第3章 电路的暂态分析-答案

在直流电路启动过程中，会产生较大的暂态电流和电压，通过暂态分析可以了解启动过程的特性 ，为电路设计和设备选型提供依据。
预测直流电路中的故障
利用暂态分析可以预测直流电路中的短路、断路等故障，从而及时采取维修措施，避免故障扩大 。
优化直流电路的控制策略
通过暂态分析可以了解直流电路在不同控制策略下的响应特性，从而选择最优的控制策略，提高 电路的控制精度和稳定性。
在暂态过程中，电阻的电压和电流会发生变 化，但电阻本身不会储存能量，因此电阻的 暂态响应是被动的，取决于外部电路的变化 。
电阻的阻值决定了电路中电流的大小， 因此在暂态过程中，电阻的阻值会影 响电流的变化速率。
电容的暂态特性
电容的充电和放电过程
当电容两端的电压发生变化时，电容会进行充电或放电， 这个过程需要一定的时间，因此电容的暂态过程相对较长。
稳态过程
电路在稳定状态下的工作过程， 此时电路中各处的电压、电流等 物理量均保持恒定或呈周期性变 化。
暂态分析的重要性
01
02
03
理解电路行为
通过暂态分析，可以深入 了解电路在开关操作、电 源变化等条件下的行为特 性。
优化电路设计
暂态分析有助于优化电路 设计，提高电路的稳定性 和可靠性，减少不必要的 能量损失和电磁干扰。
分析仿真与实验结果之间存在的误差，探 讨误差产生的原因，如元件参数不准确、 测量误差等。
改进建议
总结与反思
根据误差分析结果，提出相应的改进建议 ，如优化仿真模型、提高测量精度等，以 提高暂态分析的准确性。
对整个暂态分析的仿真与实验验证过程进行 总结与反思，总结经验教训，为后续的电路 设计与分析提供参考。
阻尼比与振荡性质
阻尼比是描述振荡衰减快慢的参数。根据阻尼比的大小，二阶电路的振荡可分为过阻尼、 临界阻尼和欠阻尼三种情况。在欠阻尼情况下，电路将呈现持续的振荡现象。

L (0 ) 0, 换路瞬间，电感元件可视为开路。 U iC 、uL 产生突变 C (0 ) 1 (0 ) (C (0 ) 0) R1 u2 (0 ) 0 uL (0 ) u1 (0 ) U ( uL (0 ) 0)
例2： 换路前电路处于稳态。 试求图示电路中各个电压和电流的初始值。
O
1 2 3
二、RL电路的零状态响应
1. 响应变化规律 1). 列方程
t=0
+ -
S +
R
uR L
di KVL : L Ri U dt 2). 解方程
U
iL + uL
-
iL (0 ) 0
R t t U U R U iL e L (1 e L ) R R R

t RC
（令 RC）
( ) (1 e c
t
uC U
t (1 e RC ) U
)
(t 0)
2.电流 iC 、uR的变化规律
uC
U
Ue

t RC
duC U iC C e t0 dt R U R U U C iC R

t
+ u t 0 R + C U _
R R
+
_
2 U 8V
t =0
iC
i1
R1 + uC 4 _
R2 iL 4
uL _
R3 + 2 i1 4 U + _ 8V
iC
R1 + uC C 4 _
R2 iL 4
+ uL L _
R3 4
解： (1) 由t = 0-电路求 uC(0–)、iL (0–) 换路前电路已处于稳态：电容元件视为开路； 由t = 0-电路可求得： 电感元件视为短路。 R1 U 4 U i L (0 ) 1A R1 R3 R R1 R3 4 4 2 4 4 44 R1 R3

一、单选题1、工程上认为R＝25Ω、L=50mH的串联电路中发生暂态过程时将持续（）。

A.0～2msB.37.5～62.5msC.6～10msD.30～50ms正确答案：C2、在换路瞬间，下列说法中正确的是（）。

A.电感电流不能跃变B.电容电流不能跃变C.电感电压必然跃变D.电容电流必然跃变正确答案：A3、电容元件是（）元件。

A.线性元件B.耗能元件C.储能元件D.以上答案都不对正确答案：C4、关于RL电路的时间常数，下面说法正确的是（）A.与R成反比，与L成正比B.与R、L成正比C.与R成正比，与L成反比D.与R、L成反比正确答案：A5、动态电路工作的全过程是（）。

A.换路—前稳态—过渡过程—后稳态B.换路—前稳态—后稳态—过渡过程C.前稳态—过渡过程—换路—后稳态D.前稳态—换路—过渡过程—后稳态正确答案：D二、判断题1、换路定理指出：电感两端的电压是不能发生跃变的，只能连续变化。

（）正确答案：×2、RC串联电路如果在C两端再并联一个电阻，则时间常数会变大。

（）正确答案：×3、三要素法只能计算全响应，不能计算零输入响应和零状态响应。

（）正确答案：×4、求解时间常数时，一定要使动态电路处于换路之前的状态。

（）正确答案：×5、动态电路在换路时一定产生过渡过程。

（）正确答案：√6、时间常数越小，电路的变化速度越慢。

（）正确答案：×。

第3章作业参考答案3-1 什么是短路功率（短路容量）？在三相短路计算时，对某短路点，短路功率的标幺值与短路电流的标幺值是否相等？为什么？答：短路功率等于短路电流有效值与短路处正常工作电压构成的三相功率，短路功率的标幺值与短路电流的标幺值是相等的。

因为："""D D B BI I S S I S I ∑*∑*====3-2 在对电网三相对称短路的起始次暂态电流进行实用计算时，采用等值法与采用叠加法的主要不同之处有哪些？答：等值法与叠加法的主要不同之处有：1) 短路前的电气量求取：等值法要求出各个电源点的次暂态电势E”， 而叠加法要求出短路点开路电压以及待求量的正常分量。

2) 网络化简：等值法针对有源网络求取各个电源对短路点的转移电抗，而叠加法针对无源网络求取整个网络对短路点的等值电抗。

3) 最后，等值法对有源网络直接求取其它待求量，而叠加法对无源网络求取其它待求量的故障分量且要加上正常分量。

3-3 电源的转移电抗是指什么？它与运算电抗有何关系？何为短路点的等值电抗？答：电源的转移电抗是指电源与短路点直接连接的电抗（中间无其它支路）。

准确描述为：某个电源对短路点的转移电抗指：除该电源电动势外，网络中其它电源电动势为0(短路)，该电源电动势与短路点电流的比值。

某个电源对短路点的运算电抗是指以该电源容量为基准的转移电抗。

转移电抗转换为计算电抗的公式为：Ni jsi ki Bs x x s =。

短路点的等值电抗是指所有电源对短路点转移阻抗的并联。

即网络对短路点的戴维南等值阻抗。

3-4 三相短路实用计算中，同步发电机如何等值？在什么情况下应该将异步电动机（综合负荷）作为电源看待？答：三相短路实用计算中，同步发电机可用直轴次暂态电抗"d x ，而电动势采用次暂态电势"E （次暂态电抗后的电势00""d E U j I x =+）。

另外在不及负荷时也可假设全网空载，全部电动势均为1且同相位。

第3章电路的暂态分析一、练习与思考详解3.1.1如果一个电感元件两端的电压为零，其储能是否也一定等于零？如果一个电容元件中的电流为零，其储能是否也一定等于零？解：（1）根据电感元件的储能公式：212W Li =，其中L 为电感元件的电感，i 为流过它的瞬时电流，电感元件的端电压di U L dt =当U ＝0时，表明0,di dt =但是i 不一定为0，即电感元件的储能不一定为零。

（2）同理：电容元件储能公式为212W Cu =，C 为元件电容值，u 为元件两端的瞬时电压，流过电容的电流c du i C dt =，当i＝0时，即0C du dt =，而u C 不一定等于0，故其储能不一定为零。

3.1.2电感元件中通过恒定电流时可视为短路，是否此时电感L 为零？电容元件两端加恒定电压时可视为开路，是否此时电容为无穷大？解：（1）电感的电感量L 取决于线圈的尺寸、匝数及其周围介质的性质，与通入何种电流无关。

在恒定电流情况下，因为d 0d I t=，故U L ＝0，可视作短路，而L ≠0。

（2）电容元件的电容量C 取决于其极板的尺寸、距离及中间介质的性质，与施加何种电压无关，在恒定电压作用下，因为d 0,d U t =故I C ＝0，可视作开路，而上x 时电容C 不是无穷大。

3.2.1确定图3-1所示电路中各电流的初始值。

换路前电路已处于稳态。

图3-1解：换路前：()()()()()L L S 6001A 2400V 00Ai i u L i ----===+===相当于短路换路后，由换路定则：()()()()()()()L L S +C L 001A603A 200031A 2A i i i i i i +-+++=====-=-=3.2.2在图3-2所示电路中，试确定在开关S 断开后初始瞬间的电压u C 和电流i C ，i1，i 2之值。

S 断开前电路已处于稳态。

图3-2解：开关S 断开前电容C 开路，根据分压定理，电容器的电压：()C 4064V 24u -=⨯=+根据换路定则，开关断开后的初始瞬间电容电压不能跃变，因此：()()()()()()C C C 1C 2004V606400A 1A 2200A u u u i i i +-++++==--====3.2.3在图3-3中，已知R ＝2Ω，电压表的内阻为2.5k Ω，电源电压U ＝4V。

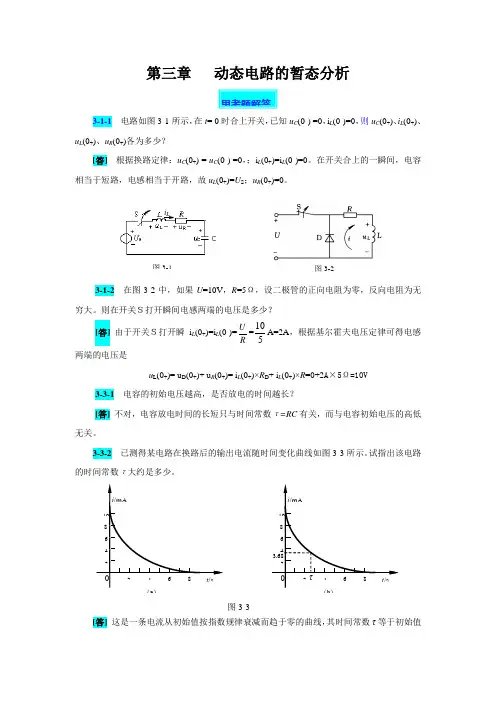
第三章 动态电路的暂态分析 3-1-1 电路如图3-1所示，在t = 0时合上开关，已知u C (0-) =0，i L (0-)=0，则u C (0+)、i L (0+)、u L (0+)、u R (0+)各为多少？[答] 根据换路定律：u C (0+) = u C (0-) =0，；i L (0+)=i L (0-)=0。

在开关合上的一瞬间，电容相当于短路，电感相当于开路，故u L (0+)=U S ；u R (0+)=0。

3-1-2 在图3-2中，如果U =10V ，R =5Ω，设二极管的正向电阻为零，反向电阻为无穷大。

则在开关Ｓ打开瞬间电感两端的电压是多少？[答] 由于开关Ｓ打开瞬i L (0+)=i L (0-)=R U =510A=2A ，根据基尔霍夫电压定律可得电感两端的电压是u L (0+)= u D (0+)+ u R (0+)= i L (0+)×R D + i L (0+)×R =0+2A ×5Ω=10V3-3-1 电容的初始电压越高，是否放电的时间越长？[答] 不对，电容放电时间的长短只与时间常数τ=RC 有关，而与电容初始电压的高低无关。

3-3-2 已测得某电路在换路后的输出电流随时间变化曲线如图3-3所示。

试指出该电路的时间常数τ大约是多少。

[答] 这是一条电流从初始值按指数规律衰减而趋于零的曲线，其时间常数τ等于初始值思考题解答 图3-3 0 2 4 6 8 2 46810i /mAt /s (a) 02 4 6 8 24 6 8 10 i /mA t /s τ 3.68(b) ii iii L 图3-1 图3-2下降了总变化量的63.2%所需的时间。

电流初始值为10mA，故下降到3.68 mA所需的时间即为时间常数τ。

据此作图如图3-3（b）所示，可知τ大约为2.7s左右。

3-3-3 在图3-4中，开关长期合在A上，如在ｔ＝0时把它合到B上。

电力系统暂态分析第三章课后答案1、什么是动力系统、电力系统、电力网？答:通常把发电企业的动力设施、设备和发电、输电、变电、配电、用电设备及相应的辅助系统组成的电能热能生产、输送、分配、使用的统一整体称为动力系统；把由发电、输电、变电、配电、用电设备及相应的辅助系统组成的电能生产、输送、分配、使用的统一整体称为电力系统；把由输电、变电、配电设备及相应的辅助系统组成的联系发电与用电的统一整体称为电力网。

2、现代电网有哪些特点?答:1、由较强的超高压系统构成主网架。

2、各电网之间联系较强,电压等级相对简化。

3、具有足够的调峰、调频、调压容量,能够实现自动发电控制,有较高的供电可靠性。

4、具有相应的安全稳定控制系统,高度自动化的监控系统和高度现代化的通信系统。

5、具有适应电力市场运营的技术支持系统,有利于合理利用能源。

3、区域电网互联的意义与作用是什么?答：1、可以合理利用能源,加强环境保护,有利于电力工业的可持续发展。

2、可安装大容量、高效能火电机组、水电机组和核电机组,有利于降低造价,节约能源,加快电力建设速度。

3、可以利用时差、温差,错开用电高峰,利用各地区用电的非同时性进行负荷调整,减少备用容量和装机容量。

4、可以在各地区之间互供电力、互通有无、互为备用,可减少事故备用容量,增强抵御事故能力,提高电网安全水平和供电可靠性。

5、能承受较大的冲击负荷,有利于改善电能质量。

6、可以跨流域调节水电,并在更大范围内进行水火电经济调度,取得更大的经济效益。

4、电网无功补偿的原则是什么?答:电网无功补偿的原则是电网无功补偿应基本上按分层分区和就地平衡原则考虑,并应能随负荷或电压进行调整,保证系统各枢纽点的电压在正常和事故后均能满足规定的要求,避免经长距离线路或多级变压器传送无功功率。

5、简述电力系统电压特性与频率特性的区别是什么?答：电力系统的频率特性取决于负荷的频率特性和发电机的频率特性(负荷随频率的变化而变化的特性叫负荷的频率特性。

第3章 电路的暂态分析练习与思考3.1.1 什么是稳态？什么是暂态？答：稳态是指电路长时间工作于某一状态，电流、电压为一稳定值。

暂态是指电路从一种稳态向另一种稳态转变的过渡过程。

3.1.2 在图3-3所示电路中，当开关S 闭合后，是否会产生暂态过程？为什么？图3-3 练习与思考3.1.2图答：不会产生暂态过程。

因为电阻是一个暂态元件，其瞬间响应仅与瞬间激励有关，与以前的状态无关，所以开关S 闭合后，电路不会产生暂态过程。

3.1.3 为什么白炽灯接入电源后会立即发光，而日光灯接入电源后要经过一段时间才发光？答：白炽灯是电阻性负载，电阻是一个暂态元件，其暂态响应仅与暂态的激励有关，与以前的状态无关；而日光灯是一个电感性负载，电感是一个记忆元件，暂态响应不仅与暂态激励有关，还与电感元件以前的工作状态有关，能量不能发生突变，所以日光灯要经过一段时间才发光。

3.2.1任何电路在换路时是否都会产生暂态过程？电路产生暂态的条件是什么？答：不是。

只有含有储能元件即电容或电感的电路，在换路时才会产生暂态过程。

电路产生暂态的条件是电路中含有储能元件，并且电路发生换路。

3.2.2若一个电感元件两端电压为零，其储能是否一定为零？若一个电容元件中的电流为零，其储能是否一定为零？为什么？答：若一个电感元件两端电压为零，其储能不一定为零，因为电感元件电压为零，由dt di Lu =只能说明电流的变化率为零，实际电流可能不为零，由221Li W L =知电感储能不为零。

若一个电容元件中的电流为零，其储能不一定为零，因为电容元件电流为零，由dt du Ci =只能说明电压变化率为零，实际电压可能不为零，由221)(Cu t W C =知电容储能不为零。

3.2.3在含有储能元件的电路中，电容和电感什么时候可视为开路？什么时候可视为短路？答：电路达到稳定状态时，电容电压和电感电流为恒定不变的值时，电容可视为开路，电感可视为短路。

3.2.4 在图3-13所示电路中，白炽灯分别和R 、L 、C 串联。

第一章电力系统分析基础知识1-2-1 对例1-2，取110kV B30,用准确和近似计算法计算参数标幺值。

U，S MVAB2解：①准确计算法：选取第二段为基本段，取U110kV，S B30MVA，则其余两段的电压基准值分B210.5别为：U B k U110kV9.5kV11B2121UB3UB2k21101106.66.6kV电流基准值：IS30BB1.8kA 13U39.5B1IS30BB0.16 23U23110BkA各元件的电抗标幺值分别为：210.530发电机：x0.260.3212309.5变压器212130T：x0.1050.121 122211031.530输电线路：x0.4800.07932110变压器211030T：x0.1050.21 24221511062.62电抗器：x0.050.456.60.330电缆线路：x0.082.50.14626.611电源电动势标幺值：E1.169.5②近似算法：取S B30MVA，各段电压电流基准值分别为：30U B110.5kV，I B 1.65kA1310.5U30B2115kV，I B0.15kA13115U30B36.3，I B 2.75kA kV13 6.3各元件电抗标幺值：210.530发电机：x0.260.26123010.5变压器212130T：x0.1050.11 12211531.530输电线路：x0.4800.07332115变压器211530T：x0.1050.21 2421151562.75电抗器：x0.050.4456.30.330电缆线路：x0.082.50.151626.311电源电动势标幺值：E 1.0510.5210.530发电机：x0.260.3212309.5变压器212130T：x0.1050.121 122211031.530输电线路：x0.4800.07932110变压器211030T：x0.1050.21 24221511062.62电抗器：x0.050.456.60.330电缆线路：x0.082.50.14626.611电源电动势标幺值：E1.169.51-3-1 在例1-4 中，若 6.3kV 母线的三相电压为：U a2 6.3c o s(s t)U a2 6.3c os(s t120)U a2 6.3c os(s t120)在空载情况下f点突然三相短路，设突然三相短路时30。

第三章 电路的暂态分析含有电感或电容储能元件的电路，在换路时会出现暂态过程。

本章研究了暂态过程中电压与电流的变化规律。

主要内容：1．暂态过程的基本概念。

2．换路定则：在换路瞬间，电容电流和电感电压为有限值的情况下，电容电压 和电感电流在换路前后的瞬间保持不变。

3．RC 电路的零输入响应、零状态响应和全响应。

4．RL 电路的零输入响应、零状态响应和全响应。

5．一阶线性电路暂态分析的三要素法：一阶线性电路在直流激励下的全响应零、 输入响应和零状态响应都可以用三要素法τte f f f t f -+∞-+∞=)]()0([)()(来求出。

6．暂态过程的应用：对于RC 串联电路，当输入矩形脉冲，若适当的选择参数 和输出，可构成微分电路或积分电路。

[练习与思考]解答3-1-1什么是稳态？什么是暂态？解：当电路的结构、元件参数及激励一定时，电路的工作状态也就一定，且电流和电压为某一稳定的值，此时电路所处的工作状态就称为稳定状态，简称为稳态。

在含有储能元件的电路中，当电路的发生换路时，由于储能元件储的能量的变化，电路将从原来的稳定状态经历一定时间变换到新的稳定状态，这一变换过程称为过渡过程，电路的过渡过程通常是很短的，所以又称暂态过程。

3-1-2什么是暂态过程？产生暂态过程的原因是什么？解：含有储能元件的电路从一个稳态转变到另一个稳态的所需的中间过程称为电路的暂态过程（过渡过程）。

暂态过程产生的内因是电路中含有储能元件，外因是电路发生换路。

3-2-1 初始值和稳态值分别是暂态过程的什么时刻的值？解：初始值是暂态过程的+=0t 时刻的值，稳态值是暂态过程的∞=t 时刻的值。

3-2-2 如何求暂态过程的初始值？解：求暂态过程初始值的步骤为:⑴首先画出换路前-=0t 的等效电路，求出-=0t 时刻电容电压)0(-C u 和电感电流)0(-L i 的值。

对直流电路，如果换路前电路处于稳态，则电容相当于开路，电感相当于短路。

⑵令： 5 = 10(1− e−105 t )
得：
t
=
−
ln 0.5 105
=
6.93×10−6 (S )
3.3.5 在图 3.09 所示电路中，I=10mA，R1=3kΩ，R2=处于稳态。求在 t≥0 时的 uC 和 i1，并作出它们随时间的变化曲线。
+
U1
−
R2
L
U2
−
解： 三要素：
iL (0+ )
= iL (0− )
=
U2 R3
=
20 40
=
0.5( A)
2
iL (∞)
=
U1 R1
+ U2 R3
=
24 60
+
20 40
=
0.4 + 0.5
=
0.9( A)
τ=L=
L
=
4
= 0.2(S)
R R1 // R2 // R3 60 //120 // 40
第三章 电路的暂态分析（B 基本题）
3.3.3 在图 3.07 所示电路中，已知 uC (0-)=0，试求：⑴t≥0 时的 uC 和 i；⑵uC 到达 5V 时 所需时间。
S
10Ω
+
t =0
10V
−
+i u−C 1μF
图3.07 习题3.3.3的图
解：⑴由题意为零状态响应问题。
−t
uC = U (1− e τ )
解： 三要素：
uC (0+ ) = uC (0− ) = 1× 20 −10 = 10(V )
uC (∞)
=
20
10 + 10

3.1 电阻元件、电感元件与电容元件 3.1.1 电阻元件。
i
+
电阻元件：消耗电能，转换为热能（电阻性） u
R
根据欧姆定律: u iR
_
即电阻元件上的电压与通过的电流成线性关系
金属导体的电阻与导体的尺寸及导体材料的
导电性能有关，表达式为：R l
S
电阻的能量 W
t
uidt
t Ri2dt 0
或与磁通的参考方向符合右手螺旋定则。
(2) 自感电动势瞬时极性的判别
i
i di 0
+-
u eL
-+
+
dt
eL实
-
eL
L di dt
<
0
eL与参考方向相反
i
+-
u eL
-+
-
eL实
+
i
di
dt 0
eL
L
di dt
>0
eL与参考方向相同
eL具有阻碍电流变化的性质
电感中出现的感应电动势表明在电感两端有电压产生， 用u表示，并规定u、I的参考方向一致，
三、初始值的确定
初始值：电路中各 u、i 在 t =0+ 时的数值。
求解要点：
(1) uC( 0+)、iL ( 0+) 的求法。 1) 先由t =0-的电路求出 uC ( 0– ) 、iL ( 0– )； 2) 根据换路定律求出 uC( 0+)、iL ( 0+) 。
换路前
换路后
t=0
因此，电容和电感在换路瞬时的uC 和iL 值可用下列关系表示：
uC (0-) = uC (0+) iL (0-) = iL（0+） 即 从t=0-到t=0+ 瞬间，电容两端的电压和流过电感的电流不能突 变，这称为换路定则。

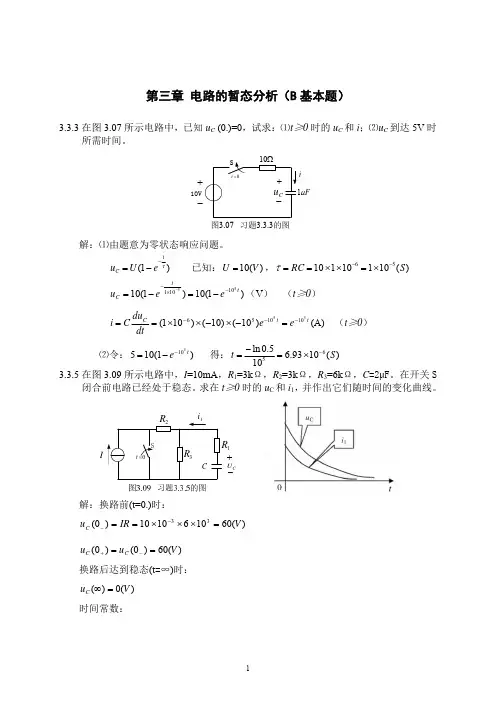
第三章 电路的暂态分析3.2.1 图3.01所示各电路在换路前都处于稳态，试求换路后其中电流i 的初始值(0)i +和稳态值()i ∞。

(b)(a)(c)(d)图3.01解： （a ）A 5.1265.0)0(5.0)0(21)0(=×===−++L L i i i A 326)(==∞i（b ）02662)0(62)0(6)0(=−=−−=−=++c c u u iA 5.1226)(=+=∞i （c ）A 6)0()0(==−+i i A 0)(=∞i（d ）A 75.04364)0(622)0(6)0(=−=−=+−=−++c c u u iA 12226)(=++=∞i3.4.1 在图3.07(a)的电路中，u 为一阶跃电压，如图3.07(b)所示，试求3i 和c u 。

设V 1)0(c =−u 。

(a)图3.07(b)解：s 102)(331312−×=++=C R R R R R τV 22224)(C =+×=∞u V 1)0()0(C C ==−+u u V 2)(500C t e t u −−=mA 75.0)(1)(4)0(31131312322323213=+++++++=+R R R R R R R R R R R R R R R R i mA 144)(3==∞imA 25.01)(5003t e t i −−=3.4.2 电路如图3.08所示，求0t ≥时(1)电容电压C u ，(2)B 点电位B v 和(3)A 点电位A v 的变化规律。

换路前电路处于稳态。

Sk 10图3.08解：(1)求0≥t 时的电容电压C uV 15255)6(0)0()0(C =×+−−==−+C u uV 5.1525510)6(6)(C =×++−−=∞u[]s 1044.010100105//)2510(6123−−×=×××+=τ故V 5.05.1)5.11(5.1)(66103.21044.0C t t e et u ×−×−−=−+=−t =0_时k 10t =0+时+6V Ωk 10（2）求0≥t 时的B 点电位B v注意，+=0t 时，由于电容中存在电流，0CC ≠=dtdu Ci 因此，10K 和5K 电阻中的电流不等。

暂态分析习题答案暂态分析习题答案是电力系统分析中的重要部分，它可以帮助我们了解电力系统在瞬态过程中的动态响应和稳定性。

在这篇文章中，我们将探讨几个常见的暂态分析习题，并给出详细的解答。

第一个习题是关于电力系统中的短路故障。

假设一个三相电力系统中发生了一次对地短路故障，故障电流为1000A，故障持续时间为0.1秒。

系统的额定电压为10kV，发电机的暂态电抗为0.2，负载的暂态电抗为0.1。

求故障后系统的电压和电流。

首先，我们需要计算故障电流的幅值。

由于故障电流为对地短路，其幅值为故障电流的三相幅值的1/√3倍。

因此，故障电流的幅值为1000A/√3 ≈ 577A。

接下来，我们可以使用短路电流计算方法来计算故障后的电压和电流。

根据短路电流计算方法，故障后的电压可以表示为：Uf = U0 - Zf * If其中，Uf为故障后的电压，U0为额定电压，Zf为系统的暂态阻抗，If为故障电流。

代入数值计算，我们得到：Uf = 10kV - (0.2 + 0.1j) * 577A ≈ 10kV - 115.4kVA ≈ 9.884kV因此，故障后系统的电压约为9.884kV。

接下来，我们可以使用功率方程来计算故障后的电流。

根据功率方程，故障后的电流可以表示为：If = (U0 - Uf) / Zf代入数值计算，我们得到：If = (10kV - 9.884kV) / (0.2 + 0.1j) ≈ 116.4A因此，故障后系统的电流约为116.4A。

第二个习题是关于电力系统中的过电压问题。

假设一个三相电力系统中，当一台发电机突然失去负载时，系统的电压会出现过电压现象。

假设系统的额定电压为10kV，发电机的暂态电抗为0.2，负载的暂态电抗为0.1。

求失去负载后系统的电压。

在失去负载时，发电机的电压会突然升高。

根据过电压计算方法，失去负载后的电压可以表示为：Uf = U0 + Zg * Ig其中，Uf为失去负载后的电压，U0为额定电压，Zg为发电机的暂态阻抗，Ig为发电机的电流。

返 回练习题题集
上一页
下一题
7在图所示电路中，开关 S 闭合前电路已处于稳态，试确 定 S 闭合后电压 uL 和电流 iL、i1、 i2 的初始值和稳态值。
L
iL
+ uL + U S 12 V -
i1
4Ω
S
i2
R1
R2
6Ω
【解】 (1)求初始值 由于 S 闭合前，电路已稳定， L 相当于短路，R2 两端的电压等于 US， R2 中的电流即 iL。因 此，根据换路定律，由换路前( S 断开时)的电路，首先求得
第三章 电路暂态分析
1、已知： S 在“1”处已 经达到稳态，在t=0时合
S
2 R 1 + _ E =6V 2k
i
i1
R1
i2
2k
R2 1k
向“2”
求:
i、i1、i 2 u C 、uL
的初始值。
-
uL
uC
解：
换路前即 t = 0 时的等效电路
+ E _ i1 R R1 R2
uC
E = 1.5mA i 1(0 ) = R +R 1
(2) 在(1)中, 若使uRL不超过220V, _ 则泄放电阻R´应选多大？
U R´ L
(3) 根据(2)中所选用的电阻R´, 试求开关接通R´后经 过多长时间，线圈才能将所储的磁能放出95%？ (4) 写出(3) 中uRL随时间变化的表示式。 解: 换路前，线圈中的电流为
(1) 开关接通R´瞬间线圈两端的电压为
uL () = 0
然后，进一步求得
U S - uL ( ) 12 - 0 i1 ( ) = = A= 3A R1 4 U S - uL ( ) 12 - 0 i2 ( ) = = A=2A R2 6 i L ( ) = i1 ( ) + i2 ( ) = ( 3 + 2) A = 5 A

第三章 三相电路一、单相选择题1．三相对称绕组在空间位置上应彼此相差（ B ）A 、60°电角度；B 、120°电角度；C 、180°电角度；D 、360°电角度。

2. 三相对称电路是指（ C ） A 、三相电源对称的电路； B 、三相负载对称的电路；C 、三相电源和三相负载均对称的电路-D 、三相电源对称和三相负载均不对称的电路。

3. 有“220V 、100W ”“220V 、25W ”白炽灯两盏，串联后接入220V 交流电源，其亮度情况是（ B ）A 、100W 灯泡最亮；B 、25W 灯泡最亮；C 、两只灯泡一样亮；D 、100W 和25W 都不亮。

4. 三相四线制供电线路，已知作星形联接的三相负载中U 相为纯电阻，V 相为纯电感，W 相为纯电容，通过三相负载的电流均为10安培，则中线电流为（ A ） A 、30安； B 、10安； C 、27.32安。

5. 在某对称星形连接的三相负载电路中，已知线电压 u t AB = V 3802sin ω，则C 相电压有效值相量 C U &为（ A ）A 、 22090∠︒ VB 、38090∠︒VC 、22090∠-︒ V D 、︒-∠90380 6．星型连接的三相对称负载，接于三相对称电源上，线电流与相电流之比为( C )。

A 、3B 、2C 、1D 、337. 额定电压为 220 V 的照明负载接于线电压为380 V 的三相四线制电源时，必须接成 ( A ) 形。

A 、YB 、 ∆C 、Y 和∆都可以D 、Y 和∆都不可以8．当三相交流发电机的三个绕组连接成星形时，若线电压V t u BC )180sin(2380-=ω，则相电压=C u ( D )。

A 、V t )30sin(2220-ω B 、 V t )30sin(2380-ωC 、 V t )120sin(2380+ωD 、30)t ω+o9.有一对称三相电动势，若U 相电动势为Vt u U )314sin(311π+=则V 相和W 相电动势分别为 （ A ） A 、V t u Vt u W V )3314sin(311)3314sin(311ππ-=+=B 、V t u Vt u W V )3314sin(311)3314sin(311ππ+=-= C 、V t u Vt u W V )6314sin(311)6314sin(311ππ+=-=D 、V t u Vt u W V )6314sin(311)6314sin(311ππ-=+=10．在三相交流电路中，三相堆成负载星形连接，三个线电流均为4A ，则中线电流为（ A ）。

i
+
u
R
-
将上式两边乘以 i，并积分之，则得
t
uidt
t Ri2dt
0
0
上式表明电能全部消耗在电阻元件上，转换为热能。电阻元件
是耗能元件。
3·1 电阻元件、电感元件与电容元件
3·1·2 电感元件
图所示是一电感元件(线圈)， 其上电压为 u。当通过电流 i 时，
将产生磁通。
设磁通通过每匝线圈，如果
第 3 章 电路的暂态分析
仅由电阻元件构成的电路，一旦接通或断开电源时，电路立即 处于稳定状态。但当电路中含有电感元件或电容元件时则不然。
譬如当RC串联电路与直流电源接通后， 电容元件被充电，其上电压uC 是逐渐增长 到稳定值 (电源电压) 的；电路中有充电电 流，它是逐渐衰减到零的。
i
+R
U
+
- C -uC
R2 R1 R2
U2

12 2 5
10 3
V
2103s
uC

10 3
(1
et
/ 21 03
)
V
所以
可见，这种电路中电压或电流的增长或衰减有一个暂态过程。
本章首讨论电阻元件、电感元件、电容元件的特征和引起暂态 过程的原因，而后讨论暂态过程中电压与电流随时间而变化的规 律和影响暂态过程快慢的电路时间常数。
3·1 电阻元件、电感元件与电容元件
3·1·1 电阻元件
在图中，u 和 i 参考方向相同，根据欧姆定律 得出 u=Ri，电阻元件的参数 R=u/i 称为电阻， 它具有对电流起阴碍作用于的物理性质。
3·3 RC电路的响应
[例题] 在图中，开关长期合在位置1上，如在 t =0时把它合到位置