基于MATLAB的发动机万有特性曲线绘制方法_周广猛

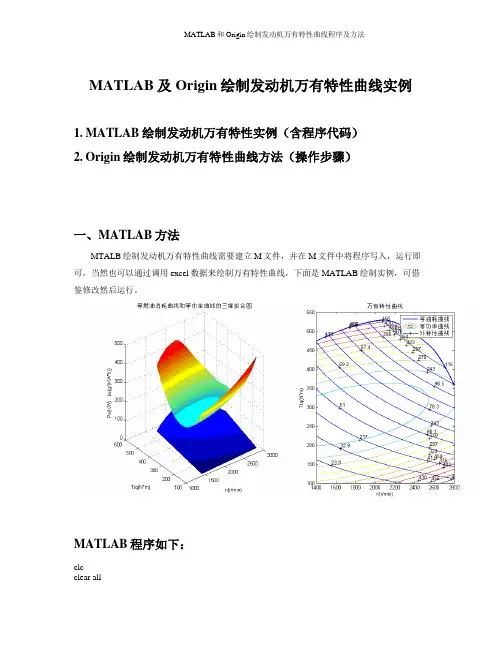
MATLAB及Origin绘制发动机万有特性曲线实例1.MATLAB绘制发动机万有特性实例（含程序代码）2.Origin绘制发动机万有特性曲线方法（操作步骤）一、MATLAB方法MTALB绘制发动机万有特性曲线需要建立M文件，并在M文件中将程序写入，运行即可，当然也可以通过调用excel数据来绘制万有特性曲线，下面是MATLAB绘制实例，可借鉴修改然后运行。

MATLAB程序如下：clcclear all%不同转速下的燃油消耗率与扭矩的曲线拟合be1=[222.8,220.4,232.4,228.5,227.8,232.6,248.5,245.9,272.4,329.7];Ttq1=[399.8,354.1,318.5,278.1,236.2,203.6,185.3,157.2,117.2,80.8];T1=80:320/9:400;%转换矩阵格式Be1=interp1(Ttq1,be1,T1,'spline');%n=1400r/min时燃油消耗率与扭矩的曲线拟合be2=[222.0,221.7,235.4,226.5,230.5,236.8,249.1,276.1,407.9,487.0];Ttq2=[409.1,365.7,328.3,284.1,243.7,203.2,164.3,123.9,83.5,39.7];T2=39:371/9:410;Be2=interp1(Ttq2,be2,T2,'spline');be3=[226.0,225.3,226.4,233.9,242.1,283.3,253.9,271.4,323.5,468.6];Ttq3=[408.3,368.3,328.3,289.0,244.4,208.8,167.7,132.1,89.5,46.1];T3=46:363/9:409;Be3=interp1(Ttq3,be3,T3,'spline');be4=[206.5,231.1,231.1,233.0,242.0,244.9,265.0,299.8,398.0,596.8];Ttq4=[425.6,380.3,332.7,290.9,244.4,205.1,160.2,114.5,68.8,30.7];T4=30:396/9:426;Be4=interp1(Ttq4,be4,T4,'spline');be5=[234.7,259.8,235.5,237.6,242.8,292.3,277.9,308.7,396.2,605.9];Ttq5=[420.7,379.6,334.6,291.6,244.4,202.8,157.5,116.0,74.1,37.8];T5=37:384/9:421;Be5=interp1(Ttq5,be5,T5,'spline');be6=[174.2,242.2,252.1,287.4,253.6,263.6,290.6,316.8,378.0,518.8];Ttq6=[404.6,360.5,322.7,283.0,243.3,205.5,162.1,124.7,86.8,52.4];T6=52:353/9:405;Be6=interp1(Ttq6,be6,T6,'spline');be7=[256.9,253.7,253.5,260.0,303.8,280.7,300.6,346.6,435.6,812.9];Ttq7=[378.0,344.7,310.3,264.3,226.1,186.8,154.2,115.3,76.3,34.1];T7=34:344/9:378;Be7=interp1(Ttq7,be7,T7,'spline');be8=[257.9,295.3,282.4,288.7,301.9,329.7,357.0,475.4,580.3,1080.1];Ttq8=[315.6,275.5,242.5,210.3,178.5,145.6,118.6,72.6,52.8,22.4];T8=22:294/9:316;Be8=interp1(Ttq8,be8,T8,'spline');B=[Be1';Be2';Be3';Be4';Be5';Be6';Be7';Be8'];N=[1400*ones(10,1);1600*ones(10,1);1800*ones(10,1);2000*ones(10,1);2200*ones(10,1);2400*ones (10,1);2600*ones(10,1);2800*ones(10,1)];Ttqn=[T1';T2';T3';T4';T5';T6';T7';T8'];G=[ones(80,1),N,Ttqn,N.^2,N.*Ttqn,Ttqn.^2];A=G\B;%A为6*1矩阵[n,Ttq]=meshgrid(1400:2800,100:600);%生成n-Ttq平面上的自变量“格点”矩阵be=A(1)+n.*A(2)++Ttq*A(3)+n.^2*A(4)+n.*Ttq*A(5)+Ttq.^2*A(6);Pe=Ttq.*n/9550;%外特性实验数据拟合Nw=[1403,1597,1797,1986,2102,2199,2303,2400,2507,2598,2700,2802]; Ttqw=[474,497,515,526,528.8,522.8,509.5,492.2,471.2,448.4,408.3,357.4]; n0=1400:2800;Ttqw_N=interp1(Nw,Ttqw,n0,'spline');h=repmat(Ttqw_N,501,1);ii=find(Ttq>h);%确定超出边界的“格点”下标be(ii)=NaN;%强制为非数Pe(ii)=NaN;%强制为非数%绘制等燃油消耗率曲线和等功率曲线三维拟合图subplot(1,2,1);mesh(n,Ttq,be);hold on;mesh(n,Ttq,Pe);axis([1000,3000,100,600,0,500]);hold on;xlabel('n(r/min)')ylabel('Ttq(N*m)')zlabel('Pe(KW) be(g/(KW*h))')title('等燃油消耗曲线和等功率曲线的三维拟合图')%绘制边界线(外特性曲线)subplot(1,2,2);plot(n0,Ttqw_N,'LineWidth',2);axis([1400,2800,100,550]);xlabel('n(r/min)');ylabel('Ttq(N*m)');title('万有特性曲线');hold on;%绘制等油耗率曲线的二维图B=contour(n,Ttq,be,11);%画等位线，并给出标识数据clabel(B);%把“等位值”沿等位线随机标识hold on;%绘制等功率曲线的二维图P=contour(n,Ttq,Pe,11);%画等位线，并给出标识数据clabel(P);%把“等位值”沿等位线随机标识legend('等油耗曲线','等功率曲线','外特性曲线')hold off二、Origin方法用origin软件绘制发动机万有特性曲线方法一、万有特性数据输入在excel中整理好发动机万有特性数据，主要包括发动机转速、扭矩、燃油消耗率及功率数据。

基于MATLAB语言的发动机万有特性曲线的绘制
黄美美;赵志伟;靳华磊;贾延涛;孙海鹏
【期刊名称】《现代制造技术与装备》
【年(卷),期】2011(000)005
【摘要】利用MATLAB语言的强大的数据处理和绘图功能,在建立发动机万有特性曲线曲面拟合数学模型的基础上,运用其矩阵运算、三维绘图等功能,进行曲线、曲面拟合,绘制了万有特性曲线.该方法具有数据处理精度高、明显直观和实用性强等优点.
【总页数】2页(P19,24)
【作者】黄美美;赵志伟;靳华磊;贾延涛;孙海鹏
【作者单位】山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100;山东省内燃机研究所,济南250100
【正文语种】中文
【相关文献】
1.基于MATLAB语言的发动机万有特性研究 [J], 关志伟;杨玲;施继红;吴明
2.基于Matlab语言的液压特性曲线的绘制 [J], 陈立胜;李业庆
3.汽车发动机万有特性曲线簇计算机绘制算法 [J], 彭炜;李志中;段明磊
4.基于MATLAB的发动机万有特性曲线绘制方法 [J], 周广猛;郝志刚;刘瑞林;陈东;管金发;张春海
5.多项式插值法绘制发动机万有特性曲线 [J], 李小华;罗福强;汤东
因版权原因，仅展示原文概要，查看原文内容请购买。

%不同转速下的燃油消耗率与扭矩的曲线拟合clear allbe1=[222.8,220.4,232.4,228.5,227.8,232.6,248.5,245.9,272.4,329.7];Ttq1=[399.8,354.1,318.5,278.1,236.2,203.6,185.3,157.2,117.2,80.8];T1=80:320/9:400; %转换矩阵格式Be1=interp1(Ttq1,be1,T1,'spline'); %n=1400r/min时燃油消耗率与扭矩的曲线拟合be2=[222.0,221.7,235.4,226.5,230.5,236.8,249.1,276.1,407.9,487.0];Ttq2=[409.1,365.7,328.3,284.1,243.7,203.2,164.3,123.9,83.5,39.7];T2=39:371/9:410;Be2=interp1(Ttq2,be2,T2,'spline');be3=[226.0,225.3,226.4,233.9,242.1,283.3,253.9,271.4,323.5,468.6];Ttq3=[408.3,368.3,328.3,289.0,244.4,208.8,167.7,132.1,89.5,46.1];T3=46:363/9:409;Be3=interp1(Ttq3,be3,T3,'spline');be4=[206.5,231.1,231.1,233.0,242.0,244.9,265.0,299.8,398.0,596.8];Ttq4=[425.6,380.3,332.7,290.9,244.4,205.1,160.2,114.5,68.8,30.7];T4=30:396/9:426;Be4=interp1(Ttq4,be4,T4,'spline');be5=[234.7,259.8,235.5,237.6,242.8,292.3,277.9,308.7,396.2,605.9];Ttq5=[420.7,379.6,334.6,291.6,244.4,202.8,157.5,116.0,74.1,37.8];T5=37:384/9:421;Be5=interp1(Ttq5,be5,T5,'spline');be6=[174.2,242.2,252.1,287.4,253.6,263.6,290.6,316.8,378.0,518.8];Ttq6=[404.6,360.5,322.7,283.0,243.3,205.5,162.1,124.7,86.8,52.4];T6=52:353/9:405;Be6=interp1(Ttq6,be6,T6,'spline');be7=[256.9,253.7,253.5,260.0,303.8,280.7,300.6,346.6,435.6,812.9];Ttq7=[378.0,344.7,310.3,264.3,226.1,186.8,154.2,115.3,76.3,34.1];T7=34:344/9:378;Be7=interp1(Ttq7,be7,T7,'spline');be8=[257.9,295.3,282.4,288.7,301.9,329.7,357.0,475.4,580.3,1080.1];Ttq8=[315.6,275.5,242.5,210.3,178.5,145.6,118.6,72.6,52.8,22.4];T8=22:294/9:316;Be8=interp1(Ttq8,be8,T8,'spline');B=[Be1';Be2';Be3';Be4';Be5';Be6';Be7';Be8'];N=[1400*ones(10,1);1600*ones(10,1);1800*ones(10,1);2000*ones(10,1);2200*ones(10,1);2400*ones (10,1);2600*ones(10,1);2800*ones(10,1)];Ttqn=[T1';T2';T3';T4';T5';T6';T7';T8'];G=[ones(80,1),N,Ttqn,N.^2,N.*Ttqn,Ttqn.^2];A=G\B; %A为6*1矩阵[n,Ttq]=meshgrid(1400:2800,100:600); %生成n-Ttq平面上的自变量“格点”矩阵be=A(1)+n.*A(2)++Ttq*A(3)+n.^2*A(4)+n.*Ttq*A(5)+Ttq.^2*A(6); %501×1401Pe=Ttq.*n/9550; %501×1401%外特性实验数据拟合Nw=[1403,1597,1797,1986,2102,2199,2303,2400,2507,2598,2700,2802]; Ttqw=[474,497,515,526,528.8,522.8,509.5,492.2,471.2,448.4,408.3,357.4]; n0=1400:2800;Ttqw_N=interp1(Nw,Ttqw,n0,'spline');h=repmat(Ttqw_N,501,1); % 501×1401矩阵ii=find(Ttq>h); %确定超出边界的“格点”下标 %155109×1be(ii)=NaN; %强制为非数Pe(ii)=NaN; %强制为非数%绘制等燃油消耗率曲线和等功率曲线三维拟合图subplot(1,2,1);mesh(n,Ttq,be);hold on;mesh(n,Ttq,Pe);axis([1000,3000,100,600,0,500]);hold on;xlabel('n(r/min)')ylabel('Ttq(N*m)')zlabel('Pe(KW) be(g/(KW*h))')title('等燃油消耗曲线和等功率曲线的三维拟合图')%绘制边界线(外特性曲线)subplot(1,2,2);plot(n0,Ttqw_N,'LineWidth',2);axis([1400,2800,100,550]);xlabel('n(r/min)');ylabel('Ttq(N*m)');title('万有特性曲线');hold on;%绘制等油耗率曲线的二维图B=contour(n,Ttq,be,11); %画等位线，并给出标识数据clabel(B); %把“等位值”沿等位线随机标识hold on;%绘制等功率曲线的二维图P=contour(n,Ttq,Pe,11); %画等位线，并给出标识数据clabel(P); %把“等位值”沿等位线随机标识legend('等油耗曲线','等功率曲线','外特性曲线')hold off%利用mesh作原始曲面N=3500:500:8000;T=1.3:-1.2/6:0.1;B=xlsread('F:\Matlab\RanJia.xls','revise5');%mesh(N,T,B)%colormap;%colorbar;%xlabel('转速n/ r*min^-^1'), ylabel('p平均有效压力/ Mpa'), zlabel('燃油消耗率z/ kg/(kw*h)')%hidden off 透明网孔%colormap; 表面小块着色%colorbar;%surf(,,,'FaceColor','red','EdgeColor','none');%camlight left; 增加光源%lighting phone 照明方式%view(-15,65) 改变视角（方位角，仰角）%利用interrp2矩阵插值函数作优化曲面N1=3500:50:8000;T1=1.3:-0.005:0.1;[N2,T2]=meshgrid(N1,T1);B1=interp2(N,T,B,N2,T2,'cubic');P1=T2.*N2/9.55;%figure;%surf(N1,T1,B1)%colormap;%colorbar;%xlabel('转速n/ r*min^-^1'), ylabel('p平均有效压力/ Mpa'), zlabel('燃油消耗率z/ kg/(kw*h)')%外特性实验数据拟合T3=[0.90,0.95,0.99,1.06,1.12,1.18,1.24,1.30,1.22,1.11];T4=interp1(N,T3,N1,'spline');W=repmat(T4,241,1); %平铺成381×91矩阵jj=find(T2>W); %确定超出边界的“格点”下标B1(jj)=NaN;%画外特性曲线plot(N1,T4,'LineWidth',2);axis([3500,8000,0.1,1.3]);hold on%画等油耗线v=[450,460,470,480,490,500,510,525,540,560];[A1,h]=contour(N2,T2,B1,v,'b:'); %N2,T2限制在X,Y轴上的范围，10为等高线条数clabel(A1,h,'manual');hold on%画等功率线[A2,h]=contour(N2,T2,P1,500:100:900,'k:'); %N2,T2限制在X,Y轴上的范围，10为等高线条数clabel(A2,h,'manual');plot(6000,1.114,'.','color','r');xlabel('转速—r/min');ylabel('扭矩—N ·m');legend('外特性曲线','等油耗线-g/(kW ·h)','等功率线-W') hold off% title('等油耗线');%xlabel('转速n/ r*min^-^1'), ylabel('p 平均有效压力/ Mpa')转速（r/min ）扭矩（N ·m ）。

%不同转速下的燃油消耗率与扭矩的曲线拟合clear allbe仁[222.8,220.4,232.4,228.5,227.8,232.6,248.5,245.9,272.4,329.7];Ttq仁[399.8,354.1,318.5,278.1,236.2,203.6,185.3,157.2,117.2,80.8];T1=80:320/9:400;%转换矩阵格式Be仁in terp1(Ttq1,be1,T1,'spli ne');% n=1400r/mi n 时燃油消耗率与扭矩的曲线拟合be2=[222.0,221.7,235.4,226.5,230.5,236.8,249.1,276.1,407.9,487.0];Ttq2=[409.1,365.7,328.3,284.1,243.7,203.2,164.3,123.9,83.5,39.7];T2=39:371/9:410;Be2=i nterp1(Ttq2,be2,T2,'spl in e');be3=[226.0,225.3,226.4,233.9,242.1,283.3,253.9,271.4,323.5,468.6];Ttq3=[408.3,368.3,328.3,289.0,244.4,208.8,167.7,132.1,89.5,46.1];T3=46:363/9:409;Be3=i nterp1(Ttq3,be3,T3,'spl in e');be4=[206.5,231.1,231.1,233.0,242.0,244.9,265.0,299.8,398.0,596.8];Ttq4=[425.6,380.3,332.7,290.9,244.4,205.1,160.2,114.5,68.8,30.7];T4=30:396/9:426;Be4=i nterp1(Ttq4,be4,T4,'spl in e');be5=[234.7,259.8,235.5,237.6,242.8,292.3,277.9,308.7,396.2,605.9];Ttq5=[420.7,379.6,334.6,291.6,244.4,202.8,157.5,116.0,74.1,37.8];T5=37:384/9:421;Be5=i nterp1(Ttq5,be5,T5,'spl in e');be6=[174.2,242.2,252.1,287.4,253.6,263.6,290.6,316.8,378.0,518.8];Ttq6=[404.6,360.5,322.7,283.0,243.3,205.5,162.1,124.7,86.8,52.4];T6=52:353/9:405;Be6=i nterp1(Ttq6,be6,T6,'spl in e');be7=[256.9,253.7,253.5,260.0,303.8,280.7,300.6,346.6,435.6,812.9];Ttq7=[378.0,344.7,310.3,264.3,226.1,186.8,154.2,115.3,76334.1];T7=34:344/9:378;Be7=i nterp1(Ttq7,be7,T7,'spl in e');be8=[257.9,295.3,282.4,288.7,301.9,329.7,357.0,475.4,580.3,1080.1];Ttq8=[315.6,275.5,242.5,210.3,178.5,145.6,118.6,72.6,52.8,22.4];T8=22:294/9:316;Be8=i nterp1(Ttq8,be8,T8,'spl in e');B=[Be1';Be2';Be3';Be4';Be5';Be6';Be7';Be8'];N=[1400*o nes(10,1);1600*o nes(10,1);1800*o nes(10,1);2000*o nes(10,1);2200* on es(10,1);2400*o nes(10,1);2600*o nes(10,1);2800*o nes(10,1)];Ttq n=[T1';T2';T3';T4';T5';T6';T7';T8'];G=[o nes(80,1),N,Ttq n,N.A2,N.*Tt qn ,Ttq n. A2];A=G\B;%A 为6*1 矩阵[n,Ttq]=meshgrid(1400:2800,100:600);% 生成n-Ttq 平面上的自变量“格点”矩阵be=A(1)+n. *A (2)++Ttq*A(3)+n.A2*A(4)+n.*Ttq*A(5)+Ttq.A2*A(6);Pe=Ttq.* n/9550;%外特性实验数据拟合Nw=[1403,1597,1797,1986,2102,2199,2303,2400,2507,2598,2700,2802];Ttqw=[474,497,515,526,528.8,522.8,509.5,492.2,471.2,448.4,408.3,357.4]; n0=1400:2800; Ttqw_N=i nterp1(Nw,Ttqw ,n 0,'spli ne');h=repmat(Ttqw_N,501,1);ii=find(Ttq>h);%确定超出边界的“格点”下标be(ii)=NaN;%强制为非数Pe(ii)=NaN;%强制为非数%绘制等燃油消耗率曲线和等功率曲线三维拟合图subplot(1,2,1);mesh( n, Ttq,be);hold on;mesh( n,Ttq,Pe);axis([1000,3000,100,600,0,500]);hold on;xlabel(' n(r/mi n)')ylabel('Ttq(N*m)')zlabel('Pe(KW) be(g/(KW*h))')title('等燃油消耗曲线和等功率曲线的三维拟合图')%绘制边界线(外特性曲线)subplot(1,2,2);plot( nO,Ttqw_N,'Li neWidth',2);axis([1400,2800,100,550]);xlabel(' n(r/mi n)');ylabel('Ttq(N*m)');title('万有特性曲线');hold on;%绘制等油耗率曲线的二维图B=contour(n,Ttq,be,11);%画等位线，并给出标识数据clabel(B);%把“等位值”沿等位线随机标识hold on;%绘制等功率曲线的二维图P=contour(n,Ttq,Pe,11);%画等位线，并给出标识数据clabel(P);%把“等位值”沿等位线随机标识lege nd('等油耗曲线','等功率曲线','外特性曲线')hold off。

MTLAB绘制发动机万有特性MAP详细程序采用MATLAB来绘制发动机MAP，通过附表1和2，将这两个表放在同一个根目录下，并编写M文件（见后面附录程序），将M文件跟附表1和2同时放在同一个不带中文的根目录下，点击运行即可。

详细绘图程序见附录。

附表1：转速扭矩燃油消耗率2500 613 221.662501 549.4 222.472500 484.3 221.462500 401.8 227.392499 300.3 242.942500 205.5 272.412498 99.1 375.582300 649.9 212.042300 578.8 212.76附表2：1168 408.821200 477.51337 5001485 514.481500 5731543 618.921401 749.821600 716.251656 749.71760 759.661885 759.952000 5001．将附表1粘贴到Excel中，并将Excel名称更改为12.xlsx文件，并将该12.xlsx 文件存放在E盘根目录下，即E:\12.xlsx2．将附表2粘贴到另外一个Excel中，并将Excel名称更改为hua.xlsx文件，并将hua.xlsx文件存放在E盘根目录下，即E:\hua.xlsx3．在MTLAB中点击File，New，Scrip新建一个M文件4. 将附录后的程序粘贴进去后点击运行，即可生成发动机MAP图。

附录程序：（注意：程序和两个Excel存放在同一个跟目录，因为程序会调用者两张表格）clearclcA=xlsread('E:\12.xlsx');%%%表示12.xlsx文件存放在E盘根目录下x=A(:,1);y=A(:,2);z=A(:,3);xi=(linspace(min(x),max(x),100));size(xi)%%%% linspace是Matlab中的一个指令，用于产生x1,x2之间的N点行矢量。

【设计研究】基于 M AT LAB 的发动机万有特性曲线绘制方法周广猛 1, 郝志刚 2, 刘瑞林 1, 陈东 3, 管金发 1, 张春海4(1. 军事交通学院汽车工程系 , 天津 300161;2. 军事交通学院训练部 , 天津300161; 3. 军事交通学院基础部 , 天津 300161;4. 兰州军区军械汽车技工训练大队 , 陕西 710111摘要 :利用 MAT LAB 数学运算能力 , , , 有曲线直观明了 , 把等燃油消耗率曲线、 , 拟合程度较高。

关键词 ; :A文章编号 :1673-6397(2009 02-0034-03U niversal Characteristics Curve Plotting Method based on MAT LABZ H O U G uang -m eng 1,H A O Z hi -gang 2, L I U Rui -lin 1,CHE N D ong 3,G U A N Jin -fa 1,Z H A NG Chun -hai 4(1. Autom obile Engineering Department , Academy of Military T ransportation , T ianjin 300161,China ;2. T raining Department ,Academy of Military T ransportation , T ianjin 300161,China ;3. G eneral C ourse Department , Academy of Military T ransportation , T ianjin 300161,China ;4. Ordnance Mechanic T raining Brigade , Lan Zhou Theater , X i ’ an 710111,China Abstract :Taking advantage of MAT LAB mathematic operation , data from engine characteristic test was processed , the method is sim ple and credible , The universal characteristics curve plotted is intuitionistic and perspicuous ,and was in g ood fit with data g ot in test.K ey Words :MATLAB ;Universal Characteristics Curve ;Plot作者简介 :周广猛 (1984- , 男 , 山东邹城人 , 在读硕士研究生 , 主要研究方向为动力机械特殊环境适应性。

基于Matlab的发动机特性研究袁坚【摘要】本文使用Matlab绘制出发动机的外特征曲线,获取发动机不同转矩特性与比油耗特性,并进行四次多项式拟合,结果表明所选取的发动机整车匹配性能较好.【期刊名称】《电子测试》【年(卷),期】2019(000)008【总页数】2页(P51-52)【关键词】Matlab;发动机;特性研究;对比分析【作者】袁坚【作者单位】比亚迪汽车工业有限公司,广东深圳,518118【正文语种】中文0 引言利用MATLAB 能够对汽车发动机的实验数据进行整理与分析，获取相应的拟合曲线，实现动态系统的建模与仿真，因此MATLAB被广泛应用于汽车工程计算中[1]。

1 发动机特性的数学模型目前，使用实验数据对发动机性能进行描述的方法主要有两种：表格法与数学模型描述法。

其中，表格法的特点为计算简单、精度较高，但该法需要的实验数据测试量较大且测量精度要求较高；数学模型描述法是通过构建发动机转速、转矩以及油耗等参数间的数学模型对发动机的性能特性进行描述，该方法的特点在于其模拟精度高低取决于建模的方法，因此该方法的应用范围更广[2]。

1.1 发动机外特性的数学模型关于发动机的外特性可以借助曲线拟合的方法来构建相关性能参数之间的关系，拟合形式多使用多项式，其中拟合通式如下：式中：y——任意一条特征曲线的纵坐标；x——任意一条特征曲线的横坐标；P——多项式的阶次；Ai——多项式拟合系数，一般通过最下二乘法确定。

Matlab中曲线拟合等相应的工具箱或Polyfit、Polyval、Polytool、Polyconf等函数均可对上述曲线拟合。

1.2 万有特性的数学模型发动机的万有特性常使用多元回归方程拟合，将发动机的有效燃油消耗率ge看成转速ne与有效转矩Me的函数，回归模型如下：式中：{a0...ak-1}——模型中待定系数；{e1...aN-1}——随机误差；N——实验数据点数；K——多项式项数（k=（l+1）（l+2）/2，l 为多项式最高幂次）。

如何用matlab绘制电机效率map图或发动机万有特性曲线第一篇：如何用matlab绘制电机效率map图或发动机万有特性曲线如何用matlab绘制电机效率map图或发动机万有特性曲线前段时间写论文，需要绘制电机效率map图，其实和发动机万有特性曲线一样。

看了好多资料都不会，问问师兄也没具体画过。

困惑中查到貌似有几个软件可以画map图，由于我比较熟悉matlab，就选用它了，可是matlab也不知道咋画呀，我查看了matlab图形处理这一块，突然发现等高线图绘制，咦这不就是高中地理学的吗和map图万有特性图本质一样吗就是contour函数啦，惊喜万分5.2.13 等值线图等值线图可用于绘制地理数据中的等高图、气象数据中的等势图等。

等值线图在二维图形中把第三维中相同大小的数据连接为等值线，一定程度上可以表示第三维的信息，同时等值线图相比三维图更容易观察数据之间的关系，被广泛的应用于各个领域。

MATLAB中提供了一系列的函数用于绘制不同形式的等高线图，其中包括： 1．contour()函数contour()函数可用于绘制二维等值线图，函数的调用格式为：θ contour(z)：输入数据z为二维矩阵，绘制数据z的等值线，绘图时等值线的数量和数值根据矩阵z的数据范围自动确定。

θ contour(z,n)：绘制等值线图，设置等值线数目为n。

θ contour(z,v)：绘制等值线图，向量v设置等值线的数值。

θ contour(x,y,z)：绘制矩阵z的等值线图，输入参数x、y用于指定绘制的等值线图的坐标轴数据，同时输入数据x、y、z必须为大小相等的矩阵。

θcontour(x,y,z,n)：为指定坐标轴的等值线图设置等值线的数目n。

θ contour(x,y,z,v)：为指定坐标轴的等值线图设置等值线的数值v。

θ contour(...,LineSpec)：输入参数LineSpec用于设置等值线的线型。

θ [c,h] = contour(...)：返回contour()函数绘制的等高线图中的等值线的数值标签c和包含所有图形对象的句柄h； 2．contourf()函数contourf()函数用于绘制带填充的二维等值线图。

基于MATLAB软件的发动机特性曲线拟合
申爱玲;邓清方
【期刊名称】《广西轻工业》
【年(卷),期】2011(027)007
【摘要】根据发动机特性试验数据,利用MATLAB强大的数据运算处理功能,基于最小二乘法原理与多元线性回归理论模型,拟合得到其外特性和万有特性曲线,可以提高计算效率,并得到较高的试验精度.
【总页数】2页(P37-38)
【作者】申爱玲;邓清方
【作者单位】邵阳学院机械与能源工程系,湖南,邵阳,422004;邵阳学院机械与能源工程系,湖南,邵阳,422004
【正文语种】中文
【中图分类】TK401
【相关文献】
1.一种基于试验数据的发动机特性曲线拟合
2.基于Matlab软件的药时曲线拟合及其程序实现
3.MATLAB曲线拟合工具箱在发动机特性拟合中的应用
4.发动机台架试验特性曲线拟合算法研究与实现
5.基于Matlab软件的药时曲线拟合及其程序实现
因版权原因，仅展示原文概要，查看原文内容请购买。