当前位置：文档之家 › 5交通流三参数之间的关系解析

5交通流三参数之间的关系解析

  • 格式：ppt
  • 大小：2.75 MB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

第七章交通流三参数之间的关系

第七章交通流三参数之间的关系

参考文献
1、任福田,刘小明,荣建等.交通工程学. 北京：人民交通 出版社,2003.7
2、刘建军.交通工程学基础. 北京：人民交通出版社, 1995.7
第七章 交通流量、速度和密度之间来自关系授课内容：1、三参数之间的关系
2、速度—密度之间的关系
3、交通流量—密度之间的关系
4、交通流量—速度之间的关系
授课要求：
掌握交通流中交通流量、速度和密度各参数之间
的关系，会分析和应用三参数之间的关系。
第一节 三参数之间的关系
一、交通流的三个参数关系
描述交通流的三个参数是交通量、速度和交通密 度，它们之间的关系可以用下式表示：
Q VK
式中：Q——交通量（辆/h）；
V——速度（km／h）；
K——交通密度（辆／km）。
二、交通量、速度和交通密度的关系曲线 由交通量、速度和交通密度三者关系图（图 7-1 ） 可见：
图7—1交通量、速度和交通密度的关系
（1）Qm是速度-流量图上的峰值，表示最大流量。
（2）Vm是流量取最大值（Q＝Qm）时的速度，称为 临界速度。
例7-1已知某公路上畅行速度Vf=80 km/h，阻塞密度Kj =105veh／km，速度一密度符合直线关系式。 求：（1）在该路段上期望得到的最大流量？ （2）此时所对应的车速是多少？ 解：（1）该路段上期望得到的最大流量为： Qm=1/4 KjVf=1/4*80*105= 2100（veh／h）
阻塞密度值：kj=1000／hd＝1000／8.05=124辆 ／km，如假定ht＝1.5s，由于 ht＝3600／Q
因此，最大通行能力Qm＝3600／1.5＝2400辆／h。 此时的速度Vm＝Qm／Km＝2400／62＝38.7km／ h。

交通流三个参数K Q V之间关系概要

交通流三个参数K Q V之间关系概要

V=60-3/4*70=7.5（km／h）
Q= KV=7.5*70=525（veh／h）
Qm=1/4 KjVf=1/4*60*80=1200（veh／h）
例7-3假定车辆平均长度为6.lm，在阻塞密度时，单车 道车辆间的平均距离为1.95m，因此车头间距h＝ 8.05m，试说明流量与密度的关系。 解：因为hd＝1000／k
第二节 速度和密度之间的关系
1934年，格林希尔兹（Greenshields）提出了 速度一密度线性模型。
K v v（ ） f 1Kj
式中：Vf－一畅行速度； Kj——阻塞密度。
这一模型较为直观、实用（图7－2），且与实 测数据拟合良好。
当 K ＝ 0 时， V 值可达理论最高速度，即畅行速度 Vf 。实际上， AE 线不与纵坐标轴相交，而是趋于该 轴因为在道路上至少有一辆车V以速度Vf行驶。这时， Vf只受道路条件限制。该图也可以表示流量，根据直 线关系，直线上任意点的纵横坐标与原点O所围成的 面积表示交通量，如运行点 C ，速度为 Vm ，密度为 Km，其交通量为 Qm＝VmKm，即图上的矩形面积。
过C点作一条平行于流量坐标轴的线，将曲线分 成两部分，这条线以上的部分，为不拥挤部分，速度 随流量的增加而降低，直至达到通行能力的流量Qm 为止，速度为Vm；这条线以下部分为拥挤部分，流 量和速度都下降。
综合以上三个参数的关系可知：当道路上交通密 度小时，车辆可自由行驶，平均车速高，交通流量不 大；随着交通密度增大，交通流量也增加，但车速下 降；当交通密度增加到最佳密度时，交通流量达到最 大值，即交通流量达到了道路的通行能力，车辆的行 驶形成了车队跟随现象，车速低且均衡；当交通密度 继续增大，即超过了最佳密度，交通流量下降，车速 明显下降，直到车速接近于零，道路出现阻塞，交通 密度达到最大值，即阻塞密度，交通流量等于零。

交通流三个参数KQV之间关系解读

交通流三个参数KQV之间关系解读

图7－3所示。
图7－3交通量和密度的关系
当交通密度为零时，流量为零，故曲线通过坐标 原点。当交通密度增加，流量增大，直至达到道路的 通行能力，即曲线C点的交通量达到最大值，对应的 交通密度为最佳密度Km；从C点起，交通密度增加， 速度下降，交通量 减少，直到阻塞密度Kj，速度等 于零，流量等于零；由坐标原点向曲线上任一点画矢 径。这些矢径的斜率，表示矢端的平均速度。通过A 点的矢径与曲线相切，其斜率为畅行速度Vf；对于密 度比Km小的点，表示不拥挤情况，而密度比Km大 的点，表示拥挤情况。
例7-2 在长400m的道路上行驶28辆车，速度-密度为直 线关系，V=60-3/4 K，
求：该道路的Vf ，Kj ，Q ，Qm 。 解：V=60-3/4 K=60（1- K/80）
Vf=60 km／h K=N/L=28/0.4=70（veh／km） V=60-3/4*70=7.5（km／h） Q= KV=7.5*70=525（veh／h） Qm=1/4 KjVf=1/4*60*80=1200（veh／h）
线同样是一条抛物线（图7-4）
图7—4 速度与流量的关系
当交通密度为零时，畅行交通流的车速就可能达 到最高车速，如图中曲线的最高点A，就是畅行速度 Vf，而流量等于零。当交通密度等于阻塞密度时，速 度等于零，流量也等于零，因此，曲线通过坐标原点。
过C点作一条平行于流量坐标轴的线，将曲线分 成两部分，这条线以上的部分，为不拥挤部分，速度 随流量的增加而降低，直至达到通行能力的流量Qm 为止，速度为Vm；这条线以下部分为拥挤部分，流 量和速度都下降。
对于式（7-6）若另dQ/dK=0，则可求出对应于 Qm的Km值：
km
1 2
k
j
从而

第六章 流量速度密度三者关系

第六章 流量速度密度三者关系
2
2
Q k jv
kj vf
v
2
2 i
13931 .65
463.92
x y k v
i i
12590 .04
20 *12590 .04 463.92 * 703.6 ( ) 1.177 2 kj 20 *13931 .65 463.92
1 1 * 703 .6 (1.177 * * 463 .92 62.47 20 20
一、概述
1. 交通流——交通体组成的粒子流。如同其它流 体一样，也可以用流量、速度、密度三个参数来 描述。
Q K V

式中：Q——流量，辆/h K——密度，辆/公里 V——区间平均速度，km/h
一、概述

三维空间曲线投影到二维 空间：
Qm
（1） Qm是u—q图上的峰值，表示 最大流量； （2）Vm是流量取最大值（Qm）时 的速度； （3）u—k图上：k↓,u↑。k→0 u u f ， 畅行速度；当 k k j 时， 时（max），车流水泄不通，u=0 时， k j 为阻塞密度； （4）对应 Qm时的密度称为最佳密
a
Vf
二、流量、速度、密度三者关系
2．Q——k关系： 抛物线关系
2
K K Q KV K V f (1 ) V f ( K ) Kj Kj
二、流量、速度、密度三者关系

当K=0, Q=0 曲线通过坐标原点。
dQ 0 dK
1 K K j Km 2

从C点起，K增加，Q减少，直到 K=Kj时，V=0 Q=0。

当车流密度小于最佳车流密度时，车流处于自由行 驶状态，平均车速高。交通量没有达到最大值，密 度增大，交通量也增大；当车流密度接近或等于最

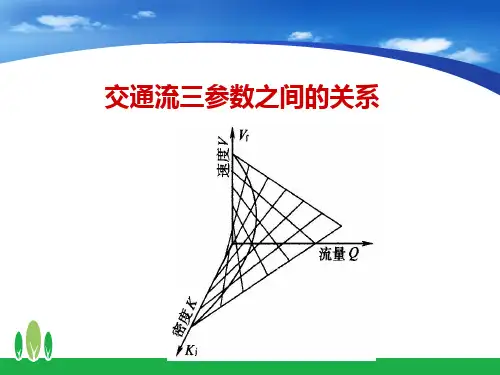
交通工程-交通流三参数之间的关系06

交通工程-交通流三参数之间的关系06

❖
V=60-3/4*70=7.5（km／h）
❖
Q= KV=7.5*70=525（veh／h）
❖ Qm=1/4 KjVf=1/4*60*80=1200（veh ／h）
❖ 4、假定车辆平均长度为6.lm，在阻塞密度时，
单车道车辆间的平均距离5m，试说明流量与密度的关系。
❖试计算该道路的最大流量。 ❖解：对照车速-密度的对数模型，可得： ❖Vm=40km/h；则Vf=80km/h； ❖Kj=82辆/km； ❖则Qm=1/4Vf*Kj=1640辆/h。
3、交通量三参数之间关系的应用
拥挤收费——交通需求管理策略
流量-密度关系曲线
交通量三参数之间关系的应用
拥挤收费
通过对驶入城市中心区的车辆征收额外的 通行费达到调节中心区交通流的目的，从 而使城市中心区的交通流运行在最佳状态。
❖ 1998年8月，新加坡政府将ERP扩充到整个中心 商业区、高速公路和交通拥挤的区域。新加坡拥 挤收费的目的非常单一，就是为了控制交通拥挤 现象，同时辅以高达130%的小汽车牌照税进一 步限制小汽车的保有，削弱了拥挤收费政策的负 面影响，增强了拥挤收费实施的效果。
❖ 技术手段
❖ 早期的ALS和RPS均采取出入收费区域出示纸质凭证 的方式运行。
实施效果： 收费区域交 通量减少了 22%；
交通事故降 低5~10%；
公交利用率 大幅提高， 增减了16条 公交线路和 200多辆公交 车。
3、交通量三参数之间关系的应用
拥挤收费需解 决的关键问题
拥挤区域、拥挤收费时段、拥挤收费 费率、收费方式等。
新加 坡电 子拥 挤收 费区 域入 口图
❖ 新加坡交通拥挤收费典型成功案例
❖ 收费水平和收益分析 ❖ 新加坡的电子收费系统(ERP)是一种单次分级

交通特性分析—交通流的基本特性及其相互关系

交通特性分析—交通流的基本特性及其相互关系
结果一致。
三流量与密度的关系
流量——密度曲线上的其他点的数值以同样的方式求出。点是表示
不拥挤情况的一个典型点。从这图来看,点的流量为1800辆/ℎ,密度为30
辆/及速度(矢径的斜率)为58/ ℎ。
点是表示拥挤情况的一个典型点。从图中看出,点的流量为1224 辆
/ℎ,密度105.6辆/及速度(矢径的斜率)为11.6/ℎ。根据定义,点的流
— — 路段长度（）
交通流三参数基本关系
车流密度大小反映一条道路上的交通密集程度。对于同一条道路,可以
不考虑车道数;对于具有不同车道数的道路,为使车流密度具有可比性，
车流密度应按单车道来定义，单位为:辆/( ·车道)。
• 交通流三参数之间的基本关系式为：
=∙
式中：
— — 平均流量（辆/ℎ）；
点。从原点 到曲线上点的向量斜率表示那一点的密度的倒
数1/ 。由 点作平行于 轴的一条直线,该直线为(上半部分)
交通流不拥挤的稳定交通流和(下半部分)拥挤路段的不稳定
交通流的分界线。
流量与速度的关系
综上所述,按格林希尔茨的速度——密度模型、流量——密度模型、
速度——流量模型可以看出, 、 、 是划分交通是否拥挤的重要特
密度由大变小时，车速会增大。关于两者之间的关系,已经由各国学者
提出了几种不同的模型。
1934年,格林希尔茨提出了速度一密度线性关系模型:

= (1 − )

式中符号意义同前。
这一模型简单直观如图所示 ,研究表明,刚才的公式表示的模型与实
测数据相关性很好。
速度与密度关系
这一模型简单直观如图所示 ,研究表明,刚才的公式表示的模型与实测数据相
速度与密度关系

交通流三个参数K Q V之间关系


过C点作一条平行于流量坐标轴的线，将曲线分 成两部分，这条线以上的部分，为不拥挤部分，速度 随流量的增加而降低，直至达到通行能力的流量Qm 为止，速度为Vm；这条线以下部分为拥挤部分，流 量和速度都下降。
综合以上三个参数的关系可知：当道路上交通密 度小时，车辆可自由行驶，平均车速高，交通流量不 大；随着交通密度增大，交通流量也增加，但车速下 降；当交通密度增加到最佳密度时，交通流量达到最 大值，即交通流量达到了道路的通行能力，车辆的行 驶形成了车队跟随现象，车速低且均衡；当交通密度 继续增大，即超过了最佳密度，交通流量下降，车速 明显下降，直到车速接近于零，道路出现阻塞，交通 密度达到最大值，即阻塞密度，交通流量等于零。
（2）此时所对应的车速是：
Vm＝Vf/2=1/2*80=40 km／h
例7-2 在长400m的道路上行驶28辆车，速度-密度为直 线关系，V=60-3/4 K， 求：该道路的Vf ，Kj ，Q ，Qm 。 解：V=60-3/4 K=60（1- K/80） Vf=60 km／h K=N/L=28/0.4=70（veh／km）
上式是二次函数关系，可用一条抛物线表示，如 图7－3所示。
图7－3交通量和密度的关系
当交通密度为零时，流量为零，故曲线通过坐标 原点。当交通密度增加，流量增大，直至达到道路的 通行能力，即曲线C点的交通量达到最大值，对应的 交通密度为最佳密度Km；从C点起，交通密度增加， 速度下降，交通量 减少，直到阻塞密度Kj，速度等 于零，流量等于零；由坐标原点向曲线上任一点画矢 径。这些矢径的斜率，表示矢端的平均速度。通过A 点的矢径与曲线相切，其斜率为畅行速度Vf；对于密 度比Km小的点，表示不拥挤情况，而密度比Km大 的点，表示拥挤情况。
参考文献

5班1组-适应 ITS的交通流参数之间的关系研究交通流三参数两两之间的关系

交通流三参数关系1理论基础交通流是由各种车辆在道路上的运动而形成的。

从宏观上来考察 ,它类似于运动着的流体 ,而且由于它的密度随时在改变,所以交通流可看成一种可压缩性的流体。

当车流因信号灯的变化而引起车流密度的改变时 ,车流中会产生车流波的传播 ,通过分析波传播过程中流量和密度、速度之间的关系,来描述车流从拥挤到消散的全过程。

1 . 1　基本函数关系文中研究对象是在无出入岔道的道路上单向行驶的车流。

在道路上选定一点作坐标原点,记作ｘ=0。

以车流运动方向作为ｘ轴的正向,则在任一时刻ｔ通过点ｘ的车流流量ｑ(ｘ,ｔ)、密度 ρ(ｘ ,ｔ)和车流速度ｖ(ｘ ,ｔ)之间有如下关系ｑ(ｘ ,ｔ) =ρ(ｘ ,ｔ)ｖ(ｘ ,ｔ) (1 )下面推导在平衡状态下(车流密度相等,车速相等)车流流量和密度之间的函数关系。

为使研究简便 ,假定如下[1 ]:(1 )初始时是平衡状态。

在平衡状态下车流速度ｖ是密度ρ的函数。

(车辆首尾相接形成堵塞的最大密度 )时 ,; ρ在接近 0时 ,车辆以最大速度自由行驶。

(2 )在平衡被破坏的过程中 ,ｔ时刻第ｉ辆车的制动力与前后两车的速度差成正比 ,与前后两车之间的距离平方成反比。

根据上述假设 ,由牛顿第二定律有转化为式中ｍ为第ｉ辆车质量。

因为ｘｉ(ｔ) -ｘｉ-1 (ｔ) 等于车流中前后两车车长与间距之和 ,即而且在平衡状态下车流始终以定速ｖ行驶 ,所以式 (2 )化为代入初始值得根据式 (1 )得流量函数显然 ,ｑ的极大值点(见图 1 )。

1 . 2　连续交通流方程对于正常运动的交通流 ,可假定流量ｑ(ｘ,ｔ)、密度 ρ(ｘ,ｔ)和速度ｖ(ｘ,ｔ)都是ｘ和ｔ的连续、可微函数。

在道路没有岔路的假定下车辆数守恒 ,因此有流入量 -流出量 =△ｘ内车辆数的变化即取极限可得这就是著名的连续交通流方程。

对于式 (4)ｑ =ｑ(ρ) ,导数可记作这样 ,方程 (5)可写成式中ｆ(ｘ)为初始密度。

交通流三参数之间的关系

三个参数之间的关系式为 Q ? Vs K
适合于所有稳定的交通流
最大流量 Qm 临界速度 （critical density ）vm 临界密度 （critical density ）Km 阻塞密度 （jam density ）Kj 自由流速度 （free-flow speed）Vf
22、、交停通车流三场参布数局之间原的则关系
交通流三参数之间的关系
2 、交通停流车三场参数布之局间原的则关系
(1) 连续流和间断流 (2) 流量-速度-密度之间的关系 (Q-V-K 关系) (3) 速度-密度之间的关系 (V-K 关系) (4) 流量-密度之间的关系 (Q-K 关系) (5) 流量-速度之间的关系 (Q-V 关系)
22、、交停通车流三场参布数局之间原的则关系
?试用格林希尔茨线性模型求该路段在密度为 30辆 ／Km 时的路段平均交通量。该道路的最大交通量 为多少？对应的速度和密度值是多少？
200
400
600
800
q (pcu /h /lane )
速度—密度线性关系模型与实测结果对比
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (b) Grenberg （对数）模型
V
?
Vm
ln
Kj K
适用于交通流密度很大时
2、停车场布局原则
(3) 速(1度) -密度之间的关系 (c) Underwood （指数）模型
) /h
50
m
v(k 40
30
20 0
南京市：龙蟠南路路段
)
ne
/la
2min Underwood 2min Greenberg
(pcu/h
5min Underwood

交通流三参数之间的关系


600
800
速度—密度线性关系模型与实测结果对比
2、停车场布局原则
(3) 速度-密度之间的关系 (1) (b) Grenberg（对数）模型
V Vm ln
Kj K
适用于交通流密度很大时
2、停车场布局原则
(3) 速度-密度之间的关系 (1) (c) Underwood（指数）模型
V Vf e
800 600 400 200 0 0
南京市：龙蟠南路路段
q (pcu /h /lane )
v (km /h )
2min 2min 5min 5min 15min 10 20 k (pcu /km /lane )
Underwood Greenberg Underwood Greenberg Underwood 30

K Km
适用于交通流密度很小时
2、停车场布局原则 交通流三参数之间的关系
(4) 流量-密度之间的关系 (1)
Q K V
K V V f (1 ) Kj
K2 Q V f (K ) Kj
2、停车场布局原则 2、交通流三参数之间的关系
(4) 流量-密度之间的关系 (1)
70 60 50 40 30 20 0 200 400 q (pcu /h /lane ) 600 800 2min 2min 5min 5min 15min Underwood Greenberg Underwood Greenberg Underwood
3、交通量三参数之间关系的应用
实施效果： 收费区域交 通量降低了 18%； 平均延误降 低了30%； 车速提高了 17km/h；
公交利用率 提高38%。
伦敦拥挤收费区域示意图（2003年以来）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

当K＝0时，V值可达理论最高速度，即畅 行速度Vf。实际上，AE线不与纵坐标轴相 交，而是趋于该轴因为在道路上至少有一 辆车 V 以速度 Vf 行驶。这时， Vf 只受道路 条件限制。该图也可以表示流量，根据直 线关系，直线上任意点的纵横坐标与原点O 所围成的面积表示交通量，如运行点C，速 度为Vm，密度为Km，其交通量为 Qm ＝VmKm，即图上的矩形面积。
Q-K-V之间的 基本关系式 Q=V*K Q：平均流量(pcu/h) V：平均车速(km/h)；K：平均车流密度(pcu/km)
怎么得出？
Q、V、K关系
三个参数之间的关系式为
Q Vs K
适合于所有稳定的交通流
最大流量 Qm
临界速度（critical density）vm 临界密度（critical density）Km 阻塞密度（jam density）Kj 自由流速度（free-flow speed）Vf
交通流三参数之间的关系
授课要求：
掌握交通流中交通流量、速度和密度各参数 之间的关系，会分析和应用三参数之间的关系。
2、停车场布局原则 交通流三参数之间的关系
(1) (2) (3) (4) (5)
连续流和间断流

流量-速度-密度之间的关系(Q-V-K关系) 速度-密度之间的关系(V-K关系) 流量-密度之间的关系(Q-K关系) 流量-速度之间的关系(Q-V关系)
800 600 400 200 0 0
南京市：龙蟠南路路段
q ( pcu /h /lane )
v ( km /h )
2min 2min 5min 5min 15min 10 20 k (pcu /km /lane )
Underwood Greenberg Underwood Greenberg Underwood 30
2 、停车场布局原则 1、 交通流三参数之间的关系
(1) (1) 极大流 量 Qm
Q－V曲线上的峰值。 流量达到极大时的速度。
(5)畅行速 度Vf
车流密度趋于零，车辆可以
(2) 临界速 度Vm
反映交通 流特性的 特征变量
畅行无阻时的平均速度。
(4)阻塞密 度 Kj
车流密集到车辆无法移 动时的密度。
K2 Q Vf (K ) Kj
对于流量与密度关系式，若令 dQ/dK=0，则可求出对应于Qm的Km 值：
km 1 kj 2
从而
Qm K mVm
K jVm 2
2 、停车场布局原则 2、 交通流三参数之间的关系
(4) 流量 (1) -密度之间的关系
70 60 50 40 30 20 0 200 400 q (pcu /h /lane ) 600 800 2min 2min 5min 5min 15min Underwood Greenberg Underwood Greenberg Underwood
2 、停车场布局原则 1、 交通流三参数之间的关系
(1) 连续流和间断流: 按照交通设施对交通流的影响，交通流 (1) 可分为连续流和间断流。 连续流：没有外部固定因素影响（交通信号设施等）的 不间断流，如高速公路基本路段上的交通流； 间断流：有外部固定因素影响的同期性交通流，如信号 交叉口或无信号交叉口处的交通流。 连续流和间断流的区 别 设施类型
高速公路、城市快速路、 多车道公路 交叉口、公共交通、 行人、自行车
交通流类型 连续流
间断流
描述参数 Q、V、K
延误、饱和流率、 损失时间
Uninterrupted Traffic Flow Interrupted Traffic Flow
2 、停车场布局原则 1、 交通流三参数之间的关系
(2) 流量-速度-密度之间的关系: Q-V-K之间的关系又称为交 (1) 通流三参数之间的基本关系。
vm 1 vf 2
从而
Qm K m vm
Kmv f 2

k jv f 4
2 、停车场布局原则 2、 交通流三参数之间的关系
(5) 流量 (1) -速度之间的关系
70 60
v ( km /h )
南京市：龙蟠南路路段
50 40 30 20 0 200 400 q (pcu /h /lane ) 600 800 2min Underwood 2min Greenberg 5min Underwood 5min Greenberg 15min Underwood
40 30 20 10 0 y = -0.054 x + 51.030
y = -0.013 x + 52.349
0
200
400 q (pcu /h /lane )
600
800
速度—密度线性关系模型与实测结果对比
2、停车场布局原则
(3) 速度 (1) -密度之间的关系 (b) Greenberg（对数）模型
2、停车场布局原则 交通流三参数之间的关系
(3) 速度 (1) -密度之间的关系 (a)格林希尔治(Green Shields)模型(线性模型)(1933年)
南京市：龙蟠南路路段
60 50
vs ( km /h ) vs ( km /h )
60 50 40 30 20 10 0
0 30 60 90 f s (辆次 /h ) 120 150
流量达到极大时的密度。
(3)最佳密 度 Km
2 、停车场布局原则 1、交通流三参数之间的关系
(3) 速度 (1) -密度之间的关系 (a)格林希尔治(Green Shields)模型(线性模型)(1933年)
K V V f (1 ) Kj
模型适用于交通流密度适中时， 当密度很大或很小时偏差大。 该模型形式简单，一直被广泛采 用。
流量—密度关系模型与实测结果对比
2 、停车场布局原则 2、 交通流三参数之间的关系
(5) 流量 (1) -速度之间的关系
V V f (1 K ) Kj
V K K j (1 ) Vf
Q K V
V2 Q K j (V ) Vf
对式求导dQ/dv=0，则可求出对应于 Qm的Km值：
V Vm ln
Kj K
适用于交通流密度很大时
2、停车场布局原则
(3) 速度 (1) -密度之间的关系 (c) Underwood（指数）模型
V Vf e

K Km
适用于交通流密度很小时
2、停车场布局原则 2、交通流三参数之间的关系
(4) 流量 (1) -密度之间的关系
Q K V
V V f (1 K ) Kj