第二个重要极限使用条件

2
).
解
因为
n 1 1 n , < +⋯+ < 2 2 2 2 n +n n +1 n +n n +1
n 1 又 lim 2 = lim = 1, n→ ∞ n + n n→ ∞ 1 1+ n n 1 lim 2 = lim = 1, 由夹逼准则得 n→ ∞ n + 1 n→ ∞ 1 1+ 2 n 1 1 1 lim ( 2 ) = 1. + +⋯+ 2 2 n→ ∞ n +1 n +2 n +n
显然 f ( n + 1) > f ( n), 所以 f ( n ) 是单调递增的 ;
1 1 1 1 f ( n) < 1 + 1 + + ⋯ + < 1 + 1 + + ⋯ + n −1 2! n! 2 2
所以 f ( n )是有界的 ; 1n 所以 lim xn 存在. 记为lim(1 + ) = e (e = 2.71828⋯ ) n→ ∞ n→∞ n
这个重要极限, 可写成 这个重要极限
lim u u→0
sinu
= 1 其中, u可以为函数.
例2.
sin kx 求 lim x →0 x
sin kx sin kx 解:lim = lim k ⋅ x →0 x →0 x kx
sin kx = k ⋅ lim x → 0 kx
= k·1= k
例3.
∵ f ( x ) g( x ) = f ( x ) g( x ) ≤ M f ( x )
∴ − M f ( x ) ≤ f ( x ) g( x ) ≤ M f ( x )

x3 + ax + b x 3 + ax + (−8 − 2a ) ∴ lim = lim 2 x →2 x→2 x −4 x2 − 4 2 ( x − 2)( x + 2 x + 4 + a) 12 + a = lim = x→2 ( x − 2)( x + 2) 4 12 + a ∴ =4 4 ∴ a = 4, b = −16
又 Q x1 = 3 < 3, 假定 x k < 3, x k + 1 = 3 + x k < 3 + 3 < 3,
∴ lim x n 存在.
n→∞
2 lim x n + 1 = lim ( 3 + x n ), n→ ∞ n→∞
2 Q x n+1 = 3 + x n , x n+1 = 3 + x n ,
存在如果推论2limlimlimlimlimlim分母的极限都是零分子1后再求极限因子先约去不为零的无穷小分母的极限都是无穷大分子再求极限分出无穷小去除分子分母先用无穷小因子分出法小结
1.5 极限的运算法则、两个重要极限 极限的运算法则、
• 一、极限的运算法则 • 二、两个重要极限 • 三、无穷小量的比较
1 2 n 1+ 2 +L+ n lim ( 2 + 2 + L + 2 ) = lim 2 n→ ∞ n n→ ∞ n n n
1 n( n + 1) 1 1 1 2 = lim = lim (1 + ) = . 2 n→ ∞ n→ ∞ 2 n n 2
例7
3 1 lim( − ) 3 x →1 1 − x 1− x

例8 求极限 解 令
arcsin x lim x 0 x
则
arcsin x t
x sin t
t 1 原式= lim t 0 sin t
思考
arctan x lim ? x 0 x arccos x lim ? x 0 x
(2)
1 x lim (1 ) e x x
1 1 1 1 1 1 n 1 xn 1 1 2! n! 2 2 1 xn 是有界的; 3 n 1 3, 2 1 n lim x n 存在. 记为 lim (1 ) e (e 2.71828) n n n
0 ( )型 0
tan x sin x 例4 求极限 lim 3 x 0 x
0 ( )型 0
tan x sin x 解 lim 3 x 0 x 1 1 sin x cos x lim x 0 x x2
sin x 1 cos x 1 lim 2 x 0 x x cos x
2
sin x 即 cos x 1, x
2
lim cos x 1,
x 0
又 lim 1 1,
x 0
sin x lim 1. x 0 x
0 ( )型 0
例2 求极限 解
tan x lim x 0 x
0 ( )型 0
tan x lim x 0 x
sin x 1 lim x 0 x cos x
1 2
cos x cos 3 x 例5 求极限 lim x 0 x2 cos x cos 3 x 解 lim x 0 x2
2 sin(2 x ) sin x lim 2 x 0 x

浅析第二个重要的极限作者：张春红来源：《知识文库》2017年第04期高等数学是从函数及其极限为基础展开研究的。

第二个重要极限跟第一个重要极限一样是极限中特殊的极限形式。

理解第二个重要极限的本质形式，是学好第二个重要极限的前提。

文章先分析第二个重要极限本质表现形式，然后分析其应用。

用事實说明第二个重要极限在高等数学和经济上的重要性第二个重要极限是型的极限类型，为导数的学习奠定了基础，在经济上用于复利的计算。

1 结构第二个重要的极限： .当时，底数趋向于1，指数趋向于无穷大，属于型的极限类型。

利用单调有界数列必有极限，可以求得极限为。

在极限中只要是无穷小就有①型的极限类型②表达式中，只要是无穷小即这说明：当及时，函数的值会无限地趋近于。

常数就是这个极限值，即.如果令公式还可以写成. （1.5.5）这两个极限式可以统一为“1加无穷小的无穷大次方的极限为”。

如：；；用求极限时，函数的特点是型幂指函数，只要中是无穷小，而指数为无穷大，两者恰好互为倒数就符合第二个重要极限的类型。

2 应用2.1公式的直接应用应用第二个重要极限求极限：例1 求解这道题属于求幂指函数的极限，先变形化简后整理成第二个重要极限的形式，然后应用第二个重要极限求出结果。

应用第二个重要极限推导指数和对数函数的求导公式：例2 求函数的导数解例3 求函数的导数解即特殊地运用导数的定义表达出指数函数和对数函数的导数形式，结合第二个重要极限，推导得出求导公式，为导数的进一步学习铺砖引路。

第二个重要的极限在推导求指数函数和对数函数的求导公式过程中，起到了举足轻重的作用。

第二个重要极限是基本初等函数求导公式得出的奠基石。

第二个重要极限在初等函数求导过程中起到了重要的桥梁纽带作用。

2.2公式的间接应用经济上连续复利计算就是以第二个重要极限为依据的：设初始本金为p （元），年利率为r，按复利付息，若一年分m次付息，则第n年末的本利和为89如果利息按连续复利计算，即计算复利的次数m趋于无穷大时， t年末的本利和可按如下公式计算若要t年末的本利和为s，则初始本金。

1 = lim (1 - t +1) -(t +1) t +
从而有
= lim ( t +
t +
-1 t (t +1) t +1
)
1) t +1 = lim (1 + t t +
= lim [(1 + 1)t (1 + 1)] = e t t
故
1) x lim (1 + x x
n1 = 1 + 1! n
xn+1 = 1 + 1 +
1 (1 - 1 ) + 1 (1 - 1 )(1 - 2 ) + 2! n+1 3! n+1 n+1
大 大
1 + ( n+1)! (1 - n1 1)(1 - n2 1)(1 - nn 1) + + +
正
比较可知
首页
xn xn+1 ( n = 1, 2 , )
那么数列{xn }的极限存在 且 lim xn = a
由条件(2) e 0 N 0 当nN 时 有 |yn-a|e 及|zn-a|e 即有 a-eyna+e a-ezna+e 由条件(1) 有 a-eynxnzna+e 即 |xn-a|e 这就证明了 lim xn =a 简要证明
6.lim(1 + x ) =
x 0 1 x
1 x 5.lim(1 - ) = x x
1 x x 0
e
-1
;
e;
7.lim(1 - x ) = e -1 .
首页 上页 返回 下页 结束

则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,（舍去）
lim n
xn
3.
14
3.两个重要极限的应用
例6： 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解： lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知：
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明：
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x

1
(1
1 )(1
2 )(1
n1 )
2! n
n! n n
n
xn

11
1 2!
1 n!

11
1 2

1 2n1

3

1 2n1

3,
{xn}是有界的; 单调上升有上界必有极限
lim n
xn
存在.
记为 lim(1 1)n e
n
n
(e 2.718281828459045) 无理数
12 23
n1 n
2 1 2, n
{ xn}是有上界的;
因此, 利用单调有界数列必收敛准则即得结论.
15
2.5 极限存在准则 两个重要极限
例 证明数列 xn 3 3 3
(n重根式)的极限存在.
证 (1) 显然 xn1 xn ,
{xn}是单调增加的; (2) x1 3 3, 假定 xk 3,
1.
8
2.5 极限存在准则 两个重要极限
0
例 lim x 0 lim
x
lim sin x 1 lim x 1
x0 x
x0 sin x
cos x 1.
x0 tan x x0 sin x
例
sin3 3 lim x0 3x
x
0
0
1 3
lxim0
sin
3
3
x
x
3
n
an

bn

cn ,求 lim n
xn .
解 法一 由于 a xn a n 3
1
以及 lima a, lim a n 3 lim a 3n a 1

第二重要极限
第二个重要极限是：n趋近于无穷大时，（1+1/n）的n次方的极限为e。

数学中的“极限”指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中。

逐渐向某一个确定的数值A不断地逼近而永远不能够重合到A （永远不能够等于A，但是取等于A已经足够取得高精度计算结果）的过程中，此变量的变化，被人为规定为永远靠近而不停止，其有一个不断地极为靠近A点的趋势。

第二个重要极限公式是：lim（1+（1/x））^x=e（x→∞）。

第二个重要极限在极限计算中占有很重要的地位，它对初等函数极限的推导至关重要，是解决未定型极限的一个重要工具。

但它形式变化多样，在学习和使用中不易把握是学生学习的难点。

第二个重要极限，它的结构独特、复杂，形式多样，计算灵活，许多实际问题都依赖于这种极限的应用，因此掌握第二个重要极限，也有利于解决生产和生活中的实际问题，在经济学中尤为重要。

第二个重要极限使用条件第二个重要极限使用条件是指在使用某种技术或方法时，必须注意其使用条件和限制，以避免出现意外和危险。

这种重要极限使用条件在很多领域都有应用，如航空、化工、医疗等领域。

在这些领域中，失误和意外往往会造成严重的后果，因此必须非常严格地遵守这些使用条件。

对于航空领域来说，第二个重要极限使用条件特别重要。

航空器在高空飞行时，受到重力、空气阻力、温度、气压等多种因素的影响，因此必须保证飞行时使用的材料和设备必须符合特定的使用条件。

例如，飞机的机翼和发动机必须能够耐受巨大的气压和温度变化，而飞行员则必须在极端的高压和低温环境下进行飞行。

因此，航空器制造商和维修人员必须严谨地考虑第二个重要极限使用条件，以保证飞机的安全性和可靠性。

在化工领域中，第二个重要极限使用条件同样至关重要。

化工生产中涉及到的材料和化学品往往具有较强的腐蚀性和毒性，一旦使用不当，就会对人员和环境造成严重的危害。

因此，化工生产企业必须要求员工必须具有良好的职业素养，严格遵守第二个重要极限使用条件，并加强安全培训和监管，以降低事故发生的概率。

在医疗领域中，临床医生和医疗保健专家也必须遵循第二个重要极限使用条件。

医疗设备和药品对人体的影响非常大，必须精确地控制使用量和使用时间。

例如，化疗药物的使用时间和用量必须经过仔细计算和监控，否则可能导致患者细胞功能异常、免疫力下降等严重后果。

临床医生必须仔细考虑患者的病情和身体状况，并根据第二个重要极限使用条件选择合适的医疗方案，以确保患者的安全和舒适度。

总之，第二个重要极限使用条件在工业生产和人类生活的多个领域中起着至关重要的作用。

在面对高风险、高技术和高负荷的工作场所中，必须严格遵守第二个重要极限使用条件，以保护人们的生命和财产安全。

不一定要x→0，但必须保 证x→x0 (或x→∞)时，另 外两个方框处是无穷小
0 (" "型, 三统一) 0
必须是一个与分子 方框处完全相同的 无穷小
机动
目录
上页
下页
返回
结束
例1. 求
tan x sin x 1 解: lim lim x 0 x x 0 x cos x sin x 1 lim 1 lim x 0 x x 0 cos x
2 x
lim(1 3x) lim (1 3x) e6 . x 0 x 0
2 x
1 3x
6
机动
目录
上页
下页
返回
结束
例8. 求
x2 x 3 5 lim 1 5 lim 解: x lim x x 3 x 3 x x 3 5x x3 x3 5 5 5 5 lim 13 lim 1 /x x e . e x x 3 x x 2 x 2 1 1 x2 x x 另解: lim lim lim x 1 3 x x x 3 3 x 1 x
第九节
第一章
两个重要极限
一、第一个重要极限 二、 第二个重要极限
机动
目录
上页
下页
返回
结束
本节教学目的
掌握重要极限 它求极限 难点 掌握重要极限 用它求极限 ，并能熟练运用 ，并能熟练运
重点
机动
目录
上页
下页
返回
结束
一、 第一个重要极限
必须是一个无穷小
sin lim 1 x x0 ( x)

令t =1x, 则:
lim(1
1
x)x
=
lim(1
1)t
=
e.
x0
t
t
此结论可推广到
1
lim1 ( x)( x) = e
xa
条件是x a时, ( x) 0，其中a可为
有限值，也可为
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
14
例5 求 lim(1 1 )x .
n2 n n2 1
又 lim n
n = lim n2 n n
1 1 1 = 1,
n
lim
n
n = lim n2 1 n
1 = 1,
1 1 n2
由夹逼定理得
lim( 1 1 L 1 ) = 1.
n n2 1 n2 2
n2 n
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
6
例2 证明数列 xn = 3 3 L 3 (n重根 式)的极限存在.
证: 显然 xn1 > xn , xn是单调递增的 ;
又 x1 = 3 3, 假定 xk 3, xk1 = 3 xk 3 3 3,
xn 是有界的 ;
原式
=
lim x (1
x 1 )x
x
=
e e 1
=
e2
2020年9月1日星期二
(20ppt,scau,L.G.YUAN)
16
三、小结
1.两个准则
夹逼准则; 单调有界准则 .
2.两个重要极限
10 lim sin x = 1; x0 x

π
（3）求极限
sin x Q cos x < < 1, x
又 lim cos x = 1,
x→0
(0 <| x |<
π
2
)
lim 1 = 1,
x →0
由夹逼法则
sin x lim = 1. x →0 x
机动
目录
上页
下页
返回
结束
例5
tan x sin x 1 (1) lim = lim ⋅ =1 x →0 x →0 x x cos x
x = 弧 AB ,
tan x = AC ,
1 1 1 ∴ sin x < x < tan x , 2 2 2
∴ sin x < x < tan x ,
(0 < x <
π
2
)
机动 目录 上页 下页 返回 结束
sin x < x < tan x ,
(0 < x < (0 < x <
π π
2 2
) )
n
证 Q x1 = 3 < 3, 假定 xk < 3, x k + 1 = 3 + x k < 3 + 3 < 3,
∴
{xn } 有上界 ;
假定 xk > xk −1 ,
又 Q x2 = 3 + 3 > 3 = x1 ,
x k + 1 = 3 + x k > 3 + x k −1 = x k
∴ {xn } 是单调递增的 ; ∴ lim xn 存在 . n→ ∞
显然 xn+1 > xn ,

即|x n-a|<e ．这就证明了 lim x n=a ． n
一、准则 I
准则 I： 如果数列{xn }、{yn}及{zn}满足下列条件：
( ynxnzn(n=1，2，3，…)，
lim (2) lim yn=a，n zn=a，
n
lim 那么数列{xn }的极限存在，且 x n=a ． n
．
例8
sin x ． x x tan x 求 lim ． x0 x 1 - cos x 例 2 求 lim ． 2 x 0 x
求 lim
5 求 lim
6
7
7 x + 5x - 3 3x 2 - 2 x - 1 求 lim ． x 2 x 3 - x 2 + 5 2x 3 - x 2 + 5 求 lim ． 2 x 3 x - 2 x - 1
例2 求lim
1 - cos x ． 2 x 0 x
2
解
x sin x 2 x sin 2 sin 1 1 1 - cos x 2 2 = lim 2 = lim lim = lim x0 x0 x2 2 x 0 1 2 2 x 0 x x2 2 2 1 2 1 = 1 = ． 2 2
n
根据准则II，数列{x n}必有极限． 这个极限我们用e 来表示．即
lim 1 + n 1 =e ． n
n
e 是个无理数，它的值是e=2.718281828459045 ···．
还可证明
1 lim1 + =e ． x x
x
第二个重要极限： lim1 + x
准则 I： 如果函数g(x)、f(x)及h(x)满足下列条件：

x0
x
2. lim xsin 1 __1__ ;
x
x
4. lim (1 1)n _e___1;
n n
27
作业
P56 1 写在书上 ; 2; 3；4 .
28
x
1 x
)
x

e
说明:
此极限也可写为
1
lim (1 z) z
e
z0
18
例7 已知 解: 原式 =
c ln 4
求 C。
ec 4
19
例8 求下列极限
解: 令 t x , 则
lim (1
t

1t )t

lim
t
1
解 原式＝
说明
：若利用

lim (1
( x)
1n）]

e
lim (1
x
1x) x

e
17
当
时, 令 x (t 1), 则
从而有

lim (1
t

t
11)(t
1)
tlim(tt 1)(t1)

t
lim (1


1t )t
1

t
lim [(1


1t )t
(1

1t )]

e
故
lim (1

k

lim
x0
sin k
k x
x
k
2.
lim tan x x0 x

lim x0
sin x
x
1 cos
x

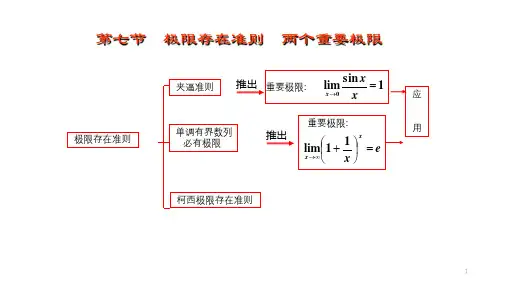
两个重要极限一、基本内容1. 第一重要极限 ：1sin lim0=→x xx特征 ：（1）是“00”型极限，但并不代表所有的“0”型；（2）无论x 趋于何值，只要0)(α→x ，就有1)(α)(αsin →x x 。

2. 第二重要极限： e x x x =+∞→)11(lim ，e x x x =+→10)1(lim ，e nnn =+∞→)11(lim特征 ：（1）是“∞1”型极限，但并不代表所有的∞1；（2）无论x 趋于何值，只要0)(α→x ，就有e x x →+)(α1)](α1[。

二、学习要求能够灵活运用两个重要极限求极限。

三、基本题型及解题方法 题型1 求“”型极限 解题方法：以第一重要极限为基础，同时要注意该重要极限的推广应用即0)(α→x ，有1)(α)(αsin lim0)(α=→x x x 。

【例1】 计算下列极限（1） 2-)1-sin(lim21x x x x +→ (2) xx xx sin 2cos 1lim0-→ 解：(1) 原式211-)1-sin(lim1+⋅=→x x x x 31= (2) 原式= x x x x sin sin 2lim 20→=xxx sin lim 20→=2题型2 求“∞1”型极限解题方法：以第二重要极限为基础，同时也要注意该重要极限的推广应用即0)(α→x ，有e x x x =+→)(α10)(α)](α1[lim 。

【例2】 计算下列极限 （1）xx x2)51(lim -∞→+； （2）()xx x 2031lim -→解：（1）原式)10(5)51(lim -⋅∞→+=xx x10)10(5)51(lim --∞→=⎥⎦⎤⎢⎣⎡+=e x xx（2）原式)6(31)31(lim -⋅-→-=xx x =6e四、同步练习 （一）填空题： 1．若53sin lim0=→kxxx ，则=k 。

2．设⎪⎪⎩⎪⎪⎨⎧>=<=0,sin 10,0,)(x x xx k x e x f x，若()x f x 0lim →存在，则=k 。

高数两个重要极限公式
1、第一个重要极限的公式：
lim sinx / x = 1 (x->0)当x→0时，sin / x的极限等于1；特别注意的是x→∞时，1 / x是无穷小，无穷小的性质得到的极限是0。

2、第二个重要极限的公式：
lim (1+1/x) ^x = e（x→∞）当x→∞时，（1+1/x）＾x的极限等于e；或当x →0时，（1+x）＾（1/x）的极限等于e。

相关性质：
1、唯一性：若数列的极限存在，则极限值是唯一的，且它的任何子列的极限与原数列的相等。

2、有界性：如果一个数列收敛（有极限），那么这个数列一定有界。

但是，如果一个数列有界，这个数列未必收敛。

3、与子列的关系：数列{xn} 与它的任一平凡子列同为收敛或发散，且在收敛时有相同的极限；数列{xn} 收敛的充要条件是：数列{xn} 的任何非平凡子列都收敛。

极限存在准则两个重要极限在极限存在准则中，有两个特别重要的极限存在定理，分别是柯西收敛准则和夹逼定理。

柯西收敛准则是极限存在定理中的一个基本定理。

它是由法国数学家柯西于19世纪初发现的，用来判定一个数列是否收敛。

柯西收敛准则的核心思想是，如果一个数列在无穷项的情况下，其任意两项之差都可以变得很小，那么这个数列是收敛的。

具体来说，柯西收敛准则可以分为两个条件：1.必要条件：如果对于任意给定的正实数ε，总存在一个正整数N，使得当n和m都大于N时，an - am，< ε，那么数列{an}是收敛的。

2.充分条件：如果数列{an}具有柯西序列的性质，即对于任意给定的正实数ε，总存在一个正整数N，使得当n和m都大于N时，an - am，< ε，则该数列一定是收敛的。

夹逼定理又称为挤压定理，是另一个极限存在定理。

它主要用于计算和证明无穷序列和函数的极限存在。

夹逼定理的核心思想是，如果一个函数在一些点的两侧有两个函数夹住，并且这两个函数的极限都存在并且相等，那么原始函数在该点处的极限也存在，并且等于这两个函数的共同极限。

具体来说，夹逼定理可以表达为以下三个条件：1.设函数f(x)，g(x)，h(x)在点a的一些去心邻域内有定义，并且对于这个去心邻域内的任意x，有g(x)≤f(x)≤h(x)。

2.如果lim(x→a)g(x) = L，并且lim(x→a)h(x) = L，那么lim(x→a)f(x)存在，并且等于L。

3.夹逼定理对于数列也成立，即如果数列{an}满足对于所有的n，有gn ≤ an ≤ hn，并且lim(n→∞)gn = L，并且lim(n→∞)hn = L，则lim(n→∞)an存在，并且等于L。

柯西收敛准则和夹逼定理是极限存在准则中非常重要的定理，它们在数学分析中有着广泛的应用。

通过这两个定理，我们可以更加准确地计算和证明函数的极限存在，并建立起更为完善和严谨的数学分析体系。