大学物理-作业与答案

[解] 取半径为 r 、 厚度为 dr 的球壳。 认为球壳内电荷分 布是均匀的
dQ 4 r 2 dr (r ) 4A r 3 dr
R Q0 4r 2 (r )dr
A 4r 3 dr R 4 A
0
R
6．如图所示，一质量 m 1.6 10 kg 的小球，带电量 q 2 10
作业 2
1． 如图所示， 把点电荷 q 从高斯面外 P 移到 R 处 OP OR ， ] O 为 S 上一点，则[ A. 穿过 S 的电通量 e 发生改变， O 处 E 变
B. e 不变， E 变。 C. e 变， E 不变。 D. e 不变， E 不变。
答案： 【B】 [解]闭合面外的电荷对穿过闭合面的电通量无贡献，或者说， 闭合面外的电荷产生的电场，穿过闭合面的电通量的代数和为零；移动点电荷，会使电荷重 新分布，或者说改变电荷的分布，因此改变了 O 点的场强。 2．半径为 R 的均匀带电球面上，电荷面密度为 ，在球面上取小面元 S ，则 S 上的电 荷受到的电场力为[ ]。
y a/ 2
y a / 2 处电场最强。
4． 如图所示， 在一无限长的均匀带点细棒旁垂直放置一均匀带电的细棒 MN 。 且二棒共面， 若二棒的电荷线密度均为 ，细棒 MN 长为 l ，且 M 端距长直细棒也为 l ，那么细棒 MN 受到的电场力为 。
答案：
[解] 坐标系建立如图： MN 上长为 dx 的元电荷 dq dx 受力 dF Edq 。 无限长带电直线场强 E
2 2 dx ln 2 ；方向沿 x 轴正向。 2 0 x 2 0
根据叠加原理， 圆心处场强可以看成是半径为 R ,电荷线密度为 的均匀带电园环 （带 电量为 Q1 2R ） 在圆心处产生的场强 E1 与放在空隙处长为 l ， 电荷线密度为 的均 匀带电棒（可以看成是点电荷 q l ）在圆心产生的场强 E 2 的叠加。即：

《大学物理I 》作业 No.03 角动量 角动量守恒定律 （A 卷）班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题[ ]1、一质点沿直线做匀速率运动时，(A) 其动量一定守恒，角动量一定为零。

(B) 其动量一定守恒，角动量不一定为零。

(C) 其动量不一定守恒，角动量一定为零。

(D) 其动量不一定守恒，角动量不一定为零。

答案：B答案解析：质点作匀速直线运动，很显然运动过程中其速度不变，动量不变，即动量守恒；根据角动量的定义v m r L⨯=，质点的角动量因参考点（轴）而异。

本题中，只要参考点（轴）位于质点运动轨迹上，质点对其的角动量即为零，其余位置均不会为零。

故(B)是正确答案。

[ ]2. 两个均质圆盘A 和B 密度分别为A ρ和B ρ，若A ρ>B ρ，两圆盘质量与厚度相同，如两盘对通过盘心且垂直于盘面的轴的转动惯量各为A J 和B J ，则 (A) A J >B J(B) B J >A J(C) A J ＝B J(D) A J 、B J 哪个大，不能确定答案：B答案解析：设A 、B 联盘厚度为d ，半径分别为A R 和B R ，由题意，二者质量相等，即B B A A d R d R ρπρπ22=因为B A ρρ>，所以22B A R R <，由转动惯量221mR J =，则B A J J <。

[ ]3．对于绕定轴转动的刚体，如果它的角速度很大，则 (A) 作用在刚体上的力一定很大 (B) 作用在刚体上的外力矩一定很大(C) 作用在刚体上的力和力矩都很大 (D) 难以判断外力和力矩的大小答案：D 答案解析：由刚体质心运动定律和刚体定轴转动定律知：物体所受的合外力和合外力矩只影响物体运动的加速度和角加速度，因此无法通过刚体运动的角速度来判断外力矩的大小，正如无法通过速度来判断物体所受外力的大小一样。

大学物理力学一、二章作业答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 质点运动学一、选择题1、一质点在xoy 平面内运动，其运动方程为2,ct b y at x +==，式中a 、b 、c 均为常数。

当运动质点的运动方向与x 轴成450角时，它的速率为[ B ]。

A ．a ；B ．a 2；C ．2c ；D ．224c a +。

2、设木块沿光滑斜面从下端开始往上滑动，然后下滑，则表示木块速度与时间关系的曲线是图1-1中的[ D ]。

3、一质点的运动方程是j t R i t R rωωsin cos +=，R 、ω为正常数。

从t ＝ωπ/到t =ωπ/2时间内该质点的路程是[ B ]。

A ．2R ；B ．R π；C ． 0；D ．ωπR 。

4、质量为0.25kg 的质点，受i t F =(N)的力作用，t =0时该质点以v=2j m/s 的速度通过坐标原点，该质点任意时刻的位置矢量是[ B ]。

A ．22t i +2j m ； B ．j t i t2323+m ；C ．j t i t343243+； D ．条件不足，无法确定。

二、填空题1、一质点沿x 轴运动，其运动方程为225t t x -+=（x 以米为单位，t 以秒为单位）。

质点的初速度为 2m/s ，第4秒末的速度为 -6m/s ，第4秒末的加速度为 -2m/s 2 。

2、一质点以π（m/s ）的匀速率作半径为5m 的圆周运动。

该质点在5s 内的平均速度的大小为 2m/s ，平均加速度的大小为 22m /5s π 。

3、一质点沿半径为0.1m 的圆周运动，其运动方程为22t +=θ（式中的θ以弧度计，t 以秒计），质点在第一秒末的速度为 0.2m/s ，切向加速度为 0.2m/s 2 。

4、一质点沿半径1m 的圆周运动，运动方程为θ=2+3t 3，其中θ以弧度计，t 以秒计。

T =2s 时质点的切向加速度为 36m/s 2 ；当加速度的方向和半径成45º角时角位移是 38rad 。

dt dx dt
dx
K
0
v0 K
K
答案 (1)3°36′；(2)0.078
解析 (1)轮胎不受路面左右方向的力，而法向力应在水平方向上．
因而有 Nsin θ＝mv21，Ncos θ＝mg，所以 tan θ＝ v21 ，代入数据可得θ＝3°36′．
R
Rg
(2)当有横向运动趋势时，轮胎与地面间有摩擦力，最大值为μN′，这里 N′为该时刻地面对车的支
Rcot α． at
(2)S＝1att2＝1Rcot α． 22
2－4 2－5
答案
R－b cc
解析 v＝s′＝b＋ct，at＝c，an＝vR2＝(b＋Rct)2，令 at＝an，得 t＝
R－b． cc
答案 北偏东 19.4°，170 km/h
解析 设下标 A 指飞机，F 指空气，E 指地面，由题可知：
v0 v
0
作业 2
ABBCF
2－2
(1)gsin θ；gcos θ；(2)－g；2 3v2；(3)v0＋bt； 2 3g
b2＋(v0＋bt)4；(4)1ct3；2ct；c2t4；(5)69.8 m/s
R2
3
R
2－3 答案 (1) Rcot α；(2)1Rcot α
at
2
解析 (1)物体的总加速度 a 为 a＝at＋an，tan α＝aant＝(aattt)2＝aRtt2，t＝ R
解析 (1)dx＝vdt，dx＝vdt＝v，adx＝vdv， adx ＝ vdv ， (－kx)dx ＝ vdv ，－1kx2＝1v2＋C，因
dv dv a
22
为质点静止于 x＝x0，所以 C＝－1kx20，所以 v＝± k(x20－x2)． 2

作业 10 稳恒磁场四1.载流长直螺线管内充满相对磁导率为r μ的均匀抗磁质，则螺线管内中部的磁感应强度B 和磁场强度H 的关系是[ ]。

A. 0B H μ>B. r B H μ=C. 0B H μ=D. 0B H μ< 答案：【D 】解：对于非铁磁质，电磁感应强度与磁场强度成正比关系H B r μμ0=抗磁质：1≤r μ，所以，0B H μ<2.在稳恒磁场中，关于磁场强度H →的下列几种说法中正确的是[ ]。

A. H →仅与传导电流有关。

B.若闭合曲线内没有包围传导电流，则曲线上各点的H →必为零。

C.若闭合曲线上各点H →均为零，则该曲线所包围传导电流的代数和为零。

D.以闭合曲线L 为边界的任意曲面的H →通量相等。

答案：【C 】解：安培环路定理∑⎰=⋅0I l d H L ρρ，是说：磁场强度H ρ的闭合回路的线积分只与传导电流有关，并不是说：磁场强度H ρ本身只与传导电流有关。

A 错。

闭合曲线内没有包围传导电流，只能得到：磁场强度H ρ的闭合回路的线积分为零。

并不能说：磁场强度H ρ本身在曲线上各点必为零。

B 错。

高斯定理0=⋅⎰⎰SS d B ρρ，是说：穿过闭合曲面，场感应强度B ρ的通量为零，或者说，.以闭合曲线L 为边界的任意曲面的B ρ通量相等。

对于磁场强度H ρ，没有这样的高斯定理。

不能说，穿过闭合曲面，场感应强度H ρ的通量为零。

D 错。

安培环路定理∑⎰=⋅0I l d H L ρρ，是说：磁场强度H ρ的闭合回路的线积分等于闭合回路包围的电流的代数和。

C 正确。

3.图11-1种三条曲线分别为顺磁质、抗磁质和铁磁质的B H -曲线，则Oa 表示 ；Ob 表示 ；Oc 表示 。

答案：铁磁质；顺磁质； 抗磁质。

图中Ob （或4.某铁磁质的磁滞回线如图11-2 所示，则'Ob ）表示 ；Oc （或'Oc ）表示 。

答案：剩磁；矫顽力。

5.螺线环中心周长10l cm =，环上线圈匝数300N =，线圈中通有电流100I mA =。

吗？
p
解：（1）循环过程中，AB 为吸热过程，CD 为放热过程
A
B
D
C
23
O
图 6-11
V
大学物理练习册—热力学
η = 1− QCD
=1−
m M mol
C p (TD
− TC )
= 1− TC
− TD
= 1− TC (1− TD TC )
Q AB
m M mol
Cp
(TB
−TA
)
TB −TA
TB (1− TA TB )
量CV=3R，求该理想气体在ab过程中的摩尔热容量（用R表示）。
解：设理想气体在 ab 过程中的摩尔热容量为 Cab ，在一微小过程中 p
d Q = Cab d T
（1）
b
由热力学第一定律有 a
d Q = d E + d A = CV d T + p dV
（2） O
V
由(1)、(2)得
C ab
= CV
J
A = Q1 − Q2 = 5.35×103 − 4.01×103 = 1.34×103 J
6-11 一定量的理想气体，经历如图 6-11 所示循环过程，其中AB和CD为等压过程，BC和DA为绝热过程。
已知B点的温度为TB=T1，C点的温度为TC=T2。（1）证明其效率为η
= 1 − T2 T1
；（2）该循环是卡诺循环
∫ ∫ AT =
V2 p dV =
V1
V2 V1
m M V mol
RT1 dV
=
m M mol
RT1
ln
V2 V1
=
p1V1 ln

方向向下。
T1 m1 ( g a1 ) 0.2 (9.8 1.96) 1.57 N 1 T2 T1 0.785 N 2 m g T2 0.1 9.8 0.785 a2 2 1.95 m s 2 m2 0.1
方向向下。
a3
方向向上。
m3 g T2 0.05 9.8 0.785 5.9 m s 2 m3 0.05
5
物体受力： 真实力：重力 mg, 、斜面对它的正压力 N 惯性力： ma0
mg N ( ma0 ) mar
mgsin ma0sin mar mgcos N ma0cos 0
解得
N m ( g 0a) c o s; ar (g a0 ) sin
A

mg N ma
x 方向： mg sin max m(ar a0 sin ) y 方向： ma y N mg cos ma0 cos 解得
N m ( g 0a) c o s; ar (g a0 ) sin
解法二： 以升降机为参考系（非惯性系） ，建立坐标系如图，
解 当雨滴均匀运动时 得 所以当速率为 4.0 m s 时
1
mg k v 2 k mg / 25
F ma mg k v 2 mg
得
16 9 mg mg 25 25 a 9 g / 25
12. 2-12 质量为 m 的物体系于长度为 R 的绳子的一个端点上，在竖直平面内绕 绳子另一端点（固定）作圆周运动．设时刻物体瞬时速度的大小为 ，绳子 与竖直向上的方向成 θ 角，如图所示。(1) 求ｔ时刻绳中的张力 T 和物体的 切向加速度 at；(2) 说明在物体运动过程中 at 的大小和方向如何变化？

x＋R， R
令dФ＝0，得Ф最大时 x＝1( 5－1)R．
dx
2
24－4 答案 μ0 ·I2(R＋d)(1＋π)－RI1，方向⊙
2π
R(R＋d)
解析 圆电流产生的磁场 B1＝μ20RI2，方向⊙，长直导线电流的磁场 B2＝2μπ0IR2，方向⊙，导体管电流
第 1 页(共 15 页)
产 生 的 磁 场 ， B3 ＝ μ0I1 ， 方 向 ， 所 以 ， 圆 心 Ｏ 点 处 的 磁 感 强 度 B ＝ B1 ＋ B2 － B3 ＝ 2π(d＋R)
B＝2Sρgtan α≈9.35×10－3 T． I
26－4 答案 πkωBR5，方向在纸面内且垂直 B 向上 5
解析 在圆盘上取一个半径为 r、宽度为 dr 的圆环，其环上电荷为 dq＝σ2πrdr，圆环以角速度ω旋 转，其圆电流为 dI＝σrωdr，其磁矩大小为 dm＝πr2dI＝πr2(kr)ωrdr，则圆环上电流所受的磁力矩为
28－4 答案 0.01 T
28－4
解析
εi＝|ddФt |，i＝Rεi＝R1|ddФt |，而
i＝dq，得 dt
dq＝idt＝1|dФ|， R
Q dq ＝1
0
R
0
dФ，Q＝1Ф， R
Ф＝RQ＝π×10－5 Wb，因为Ф＝πr2B，所以 B＝0.01 T．
答案 －μ0Ivln a＋b，方向为 N→M，μ0Ivln a＋b
dM＝Bdm＝πkωr4dr，所以，圆盘所受总磁力矩 M＝ dM ＝ R πkωr4dr＝πkωBR5，M 的方向在纸面
0
5
内且垂直 B 向上．
26－5 答案 (1)πa2BI0sin2 ωt；(2)1BI0ωπa2 2

A在时间t内作匀加速运动，t秒末的速度vA＝at．当子弹射入B时，B将加速
而A则以vA的速度继续向右作匀速直线运动．
vA＝at＝6 m/s
取A、B和子弹组成的系统为研究对象，系统所受合外力为零，故系统的动
量守恒，子弹留在B中后有
mv 0 mAv A (m mB )v B
vB

mv 0 mAv A m mB
量m1=
1m 2
的小球.将右边小球约束,使之不动. 使左边两小球绕竖直轴对称匀速
地旋转, 如图所示.则去掉约束时, 右边小球将向上运动, 向下运动或
保持不动?说明理由.
答：右边小球不动
理由：右边小球受约束不动时，

在左边对任一小球有
1m 2
1
ｍ2
m
m
式中T1为斜悬绳中张 力，这时左边绳竖直
T1 cos m1g 0
质量以及滑轮与其轴之间的摩擦都可忽略不
计，绳子不可伸长，m1与平面之间的摩擦也
可不计，在水平外力F的作用下，物体m1与
F
m1
T
m2
F m2 g
m2的加速度a＝___m__1____m__2___，
绳中的张力T＝_m__1m__2m__2_(_F____m_1_g_)_．
4.质量相等的两物体A和B，分别固定在弹簧的两端， A 竖直放在光滑水平面C上，如图所示．弹簧的质量 与物体A、B的质量相比，可以忽略不计．若把支持 面C迅速移走，则在移开的一瞬间，
dx dt dx
10 6x2 2 vdv
v
2 vdv
4 (10 6x2 )dx v 13m/ s
dx 0
0
解2：用动能定理，对物体

行于ab边，bc的长度为l。当金属框架绕ab边以匀角速度w 转动时，
aUbcc=回__路__中__-的_1_感_B_应_w_l电_2_动__势。 = 0
2
，a、c两点间的电势差Ua –
B
解：任意时刻通过三角形磁通量为零，所以 回路的感应电动势为零。
b
l c
ab bc ca 0
w
- ca
5．载有电流的I长直导线附近，放一导体半圆环MeN与
长直导线共面，且端点MN的连线与长直导线垂直。半 圆环的半径为b，环心O与导线相距a。设半圆环以速度
平行导线平移，求半圆环内感应电动势的大小和方向以
及MN两端的电压UM -UN。
解(1) 弧MN 直NM 0
弧MN 直MN ab Bdx ab 0 I ln a b 2π a b
边重合。求：（1）任意时刻矩形线框内的动生电动
势；（2）任意时刻矩形线框内的感应电动势。
dΦ B dS Bldx
ab
Bldx
ab 0I (t ) ldx
a
a
0I
(
t2)πxt
ln
a
b
I (t )
a
b
l
动
dΦ dt
0I (t)2πln a b
2π
a
a
18
5．如图所示，真空中一长直导线通有电流I=I（t），
3．两根无限长平行直导线载有大小相等方向相 反的电流I，I 以 dI/dt 的变化率增长，一矩形线 圈位于导线平面内(如图)，则
A． 线圈中无感应电流； B． 线圈中感应电流为顺时针方向； C． 线圈中感应电流为逆时针方向； D．线圈中感应电流方向不确定。
I
I
4．在无限长的载流直导线附近放置一矩形闭合线圈， 开始时线圈与导线在同一平面内，且线圈中两条边与导 线平行，当线圈以相同的速率作如图所示的三种不同方 向的平动时，线圈中的感应电流（ ）

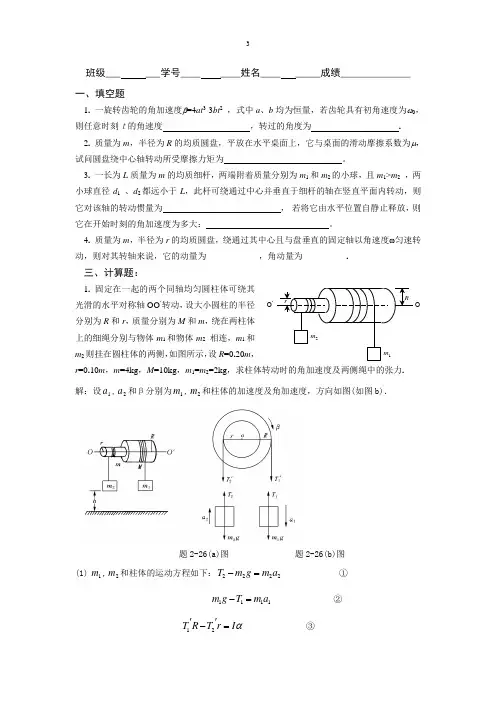
班级___ ___学号____ ____姓名____ _____成绩______________ 一、填空题1. 一旋转齿轮的角加速度β=4at 3-3bt 2 ，式中a 、b 均为恒量，若齿轮具有初角速度为ω0，则任意时刻ｔ的角速度 ，转过的角度为 .2. 质量为m ，半径为R 的均质圆盘，平放在水平桌面上，它与桌面的滑动摩擦系数为μ，试问圆盘绕中心轴转动所受摩擦力矩为 。

3. 一长为L 质量为m 的均质细杆，两端附着质量分别为m 1和m 2的小球，且m 1>m 2 ，两小球直径d 1 、d 2都远小于L ，此杆可绕通过中心并垂直于细杆的轴在竖直平面内转动，则它对该轴的转动惯量为 ， 若将它由水平位置自静止释放，则它在开始时刻的角加速度为多大： 。

4. 质量为m ，半径为r 的均质圆盘，绕通过其中心且与盘垂直的固定轴以角速度ω匀速转动，则对其转轴来说，它的动量为____________，角动量为__________.三、计算题：1. 固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴OO ’转动，设大小圆柱的半径分别为R 和r ，质量分别为M 和m ，绕在两柱体上的细绳分别与物体m 1和物体m 2 相连，m 1和m 2则挂在圆柱体的两侧，如图所示，设R =0.20m ，r =0.10m ，m =4kg ，M =10kg ，m 1=m 2=2kg ，求柱体转动时的角加速度及两侧绳中的张力. 解：设1a ,2a 和β分别为1m ,2m 和柱体的加速度及角加速度，方向如图(如图b)．题2-26(a)图 题2-26(b)图(1) 1m ,2m 和柱体的运动方程如下：2222a m g m T =- ①1111a m T g m =- ②12T R T r I α''-= ③rRO ’Om 2m 1式中 112221,,,T T T T a r a R αα''==== 而 222121mr MR I += 由上式求得122212222220.220.129.811100.2040.1020.2020.10226.13rad s Rm rm gI m R m r β--=++⨯-⨯=⨯⨯⨯+⨯⨯+⨯+⨯=⋅(2)由①式 22220.10 6.1329.820.8T m r m g α=+=⨯⨯+⨯=N 由②式11129.820.2. 6.1317.1T m g m R α=-=⨯-⨯⨯=N2. 计算题3-13图所示系统中物体的加速度．设滑轮为质量均匀分布的圆柱体，其质量为M ，半径为r ，在绳与轮缘的摩擦力作用下旋转，忽略桌面与物体间的摩擦，设1m ＝50kg ，2m ＝200 kg,M ＝15 kg, r ＝0.1 m解: 分别以1m ,2m 滑轮为研究对象，受力图如图(b)所示．对1m ,2m 运用牛顿定律，有a m T g m 222=- ① a m T 11= ②对滑轮运用转动定律，有α)21(212Mr r T r T =- ③又， αr a = ④联立以上4个方程，得 2212s m 6.721520058.92002-⋅=++⨯=++=M m m g m a题3-13(a)图 题3-13(b)图3. 如图质量为M ，长为L 的均匀直杆可绕O 轴在竖直平面内无摩擦地转动，开始时杆处于自由下垂位置，一质量为m 的弹性小球水平飞来与杆下端发生完全弹性碰撞，若M >3m ，且碰撞后，杆上摆的最大角度为θ=30，则求：(A)小球的初速度v 0，(B)碰撞过程中杆给小球的冲量. （教材）解: (1)设小球的初速度为0v ，棒经小球碰撞后得到的初角速度为ω，而小球的速度变为v ，按题意，小球和棒作弹性碰撞，所以碰撞时遵从角动量守恒定律和机械能守恒定律，可列式：mvl I l mv +=ω0 ①2220212121mv I mv +=ω ② 上两式中231Ml I =，碰撞过程极为短暂，可认为棒没有显著的角位移；碰撞后，棒从竖直位置上摆到最大角度o30=θ，按机械能守恒定律可列式：)30cos 1(2212︒-=lMg I ω ③ 由③式得 2121)231(3)30cos 1(⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-=l g I Mgl ω 由①式 mlI v v ω-=0 ④ 由②式 mI v v 2202ω-= ⑤所以 22001)(2ωωmv ml I v -=-求得glmM m m Ml ml I l v +-=+=+=31232(6)311(2)1(220ωω(2)相碰时小球受到的冲量为 ⎰-=∆=0d mv mv mv t F由①式求得 ωωMl l I mv mv t F 31d 0-=-=-=⎰gl M 6)32(6--=负号说明所受冲量的方向与初速度方向相反．m v MOL。

引言概述：正文内容：一、力学1.牛顿三定律的应用解释牛顿第一定律的原理，并给出实际应用的例子。

找出物体的质心，并计算其位置坐标。

利用牛顿第二定律计算物体所受的合力和加速度。

2.作用力和反作用力解释作用力和反作用力的概念，并给出相关案例。

计算物体所受的作用力和反作用力的大小和方向。

应用牛顿第三定律解决实际问题。

3.动能和动能守恒计算物体的动能，并解释其物理意义。

说明动能守恒定律的原理，给出相应的实例。

利用动能守恒定律解决能量转化问题。

4.力学振动和波动解释简谐振动的特征和公式，并计算相关参数。

介绍波的基本概念和性质，并给出波动方程的解释。

分析机械波的传播和干涉现象。

5.万有引力和天体运动介绍万有引力定律的公式和原理。

计算引力和重力的大小和方向。

描述行星运动的轨道和速度，并解释开普勒定律。

二、热学1.理想气体定律和状态方程解释理想气体和实际气体的区别。

推导理想气体定律，解释每个变量的含义。

计算理想气体的性质和状态。

2.热力学第一定律和功解释热力学第一定律的原理，并给出相应公式。

计算系统的内能变化和热量的传递。

分析功的定义和计算方法。

3.热力学第二定律和熵介绍热力学第二定律的概念和表述方法。

计算熵的变化和热力学过程的可逆性。

解释热力学第二定律对能量转化的限制。

4.热传导和热辐射分析热传导的机制和方法，并计算热传导的速率。

描述热辐射的特性和功率密度。

利用热传导和热辐射解决实际问题。

5.热力学循环和效率给出常见热力学循环的定义和示意图。

计算热力学循环的效率和功率输出。

分析热力学循环的改进方法和应用。

三、电磁学1.静电场和电势描述静电场的特性和形成原理，并给出电势的定义。

计算电场和电势的大小和方向。

利用电势差解决电荷移动和电场中的工作问题。

2.电场和电场强度推导库仑定律和电场强度公式。

计算由点电荷、带电导体和带电平面产生的电场。

分析电场中带电粒子受力和加速度。

3.电容和电容器解释电容和电容器的概念和原理，并计算其电容量。

v d dr tt22i1 j3 (m)/s
a d dvtt28j(m2/)s
大学物理
3、质点作直线运动，加速度 a2Asint，已知
t 0时质点初始状态为x 0
动学方程为xAsi n .t0
、v0 A、该质点运
解：
vv0
t
a
0
dt A
t2As
0
intdt
AAcostA
Acost
t
t
即 a2ct, t a 2c
vx vy
vvx 2vy 2a24c2t22a
大学物理
5、一飞机在跑道上跑过500米后，即升空，如果它在跑
前是静止的，以恒定加速度运动，升空前跑了30秒，则
当它升空时的速度为 v 100 m/s
.
3
解： x 1 at 2 2
a2t2x2 352 000190m2/s
答：B
v(m / s)
2
0到7秒的位移为：
0
r 2 22 2 2 2 2 3 1 i 3 .5 im1
坐标为：x23 .55 .5 m
t(s) 24 5 7
大学物理
3、一质点沿x轴运动的规律是 xt24t5,其中x以m 计，t以s计，则前3s内它的位移和路程分别是
(A)位移和路程都是3m. (B) 位移和路程都是-3m .
dvy dy
则
a vy
dvy dy
kvy2
分离变量得 :
dvy kdy vy
两边积分得 :
v dvy
y
k dy
v v0 y
0
v v0eky
大学物理
3、一质点沿半径为1 m 的圆周运动，运动方程
为 23t，3 式中以弧度计，t以秒计，求：(1) t＝2 s

理想气体状态方程5-1一容器内储有氧气，其压强为1.01⨯105Pa ，温度为270C ，求：（1）气体分子的数密度；（2）氧气的质量密度；（3）氧分子的质量；（4）分子间的平均距离（设分子均匀等距分布）。

解：(1) nkT p =，325235/m 1044.2)27273(1038.11001.1⨯=+⨯⨯⨯==-kT p n (2) R M mT pV mol= ，335mol kg/m 30.1)27273(31.810321001.1=+⨯⨯⨯⨯===∴-RT pM V m ρ (3) n m O 2=ρ ， kg 1033.51044.230.126252-⨯=⨯==∴nm O ρ(4) m 1045.31044.21193253-⨯=⨯==n d 5-2在容积为V 的容器中的气体，其压强为p 1，称得重量为G 1。

然后放掉一部分气体，气体的压强降至p 2，再称得重量为G 2。

问在压强p 3下，气体的质量密度多大？ 解： 设容器的质量为m ，即放气前容器中气体质量为m g G m -=11，放气后容器中气体质量为m gG m -=22。

由理想气体状态方程有RT M m g G RT M m V p mol 1mol 11-==， RT M mg G RT M m V p mol2mol 22-==上面两式相减得V p p G G g M RT )()(1212mol -=-， )(1212m o lp p G G gV RT M --= 当压强为3p 时， 121233mol 3p p G G gV p RT p M V m --⋅===ρ 压强、温度的微观意义5-3将2.0⨯10-2kg 的氢气装在4.0⨯10-3m 2的容器中，压强为3.9⨯105Pa ，则氢分子的平均平动动能为多少？ 解： RT M mpV mol=，mR pV M T mol=∴J 1088.331.8102100.4109.31021038.123232322235323mol -----⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯===mR pV M k kT t ε 5-4体积33m 10-=V ，压强Pa 105=p 的气体分子平均平动动能的总和为多少？ 解：kT Nt 23=∑ε，其中N 为总分子数。

习题一一、选择题1．如图所示，半径为R 的圆环开有一小空隙而形成一圆弧，弧长为L ，电荷Q -均匀分布其上。

空隙长为()L L R ∆∆<<，则圆弧中心O 点的电场强度和电势分别为 [ ] （Ａ）200,44Q L Qi R L Rπεπε-∆-； （Ｂ）2200,84Q L Qi R L Rπεπε-∆-； （Ｃ）200,44Q L Qi R L Rπεπε∆； （Ｄ）200,44Q L Q Li R L RLπεπε-∆-∆。

答案：A解：闭合圆环中心场强为0，则圆弧产生的场强与空隙在圆心处产生的场强之和为0。

由于空隙 ∆l 非常小，可视为点电荷，设它与圆弧电荷密度相同，则所带电荷为/Q L L -∆，产生的场强为204Q L i R L πε∆，所以圆弧产生的场强为204OQ LE i R Lπε-∆=；又根据电势叠加原理可得04O Q U Rπε-= .2．有两个电荷都是＋q 的点电荷，相距为2a 。

今以左边的点电荷所在处为球心，以a 为半径作一球形高斯面。

在球面上取两块相等的小面积S 1和S 2，其位置如图所示。

设通过S 1和S 2的电场强度通量分别为1Φ和2Φ，通过整个球面的电场强度通量为S Φ，则［ ］ （A ）120, /S q εΦ>ΦΦ=； （B ）120, 2/S q εΦ<ΦΦ=；（C ）120, /S q εΦ=ΦΦ=； （D ）120, /S q εΦ<ΦΦ=。

答案：D解：由高斯定理知0Φ=S q 。

由于面积S 1和S 2相等且很小，场强可视为均匀。

根据场强叠加原理，120,0E E =<，所以12Φ0,Φ0=>。

3．半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为 [ ]答案：B2∝2∝rRr R解：由高斯定理知均匀带电球体的场强分布为()302041 ()4qrr R R E q r R r πεπε⎧<⎪⎪=⎨⎪>⎪⎩，所以选（B ）。

第十二章 机械波12-1 一平面简谐纵波沿着线圈弹簧传播．设波沿着x 轴正向传播，弹簧中某圈的最大位移为3.0 cm ，振动频率为25 Hz ，弹簧中相邻两疏部中心的距离为24 cm ．当t = 0时，在x = 0处质元的位移为零并向x 轴正向运动．试写出该波的表达式．（答案：]21)6/(50cos[100.32π--π⨯=-x t y (SI)）12-2 一平面简谐波沿x 轴正向传播，波的振幅A = 10 cm ，波的角频率ω = 7π rad/s.当t = 1.0 s 时，x = 10 cm 处的a 质点正通过其平衡位置向y 轴负方向运动，而x = 20 cm 处的b 质点正通过y = 5.0 cm 点向y 轴正方向运动．设该波波长λ >10 cm ，求该平面波的表达式．（答案：]3112.07cos[1.0π+π-π=x t y (SI)）12-3 一平面简谐波沿x 轴正向传播，其振幅为A ，频率为ν ，波速为u ．设t = t ＇时刻的波形曲线如图所示．求(1) x = 0处质点振动方程；(2) 该波的表达式．（答案：]21)(2cos[π+'-π=t t A y ν；]21)/(2cos[π+-'-π=u x t t A y ν）12-4 一列平面简谐波在媒质中以波速u = 5 m/s 沿x 轴正向传播，原点O 处质元的振动曲线如图所示．(1) 求解并画出x = 25 m 处质元的振动曲线． (2) 求解并画出t = 3 s 时的波形曲线．（答案：)321cos(1022π-π⨯=-t y ，(SI)，图略；)10/cos(1022x y π-π⨯=-，(SI)，图略）12-5 已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程； (2) 求x 1，x 2两点间的振动相位差；(3) 求x 1点在t = 4 s 时的振动位移．（答案：)7.3125cos(25.010-==t y x (SI)，)25.9125cos(25.025-==t y x (SI)；-5.55 rad ；0.249 m ）12-6 一横波方程为 )(2cosx ut A y -π=λ， 式中A = 0.01 m ，λ = 0.2 m ，u = 25 m/s ，求t = 0.1 s 时在x = 2 m 处质点振动的位移、速度、加速度．（答案：-0.01 m ，0 m/s ，6.17×103 m/s 2）xu O t =t ′y12-7 如图，一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播，已知A 点的振动方程为 t y π4c o s 1032-⨯= (SI)． (1) 以A 点为坐标原点写出波的表达式；(2) 以距A 点5 m 处的B 点为坐标原点，写出波的表达式．（答案：)]20/([4cos 1032x t y +π⨯=- (SI)；])20(4cos[1032π-+π⨯=-xt y (SI)）12-8 一平面简谐波沿x 轴正向传播，其振幅和角频率分别为A 和ω ，波速为u ，设t = 0时的波形曲线如图所示．(1) 写出此波的表达式． (2) 求距O 点分别为λ / 8和3λ / 8 两处质点的振动方程．(3) 求距O 点分别为λ / 8和3λ / 8 两处质点在t = 0时的振动速度．（答案：]21)/(cos[π+-=u x t A y ωω；)4/cos(π+=t A y ω，)4/cos(π-=t A y ω；2/2ωA -，2/2ωA ）12-9 如图，一平面简谐波沿Ox 轴传播，波动表达式为])/(2cos[φλν+-π=x t A y (SI)，求 (1) P 处质点的振动方程；(2) 该质点的速度表达式与加速度表达式．（答案：])/(2cos[φλν++=L t A y P π；])/(2sin[2φλνπν++π-=L t A P v ，])/(2cos[422φλνν++ππ-=L t A a P ）12-10 某质点作简谐振动，周期为2 s ，振幅为0.06 m ，t = 0 时刻，质点恰好处在负向最大位移处，求(1) 该质点的振动方程； (2) 此振动以波速u = 2 m/s 沿x 轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；(3) 该波的波长．（答案： )cos(06.00ππ+=t y (SI)；])21(cos[06.0ππ+-=x t y (SI)；4m ）12-11 图示一平面简谐波在t = 0 时刻的波形图，求 (1) 该波的波动表达式； (2) P 处质点的振动方程．（答案：]2)4.05(2cos[04.0π--π=x t y (SI)； )234.0cos(04.0ππ-=t y P (SI)）ABxuxuOyOP(m) -12-12 图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图．已知波速为u ，求(1) 坐标原点处介质质点的振动方程；(2) 该波的波动表达式．（答案：)218/cos(0π-π=t A y (SI)；]21)16016(2cos[π-+π=x t A y (SI)）12-13 如图所示为一平面简谐波在t = 0 时刻的波形图，设此简谐波的频率为250 Hz ，且此时质点P 的运动方向向下，求(1) 该波的表达式；(2) 在距原点O 为100 m 处质点的振动方程与振动速度表达式． （答案：]41)200250(2cos[π++π=x t A y (SI)； )45500cos(1π+π=t A y ，)45500cos(500π+ππ-=t A v (SI)）12-14 如图所示，一简谐波向x 轴正向传播，波速u = 500 m/s ，x 0 = 1 m, P 点的振动方程为)21500cos(03.0π-π=t y (SI).(1) 按图所示坐标系，写出相应的波的表达式； (2) 在图上画出t = 0时刻的波形曲线．（答案：)21500cos(03.0x t y π-π+π= (SI)；x x y π=sin 03.0)0,(）12-15 一平面简谐波，频率为300 Hz ，波速为340 m/s ，在截面面积为3.00×10-2 m 2的管内空气中传播，若在10 s 内通过截面的能量为2.70×10-2 J ，求(1) 通过截面的平均能流； (2) 波的平均能流密度；(3) 波的平均能量密度．（答案：2.70×10-3 J/s ；9.00×10-2 J /(s ·m 2)；2.65×10-4 J/m 3）12-16 已知点波源向外发射球面波，波速为v 0，波源振动的角频率为ω ，初相为零．距波源为 1 m 处质点的振幅为A 0．设介质均匀且不吸收能量，试写出球面波的波动表达式．（答案：)]}/([cos{)/(0v r t r A y -=ω (SI)）12-17 如图所示，S 1，S 2为两平面简谐波相干波源．S 2的相位比S 1的相位超前π/4 ，波长λ = 8.00 m ，r 1 = 12.0 m ，r 2 = 14.0 m ，S 1在P 点引起的振动振幅为0.30 m ，S 2在P 点引起的振动振幅为0.20 m ，求P 点的合振幅．（答案：0.464m ）12-18 如图所示，两相干波源在x 轴上的位置为S 1和S 2，其间距离为d = 30 m ，S 1位于坐标原点O ．设波只沿x 轴正负方向传播，单独传播时强度保持不变．x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点．求两波的波长和两波源间最小相位差．（答案：6m ；± π ）12-19 图中A 、B 是两个相干的点波源，它们的振动相位差为π（反相）．A 、B 相距 30 cm ，观察点P 和B 点相距 40 cm ，且AB PB ⊥．若发自A 、B 的两波在P 点处最大限度地互相削弱，求波长最长能是多少．（答案：10 cm ）12-20 如图所示，两列相干波在P 点相遇．一列波在B 点引起的振动是 t y π⨯=-2cos 103310 (SI)；另一列波在C 点引起的振动是)212cos(103320π+π⨯=-t y (SI)； 令=BP 0.45 m ，=CP 0.30 m ，两波的传播速度u = 0.20 m/s ，不考虑传播途中振幅的减小，求P 点的合振动的振动方程．（答案：)212cos(1063ππ-⨯=-t y ）12-21 一平面简谐波沿Ox 轴正方向传播，波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播，波的表达式为 )/(2cos 2λνx t A y +π= 求：(1) x = λ /4 处介质质点的合振动方程；(2) x = λ /4 处介质质点的速度表达式．（答案：)212cos(π+π=t A y ν；)2cos(2πππ+=t A v νν）12-22 一驻波中相邻两波节的距离为d = 5.00 cm ，质元的振动频率为ν =1.00×103 Hz ，求形成该驻波的两个相干行波的传播速度u 和波长λ ．（答案：u = 100 m/s ，λ = 0.10 m ）12-23 两波在一很长的弦线上传播，其表达式分别为：)244(31cos 1000.421t x y -π⨯=- (SI))244(31cos 1000.422t x y +π⨯=- (SI)PSS求： (1) 两波的频率、波长、波速； (2) 两波叠加后的节点位置； (3) 叠加后振幅最大的那些点的位置．（答案：ν = 4 Hz ，λ = 1.50 m ，u = λν = 6.00 m/s ；)21(3+±=n x m , n = 0，1，2，3, …； 4/3n x ±= m , n = 0，1，2，3, …）12-24 设入射波的表达式为 )(2cos 1TtxA y +π=λ，在x = 0处发生反射，反射点为一固定端．设反射时无能量损失，求(1) 反射波的表达式； (2) 合成的驻波的表达式；(3) 波腹和波节的位置． （答案：])//(2cos[2π+-π=T t x A y λ；)21/2cos()21/2cos(2ππππ-+=T t x A y λ；波腹位置：λ)21(21-=n x , n = 1, 2, 3, 4,…；波节位置：λn x 21=, n = 1, 2, 3, 4,…）12-25 一弦上的驻波表达式为 t x y ππ⨯=-550c o s )6.1(c o s 1000.32 (SI)．(1) 若将此驻波看作传播方向相反的两列波叠加而成，求两波的振幅及波速； (2) 求相邻波节之间的距离；(3) 求t = t 0 = 3.00×10-3 s 时，位于x = x 0 = 0.625 m 处质点的振动速度．（答案：A = 1.50×10-2 m ，u = 343.8 m/s ；0.625 m ；－46.2m/s ）12-26 在弹性媒质中有一沿x 轴正向传播的平面波，其表达式为)214cos(01.0π-π-=x t y (SI)．若在x = 5.00 m 处有一媒质分界面，且在分界面处反射波相位突变π，设反射波的强度不变，试写出反射波的表达式．（答案：)214cos(01.0π+π+=x t y (SI)）12-27 火车以u = 30 m/s 的速度行驶，汽笛的频率为ν0 = 650 Hz ．在铁路近旁的公路上坐在汽车里的人在下列情况听到火车鸣笛的声音频率分别是多少？ (1) 汽车静止； (2) 汽车以v = 45 km/h 的速度与火车同向行驶．（设空气中声速为V = 340 m/s ） （答案：火车迎面而来713Hz ，火车背离而去597Hz ；汽车在前687Hz ；火车在前619Hz ）12-28 甲火车以43.2 km/h 速度行驶，其上一乘客听到对面驶来的乙火车鸣笛声的频率为512 Hz ；当这一火车过后，听到其鸣笛声的频率为428 Hz ．求乙火车上的乘客听到乙火车鸣笛的频率和乙火车对于地面的速度（设空气中声波的速度为340 m/s ）．（答案：468 Hz ，18.4 m/s ）12-29 一个观察者站在铁路附近，听到迎面开来的火车汽笛声的频率为640 Hz ，当火车驶过他身旁后，听到汽笛声的频率降低为530 Hz ．问火车的时速为多少？（设空气中声速为330 m/s ）（答案：31.0 m /s ）12-30 甲和乙两个声源的频率均为500 Hz．甲静止不动，乙以40 m/s的速度远离甲．在甲乙之间有一观察者以20 m/s的速度向着乙运动．此观察者听到的声音的拍频是多少？（已知空气中的声速为330 m/s）（答案：3.3 Hz）12-31 一人手执一频率为400 Hz的声源以2.0 m/s的速度正对一高墙运动．声音在空气中的速度为330 m/s．此人听到的声音的拍频是多少？（答案：4.88 Hz）。

No.1 运动的描述一、选择题1. 一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一段时间内的平均速度为v，平均速率为v ，它们之间的关系有 [ D ](A) v v v v ==, (B) v v v v =≠, (C) v v v v ≠≠,(D) v v v v ≠=,注意：①平均速度t r∆∆= v ，矢量。

②平均速率t ∆∆=sv ，标量。

③一般情况下，|||r |s ∆≠∆。

④瞬时速度tr ∆∆=→∆0t lim v 。

⑤瞬时速率|v |v=（即瞬时速率是瞬时速度的大小，这与平均速度和平均速率的关系不同） 2. 某物体的运动规律为kt tv -=d d ，式中的k 为大于零的常数。

当t ＝0时，初速为0v ，则速度v 与t 的函数关系是 [ B ](A) 0221v kt v += (B) 0221v kt v +-=注意：①求积分。

3. 一质点在平面上运动，已知质点位置矢量的表示式为j bt i at r 22+=（其中a 、b 为常量）则该质点作 [ B ] (A) 匀速直线运动 (B) 变速直线运动 (C) 抛物线运动 (D) 一般曲线运动 注意：①求导数。

②求运动方程。

4.一运动质点在某瞬时位于矢径),(y x r的端点处，其速度大小为 [ D ]（C ）tr d d( D)22)d d ()d d (ty tx +注意：①即求模长。

二、填空题★1. 一质点的运动方程为SI)(62t t x -=，则在t 由0至4 s 的时间间隔内，质点的位移大小为8m ，在t 由0到4 s 的时间间隔内质点走过的路程为 10 m 。

注意：①陷阱，4秒内并不是一直在往前，中间存在一个先去后返的过程。

2. ()()t t r t r ∆+与为某质点在不同时刻的位置矢量，试在两个图中分别画出三、计算题1.（p36 习题1.6）一质点在xy 平面上运动，运动函数84,22-==t y t x （采用国际单位制）。