2012年下概率论试卷

东莞理工学院（本科）试卷（C 卷）2011 --2012 学年第二学期《概率论与数理统计》试卷（答案）开课单位：计算机学院数学教研室 ，考试形式：闭卷，允许带 计算器 入场一、填空题（共70分 每空21、已知()0.4,()0.5,()0.4,P A P B P A B ===则)(B A P ＝ 0.7 。

2、已知3.0)(7.0)(=-=B A P A P ，，则)(B A P ＝ 0.6 。

3、甲、乙两人独立的对同一目标各射击一次，其命中率分别为0.6 和0.5，现已知目标被命中，则它是乙射中的概率是 85 4、一批产品共有6件正品2件次品，从中不放回任取两件，则两件都是正品的概率为 2815 5、某种动物活到25岁以上的概率为0.8，活到30岁的概率为0.4，则现年25岁的这种动物活到30岁以上的概率是 0.5 。

6、设一电路由三个相互独立且串联的电子元件构成，它们被损坏而发生断路概率均为p ，则电路发生断路的概率是 3)1(1p --。

7、已知某对夫妇有三个小孩，则男孩的个数Y 服从的分布为 )5.0 ,3(B ，恰有两个男孩的概率为83，在已知至少有一个女孩的条件下，至少还有一个男孩的概率为76。

8、已知工厂A B 、生产产品的次品率分别为1%和2%，现从由A B 、的产品分别占60%和40%的一批产品中随机抽取一件，则该产品是次品的概率为 1.4% ；若随机地从这批产品中抽出一件，检验出为次品，则该次品属于A 厂生产的概率是 73 9、指数分布又称为寿命分布，经常用来描述电子器件的寿命。

设某款电器的寿命（单位：小时）的密度函数为⎩⎨⎧>=-其它 ,00 ,002.0)(002.0t e t f t 则这种电器没有用到1000小时就坏掉的概率为21--e ，这种电器的寿命的标准差为 500 小时。

10、设随机变量X 服从参数为λ的泊松分布，}1{}2{===X P X P ，则=EX 2。

第 1 页 共 3 页一、单项选择题（每小题3分，共21分）1．对于事件B A ,，若∅=B A ，则下列说法中正确的是 （ ） A 、B A ,为对立事件B 、0)(=A P 或0)(=B PC 、B A ,互不相容D 、B A ,独立2．设随机变量X 的分布函数为)(x F ，下列说法中错误的是 （ ） A 、)(x F 是不减函数B 、)(x F 必为),(+∞-∞上的连续函数C 、0)(=-∞FD 、1)(≤x F3．设连续型二维随机变量的联合概率密度函数为),(y x f ，则必有 （ ）A 、1),(0≤≤y x fB 、),(y x f 为xOy 平面上的连续函数C 、1),(=⎰⎰+∞∞-+∞∞-dxdy y x f D 、1),(=+∞+∞f4．设Y X ,是两个随机变量，则下式中一定成立的是 （ ）A 、)()()(Y E X E Y X E +=+B 、)()()(Y E X E XY E =C 、)()()(YD X D Y X D +=+ D 、)()()(Y D X D XY D =5．随机变量 n X X X ,,,21 相互独立，服从同一分布，且具有期望和方差，0)(,)(2>==σμk k X D X E ，当n 充分大时，近似服从)1,0(N 的是 （ ）A 、σμn n Xnk k∑=-1B 、21σμn n Xnk k∑=-C 、σμn n Xnk k∑=-1D 、21σμn n Xnk k∑=-6．设4321,,,X X X X 是来自均值为θ的指数分布的样本，其中θ未知， 以下估计量中哪个不是θ的无偏估计量？ （ ） A 、443211X X X X T +++=B 、722343211X X X X T +++=C 、3643211X X X X T +++=D 、5243211X X X X T +++= 7．对于一个原假设为0H 的假设检验问题，有可能犯的第一类错误是指（ ）A 、0H 成立时，检验结果接受0HB 、0H 成立时，检验结果拒绝0HC 、0H 不成立时，检验结果接受0HD 、0H 不成立时，检验结果拒绝0H二、填空题（每小题3分，共24分）1．设C B A ,,为三个事件，则事件“C B A ,,都不发生” 可以用C B A ,,的运算关系表示为 ．2．10片药片中有5片是安慰剂，从中任取2片，其中至少有1片是安慰剂的概率为 ．3．三人独立地去破译一份密码，各人能译出的概率分别为3.0,2.0,1.0， 三人中至少有一人能将此密码译出的概率为 ．第 2 页 共 3 页4．一射击运动员每次射击命中的概率为7.0，以X 表示他首次命中时 累计已射击的次数，则{}3=X P 为 ．5．随机变量X 在4,3,2,1中等可能地取一个值，随机变量Y 在X ~1中 等可能地取一个整数值，则{}4=Y P 为 ． 6．随机变量)2,0(~U X ，则=)(X D ． 7．总体)6(~2χX ，1021,,,X X X 是来自X 的样本，则=)(X D．8．设n X X X ,,,21 是来自正态总体),(2σμN 的样本，X 是样本均值， 则~X ．三、解答题（第1题8分，第2题9分，共17分）1．对以往的数据分析结果表明，当机器调整得良好时，产品的合格率为80%，而当机器发生某种故障时，产品的合格率为30%．每天早上机器开动时，机器调整良好的概率为90%．（1）求每天早上第一件产品是合格品的概率；（2）若某天早上第一件产品是合格品，求此时机器调整良好的概率．2．设随机变量X 具有概率密度⎪⎩⎪⎨⎧<≤<≤-=其它,031,10,1)(x kxx xx f（1）确定常数k ； （2）求()20<<X P ．四、解答题（第1题10分，第2题10分，共20分）1．设随机变量X 与Y 的联合分布律为 求：（1）常数a 值；（2）X 与Y 是否独立？为什么？(3) 设Y X Z +=，求Z 的分布律．第 3 页 共 3 页X （以年计）服从指数分布，概率密度为⎪⎪≤>-0,00,313x x e x．1000800元，试求厂方出售一台设备净赢利的数学期望．五、解答题（第1题8分，第2题10分，共18分）X 具有分布律 )1<<θ为未知参数．,2,1,3321===x x x 求θ的矩估计值．2．某批铁矿石的9个样品中的含铁量，经测定为（%）35 36 36 38 38 39 39 40 41设测定值总体服从正态分布，但参数均未知， （1）求样本均值和样本标准差；（2）在01.0=α下能否接受假设：这批铁矿石的含铁量的均值为39%？ （3554.3)8(005.0=t ）。

概率论与数理统计练习一一、选择题（本大题共7 小题，每小题 3 分，共 21 分）1. 设A ，B 为随机事件, 若P (A )=P (B )>0.5, 则 （ ）(A) A ，B 互不相容； (B) A ，B 非互不相容； (C) A ，B 相互独立； (D) A ，B 非相互独立.2.设2(,4)X N μ ，2(,5)Y N μ ，1(4)p P X μ=≤- ，2(5)p P Y μ=≥+，则（ ）(A) 对任意实数μ，都有12p p =； (B) 对任意实数μ，都有12p p <； (C) 只对μ的个别值，才有12p p = ； (D) 对任意实数μ，都有12p p >；3.己知随机变量X 服从区间[5,10]上的均匀分布, 则 （ ） (A) 2(9)0.3P X <= ； (B) 2(9)0.15P X <=； (C) 2(9)0P X ≤= ； (D)｛7X =｝是不可能事件. 4．对随机变量X ，关于EX ，EX 2合适的值为 （ ） (A)3，8 (B) 3， 10 (C) 3，-8 (D) 3，-105. 已知随机变量X ,Y 相互独立，且都服从标准正态分布，则22X Y +服从( )(A) 自由度为1的2χ分布； (B) 自由度为2的2χ分布； (C) 自由度为1的F 分布；(D) 自由度为2的F 分布.6. 样本(X 1,X 2,X 3)取自总体X ，E (X )=μ，D (X )=2σ，则有 ( ) (A) X 1+X 2+X 3是μ的无偏估计量；(B)1233X X X ++是μ的无偏估计量；(C) 22X 是2σ的无偏估计量；(D) 21233X X X ++⎛⎫ ⎪⎝⎭是2σ的无偏估计量.7. 设总体X 服从二项分布),1(p B ，n X X ,,1 是来自总体X 的一个样本，则)(nkX P ==（ ）。

（A ）p （B ）p -1（C ）k n k k n p p C --)1( （D ）k n k kn p p C --)1(.二、填空题（本大题共7小题，每小题 3 分，共 21 分）1．设()P λX （泊松分布），且()(1)21E X X --=⎡⎤⎣⎦，则λ= .2.设X的概率密度为2()x f x -=，则()E X = ，()D X ＝ . 3．若事件A 和事件B 相互独立, P()=A α，P(B)=0.3，P(A B)=0.7 ，则α= .4．已知随机变量X 与Y 的联合分布律为 则(1)P X Y +== .5. 设X 的分布函数为⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤-<≤<=5.1,15.11,2110,20,0)(x x x x xx x F ，则=≤<}3.14.0{X P 。

暨 南 大 学 考 试 试 卷 答 案得分 评阅人 一、 选择题（共10小题，每小题2分，共20分,请将答案写在答题框内）题号12 3 4 5 6 7 8 9 10 答案 C BBDBABADC1．设、、为三个事件，则事件“、、中恰有两个发生”可表示为( C ). A ．； B.； C.； D.2.. 设在 Bernoulli 试验中,每次试验成功的概率为，重复独立进行3 次试验, 至少失败一次的概率为 ( B ). A. ; B. ;C.; D..教 师填 写2011 - 2012 学年度 第 二 学期 课程名称：《 概率论与数理统计 》（内招）授课教师姓名：黄颖强、范旭乾、张培爱、邱青、 刘春光、王文杰、夏良辉 考试时间: 2012年 7 月 6 日课程类别必修[ √] 选修[ ] 考试方式开卷[ ] 闭卷[ √ ]试卷类别[ A ] 共 7 页考生填写)级(班 专业 ) 校(学院[ ]外招] √[内招 学号 姓名题 号 一 二 三 四 五 六 七 八 九 十 总 分得 分3. 设是相互独立且具有相同分布的随机变量序列, 若,方差存在,则( B ).A. B. C. D. .4. 设随机变量X的概率密度为, 则方差D(X)= ( D )A. 9；B. 3；C. ；D. .5. 设随机变量的概率密度函数，则的概率密度函数为（ B ）．A． B． C．D．6. 设且，则（ A ）A．0.15 B. 0.30 C. 0.45 D. 0.67．设，则（ B ）（设）．A． B． C． D．8．设总体，其中未知，为来自总体X的一个样本，则以下关于的四个无偏估计：=，中，哪一个最有效？（A ）A．；B．；C．；D．9. 设为总体的一个样本,为样本均值,, 则下列结论中正确的是 ( D ).A. ；B. ；C. ；D. .10. 在假设检验中,记为原假设，则犯第一类错误指的是（ C ）.A. 正确，接受；B. 不正确，拒绝；C. 正确，拒绝；D. 不正确，接受得分评阅人二、填空题（共9小题, 每空3分, 共30分, 请将答案写在答题框内）题号 1 2 3 4 5 6 7 8 9答案6/7 55 19 2/9, 1/9 3/4 0.5=1/1. 假设是两个相互独立的事件, 若则.2.若,则它的概率函数在 55 取得最大值.3.若则19 .4.设，的联合分布律为X1 2Y123且X，Y相互独立，则=，.5. 设由切比雪夫不等式知.6. 设是次独立试验中事件发生的次数，是事件在每次试验中发生的概率，则= 0.5 .7. 若随机变量相互独立, 且则.8. 若随机变量, 则.9. 设总体的分布密度为, 现从中抽取个样本, 测得观测值分别为, 则参数的最大似然估计为.得分评阅人三、计算题（共 5 小题，每小题9分，共45分）1.甲罐中有一个白球，二个黑球，乙罐中有一个白球，四个黑球，现掷一枚均匀的硬币，如果得正面就从甲罐中任取一球，如果得反面就从乙罐中任取一球，若已知取的球是白球，试求此球是甲罐中取出的概率。

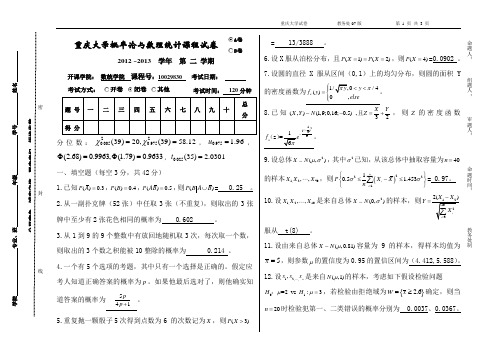
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院： 数统学院 课程号：10029830 考试日期：考试方式：开卷闭卷 其他 考试时间： 120分钟分位数：220.0050.975(39)20,(39)58.12χχ==，0.975 1.96u =，(2.68)0.9963,(1.79)0.9633Φ=Φ=，0.025(35) 2.0301t =一、填空题（每空3分，共42分）1.已知()0.3P A =，()0.4P B =，()0.5P AB =，则()P B A B ⋃= 0.25 。

2.从一副扑克牌（52张）中任取3张（不重复），则取出的3张牌中至少有2张花色相同的概率为 0.602 。

3.从1到9的9个整数中有放回地随机取3次，每次取一个数，则取出的3个数之积能被10整除的概率为 0.214 。

4.一个有5个选项的考题，其中只有一个选择是正确的。

假定应 考人知道正确答案的概率为p 。

如果他最后选对了，则他确实知道答案的概率为541pp +。

5.重复抛一颗骰子5次得到点数为6 的次数记为X ，则(3)P X >= 13/3888 。

6.设X 服从泊松分布，且(1)(2)P X P X ===，则(4)P X ==0.0902 。

7.设圆的直径X 服从区间（0,1）上的均匀分布，则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。

8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且，则Z 的密度函数21()36z Z f --（z ）。

9.设总体2(,)X N μσ，其中2σ已知，从该总体中抽取容量为40n =的样本1,240,,X X X ，则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。

10.设1,210,,X X X 是来自总体2(0,)XN σ的样本，则Y =服从 t(8) 。

2012年10月真题讲解一、前言学员朋友们，你们好！现在，对《全国2012年10月高等教育自学考试概率论与数理统计（经管类）试题》进行必要的分析，并详细解答，供学员朋友们学习和应试参考。

三点建议：一是在听取本次串讲前，请对课本内容进行一次较全面的复习，以便取得最佳的听课效果；二是在听取本次串讲前，务必将本套试题独立地做一遍，以便了解试题考察的知识点，与以及个人对课程全部内容的掌握情况，有重点的听取本次串讲；三是，在听取串讲的过程中，对重点、难点的题目，应该反复多听几遍，探求解题规律，提高解题能力。

一点说明：本次串讲所使用的课本是2006年8月第一版。

二、考点分析1.总体印象对本套试题的总体印象是：内容比较常规，有的题目比较新鲜，个别题目难度稍大。

内容比较常规：① 概率分数偏高，共74分；统计分数只占26分，与今年7月的考题基本相同，以往考题的分数分布情况稍有不同；② 除《回归分析》仅占2分外，对课本中其他各章内容都有涉及；③几乎每道题都可以在课本上找到出处。

如果粗略的把题目难度划分为易、中、难三个等级，本套试题容易的题目约占24分，中等题目约占60分，稍偏难题目约占16分，包括计算量比较大额题目。

2.考点分布按照以往的分类方法：事件与概率约18分，一维随机变量（包括数字特征）约22分，二维随机变量（包括数字特征）约30分，大数定律4分，统计量及其分布6分，参数估计6分，假设检验12分，回归分析2分。

考点分布的柱状图如下三、试题详解选择题部分一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其选出并将“答题纸”的相应代码涂黑。

错涂、多涂或未涂均无分。

1.已知事件A，B，A∪B的概率分别为0.5，0.4，0.6，则P（A）=A.0.1B.0.2C.0.3D.0.5[答疑编号918150101]【答案】B【解析】因为，所以，而，所以，即；又由集合的加法公式P（AB）=P（A）+P（B）-P（A∪B）=0.5+0.4-0.6=0.3，所以＝0.5－0.3＝0.2，故选择B.[快解] 用Venn图可以很快得到答案：【提示】1. 本题涉及集合的运算性质：（i）交换律：A∪B=B∪A,AB=BA；（ii）结合律：（A∪B）∪C=A∪（B∪C）,（AB）C=A（BC）；（iii）分配律：（A∪B）∩C=（A∩C）∪（B∩C），（A∩B）∪C=（A∪C）∩（B∪C）；（iv）摩根律（对偶律）,.2.本题涉及互不相容事件的概念和性质：若事件A与B不能同时发生，称事件A与B互不相容或互斥，可表示为A∩B＝，且P（A∪B）=P（A）+P（B）.3.本题略难，如果考试时遇到本试题的情况，可先跳过此题，有剩余时间再考虑。

系别 专业 年级 姓名 学号┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈密┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈封┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈线┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈安阳师范学院 专 业 概率论与数理统计 课2011——2012学年度第二学期期末考查试卷(B 卷)一、判断题（在题前的括号内打√或×，每小题2分，共20分）（ ）1.若P (A )=1，则A 一定为必然事件. （ ）2.若P (A )=0,则A 与任何事件都相互独立. （ ）3.设ξ为随机变量,若()D ξ=0,则X 为常数．（ ）4.F (x )是随机变量的分布函数,则F (x )是x 的非增函数. （ ）5.若ξ与η相互独立，则ξ与η的相关系数0ρ=. （ ）6.如果随机变量~(20,0.3)b ξ，则() 4.2.D ξ=. （ ）7. 设~(1,2)N ξ-，则(1)0.5P ξ>=.（ ）8.若,)ξη（服从二维正态分布，且ξ与η不相关，则ξ与η一定相互独立. （ ）9.若ξ与η相互独立，且方差都存在，则()()D D ξηξη+=-.（ ）10.如果12,,ξξ…是相互独立，都服从参数为5的泊松分布，则01.051lim 1=⎭⎬⎫⎩⎨⎧≥-∑=∞→n k k n X n P .二、填空题（每小题2分，共２0分）1.在1个，求其为次品的概率 .2. 已知事件,A B 互不相容，则()P AB 的值是 .3.某家庭有两个小孩，已知该家至少有一个是女孩，则“此家另一个也是女孩”的概率为 .4设连续随机变量ξ的分布函数为20,0;(),01;1, 1.x F x Ax x x <⎧⎪=≤<⎨⎪≥⎩则常数A= .5.设ξ为一随机变量，()2E ξ=-,2()5E ξ=，求(13)D ξ-= .6.设随机变量ξ～(5,9)N ，则c =_______时，()12P c ξ>=.7.设随机变量ξ与η相互独立，且(1,3)N ξ ，(2,4)N ξ ，235Z ξη=--，则()D Z = .8. 已知随机变量ξ的密度函数为;()0.xce x t p x x t -⎧>=⎨≤⎩ ，则常数c 为 .9.设ξ服从参数为2的泊松分布，32ηξ=-，则ov(,)C ξη= .10.已知随机变量ξ~N (0,1)，η~N (3,5)，且ξ与η相互独立，随机变量21Z ξη=-+，则Z ~_________.三、单项选择题 (每小题2分, 共10分)1. 设A 、B 、C 为三个相互独立的随机事件，且0<P(C)<1，则下列给定的事件中不相互独立的是（ ）（A ）C B A 与⋃ （B ）C AC 与 （C ）A-B 与C （D ）AB 与C2. 设随机变量,)~(3,2,4,9,0.5)N ξη（，则（ ）（A ）()6E ξη= （B ）()9E ξη= （C ）()12E ξη= （D ）()15E ξη=3. 设随机变量12,,,,n ξξξ 相互独立，根据辛钦大数定律，当n →+∞时，X 要是依概率收敛于其数学期望，需要随机变量序列{}n X 还满足（ ）（A ）有相同的数学期望 （B ）有相同的方差（C ）服从相同的分布 （D ）期望和方差均相同但未必服从相同分布4.下列n P 能成为概率分布（即分布列或分布律）的是（ ）（A ）1(2)n P n n =≥ （B ）1(1)(2)n P n n n =-≥ （C ）21(2)n P n n =≥ （D ）1(1)(2)n P n n n =+≥5. 设~(10)t η，则()E η=（ ）（A ）0 （B ）10 （C ）5（D ）20 四、计算题（每小题10分，共４0分）1. 设二维离散型随机变量(,)ξη的联合分布列为问其中α、β取何值时ξ与η相互独立？（10分）2. 设随机变量,)ξη（的密度函数为221,1(,)0,x y p x y π⎧+<⎪=⎨⎪⎩其他（！）求()X p x ,()Y p y （4分）；（2）判断ξ与η的独立性（2分）；（3）求ov(,)C ξη（4分）.3. 设随机变量,)ξη（的密度函数为()1(),0,0;(,)20,.x y x y ex y p x y -+⎧+>>⎪=⎨⎪⎩其它（1）问ξ与η是否相互独立； （2）求Z ξη=+的密度函数()Z p t .4．设某厂一车床生产的纽扣，据经验其直径服从正态分布2(,)N μσ，0σ未知．为了检验这一车床生产是否正常，现抽取容量37n =的子样，其子样均值26.56x =，29nS =且生产正常时026μμ==，而生产不正常时0μμ≠．要求在显著性水平0.05α=下检验生产是否正常（()()0.9750.9536 2.0281,36 1.6883t t ==）．（10分）五、证明题（每小题10分，共50分）设0()1,0()1P A P B <<<<，试证：A 与B 独立的充要条件是(|)(|)1P A B P A B +=．。

2012年概率论考研真题与答案1. （2012年数学一）设随机变量X 与Y 相互独立，且分别服从参数为1与4的指数分布，则{}P X Y <=_________. 【A 】A ．15 B. 13 C. 25 D. 45解：X 与Y 的概率密度函数分别为：,0()0,0x X e x f x x -⎧>=⎨≤⎩， 44,0()0,0y Y e y f y y -⎧>=⎨≤⎩ 因为X 与Y 相互独立，所以X 与Y 的联合密度函数为44,0,0(,)()()0,x y X Y e x y f x y f x f y --⎧>>=⋅=⎨⎩其他 {}40(,)4x y xx yP X Y f x y dxdy dx e dy +∞+∞--<∴<==⎰⎰⎰⎰450145xyx xe dx edy e dx +∞+∞+∞---===⎰⎰⎰2. （2012年数学一）将长度为1m 的木棒随机地截成两段，则两段长度的相关系数为______.A ．1 B.12 C. 12- D. 1- 答案：D.解：设两段长度分别为X 和Y ，显然满足1X Y +=，即1Y X =-+，故两者是线性关系，且是负相关，所以相关系数为1-.3. （2012年数学三）设随机变量X 与Y 相互独立，且都服从区间(0,1)上的均匀分布，{}221P X Y +≤=_________. 【D 】A ．14 B. 12 C. 8π D. 4π解：X 与Y 的概率密度函数分别为：1,01()0,X x f x <<⎧=⎨⎩其他， 1,01()0,Y y f y <<⎧=⎨⎩其他又X 与Y 相互独立，所以X 与Y 的联合密度函数为1,0,1(,)()()0,X Y x y f x y f x f y <<⎧=⋅=⎨⎩其他， 从而 {}222211(,)4D x y P X Y f x y dxdy S π+≤+≤===⎰⎰.4. （2012年数学三）设1234,,,X X X X 为来自总体2(1,)(0)N σσ>的简单随机样本，则统计量12342X X X X -+- 的分布为_________. 【B 】A. (0,1)NB. (1)tC.2(1)χ D. (1,1)F解：因为2(1,)i X N σ ，所以212(0,2)X X N σ-(0,1)N 234(2,2)X X N σ+(0,1)N ，22342(2)(1)2X X χσ+- . 因为1234,,,X X X X2342(2)2X X σ+-也相互独立， 从而1234(1)2X X t X X -=+-5. （2012年数学一、三）设,,A B C 是随机事件，A 与C 互不相容，11(),()23P AB P C ==，则()____P AB C =. 【34】解：由于A 与C 互不相容，所以AC φ=，则ABC φ=，从而()0P ABC =;10()()()32()14()()13P ABC P AB P ABC P AB C P C P C --====-6. （2012年数学一、三）设二维离散型随机变量(,)X Y 的概率分布为（1）求{}2P X Y =；（2）求(,)Cov X Y Y -.解：（1）{}{}{}120,02,14P X Y P X Y P X Y ====+===.（2） 由(,)X Y 的概率分布可得,,X Y XY 的概率分布分别为，，所以 23EX =,1EY =,2522,,()333EY DY E XY ===(,)()0Cov X Y E XY EX EY =-⋅=故： 2(,)(,)3Cov X Y Y Cov X Y DY -=-=-7. （2012年数学一）设随机变量X 和Y 相互独立且分别服从正态分布2(,)N μσ和2(,2)N μσ，其中σ是未知参数且0σ>. 设Z X Y =-. （1）求Z 的概率密度2(,)f z σ；（2）设12,,,n Z Z Z 是来自总体Z 的简单随机样本，求2σ的最大似然估计量2σ；（3）证明 2σ是2σ的无偏估计量. 解：（1） 因为2(,)X N μσ ，2(,2)Y N μσ ，且X 和Y 相互独立，故2(0,3)Z X Y N σ=-2226(;),z f z z R σσ-∴=∈（2）似然函数为 2116221()(;)ni i nz i i L f z σσσ=-=∑==∏两边取对数，得222211l n ()l n 26nii nL n zσσσ==--∑关于2σ求导，得2222221ln ()1+26()nii d L n z d σσσσ=-=∑ 令22ln ()0,d L d σσ= 解得λ的最大似然估计值 22113n i i z n σ==∑ 因此，λ的最大似然估计量 22113n i i Z n σ==∑（3） 2221111()()()33n n i i i i E E Z E Z n n σ====∑∑2221111[()()]333n n i i i i E Z D Z n n σσ===+==∑∑ 故 2σ是2σ的无偏估计量. 8. （2012年数学三）设随机变量X 与Y 相互独立，且都服从参数为1的指数分布. 记{}max ,U X Y =，{}min ,V X Y =，则（1）求V 的概率密度()V f v ；（2）求()E U V +. 解：（1） X 与Y 的分布函数均为1,0()0,0x e x F x x -⎧-≥=⎨<⎩{}min ,V X Y =的分布函数为{}{}{}{}()min ,1min ,V F v P X Y v P X Y v =≤=-> {}21,1(1())P X v Y v F v =->>=--21,00,0v e v v -⎧-≥=⎨<⎩故V 的概率密度为22,0()()0,0v V V e v f v F v v -⎧>'==⎨≤⎩（2） min(,)max(,)U V X Y X Y X Y +=+=+()()()()2E U V E X Y E X E Y ∴+=+=+=.。

商学院2011/2012学年第二学期考试试卷(B)课程名称： 概率论与数理统计 考试方式： 闭卷 完成时限： 120分钟班级名称： 学号： ： .一、单项选择题（每小题2分，共10分）1、设在一次试验中事件A 发生的概率为p ，现重复独立进行n 次试验，则事件A 至少发生一次的概率为（ ）。

（A ）n p -1（B ）n p（C ）n p )1(1--（D ）n p )1(-2、设A ，B 为两事件，则A －B 不等于（ ）。

（A ）B A（B ）B A（C ）AB A -（D ）B B A -)(Y3、如果随机变量X 与Y 满足:)(Y X D +)(Y X D -=,则下列式子正确的是（ ）。

（A ）X 与Y 相互独立 （B ）X 与Y 不相关 （C ）0=DY（D ）0=⋅DY DX4、设两个相互独立的随机变量X 和Y 的方差分别为4和2，则随机变量Y X 23-的方差是（ ）。

（A ）8（B ）16（C ）28 （D ）445、设总体)1,0(~N X ，n X X X ,,,21⋅⋅⋅为其样本，又S X ,分别为样本均值及样本标准差,则（ ）。

（A ）)1,0(~N X （B ）)1,0(~N X n （C ）)(~212n X ni i χ∑= （D ）)1(~-n t SX二、填空题（每小题2分，共16分）1、设B A ,为随机事件，7.0)(=A P ，3.0)(=-B A P ，则=)(AB P ________。

2、设随机变量X 服从参数为λ的泊松分布,且已知1)]2)(1[(=--X X E ，则=λ_______。

3、若随机变量X 的概率密度为)( e21)(4)3(2+∞<<-∞=+-x x f x π,则有=Y)1,0(~___________N 。

4、设随机变量X ,Y 的方差分别为25=DX ,36=DY ,相关系数4.0=XY ρ,则),(Y X Cov = 。

2012年10月全国自考概率论与数理统计（经管类）真题试卷(题后含答案及解析)题型有：1. 单项选择题 2. 填空题 3. 计算题 4. 综合题 5. 应用题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．已知事件A，B，A∪B的概率分别为0．5，0．4，0．6，则P(AB)=( ) A．0．1B．0.2C．0.3D．0.5正确答案：B2．设F(x)为随机变量X的分布函数，则有( )A．F(一∞)=0，F(+∞)=0B．F(一∞)=1，F(+∞)=0C．F(-∞)=0，F(+∞)=1D．F(-∞)=1，F(+∞)=1正确答案：C解析：本题是分布函数的基本性质，应牢记．答案为C3．设二维随机变量(X，Y)服从区域D：x2+y2≤1上的均匀分布，则(X，Y)的概率密度为( )A．B．C．D．正确答案：D解析：本题是典型的利用区域面积来求其概率密度的题，在历年考题中出现多次，F(x，y)=答案为D4．设随机变量X服从参数为2的指数分布，则E(2X-1)=( )A．0B．1C．3D．4正确答案：A解析：指数分布的期望E(X)=,再根据期望的性质易知E(2X一1)=2E(X)一1=2×一1=0．答案为A5．设二维随机变量(X，Y)的分布律则D(3X)=( )A．B．2C．4D．6正确答案：B解析：本题可先求出随机变量X的边缘分布，，故EX=，再根据方差性质可知D(3X)=9D(X)=2．答案为B．6．设X1，X2，…，Xn…为相互独立同分布的随机变量序列，且E(X1)=0，D(X1)=1，则=( )A．0B．0.25C．0.5D．1正确答案：C解析：本题可由中心极限定理得答案为C7．设x1，x2，…，xn为来自总体N(μ，σ2)的样本，μ，σ2是未知参数，则下列样本函数为统计量的是( )A．B．C．D．正确答案：D解析：统计量中要求不含任何未知参数，故含μ，σ两参数的选项均被排除．答案为D．8．对总体参数进行区间估计，则下列结论正确的是( )A．置信度越大，置信区间越长B．置信度越大，置信区间越短C．置信度越小，置信区间越长D．置信度大小与置信区间长度无关正确答案：A解析：当置信度1-α增大，又样本容置n固定时，置信区间长度增大，区间估计精度减低。

湖南人文科技学院 数学系 数学与应用数学、信息与计算科学专业 2012 级2013---2014学年第二学期概率论与数理统计课程考试试卷A分钟一、单项选择题（本大题共5小题，每小题3分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题干的括号内。

多选无分。

1．设B A ,是任意2个事件，则=-)(B A P （ C）．（A ）)()(B P A P -； （B ）()()()P A P B P AB -+；（C ）)()(AB P A P -； （D ）)()()(AB P B P A P -+．2．设n x x x ,,,21 是来自正态总体),(2σμN （σ未知）的样本，对均值μ考虑如下的检验0100::μμμμ≠=H vs H ，则显著性水平为α的拒绝域是（ A ）（记t =）A ．2{;(1)}W t t t n α=≥- Ｂ．{;(1)}W t t t n α=≥-Ｃ．1{;(1)}W t t t n α-=≤- D ．2{;(1)}W t t t n α=≤-3．设总体X ~2(1,)N σ,12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, 则为参数2σ的无偏估计量的是( Ａ )(A) 211()1n i i X X n =--∑; (B) 211()ni i X X n =-∑; (C) 211nii X n =∑; (D) 2X4．若随机变量X 和Y 的协方差等于0，则以下结论正确的是（ Ｂ ）．)(A X 和Y 相互独立； )(B )()()(Y D X D Y X D +=+；)(C )()()(Y D X D Y X D -=-； )(D )()()(Y D X D XY D ⋅=．5设随机变量X 与Y 均服从正态分布，)5,(~),4,(~22μμN Y N X ；记},4{1-≤=μX p p }5{2+≥=μY p p ，则有（ Ａ）．)(A 对任何实数μ，都有21p p =； )(B 对任何实数μ，都有21p p < ；)(C 只对个别μ值，才有21p p =； )(D 对任何实数μ，都有21p p >． 二、填空题（本大题共5小题，每小题 3分，共15分） 1．随机变量X ~)4,(μN ，且5)(2=X E ，则X 2(1)x ±-2．设Y X ,独立且均服从正态分布),0(2σN ，且41)2,2(=-≤≤Y X P ，则=->>)2,2(Y X P 14 ． 3．设 ，n X X X ,,,21为独立同分布的随机变量序列，且),2,1( =i X i 服从参数为2的指数分布，则∞→n 当时，∑==n i i n X n Y 121依概率收敛于 12． 4. 设(1521,,,X X X )是来自正态总体()9,0N 的简单随机样本，则统计量 2152122112102221 21X X X X X X Y ++++++= 的概率分布是(10,5)F ．（只填Ｆ分布得２分.） 5. 设总体n X X X N X ,,,),,(~212⋅⋅⋅σμ是来自X 的一个样本∑==n i i X n X 11，参数2,σμ都是未知的，则2σ的矩估计量为 22211()n n i i i i x x x x n n ==--∑∑或 三、判断题(每小题2分，共12分对的打“√”，错的打“×”) 1．设X ~(,1)N μ,则满足{}{}22P X P X >=≤的参数μ=2 （√ ） 2．设随机变量)1,0(~),1,0(~N Y N X ，则22Y X +服从2χ分布； （× ） 3. 设随机变量X 与Y 相互独立，且),(~1p n B X ，),(~2p n B Y ，则~Y X +)2,(21p n n B +；（× ）4. 设A,B,C 是三个事件,如果有 ()()()()()()()()()P AB P A P B P BC P B P C P AC P A P C =⎧⎪=⎨⎪=⎩, 则称A,B,C 相互独立 ( × )5. 设0＜P(A)＜1，0＜P(B)＜1，且A 、B 两事件相互独立，则必有A 与B 互斥事件； (× )6. 设总体),(~2σμN X ，2σ未知，X 为样本均值，,)(1122∑=-=n i i n X X n S,)(11122∑=--=ni i X X n S 检验假设00:μμ=H 时采用的统计量是n X Z /0σμ-= （ × ）（以下各题要有详细过程，只写结果不给分）。

第⼆学期概率论与数理统计试卷参考答案重庆⼤学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年第⼆学期开课学院：数统学院课程号：10029830 考试⽇期：考试⽅式：开卷闭卷其他考试时间： 120分钟分位数：220.0050.975(39)20,(39)58.12χχ==，0.975 1.96u =，(2.68)0.9963,(1.79)0.9633Φ=Φ=，0.025(35) 2.0301t =⼀、填空题（每空3分，共42分）1.已知()0.3P A =，()0.4P B =，()0.5P AB =，则()P B A B ?= 0.25 。

从⼀副扑克牌（52张）中任取3张（不重复），则取出的3张牌中⾄少有2张花⾊相同的概率为 0.602 。

从1到9的9个整数中有放回地随机取3次，每次取⼀个数，则取出的3个数之积能被10整除的概率为 0.214 。

4.⼀个有5个选项的考题，其中只有⼀个选择是正确的。

假定应考⼈知道正确答案的概率为p 。

如果他最后选对了，则他确实知道答案的概率为541pp +。

5.重复抛⼀颗骰⼦5次得到点数为 6 的次数记为X ，则(3)P X > = 13/3888 。

6.设X 服从泊松分布，且(1)(2)P X P X ===，则(4)P X ==0.0902 。

7.设圆的直径X 服从区间（0,1）上的均匀分布，则圆的⾯积Y的密度函数为1//4()0 ,Y y f y elseπ?<。

8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且，则Z 的密度函数21()36z Zf --（z ）。

9.设总体2(,)X N µσ，其中2σ已知，从该总体中抽取容量为40n =的样本1,240,,X X X ，则()222110.5 1.453n i i P X X n σσ=??≤-≤∑= 0.97。

10.设1,210,,X X X 是来⾃总体2(0,)XN σ的样本，则Y =服从 t(8) 。

上海第二工业大学 （试卷编号： ） 2011-2012学年第二学期 期末 考试 《概率论与数理统计》试卷 姓名： 学号： 班级： 成绩：一、填空题（每题3分，共15分）1．已知(/)()P A B P A =，则A B 与的关系是 。

2.若12(),()X P Y P λλ，且,X Y 相互独立，则X Y +服从的分布是 。

3．将一枚硬币重复抛掷3次，则正、反面都至少出现一次的概率为 。

4．设总体X 以等概率θ1取值θ,,2,1 ，则未知参数θ的矩估计量为_ ____。

5．设2(,)X N μσ，其分布函数为()F x ，则有(+)()=F x F x μσμσ+- 。

二、选择题（每题3分，共15分）1．已知事件A 、B 满足：()()()()0.2,0.5,0.8,P AB P B P A B P A B ====则（ ）。

（A ）0.7 （B ）0.3 （C ）0.6 （D ）0.82.设随机变量x X ~f (x )e ,(x 0)λλ-=>，已知()1/2E X =，若~()Y P λ，则下列计算 正确的是 （ ）（A ）()2,()4E Y D Y == （B ）(22)6D Y --=-（C ）2()4E Y = （D ）2(+1)11E Y =3. 从总体2~(,)X N μσ中抽取简单随机样本12,,......,n X X X ，以下结论错误的是（ ） （A ）11ni i X n =∑服从正态分布 （B ）2211()ni i X X σ=-∑服从2()n χ（C ）211()ni i D X n n σ==∑（D ）11()ni i E X n μ==∑4.连续型随机变量的分布函数,0()0,0x a be x F x x -⎧+>=⎨≤⎩，其中的常数,a b 的值为（）（A ）1,1a b == （B ）0,1a b == （C ）1,1a b ==- （D ）1,1a b =-=5．关于正态分布的结论中错误的是（ ）（A ）服从正态分布的随机变量的任一线性变换后仍然服从正态分布。

东莞理工学院（本科）试卷（B 卷）2011 --2012 学年第二学期《概率论与数理统计》试卷（答案）开课单位：计算机学院数学教研室 ，考试形式：闭卷，允许带 计算器 入场一、填空题（共70分 每空21、A 、B 是两个随机事件，已知4.0)(=A P ，5.0)(=B P 。

若A 与B 相互独立，则=+)(B A P 0.7 ；若 1.0)(=-B A P ，则P( A | B ) = 0.6 。

2、已知事件A ，B 满足)()(B A P AB P =，且3.0)(=A P ，则=)(B P 0.7 。

3、.抛掷两颗骰子,用X 和Y 分别表示它们的点数(向上的面上的点数),则这两颗骰子的点数和为5的概率是91。

4、袋中有6只白球,4只红球,从中抽取两只。

如果作不放回抽样,则抽得的两个球颜色不同的概率为158；如果作放回抽样,则抽得的两个球颜色不同的概率为 0.48 。

5、已知某对夫妇有四个小孩，则男孩的个数Y 服从的分布为 )5.0 ,4(B ，恰有两个男孩的概率为 83，在已知至少有一个女孩的条件下，至少还有一个男孩的概率为1514。

6、有甲乙两台设备生产相同的产品，甲生产的产品占70%，次品率为1%；乙生产的产品占30%，次品率为2%。

(1) 若随机地从这批产品中抽出一件,抽到次品的概率为 1.3% ；（2）若随机地从这批产品中抽出一件，检验出为次品，则该次品属于甲厂生产的概率是137。

7、指数分布又称为寿命分布，经常用来描述电子器件的寿命。

设某款电器的寿命（单位：小时）的密度函数为⎩⎨⎧>=-其它 ,00 ,002.0)(002.0t e t f t 则这种电器没有用到500小时就坏掉的概率为11--e ，这种电器的平均寿命为 500 小时。

8、假设某公路上每分钟通过的汽车数可以用泊松(Poisson)分布)9(P 来描述。

则该公路在某一分钟至少有一辆汽车通过的概率为91--e 。

东莞理工学院（本科）试卷（D 卷）2011 --2012 学年第二学期《概率论与数理统计》试卷（答案）开课单位：计算机学院数学教研室 ，考试形式：闭卷，允许带 计算器 入场一、选择填空题（共70分 每空21、设A 、B 为两个事件，P(A)=0.5，P(A-B)=0.2，则P(B A )为( C ) （A ）0.2 （B ）0.3 （C ）0.7 （D ）0.82、A 、B 是两个随机事件，P( A ) = 0.3，P( B ) = 0.4，且A 与B 互不相容,则P （B A ）等于（ D ） (A) 0 (B) 42.0 (C) 88.0 (D)13、已知P(A)=0.5,P(B)=0.6,且A 与B 相互独立,则)(B A P 等于（ C ） （A ）0.6 （B ）0.7 （C ）0.8 （D ）0.94、事件A 、B 相互独立，)(A P =0.3，)(A B P =0.6，则)(A P +)(B P 等于（ C ） （A ）0.5 （B ）0.3 （C ）0.9 （D ）15、设A 、B 为两个事件，则B A -表示( D ) （A ）“A发生且B 不发生” （B ）“A、B 都不发生” （C ）“A、B 都发生”（D ）“A不发生或者B 发生”6、 某事件发生的概率为10，如果试验10次，则该事件（D ）（A ）一定会发生1次 （ B ） 一定会发生10次 （C ） 至少会发生1次 （D ）发生的次数是不确定的 7、已知离散型随机变量X 概率函数为1)(+==i pi X P ，1 ,0=i ，则p 的值为( A )（A ）(-1+5)／2 （ B ）(1+5)／2 （ C ）(-l ±5)／2 （ D ） 1／2 8、某大学统计系06级3班共有60名同学。

至少有2名同学生日相同的概率为（ D ） （一年按365天计算）（A ） 6060!365（B ） 6036560365P （ C ）!36560365P （ D ） 60365601365P -9、 红星游乐园入口处的每辆汽车的载客人数服从2λ=的泊松分布，今任意观察一辆到达公园门口的汽车，车中无乘客的概率为（A ）（A ） 2e- （B ） 2 （C ） 2e （ D ）!22-e10、某食品超市的牛奶销售量服从正态分布，每天平均销售200公斤，标准差为20公斤。

海南大学2012-2013学年第二学期试卷科目：《概率论与数理统计》试题(A 卷)考试说明：本课程为闭卷考试，答案一律答在后面的答题纸上，答在其它地方无效，可携带 计算器 。

一、选择题（每题3分，共15分，选择正确答案的编号，将答案写在答题纸上）1、设,,A B C 为三个事件，则,,A B C 中不多于一个发生可表示为（a ） (A) AB BC AC ； （B ）A B C ； （C ）AB BC AC ； （D ）A B C .2、设A 与B 是两个事件，则下列关系正确的是（ b ）.（A ）()A B B A -=； （B ）()AB A B A +-=； （C ）()A B B A -=； （D ）()ABA B A -=. 3、设随机变量~(0,1)X N ，~(2,1)Y N ，且X 与Y 相互独立，则21Z X Y =++服从（d ）(A) ~(2,5)Y N ； （B ）~(3,4)Y N ； （C ）~(2,4)Y N ； （D ）~(3,5)Y N .4、设~(),X t n 则2X 服从（ 略 ）分布(A) 2()n χ； （B ）(1,)F n ； （C ）(,1)F n ； （D ）(1,1)F n -. 5、设随机变量X 与Y 相互独立，则下列结论不正确的是 ( d )(A) (,)0Cov X Y =； （B ）X 与Y 不相关；（C ）()()()D X Y D X D Y -=+； （D ()()()D XY D X D Y =.二、填空题（每题3分，共15分，将答案写在答题纸上）1、设,A B 是两事件，()0.2P A =，若B A ⊃，则()P A B =0.8 .2、袋中有3个白球，6个黑球，它们除颜色不同外，其他没有差别，每次从中任取一个，则第7次取到白球的概率为__1/3___.3、假设2~(1)X χ，~(2,9)Y N ，且X 与Y 相互独立，则()D X Y +=_10_____.4、设随机变量~(10,0.4)X B ，则根据切比雪夫不等式有{}()2P X E X -≥≤__0.1____.5、设~(0,3)X N ，~(0,6)Y U ，0.5XY ρ=，则(2)D X Y -=12______.三、计算题（每题10分，共70分，将答案写在答题纸上）（注意：答题时要列出详细运算步骤并计算出中间运算数值和最终计算结果）1、一道选择题有4个答案，其中仅有1个正确，假设一名学生知道正确答案的概率为14. （1）求该学生答对的概率；1/4（2）若已知该学生答对了，求他确实知道答案的概率.知啊到答案事件设为A 不知道答案事件设为B 玩呗时间组 设学生答对的事件为C 1/42、某射手有3发子弹，射一次命中的概率为13，如果命中了就停止射击，否则一直射到子弹用尽. 设X 表示耗用的子弹数.试求：（1）X 的分布律； （2）分布函数()F x ； （3）至少需要耗用2发子弹的概率.3、设连续型随机变量X 的概率密度为,01()2,120,Ax x f x x x ≤<⎧⎪=-≤<⎨⎪⎩其他试求：（1）系数A ；（2）分布函数()F x ；（3）{0.4 1.2}P X <<.4、设二维随机变量(,)X Y 的密度函数为8,01(,)0,xy x y f x y ≤≤≤⎧=⎨⎩其他 （1）求X 和Y 的边缘密度；（2）判断X 和Y 是否独立，并说明理由.5、已知二元离散型随机变量(,)X Y 的联合概率分布如下表所示：试求()E X ，()E Y ，()D X ，()D Y ，及X 与Y 的相关系数XY ρ.6、 设总体X 服从参数为λ泊松分布，即{}!x P Xx e x λλ-==，0,1,2,.x =12,,,n X X X 是X的样本，求λ的矩估计量和极大似然估计量.7、设某次考试的学生成绩2~(,)X N μσ，其中已知10σ=分. 现从中随机抽取25名学生的成绩，得其平均成绩为72分. 问在显著性水平0.05α=下，是否可以认为此次考试中考生的平均成绩为75分?(注：计算中可能用到0.0251.96u=)。

试卷编号 课程名称：概率论与数理统计 考试时间：110 分钟:名姓一、选择题(本大题共5小题，每小题3分，总计15分) 1、甲、乙两乒乓球队各有运动员三男二女 ，其中甲队一男与乙队一女是种子选手 ，现在两队进行混 合双打比赛，则两个种子选手都上场的概率是 () :号学••业专级年----- 装---------A. 1 ；B. 6 5 36C. _5_ 12D. 2、下列关系式中成立的个数 (1)A U B=(A B )U B (3)若 A U B ，贝U A=AB A.1个 B.2个 (2)(AuB)nC= A n ⑷若 AB=0，且 C U A ，贝U BC=0 C.3个 D.4个 3、已知随机变量 X 的概率密度为f x (x),令Y=-2X ,则丫的概率密度f Y (y)为(). y 1 y 1 y A. 2f x (—2y)； B. f x (-T)； C. 一7 f x(——)； D. -f x(——). 2 2 2 2 2 4、设随机变量 X 的概率密度为P(X),且P {x >0} = 1,则必有( A. p(x)在(0,+处内大于零； -be C. 4 P(x)dx =1; ). B . D. 5.设随机变量X ~N(A,cr 2),则随CT 的增大，概率 (A )单调增大 (B )单调减小 p(x)在(一处,0 )内小于零； p(x)在(0,+处)上单调增加. p{X-4 (C )保持不变 (D ) 增减不定 二、填空题(本大题共5小题，每小题3分，总计15分) 若卩(A) =0.4, P( AB) =0.3,则 P(A U B)= 设连续型随机变量 F(x)M 0, 1、 2、 X 的分布函数为 X >0; X <0. 则当x>0时，X 的概率密度f(x) = 设随机变量X 的分布函数为 0, F(x)={x 2, h , xcO; 0<x <1;以丫表示对X 的3次独立重复观测中 X 纣.五(10分)、若随机变量K~N(A,cr 2),而方程+ 4x + K = 0无实根的概率为0.5，试求卩事件{ X < !}出现的次数，则P{Y=2} =2 4、从长度为 1、3、5、7、9五条线段中任取三条能构成三角形的概率是5、随机变量 X 的所有可能取值为 0和X ,且P {X =0}=0.8, E(X)=1,则x = 三(10分)、 设一批混合麦种中一、二、三、四等品分别占率依次为,0.98, 0.95, 0.9, 0.85.求这批麦种的发芽率； 94%、3%、2%、1%,,四个等级的发芽 若取一粒能发芽，它是二等品的概率是多少？ 四(15分)、设随机变量X, E(X)=工，且12『ax +b,P(x) =\10,求a 与b 的值,并求分布函数F (x).0 <x<1; 其它.六（15分）、•某单位招聘员工，共有10000人报考。