全国版2019版高考数学一轮复习坐标系与参数方程第2讲参数方程学案

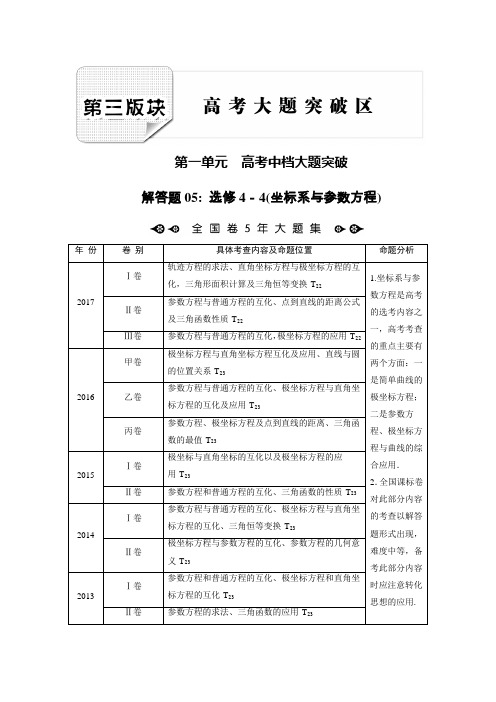
第一单元高考中档大题突破解答题05: 选修4－4(坐标系与参数方程)年份卷别具体考查内容及命题位置命题分析2017 Ⅰ卷轨迹方程的求法、直角坐标方程与极坐标方程的互化，三角形面积计算及三角恒等变换·T221.坐标系与参数方程是高考的选考内容之一，高考考查的重点主要有两个方面：一是简单曲线的极坐标方程；二是参数方程、极坐标方程与曲线的综合应用．2．全国课标卷对此部分内容的考查以解答题形式出现，难度中等，备考此部分内容时应注意转化思想的应用. Ⅱ卷参数方程与普通方程的互化、点到直线的距离公式及三角函数性质·T22Ⅲ卷参数方程与普通方程的互化，极坐标方程的应用·T222016 甲卷极坐标方程与直角坐标方程互化及应用、直线与圆的位置关系·T23乙卷参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化及应用·T23丙卷参数方程、极坐标方程及点到直线的距离、三角函数的最值·T232015 Ⅰ卷极坐标与直角坐标的互化以及极坐标方程的应用·T23Ⅱ卷参数方程和普通方程的互化、三角函数的性质·T232014 Ⅰ卷参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化、三角恒等变换·T23Ⅱ卷极坐标方程与参数方程的互化、参数方程的几何意义·T232013 Ⅰ卷参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化·T23Ⅱ卷参数方程的求法、三角函数的应用·T23基本考点——极坐标方程1．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r ，则圆的方程为：ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程： (1)当圆心位于极点，半径为r ：ρ＝r ； (2)当圆心位于M (a,0)，半径为a ：ρ＝2a cos θ； (3)当圆心位于M (a, π2)，半径为a ：ρ＝2a sin θ.2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴与此直线所成的角为α， 则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)． 几个特殊位置的直线的极坐标方程： (1)直线过极点：θ＝θ0和θ＝π＋θ0；(2)直线过点M (a,0)且垂直于极轴：ρcos θ＝a ； (3)直线过M (b, π2)且平行于极轴：ρsin θ＝b .1．(2017·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．解：(1)设P 的极坐标为(ρ，θ)(ρ>0)，M 的极坐标为(ρ1，θ)(ρ1>0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ. 由|OM |·|OP |＝16得C 2的极坐标方程为ρ＝4cos θ(ρ>0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB >0)．由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积S ＝12|OA |·ρB ·sin ∠AOB ＝4cos α·⎪⎪⎪⎪sin α－π3 ＝2⎪⎪⎪⎪sin2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.2．(2016·全国乙卷)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t ，(t 为参数，a >0)，在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a .解：(1)消去参数t 得到C 1的普通方程x 2＋(y －1)2＝a 2，则C 1是以(0,1)为圆心，a 为半径的圆．将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ.若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0， 由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0， 从而1－a 2＝0，解得a ＝－1(舍去)，a ＝1.当a ＝1时，极点也为C 1，C 2的公共点，在C 3上． 所以a ＝1.极坐标方程与普通方程的互化技巧(1)巧用极坐标方程两边同乘以ρ或同时平方技巧，将极坐标方程构造成含有ρcos θ，ρsin θ，ρ2的形式，然后利用公式代入化简得到普通方程．(2)巧借两角和差公式，转化ρsin(θ±α)或ρcos(θ±α)的结构形式，进而利用互化公式得到普通方程．(3)将直角坐标方程中的x 转化为ρcos θ，将y 换成ρsin θ，即可得到其极坐标方程．常考热点——参数方程与极坐标的综合几种常见曲线的参数方程(1)圆：以O ′(a ，b )为圆心，r 为半径的圆的参数方程是⎩⎪⎨⎪⎧x ＝a ＋r cos α，y ＝b ＋r sin α，其中α是参数．当圆心在(0,0)时，方程为⎩⎪⎨⎪⎧x ＝r cos α，y ＝r sin α，其中α是参数．(2)椭圆：椭圆x 2a 2＋y 2b 2＝1(a >b >0)的参数方程是⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ，其中φ是参数．椭圆x 2b 2＋y 2a 2＝1(a >b >0)的参数方程是⎩⎪⎨⎪⎧x ＝b cos φ，y ＝a sin φ，其中φ是参数．(3)直线：经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程是⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α，其中t是参数．1．(2017·全国卷Ⅰ)选修4－4：坐标系与参数方程在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . 解：(1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎨⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点 (3cos θ，sin θ )到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917. 由题设得a ＋917＝17，所以a ＝8；当a <－4时，d 的最大值为－a ＋117.由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.2．(2017·大庆二模)在直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－35t ＋2y ＝45t(t 为参数)，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝a sin θ.(1)若a ＝2，求圆C 的直角坐标方程与直线l 的普通方程； (2)设直线l 截圆C 的弦长等于圆C 的半径长的3倍，求a 的值． 解：(1)当a ＝2时，ρ＝a sin θ转化为ρ＝2sin θ， 整理成直角坐标方程为：x 2＋(y －1)2＝1，直线l 的参数方程⎩⎨⎧x ＝－35t ＋2y ＝45t(t 为参数)．转化成直角坐标方程为4x ＋3y －8＝0.(2)圆C 的极坐标方程转化成直角坐标方程为x 2＋⎝⎛⎭⎫y －a 22＝a 24， 直线l 截圆C 的弦长等于圆C 的半径长的3倍， 所以：d ＝|3a2－8|5＝12·|a |2，2|3a －16|＝5|a |，利用平方法解得：a ＝32或3211.1．(2017·全国卷Ⅲ)在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝m k ，(m 为参数)．设l 1与l 2的交点为P ，当 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．解：(1)消去参数t 得l 1的普通方程l 1：y ＝ (x －2)； 消去参数m 得l 2的普通方程l 2：y ＝1k(x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k (x －2)，y ＝1k (x ＋2)，消去 得x 2－y 2＝4(y ≠0)，所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0<θ<2π，θ≠π)，联立⎩⎪⎨⎪⎧ρ2(cos 2θ－sin 2θ)＝4，ρ(cos θ＋sin θ)－2＝0得cos θ－sin θ＝2(cos θ＋sin θ)． 故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以交点M 的极径为 5.2．(2017·承德二模)在直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2cos θy ＝2sin θ(θ为参数)，直线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1＋ty ＝2＋t (t 为参数)．(1)若直线C 1与圆O 相交于A ，B ，求弦长|AB |；(2)以该直角坐标系的原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，圆C 2的极坐标方程为ρ＝2cos θ＋23sin θ，圆O 和圆C 2的交点为P ，Q ，求弦PQ 所在直线的直角坐标方程．解：(1)由直线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1＋ty ＝2＋t(t 为参数)消去参数t ，可得：x －y ＋1＝0，即直线C 1的普通方程为x －y ＋1＝0.圆O 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θy ＝2sin θ(θ为参数)，根据sin 2θ＋cos 2θ＝1消去参数θ，可得：x 2＋y 2＝2.那么圆心到直线的距离d ＝12＝22， 故得弦长|AB |＝2r 2－d 2＝ 6.(2)圆C 2的极坐标方程为ρ＝2cos θ＋23sin θ，利用ρ2＝x 2＋y 2，ρcos θ＝x ，ρsin θ＝y ，可得圆C 2的普通方程为x 2＋y 2＝2x ＋23y . ∵圆O 为：x 2＋y 2＝2.∴弦PQ 所在直线的直角坐标方程为2＝2x ＋23y ，即x ＋3y －1＝0.3．(2017·河南六市一模)在直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－5＋22ty ＝5－22t (t 为参数)若以O 点为极点，x 轴正半轴为极轴建立极坐标系，则曲线C 的极坐标方程为ρ＝4cos θ.(1)求曲线C 的直角坐标方程及直线l 的普通方程；(2)将曲线C 上各点的横坐标缩短为原来的12，再将所得曲线向左平移1个单位，得到曲线C 1，求曲线C 1上的点到直线l 的距离的最小值．解：(1)由ρ＝4cos θ，得出ρ2＝4ρcos θ，化为直角坐标方程x 2＋y 2＝4x ， 即曲线C 的方程为(x －2)2＋y 2＝4，直线l 的方程是：x ＋y ＝0.(2)将曲线C 横坐标缩短为原来的12，再向左平移1个单位，得到曲线C 1的方程为4x 2＋y 2＝4，设曲线C 1上的任意点(cos θ，2sin θ)，到直线l 距离d ＝|cos θ＋2sin θ|2＝5|sin (θ＋α)|2.当sin(θ＋α)＝0时，到直线l 距离的最小值为0.4．(2017·南阳二模)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝12ty ＝1－32t (t为参数)．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝2sin θ.(1)判断直线l 与圆C 的交点个数；(2)若圆C 与直线l 交于A ，B 两点，求线段AB 的长度．解：(1)∵直线l 的参数方程为⎩⎨⎧x ＝12t y ＝1－32t (t 为参数)．∴消去参数t 得直线l 的普通方程为3x ＋y －1＝0， ∵圆C 的极坐标方程为ρ＝2sin θ，即ρ2＝2ρsin θ，∴由ρ2＝x 2＋y 2，ρsin θ＝y ，得圆C 的直角坐标方程为x 2＋y 2－2y ＝0. ∵圆心(0,1)在直线l 上， ∴直线l 与圆C 的交点个数为2. (2)由(1)知圆心(0,1)在直线l 上， ∴AB 为圆C 的直径，∵圆C 的直角坐标方程为x 2＋y 2－2y ＝0. ∴圆C 的半径r ＝12×4＝1，∴圆C 的直径为2，∴|AB |＝2.5．(2017·厦门二模)在平面直角坐标系中，以原点为极点，x 轴正半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位．已知曲线C 的极坐标方程为ρ＝2cos θ，直线l的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t cos αy ＝t sin α(t 为参数，α为直线的倾斜角)．(1)写出直线l 的普通方程和曲线C 的直角坐标方程； (2)若直线l 与曲线C 有唯一的公共点，求角α的大小． 解：(1)当α＝π2时，直线l 的普通方程为x ＝－1；当α≠π2时，直线l 的普通方程为y ＝tan α·(x ＋1)．由ρ＝2cos θ，得ρ2＝2ρcos θ，所以x 2＋y 2＝2x ，即为曲线C 的直角坐标方程．(2)把x ＝－1＋t cos α，y ＝t sin α代入x 2＋y 2＝2x ，整理得t 2－4t cos α＋3＝0.当α＝π2时，方程化为：t 2＋3＝0，方程不成立，当α≠π2时，由Δ＝16cos 2α－12＝0，得cos 2α＝34，所以cos α＝32或cos α＝－32， 故直线l 倾斜角α为π6或5π6.6．(2017·梅州二模)已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝－2＋2cos θy ＝2sin θ(θ为参数)，以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程是ρ＝4sin θ.(1)求曲线C 1与C 2交点的平面直角坐标；(2)A ，B 两点分别在曲线C 1与C 2上，当|AB |最大时，求△OAB 的面积(O 为坐标原点)．解：(1)∵曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝－2＋2cos θy ＝2sin θ(θ为参数)，∴曲线C 1的平面直角坐标方程为(x ＋2)2＋y 2＝4. 又由曲线C 2的极坐标方程是ρ＝4sin θ， 得ρ2＝4ρsin θ，∴x 2＋y 2＝4y ，把两式作差，得y ＝－x ，代入x 2＋y 2＝4y ，得2x 2＋4x ＝0，解得⎩⎪⎨⎪⎧ x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝－2y ＝2，∴曲线C 1与C 2交点的平面直角坐标为(0,0)，(－2,2)．(2)如图，由平面几何知识可知：当A ，C 1，C 2，B 依次排列且共线时，|AB |最大，此时|AB |＝22＋4，O 到AB 的距离为2，∴△OAB 的面积为S ＝12(22＋4)·2＝2＋2 2.。

第2讲 参数方程【20XX 年高考会这样考】考查直线、圆和圆锥曲线的参数方程以及简单的应用问题． 【复习指导】复习本讲时，应紧紧抓住直线的参数方程、圆的参数方程、圆锥曲线的参数方程的建立以及各参数方程中参数的几何意义，同时要熟练掌握参数方程与普通方程互化的一些方法.基础梳理1．参数方程的意义在平面直角坐标系中，如果曲线上的任意一点的坐标x ，y 都是某个变量的函数⎩⎨⎧x ＝f (t )，y ＝f (t )，并且对于t 的每个允许值，由方程组所确定的点M (x ，y )都在这条曲线上，则该方程叫曲线的参数方程，联系变数x ，y 的变数t 是参变数，简称参数．相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程． 2．常见曲线的参数方程的一般形式(1)经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程为⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．设P 是直线上的任一点，则t 表示有向线段P 0P →的数量． (2)圆的参数方程⎩⎨⎧x ＝r cos θ，y ＝r sin θ(θ为参数)．(3)圆锥曲线的参数方程椭圆x 2a 2＋y 2b 2＝1的参数方程为⎩⎨⎧x ＝a cos θ，y ＝b sin θ(θ为参数)．双曲线x 2a 2－y 2b 2＝1的参数方程为⎩⎨⎧x ＝a sec φ，y ＝tan φ(φ为参数)．抛物线y 2＝2px 的参数方程为⎩⎨⎧x ＝2pt 2，y ＝2pt(t 为参数)． 双基自测1．极坐标方程ρ＝cos θ和参数方程⎩⎨⎧x ＝－1－t ，y ＝2＋t (t 为参数)所表示的图形分别是( )．A ．直线、直线B ．直线、圆C ．圆、圆D ．圆、直线解析 ∵ρcos θ＝x ，∴cos θ＝x ρ代入到ρ＝cos θ，得ρ＝xρ，∴ρ2＝x ，∴x 2＋y 2＝x 表示圆．又∵⎩⎪⎨⎪⎧x ＝－1－t ，y ＝2＋t ，相加得x ＋y ＝1，表示直线．答案 D2．若直线⎩⎨⎧x ＝1－2t ，y ＝2＋3t (t 为实数)与直线4x ＋ky ＝1垂直，则常数k ＝________.解析 参数方程⎩⎪⎨⎪⎧x ＝1－2t ，y ＝2＋3t ，所表示的直线方程为3x ＋2y ＝7，由此直线与直线4x ＋ky ＝1垂直可得－32×⎝ ⎛⎭⎪⎫－4k ＝－1，解得k ＝－6.答案 －63．二次曲线⎩⎨⎧x ＝5cos θ，y ＝3sin θ(θ是参数)的左焦点的坐标是________．解析 题中二次曲线的普通方程为x 225＋y 29＝1左焦点为(－4,0)． 答案 (－4,0)4．(2011·广州调研)已知直线l 的参数方程为：⎩⎨⎧x ＝2t ，y ＝1＋4t (t 为参数)，圆C 的极坐标方程为ρ＝22sin θ，则直线l 与圆C 的位置关系为________．解析 将直线l 的参数方程：⎩⎪⎨⎪⎧x ＝2t ，y ＝1＋4t 化为普通方程得，y ＝1＋2x ，圆ρ＝22sin θ的直角坐标方程为x 2＋(y －2)2＝2，圆心(0，2)到直线y ＝1＋2x 的距离为2－11＋4，因为该距离小于圆的半径，所以直线l 与圆C 相交．答案 相交5．(2011·广东)已知两曲线参数方程分别为⎩⎨⎧x ＝5cos θ，y ＝sin θ(0≤θ＜π)和⎩⎪⎨⎪⎧x ＝54t 2，y ＝t(t ∈R )，它们的交点坐标为________． 解析 由⎩⎪⎨⎪⎧x ＝5cos θ，y ＝sin θ(0≤θ＜π)得，x 25＋y 2＝1(y ≥0)由⎩⎨⎧x ＝54t 2，y ＝t(t ∈R )得，x ＝54y 2，∴5y 4＋16y 2－16＝0. 解得：y 2＝45或y 2＝－4(舍去)．则x ＝54y 2＝1又θ≥0，得交点坐标为⎝ ⎛⎭⎪⎫1，255. 答案 ⎝⎛⎭⎪⎫1，255考向一 参数方程与普通方程的互化【例1】►把下列参数方程化为普通方程： (1)⎩⎨⎧x ＝3＋cos θ，y ＝2－sin θ；(2)⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝5＋32t .[审题视点] (1)利用平方关系消参数θ； (2)代入消元法消去t .解 (1)由已知⎩⎨⎧cos θ＝x －3，sin θ＝2－y ，由三角恒等式cos 2θ＋sin 2θ＝1,可知(x －3)2＋(y －2)2＝1，这就是它的普通方程． (2)由已知t ＝2x －2，代入y ＝5＋32t 中，得y ＝5＋32(2x －2)，即3x －y ＋5－3＝0就是它的普通方程．参数方程化为普通方程：化参数方程为普通方程的基本思路是消去参数，常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法，参数方程通过代入消元或加减消元消去参数化为普通方程，不要忘了参数的范围．【训练1】(2010·陕西)参数方程⎩⎨⎧x ＝cos α，y ＝1＋sin α(α为参数)化成普通方程为________．解析 由⎩⎪⎨⎪⎧ x ＝cos α，y ＝1＋sin α，得⎩⎪⎨⎪⎧x ＝cos α， ①y －1＝sin α， ②①2＋②2得：x 2＋(y －1)2＝1. 答案 x 2＋(y －1)2＝1考向二 直线与圆的参数方程的应用【例2】►已知圆C ：⎩⎨⎧ x ＝1＋cos θ，y ＝sin θ(θ为参数)和直线l ：⎩⎨⎧x ＝2＋t cos α，y ＝3＋t sin α(其中t 为参数，α为直线l 的倾斜角)．(1)当α＝2π3时，求圆上的点到直线l 距离的最小值； (2)当直线l 与圆C 有公共点时，求α的取值范围．[审题视点] (1)求圆心到直线l 的距离，这个距离减去圆的半径即为所求；(2)把圆的参数方程化为直角坐标方程，将直线的参数方程代入得关于参数t 的一元二次方程，这个方程的Δ≥0.解 (1)当α＝2π3时，直线l 的直角坐标方程为3x ＋y －33＝0，圆C 的圆心坐标为(1,0)，圆心到直线的距离d ＝232＝3，圆的半径为1，故圆上的点到直线l 距离的最小值为3－1.(2)圆C 的直角坐标方程为(x －1)2＋y 2＝1，将直线l 的参数方程代入圆C 的直角坐标方程，得t 2＋2(cos α＋3sin α)t ＋3＝0，这个关于t 的一元二次方程有解，故Δ＝4(cos α＋3sin α)2－12≥0，则sin 2⎝ ⎛⎭⎪⎫α＋π6≥34，即sin ⎝ ⎛⎭⎪⎫α＋π6≥32或sin⎝ ⎛⎭⎪⎫α＋π6≤－32.又0≤α＜π，故只能sin ⎝ ⎛⎭⎪⎫α＋π6≥32，即π3≤α＋π6≤2π3，即π6≤α≤π2.如果问题中的方程都是参数方程，那就要至少把其中的一个化为直角坐标方程．【训练2】 已知直线l 的参数方程为⎩⎨⎧x ＝1＋t ，y ＝4－2t (参数t ∈R )，圆C 的参数方程为⎩⎨⎧x ＝2cos θ＋2，y ＝2sin θ(参数θ∈[0,2π])，求直线l 被圆C 所截得的弦长． 解 由⎩⎨⎧ x ＝1＋t ，y ＝4－2t 消参数后得普通方程为2x ＋y －6＝0，由⎩⎨⎧x ＝2cos θ＋2，y ＝2sin θ消参数后得普通方程为(x －2)2＋y 2＝4，显然圆心坐标为(2,0)，半径为2.由于圆心到直线2x ＋y －6＝0的距离为d ＝|2×2＋0－6|22＋1＝255，所以所求弦长为222－⎝⎛⎭⎪⎫2552＝855. 考向三 圆锥曲线的参数方程的应用【例3】►求经过点(1,1)，倾斜角为135°的直线截椭圆x 24＋y 2＝1所得的弦长．[审题视点] 把直线方程用参数表示，直接与椭圆联立，利用根与系数的关系及弦长公式可解决．解由条件可知直线的参数方程是⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t(t 为参数)，代入椭圆方程可得⎝ ⎛⎭⎪⎫1－22t 24＋⎝⎛⎭⎪⎫1＋22t 2＝1， 即52t 2＋32t ＋1＝0.设方程的两实根分别为t 1、t 2，则由二次方程的根与系数的关系可得⎩⎪⎨⎪⎧t 1＋t 2＝－625，t 1t 2＝25，则直线截椭圆的弦长是|t 1－t 2|＝(t 1＋t 2)2－4t 1t 2＝⎝ ⎛⎭⎪⎫－6252－4×25＝425.普通方程化为参数方程：化普通方程为参数方程的基本思路是引入参数，即选定合适的参数t ，先确定一个关系x ＝f (t )(或y ＝φ(t ))，再代入普通方程F (x ，y )＝0，求得另一关系y ＝φ(t )(或x ＝f (t ))．一般地，常选择的参数有角、有向线段的数量、斜率，某一点的横坐标(或纵坐标)．普通方程化为参数方程需要引入参数，选择的参数不同，所得的参数方程也不一样．【训练3】(2011·南京模拟)过点P (－3,0)且倾斜角为30°的直线和曲线⎩⎪⎨⎪⎧x ＝t ＋1t ，y ＝t －1t(t 为参数)相交于A 、B 两点，求线段AB 的长．解直线的参数方程为⎩⎪⎨⎪⎧x ＝－3＋32s ，y ＝12s(s 为参数)，又曲线⎩⎪⎨⎪⎧x ＝t ＋1t ，y ＝t －1t(t 为参数)可以化为x 2－y 2＝4，将直线的参数方程代入上式，得s 2－63s ＋10＝0，设A 、B 对应的参数分别为s 1，s 2.∴s 1＋s 2＝63，s 1s 2＝10.∴|AB |＝|s 1－s 2|＝(s 1＋s 2)2－4s 1s 2＝217.如何解决极坐标方程与参数方程的综合问题从近两年的新课标高考试题可以看出，对参数方程的考查重点是直线的参数方程、圆的参数方程和圆锥曲线的参数方程的简单应用，特别是利用参数方程解决弦长和最值等问题，题型为填空题和解答题．【示例】►(本题满分10分)(2011·新课标全国)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎨⎧x ＝2cos α，y ＝2＋2sin α(α为参数)．M 是C 1上的动点，P 点满足OP →＝2OM →，P 点的轨迹为曲线C 2.(1)求C 2的方程；(2)在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线θ＝π3与C 1的异于极点的交点为A ，与C 2的异于极点的交点为B ，求|AB |.第(1)问：利用代入法；第(2)问把曲线C 1、曲线C 2均用极坐标表示，再求射线θ＝π3与曲线C 1、C 2的交点A 、B 的极径即可． [解答示范] (1)设P (x ，y )，则由条件知M ⎝ ⎛⎭⎪⎫x 2，y 2.由于M 点在C 1上，所以⎩⎪⎨⎪⎧x 2＝2cos α，y2＝2＋2sin α，即⎩⎨⎧x ＝4cos α，y ＝4＋4sin α. 从而C 2的参数方程为⎩⎨⎧x ＝4cos α，y ＝4＋4sin α(α为参数)．(5分)(2)曲线C 1的极坐标方程为ρ＝4sin θ，曲线C 2的极坐标方程为ρ＝8sin θ. 射线θ＝π3与C 1的交点A 的极径为ρ1＝4sin π3， 射线θ＝π3与C 2的交点B 的极径为ρ2＝8sin π3. 所以|AB |＝|ρ2－ρ1|＝2 3.(10分)很多自主命题的省份在选考坐标系与参数方程中的命题多以综合题的形式命题，而且通常将极坐标方程、参数方程相结合，以考查考生的转化与化归的能力．【试一试】(2011·江苏)在平面直角坐标系xOy 中，求过椭圆⎩⎨⎧x ＝5cos φ，y ＝3sin φ(φ为参数)的右焦点，且与直线⎩⎨⎧x ＝4－2t ，y ＝3－t (t 为参数)平行的直线的普通方程．[尝试解答] 由题设知，椭圆的长半轴长a ＝5，短半轴长b ＝3，从 而c ＝a 2－b 2＝4，所以右焦点为(4,0)．将已知直线的参数方程化为普通方程：x －2y ＋2＝0.故所求直线的斜率为12，因此其方程为y ＝12(x －4)，即x －2y －4＝0..精品资料。

第二节 参数方程[考纲传真] (教师用书独具)1.了解参数方程，了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第201页)[基础知识填充]1．曲线的参数方程(1)一般地，在取定的坐标系中，如果曲线上任意一点的坐标(x ，y )都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )，并且对于t 取的每一个允许值，由方程组所确定的点P (x ，y )都在这条曲线上，那么方程组就叫作这条曲线的参数方程，联系x ，y 之间关系的变数t 叫作参变数，简称参数．相对于参数方程，我们直接用坐标(x ，y )表示的曲线方程f (x ，y )＝0叫作曲线的普通方程．(2)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数，从参数方程得到普通方程．2．常见曲线的参数方程和普通方程点的轨迹 普通方程参数方程直线y －y 0＝tan α(x －x 0) ⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)圆 x 2＋y 2＝r 2 ⎩⎪⎨⎪⎧ x ＝r cos θ，y ＝r sin θ(θ为参数)椭圆x 2a 2＋y 2b 2＝1(a >b >0) ⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ(φ为参数)[意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( )(3)方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝1＋2sin θ表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t(t 为参数)，点M 在椭圆上，对应参数t＝π3，点O 为原点，则直线OM 的斜率为 3.( ) [答案] (1)√ (2)√ (3)√ (4)×2．(教材改编)曲线⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( ) A ．在直线y ＝2x 上 B ．在直线y ＝－2x 上 C ．在直线y ＝x －1上 D ．在直线y ＝x ＋1上B [由⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ，得⎩⎪⎨⎪⎧cos θ＝x ＋1，sin θ＝y －2，所以(x ＋1)2＋(y －2)2＝1.曲线是以(－1,2)为圆心，1为半径的圆， 所以对称中心为(－1,2)，在直线y ＝－2x 上．] 3．(教材改编)在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)的普通方程为________．x －y －1＝0 [由x ＝2＋22t ，且y ＝1＋22t ， 消去t ，得x －y ＝1，即x －y －1＝0.] 4．椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，过左焦点F 1的直线l 与C 相交于A ，B ，则|AB |min ＝________.185 [由⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，消去参数φ得x 225＋y 29＝1，当AB ⊥x 轴时，|AB |有最小值． 所以|AB |min ＝2×95＝185.]5．(2017·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值．[解] 直线l 的普通方程为x －2y ＋8＝0. 因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋(－2)2＝2(s －2)2＋45. 当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上的点P 到直线l 的距离取到最小值455.(对应学生用书第202页)参数方程与普通方程的互化(1)求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t(t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数．(2)在平面直角坐标系xOy 中，若直线l ：⎩⎪⎨⎪⎧x ＝t ，y ＝t －a(t 为参数)过椭圆C ：⎩⎪⎨⎪⎧x ＝3cos φ，y ＝2sin φ(φ为参数)的右顶点，求常数a 的值.【导学号：79140389】[解] (1)将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α得圆x 2＋y 2＝9.又圆心(0,0)到直线x ＋y －1＝0的距离d ＝22<3. 因此直线与圆相交，故直线与曲线有2个交点． (2)直线l 的普通方程为x －y －a ＝0， 椭圆C 的普通方程为x 29＋y 24＝1，所以椭圆C 的右顶点坐标为(3,0)，若直线l 过(3,0)， 则3－a ＝0，∴a ＝3.[规律方法] 化参数方程为普通方程的基本思路是消去参数，常用的消参方法有代入消去法、加减消去法、恒等式三角的或代数的消去法.另外，消参时要注意参数的范围. 普通方程化为参数方程时，先分清普通方程所表示的曲线类型，结合常见曲线的参数方程直接写出.[跟踪训练] 如图2，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程．图2[解] 圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ， 则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．参数方程的应用(2017·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ(θ为参数)，直线l 经过点P (1,2)，倾斜角α＝π6.(1)写出圆C 的普通方程和直线l 的参数方程；(2)设直线l 与圆C 相交于A ，B 两点，求|PA |·|PB |的值．[解] (1)由⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ，消去θ，得圆C 的普通方程为x 2＋y 2＝16. 又直线l 过点P (1,2)且倾斜角α＝π6，所以l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos π6，y ＝2＋t sin π6，即⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t (t 为参数)．(2)把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t代入x 2＋y 2＝16，得⎝⎛⎭⎪⎫1＋32t 2＋⎝ ⎛⎭⎪⎫2＋12t 2＝16，t 2＋(3＋2)t －11＝0，所以t 1t 2＝－11，由参数方程的几何意义，|PA |·|PB |＝|t 1t 2|＝11. [规律方法]1解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有关的问题，如最值、范围等.2根据直线的参数方程的标准式中t 的几何意义，有如下常用结论： 过定点M 0的直线与圆锥曲线相交，交点为M 1，M 2，所对应的参数分别为t 1，t 2. ①弦长l ＝|t 1－t 2|； ②弦M 1M 2的中点⇒t 1＋t 2＝0； ③|M 0M 1||M 0M 2|＝|t 1t 2|.⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . [解] (1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8;当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.极坐标方程与参数方程的综合应用(2018·石家庄质检(二))在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋a cos β，y ＝a sin β(a >0，β为参数)．以O 为极点，x 轴的正半轴为极轴，建立极坐标系，直线l 的极坐标方程ρcos ⎝⎛⎭⎪⎫θ－π3＝32.(1)若曲线C 与l 只有一个公共点，求a 的值；(2)A ，B 为曲线C 上的两点，且∠AOB ＝π3，求△OAB 的面积最大值．[解] (1)曲线C 是以(a,0)为圆心，以a 为半径的圆， 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 只有一个公共点，则可得|a －3|2＝a ，解得a ＝－3(舍)，a ＝1. 所以a ＝1.(2)法一：曲线C 的极坐标方程为ρ＝2a cos θ(a >0)， 设A 的极角为θ，B 的极角为θ＋π3，则S △OAB ＝12|OA |·|OB |sin π3＝34|2a cos θ|·⎪⎪⎪⎪⎪⎪2a cos ⎝⎛⎭⎪⎫θ＋π3＝3a 2⎪⎪⎪⎪⎪⎪cos θcos ⎝⎛⎭⎪⎫θ＋π3，∵cos θcos ⎝ ⎛⎭⎪⎫θ＋π3＝12cos 2θ－32sin θcos θ ＝12·cos 2θ＋12－34sin 2θ ＝12⎝ ⎛⎭⎪⎫12cos 2θ－32sin 2θ＋14 ＝12cos ⎝⎛⎭⎪⎫2θ＋π3＋14，所以当θ＝－π6时，12cos ⎝ ⎛⎭⎪⎫2θ＋π3＋14取得最大值34.△OAB 的面积最大值为33a24.法二：因为曲线C 是以(a,0)为圆心，以a 为半径的圆，且∠AOB ＝π3，由正弦定理得|AB |sinπ3＝2a ，所以|AB |＝3a .由余弦定理得|AB |2＝3a 2＝|OA |2＋|OB |2－|OA |·|OB | ≥|OA |·|OB |，所以S △OAB ＝12|OA |·|OB |sin π3≤12×3a 2×32＝33a 24， 所以△OAB 的面积最大值为33a 24.[规律方法] 处理极坐标、参数方程综合问题的方法 1涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然，还要结合题目本身特点，确定选择何种方程.2数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的.1⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ(其中φ为参数)．以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ(tan α·cos θ－sin θ)＝1(α是常数，0<α<π，且α≠π2)，点A ，B (A 在x 轴的下方)是曲线C 1与C 2的两个不同交点．(1)求曲线C 1的普通方程和C 2的直角坐标方程； (2)求|AB |的最大值及此时点B 的坐标.【导学号：79140390】[解] (1)∵⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，∴x 24＋y 2＝1， 由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得曲线C 2的直角坐标方程为y ＝tan α·x －1.(2)由(1)得曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α(t 是参数)，设A (t 1cos α，－1＋t 1sin α)，B (t 2cos α，－1＋t 2sin α)，将C 2：⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α，代入x 24＋y 2＝1，整理得t 2(1＋3sin 2α)－8t sin α＝0， ∴t 1＝0，t 2＝8sin α1＋3sin 2α， ∴|AB |＝|t 1－t 2|＝8|sin α|1＋3sin 2α ＝83|sin α|＋1|sin α|≤823＝433(当且仅当sin α＝33取等号)， 当sin α＝33时，∴0<α<π，且α≠π2， ∴cos α＝±63， ∴B ⎝ ⎛⎭⎪⎫±423，13， ∴|AB |的最大值为433，此时点B 的坐标为⎝ ⎛⎭⎪⎫±423，13.。

第2讲 参数方程一、知识梳理1．参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式，一般地，可以通过消去参数，从参数方程得到普通方程．(2)如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么⎩⎪⎨⎪⎧x ＝f （t ），y ＝g （t ）就是曲线的参数方程，在参数方程与普通方程的互化中，必须使x ，y 的取值X 围保持一致．2．直线、圆和圆锥曲线的参数方程 名称普通方程参数方程直线 y －y 0＝k (x －x 0)⎩⎪⎨⎪⎧x ＝x 0＋t cos αy ＝y 0＋t sin α (t 为参数)圆 (x －x 0)2＋(y －y 0)2＝r2⎩⎪⎨⎪⎧x ＝x 0＋r cos θy ＝y 0＋r sin θ (θ为参数且0≤θ<2π)椭圆x 2a 2＋y 2b 2＝1(a >b >0) ⎩⎪⎨⎪⎧x ＝a cos t y ＝b sin t (t 为参数且0≤t <2π)常用结论经过点P (x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．若A ，B 为直线l 上的两点，其对应的参数分别为t 1，t 2，线段AB 的中点为M ，点M 所对应的参数为t 0，则以下结论在解题中经常用到：(1)t 0＝t 1＋t 22；(2)|PM |＝|t 0|＝⎪⎪⎪⎪⎪⎪t 1＋t 22；(3)|AB |＝|t 2－t 1|； (4)|PA |·|PB |＝|t 1·t 2|. 二、习题改编1．(选修4­4P22例1改编)已知曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3t ，y ＝2t 2＋1(t 为参数)，点M (－6，a )在曲线C 上，则a ＝．解析：由题意得⎩⎪⎨⎪⎧－6＝3t ，a ＝2t 2＋1，所以⎩⎪⎨⎪⎧t ＝－2，a ＝9. 答案：92．(选修4­4P36例1改编)在直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝22t (t 为参数)，与圆C ：(x －3)2＋(y －3)2＝4交于A ，B 两点，求|AB |.解：将直线l 的参数方式代入圆C 的直角坐标方程，得⎝ ⎛⎭⎪⎫22t －12＋⎝ ⎛⎭⎪⎫22t －32＝4，即t 2－42t ＋6＝0，设两交点A ，B 所对应的参数分别为t 1，t 2，从而t 1＋t 2＝42，t 1t 2＝6，则|AB |＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2＝2 2.一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝f （t ），y ＝g （t ）中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( )(3)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t (t 为参数)，点M 在椭圆上，对应参数t ＝π3，点O 为原点，则直线OM 的斜率为 3.( )答案：(1)√ (2)√ (3)× 二、易错纠偏常见误区(1)不注意互化的等价性致误； (2)直线参数方程中参数t 的几何意义不清致误．1．在平面直角坐标系中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋sin 2θ，y ＝－1＋cos 2θ(θ为参数)，求曲线C 的普通方程． 解：由x ＝2＋sin 2θ，0≤sin 2θ≤1 ⇒2≤2＋sin 2θ≤3⇒2≤x ≤3，⎩⎪⎨⎪⎧x ＝2＋sin 2θ，y ＝－1＋cos 2θ⇒⎩⎪⎨⎪⎧x －2＝sin 2θ，y ＝－1＋1－2sin 2θ⇒⎩⎪⎨⎪⎧x －2＝sin 2θy ＝－2sin 2θ⇒2x ＋y －4＝0(2≤x ≤3)． 2．在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝2＋t ，y ＝1＋3t(t 为参数)，曲线C 的普通方程为(x －4)2＋(y －3)2＝4，设点M (2，1)，直线l 与曲线C 相交于A ，B 两点，求|MA |·|MB |的值．解：设点A ，B 对应的参数分别为t 1，t 2，将⎩⎨⎧x ＝2＋t ，y ＝1＋3t(t 为参数)代入(x －4)2＋(y －3)2＝4， 得t 2－(3＋1)t ＋1＝0， 所以t 1t 2＝1，直线l ：⎩⎨⎧x ＝2＋ty ＝1＋3t(t 为参数)，可化为⎩⎪⎨⎪⎧x ＝2＋12（2t ）y ＝1＋32（2t ），所以|MA |·|MB |＝|2t 1||2t 2|＝4|t 1t 2|＝4.参数方程与普通方程的互化(师生共研)已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t ，y ＝3＋sin t(t 为参数)，曲线C 2：⎩⎪⎨⎪⎧x ＝8cos θ，y ＝3sin θ(θ为参数)．化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线．【解】 曲线C 1：(x ＋4)2＋(y －3)2＝1， 曲线C 2：x 264＋y 29＝1， 曲线C 1是以(－4，3)为圆心，1为半径的圆；曲线C 2是中心为坐标原点，焦点在x 轴上，长半轴长是8，短半轴长是3的椭圆．将参数方程化为普通方程的方法(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等．对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin 2θ＋cos 2θ＝1等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解．1．求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t (t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数． 解：将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α得圆x 2＋y 2＝9. 又圆心(0，0)到直线x ＋y －1＝0的距离d ＝22<3. 因此直线与圆相交，故直线与曲线有2个交点．2．如图，以过原点的直线的倾斜角θ为参数，求圆x 2＋y 2－x ＝0的参数方程．解：圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ，则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．参数方程的应用(师生共研)(2019·高考全国卷Ⅰ)在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝1－t 21＋t2，y ＝4t1＋t2(t为参数)．以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 的极坐标方程为2ρcos θ＋3ρsin θ＋11＝0.(1)求C 和l 的直角坐标方程； (2)求C 上的点到l 距离的最小值．【解】 (1)因为－1<1－t 21＋t 2≤1，且x 2＋⎝ ⎛⎭⎪⎫y 22＝⎝ ⎛⎭⎪⎫1－t 21＋t 22＋4t 2（1＋t 2）2＝1，所以C 的直角坐标方程为x 2＋y 24＝1(x ≠－1)．l 的直角坐标方程为2x ＋3y ＋11＝0.(2)由(1)可设C 的参数方程为⎩⎪⎨⎪⎧x ＝cos α，y ＝2sin α(α为参数，－π<α<π)．C 上的点到l 的距离为|2cos α＋23sin α＋11|7＝4cos ⎝⎛⎭⎪⎫α－π3＋117.当α＝－2π3时，4cos(α－π3)＋11取得最小值7，故C 上的点到l 距离的最小值为7.(1)解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上和动点有关的问题，如最值、X 围等．(2)根据直线的参数方程的标准式中t 的几何意义，有如下常用结论：过定点M 0的直线与圆锥曲线相交，交点为M 1，M 2，所对应的参数分别为t 1，t 2，①弦长l ＝|t 1－t 2|；②M 0为弦M 1M 2的中点⇒t 1＋t 2＝0；③|M 0M 1|·|M 0M 2|＝|t 1t 2|.1．已知曲线C 的普通方程为x 212＋y 24＝1，求曲线C 的内接矩形周长的最大值．解：由曲线C 的直角坐标方程为x 212＋y 24＝1，可设曲线C 上的动点A (23cos α，2sin α)，0<α<π2，则以A 为顶点的内接矩形的周长为4(23cos α＋2sin α)＝16sin(α＋π3)，0<α<π2.因此该内接矩形周长的最大值为16，当且仅当α＝π6时取得最大值．2．(2020·某某第一次诊断性检测)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝12t ，y ＝32t －1(t 为参数)．在以坐标原点O 为极点，x 轴的正半轴为极轴，且与直角坐标系长度单位相同的极坐标系中，曲线C 的极坐标方程是ρ＝22sin ⎝⎛⎭⎪⎫π4＋θ.(1)求直线l 的普通方程与曲线C 的直角坐标方程；(2)设点P (0，－1)，若直线l 与曲线C 相交于A ，B 两点，求|PA |＋|PB |的值． 解：(1)将直线l 的参数方程消去参数t 并化简， 得直线l 的普通方程为3x －y －1＝0. 曲线C 的极坐标方程可化为ρ2＝22ρ⎝⎛⎭⎪⎫22sin θ＋22cos θ，即ρ2＝2ρsin θ＋2ρcos θ，所以x 2＋y 2＝2y ＋2x ， 故曲线C 的直角坐标方程为(x －1)2＋(y －1)2＝2. (2)将直线l 的参数方程代入(x －1)2＋(y －1)2＝2中， 得⎝ ⎛⎭⎪⎫12t －12＋⎝ ⎛⎭⎪⎫32t －22＝2，化简，得t 2－(1＋23)t ＋3＝0.可得Δ>0，所以此方程的两根为直线l 与曲线C 的交点A ，B 对应的参数t 1，t 2. 由根与系数的关系，得t 1＋t 2＝23＋1，t 1t 2＝3，故t 1，t 2同正．由直线的参数方程中参数的几何意义，知|PA |＋|PB |＝|t 1|＋|t 2|＝t 1＋t 2＝23＋1.极坐标与参数方程的综合问题(师生共研)(一题多解)(2020·某某省适应性考试)曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋2cos α，y ＝2sin α(α为参数)，在以原点O 为极点，x 轴的非负半轴为极轴的极坐标系中，曲线C 2的极坐标方程为ρcos 2θ＝sin θ.(1)求曲线C 1的极坐标方程和曲线C 2的直角坐标方程；(2)过原点且倾斜角为α(π6<α≤π4)的射线l 与曲线C 1，C 2分别相交于A ，B 两点(A ，B 异于原点)，求|OA |·|OB |的取值X 围．【解】 (1)曲线C 1的普通方程为(x －2)2＋y 2＝4， 即x 2＋y 2－4x ＝0，故曲线C 1的极坐标方程为ρ2＝4ρcos θ，即ρ＝4cos θ.由曲线C 2的极坐标方程为ρcos 2θ＝sin θ，两边同乘以ρ，得ρ2cos 2θ＝ρsin θ，故曲线C 2的直角坐标方程为x 2＝y .(2)法一：射线l 的极坐标方程为θ＝α，π6<α≤π4，把射线l 的极坐标方程代入曲线C 1的极坐标方程得|OA |＝ρ＝4cos α， 把射线l 的极坐标方程代入曲线C 2的极坐标方程得|OB |＝ρ＝sin αcos 2α， 所以|OA |·|OB |＝4cos α·sin αcos 2α＝4tan α， 因为π6<α≤π4，所以|OA |·|OB |的取值X 围是⎝⎛⎦⎥⎤433，4. 法二：射线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，π6<α≤π4)．把射线l 的参数方程代入曲线C 1的普通方程得t 2－4t cos α＝0. 解得t 1＝0，t 2＝4cos α.故|OA |＝|t 2|＝4cos α. 同理可得|OB |＝sin αcos 2α， 所以|OA |·|OB |＝4cos α·sin αcos 2α＝4tan α， 因为π6<α≤π4，所以|OA |·|OB |的取值X 围是⎝⎛⎦⎥⎤433，4.处理极坐标、参数方程综合问题的方法(1)涉及参数方程和极坐标的综合问题时，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．(2)数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的．(一题多解)(2020·某某市模拟考试)在平面直角坐标系xOy 中，曲线C的参数方程为⎩⎨⎧x ＝3cos α，y ＝1＋3sin α(α为参数)，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρsin ⎝⎛⎭⎪⎫θ＋π6＝2 3.(1)求曲线C 的普通方程和直线l 的直角坐标方程；(2)射线OP 的极坐标方程为θ＝π6(ρ≥0)，若射线OP 与曲线C 的交点为A ，与直线l的交点为B ，求线段AB 的长．解：(1)由⎩⎨⎧x ＝3cos α，y ＝1＋3sin α，可得⎩⎨⎧x ＝3cos α，y －1＝3sin α，所以x 2＋(y －1)2＝3cos 2α＋3sin 2α＝3， 所以曲线C 的普通方程为x 2＋(y －1)2＝3.由ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝23，可得ρ⎝ ⎛⎭⎪⎫32sin θ＋12cos θ＝23， 所以32ρsin θ＋12ρcos θ－23＝0， 所以直线l 的直角坐标方程为x ＋3y －43＝0. (2)法一：曲线C 的方程可化为x 2＋y 2－2y －2＝0， 所以曲线C 的极坐标方程为ρ2－2ρsin θ－2＝0. 由题意设A ⎝⎛⎭⎪⎫ρ1，π6，B ⎝ ⎛⎭⎪⎫ρ2，π6，将θ＝π6代入ρ2－2ρsin θ－2＝0，可得ρ2－ρ－2＝0，所以ρ＝2或ρ＝－1(舍去)，即ρ1＝2， 将θ＝π6代入ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝23， 可得ρ＝4，即ρ2＝4， 所以|AB |＝|ρ1－ρ2|＝2.法二：因为射线OP 的极坐标方程为θ＝π6(ρ≥0)，所以射线OP 的直角坐标方程为y ＝33x (x ≥0)， 由⎩⎪⎨⎪⎧x 2＋（y －1）2＝3，y ＝33x （x ≥0），解得A (3，1)， 由⎩⎪⎨⎪⎧x ＋3y －43＝0y ＝33x （x ≥0），解得B (23，2)，所以|AB |＝（23－3）2＋（2－1）2＝2.[基础题组练]1．在平面直角坐标系中，以原点为极点，x 轴正半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位．已知曲线C 的极坐标方程为ρ＝2cos θ，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t cos α，y ＝t sin α(t 为参数，α为直线的倾斜角)． (1)写出直线l 的普通方程和曲线C 的直角坐标方程； (2)若直线l 与曲线C 有唯一的公共点，求角α的大小． 解：(1)当α＝π2时，直线l 的普通方程为x ＝－1；当α≠π2时，直线l 的普通方程为y ＝(x ＋1)tan α.由ρ＝2cos θ，得ρ2＝2ρcos θ， 所以x 2＋y 2＝2x ，即为曲线C 的直角坐标方程．(2)把x ＝－1＋t cos α，y ＝t sin α代入x 2＋y 2＝2x ，整理得t 2－4t cos α＋3＝0. 由Δ＝16cos 2α－12＝0，得cos 2α＝34，所以cos α＝32或cos α＝－32， 故直线l 的倾斜角α为π6或5π6.2．以极点为原点，以极轴为x 轴正半轴建立平面直角坐标系，已知曲线C 的极坐标方程为ρ＝10，曲线C ′的参数方程为⎩⎪⎨⎪⎧x ＝3＋5cos α，y ＝－4＋5sin α，(α为参数)．(1)判断两曲线C 和C ′的位置关系；(2)若直线l 与曲线C 和C ′均相切，求直线l 的极坐标方程． 解：(1)由ρ＝10得曲线C 的直角坐标方程为x 2＋y 2＝100，由⎩⎪⎨⎪⎧x ＝3＋5cos α，y ＝－4＋5sin α得曲线C ′的普通方程为(x －3)2＋(y ＋4)2＝25.曲线C 表示以(0，0)为圆心，10为半径的圆； 曲线C ′表示以(3，－4)为圆心，5为半径的圆．因为两圆心间的距离5等于两圆半径的差，所以圆C 和圆C ′的位置关系是内切．(2)由(1)建立方程组⎩⎪⎨⎪⎧x 2＋y 2＝100，（x －3）2＋（y ＋4）2＝25， 解得⎩⎪⎨⎪⎧x ＝6，y ＝－8，可知两圆的切点坐标为(6，－8)，且公切线的斜率为34，所以直线l 的直角坐标方程为y ＋8＝34(x －6)，即3x －4y －50＝0，所以极坐标方程为3ρcos θ－4ρsin θ－50＝0.3．(2020·某某市第二次诊断性检测)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，α为倾斜角)，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝4＋2cos β，y ＝2sin β(β为参数，β∈[0，π])．以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系．(1)写出曲线C 的普通方程和直线l 的极坐标方程； (2)若直线l 与曲线C 恰有一个公共点P ，求点P 的极坐标．解：(1)由曲线C 的参数方程⎩⎪⎨⎪⎧x ＝4＋2cos βy ＝2sin β，得(x －4)2＋y 2＝4.因为β∈[0，π]，所以曲线C 的普通方程为(x －4)2＋y 2＝4(y ≥0)． 因为直线l 的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，α为倾斜角)，所以直线l 的倾斜角为α，且过原点O (极点)． 所以直线l 的极坐标方程为θ＝α，ρ∈R . (2)由(1)可知，曲线C 为半圆弧．若直线l 与曲线C 恰有一个公共点P ，则直线l 与半圆弧相切． 设P (ρ，θ)(ρ>0)．由题意，得sin θ＝24＝12，故θ＝π6.而ρ2＋22＝42，所以ρ＝2 3.所以点P 的极坐标为⎝⎛⎭⎪⎫23，π6. 4．(2020·某某省质量检查)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋35t ，y ＝1＋45t(t 为参数)．以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ2＝21＋sin 2θ，点P 的极坐标为⎝⎛⎭⎪⎫2，π4. (1)求曲线C 的直角坐标方程和点P 的直角坐标；(2)设l 与C 交于A ，B 两点，线段AB 的中点为M ，求|PM |. 解：(1)由ρ2＝21＋sin 2θ得ρ2＋ρ2sin 2θ＝2，① 将ρ2＝x 2＋y 2，y ＝ρsin θ代入①并整理得，曲线C 的直角坐标方程为x 22＋y 2＝1.设点P 的直角坐标为(x ，y )，因为点P 的极坐标为⎝ ⎛⎭⎪⎫2，π4， 所以x ＝ρcos θ＝2cos π4＝1，y ＝ρsin θ＝2sin π4＝1.所以点P 的直角坐标为(1，1)．(2)将⎩⎪⎨⎪⎧x ＝1＋35t ，y ＝1＋45t 代入x 22＋y 2＝1，并整理得41t 2＋110t ＋25＝0，Δ＝1102－4×41×25＝8 000>0，故可设方程的两根分别为t 1，t 2，则t 1，t 2为A ，B 对应的参数，且t 1＋t 2＝－11041.依题意，点M 对应的参数为t 1＋t 22，所以|PM |＝⎪⎪⎪⎪⎪⎪t 1＋t 22＝5541.5．(2020·某某省湘东六校联考)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝7－t ，y ＝－2＋t (t 为参数)．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C ：ρ＝42sin ⎝⎛⎭⎪⎫θ＋π4.(1)求直线l 的普通方程和曲线C 的直角坐标方程；(2)设曲线C 与直线l 的交点为A ，B ，Q 是曲线C 上的动点，求△ABQ 面积的最大值．解：(1)由⎩⎪⎨⎪⎧x ＝7－t ，y ＝－2＋t 消去t 得x ＋y －5＝0，所以直线l 的普通方程为x ＋y －5＝0.由ρ＝42sin ⎝ ⎛⎭⎪⎫θ＋π4＝4sin θ＋4cos θ，得ρ2＝4ρsin θ＋4ρcos θ，化为直角坐标方程为x 2＋y 2＝4x ＋4y ，所以曲线C 的直角坐标方程为(x －2)2＋(y －2)2＝8.(2)由(1)知，曲线C 是以(2，2)为圆心，22为半径的圆，直线l 过点P (3，2)，可知点P 在圆内．将直线l 的参数方程化为⎩⎪⎨⎪⎧x ＝7－22t y ＝－2＋22t ，代入圆的直角坐标方程，得t 2－92t ＋33＝0.设A ，B 对应的参数分别为t 1，t 2，则t 1＋t 2＝92，t 1t 2＝33， 所以|AB |＝|t 2－t 1|＝（t 1＋t 2）2－4t 1t 2＝30. 又圆心(2，2)到直线l 的距离d ＝|2＋2－5|2＝22，所以△ABQ 面积的最大值为12×30×⎝ ⎛⎭⎪⎫22＋22＝5152. 6．(2020·某某第三次调研测试)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t (t 为参数)，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρsin 2θ＝4cos θ.(1)求曲线C 1的普通方程与曲线C 2的直角坐标方程；(2)若C 1与C 2交于A ，B 两点，点P 的极坐标为⎝⎛⎭⎪⎫2，π4，求1|PA |＋1|PB |的值．解：(1)曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t ，(t 为参数)，两式相加消去t 可得普通方程为x ＋yρcos θ＝x ，ρsin θ＝y ，曲线C 2的极坐标方程为ρsin 2θ＝4cos θ，可得曲线C 2的直角坐标方程为y 2＝4x .(2)把曲线C 1的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t(t 为参数)代入y 2＝4x ，得t 2＋62t －6＝0，设t 1，t 2是A ，B 对应的参数，则t 1＋t 1＝－62，t 1·t 2＝－6，所以1|PA |＋1|PB |＝|PA |＋|PB ||PA |·|PB |＝|t 1－t 2||t 1·t 2|＝（t 1＋t 2）2－4t 1·t 2|t 1·t 2|＝966＝263.[综合题组练]1．(2020·某某某某第一次(3月)双基测试)在平面直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α⎝ ⎛⎭⎪⎫t 为参数且t >0，α∈⎝ ⎛⎭⎪⎫0，π2，曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝cos β，y ＝1＋sin β⎝ ⎛⎭⎪⎫β为参数，且β∈⎝ ⎛⎭⎪⎫－π2，π2，以O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C3的极坐标方程为ρ＝1＋cos θ⎝ ⎛⎭⎪⎫θ∈⎝⎛⎭⎪⎫0，π2，曲线C 4的极坐标方程为ρcos θ＝1.(1)求C 3与C 4的交点到极点的距离；(2)设C 1与C 2交于P 点，C 1与C 3交于Q 点，当α在⎝⎛⎭⎪⎫0，π2上变化时，求|OP |＋|OQ |的最大值．解：(1)联立⎩⎪⎨⎪⎧ρ＝1＋cos θ⎝ ⎛⎭⎪⎫θ∈⎝ ⎛⎭⎪⎫0，π2，ρcos θ＝1得ρ2－ρ－1＝0，解得ρ＝1＋52，即交点到极点的距离为1＋52.(2)曲线C 1的极坐标方程为θ＝α⎝ ⎛⎭⎪⎫α∈⎝ ⎛⎭⎪⎫0，π2，ρ>0，曲线C 2的极坐标方程为ρ＝2sin θ，θ∈⎝ ⎛⎭⎪⎫0，π2，联立C 1，C 2的极坐标方程得ρ＝2sin α，α∈⎝⎛⎭⎪⎫0，π2，即|OP |＝2sin α，α∈⎝⎛⎭⎪⎫0，π2，曲线C 1与曲线C 3的极坐标方程联立得ρ＝1＋cos α，α∈⎝ ⎛⎭⎪⎫0，π2，即|OQ |＝1＋cos α，α∈⎝⎛⎭⎪⎫0，π2，所以|OP |＋|OQ |＝1＋2sin α＋cos α＝1＋5sin(α＋φ)，其中φ的终边经过点(2，1)，当α＋φ＝π2＋2k π，k ∈Z 时，|OP |＋|OQ |取得最大值，为1＋ 5.2．(2020·原创冲刺卷二)在直角坐标系xOy 中，直线C 1：x ＋y ＝4，曲线C 2：⎩⎨⎧x ＝2cos αy ＝3sin α(α为参数)．在同一平面直角坐标系中，曲线C 2上的点经过坐标变换⎩⎪⎨⎪⎧x ′＝12x ＋1，y ′＝33y ，得到曲线C 3，以原点为极点，x 轴的正半轴为极轴建立极坐标系．(1)求直线C 1的极坐标方程和曲线C 3的极坐标方程；(2)若射线l ：θ＝α(ρ>0)分别交C 1与C 3于A ，B 两点，求|OB ||OA |的取值X 围．解：(1)由C 1：x ＋y ＝4，得直线C 1的极坐标方程为ρcos θ＋ρsin θ＝4， 由曲线C 2的参数方程得其普通方程为x 24＋y 23＝1，由⎩⎪⎨⎪⎧x ′＝12x ＋1，y ′＝33y可得⎩⎨⎧x ＝2（x ′－1），y ＝3y ′，将其代入x 24＋y 23＝1，可得(x ′－1)2＋y ′2＝1，所以曲线C 3的极坐标方程为ρ＝2cos θ. (2)设A (ρ1，α)，B (ρ2，α)，则－π4<α<π2，由题可得ρ1＝4cos α＋sin α，ρ2＝2cos α，所以|OB ||OA |＝ρ2ρ1＝14×2cos α(cos α＋sin α)＝14(cos 2α＋sin 2α＋1)＝14⎣⎢⎡⎦⎥⎤2cos ⎝ ⎛⎭⎪⎫2α－π4＋1，因为－π4<α<π2，所以－22<cos ⎝⎛⎭⎪⎫2α－π4≤1，所以0<14⎣⎢⎡⎦⎥⎤2cos ⎝ ⎛⎭⎪⎫2α－π4＋1≤14(2＋1)． 所以|OB ||OA |的取值X 围是⎝ ⎛⎦⎥⎤0，14（2＋1）.。

第二节 参数方程[考纲传真] (教师用书独具)1.了解参数方程，了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第201页)[基础知识填充]1．曲线的参数方程(1)一般地，在取定的坐标系中，如果曲线上任意一点的坐标(x ，y )都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )，并且对于t 取的每一个允许值，由方程组所确定的点P (x ，y )都在这条曲线上，那么方程组就叫作这条曲线的参数方程，联系x ，y 之间关系的变数t 叫作参变数，简称参数．相对于参数方程，我们直接用坐标(x ，y )表示的曲线方程f (x ，y )＝0叫作曲线的普通方程．(2)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数，从参数方程得到普通方程．2．常见曲线的参数方程和普通方程[意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( ) (3)方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝1＋2sin θ表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t(t 为参数)，点M 在椭圆上，对应参数t＝π3，点O 为原点，则直线OM 的斜率为 3.( ) [答案] (1)√ (2)√ (3)√ (4)×2．(教材改编)曲线⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( ) A ．在直线y ＝2x 上 B ．在直线y ＝－2x 上 C ．在直线y ＝x －1上D ．在直线y ＝x ＋1上B [由⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ，得⎩⎪⎨⎪⎧cos θ＝x ＋1，sin θ＝y －2，所以(x ＋1)2＋(y －2)2＝1.曲线是以(－1,2)为圆心，1为半径的圆， 所以对称中心为(－1,2)，在直线y ＝－2x 上．] 3．(教材改编)在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)的普通方程为________．x －y －1＝0 [由x ＝2＋22t ，且y ＝1＋22t ， 消去t ，得x －y ＝1，即x －y －1＝0.] 4．椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，过左焦点F 1的直线l 与C 相交于A ，B ，则|AB |min ＝________.185 [由⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，消去参数φ得x 225＋y 29＝1，当AB ⊥x 轴时，|AB |有最小值． 所以|AB |min ＝2×95＝185.]5．(2017·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值．[解] 直线l 的普通方程为x －2y ＋8＝0. 因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋(－2)2＝2(s －2)2＋45. 当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上的点P 到直线l 的距离取到最小值455.(对应学生用书第202页)(1)求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t(t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数．(2)在平面直角坐标系xOy中，若直线l ：⎩⎪⎨⎪⎧x ＝t ，y ＝t －a (t 为参数)过椭圆C ：⎩⎪⎨⎪⎧x ＝3cos φ，y ＝2sin φ(φ为参数)的右顶点，求常数a 的值.【导学号：79140389】[解] (1)将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α得圆x 2＋y 2＝9.又圆心(0,0)到直线x ＋y －1＝0的距离d ＝22<3.因此直线与圆相交，故直线与曲线有2个交点． (2)直线l 的普通方程为x －y －a ＝0， 椭圆C 的普通方程为x 29＋y 24＝1，所以椭圆C 的右顶点坐标为(3,0)，若直线l 过(3,0)， 则3－a ＝0，∴a ＝3.法、加减消去法、恒等式三角的或代数的消去法普通方程化为参数方程时，先分清普通方程所表示的曲线类型，图2[解] 圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ， 则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．(2017·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ(θ为参数)，直线l 经过点P (1,2)，倾斜角α＝π6.(1)写出圆C 的普通方程和直线l 的参数方程；(2)设直线l 与圆C 相交于A ，B 两点，求|PA |·|PB |的值．[解] (1)由⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ，消去θ，得圆C 的普通方程为x 2＋y 2＝16. 又直线l 过点P (1,2)且倾斜角α＝π6，所以l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos π6，y ＝2＋t sin π6，即⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t (t 为参数)．(2)把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t代入x 2＋y 2＝16，得⎝⎛⎭⎪⎫1＋32t 2＋⎝ ⎛⎭⎪⎫2＋12t 2＝16，t 2＋(3＋2)t －11＝0，所以t 1t 2＝－11，由参数方程的几何意义，|PA |·|PB |＝|t 1t 2|＝11. 解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有关的问题，如最值、根据直线的参数方程的标准式中过定点M ①弦长l⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t(t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . [解] (1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8;当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.(2018·石家庄质检(二))在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋a cos β，y ＝a sin β(a >0，β为参数)．以O 为极点，x 轴的正半轴为极轴，建立极坐标系，直线l 的极坐标方程ρcos ⎝⎛⎭⎪⎫θ－π3＝32.(1)若曲线C 与l 只有一个公共点，求a 的值；(2)A ，B 为曲线C 上的两点，且∠AOB ＝π3，求△OAB 的面积最大值．[解] (1)曲线C 是以(a,0)为圆心，以a 为半径的圆， 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 只有一个公共点，则可得|a －3|2＝a ，解得a ＝－3(舍)，a ＝1. 所以a ＝1.(2)法一：曲线C 的极坐标方程为ρ＝2a cos θ(a >0)， 设A 的极角为θ，B 的极角为θ＋π3，则S △OAB ＝12|OA |·|OB |sin π3＝34|2a cos θ|·⎪⎪⎪⎪⎪⎪2a cos ⎝⎛⎭⎪⎫θ＋π3＝3a 2⎪⎪⎪⎪⎪⎪cos θcos ⎝⎛⎭⎪⎫θ＋π3，∵cos θcos ⎝ ⎛⎭⎪⎫θ＋π3＝12cos 2θ－32sin θcos θ ＝12·cos 2θ＋12－34sin 2θ ＝12⎝ ⎛⎭⎪⎫12cos 2θ－32sin 2θ＋14 ＝12cos ⎝⎛⎭⎪⎫2θ＋π3＋14，所以当θ＝－π6时，12cos ⎝ ⎛⎭⎪⎫2θ＋π3＋14取得最大值34.△OAB 的面积最大值为33a24.法二：因为曲线C 是以(a,0)为圆心，以a 为半径的圆，且∠AOB ＝π3，由正弦定理得|AB |sinπ3＝2a ，所以|AB |＝3a .由余弦定理得|AB |2＝3a 2＝|OA |2＋|OB |2－|OA |·|OB | ≥|OA |·|OB |，所以S △OAB ＝12|OA |·|OB |sin π3≤12×3a 2×32＝33a 24， 所以△OAB 的面积最大值为33a 24.涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用意义，直接求解，能达到化繁为简的解题目的[跟踪训练1⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ(其中φ为参数)．以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ(tan α·cos θ－sin θ)＝1(α是常数，0<α<π，且α≠π2)，点A ，B (A 在x 轴的下方)是曲线C 1与C 2的两个不同交点．(1)求曲线C 1的普通方程和C 2的直角坐标方程； (2)求|AB |的最大值及此时点B 的坐标.【导学号：79140390】[解] (1)∵⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，∴x 24＋y 2＝1，由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得曲线C 2的直角坐标方程为y ＝tan α·x －1.(2)由(1)得曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α(t 是参数)，设A (t 1cos α，－1＋t 1sin α)，B (t 2cos α，－1＋t 2sin α)，将C 2：⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α，代入x 24＋y 2＝1，整理得t 2(1＋3sin 2α)－8t sin α＝0， ∴t 1＝0，t 2＝8sin α1＋3sin α， ∴|AB |＝|t 1－t 2|＝8|sin α|1＋3sin 2α ＝83|sin α|＋1|sin α|≤823＝433(当且仅当sin α＝33取等号)， 当sin α＝33时，∴0<α<π，且α≠π2， ∴cos α＝±63， ∴B ⎝ ⎛⎭⎪⎫±423，13， ∴|AB |的最大值为433，此时点B 的坐标为⎝ ⎛⎭⎪⎫±423，13.。

一.自我诊断 知己知彼1. 若圆M 的方程为422=+y x ，则圆M 的参数方程为 ．【答案】)(sin 2cos 2为参数ααα⎩⎨⎧==y x 【解析】由圆M 的方程224x y +=,可知圆心()0,0,半径为 2.所以圆M 的参数方程为:)(sin 2cos 2为参数ααα⎩⎨⎧==y x . .2．已知圆M ：x 2+y 2-2x -4y +1=0，则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）的距离为 ．【答案】2【解析】由于圆M 的标准方程为：22(1)(2)4x y -+-=，所以圆心(1,2)M ，又因为直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）消去参数t 得普通方程为3450x y --=，由点到直线的距离公式得所求距离2d ==；故答案为：2．3在极坐标系中，点（2，6π）到直线θρsin ＝2的距离等于________． 【答案】1【解析】在极坐标系中，点（2，6π1），直线θρsin ＝2对应直角坐标系中的方程为y ＝2，所以点到直线的距离为1．4设曲线C 的参数方程为4cos 14sin x a y θθ=+⎧⎨=+⎩（θ是参数，0>a ），直线l 的极坐标方程为3cos 4sin 5ρθρθ+=，若曲线C 与直线l 只有一个公共点，则实数a 的值是 ．【答案】7【解析】曲线C 的普通方程为()()22116x a y -+-=，直线l 的普通方程3450x y +-=，直线l 与圆C 相切，则圆心(),1a 到l 的距离345475a d d +-==⇒= 5．直角坐标系xOy 中，圆C的参数方程是cos ,(1sin ,x y θθθ⎧=⎪⎨=+⎪⎩为参数），以原点为极点，x轴的正半轴为极轴建立坐标系，则圆心C 的极坐标是 ． 【答案】)6,2(π【解析】由圆C的参数方程是cos ,(1sin ,x y θθθ⎧=⎪⎨=+⎪⎩为参数）得⎩⎨⎧-=-=1sin 3cos y x θθ可得圆的标准方程为1)1()3(22=-+-y x ，圆心坐标为)1,3(，离圆心的距离33tan ,21)3(22==+=θρ，由题意6πθ=，则圆心C 的极坐标是)6,2(π．二.温故知新 夯实基础1．平面直角坐标系设点P (x ，y )是平面直角坐标系中的任意一点，在变换φ：⎪⎩⎪⎨⎧==0>,0>,''λμλλy y x x 的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换． 2．极坐标系(1)极坐标与极坐标系的概念在平面内取一个定点O ，自点O 引一条射线Ox ，同时确定一个长度单位和计算角度的正方向(通常取逆时针方向)，这样就建立了一个极坐标系．点O 称为极点，射线Ox 称为极轴．平面内任一点M 的位置可以由线段OM 的长度ρ和从射线Ox 到射线OM 的角度θ来刻画(如图所示)．这两个数组成的有序数对(ρ，θ)称为点M 的极坐标．ρ称为点M 的极径，θ称为点M 的极角．一般认为ρ≥0.当极角θ的取值范围是[0,2π)时，平面上的点(除去极点)就与极坐标(ρ，θ)(ρ≠0)建立一一对应的关系．我们设定，极点的极坐标中，极径ρ＝0，极角θ可取任意角．(2)极坐标与直角坐标的互化设M 为平面内的一点，它的直角坐标为(x ，y )，极坐标为(ρ，θ)．由图可知下面关系式成立：⎩⎨⎧==θρθρsin cos y x 或⎪⎩⎪⎨⎧≠=+=0,tan 222x x yy x θρ，这就是极坐标与直角坐标的互化公式． 3．常见曲线的极坐标方程4.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数从参数方程得到普通方程．(2)如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么⎩⎨⎧==)()(t g y t f x 就是曲线的参数方程．5．常见曲线的参数方程和普通方程三.典例剖析 思维拓展考点一 坐标系例1在平面直角坐标系xOy 中，直线l 的参数方程为12,22x t y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数），又以O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos24sin 30ρθρθ+-=．（1）求曲线C 的直角坐标方程；（2）设直线l 与曲线C 方程相交于A ，B 两点，求||AB ．【答案】（1）曲线C 的直角坐标方程为22(2)1y x --=；（2）||AB = 【解析】（1）曲线C 的极坐标方程2cos24sin 30ρθρθ+-=， 化为2222cossin 4sin 30ρθρθρθ-+-=，即22430x y y -+-=．∴曲线C 的直角坐标方程为22(2)1y x --=．（2）将直线l的参数方程12,22x t y ⎧=-+⎪⎪⎨⎪=+⎪⎩（t 为参数），代入曲线C 方程得24100t t +-=，设A ，B 对应的参数分别为1t ，2t ，则124t t +=-，1210t t =-，所以12||||AB t t =-= 【方法点拨】（1）由极坐标与直角坐标相互转化公式cos sin x y ρθρθ=⎧⎨=⎩，可求出曲线C 的直角坐标方程；（2）将直线l 的参数方程代入曲线C 的方程并整理可得关于t 的一元二次方程，利用韦达定理可得12t t +，12t t ，运用直线的参数方程的几何意义可知，12||||AB t t =-，代入即可得出所求的结果．考点二 参数方程例1已知曲线C 的极坐标方程式2cos ρθ=，以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线L的参数方程是212x m y t ⎧=+⎪⎪⎨⎪=⎪⎩，（t 为参数）． （1）求曲线C 的直角坐标方程和直线L 的普通方程；（2）设点(,0)P m ，若直线L 与曲线C 交于两点,A B ，且||||1P A P B ⋅=，求实数m 的值． 【答案】（1）曲线C 的直角坐标方程为222x y x +=，直线L的普通方程为x m =+；（2）1m =【解析】（1）曲线C 的极坐标方程是2cos ρθ=，化为22cos ρρθ=，可得直角坐标方程：222x y x +=．直线L的参数方程是12x m y t ⎧=+⎪⎪⎨⎪=⎪⎩，（t 为参数），消去参数t可得x m =+． （2）把12x t m y t ⎧=+⎪⎪⎨⎪=⎪⎩，（t 为参数），代入方程：222x y x +=，化为：2220t t m m ++-=，由0∆>，解得13m -<<．∴2122t t m m =-．∵12||||1PA PB t t ⋅==，∴221m m -=，解得1m =0∆>．∴实数1m =【方法点拨】（1）利用y x y x ==+=θρθρρsin ,cos ,222，即可将极坐标方程化为平面直角坐标系方程；消去参数t 即可将直线的参数方程化为普通方程；（2）将直线的参数方程代入曲线C 的普通方程得到一个含t 且关于x 的一元二次方程2220t t m m ++-=，然后利用参数t 的几何意义知，12||||1PA PB t t ⋅==22m m =-，并由t 的范围（利用判别式大于零求范围）求出值域即可． 例2. 在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴的非负半轴为极轴，建立极坐标系．曲线C 的极坐标方程是4cos (0)2πρθθ=≤≤，直线l 的参数方程是3cos 6()sin6x t t y t ππ⎧=-+⎪⎪⎨⎪=⎪⎩为参数． （1）求直线l 的直角坐标方程和曲线C 的参数方程； （2）求曲线C 上的动点M 到直线l 的距离的范围． 【答案】（1）30x +=，22cos 2sin x y αα=+⎧⎨=⎩（α为参数，0απ≤≤）；（2）17,22⎡⎤⎢⎥⎣⎦．【解析】（1）直线:3l x +=，即：30x += 由24cos ρρθ=得：224x y x +=，即：22(2)4x y -+=0,sin 02y πθρθ≤≤∴=≥ .故C 的参数方程为：22cos (0)2sin x y ααπα=+⎧≤≤⎨=⎩ （2）设点(22cos ,2sin )M αα+到直线30x +=的距离为dd ==54sin()1654sin()(0)226παπααπ--⎛⎫==--≤≤ ⎪⎝⎭51sin()166626ππππαα-≤-≤-≤-≤ 时,min max 117sin()1,,sin(),62622d d ππαα∴-==-=-=时时点M 到直线l 的距离的范围是17,22⎡⎤⎢⎥⎣⎦【方法点拨】（1）消去t 可得直线l 的直角坐标方程，利用cos x ρθ=，sin y ρθ=代入曲线C 的极坐标方程可得曲线C 的直角坐标方程，进而引入参数α可得曲线C 的参数方程；（2）先计算点M 到直线l 的距离，再利用三角函数的性质可得点M 到直线l 的距离的范围．考点三 综合问题例1在直角坐标系xOy 中，直线l 的参数方程为{(2x tcos t y tsin αα==+为参数， 0απ≤<），曲线C 的参数方程为2{(22x cos y cos βββ==+为参数），以坐标原点O 为极点， x 轴正半轴为极轴建立极坐标系.（1）求曲线C 的极坐标方程；（2）设C 与l 交于,M N 两点（异于原点），求OM ON +的最大值.【答案】（1）曲线C 的极坐标方程为24sin ρρθ=；（2）【解析】（1）曲线C 的普通方程为()2224x y +-=，化简得224x y y +=，则24sin ρρθ=，所以曲线C 的极坐标方程为24sin ρρθ=. （2）由直线l 的参数方程可知，直线l 必过点()0,2，也就是圆C 的圆心，则2MON π∠=，不妨设()12,,,2M N πρθρθ⎛⎫+⎪⎝⎭，其中0,2πθ⎛⎫∈ ⎪⎝⎭，则()1244424OM ON sin sin sin cos ππρρθθθθθ⎛⎫⎛⎫+=+=++=+=+ ⎪ ⎪⎝⎭⎝⎭ ，所以当4πθ=， OM ON +取得最大值为【方法点拨】(1)由题意可得曲线C 的普通方程为()2224x y +-=，将其转化为极坐标方程即24sin ρρθ=.(2)由参数方程可知直线l 过圆C 的圆心，则2MON π∠=，设()12,,,2M N πρθρθ⎛⎫+⎪⎝⎭，其中0,2πθ⎛⎫∈ ⎪⎝⎭，则4OM ON πθ⎛⎫+=+ ⎪⎝⎭，由三角函数的性质可得OM ON +取得最大值为例2. 在平面直角坐标系xOy 中，以O 为极点， x 轴的正半轴为极轴，建立极坐标系．曲线1C 的极坐标方程为()223sin 12ρθ+=，曲线2C 的参数方程为1{x tcos y tsin αα=+=（t 为参数），0,2πα⎛⎫∈ ⎪⎝⎭． （Ⅰ）求曲线1C 的直角坐标方程，并判断该曲线是什么曲线？（Ⅱ）设曲线2C 与曲线1C 的交点为A ， B ， ()1,0P ，当72PA PB +=时，求cos α的值．【答案】(1) 见解析；（2）cos α=. 【解析】 (1) 由()223sin 12ρθ+=得22143x y +=，该曲线为椭圆. （2）将1{x tcos y tsin αα=+=代入22143x y +=得()224cos 6cos 90t t αα-+-=，由直线参数方程的几何意义，设12,PA t PB t ==， 1226cos ,4cos t t αα-+=-12294cos t t α-=-，所以1221274c o s 2P A P B t t t α+=-==-，从而24c o s 7α=，由于0,2πα⎛⎫∈ ⎪⎝⎭，所以cos 7α=. 【方法点拨】（1）根据极坐标与直角坐标间的转化公式，可得1C 的直角坐标方程. (2) 由直线参数方程的几何意义得1272PA PB t t +=-=，可得解.例3. 在直角坐标系xoy 中，曲线1C 的参数方程为{x y sin αα==，（ α为参数），以原点O为极点，x 轴正半轴为极轴，建立极坐标系，曲线2C 的极坐标方程为sin 4πρθ⎛⎫+= ⎪⎝⎭.（1）求曲线1C 的普通方程与曲线2C 的直角坐标方程；（2）设P 为曲线1C 上的动点，求点P 到2C 上点的距离的最小值.【答案】（1）2213x y +=， 80x y +-=（2）【解析】（1）由曲线1C ：{ x y sin αα==得 cos y sin αα==即：曲线1C 的普通方程为： 2213x y += 由曲线2C ：sin 4πρθ⎛⎫+= ⎪⎝⎭得：()sin cos 2ρθθ+=即:曲线2C 的直角坐标方程为： 80x y +-=（2）由（1）知椭圆1C 与直线2C 无公共点，椭圆上的点),sin Pαα到直线80x y +-=的距离为d ==所以当sin 13πα⎛⎫+= ⎪⎝⎭时， d的最小值为【方法点拨】（1）对于1C ，利用22cos sin 1αα+=，化简得2213x y +=，对于2C ，展开后利用极坐标与直角坐标转化公式，化简的80x y +-=.（2）直接利用点到直线距离公式，求出距离，并用辅助角公式化简，利用三角函数最值求得距离的最小值.四.举一反三 成果巩固考点一 坐标系1. 已知圆C 的参数方程为cos ,(1sin .x y ααα=⎧⎨=+⎩为参数），直线l 的极坐标方程为sin 1ρθ=，则直线l 与圆C 的交点的直角坐标为 ．【答案】)1,1(±【解析】圆C 的普通方程为()2211x y +-=，直线l 的普通方程为1y =，所以交点为)1,1(±2. 将曲线22132x y +=按ϕ：1',3{ 1'2x x y y==变换后的曲线的参数方程为（ ） A. 3,{ 2x cos y sin θθ==B. ,{x y θθ== C. 1,3{ 12x cos y sin θθ==D. ,3{ x cos y sin θθ==【答案】D【解析】由变换ϕ： 1',3{ 1'2x x y y==可得： 3',{ 2'x x y y ==,代入曲线22132x y +=可得： ()()2232132x y ''+=，即为： 22321,x y +=令,{2x y sin θθ==(θ为参数)即可得出参数方程.故选：D.考点二 参数方程1. 若P ),(n m 为椭圆上的点，则n m +的取值范围是 ．【答案】[]2,2- 【解析】依题意可得sin m n θθ⎧=⎪⎨=⎪⎩,1sin 2sin 2sin 23m n πθθθθθ⎫⎛⎫∴+=+=+=+⎪ ⎪⎪⎝⎭⎝⎭, R θ∈ , []sin 1,13πθ⎛⎫∴+∈- ⎪⎝⎭, []2sin 2,23πθ⎛⎫∴+∈- ⎪⎝⎭.即[]2,2m n +∈-2. 在直角坐标系xOy 中，曲线1C 的方程是5222=+y x ，2C 的参数方程是⎪⎩⎪⎨⎧-==ty tx 3（t为参数），则1C 与2C 交点的直角坐标是 ． 【答案】)1 , 3(-【解析】由⎪⎩⎪⎨⎧-==ty t x 3消去参数t ，得2C的普通方程为(0)3y x x =-≥，代入1C 方程5222=+y x 整理得：23x =，解得x =1y =-，因此交点为1)-.3. 参数方程sin cos 2x y θθ=⎧⎨=⎩（θ为参数）化为普通方程为 ．【答案】212y x =-，[1,1]x ∈-【解析】由2cos 212sin θθ=-得212y x =-，又sin [1,1]θ∈-，所以[1,1]x ∈-，因此普通方程为212y x =-，[1,1]x ∈-考点三 综合问题例1. 已知在平面直角坐标系xOy 中，直线l 的参数方程是{ 26x t y t ==+（t 是参数），以原点O 为极点，x 轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 的极坐标方程为ρθ=．（1）求直线l 的普通方程与曲线C 的直角坐标方程；（2）设(),M x y 为曲线C 上任意一点，求x y +的取值范围． 【答案】（1）260x y -+=，(222x y +=（2）2⎡-⎣【解析】（1）由{26x t y t ==+，得26y x =+，故直线l 的普通方程为260x y -+=，由ρθ=，得2cos ρθ=，所以22x y +=，即(222x y +=，故曲线C的普通方程为(222x y +=；（2）据题意设点)2os 2s i nMθθ，则2o 2s i n 22s i n4x y πθθθ⎛⎫+=+⎪⎝⎭，所以x y +的取值范围是2⎡-⎣．例2. 在直角坐标系xOy 中，曲线C的参数方程为2{ 12x cos y sin αα==+ (α为参数)，以平面直角坐标系的原点为极点， x 轴的正半轴为极轴建立极坐标系.(1)求曲线C 的极坐标方程；(2)过原点O 的直线12,l l 分别与曲线C 交于除原点外的,A B 两点，若3AOB π= ，求AO B 的面积的最大值.【答案】(1) 4sin 3πρθ⎛⎫=+⎪⎝⎭；(2) . 【解析】 (1)曲线C的普通方程为(()2214x y +-=，即2220x y y +--=，所以，曲线C的极坐标方程为2cos 2sin 0ρθρθ--=，即4sin 3πρθ⎛⎫=+⎪⎝⎭. (2)不妨设()1,A ρθ， 2,3B πρθ⎛⎫+⎪⎝⎭， ,33ππθ⎛⎫∈-⎪⎝⎭. 则14sin 3πρθ⎛⎫=+⎪⎝⎭， 224sin 3πρθ⎛⎫=+⎪⎝⎭， AOB 的面积12112sin sin sin 232333S OA OB ππππρρθθθ⎛⎫⎛⎫=⋅==++= ⎪ ⎪⎝⎭⎝⎭所以，当0θ=时， AOB的面积取最大值为.例3. 在直角坐标系xOy 中，曲线C的参数方程是1,{ x y αα=+=（α为参数），以该直角坐标系的原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为sin cos 0m θρθ-+=.（1）写出曲线C 的普通方程和直线l 的直角坐标方程；（2）设点(),0P m ，直线l 与曲线C 相交于,A B 两点，且1PA PB =，求实数m 的值.【答案】（1）曲线C 的普通方程为()2212x y -+=，直线l 的直角坐标方程为)y x m =-；（2）1m =0m =或2m =.【解析】（1）()221,{12x x y y αα=+⇒-+==，故曲线C 的普通方程为()2212x y -+=.直线l)3x m y x m -+⇒=-. （2）直线l的参数方程可以写为,{12x m y t =+=（t 为参数）.设,A B 两点对应的参数分别为12,t t ，将直线l 的参数方程代入曲线C 的普通方程()2212x y -+=可以得到2221122m t t ⎛⎫⎛⎫+-+= ⎪ ⎪ ⎪⎝⎭⎝⎭)()21120m t m -+--=，所以()212121PA PB t t m ==--= 2211m m ⇒--= 2220m m ⇒-==或220m m -=，解得1m =±0m =或2m =.五.分层训练 能力进阶【基础达标】1. 曲线⎩⎨⎧==θθsin 4cos 5y x （θ为参数）的焦距是 ．【答案】6【解析】消参后化为：14522=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛y x ，整理为1162522=+y x ，所以焦距6162522=-=c ．2. 已知直线l 的方程为2)4sin(=+πθρ，曲线C 的方程为()为参数θθθ⎩⎨⎧==sin cos y x ． （1）把直线l 和曲线C 的方程分别化为直角坐标方程和普通方程；（2）求曲线C 上的点到直线l 距离的最大值．【答案】（1）2=+y x ，122=+y x ；（2）12+=l ．【解析】（1）222cos 22sin =⎪⎪⎭⎫⎝⎛⋅+⋅θθρ，根据⎩⎨⎧==θρθρsin cos y x ，代入得：2=+y x 根据1cos sin 22=+θθ，消参后的方程是：122=+y x ．（2）直线与圆相离，所以圆上的点到直线的最大距离是圆心到直线的距离加半径，即222==d ，那么最大距离就是12+=l3. 已知曲线C 的极坐标方程是ρ=4cosθ，以极点为平面直角坐标系的原点，极轴为χ轴的正半轴，建立平面直角坐标系，直线l 的参数方程是⎪⎩⎪⎨⎧+==t m x ty 2222（t 是参数）．（Ⅰ）将曲线C 的极坐标方程化为直角坐标方程，直线l 的参数方程化为普通方程； （Ⅱ）若直线l 与曲线C 相交于A 、B 两点，且|AB |=14，试求实数m 的值． 【答案】（Ⅰ）2240x y x +-=，y x m =-；（Ⅱ）1或3．【解析】（Ⅰ）曲线C 的极坐标方程是ρ=4cos θ化为直角坐标方程为：0422=-+x y x 直线l 的直角坐标方程为：m x y -=（5分）（Ⅱ）解法一：由（Ⅰ）知：圆心的坐标为（2，0），圆的半径R =2， 圆心到直线l 的距离22)214(222=-=d ，∴ 1222202=-⇒=--m m ∴ 31==m m 或解法二：把22x m y ⎧=+⎪⎪⎨⎪=⎪⎩（t 是参数）代人方程2x 042=-+x y得222)40t m t m m -+-=∵ m m t t m t t 42(222121-=--=+），∴ 21221214)(t t t t t t AB -+=-=∴ []14)442(222=---=m m m （）∴ 31==m m 或【能力提升】1. 把下列参数方程化为普通方程，并说明它们各表示什么曲线：⑴⎩⎨⎧==ϕϕsin 4cos 5y x （ϕ为参数）； ⑵⎩⎨⎧=-=ty tx 431（t 为参数）【答案】⑴1162522=+y x ∴曲线是长轴在x 轴上且为10，短轴为8，中心在原点的椭圆.⑵0434=-+y x ，它表示过（0，43）和(1, 0)的一条直线. 【解析】本题主要是考查参数方程化为普通方程，（1）对两个式子中右边的系数挪到左边，利用三角函数的平方关系式消去ϕ整理即得到；（2）可以代入消元或加减消元消去t 得普通方程.解：⑴．∵⎩⎨⎧==ϕϕsin 4cos 5y x ∴⎪⎩⎪⎨⎧==ϕϕsin 4cos 5y x两边平方相加，得ϕϕ2222sin cos 1625+=+y x 即 1162522=+y x ∴曲线是长轴在x 轴上且为10，短轴为8，中心在原点的椭圆.⑵．∵⎩⎨⎧=-=ty t x 431∴由4y t =代入t x 31-=，得 431y x ⋅-=∴0434=-+y x∴它表示过（0，43）和(1, 0)的一条直线. 2. 在平面直角坐标系xoy 中,直线l 的参数方程为(t 为参数),若以该直角坐标系的原点O 为极点x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为.(1)求直线l 的普通方程与曲线C 的直角坐标方程 (2)已知直线l 与曲线C 交于A 、B 两点,设F(1,0),求的值【答案】(1)..(2)1.【解析】 (1)直线的参数方程为，消去参数，得普通方程.曲线C 的极坐标方程为，直角坐标方程为.参考解法1：直线l 的参数方程为，代入，整理可得设对应的参数分别为，则3. 在平面直角坐标系xOy 中，已知点()2+cos ,sin P αα（α为参数）.以O 为极点，x 轴的正半轴为极轴，取相同的长度单位建立极坐标系，直线l 的极坐标方程为sin 4πρθ⎛⎫+= ⎪⎝⎭. （1）求点P 的轨迹C 的方程及直线l 的直角坐标方程； （2）求曲线C 上的点到直线l 的距离的最大值.【答案】（1）P 点的轨迹C 的方程为()2221x y -+=，直线l 的直角坐标方程为40x y +-=；（2）曲线C 上的点到直线l 1. 【解析】（1）设点(),P x y ，所以2{x cos y sin αα=+=，（ α为参数）， 消去参数，得()2221x y -+=，即P 点的轨迹C 的方程为()2221x y -+=直线:sin 4l πρθ⎛⎫+= ⎪⎝⎭cos sin 4ρθρθ⇒+= 4x y ⇒+=, 所以直线l 的直角坐标方程为40x y +-=.（2）由（1），可知P 点的轨迹C 是圆心为()2,0，半径为1的圆，则圆心C 到直线l 的距离为1d r ==>=.所以曲线C 上的点到直线l 1.4. 在平面直角坐标系xoy 中，曲线1C 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x （0>>b a ，ϕ为参数），在以O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线2C 是圆心在极轴上，且经过极点的圆 已知曲线1C 上的点)23,1(M 对应的参数3πϕ=，射线3πθ=与曲线2C 交于点)3,1(πD（1）求曲线1C ，2C 的方程； （2）若点),(1θρA ，)2,(2πθρ+B 在曲线1C 上，求222111ρρ+的值【答案】（1）曲线1C 的方程为⎩⎨⎧==ϕϕsin cos 2y x （ϕ为参数），1422=+y x ； 曲线2C 的方程为θρcos 2=,或1)1(22=+-y x ；（2）54【解析】（I ）将)23,1(M 及对应的参数3πϕ=，代入⎩⎨⎧==ϕϕsin cos b y a x ，得⎪⎪⎩⎪⎪⎨⎧==3sin 233cos 1ππb a ， 即⎩⎨⎧==12b a ， 2分所以曲线1C 的方程为⎩⎨⎧==ϕϕsin cos 2y x （ϕ为参数），或1422=+y x 3分 设圆2C 的半径为R ,由题意,圆2C 的方程为θρcos 2R =,(或222)(R y R x =+-) 将点)3,1(πD 代入θρcos 2R =, 得3cos21πR =,即1=R(或由)3,1(πD ,得)23,21(D ,代入222)(R y R x =+-,得1=R ), 所以曲线2C 的方程为θρcos 2=,或1)1(22=+-y x 5分 （II ）因为点),(1θρA ，)2,(2πθρ+B 在在曲线1C 上,所以1sin 4cos 221221=+θρθρ,1cos 4sin 222222=+θρθρ,所以45)cos 4sin ()sin 4cos (1122222221=+++=+θθθθρρ。

坐标系与参数方程第1课坐标系[过双基]1．平面直角坐标系中的坐标伸缩变换设点P (x ，y )是平面直角坐标系中的任意一点，在变换 φ：⎩⎪⎨⎪⎧x ′＝λ·x λ＞，y ′＝μ·yμ＞的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换，简称伸缩变换．2．极坐标系的概念 (1)极坐标系如图所示，在平面内取一个定点O ，叫做极点；自极点O 引一条射线Ox ，叫做极轴；再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系．(2)极坐标①极径：设M 是平面内一点，极点O 与点M 的距离|OM |叫做点M 的极径，记为ρ. ②极角：以极轴Ox 为始边，射线OM 为终边的角xOM 叫做点M 的极角，记为θ. ③极坐标：有序数对(ρ，θ)叫做点M 的极坐标，记作M (ρ，θ)． 3．极坐标与直角坐标的互化设M 是平面内任意一点，它的直角坐标是(x ，y )，极坐标是(ρ，θ)，则它们之间的关系为：⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ；⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝y x x4．常见曲线的极坐标方程1．点P 的直角坐标为(1，－3)，则点P 的极坐标为________．解析：因为点P (1，－3)在第四象限，与原点的距离为2，且OP 与x 轴所成的角为－π3，所以点P 的极坐标为⎝⎛⎭⎪⎫2，－π3.答案：⎝⎛⎭⎪⎫2，－π32．在极坐标系中，圆ρ＝2cos θ的垂直于极轴的两条切线方程分别为________． 解析：把圆ρ＝2cos θ的方程化为(x －1)2＋y 2＝1知，圆的垂直于极轴的两条切线方程分别为x ＝0和x ＝2，从而得这两条切线的极坐标方程为θ＝π2(ρ∈R)和ρcos θ＝2.答案：θ＝π2(ρ∈R)和ρcos θ＝23．(2017·北京高考)在极坐标系中，点A 在圆ρ2－2ρcos θ－4ρsin θ＋4＝0上，点P 的坐标为(1,0)，则|AP |的最小值为________．解析：将圆的极坐标方程化为直角坐标方程为x 2＋y 2－2x －4y ＋4＝0，即(x －1)2＋(y －2)2＝1，圆心为(1,2)，半径r ＝1.因为点P (1,0)到圆心的距离d ＝－2＋－2＝2>1，所以点P 在圆外，所以|AP |的最小值为d －r ＝2－1＝1.答案：14．(2017·天津高考)在极坐标系中，直线4ρcos ⎝ ⎛⎭⎪⎫θ－π6＋1＝0与圆ρ＝2sin θ 的公共点的个数为________．解析：依题意，得4ρ⎝⎛⎭⎪⎫32cos θ＋12sin θ＋1＝0，即23ρcos θ＋2ρsin θ＋1＝0， 所以直线的直角坐标方程为23x ＋2y ＋1＝0. 由ρ＝2sin θ，得ρ2＝2ρsin θ， 所以圆的直角坐标方程为x 2＋y 2＝2y ， 即x 2＋(y －1)2＝1，其圆心(0,1)到直线23x ＋2y ＋1＝0的距离d ＝|2×1＋1|32＋22＝34<1，则直线与圆相交，故直线与圆的公共点的个数是2. 答案：25．在极坐标系中，过点A ⎝ ⎛⎭⎪⎫1，－π2引圆ρ＝8sin θ的一条切线，则切线长为________．解析：点A ⎝ ⎛⎭⎪⎫1，－π2的极坐标化为直角坐标为A (0，－1)，圆ρ＝8sin θ的直角坐标方程为x 2＋y 2－8y ＝0， 圆的标准方程为x 2＋(y －4)2＝16， 点A 与圆心C (0,4)的距离为|AC |＝5， 所以切线长为|AC |2－r 2＝3. 答案：3[清易错]1．极坐标方程与直角坐标方程的互化易错用互化公式．在解决此类问题时考生要注意两个方面：一是准确应用公式，二是注意方程中的限制条件．2．在极坐标系下，点的极坐标不唯一性易忽视．注意极坐标(ρ，θ)(ρ，θ＋2k π)(k ∈Z)，(－ρ，π＋θ＋2k π)(k ∈Z)表示同一点的坐标．1．若圆C 的极坐标方程为ρ2－4ρcos ⎝ ⎛⎭⎪⎫θ－π3－1＝0，若以极点为原点，以极轴为x轴的正半轴建立相应的平面直角坐标系xOy ，则在直角坐标系中，圆心C 的直角坐标是________．解析：因为ρ2－4ρcos ⎝ ⎛⎭⎪⎫θ－π3－1＝0，所以ρ2－2ρcos θ－23ρsin θ－1＝0，即x 2＋y 2－2x －23y －1＝0，因此圆心坐标为(1，3)．答案：(1，3)2．圆ρ＝5cos θ－53sin θ的圆心的极坐标为________． 解析：将方程 ρ＝5cos θ－53sin θ两边都乘以ρ得： ρ2＝5ρcos θ－53ρsin θ，化成直角坐标方程为x 2＋y 2－5x ＋53y ＝0. 圆心的坐标为⎝ ⎛⎭⎪⎫52，－532，化成极坐标为⎝⎛⎭⎪⎫5，5π3.答案：⎝⎛⎭⎪⎫5，5π3(答案不唯一)平面直角坐标系下图形的伸缩变换[典例] (1)在同一平面直角坐标系中，已知伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y .求点A ⎝ ⎛⎭⎪⎫13，－2经过φ变换所得的点A ′的坐标．(2)求直线l ：y ＝6x 经过φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，变换后所得到的直线l ′的方程．[解] (1)设A ′(x ′，y ′)，由伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，得到⎩⎪⎨⎪⎧x ′＝3x ，y ′＝12y ，由于点A 的坐标为⎝ ⎛⎭⎪⎫13，－2，于是x ′＝3×13＝1，y ′＝12×(－2)＝－1，∴A ′(1，－1)为所求．(2)设直线l ′上任意一点P ′(x ′，y ′)， 由上述可知，将⎩⎪⎨⎪⎧x ＝13x ′，y ＝2y ′代入y ＝6x 得2y ′＝6×⎝ ⎛⎭⎪⎫13x ′，∴y ′＝x ′，即y ＝x 为所求． [方法技巧]伸缩变换的解题方法平面上的曲线y ＝f (x )在变换φ：⎩⎪⎨⎪⎧x ′＝λx λ，y ′＝μy μ的作用下得到的方程的求法是将⎩⎪⎨⎪⎧x ＝x ′λ，y ＝y ′μ代入y ＝f (x )，得y ′μ＝f ⎝⎛⎭⎪⎫x ′λ，整理之后得到y ′＝h (x ′)，即为所求变换之后的方程．[即时演练]1．求椭圆x 24＋y 2＝1，经过伸缩变换⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y后的曲线方程．解：由⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y得⎩⎪⎨⎪⎧x ＝2x ′，y ＝y ′.①将①代入x 24＋y 2＝1，得4x ′24＋y ′2＝1，即x ′2＋y ′2＝1.因此椭圆x 24＋y 2＝1经伸缩变换后得到的曲线方程是x 2＋y 2＝1. 2．若函数y ＝f (x )的图象在伸缩变换φ：⎩⎪⎨⎪⎧x ′＝2x ，y ′＝3y 的作用下得到曲线的方程为y ′＝3sin ⎝⎛⎭⎪⎫x ′＋π6，求函数y ＝f (x )的最小正周期．解：由题意，把变换公式代入曲线y ′＝3sin ⎝⎛⎭⎪⎫x ′＋π6得3y ＝3sin ⎝⎛⎭⎪⎫2x ＋π6，整理得y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π6，故f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6. 所以y ＝f (x )的最小正周期为2π2＝π.极坐标与直角坐标的互化[典例] 系．直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫π4－θ＝22，直线与曲线C ：ρsin 2θ＝8cos θ相交于不同的两点A ，B ，求|AB |的值．[解] l ：ρsin ⎝⎛⎭⎪⎫π4－θ＝22⇒22ρcos θ－22ρsin θ＝22⇒x －y －1＝0，C 的直角坐标方程是y 2＝8x .由⎩⎪⎨⎪⎧y 2＝8x ，x －y －1＝0，可得x 2－10x ＋1＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝10，x 1x 2＝1， 所以AB 的长为1＋1·102－4＝8 3. [方法技巧]1．极坐标与直角坐标互化公式的3个前提条件(1)取直角坐标系的原点为极点． (2)以x 轴的非负半轴为极轴． (3)两种坐标系规定相同的长度单位． 2．直角坐标化为极坐标的注意点(1)根据终边相同的角的意义，角θ的表示方法具有周期性，故点M 的极坐标(ρ，θ)的形式不唯一，即一个点的极坐标有无穷多个．当限定ρ≥0，θ∈[0,2π)时，除极点外，点M 的极坐标是唯一的．(2)当把点的直角坐标化为极坐标时，求极角θ应注意判断点M 所在的象限(即角θ的终边的位置)，以便正确地求出角θ∈[0,2π)的值．[即时演练]在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴建立极坐标系．曲线C 的极坐标方程为ρcos ⎝⎛⎭⎪⎫θ－π3＝1(0≤θ<2π)，M ，N 分别为C 与x 轴，y 轴的交点． (1)写出C 的直角坐标方程，并求M ，N 的极坐标； (2)设MN 的中点为P ，求直线OP 的极坐标方程． 解：(1)由ρcos ⎝⎛⎭⎪⎫θ－π3＝1，得ρ⎝ ⎛⎭⎪⎫12cos θ＋32sin θ＝1.从而C 的直角坐标方程为12x ＋32y ＝1，即x ＋3y －2＝0.当θ＝0时，ρ＝2，所以M (2,0)． 当θ＝π2时，ρ＝233，所以N ⎝ ⎛⎭⎪⎫233，π2.(2)M 点的直角坐标为(2,0)．N 点的直角坐标为⎝ ⎛⎭⎪⎫0，233. 所以P 点的直角坐标为⎝ ⎛⎭⎪⎫1，33， 则P 点的极坐标为⎝⎛⎭⎪⎫233，π6. 所以直线OP 的极坐标方程为θ＝π6(ρ∈R)．极坐标方程的应用[典例] 已知曲线C 1：x ＋3y ＝3和C 2：⎩⎨⎧x ＝6cos φ，y ＝2sin φ(φ为参数)．以原点O为极点，x 轴的正半轴为极轴建立极坐标系，且两种坐标系中取相同的长度单位．(1)把曲线C 1和C 2的方程化为极坐标方程；(2)设C 1与x ，y 轴交于M ，N 两点，且线段MN 的中点为P .若射线OP 与C 1，C 2交于P ，Q 两点，求P ，Q 两点间的距离．[解] (1)C 1：ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32，C 2：ρ2＝61＋2sin 2θ. (2)∵M (3，0)，N (0,1)， ∴P ⎝⎛⎭⎪⎫32，12， ∴OP 的极坐标方程为θ＝π6，把θ＝π6代入ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32得ρ1＝1，P ⎝ ⎛⎭⎪⎫1，π6. 把θ＝π6代入ρ2＝61＋2sin 2θ得ρ2＝2，Q ⎝ ⎛⎭⎪⎫2，π6. ∴|PQ |＝|ρ2－ρ1|＝1，即P ，Q 两点间的距离为1. [方法技巧]曲线的极坐标方程的求解策略在已知极坐标方程求曲线交点、距离、线段长等几何问题时，如果不能直接用极坐标解决，或用极坐标解决较麻烦，可将极坐标方程转化为直角坐标方程解决．[即时演练]在直角坐标系xOy 中，圆C 的普通方程为(x －1)2＋y 2＝1.以O 为极点，x 轴的非负半轴为极轴建立极坐标系．(1)求圆C 的极坐标方程；(2)直线l 的极坐标方程是ρ(sin θ＋3cos θ)＝33，射线OM ：θ＝π3与圆C 的交点为O ，P ，与直线l 的交点为Q ，求线段PQ 的长．解：(1)因为圆C 的普通方程为(x －1)2＋y 2＝1， 又x ＝ρcos θ，y ＝ρsin θ， 所以圆C 的极坐标方程是ρ＝2cos θ. (2)设(ρ1，θ1)为点P 的极坐标， 则有⎩⎪⎨⎪⎧ρ1＝2cos θ1，θ1＝π3，解得⎩⎪⎨⎪⎧ρ1＝1，θ1＝π3.设(ρ2，θ2)为点Q 的极坐标，则有⎩⎪⎨⎪⎧ρ2θ2＋3cos θ2＝33，θ2＝π3，解得⎩⎪⎨⎪⎧ρ2＝3，θ2＝π3.由于θ1＝θ2，所以|PQ |＝|ρ1－ρ2|＝2，即线段PQ 的长为2.1．(2017·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为⎝⎛⎭⎪⎫2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．解：(1)设P 的极坐标为(ρ，θ)(ρ＞0)，M 的极坐标为(ρ1，θ)(ρ1＞0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16，得C 2的极坐标方程ρ＝4cos θ(ρ＞0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB ＞0)，由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积 S ＝12|OA |·ρB ·sin∠AOB ＝4cos α·⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3 ＝2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.2．(2015·全国卷Ⅰ)在直角坐标系xOy 中，直线C 1：x ＝－2，圆C 2：(x －1)2＋(y －2)2＝1，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．(1)求C 1，C 2的极坐标方程；(2)若直线C 3的极坐标方程为θ＝π4(ρ∈R)，设C 2与C 3的交点为M ，N ，求△C 2MN 的面积．解：(1)因为x ＝ρcos θ，y ＝ρsin θ， 所以C 1的极坐标方程为ρcos θ＝－2，C 2的极坐标方程为ρ2－2ρcos θ－4ρsin θ＋4＝0.(2)将θ＝π4代入ρ2－2ρcos θ－4ρsin θ＋4＝0，得ρ2－32ρ＋4＝0，解得ρ1＝22，ρ2＝ 2. 故ρ1－ρ2＝2，即|MN |＝ 2.由于C 2的半径为1，所以△C 2MN 的面积为12.3．(2016·北京高考改编)在极坐标系中，直线ρcos θ－3ρsin θ－1＝0与圆ρ＝2cos θ交于A ，B 两点，求|AB |.解：∵x ＝ρcos θ，y ＝ρsin θ， ∴直线的直角坐标方程为x －3y －1＝0. ∵ρ＝2cos θ，∴ρ2(sin 2θ＋cos 2θ)＝2ρcos θ， ∴x 2＋y 2＝2x .∴圆的直角坐标方程为(x －1)2＋y 2＝1. ∵圆心(1,0)在直线x －3y －1＝0上， ∴AB 为圆的直径，∴|AB |＝2.4．(2015·安徽高考改编)在极坐标系中，求圆ρ＝8sin θ上的点到直线θ＝π3(ρ∈R)距离的最大值．解：圆ρ＝8sin θ即ρ2＝8ρsin θ， 化为直角坐标方程为x 2＋(y －4)2＝16， 直线 θ＝π3即tan θ＝3，化为直角坐标方程为3x －y ＝0， 圆心(0,4)到直线的距离为|－4|4＝2，所以圆上的点到直线距离的最大值为2＋4＝6.5．(2015·北京高考改编)在极坐标系中，求点⎝⎛⎭⎪⎫2，π3到直线ρ(cos θ＋3sin θ)＝6的距离．解：点⎝⎛⎭⎪⎫2，π3的直角坐标为()1，3，直线ρ(cos θ＋3sin θ)＝6的直角坐标方程为x ＋3y －6＝0. 所以点(1，3)到直线的距离d ＝|1＋3×3－6|12＋32＝22＝1.1．在极坐标系中，直线ρ(sin θ－cos θ)＝a 与曲线ρ＝2cos θ－4sin θ相交于A ，B 两点，若|AB |＝23，求实数a 的值．解：直线的极坐标方程化为直角坐标方程为x －y ＋a ＝0， 曲线的极坐标方程化为直角坐标方程为(x －1)2＋(y ＋2)2＝5， 所以圆心C 的坐标为(1，－2)，半径r ＝5， 所以圆心C 到直线的距离为 |1＋2＋a |2＝ r 2－⎝⎛⎭⎪⎫|AB |22＝2，解得a ＝－5或a ＝－1. 故实数a 的值为－5或－1.2．在极坐标系中，求直线ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1与圆ρ＝4sin θ的交点的极坐标． 解：ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1化为直角坐标方程为3x －y ＝2，即y ＝3x －2.ρ＝4sin θ可化为x 2＋y 2＝4y ， 把y ＝3x －2代入x 2＋y 2＝4y ， 得4x 2－83x ＋12＝0， 即x 2－23x ＋3＝0， 所以x ＝3，y ＝1.所以直线与圆的交点坐标为(3，1)，化为极坐标为⎝⎛⎭⎪⎫2，π6. 3．(2018·长春模拟)已知圆O 1和圆O 2的极坐标方程分别为ρ＝2，ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2.(1)把圆O 1和圆O 2的极坐标方程化为直角坐标方程； (2)求经过两圆交点的直线的极坐标方程． 解：(1)由ρ＝2知ρ2＝4，所以x 2＋y 2＝4； 因为ρ2－22ρcos ⎝⎛⎭⎪⎫θ－π4＝2，所以ρ2－22ρ⎝⎛⎭⎪⎫cos θcos π4＋sin θsin π4＝2，所以x 2＋y 2－2x －2y －2＝0.(2)将两圆的直角坐标方程相减，得经过两圆交点的直线方程为x ＋y ＝1. 化为极坐标方程为ρcos θ＋ρsin θ＝1， 即ρsin ⎝ ⎛⎭⎪⎫θ＋π4＝22. 4．已知曲线C 的参数方程为⎩⎨⎧x ＝2＋5cos α，y ＝1＋5sin α(α为参数)，以原点O 为极点，x 轴正半轴为极轴建立极坐标系．(1)求曲线C 的极坐标方程；(2)设l 1：θ＝π6，l 2：θ＝π3，若l 1，l 2与曲线C 相交于异于原点的两点 A ，B ，求△AOB 的面积．解：(1)∵曲线C 的参数方程为⎩⎨⎧x ＝2＋5cos α，y ＝1＋5sin α(α为参数)，∴曲线C 的普通方程为(x －2)2＋(y －1)2＝5，将⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ，代入并化简得ρ＝4cos θ＋2sin θ，即曲线C 的极坐标方程为ρ＝4cos θ＋2sin θ. (2)在极坐标系中，C ：ρ＝4cos θ＋2sin θ， ∴由⎩⎪⎨⎪⎧θ＝π6，ρ＝4cos θ＋2sin θ，得|OA |＝23＋1，同理：|OB |＝2＋ 3. 又∵∠AOB ＝π6，∴S △AOB ＝12|OA |·|OB |sin ∠AOB ＝8＋534，即△AOB 的面积为8＋534.5．在坐标系中，曲线C ：ρ＝2a cos θ(a >0)，直线l ：ρcos θ－π3＝32，C 与l 有且只有一个公共点．(1)求a 的值；(2)若原点O 为极点，A ，B 为曲线C 上两点，且∠AOB ＝π3，求|OA |＋|OB |的最大值．解：(1)由已知在直角坐标系中，C ：x 2＋y 2－2ax ＝0⇒(x －a )2＋y 2＝a 2(a >0)； l ：x ＋3y －3＝0.因为C 与l 只有一个公共点，所以l 与C 相切， 即|a －3|2＝a ，则a ＝1. (2)设A (ρ1，θ)，则B ⎝⎛⎭⎪⎫ρ2，θ＋π3， ∴|OA |＋|OB |＝ρ1＋ρ2＝2cos θ＋2cos ⎝ ⎛⎭⎪⎫θ＋π3＝3cos θ－3sin θ＝23cos ⎝⎛⎭⎪⎫θ＋π6.所以，当θ＝－π6时，(|OA |＋|OB |)max ＝2 3.6．在平面直角坐标系xOy 中，直线C 1：3x ＋y －4＝0，曲线C 2：x 2＋(y －1)2＝1，以原点O 为极点，x 轴正半轴为极轴建立极坐标系．(1)求C 1，C 2的极坐标方程；(2)若曲线C 3的极坐标方程为θ＝α⎝⎛⎭⎪⎫ρ>0，0<α<π2，且曲线C 3分别交C 1，C 2于点A ，B ，求|OB ||OA |的最大值． 解：(1)∵x ＝ρcos θ，y ＝ρsin θ，∴C 1：3ρcos θ＋ρsin θ－4＝0，C 2：ρ＝2sin θ. (2)曲线C 3为θ＝α⎝ ⎛⎭⎪⎫ρ>0，0<α<π2， 设A (ρ1，α)，B (ρ2，α)，ρ1＝43cos α＋sin α，ρ2＝2sin α，则|OB ||OA |＝ρ2ρ1＝14×2sin α(3cos α＋sin α) ＝142sin2α－π6＋1， ∴当α＝π3时，⎝ ⎛⎭⎪⎫|OB | |OA |max ＝34. 7．平面直角坐标系xOy 中，曲线C 1的方程为x 23＋y 2＝1，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝4sin ⎝ ⎛⎭⎪⎫θ＋π3，射线OM 的极坐标方程为θ＝α0(ρ≥0)．(1)写出曲线C 1的极坐标方程和曲线C 2的直角坐标方程；(2)若射线OM 平分曲线C 2，且与曲线C 1交于点A ，曲线C 1上的点满足∠AOB ＝π2，求|AB |.解：(1)曲线C 1的极坐标方程为ρ2＝31＋2sin 2θ， 曲线C 2的直角坐标方程为(x －3)2＋(y －1)2＝4. (2)曲线C 2是圆心为(3，1)，半径为2的圆， ∴射线OM 的极坐标方程为θ＝π6(ρ≥0)，代入ρ2＝31＋2sin 2θ，可得ρ2A ＝2. 又∠AOB ＝π2，∴ρ2B ＝65，∴|AB |＝|OA |2＋|OB |2＝ρ2A ＋ρ2B ＝455.8．已知在一个极坐标系中点C 的极坐标为⎝⎛⎭⎪⎫2，π3.(1)求出以C 为圆心，半径长为2的圆的极坐标方程(写出解题过程)并画出图形； (2)在直角坐标系中，以圆C 所在极坐标系的极点为原点，极轴为x 轴的正半轴建立直角坐标系，点P 是圆C 上任意一点，Q (5，－3)，M 是线段PQ 的中点，当点P 在圆C 上运动时，求点M 的轨迹的普通方程．解：(1)作出图形如图所示，设圆C 上任意一点A (ρ，θ)，则∠AOC ＝θ－π3或π3－θ.由余弦定理得，4＋ρ2－4ρcos θ－π3＝4，∴圆C 的极坐标方程为ρ＝4cos ⎝⎛⎭⎪⎫θ－π3. (2)在直角坐标系中，点C 的坐标为(1，3)，可设圆C 上任意一点P (1＋2cos α，3＋2sin α)，设M (x ，y )，由Q (5，－3)，M 是线段PQ 的中点，得点M的轨迹的参数方程为⎩⎪⎨⎪⎧x ＝6＋2cos α2，y ＝2sin α2(α为参数)，即⎩⎪⎨⎪⎧x ＝3＋cos α，y ＝sin α(α为参数)，∴点M 的轨迹的普通方程为(x －3)2＋y 2＝1.第2课参数方程[过双基]1．参数方程的概念一般地，在平面直角坐标系中，如果曲线C 上任意一点P 的坐标x ，y 是某个变数t 的函数：⎩⎪⎨⎪⎧x ＝f t ，y ＝g t ，并且对于t 的每一个允许值，由函数式⎩⎪⎨⎪⎧x ＝ft ，y ＝g t所确定的点P (x ，y )都在曲线C 上，那么方程⎩⎪⎨⎪⎧x ＝ft ，y ＝g t叫做这条曲线的参数方程，变数t 叫做参变数，简称参数．相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程．2．直线、圆、椭圆的参数方程(1)过点M (x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．(2)圆心在点M 0(x 0，y 0)，半径为r 的圆的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数)．(3)椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的参数方程为⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ(φ为参数)．[小题速通] 1．参数方程⎩⎪⎨⎪⎧x ＝2－t ，y ＝－1－2t(t 为参数)与极坐标方程ρ＝sin θ所表示的图形分别是________．解析：将参数方程⎩⎪⎨⎪⎧x ＝2－t ，y ＝－1－2t 消去参数t ，得2x －y －5＝0，对应图形为直线．由ρ＝sin θ，得ρ2＝ρsin θ，即x 2＋y 2＝y ，即x 2＋⎝ ⎛⎭⎪⎫y －122＝14，对应图形为圆．答案：直线、圆2．曲线⎩⎪⎨⎪⎧x ＝sin θ，y ＝sin 2θ(θ为参数)与直线y ＝x ＋2的交点坐标为________．解析：曲线的直角坐标方程为y ＝x 2.将其与直线方程联立得⎩⎪⎨⎪⎧y ＝x 2，y ＝x ＋2，∴x 2－x －2＝0，∴x ＝－1或x ＝2.由x ＝sin θ知，x ＝2不合题意．∴x ＝－1，y ＝1，∴交点坐标为(－1,1)．答案：(－1,1)3．设曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋3cos θ，y ＝－1＋3sin θ(θ为参数)，直线l 的方程为x －3y ＋2＝0，则曲线C 上到直线l 距离为71010的点的个数为________．解析：∵曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝2＋3cos θ，y ＝－1＋3sin θ(θ为参数)，∴(x －2)2＋(y ＋1)2＝9， ∴圆心(2，－1)到直线l 的距离d ＝|2＋3＋2|1＋9＝710＝71010.又∵71010<3，141010>3，∴有2个点．答案：24．参数方程⎩⎪⎨⎪⎧x ＝2t 21＋t2，y ＝4－2t21＋t2(t 为参数)化为普通方程为________．解析：∵x ＝2t21＋t 2，y ＝4－2t 21＋t 2＝＋t 2－6t 21＋t 2＝4－3×2t21＋t 2＝4－3x .又x ＝2t21＋t 2＝＋t 2－21＋t 2＝2－21＋t2∈[0,2)，∴x ∈[0,2)，∴所求的普通方程为3x ＋y －4＝0(x ∈[0,2))． 答案：3x ＋y －4＝0(x ∈[0,2))[清易错]1．在参数方程与普通方程的互化中，必须使x ，y 的取值范围保持一致，否则不等价．2．直线的参数方程中，参数t 的系数的平方和为1时，t 才有几何意义且其几何意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离，即|M 0M |＝|t |.1．直线y ＝x －1上的点到曲线⎩⎪⎨⎪⎧x ＝－2＋cos θ，y ＝1＋sin θ上的点的最近距离是________．解析：由⎩⎪⎨⎪⎧x ＝－2＋cos θ，y ＝1＋sin θ得⎩⎪⎨⎪⎧cos θ＝x ＋2，sin θ＝y －1，∴(x ＋2)2＋(y －1)2＝1，∴圆心坐标为(－2,1)， 故圆心到直线x －y －1＝0的距离d ＝42＝22，∴直线上的点到圆上的点的最近距离是d －r ＝22－1. 答案：22－12．直线⎩⎪⎨⎪⎧x ＝4＋at ，y ＝bt(t 为参数)与圆⎩⎨⎧x ＝2＋3cos θ，y ＝3sin θ(θ为参数)相切，则切线的倾斜角为________．解析：直线的普通方程为bx －ay －4b ＝0，圆的普通方程为(x －2)2＋y 2＝3，因为直线与圆相切，则圆心(2,0)到直线的距离为3，从而有 3＝|2b －a ·0－4b |a 2＋b2，即3a 2＋3b 2＝4b 2，所以b ＝±3a ，而直线的倾斜角α的正切值tan α＝ba，所以tan α＝±3，因此切线的倾斜角π3或2π3.答案：π3或2π3参数方程与普通方程的互化[典例] 已知椭圆C ：x 24＋y 23＝1，直线l ：⎩⎨⎧x ＝－3＋3t ，y ＝23＋t ，(t 为参数)．(1)写出椭圆C 的参数方程及直线l 的普通方程；(2)设A (1,0)，若椭圆C 上的点P 满足到点A 的距离与其到直线l 的距离相等，求点P 的坐标．[解] (1)椭圆C ：⎩⎨⎧x ＝2cos θ，y ＝3sin θ(θ为参数)，直线l ：x －3y ＋9＝0.(2)设P (2cos θ，3sin θ)，则|AP |＝ θ－2＋3sin θ2＝2－cos θ，点P 到直线l 的距离d ＝|2cos θ－3sin θ＋9|2＝2cos θ－3sin θ＋92.由|AP |＝d ，得3sin θ－4cos θ＝5，又sin 2θ＋cos 2θ＝1，得sin θ＝35，cos θ＝－45.故P ⎝ ⎛⎭⎪⎫－85，335.[方法技巧]将参数方程化为普通方程的方法(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等，对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin 2θ＋cos 2θ＝1等．(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解． [即时演练]将下列参数方程化为普通方程． (1)⎩⎪⎨⎪⎧x ＝3k 1＋k 2，y ＝6k21＋k2(k 为参数)；(2)⎩⎪⎨⎪⎧x ＝1－sin 2θ，y ＝sin θ＋cos θ(θ为参数)．解：(1)两式相除，得k ＝y2x ，将其代入x ＝3k1＋k 2，得x ＝3·y2x1＋⎝ ⎛⎭⎪⎫y 2x 2， 化简得所求的普通方程是4x 2＋y 2－6y ＝0(y ≠6)．(2)由(sin θ＋cos θ)2＝1＋sin 2θ＝2－(1－sin 2θ)， 得y 2＝2－x .又x ＝1－sin 2θ∈[0,2]， 故所求的普通方程为y 2＝2－x ，x ∈[0,2]．参数方程[典例] 种坐标系取相同的单位长度．已知曲线C ：ρsin 2θ＝2a cos θ(a >0)，过点P (－2，－4)的直线l 的参数方程为⎩⎨⎧x ＝－2＋2t ，y ＝－4＋2t(t 为参数)，直线l 与曲线C 分别交于M ，N ，若|PM |，|MN |，|PN |成等比数列，求实数a 的值．[解] 曲线C 的直角坐标方程为y 2＝2ax (a >0)， 将直线l 的参数方程化为⎩⎪⎨⎪⎧x ＝－2＋22t ′，y ＝－4＋22t ′(t ′为参数)，代入曲线C 的方程得：12t ′2－(42＋2a )t ′＋16＋4a ＝0， 则Δ>0，即a >0或a <－4.设交点M ，N 对应的参数分别为t 1′，t 2′，则t 1′＋t 2′＝2(42＋2a )，t 1′t 2′＝2(16＋4a )， 若|PM |，|MN |，|PN |成等比数列， 则|t 1′－t 2′|2＝|t 1′t 2′|， 解得a ＝1或a ＝－4(舍去)， 所以满足条件的a ＝1. [方法技巧](1)解决直线与圆的参数方程的应用问题时，一般是先化为普通方程，再根据直线与圆的位置关系来解决问题．(2)对于形如⎩⎪⎨⎪⎧x ＝x 0＋at ，y ＝y 0＋bt (t 为参数)．当a 2＋b 2≠1时，应先化为标准形式后才能利用t 的几何意义解题． [即时演练]已知直线l ：x ＋y －1＝0与抛物线y ＝x 2相交于A ，B 两点，求线段AB 的长度和点M (－1,2)到A ，B 两点的距离之积．解：因为直线l 过定点M ，且l 的倾斜角为3π4，所以它的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t cos 3π4，y ＝2＋t sin 3π4(t 为参数)，即⎩⎪⎨⎪⎧x ＝－1－22t ，y ＝2＋22t (t 为参数)，把它代入抛物线的方程，得t 2＋2t －2＝0， 由根与系数的关系得t 1＋t 2＝－2，t 1·t 2＝－2， 由参数t 的几何意义可知|AB |＝|t 1－t 2|＝10， |MA |·|MB |＝|t 1t 2|＝2.[典例] (2017·全国卷Ⅲ)在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝mk(m 为参数)．设l 1与l 2的交点为P ，当k变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．[解] (1)消去参数t 得l 1的普通方程l 1：y ＝k (x －2)； 消去参数m 得l 2的普通方程l 2：y ＝1k(x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k x －，y ＝1kx ＋消去k 得x 2－y 2＝4(y ≠0)．所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0＜θ＜2π，θ≠π)．联立⎩⎨⎧ρ22θ－sin 2θ＝4，ρθ＋sin θ－2＝0得cos θ－sin θ＝2(cos θ＋sin θ)． 故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以交点M 的极径为 5.[方法技巧]处理极坐标、参数方程综合问题的方法(1)涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．(2)数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的．[即时演练]在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为：ρ＝4cos θ1－cos 2θ，直线的参数方程是⎩⎪⎨⎪⎧x ＝2＋t cos α，y ＝2＋t sin α.(α为参数，0≤α<π)．(1)求曲线C 的直角坐标方程；(2)设直线与曲线C 交于两点A ，B ，且线段AB 的中点为M (2，2)，求α.解：(1)曲线C ：ρ＝4cos θ1－cos 2θ，即ρsin 2θ＝4cos θ，于是有ρ2sin 2θ＝4ρcos θ，化为直角坐标方程为y 2＝4x .(2)法一： 把x ＝2＋t cos α，y ＝2＋t sin α代入y 2＝4x ， 得(2＋t sin α)2＝4(2＋t cos α)， 即t 2sin 2α＋(4sin α－4cos α)t －4＝0.由AB 的中点为M (2,2)得t 1＋t 2＝0，有4sin α－4cos α＝0，所以k ＝tan α＝1. 由0≤α<π，得α＝π4.法二：设A (x 1，y 1)，B (x 2，y 2)，则⎩⎪⎨⎪⎧y 21＝4x 1，y 22＝4x 2⇒(y 1＋y 2)(y 1－y 2)＝4(x 1－x 2)．∵y 1＋y 2＝4，∴k 1＝tan α＝y 1－y 2x 1－x 2＝1， 由0≤α<π，得α＝π4.1．(2017·全国卷Ⅰ)在直角坐标系xOy 中，曲线C的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . 解：(1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0，由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0， 故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17. 当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，解得a ＝8；当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，解得a ＝－16.综上，a ＝8或a ＝－16.2．(2016·全国卷Ⅱ)在直角坐标系xOy 中，圆C 的方程为(x ＋6)2＋y 2＝25. (1)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程；(2)直线l 的参数方程是⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数)，l 与C 交于A ，B 两点，|AB |＝10，求l 的斜率．解：(1)由x ＝ρcos θ，y ＝ρsin θ可得圆C 的极坐标方程为 ρ2＋12ρcos θ＋11＝0.(2)法一：在(1)中建立的极坐标系中，直线l 的极坐标方程为θ＝α(ρ∈R)． 设A ，B 所对应的极径分别为ρ1，ρ2， 将l 的极坐标方程代入C 的极坐标方程得 ρ2＋12ρcos α＋11＝0，于是ρ1＋ρ2＝－12cos α，ρ1ρ2＝11.|AB |＝|ρ1－ρ2|＝ρ1＋ρ22－4ρ1ρ2＝144cos 2α－44.由|AB |＝10得cos 2α＝38，tan α＝±153.所以直线l 的斜率为153或－153. 法二：由直线l 的参数方程⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数)，消去参数得y ＝x ·tan α.设直线l 的斜率为k ， 则直线l 的方程为kx －y ＝0. 由圆C 的方程(x ＋6)2＋y 2＝25知， 圆心坐标为(－6,0)，半径为5.又|AB |＝10，由垂径定理及点到直线的距离公式得 |－6k |1＋k2＝25－⎝ ⎛⎭⎪⎫1022，即36k 21＋k 2＝904，整理得k 2＝53，解得k ＝±153，即直线l 的斜率为±153. 3．(2015·全国卷Ⅱ)在直角坐标系xOy 中，曲线C 1：⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数，t ≠0)，其中0≤α＜π.在以O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝2sin θ，C 3：ρ＝23cos θ.(1)求C 2与C 3交点的直角坐标；(2)若C 1与C 2相交于点A ，C 1与C 3相交于点B ，求|AB |的最大值． 解：(1)曲线C 2的直角坐标方程为x 2＋y 2－2y ＝0， 曲线C 3的直角坐标方程为x 2＋y 2－23x ＝0.联立⎩⎨⎧x 2＋y 2－2y ＝0，x 2＋y 2－23x ＝0，解得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝32，y ＝32.所以C 2与C 3交点的直角坐标为(0,0)和⎝⎛⎭⎪⎫32，32. (2)曲线C 1的极坐标方程为θ＝α(ρ∈R ，ρ≠0)， 其中0≤α＜π.因此A 的极坐标为(2sin α，α)，B 的极坐标为(23cos α，α)． 所以|AB |＝|2sin α－23cos α|＝4⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3. 当α＝5π6时，|AB |取得最大值，最大值为4.4．(2014·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为ρ＝2cos θ，θ∈⎣⎢⎡⎦⎥⎤0，π2.(1)求C 的参数方程；(2)设点D 在C 上，C 在D 处的切线与直线l ：y ＝3x ＋2垂直，根据(1)中你得到的参数方程，确定D 的坐标．解：(1)C 的普通方程为(x －1)2＋y 2＝1(0≤y ≤1)．可得C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋cos t ，y ＝sin t (t 为参数，0≤t ≤π)．(2)设D (1＋cos t ，sin t )．由(1)知C 是以G (1,0)为圆心，1为半径的上半圆． 因为G 在点D 处的切线与l 垂直，所以直线GD 与l 的斜率相同，tan t ＝3，t ＝π3.故D 的直角坐标为⎝ ⎛⎭⎪⎫1＋cos π3，sin π3，即⎝ ⎛⎭⎪⎫32，32.1．(2017·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t 2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C上的动点，求点P 到直线l 的距离的最小值．解：直线l 的普通方程为x －2y ＋8＝0. 因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋－2＝s －22＋45.当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上点P 到直线l 的距离取到最小值455.2．已知曲线C 1：⎩⎪⎨⎪⎧x ＝－4＋cos t ，y ＝3＋sin t (t 为参数)，曲线C 2：⎩⎪⎨⎪⎧x ＝8cos θ，y ＝3sin θ(θ为参数)．(1)化C 1，C 2的方程为普通方程，并说明它们分别表示什么曲线；(2)若C 1上的点P 对应的参数为t ＝π2，Q 为C 2上的动点，求PQ 中点M 到直线C 3：⎩⎪⎨⎪⎧x ＝3＋2t ，y ＝－2＋t(t 为参数)的距离的最小值．解：(1)曲线C 1：(x ＋4)2＋(y －3)2＝1，曲线C 2：x 264＋y 29＝1，曲线C 1是以(－4,3)为圆心，1为半径的圆；曲线C 2是以坐标原点为中心，焦点在x 轴上，长半轴长是8，短半轴长是3的椭圆． (2)当t ＝π2时，P (－4,4)，Q (8cos θ，3sin θ)，故M －2＋4cos θ，2＋32sin θ.曲线C 3为直线x －2y －7＝0，M 到C 3的距离d ＝55|4cos θ－3sin θ－13|，从而当cos θ＝45，sin θ＝－35时，d 取最小值855.3．在平面直角坐标系xOy 中，C 1的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t (t 为参数)，在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，C 2的极坐标方程ρ2－2ρcos θ－3＝0.(1)说明C 2是哪种曲线，并将C 2的方程化为普通方程；(2)C 1与C 2有两个公共点A ，B ，点P 的极坐标⎝⎛⎭⎪⎫2，π4，求线段AB 的长及定点P 到A ，B 两点的距离之积．解：(1)C 2是圆，C 2的极坐标方程ρ2－2ρcos θ－3＝0， 化为普通方程为x 2＋y 2－2x －3＝0，即(x －1)2＋y 2＝4. (2)点P 的直角坐标为(1,1)，且在直线C 1上， 将C 1的参数方程⎩⎪⎨⎪⎧x ＝1－22t ，y ＝1＋22t (t 为参数)代入x 2＋y 2－2x －3＝0，得⎝ ⎛⎭⎪⎫1－22t 2＋⎝ ⎛⎭⎪⎫1＋22t 2－2⎝⎛⎭⎪⎫1－22t －3＝0，化简得t 2＋2t －3＝0. 设A ，B 对应的参数分别为t 1，t 2， 则t 1＋t 2＝－2，t 1·t 2＝－3， 所以|AB |＝|t 1－t 2|＝t 1＋t 22－4t 1t 2＝2＋12＝14，定点P 到A ，B 两点的距离之积|PA |·|PB |＝|t 1t 2|＝3.4．在平面直角坐标系xOy 中，已知圆C 的参数方程为⎩⎪⎨⎪⎧x ＝1＋2cos θ，y ＝2sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝5－2t ，y ＝3－t (t 为参数)，定点P (1,1)．(1)以原点O 为极点，x 轴的非负半轴为极轴，单位长度与平面直角坐标系下的单位长度相同建立极坐标系，求圆C 的极坐标方程；(2)已知直线l 与圆C 相交于A ，B 两点，求||PA |－|PB ||的值． 解：(1)依题意得圆C 的一般方程为(x －1)2＋y 2＝4，将x ＝ρcos θ，y ＝ρsin θ代入上式得ρ2－2ρcos θ－3＝0， 所以圆C 的极坐标方程为ρ2－2ρcos θ－3＝0.(2)因为定点P (1,1)在直线l 上，所以直线l 的参数方程可表示为⎩⎪⎨⎪⎧x ＝1－255t ，y ＝1－55t (t 为参数)．代入(x －1)2＋y 2＝4，得t 2－255t －3＝0. 设点A ，B 分别对应的参数为t 1，t 2， 则t 1＋t 2＝255，t 1t 2＝－3.所以t 1，t 2异号，不妨设t 1>0，t 2<0， 所以|PA |＝t 1，|PB |＝－t 2， 所以||PA |－|PB ||＝|t 1＋t 2|＝255.5．已知直线l ：⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝32t(t 为参数)，曲线C 1：⎩⎪⎨⎪⎧x ＝cos θ，y ＝sin θ(θ为参数)．(1)设l 与C 1相交于A ，B 两点，求|AB |；(2)若把曲线C 1上各点的横坐标压缩为原来的12倍，纵坐标压缩为原来的32倍，得到曲线C 2，设点P 是曲线C 2上的一个动点，求它到直线l 距离的最小值．解：(1)由已知得l 的普通方程为y ＝3(x －1)，C 1的普通方程为x 2＋y 2＝1， 联立方程⎩⎨⎧y ＝3x －，x 2＋y 2＝1解得l 与C 1的交点为A (1,0)，B ⎝ ⎛⎭⎪⎫12，－32，则|AB |＝1.(2)由题意，得C 2的参数方程为⎩⎪⎨⎪⎧x ＝12cos θ，y ＝32sin θ(θ为参数)，故点P 的坐标为⎝ ⎛⎭⎪⎫12cos θ，32sin θ，从而点P 到直线l 的距离是 d ＝⎪⎪⎪⎪⎪⎪32cos θ－32sin θ－32＝342sin ⎝⎛⎭⎪⎫θ－π4＋2，当sin ⎝ ⎛⎭⎪⎫θ－π4＝－1时，d 取得最小值，且最小值为23－64.6．在直角坐标系xOy 中，直线l的参数方程为⎩⎪⎨⎪⎧x ＝t －1，y ＝t ＋2(t 为参数)．在以原点O为极点，x 轴的正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρ＝31＋2cos 2θ.(1)直接写出直线l 的普通方程、曲线C 的直角坐标方程； (2)设曲线C 上的点到直线l 的距离为d ，求d 的取值范围． 解：(1)直线l 的普通方程为x －y ＋3＝0，曲线C 的直角坐标方程为3x 2＋y 2＝3. (2)∵曲线C 的直角坐标方程为3x 2＋y 2＝3， 即x 2＋y 23＝1，∴曲线C 上的点的坐标可表示为(cos α，3sin α)， ∴d ＝|cos α－3sin α＋3|2＝⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫π6－α＋32＝2sin ⎝ ⎛⎭⎪⎫π6－α＋32.∴d 的最小值为12＝22，d 的最大值为52＝522.∴22≤d ≤522，即d 的取值范围为⎣⎢⎡⎦⎥⎤22，522. 7．平面直角坐标系xOy 中，曲线C ：(x －1)2＋y 2＝1.直线l 经过点P (m,0)，且倾斜角为π6，以O 为极点，x 轴正半轴为极轴，建立极坐标系． (1)写出曲线C 的极坐标方程与直线l 的参数方程；(2)若直线l 与曲线C 相交于A ，B 两点，且|PA |·|PB |＝1，求实数m 的值．解：(1)曲线C 的直角坐标方程为：(x －1)2＋y 2＝1，即x 2＋y 2＝2x ，即ρ2＝2ρcos θ， 所以曲线C 的极坐标方程为ρ＝2cos θ. 直线l 的参数方程为⎩⎪⎨⎪⎧x ＝m ＋32t ，y ＝12t (t 为参数)．(2)设A ，B 两点对应的参数分别为t 1，t 2，将直线l 的参数方程代入x 2＋y 2＝2x 中， 得t 2＋(3m －3)t ＋m 2－2m ＝0， 所以t 1t 2＝m 2－2m ， 由题意得|m 2－2m |＝1，解得m ＝1或m ＝1＋2或m ＝1－ 2. 8．已知直线的参数方程是⎩⎪⎨⎪⎧x ＝22t ，y ＝22t ＋42(t 是参数)，圆C 的极坐标方程为ρ＝4cos ⎝⎛⎭⎪⎫θ＋π4.(1)求圆心C 的直角坐标；(2)由直线l 上的点向圆C 引切线，求切线长的最小值． 解：(1)∵ρ＝4cos ⎝ ⎛⎭⎪⎫θ＋π4＝22cos θ－22sin θ， ∴ρ2＝22ρcos θ－22ρsin θ，∴圆C 的直角坐标方程为x 2＋y 2－22x ＋22y ＝0， 即(x －2)2＋(y ＋2)2＝4， ∴圆心的直角坐标为(2，－2)． (2)直线l 上的点向圆C 引切线，则切线长为⎝ ⎛⎭⎪⎫22t －22＋⎝ ⎛⎭⎪⎫22t ＋42＋22－4 ＝t 2＋8t ＋48＝t ＋2＋32≥42，∴直线l 上的点向圆C 引的切线长的最小值为4 2.。