多人行程

1、 五年级行程问题：多人行程难度：高难度答：2、五年级行程问题：二次相遇、追及问题 难度：中难度答3、 六年级行程问题：多次相遇、追及问题 难度：高难度答：4、 四年级行程问题：火车过桥甲、乙、丙三人都从A 地到B 地。

早上七点，甲、乙两人一起从甲地出发，甲每小时行6千米，乙每小时行5千米。

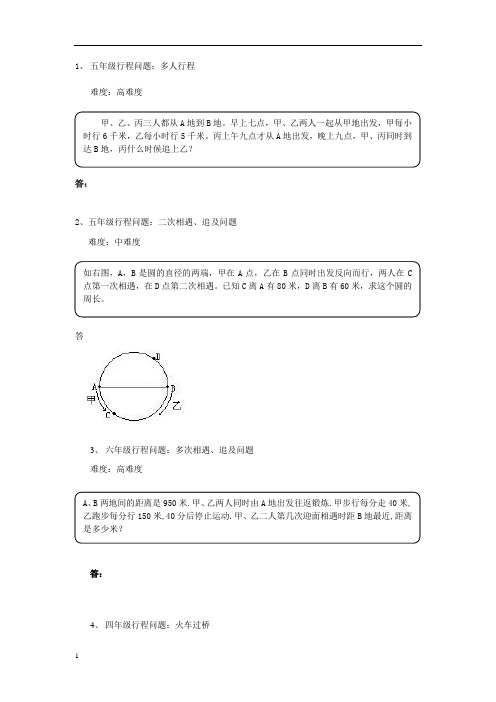
丙上午九点才从A 地出发，晚上九点，甲、丙同时到达B 地，丙什么时候追上乙？如右图，A ，B 是圆的直径的两端，甲在A 点，乙在B 点同时出发反向而行，两人在C 点第一次相遇，在D 点第二次相遇。

已知C 离A 有80米，D 离B 有60米，求这个圆的周长。

A 、B 两地间的距离是950米.甲、乙两人同时由A 地出发往返锻炼.甲步行每分走40米,乙跑步每分行150米,40分后停止运动.甲、乙二人第几次迎面相遇时距B 地最近,距离是多少米？难度：中难度两列火车相向而行，甲车每小时行36千米，乙车每小时行54千米。

两车错车时，甲车上一乘客发现：从乙车车头经过他的车窗时开始到乙车车尾经过他的车窗共用了14秒，求乙车的车长。

答：5、六年级行程问题：环形跑道难度：高难度周长为400米的圆形跑道上，有相距100米的A，B两点．甲、乙两人分别从A，B 两点同时相背而跑，两人相遇后，乙即转身与甲同向而跑，当甲跑到A时，乙恰好跑到B．如果以后甲、乙跑的速度和方向都不变，那么甲追上乙时，甲从出发开始，甲共跑了多少米?答：6、五年级行程问题：流水行船难度：高难度静水中，甲船的速度是24千米/小时，乙船的速度是20千米/小时，乙船先从某港开出，顺水航行3小时，甲船从这个港口同方向开出，如水流速度是4千米/小时，甲船几小时可以追上乙船？7、四年级行程问题：简单的相遇、追及问题难度：中难度甲车每小时行40千米，乙车每小时行60千米，甲车从A地、乙车从B地同时出发相向而行，两车相遇后4.5时，甲车到达B地，A、B两地相距多少千米？1、×年级多人行程习题答案：解答：甲先行多少米6×（9-7）＝12（千米）丙用多少时间追上甲21－9＝12（小时）丙每小时行多少千米12÷12+6＝7（千米）丙追上乙用多少小时？5×（9-7）÷（7-5）＝5丙什么时候追上乙 9+5＝14时答：丙下午2时。

(行程问题) 多人行程1、五年级行程问题：多人行程难度：高难度甲、乙、丙三辆车同时从A地出发到B地去，甲、乙两车的速度分别为60千米／时和48千米／时。

有一辆迎面开来的卡车分别在他们出发后6时、7时、8时先后与甲、乙、丙三辆车相遇。

求丙车的速度。

答：2、五年级行程问题：多人行程难度：高难度李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到。

0.5小时后，营地老师闻讯前来迎接，每小时比李华多走1.2千米，又经过了1.5小时，张明从学校骑车去营地报到。

结果3人同时在途中某地相遇。

问：张明每小时行驶多少千米？答：3、四年级行程问题：多人行程难度：高难度小红和小强同时从家里出发相向而行．小红每分走52米，小强每分走70米，二人在途中的A处相遇．若小红提前4分出发，且速度不变，小强每分走90米，则两人仍在A处相遇．小红和小强两人的家相距多少米？答：五年级行程问题：多人行程难度：高难度甲、乙、丙是一条路上的三个车站，乙站到甲、丙两站的距离相等，小强和小明同时分别从甲、丙两站出发相向而行，小强经过乙站100米时与小明相遇，然后两人又继续前进，小强走到丙站立即返回，经过乙站300米时又追上小明，问：甲、乙两站的距离是多少米？答：4、五年级行程问题：多人行程难度：高难度甲、乙、丙三人都从A地到B地。

早上七点，甲、乙两人一起从甲地出发，甲每小时行6千米，乙每小时行5千米。

丙上午九点才从A地出发，晚上九点，甲、丙同时到达B地，丙什么时候追上乙？答：1、五年级多人行程习题答案：解答：解题思路：（多人相遇问题要转化成两两之间的问题，咱们的相遇和追击公式也是研究的两者。

另外ST图也是很关键）第一步：当甲经过6小时与卡车相遇时，乙也走了6小时，甲比乙多走了6⨯60-48⨯6=72千米；（这也是现在乙车与卡车的距离）第二步：接上一步，乙与卡车接着走1小时相遇，所以卡车的速度为72-48⨯1=24第三步：综上整体看问题可以求出全程为：（60+24）⨯6=504或（48+24）⨯7=504第四步：收官之战：504÷8-24=39（千米）注意事项：画图时，要标上时间，并且多人要同时标，以防思路错乱！2、五年级多人行程习题答案：解答：老师出发时和李华相距20.4-4×0.5=18.4千米，再过18.4÷（4+4+1.2）=2小时相遇，相遇地点距学校2×4+2=10千米，张明行驶的时间为0.5小时，因此张明的速度为10÷0.5=20千米/时。

⼩学五年级⾏程问题：多⼈⾏程（⾼等难度）⼩学五年级⾏程问题：多⼈⾏程（⾼等难度）⾏程问题是⼩学奥数中变化最多的⼀个专题，不论在奥数竞赛中还是在“⼩升初”的升学考试中，都拥有⾮常重要的地位。

⾏程问题中包括：⽕车过桥、流⽔⾏船、沿途数车、猎狗追兔、环形⾏程、多⼈⾏程，等等。

每⼀类问题都有⾃⼰的特点，解决⽅法也有所不同，但是，⾏程问题⽆论怎么变化，都离不开“三个量，三个关系”：这三个量是：路程(s)、速度(v)、时间(t)三个关系：1. 简单⾏程：路程 = 速度× 时间2. 相遇问题：路程和 = 速度和× 时间3. 追击问题：路程差 = 速度差× 时间牢牢把握住这三个量以及它们之间的三种关系，就会发现解决⾏程问题还是有很多⽅法可循的。

如“多⼈⾏程问题”，实际最常见的是“三⼈⾏程”例1：有甲、⼄、丙三⼈同时同地出发，绕⼀个花圃⾏⾛，⼄、丙⼆⼈同⽅向⾏⾛，甲与⼄、丙相背⽽⾏。

甲每分钟⾛40⽶，⼄每分钟⾛38⽶，丙每分钟⾛36⽶。

在途中，甲和⼄相遇后3分钟和丙相遇。

问：这个花圃的周长是多少⽶?分析：这个三⼈⾏程的问题由两个相遇、⼀个追击组成，题⽬中所给的条件只有三个⼈的速度，以及⼀个“3分钟”的时间。

第⼀个相遇：在3分钟的时间⾥，甲、丙的路程和为(40+36)×3=228(⽶)第⼀个追击：这228⽶是因为在开始到甲、⼄相遇的时间⾥，⼄、丙两⼈的速度差造成的，是逆向的追击过程，可求出甲、⼄相遇的时间为228÷(38-36)=114(分钟)第⼆个相遇：在114分钟⾥，甲、⼄⼆⼈⼀起⾛完了全程所以花圃周长为(40+38)×114=8892(⽶)我们把这样⼀个抽象的三⼈⾏程问题分解为三个简单的问题，使解题思路更加清晰。

总之，⾏程问题是重点，也是难点，更是锻炼思维的好⼯具。

只要理解好“三个量”之间的“三个关系”，解决⾏程问题并⾮难事!。

多人旅游策划方案随着人们的生活水平提高及工作压力增加，旅游已成为人们生活中必不可少的一部分。

然而，如何规划一次完善的旅游，让每一个旅游者都满意，却是一项不容易的任务。

特别是在当今经济情况下，如何做到旅游省钱又有趣呢？因此，在本文中，我们将为大家提供一些多人旅游策划方案，帮助大家打造一次不同寻常的旅游之旅。

1. 目的与预算在规划旅游之前，首先需要明确目的地以及旅游活动预算。

旅游目的地应该根据不同人的兴趣来选择，特别是多人同行时，应该根据各自的需求和兴趣来规划旅游路线。

同时，还要确立旅游花费的预算，从而避免旅游计划过于超预算。

2. 选择住宿方式在旅游规划中，住宿是必不可少的一部分。

选择合适的住宿方式可以有效的避免因住宿问题造成的旅行不便。

对于多人旅游来讲，可以选择住宿公寓、酒店、旅馆等等。

而在这些住宿方式之中，选择性价比高的，可以帮助我们省下相应的开支。

3. 安排行程在旅游的时候，一个合理的行程能够让我们更充分的发掘旅游地点所能提供的东西，同时减少等待时间，让行程更加顺畅。

对于多人旅游来讲，需要考虑每一个人的利益，因此在安排行程的时候，可以选择拜访一些别具特色的景点和当地特色的活动，以吸引大家的兴趣。

4. 挑选饮食项目在旅游的时候，饮食也是必不可少的一部分。

提早安排饮食，可以帮助规避因寻找餐落而打乱行程的情况。

预先考虑当地的餐饮特色，挑选一些具有风味和个性的小餐馆或市场，可以让大家品尝到更加正宗的当地美食。

5. 联系当地旅游人员当我们旅游的时候，可以选择当地的旅游人员协助我们旅游，并有带领我们认识当地的文化和习俗，从而更深入的体验当地的生活。

同时，当地的旅游人员会推荐一些适合当地的自由活动，帮助大家更好的度过旅游时光。

6. 做好準备在旅游之前，我们还需要做好一些准备工作，包括准备出行所必须的物品，如护照、驾驶执照等等；另外，还可以在旅游过程中，及时查看天气以及当地旅游资源的更新情况，以便做出相应的调整。

盈亏问题盈亏问题的数量关系是：（1）（盈＋亏）÷两次分配差=份数（大盈－小盈）÷两次分配差=份数（大亏－小亏）÷两次分配差=份数（2）每次分得的数量×份数＋盈=总数量每次分得的数量×份数－亏=总数量例1 小朋友分糖果，若每人分4粒则多9粒；若每人分5粒则少6粒。

问：有多少个小朋友分多少粒糖？分析：由题目条件可以知道，小朋友的人数与糖的粒数是不变的。

比较两种分配方案，第一种方案每人分4粒就多9粒，第二种方案每人分5粒就少6粒，两种不同的方案一多一少相差9＋6＝15（粒）。

相差的原因在于两种方案的分配数不同，第一种方案每人分4粒，第二种方案每人分5粒，两次分配数之差为5－4＝1（粒）。

每人相差1粒，多少人相差15粒呢？由此求出小朋友的人数为15÷1＝15（人），糖果的粒数为4×15＋9＝69（粒）。

解：（9＋6）÷（5-4）＝15（人），4×15＋9＝69（粒）。

答：有15个小朋友，分69粒糖。

例2：学校将一批铅笔奖给三好学生。

如果每人奖9支，则缺45支；如果每人奖7支，则缺7支。

三好学生有多少人？铅笔有多少支？分析与解答：这是两亏的问题。

由题意可知：三好学生人数和铅笔支数是不变的。

比较两种分配方案，结果相差45－7=38支。

这是因为两种分配方案每人得到的铅笔相差9－7=2支。

所以，三好学生有38÷2=19人，铅笔有9×19－45=126支。

例3：有一些少先队员到山上去种一批树。

如果每人种16棵，还有24棵没种；如果每人种19棵，还有6棵没有种。

问有多少名少先队员？有多少棵树？分析与解答：这是两盈的问题。

由题意可知：少先队员的人数和树的棵数是不变的。

比较两种分配方案，结果相差24－6=18棵，这是因为两种分配方案每人种的树相差19－16=3棵。

所以，少先队员有18÷3=6名，树有16×6＋24=120棵。

【#小学奥数# 导语】行程问题是小学奥数中的一大基本问题。

行程问题有相遇问题、追及问题等近十种，是问题类型较多的题型之一。

行程问题包含多人行程、二次相遇、多次相遇、火车过桥、流水行船、环形跑道、钟面行程、走走停停、接送问题等。

以下是?无忧考网整理的《小学三年级奥数多人行程练习题》相关资料，希望帮助到您。

1.小学三年级奥数多人行程练习题1、小明上午九点上山，每小时走3千米，在山顶休息1小时后开始沿原路下山，每小时走4千米，下午一点半到达山下，问他共走了____千米。

【答案解析】上午九点上山下午1点半下山，用时4.5小时，除去休息的一个小时，上山和下山共用时3.5小时。

上山速度3千米/小时，下山速度4千米/小时，则上山用2小时，下山用1.5小时，路程应为3×2×2=12（千米）。

2、某人从甲地到乙地，先骑12小时摩托车，再骑9小时自行车正好到达。

返回时，先骑21小时自行车，再骑8小时摩托车也正好到达。

从甲地到乙地如果全骑摩托车需要多少时间？摩托车的速度是xkm/h，自行车速是ykm/h。

21y+8x=12x+9y4x=12yx=3y所以摩托车共需12+9/3=15小时2.小学三年级奥数多人行程练习题1、两人合修一条长16。

8千米的公路，计划12天完成，甲队每天修0。

8千米，乙队每天修多少千米？2、一列火车从车头到车尾全长240米，以每秒15米的速度通过一座长600米的大桥，一共用了几秒？3、小明站在铁路道口的一边，这时一列火车正好用了15秒经过，现在知道这列火车经过一座1200米的大桥用了75秒，那么这列火车的长度是多少米？4、快车和慢车同时从甲、乙两地相对开出，已知快车每小时行40千米，经过3小时，快车已驶过中点25千米，这时与慢车还相距7千米，慢车每小时行多少千米？5、兄妹两人同时离家去上学，哥哥每分钟走90米，妹妹每分钟走60米，哥哥到校门时，突然发现忘记带课本，立即沿原路回家去取，行至离学校180米处与妹妹相遇，问他们家离学校有多远？3.小学三年级奥数多人行程练习题1、一条街上，一个骑车人与一个步行人同向而行，骑车人的速度是步行人速度的3倍，每隔10分钟有一辆公共汽车超过行人，每隔20分钟有一辆公共汽车超过骑车人．如果公共汽车从始发站每次间隔同样的时间发一辆车，那么间隔多少分钟发一辆公共汽车？2、在地铁车站中，从站台到地面有一架向上的自动扶梯。

第十三讲·火车过桥与多人行程一、火车过树(植树问题)二、火车过人1. 相遇2. 追及三、火车过桥(典型)四、火车过火车(错车问题)1. 相遇2. 追及【学习目标】1. 掌握四大火车行程的基本问题与公式，注意确定路程和速度的方法与技巧.2. 掌握综合类的火车行程问题，注意使用比较加减法，并注意其中与植树问题的综合考察。

【重点难点】1. 火车行程中的相遇与追及路程的判断.2. 分析火车行程问题中的速度和与速度差的使用.3. 分析火车行程与其他行程问题的综合与判断。

【例1】一列火车长280米，铁路沿线的绿化带每两棵树之间相隔2米，这列火车从车头到第1棵树到车尾离开第61棵树用了15秒钟，这列火车每分钟行多少米？【巩固】小李在铁路旁边沿铁路方向的公路上散步，他散步的速度是 1.5米/秒，这时迎面开来一列火车，从车头到车尾经过他身旁共用了20秒，已知火车全长390米，求火车的速度。

【例2】小张沿着一条与铁路平行的笔直小路行走，这时有一列长460米的火车从他背后开来，他在行进中测出火车从他身边通过的时间是20秒，而在这段时间内，他行走了40米. 求这列火车的速度是多少？【例3】一个车队以6米/秒的速度缓缓通过一座长250米的大桥，共用152秒，已知每辆车长6米，两车间隔10米，问：这个车队共有多少辆车？【例4】列车通过250米的隧道用25秒，通过210米长的隧道用23秒，又知列车的前方有一辆与它同向行驶的货车，货车车身长320米，速度为每秒17米，列车与货车从相遇到相离需要多少秒？【例5 】(2007年第十二届“华杯赛”初赛)李云靠窗坐在一列时速60千米的火车里，看到一辆有30节车厢的货车迎面驶来，当货车车头经过窗口时，他开始计时，直到最后一节车厢驶过窗口时，所计的时间是18秒。

已知货车每节车厢长15.8米，车厢间距1.2米，货车车头长10米。

问货车行驶的速度是多少？【例6】有两列同方向行驶的火车，快车每秒行30米，慢车每秒行22米。

奥数比例中的行程问题一、什么是奥数比例中的行程问题呢？哎呀，小伙伴们，这个奥数比例中的行程问题啊，就像是一场有趣的冒险。

想象一下，你有一个小木偶，它要在不同的路程里跑来跑去，而且速度还不一样呢。

比如说，小木偶在一段路程里跑得可快啦，就像一阵小旋风；在另一段路程里呢，又慢腾腾的，像只小蜗牛。

这里面就涉及到比例关系啦。

如果把路程看成是一堆小饼干，速度就是小木偶吃饼干的速度，那时间呢，就是小木偶吃完这些饼干需要多久。

这个时间、速度和路程之间的关系，就可以用比例来表示啦。

二、一些常见的题型类型1. 简单的速度比例问题比如说，小木偶A的速度是小木偶B速度的2倍，它们同时出发，走同样的路程。

那小木偶A和小木偶B所用的时间比例是多少呢？这就很有趣啦，就像两个小朋友比赛跑步，一个跑得快，一个跑得慢，那他们到达终点的时间肯定不一样。

根据速度和时间成反比的关系，小木偶A的速度是小木偶B的2倍，那么小木偶A所用的时间就是小木偶B的1/2。

2. 往返行程中的比例问题小木偶从A地出发到B地，然后再从B地返回A地。

去的时候速度是v1，回来的时候速度是v2，那往返的平均速度是多少呢？这可不能简单地把v1和v2相加除以2哦。

我们要根据路程和时间的关系来算。

设A到B的路程是s，那么去的时间就是s/v1，回来的时间就是s/v2，往返的总路程是2s，总时间是s/v1 + s/v2，通过化简就能得到平均速度的表达式啦。

3. 多人行程中的比例问题假设有小木偶A、小木偶B和小木偶C。

小木偶A和小木偶B从甲地出发，小木偶C从乙地出发，相向而行。

小木偶A的速度是v1，小木偶B的速度是v2，小木偶C的速度是v3。

当小木偶A和小木偶C相遇的时候，小木偶B和他们的距离是多少呢？这就要考虑到他们的速度比例和行走的时间啦。

因为相遇的时候，小木偶A和小木偶C行走的时间是相同的，根据路程 = 速度×时间，我们可以算出他们各自走的路程，然后再根据小木偶B的速度和时间，就能算出小木偶B和他们的距离啦。

★这篇【⼩学⽣经典奥数题：多⼈⾏程问题】是为⼤家收集的，以下内容仅供参考！奥数题多⼈⾏程问题多⼈⾏程---这类问题主要涉及的⼈数为3⼈，主要考察的问题就是求前两个⼈相遇或追及的时刻，第三个⼈的位置，解题的思路就是把三⼈问题转化为寻找两两⼈之间的关系。

下⾯是精品学习⼩编整理的多⼈⾏程问题的经典题型，供⼤家参考。

1.有甲、⼄、丙三⼈同时同地出发，绕⼀个花圃⾏⾛，⼄、丙⼆⼈同⽅向⾏⾛，甲于⼄、丙背向⽽⾏。

甲每分40⽶，⼄每分38⽶，丙每分36⽶。

出发后，甲和⼄相遇后3分钟⼜与丙相遇。

这花圃的周长是多少?2.甲、⼄、丙三⼈⾏路，甲每分钟⾛60⽶，⼄每分钟⾛50⽶，丙每分钟⾛40⽶。

甲从A地，⼄和丙从B出发相向⽽⾏，甲和⼄相遇后，过了15分钟⼜与丙相遇，求A、B两地的距离。

3.有3个⾃⾏车运动员，他们进⾏⼀项从A城到B城的接⼒游戏，甲运动员先从A城出发，以每⼩时27千⽶的速度骑了34分钟，接着⼄运动员以每⼩时36千⽶的速度骑了25分钟，然后丙运动员⼜以30千⽶的速度骑了28分钟到达B城。

求A,B两城之间的距离是多少?4.甲、⼄两地是电车始发站，每隔⼀定时间两地同时各发出⼀辆电车，⼩张和⼩王分别骑车从甲、⼄两地出发，相向⽽⾏.每辆电车都隔4分钟遇到迎⾯开来的⼀辆电车;⼩张每隔5分钟遇到迎⾯开来的⼀辆电车;⼩王每隔6分钟遇到迎⾯开来的⼀辆电车.已知电车⾏驶全程是56分钟，那么⼩张与⼩王在途中相遇时他们已⾏⾛了分钟.5.甲⼄丙三⼈同时从东村去西村，甲骑⾃⾏车每⼩时⽐⼄快12公⾥，⽐丙快15公⾥，甲⾏3.5⼩时到达西村后⽴刻返回。

在距西村30公⾥处和⼄相聚，问：丙⾏了多长时间和甲相遇?6.有甲、⼄、丙三⼈，甲从东村，⼄丙从西村同时出发相向⽽⾏，途中，甲与⼄相遇6分钟后，⼜与丙相遇。

已知甲每分钟⾛100⽶，⼄每分钟⾛80⽶，丙每分钟⾛75⽶。

求东西两村相距多少⽶?7.甲⼄丙三⼈⾏⾛的速度分别为每分钟30⽶、40⽶和50⽶。

多人开车旅行方案多人开车旅行方案旅行是一种让人放松心情、体验不一样生活的方式，而开车旅行是一种自由自在的旅行方式，可以随时停下来欣赏风景，也可以随意改变行程。

以下是一个适合多人开车旅行的方案。

首先，确定旅行的目的地和行程。

多人开车旅行要考虑每个人的兴趣，协商好每天的行程安排。

可以选择一些景点丰富、风景优美的目的地，如云南丽江，长白山等。

接着，确定旅行的日期和时间。

多人开车旅行需要考虑每个人的工作或学习时间，选择一个适合的节假日或周末出行。

然后，准备好所需物品。

多人开车旅行需要准备充足的食品和水，在行程中可能会遇到没有餐馆的地方，所以最好自备一些干粮。

同时还需要准备好防晒霜、帽子、太阳镜等防晒用品，以及药品和急救箱等紧急情况下需要的物品。

再次，选择适合的交通工具。

多人开车旅行最好选择一辆宽敞舒适的车辆，这样可以容纳更多的人和行李。

还可以考虑租一辆房车，这样可以在路上直接住宿，更加方便。

最后，安排好住宿和就餐。

多人开车旅行需要提前预订好住宿，尤其是在旅游旺季，预订旅馆或者民宿可以保证有一个安全舒适的住处。

在行程中，要合理安排就餐时间和地点，可以尝试当地的特色美食。

在旅行过程中，要注意安全。

多人开车旅行一定要遵守交通规则，确保驾车人合法驾驶，不超速，不酒驾，不疲劳驾驶。

还要经常检查车况，确保车辆的安全。

在旅行中，多人之间要相互照顾，遇到任何问题都要及时沟通和解决。

旅行的目的是为了放松心情，享受美好的时光，所以要保持愉快的心情，不要计较小事。

以上是一个适合多人开车旅行的方案，希望能够帮助到你。

祝你们旅途愉快！。