湖北省江汉2017届高三上学期10月月考试题数学理Word版含答案

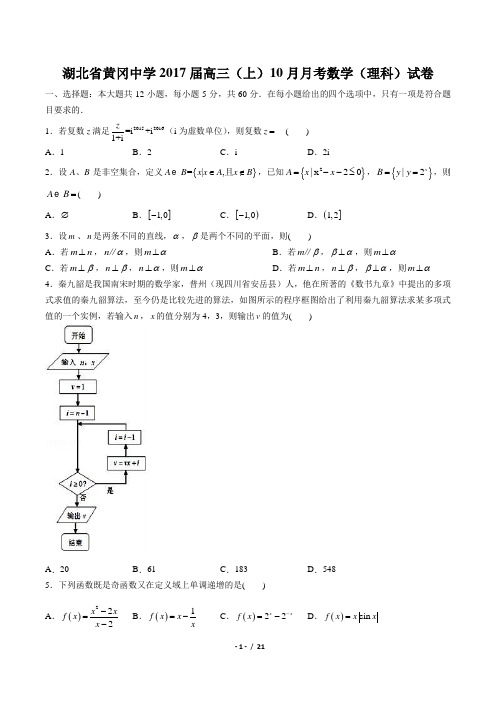
湖北省江汉平原高级中学2017届高三年级上学期10月月考数学（文科）试题★祝考试顺利★时间：120分钟 分值150分_第I 卷（选择题共60分）一、选择题（本大题12小题，每小题5分，共60分）1．若函数)1,0(),1(log )(≠>+=a a x x f a 且的定义域和值域都是[0,1]，则a=（ ）A.21B. 2C.22 D. 22．已知{}(,)1,1x y x y Ω=≤≤，A 是由曲线y x =与2y x =围成的封闭区域，若向Ω上随机投一点p ，则点p 落入区域A 的概率为（ ） A.16 B. 18 C. 112 D.1243．某人从甲地去乙地共走了500m ，途经一条宽为x m 的河流，该人不小心把一件物品丢在途中，若物品掉在河里就找不到，物品不掉在河里，则能找到，已知该物品能被找到的概率为45，则河宽为（ ）80m Ｂ．100m Ｃ．40m Ｄ．50m4．设1,0()2,0xx x f x x ⎧≥⎪=⎨<⎪⎩，则((2))f f -=（ ） A ．1- B ．14 C ．12 D ．325．函数2211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩，，，，≤则))2((f f 的值为A ．-1B ．-3C ．0D ．-86．已知函数()f x 是定义在R 上的奇函数，它的图象关于直线1x =对称，且()(01)f x x x =<≤，则当(5,7]x ∈时，()y f x =的解析式是（ ）A ．()2f x x =-B ．()4f x x =-C ．()6f x x =-D ．()8f x x =- 7．已知f(x)＝14x 2＋sin(2π＋x)，f′(x)为f(x)的导函数，则f′(x)的图象是( )8．函数2()34lg(1)f x x x x=-+++-的定义域是（）A．[-1，4] B．(]1,4-C．[1，4] D．(]1,49．函数2()lg2xf xx-=+的定义域为（）A．(),2(2,)-∞-+∞B．(,2)-∞C．(2,2)- D．()2,-+∞10．某几何体三视图如图所示，则该几何体的体积为（）A．82π- B．8π- C．82π- D．84π-11．一个直棱柱的对角线长是9 cm和15 cm,高是5 cm,若它的底面是菱形,则这个直棱柱的侧面积是( )A.160 cm2B.320 cm2C.cm2 D. cm212．如图，是CCTV 青年歌手大奖赛上某位选手得分的茎叶图，去掉一个最高分和一个最低分后，所剩数据的方差为 A ．647B ．9C ．738D ．780第II 卷（非选择题）二、填空题（本大题共4个小题，每题5分，满分20分） 13．若函数()11x mf x a =+-是奇函数，则m 为__________。

2016-2017学年湖北省部分重点中学高三（上)月考数学试卷(理科）一、选择题:本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合A={x｜｜x﹣1｜＜2｝，B={y|y=2x，x∈[0，2］}，则A∩B=（）A．［0，2]B．（1，3）C．［1,3）D．（1，4）2．已知复数z=﹣2i（其中i为虚数单位)，则|z｜=(）A．3B．3C．2D．23．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α,m∥β，则α∥βD．若m⊥α,n⊥α,则m∥n4．己知命题P:∀x∈(2，3），x2+5＞ax是假命题，则实数a的取值范围是（）A．［，+∞） B．[，+∞) C．［，+∞）D．（﹣∞,］5．把5件不同产品摆成一排,若产品A与产品B相邻,且产品A与产品C不相邻，则不同的摆法有（)种．A．12 B．24 C．36 D．486．若a=ln2,b=，c=sinxdx,则a，b，c的大小关系(）A．a＜b＜c B．b＜a＜c C．c＜b＜a D．b＜c＜a7．己知等比数列{a n}满足a1=2，a1+a3+a5=14,则++=(）A．B．C．D．8．在（x﹣）5的展开式中x3的系数等于﹣5,则该展开式项的系数中最大值为(）A．5 B．10 C．15 D．209．一个空间几何体的三视图如图所示，则该几何体的体积为（）A．B．C．40 D．8010．如图，F1、F2是双曲线﹣=1（a＞0）的左、右焦点，过F1的直线l与双曲线交于点A、B，若△ABF2为等边三角形,则△BF1F2的面积为（）A．8 B．8C．8D．1611．若函数是R上的单调减函数,则实数a的取值范围是（）A．(﹣∞，2）B．C．(0，2）D．12．设定义域为R的函数，若关于x的方程f2（x）+bf（x）+c=0有三个不同的解x1，x2，x3，则的值是（）A．1 B．3 C．5 D．10二、填空题：本大题共4小题，每小题5分,共20分请将答案填在答题卡对应题号的位置上，答错位置，书写不清，模棱两可均不得分13．已知向量,的夹角为,且丨丨=，丨丨=2,则丨﹣丨=．14．已知{a n｝是等差数列，S n是其前n项和，若a1+a22=﹣3，S5=10，则a9的值是．15．已知矩形A BCD的周长为18，把它沿图中的虚线折成正六棱柱，当这个正六棱柱的体积最大时，它的外接球的表面积为．16．已知f(x）=(x＞0），f1(x）=f(x），f n（x)=f（f n（x))，n∈N＊，则f s（x）在[，+11]上的最小值是．三、解答题：本大题共5小题，共60分.解答应写出文字说明、证明过程或演算步骤．17．在△ABC中，角A，B，C的对边分别为a，b，c,已知c=2，．(1）若△ABC的面积为,求a，b；(2）若sinC+sin（B﹣A）=sin2A,求a，b．18．某公司计划购买2台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图：以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X 表示2台机器三年内共需更换的易损零件数，n表示购买2台机器的同时购买的易损零件数．(Ⅰ）求X的分布列；(Ⅱ）若要求P（X≤n)≥0.5,确定n的最小值;（Ⅲ)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一，应选用哪个？19．如图,在直三棱柱ABC﹣A1B1C1中，平面A1BC⊥侧面A1ABB1,且AA1=AB=2．（1)求证：AB⊥BC；(2）若直线AC与平面A1BC所成的角为,求锐二面角A﹣A1C﹣B的大小．20．如图，椭圆=1（a＞b＞0)的一个焦点是F(1,0)，O为坐标原点．(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；（Ⅱ）设过点F的直线l交椭圆于A、B两点．若直线l绕点F任意转动，值有|OA|2+|OB｜2＜|AB｜2，求a的取值范围．。

2016-2017学年湖北省江汉平原高中高三（上）月考物理试卷（10月份）一、选择题（本大题12小题，每小题4分，共48分）1．如图所示，用长为l的绳子一端系着一个质量为m的小球，另一端固定在O点，拉小球至A点，此时绳偏离竖直方向θ，空气阻力不计，松手后小球经过最低点时的速率为（）A． B．C．D．2．如图所示，铁板AB与水平地面间的夹角为θ，一块磁铁吸附在铁板下方．在缓慢抬起铁块B端使θ角增加（始终小于90°）的过程中，磁铁始终相对铁板静止．则下列说法正确的是（）A．磁铁所受合外力逐渐减小B．磁铁始终受到三个力的作用C．磁铁受到的摩擦力逐渐减小 D．铁板对磁铁的弹力逐渐增大3．如图所示，用同样的力F拉同一物体，在甲（光滑水平面）、乙（粗糙水平面）、丙（光滑斜面）、丁（粗糙斜面）上通过同样的距离，则拉力F的做功情况是（）A．甲中做功最少 B．丁中做功最多 C．做功一样多D．无法比较4．人推着一辆自行车在水平道路上前进，自行车受到的力中做正功的是（）A．重力 B．摩擦力C．支持力D．人的推力5．如图所示，质量为m的物体置于光滑水平面上，一根绳子跨过定滑轮一端固定在物体上，另一端在力F作用下，以恒定速度v0竖直向下运动．物体由静止开始运动到绳与水平方向夹角α=45°过程中，绳中拉力对物体做的功为（）A ． mv 02B ．mv 02C ． mv 02D ． mv 026．如图所示，在原来静止的木箱内的水平底面上放着物体A ，A 被一伸长的弹簧（弹簧轴线沿水平方向）拉住而静止，在以后的运动中发现物体A 被向右拉动了，则木箱的运动情况可能是（ ）A ．加速下降B ．加速上升C ．匀速向右运动D ．加速向左运动7．如图所示，一人用200N 的力通过绳子和定滑轮拉一个静止在地面上重600N 的物体，则绳子对物体的拉力F r 和物体所受地面的支持力F N （ ）A ．F r =200N ，F N =400NB ．F r =600N ，F N =200NC ．F r =200N ，F N =200ND ．F r =400N ，F N =200N8．一辆汽车在水平公路上转弯，沿曲线由M 向N 行驶，速度逐渐减小．图中分别画出了汽车转弯时所受合力F 的四种方向，其中你认为正确的是（ ）A ．B ．C ．D ．9．汽车以20m/s 的速度做匀速直线运动，刹车后的加速度大小为5m/s 2，那么开始刹车后2s 与开始刹车后6s 汽车通过的位移大小之比为（ ）A ．1：4B ．3：5C ．3：4D ．5：910．蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动，如图甲所示．质量为m 的小球，从离弹簧上端高h 处自由下落，接触弹簧后继续向下运动．以小球刚开始下落计时，以竖直向下为正方向，小球的速度v 随时间t 变化的图线如图乙所示．图线中的OA 段为直线，与曲线ABCD 相切于A 点．不考虑空气阻力，则关于小球的运动过程，下列说法中正确的是（ ）A ．下落h 高度时小球速度最大B．小球在t4时刻所受弹簧弹力大于2mgC．t2﹣t1＞t3﹣t2D．球在t1到t4的时间内重力势能减小量大于弹簧弹性势能的增加量11．一物块在水平外力F的作用下沿水平面做直线运动，其运动的v﹣t图象如图所示．设0～t l、t l～t2、t2以后F的大小分别为F1、F2、F3，关于这三个力的大小关系，下列说法正确的是（）A．F1=F2=F3 B．F1=F3＜F2C．F1＜F2＜F3D．F1＜F3＜F212．据报道，一个国际研究小组借助于智利的天文望远镜，观测到了一组双星系统，它们绕两者连线上的某点O做匀速圆周运动，如图所示．假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质，达到质量转移的目的，在演变过程中两者球心之间的距离保持不变，双星平均密度可视为相同．则在最初演变的过程中（）A．它们做圆周运动的万有引力保持不变B．它们做圆周运动的角速度不断变小C．体积较大的星体圆周运动轨迹的半径变大，线速度变大D．体积较大的星体圆周运动轨迹的半径变小，线速度变大二、实验题（14分）13．如图，在“测定匀变速直线运动加速度”实验中得到的一条纸带上，从O点开始记录几个计数点，依次编为1、2、3、4、5、6，这些相邻的计数点之间还有四个点未画出（打点计时器的电源频率是50Hz），测得s1=1.22cm，s2=2.00cm，s3=2.78cm，s4=3.62cm，s5=4.40cm，s6=5.18cm．．试根据纸带求解以下问题：（1）接通电源与让释放纸带，这两个操作的先后顺序应当是A．先接通电源，后释放纸带B．先释放纸带，后接通电源C．释放纸带的同时接通电源D．先接通电源或先释放纸带都可以（2）电火花计时器所使用的电源电压是V（3）与小车相连的是纸带的端（选填“左”或“右”）；（4）两相邻计数点间的时间间隔T=s；（5）A点处瞬时速度的大小v A=m/s；（6）利用逐差法求小车运动加速度的表达式为：；（请用S1、S2、…、S6和T来表示）（7）求出的加速度的大小为：a=m/s2．三、计算题（42分）14．在大风的情况下，一小球m自A点竖直向上抛出，其运动轨迹如图所示．小球运动轨迹上A、B两点在同一水平线上，M点为轨迹的最高点．若风力的大小恒定、方向水平向右，小球抛出时的动能为4J，在M点时它的动能为2J，不计其它的阻力．求：（1）小球水平位移S1与S2的比值（2）小球所受风力F与重力G的比（结果可用根式表示）（3）小球落回到B点时重力的瞬时功率P的表达式．15．高速连续曝光照相机可在底片上重叠形成多个图象，现利用这种照相机对某款家用汽车的加速性能进行研究．如图为汽车做匀加速直线运动时的三次曝光照片，照相机每两次曝光的时间间隔为1.0s，已知该汽车的质量为2000kg，额定功率为90kW，假设汽车运动过程中所受的阻力恒为1500N．（1）试利用上图，求该汽车的加速度；（2）求汽车所能达到的最大速度是多大？（3）若汽车由静止以此加速度开始做匀加速直线运动，匀加速运动状态最多能保持多长时间？16．某物体沿一条直线运动：（1）若前一半时间内的平均速度为v1，后一半时间内的平均速度为v2，求全程的平均速度．（2）若前一半位移的平均速度为v1，后一半位移的平均速度为v2，全程的平均速度又是多少？17．有一个用直流电动机提升重物的装置，重物的质量m=50kg，电路电压为120V，当电动机以v=0.9m/s的恒定速度向上提升重物时，电路中的电流I=5A，（取g=10m/s2）求：（1）电动机线圈的电阻R等于多少．（2）电动机对该重物的最大提升速度是多少．（3）若因故障电动机不能转动，这时通过电动机的电流是多大，电动机消耗的电功率又为多大．2016-2017学年湖北省江汉平原高中高三（上）月考物理试卷（10月份）参考答案与试题解析一、选择题（本大题12小题，每小题4分，共48分）1．如图所示，用长为l的绳子一端系着一个质量为m的小球，另一端固定在O点，拉小球至A点，此时绳偏离竖直方向θ，空气阻力不计，松手后小球经过最低点时的速率为（）A． B．C．D．【考点】机械能守恒定律；向心力．【分析】小球摆动过程中，受到重力和拉力；只有重力做功，机械能守恒，根据机械能守恒定律列式求解即可【解答】解：小球从A到最低点的过程中，只有重力做功，机械能守恒，故有：mgL（1﹣cosθ）=mv2解得：v=故选：B．【点评】本题关键明确摆球摆动过程机械能守恒，根据机械能守恒定律列式即可求解．2．如图所示，铁板AB与水平地面间的夹角为θ，一块磁铁吸附在铁板下方．在缓慢抬起铁块B端使θ角增加（始终小于90°）的过程中，磁铁始终相对铁板静止．则下列说法正确的是（）A．磁铁所受合外力逐渐减小B．磁铁始终受到三个力的作用C．磁铁受到的摩擦力逐渐减小 D．铁板对磁铁的弹力逐渐增大【考点】共点力平衡的条件及其应用；摩擦力的判断与计算；物体的弹性和弹力．【分析】对铁块受力分析，受重力、磁力支持力和摩擦力，根据平衡条件列式求解出支持力和摩擦力的表达式后分析．【解答】解：对铁块受力分析，受重力G、磁力F、支持力N和摩擦力f，如图由于始终平衡，故合力为零，故A错误B错误；根据平衡条件，有：mgsinθ﹣f=0F﹣mgcosθ﹣N=0解得：f=mgsinθN=F﹣mgcosθ由于θ不断变大，故f不断变大，N不断变大，故C错误，D正确；故选：D．【点评】本题关键是对滑块受力分析，然后根据平衡条件并运用正交分解法列式求解，注意三力平衡通常用合成法，三力以上用正交分解法．3．如图所示，用同样的力F拉同一物体，在甲（光滑水平面）、乙（粗糙水平面）、丙（光滑斜面）、丁（粗糙斜面）上通过同样的距离，则拉力F的做功情况是（）A．甲中做功最少 B．丁中做功最多 C．做功一样多D．无法比较【考点】功的计算．【分析】通过功的公式W=Fscosθ去比较做功的大小．【解答】解：四种情况拉力相同，位移相同，拉力与位移同向，所以做功一样多．故C正确，A、B、D错误．故选C．【点评】解决本题的关键掌握功公式W=Fscosθ，会利用功的公式比较做功的大小．4．人推着一辆自行车在水平道路上前进，自行车受到的力中做正功的是（）A．重力 B．摩擦力C．支持力D．人的推力【考点】功的计算．【分析】分析自行车在运动中受力情况，根据功的公式判定做功情况．【解答】解：人推着自行车前进时，自行车受重力、支持力、人的推力及摩擦力的作用；重力和支持力与运动方向相互垂直，不做功；由于是人的推动才使自行车前进，则自行车受到的摩擦力均向后；故摩擦力做负功；只有人的推力与运动方向相同，推力做正功；故选：D．【点评】本题考查功的计算及受力分析的应用，要注意明确自行车在推行与骑行时的区别．5．如图所示，质量为m的物体置于光滑水平面上，一根绳子跨过定滑轮一端固定在物体上，另一端在力F作用下，以恒定速度v0竖直向下运动．物体由静止开始运动到绳与水平方向夹角α=45°过程中，绳中拉力对物体做的功为（）A．mv02B．mv02 C．mv02D．mv02【考点】功的计算．【分析】由于力F做匀速运动，将物体的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动，根据沿绳子方向的运动速度和平行四边形定则求解物体的速度，再运用动能定理求解．【解答】解：一根绳子跨过定滑轮一端固定在物体上，另一端在力F作用下，以恒定速度v0竖直向下运动．将物体的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动，则由三角函数可解得：运动到绳与水平方向夹角α=45°时物体的速度v==v0物体由静止开始运动到绳与水平方向夹角α=45°过程中，物体只受绳子拉力做功，运用动能定理得W=mv2﹣0=mv02．故选B．【点评】本题关键是正确地找出物体的合运动与分运动，然后根据运动分解的平行四边形定则，得到物体速度的大小．6．如图所示，在原来静止的木箱内的水平底面上放着物体A，A被一伸长的弹簧（弹簧轴线沿水平方向）拉住而静止，在以后的运动中发现物体A被向右拉动了，则木箱的运动情况可能是（）A．加速下降 B．加速上升 C．匀速向右运动 D．加速向左运动【考点】超重和失重．【分析】对物体进行受力分析，可知物体在水平方向受弹力及摩擦力，只有摩擦力减小时物体才会向右运动，分析升降机的运动情况可得出摩擦力的变化是否符合题意．【解答】解：A、加速下降，升降机有向下的加速度，失重，物体对地板的正压力减小；这时的最大静摩擦力小于电梯静止时的静摩擦力，而弹簧的弹力又未改变，故在这种情况下A 可能被拉向右方；故A正确；B、加速上升物体具有向上的加速度，超重，增大了物体与地板间的最大静摩擦力，弹簧不会拉向右方，故B错误；C、匀速向右运动时，物体对地面的压力不变；故物体不会产生运动；故C错误；D、加速向左运动时，物体由于惯性的作用相对于木箱会有向右的运动趋势；故D正确；故选：AD．【点评】本题考查了超重和失重，关键是掌握：超重时具有向上加速度，失重时具有向下加速度．7．如图所示，一人用200N的力通过绳子和定滑轮拉一个静止在地面上重600N的物体，则绳子对物体的拉力F r和物体所受地面的支持力F N（）A．F r=200N，F N=400N B．F r=600N，F N=200NC．F r=200N，F N=200N D．F r=400N，F N=200N【考点】共点力平衡的条件及其应用；力的合成与分解的运用．【分析】用200N的力通过绳子和定滑轮拉一个静止在地面上重600N的物体，人和物体都处于静止状态，以人为研究对象，分析受力，由平衡条件求出地面对人的支持力．【解答】解：人用200N的力拉绳子，所以绳子对物体的拉力是200N；以物体为研究对象，物体受到重力、向上的拉力和地面的支持力，拉力等于200N，重力等于600N，由平衡条件得地面对物体的支持力F N=G﹣F=600N﹣200N=400N；故选：A【点评】本题属于容易题，人和物体都处于静止状态，要善于选择研究对象，分析受力是学习力学的基本功．8．一辆汽车在水平公路上转弯，沿曲线由M向N行驶，速度逐渐减小．图中分别画出了汽车转弯时所受合力F的四种方向，其中你认为正确的是（）A．B．C．D．【考点】物体做曲线运动的条件．【分析】汽车在水平的公路上转弯，所做的运动为曲线运动，故在半径方向上合力不为零且是指向圆心的；又是做减速运动，故在切线上合力不为零且与瞬时速度的方向相反，分析这两个力的合力，即可看出那个图象时对的．【解答】解：汽车从M 点运动到N ，曲线运动，必有些力提供向心力，向心力是指向圆心的；汽车同时减速，所以沿切向方向有与速度相反的合力；向心力和切线合力与速度的方向的夹角要大于90°，所以选项ABD 错误，选项C 正确．故选：C ．【点评】解决此题关键是要沿半径方向上和切线方向分析汽车的受力情况，在水平面上，减速的汽车受到水平的力的合力在半径方向的分力使汽车转弯，在切线方向的分力使汽车减速，知道了这两个分力的方向，也就可以判断合力的方向了．9．汽车以20m/s 的速度做匀速直线运动，刹车后的加速度大小为5m/s 2，那么开始刹车后2s 与开始刹车后6s 汽车通过的位移大小之比为（ ）A ．1：4B ．3：5C ．3：4D ．5：9【考点】匀变速直线运动的位移与时间的关系．【分析】先求出汽车刹车到停止的时间，因为汽车速度为零后不再运动，然后根据匀变速直线运动的位移时间公式求出刹车后的位移．【解答】解：汽车刹车到停止的时间：t 0=＞2s所以2s 内的位移：x 1=v 0t 1+at 12=20×2﹣×5×22m=30m ．而6s ＞4s ，4s 后汽车停止运动，所以6s 内的位移等于4s 内的位移x 2=v 0t 0+=20×4﹣×5×42m=40m则：．故C 正确，A 、B 、D 错误． 故选：C ．【点评】本题属于刹车问题，关键要求出汽车刹车到停止的时间，因为汽车速度为零后不再运动．10．蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动，如图甲所示．质量为m 的小球，从离弹簧上端高h 处自由下落，接触弹簧后继续向下运动．以小球刚开始下落计时，以竖直向下为正方向，小球的速度v 随时间t 变化的图线如图乙所示．图线中的OA 段为直线，与曲线ABCD 相切于A 点．不考虑空气阻力，则关于小球的运动过程，下列说法中正确的是（ ）A ．下落h 高度时小球速度最大B ．小球在t 4时刻所受弹簧弹力大于2mgC ．t 2﹣t 1＞t 3﹣t 2D ．球在t 1到t 4的时间内重力势能减小量大于弹簧弹性势能的增加量【考点】机械能守恒定律．【分析】分清小球的运动形式，OA 过程是自由落体，A 的坐标就是自由下落的高度，此时的加速度也就是自由落体加速度；AB 过程，重力大于弹簧的弹力，小球做变加速直线运动，加速度小于g ．B 点是速度最大的地方，此时重力和弹力相等，合力为零，加速度也就为零；C 点的速度与A 点相同，D 点时速度减为零，弹簧被压缩到最低点，弹簧的弹力最大．【解答】解：A 、由图可知，A 是下降h 高度时的位置，而AB 过程，重力大于弹簧的弹力，小球做变加速直线运动，加速度小于g ．B 点是速度最大的地方，故A 错误；B 、由C 中知C 点与A 点是对称的点，由A 点到B 点的弹簧长度变化，由对称性得由B到C 的弹簧长度再变化，故到达D 点时形变量要大于2，所以弹力大于2mg ，故B 正确；D 、小球在B 点时，a=0，即mg=k △x B ，AB 过程，合外力：F 合=mg ﹣k △x=k （△x B ﹣△x ）=kx 球B ，x 球B 为球所处位置到平衡位置B 的距离，同理可得BC 过程也满足上述关系，故小球在AC 之间做简谐运动，故t 2﹣t 1=t 3﹣t 2，故C 错误；D 、小球在t 1时刻具有动能和重力势能，t 4时刻具有弹性势能，根据能量关系，从t 1到t 4的时间内重力势能减小量与在t 1时刻具有动能之和等于t 4时刻弹簧弹性势能的增加量，故小球在t 1到t 4的时间内重力势能减小量小于弹簧弹性势能的增加量，故D 错误； 故选：B【点评】此题考查了牛顿第二定律及能量守恒定律的应用；解决本题的关键知道小球在整个过程中的运动情况，结合图象，综合牛顿第二定律进行分析求解，知道系统在整个过程中，只受重力和弹簧弹力作用，系统机械能守恒．11．一物块在水平外力F 的作用下沿水平面做直线运动，其运动的v ﹣t 图象如图所示．设0～t l 、t l ～t 2、t 2以后F 的大小分别为F 1、F 2、F 3，关于这三个力的大小关系，下列说法正确的是（ ）A ．F 1=F 2=F 3B ．F 1=F 3＜F 2C ．F 1＜F 2＜F 3D ．F 1＜F 3＜F 2【考点】牛顿第二定律；匀变速直线运动的图像．【分析】根据图象得到物体各个时间段的运动规律，然后根据牛顿第二定律列式分析．【解答】解：0～t l 时间段，物体匀速运动，故拉力等于摩擦力，即F 1=f ；t l ～t 2时间段，物体加速运动，根据牛顿第二定律，有F 2﹣f=ma ；t 2以后的时间段，物体重新匀速运动，故拉力等于摩擦力，即F 3=f ；故选B ．【点评】本题关键根据图象得到物体的运动规律，然后根据共点力平衡条件和牛顿第二定律列式求解．12．据报道，一个国际研究小组借助于智利的天文望远镜，观测到了一组双星系统，它们绕两者连线上的某点O 做匀速圆周运动，如图所示．假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质，达到质量转移的目的，在演变过程中两者球心之间的距离保持不变，双星平均密度可视为相同．则在最初演变的过程中（ ）A．它们做圆周运动的万有引力保持不变B．它们做圆周运动的角速度不断变小C．体积较大的星体圆周运动轨迹的半径变大，线速度变大D．体积较大的星体圆周运动轨迹的半径变小，线速度变大【考点】万有引力定律及其应用．【分析】双星绕两者连线的一点做匀速圆周运动，由相互之间万有引力提供向心力，根据万有引力定律、牛顿第二定律和向心力进行分析．【解答】解：A、设体积较小的星体质量为m1，轨道半径为r1，体积大的星体质量为m2，轨道半径为r2．双星间的距离为L．转移的质量为△m．万有引力：F=，结合二项式定理可知，二者的质量越接近，万有引力越大．故A错误；B、对m1：G=（m1+△m）ω2r1①对m2：G=（m2﹣△m）ω2r2②由①②得：ω=，总质量m1+m2不变，两者距离L不变，则角速度ω不变．由②得：ω2r2=，ω、L、m1均不变，△m增大，则r2增大，即体积较大星体圆周运动轨迹半径变大．由v=ωr2得线速度v也增大．故C正确．BD错误．故选：C．【点评】本题是双星问题，要抓住双星系统的条件：角速度与周期相同，运用牛顿第二定律采用隔离法进行研究．二、实验题（14分）13．如图，在“测定匀变速直线运动加速度”实验中得到的一条纸带上，从O点开始记录几个计数点，依次编为1、2、3、4、5、6，这些相邻的计数点之间还有四个点未画出（打点计时器的电源频率是50Hz），测得s1=1.22cm，s2=2.00cm，s3=2.78cm，s4=3.62cm，s5=4.40cm，s6=5.18cm．．试根据纸带求解以下问题：（1）接通电源与让释放纸带，这两个操作的先后顺序应当是AA．先接通电源，后释放纸带B．先释放纸带，后接通电源C．释放纸带的同时接通电源D．先接通电源或先释放纸带都可以（2）电火花计时器所使用的电源电压是220V（3）与小车相连的是纸带的左端（选填“左”或“右”）；（4）两相邻计数点间的时间间隔T=0.1s；（5）A点处瞬时速度的大小v A=0.32m/s；（6）利用逐差法求小车运动加速度的表达式为：a=；（请用S1、S2、…、S6和T来表示）（7）求出的加速度的大小为：a=0.80m/s2．【考点】测定匀变速直线运动的加速度．【分析】打点计时器使用的是交流电源，实验操作中应先接通电源后释放纸带．根据相邻的相等时间间隔位移大小变化，从而来判断小车与纸带相连端．纸带实验中，若纸带匀变速直线运动，测得纸带上的点间距，利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度和加速度．【解答】解：（1）先接通电源，后释放纸带，以便纸带能充分运用，故A正确，BCD错误；（2）电火花计时器所使用的电源电压是220V交流电；（3）如果小车做匀加速运动，则相对时间间隔内，位移越来越大，所以纸带的左端与小车相连；（4）纸带上每打5个点取一个作为计数点，则T=0.1s，（5）利用匀变速直线运动的推论得：v A===0.32m/s；（6、7）根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，得：s4﹣s1=3a1T2s5﹣s2=3a2T2s6﹣s3=3a3T2为了更加准确的求解加速度，我们对三个加速度取平均值得：a=（a1+a2+a3）即小车运动的加速度计算表达式为：a=代入数据得：a==0.80m/s2故答案为：（1）A，（2）220；（3）左；（4）0.1，（5）0.32；（6）a=；（7）0.80．【点评】要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．三、计算题（42分）14．在大风的情况下，一小球m自A点竖直向上抛出，其运动轨迹如图所示．小球运动轨迹上A、B两点在同一水平线上，M点为轨迹的最高点．若风力的大小恒定、方向水平向右，小球抛出时的动能为4J，在M点时它的动能为2J，不计其它的阻力．求：（1）小球水平位移S1与S2的比值（2）小球所受风力F与重力G的比（结果可用根式表示）（3）小球落回到B点时重力的瞬时功率P的表达式．【考点】功率、平均功率和瞬时功率；运动的合成和分解．【分析】（1）小球在竖直方向上做竖直上抛运动，根据对称性可知从A点至M点和从M点至B点的时间t相等．小球在水平方向上做初速为零的匀加速运动，由运动学公式位移公式，运用比例法求出x1与x2之比；（2）对小球的运动过程分析，根据水平方向和竖直方向的运动，利用牛顿第二定律及运动学公式可求得两力的比值；（3）根据竖直上抛运动的对称性，得到小球到达B点时竖直速度，再求重力的瞬时功率P．【解答】解：（1）因小球竖直方向做竖直上抛运动，Y方向上升和下落时间相等，即A→M 和M→B的时间相等．在水平方向，小球做初速度为零的匀加速运动，根据S=at2有：S1=at2S2=a（2t）2﹣S1由上两式得S1：S2=1：3（2）A→M的过程，在水平方向有：v M=a x t=t竖直方向有：v A=a y t=t由mv M2：mv A2=2：4由上三式得=，=（3）根据上抛运动的对称性，B点竖直速度大小等于v A′=v A由题小球落回到B点时重力的瞬时功率为：P=mgv A′由上得：P=（W）答：（1）小球水平位移S1与S2的比值是1：3．（2）小球所受风力F与重力G的比是：2．（3）小球落回到B点时重力的瞬时功率P的表达式为P=（W）．【点评】本题运用运动的合成和分解法处理，抓住竖直方向上运动的对称性得到时间关系是关键．对于第2题，也可以求出重力加速度与风力加速度形成合加速度，再由运动学公式和牛顿第二定律结合求解．15．高速连续曝光照相机可在底片上重叠形成多个图象，现利用这种照相机对某款家用汽车的加速性能进行研究．如图为汽车做匀加速直线运动时的三次曝光照片，照相机每两次曝光的时间间隔为1.0s，已知该汽车的质量为2000kg，额定功率为90kW，假设汽车运动过程中所受的阻力恒为1500N．（1）试利用上图，求该汽车的加速度；（2）求汽车所能达到的最大速度是多大？（3）若汽车由静止以此加速度开始做匀加速直线运动，匀加速运动状态最多能保持多长时间？【考点】功率、平均功率和瞬时功率；匀变速直线运动的速度与位移的关系．【分析】（1）根据连续相等时间内的位移之差是一恒量，求出汽车的加速度大小．（2）当牵引力等于阻力时，速度最大，根据阻力的大小得出牵引力的大小，从而根据P=Fv 求出最大速度的大小．（3）先求出匀加速运动的最大速度，再根据v=at求解时间．【解答】解：（1）由运动学公式得：（2）当达到最大速度时，汽车做匀速运动，F=f=1500N，由P=Fv m得：（3）由牛顿第二定律得：F=ma+f=4500 N由功率关系为：由v1=at得：答：（1）该汽车的加速度为1.6m/s2；（2）汽车所能达到的最大速度是60m/s；（3）匀加速运动状态最多能保持12.5s时间．【点评】该题是汽车启动的问题与标尺问题相结合的题目，是一道理论联系实际的重要的题型，解决本题的关键知道功率与牵引力的关系，理清汽车的运动规律，知道牵引力与阻力相等时，速度最大．。

湖北省江汉平原高级中学2017届高三年级上学期10月月考数学（理科）试题★祝考试顺利★时间：120分钟 分值150分_第I 卷（选择题共60分）一、选择题（本大题12小题，每小题5分，共60分） 1．一个棱锥的三视图如右图所示，则它的体积为( )A ．12 B ．32 C ．1 D ．132．已知集合A ＝{－1，0，1}，B ＝{—2，—1，0}，则A ∩B 等于 （ ） A ．{0} B ．{－1，0，1} C ．{0，1} D ．{－1，0} 3．等差数列{}n a 中，12010=S ，那么101a a +的值是（ ） A ．12B ．24C ．36D ．484．设曲线11x y x +=-在点(3,2)处的切线与直线ax ＋y ＋1＝0垂直，则a ＝( )． A ．2 B ．－2 C ． 12- D. 125． 已知点A (1，2)、B （3，1），线段AB 的垂直平分线的方程是( )A. 524=+y xB. 52=-y xC. 52=+y xD. 524=-y x6．若x 的方程x 2-x+a=0和x 2-x+b=0(a ≠b)的四个根可组成首项为41的等差数列,则a+b 的值为( ) A.83 B.2411 C.2413 D.7231 7．平面向量a 与b 的夹角为30°，已知(1,2,2a b =-=，则a b +=（ ） A ．3．6 C ．3138．ABC △的内角A B C ，，的对边分别为a b c ，，，若26c b ==，，120B =则a 等于（ ）．A 6．2 C 3 D 29．已知函数)(x f y = 是偶函数，)(xg y =是奇函数，它们的定义域为],[ππ-，且它们在],0[π∈x 上的图象如右图所示，则不等式0)()(>x g x f 的解集为 A ．),3()0,3(πππ⋃- B ．)3,0()3,(πππ⋃-- C ．),4()0,4(πππ⋃-D ．),3()3,(ππππ⋃--10．将两个数a=2, b=-6交换，使a=-6, b=2，下列语句正确的是( )A ．B ．C ．D ．11．设等差数列}{n a 的前n 项和为=+++==1413121184,20,8,a a a a S S S n 则若（ ） A ．18 B ．17 C ．16 D ．1512．在直径为4的圆内接矩形中，最大的面积是（ ）第II 卷（非选择题）二、填空题（本大题共4个小题，每题5分，满分20分）13．已知定义在R 上的偶函数f （x ），当x ＞0时，f （x ）＝－x 3＋1，则f （－2）与f （3）的乘积为________ 14．如图是函数()sin(),(0,0,||)2f x A x A πωϕωϕ=+>><的图象，则其解析式是_________.xy π6π35π63- 3O15．（2010•西城区一模）已知圆C 的参数方程为（θ为参数），若P 是圆C 与y 轴正半轴的交点，以原点为极点，x 轴的正半轴为极轴建立极坐标系，求过点P 的圆C 的切线的极坐标方程．16．已知函数)(x f 是R 上的偶函数，且在（0，+∞）上有f '（x ）> 0，若f （－1）= 0，那么关于x的不等式x f （x ）< 0 的解集是____________． 三、解答题（70分） 17．（本题满分10分）选修4-4：坐标系与参数方程已知极坐标系的极点在直角坐标系的原点处，极轴与x 轴非负半轴重合．直线l 的参数方程为：⎪⎪⎩⎪⎪⎨⎧=+-=t y t x 21231（t 为参数），曲线C 的极坐标方程为：θρcos 4=．（1）写出曲线C 的直角坐标方程，并指明C 是什么曲线； （2）设直线l 与曲线C 相交于Q P ,两点，求PQ 的值．218．（本题12分）某班有学生50人，其中男同学30人，用分层抽样的方法从该班抽取5人去参加某社区服务活动．（1）求从该班男女同学在各抽取的人数；（2）从抽取的5名同学中任选2名谈此活动的感受，求选出的2名同学中恰有1名男同学的概率． 19．（本题12分）如图1，在直角梯形ABCD 中，AD BC ∥，π122BAD AB BC AD a ∠====，，E 是AD的中点，O 是AC 与BE 的交点，将ABE ∆沿BE 折起到图2中1A BE ∆的位置，得到四棱锥1A BCDE -.（Ⅰ） 证明：CD ⊥平面1A OC ；（Ⅱ） 若平面1A BE ⊥平面BCDE ，四棱锥1A BCDE -的体积为362a 的值. 20．（本题12分）已知()2122f x x x x =-++++. （Ⅰ）求证：()5f x ≥；（Ⅱ）若对任意实数()229,1521x f x a a -<++都成立，求实数a 的取值范围.21．（本题满分12分）对于函数()f x ,若存在0x R ∈使得00()f x x =成立,则称0x 为()f x 的不动点已知函数2()(1)1(0)f x ax b x b a =+++-≠ （1）若1,3a b ==,求函数()f x 的不动点；（2）若对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围；（3）在（2）的条件下,若()y f x =图象上A 、B 两点的横坐标是函数()f x 的不动点,且A 、B 两点关于直线2121y kx a =++对称,求b 的最小值22．（本题12分）已知椭圆1C :22221x y a b+=（0a b >>）经过点()1,e ，其中e 是椭圆1C 的离心率，以原点O 为圆心，以椭圆1C 的长轴长为直径的圆2C 与直线20x y -+=相切． （Ⅰ）求椭圆1C 和圆2C 的方程；（Ⅱ）过椭圆1C 的右焦点F 的直线1l 与椭圆1C 交于点A ，B ，过F 且与直线1l 垂直的直线2l 与圆2C 交于点C ，D ，以A ，B ，C ，D 为顶点的四边形的面积记为S ，求S 的取值范围．答案选择：1_5ADBDB 6_10DDDBB 11_12 AD 填空： 13．18214．3sin(2)3y x π=+15．16．)1,0()1,(⋃--∞17．（1）()4222=+-y x ，它是以()0,2为圆心，半径为2的圆．（2）721=-=t t PQ ．18．（1）2人（2）19．6解：（Ⅰ） 在图1中，AD ∥BC ，1AB BC ==，1AE =，2BAD π∠=，所以BE AC ⊥，即在图2中， 1,BE AO BE OC ⊥⊥．又1AO OC O=，所以BE⊥平面1A OC，又CD BE，所以CD⊥平面1A OC. 4分（Ⅱ）由已知，平面1A BE⊥平面BCDE，又由（Ⅰ）知，1,BE AO BE OC⊥⊥，所以1AOC∠为二面角1--CA BE的平面角，所以12AOCπ∠=.如图，以O为原点，建立空间直角坐标系，因为111A B A E BC ED====，BC ED∥，所以1222(,0,0)(,0,0)(0,0,)B E A-，，，2(0,,0),C22(,,0),BC=-122(0,,)AC=-，(2,0,0)CD BE==-.设平面1A BC的法向量1111(,,)n x y z=，平面1ACD的法向量2222(,,)n x y z=，平面1A BC与平面1ACD夹角为θ，由111n BCn AC⎧⋅=⎪⎨⋅=⎪⎩，，得1111x yy z-+=⎧⎨-=⎩，，取1(1,1,1)n=，由221n CDn A C⎧⋅=⎪⎨⋅=⎪⎩，，得222xy z=⎧⎨-=⎩，，取2(0,1,1)n=，从而126cos|cos,|32n nθ=〈〉==⨯，即平面1A BC与平面1ACD夹角的余弦值为6.20．（Ⅰ）见解析；（Ⅱ）2±≠a ．解：（Ⅰ）∵()43,25,2127,1243,2x x x f x x x x x --≤-⎧⎪-<≤-⎪=⎨+-<≤⎪⎪+>⎩，∴()f x 的最小值为5，∴()5f x ≥(Ⅱ)解：由（Ⅰ）知：()152f x -的最大值等于5. ∵()222299111511a a a a +=++-≥-=++，“=”成立()22911=a a ⇔++， 即a =a =2291aa ++取得最小值a ≠22951a a +>+，又∵对任意实数x ，()2291521-f x a a <++都成立，∴a ≠.∴a 的取值范围为a ≠ 21． （1）2,1-- （2）01a <<（3）min 4b =-22．（Ⅰ）2212x y +=，222xy +=（Ⅱ）2,⎡⎣ 解：（Ⅰ）由已知得222222211c a a b a a b c ⎧+=⎪⎪=⎪=+⎪⎩，解得1a b ⎧=⎪⎨=⎪⎩ 所以椭圆1C 的方程为2212x y +=，圆2C 的方程为222x y +=． （Ⅱ）若直线AB 的斜率不存在，由12l l ⊥，得22b aAB ==CD =，此时122S ==．若直线AB 的斜率为0，由12l l ⊥，得AB =，CD 2==，此时122S ==． 若直线AB 的斜率存在且不为0，设1l 的方程为()1y k x =-．设()11,x y A ，()22,x y B ，()22121x y y k x ⎧+=⎪⎨⎪=-⎩，消y 得()2222124220k x k x k +-+-=，所以2122412k x x k +=+，21222212k x x k-=+， ()()42221641222880k k k k ∆=-+-=+>．12x AB ==-=== 又2l 的方程为()11y x k=--，即10x ky +-=，得CD ==11CD 22S =AB ⨯== 因为20k >，S =关于2k 是单调递减函数，(2,S =． 综上得，S 的取值范围是2,⎡⎣．。

湖北省老河口市江山中学2017届高三年级上学期10月月考数学（理科）试题 ★祝考试顺利★时间：120分钟 分值150分_第I 卷（选择题共60分）一、选择题（本大题12小题，每小题5分，共60分）1．设命题:p 函数x y 1=在定义域上为减函数；命题:q ,(0,)a b ∃∈+∞,当1a b +=时,113a b +=，以下说法正确的是A ．p ∨q 为真B ．p ∧q 为真C ．p 真q 假D ．p ，q 均假 2．已知集合A={x|ax ﹣1=0}，B={x|1＜log 2x≤2，x ∈N}，且A ∩B=A ，则a 的所有可能值组成的集合是（ ）A ．Φ B． C ． D ．3．已知S n 是等差数列{a n }的前n 项和，若a 7=9a 3，则=（ ）A ．9B ．5C ．D ．4．一只小蜜蜂在一个棱长为3的正方体内自由飞行，若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于1，称其为“安全飞行”，则蜜蜂“安全飞行”的概率为（ ）A ．427B ．19C ．49D ．1275．已知集合{}1,A a =，{}1,2,3B =，则“3a =”是“A B ⊆”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件6．512x x ⎛⎫++ ⎪⎝⎭的展开式中，2x 的系数为（ ） （A ）45 （B ）60 （C ）90 （D ）1207．从一副扑克牌（54张）中抽取一张牌，抽到牌“K ”的概率是 （ ）A ．1/54B ．1/27C ．1/18D ．2/278．下列向量组中,能作为表示它们所在平面内所有向量的基底的是（ ）．A ．(0,0)=a ，(1,2)=-bB ．(1,2)=-a ，(2,4)=-bC ．(3,5)=a ，(6,10)=bD ．(2,3)=-a ，(6,9)=b9．设向量(),1a x =，()4,b x =，1a b ⋅=-，则实数x 的值是（ ）A. 2-B. 1-C. 13-D. 15- 10．已知函数22,(1)(),()(,)(21)36,(1)x ax x f x f x a x a x -+≤=-∞+∞--+>⎧⎨⎩若在上是增函数，则实数a 的取值范围是（ ）A ．1(,1]2B ．1(,)2+∞C ．[1,)+∞D ．[1,2] 11．点(,0)F c 为双曲线22221(0,0)x y a b a b-=>>的右焦点，点P 为双曲线左支上一点，线段PF 与圆2224b x y +=相切于点Q ，且1=2PQ PF ，则双曲线的离心率等于（ ） A ．2 B ．3 C ．5 D ．212．函数()ln x f x x e =+的零点所在的区间是(A)(10,e )(B)(1,1e ) (C)(1,e ) (D)(,e ∞)第II 卷（非选择题）二、填空题（本大题共4个小题，每题5分，满分20分）13．已知实数x y ，满足2203x y x y y +⎧⎪-⎨⎪⎩≥，≤，≤≤，则2z x y =-的取值范围是________．14．用二分法研究函数f(x)＝x 3＋3x －1的零点时，第一次经计算f(0)<0，f(0.5)>0可得其中一个零点x 0∈________，第二次应计算________．15．抛物线x y 42=上点M 到焦点距离为3，则点M 的横坐标为__***** _ 16．若复数z 满足iz=1（其中i 为虚数单位），则|z|= _________ ．三、解答题（70分）17．（本题12分）给出下面两个命题，命题p ：方程+=1表示焦点在x 轴上的椭圆命题q ：双曲线﹣=1的离心率e ∈（1，2）已知￢p ∨￢q 为假，求实数m 的取值范围．18．（本题12分）在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，若1sin sin cos cos 2B C B C -=． （Ⅰ）求角A ；（Ⅱ）若2,23a b c =+=，求ABC ∆的面积． 19．（13分）设命题p ：方程01)2(442=+-+x a x 无实数根；命题q ：函数2ln(1)y x ax =++的定义域是R ．如果命题q p 或为真命题，求实数a 的取值范围．20．（8分）做投掷2颗骰子试验，用（x ，y ）表示点P 的坐标，其中x 表示第1颗骰子出现的点数，y 表示第2颗骰子出现的点数.（I ）求点P 在直线y = x 上的概率； （II ）求点P 满足x+y ≥10的概率；21．（本题12分）（1）已知：正数a ，b ，x ，y 满足a+b=10，1=+yb x a ，且x+y 的最小值为18，求a ，b 的值．（2）若不等式)(22y x a xy x +≤+对一切正数x 、y 恒成立，求正数a 的最小值．22．（本题满分10分）解下列不等式：（1）7522≤-<x （2）111+>-x x答案选择：1_5 DDADA 6_10 DDDDD 11_12 CA13．[]57-， 14．(0,0.5) f(0.25) 15．2 16．1． 17．7＜m ＜1518．（Ⅰ）=60A ；（Ⅱ）233ABC S ∆=． 19．23a -<<20．（1）61 （2）61 21．（1）2,8;8,2a b a b ====；（2）2min =a22．（1）⎭⎬⎫⎩⎨⎧≤<<≤-∈627231|x x R x 或 （2）()()2,12,⋃-∞-。

{=|A B x x∈A B=(．∅．设m、n2x y 的最大值是20162016b x ++．已知向量(cos ,sin a α=(cos ,sin b β=，则a 与a b +的夹角为 B ．61na ++，则，1AF AB =，1CE CA =，1BD BC =，则D E D F 的12n na +++=12n n a +++=1222n na n +++=+，12n n a -++=12n +=⇒2n n +++⨯()21n ++-，12n +++-)2124n ++．）证明：设FC 的中点为GI IH I =，∴GIH 面GH ABC ∥面）解：连接OO 故()(2,2,0,0,1,BC BF =--=-设(),,n x y z =是平面BCF 的一个法向量，则2n BC x n BF y ⎧=-⎪⎨=-+⎪⎩，则(3,n =-又平面ABC 的一个法向量(OO'0,0,='7,'7'n OO n OO n OO ==， O 的余弦值为()1e ln 2ln3ln 2ln 1ln nn n n ++>++-+++-{A B=x|x ∈，{|B y =AB A =⋂故选：B ．【考点】空间中直线与平面之间的位置关系．n α，则m m α，故A m β，βα⊥α或m ⊂αm α，故B 错误． β⊥，n ⊥，则m α⊥，正确．n ⊥，n ⊥⊂α或m α，故D7．【考点】简单线性规划．，解得：，即赋值为即可．20162016b x ++【考点】平面向量数量积的运算．【分析】设向量与的夹角为【解答】解：∵向量(cos ,sin a α=，(cos ,sin b β=，设向量a 与b 的夹角为∴()2a ab a a b 1cos +=+=+θ，222222cos a b a a b b θ+=++=+()1cos cos ,22cos a a ba a ba ab ++++==+0π， ∴a 与a b +的夹角3π． ． 【考点】余弦函数的对称性．11a ⎛++ -⎝11n a ⎛++ -⎝，1AF AB =，1CE CA =，1BD BC =，所以：1,DE ⎛=- ，1,DF ⎛=- 所以：311DE DF ⋅=-+=- 故答案为：14-1612n n a +++=122n n a +++=， 12n n a -++=12n +=⇒2n n +++⨯()21n ++-，12n +++-2+故()(2,2,0,0,1,BC BF =--=-设(),,n x y z =是平面BCF 的一个法向量，则2n BC x n BF y ⎧⋅=-⎪⎨⋅=-+⎪⎩，则(3,n =-又平面ABC 的一个法向量(OO'0,0,='7,'7'n OO n OO n OO ==， O 的余弦值为71,2,，由累加法﹣在（()1ln 2ln3ln 2ln 1ln ne n n n ++>++-+++-。

湖北省江汉平原高级中学2017届高三年级上学期10月月考数学（文科）试题★祝考试顺利★ 时间：120分钟 分值150分_第I 卷（选择题共60分）一、选择题（本大题12小题，每小题5分，共60分）1．若函数)1,0(),1(log )(≠>+=a a x x f a 且的定义域和值域都是[0,1]，则a=（ ）A.21B. 2C.22 D. 22．已知{}(,)1,1x y x y Ω=≤≤，A 是由曲线y x =与2y x =围成的封闭区域，若向Ω上随机投一点p ，则点p 落入区域A 的概率为（ ） A.16 B. 18 C. 112 D.1243．某人从甲地去乙地共走了500m ，途经一条宽为x m 的河流，该人不小心把一件物品丢在途中，若物品掉在河里就找不到，物品不掉在河里，则能找到，已知该物品能被找到的概率为45，则河宽为（ ）80m Ｂ．100m Ｃ．40m Ｄ．50m4．设10()2,0xx f x x ⎧≥⎪=⎨<⎪⎩，则((2))f f -=（ ） A ．1- B ．14 C ．12 D ．325．函数2211()31x x f x x x x ⎧-⎪=⎨-->⎪⎩，，，，≤则))2((f f 的值为A ．-1B ．-3C ．0D ．-86．已知函数()f x 是定义在R 上的奇函数，它的图象关于直线1x =对称，且()(01)f x x x =<≤，则当(5,7]x ∈时，()y f x =的解析式是（ ）A ．()2f x x =-B ．()4f x x =-C ．()6f x x =-D ．()8f x x =-7．已知f(x)＝14x 2＋sin(2π＋x)，f′(x)为f(x)的导函数，则f′(x)的图象是( )8．函数()lg(1)f x x =-的定义域是 （ ）A ．[-1，4]B ．(]1,4- C ．[1，4] D ．(]1,49．函数2()lg2xf x x -=+的定义域为 （ ）A ．(),2(2,)-∞-+∞ B ．(,2)-∞C ．(2,2)-D ．()2,-+∞10．某几何体三视图如图所示，则该几何体的体积为（ ）A ．82π-B ．8π-C ．82π-D ．84π-11．一个直棱柱的对角线长是9 cm 和15 cm,高是5 cm,若它的底面是菱形,则这个直棱柱的侧面积是( )A.160 cm 2B.320 cm2C.cm2D.cm 212．如图，是CCTV 青年歌手大奖赛上某位选手得分的茎叶图，去掉一个最高分和一个最低分后，所剩数据的方差为 A ．647B ．9C ．738 D ．780第II 卷（非选择题）二、填空题（本大题共4个小题，每题5分，满分20分） 13．若函数()11x mf x a =+-是奇函数，则m 为__________。