数理统计考试点汇总

根据数理统计知识点归纳总结(精华版)
1. 引言
本文旨在对数理统计的基本知识点进行归纳总结，帮助读者快速了解数理统计的核心概念和方法。

2. 概率论基础
- 概率的基本定义和性质
- 随机事件的运算规则
- 条件概率和独立性
- 贝叶斯定理
3. 随机变量和分布
- 随机变量的定义和分类
- 离散型随机变量和连续型随机变量
- 常见离散型分布（如伯努利分布、二项分布、泊松分布）
- 常见连续型分布（如均匀分布、正态分布、指数分布）
4. 数理统计的基本概念
- 总体和样本的概念
- 估计与抽样分布
- 统计量和抽样分布
5. 参数估计
- 点估计的定义和性质
- 常见的点估计方法（如最大似然估计、矩估计）
- 区间估计的基本原理和方法
6. 假设检验
- 假设检验的基本思想和步骤
- 单侧检验和双侧检验
- 假设检验中的错误类型和显著性水平
- 常见的假设检验方法（如正态总体均值的检验、两样本均值的检验）
7. 相关分析
- 相关系数的定义和计算方法
- 相关分析的假设检验
- 线性回归分析的基本原理和方法
8. 统计软件的应用
- 常见的统计软件介绍（如SPSS、R、Python）
- 统计软件的基本操作（如数据导入、数据处理、统计分析）
9. 结语
本文对数理统计的核心知识点进行了简要的概括，供读者参考和研究。

通过研究数理统计，读者可以更好地理解和应用统计学在实际问题中的作用，提高数据分析和决策能力。

以上是根据数理统计知识点的归纳总结，希望有助于您对数理统计的理解和学习。

如需深入了解各个知识点的具体内容，请参考相关教材或课程。

概率论与数理统计总复习知识点归纳1.概率论的基础概念-随机事件、样本空间和事件的关系。

-频率和概率的关系，概率的基本性质。

-古典概型和几何概型的概念。

-条件概率和乘法定理。

-全概率公式和贝叶斯公式。

-随机变量和概率分布函数的概念。

-离散型随机变量和连续型随机变量的定义、概率质量函数和概率密度函数的性质。

2.随机变量的数字特征-随机变量的数学期望、方差、标准差和切比雪夫不等式。

-协方差、相关系数和线性变换的数学期望和方差公式。

-两个随机变量的和、差、积的数学期望和方差公式。

3.大数定律和中心极限定理-大数定律的概念和三级强大数定律。

-中心极限定理的概念和中心极限定理的两种形式。

4.数理统计的基本概念和方法-总体、样本和抽样方法的概念。

-样本统计量和抽样分布的概念。

-点估计和区间估计的概念。

-假设检验的基本思想和步骤。

-正态总体的参数的假设检验和区间估计。

5.参数估计和假设检验的方法和推广-极大似然估计的原理和方法。

-矩估计的原理和方法。

-最小二乘估计的原理和方法。

-一般参数的假设检验和区间估计。

6.相关分析和回归分析-相关系数和线性相关的概念和性质。

-回归分析的一般原理。

-简单线性回归的估计和检验。

7.非参数统计方法-秩和检验和符号检验的基本思想和应用。

-秩相关系数的计算和检验。

8.分布拟合检验和贝叶斯统计-卡方拟合检验的原理和方法。

-正态总体参数的拟合优度检验。

-贝叶斯估计的基本思想和方法。

9.时间序列分析和质量控制-时间序列的基本性质和分析方法。

-时间序列预测的方法和模型。

-质量控制的基本概念和控制图的应用。

以上是概率论与数理统计总复习知识点的归纳，希望对你的复习有所帮助。

概率论与数理统计考点归纳1. 引言概率论与数理统计是数学中的两个重要分支，它们研究随机现象的规律和利用数据推断总体特征。

在实际应用中，概率论与数理统计广泛应用于自然科学、社会科学、工程技术等领域。

本文将从以下几个方面对概率论与数理统计的考点进行归纳和总结。

2. 概率论考点2.1 随机变量与概率分布•随机变量的定义、分类和常见概率分布：离散随机变量、连续随机变量、二项分布、泊松分布、正态分布等。

•期望、方差和协方差的定义和性质，以及它们与随机变量的关系。

•大数定律和中心极限定理的概念和应用。

2.2 一维随机变量的分布特征•分布函数、概率密度函数和概率质量函数的定义和性质。

•分位数和分位点的概念和计算方法。

•随机变量的矩、协方差和相关系数的定义和计算。

•常见分布的特征：均匀分布、指数分布、正态分布等。

2.3 多维随机变量的分布特征•多维随机变量的联合分布、边缘分布和条件分布的定义和性质。

•多维随机变量的矩、协方差矩阵和相关系数矩阵的定义和计算。

•多维正态分布的定义和性质，以及多维正态分布的应用。

2.4 随机变量的函数的分布特征•随机变量函数的分布：线性变换、和、积、商的分布。

•随机变量函数的期望、方差和协方差的计算方法。

3. 数理统计考点3.1 抽样与抽样分布•抽样的概念和方法：随机抽样、简单随机抽样、系统抽样、分层抽样、整群抽样等。

•抽样分布的概念和性质：样本均值的抽样分布、样本比例的抽样分布、样本方差的抽样分布等。

•中心极限定理在抽样分布中的应用。

3.2 参数估计•点估计的概念和方法：矩估计、最大似然估计等。

•点估计的性质：无偏性、有效性、一致性等。

•置信区间的定义和计算方法。

3.3 假设检验•假设检验的基本步骤：建立原假设和备择假设、选择检验统计量、确定显著性水平、计算拒绝域、做出判断。

•假设检验的错误和功效：第一类错误、第二类错误和功效的概念和计算。

•常见假设检验方法：正态总体均值的假设检验、正态总体方差的假设检验、两样本均值的假设检验等。

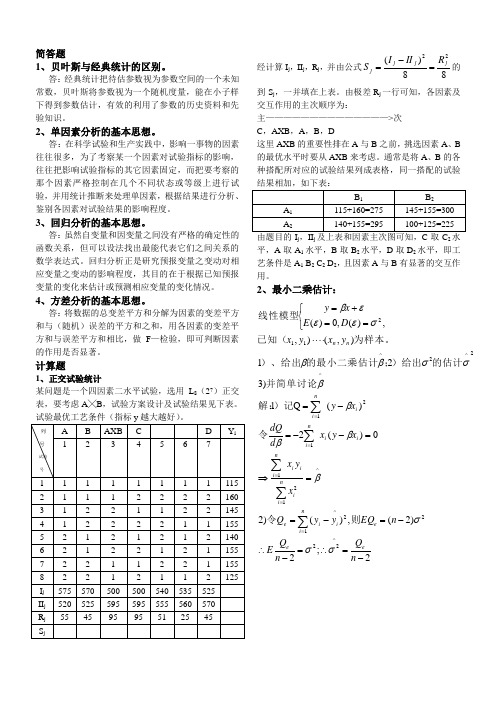
简答题1、贝叶斯与经典统计的区别。

答：经典统计把待估参数视为参数空间的一个未知常数，贝叶斯将参数视为一个随机度量，能在小子样下得到参数估计，有效的利用了参数的历史资料和先验知识。

2、单因素分析的基本思想。

答：在科学试验和生产实践中，影响一事物的因素往往很多，为了考察某一个因素对试验指标的影响，往往把影响试验指标的其它因素固定，而把要考察的那个因素严格控制在几个不同状态或等级上进行试验，并用统计推断来处理单因素，根据结果进行分析、鉴别各因素对试验结果的影响程度。

3、回归分析的基本思想。

答：虽然自变量和因变量之间没有严格的确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达式。

回归分析正是研究预报变量之变动对相应变量之变动的影响程度，其目的在于根据已知预报变量的变化来估计或预测相应变量的变化情况。

4、方差分析的基本思想。

答：将数据的总变差平方和分解为因素的变差平方和与（随机）误差的平方和之和，用各因素的变差平方和与误差平方和相比，做F—检验，即可判断因素的作用是否显著。

计算题1、正交试验统计某问题是一个四因素二水平试验，选用L8（27）正交表，要考虑A╳B，试验方案设计及试验结果见下表。

试验最优工艺条件（指标y越大越好）。

经计算I j，II j，R j，并由公式88)(22jjjjRIIIS=-=的到S j，一并填在上表。

由极差R j一行可知，各因素及交互作用的主次顺序为：主——————————————>次C，AXB，A，B，D这里AXB的重要性排在A与B之前，挑选因素A、B的最优水平时要从AXB来考虑。

通常是将A、B的各种搭配所对应的试验结果列成表格，同一搭配的试验结果相加，如下表：由题目的I j，II j及上表和因素主次图可知，C取C2水平，A取A1水平，B取B2水平，D取D2水平，即工艺条件是A1 B2 C2 D2，且因素A与B有显著的交互作用。

2、最小二乘估计：2;2)2(,)()2)(2)(Q1)321),(),,)(,0)(^22212^^121121^2^2^112-=∴=-∴-=-==⇒=--=-=⋅⋅⋅⋅⎩⎨⎧==+=∑∑∑∑∑=====nQnQEnEQyyQxyxxyxddQxyyxyxDExyeeeniiieniiiiniiiniininnσσσβββββσσββσεεεβ则令令）记解：并简单讨论的估计）给出；的最小二乘估计）、给出为样本。

（完整版）数理统计考试题及答案1、离散型随机变量X 的分布律为P （X=x i ）=p i ，i=1.2…..，则11=∑=ni ip2、设两个随机变量X ，Y 的联合分布函数F （x ，y ），边际分布Fx （x ），Fy （y ），则X 、Y 相互独⽴的条件是)()(),(y F x F y x F Y X ?=3、 X 1,X 2,….X 10是总体X~N （0，1）的样本，若2102221X X X +++=ξ,则ξ的上侧分位数025.0ξ=解：因为X~N （0，1），所以2102221X X X +++=ξ~)10(2χ，查表得025.0ξ=20.54、设X~N （0，1），若Φ（x ）=0.576，则Φ（-x ）= 解：Φ（-x ）=1-Φ（x ）=1-0.576=0.4245、设X 1,X 2,….X n 是总体),(~2σµN X 的样本，∑=-=ni iXY 122)(1µσ，则EY=n解：∑=-=ni iXY 122)(1µσ~)(2n χ，E 2χ=n ，D 2χ=2n⼆、设设X 1,X 2,….X n 是总体),(~2σµN X 的样本，∑=-=612)(51i i X X s ，试求)5665.2(22σ≤s P 。

解：因为),(~2σµN X ，所以有)5(~)(126122χσ∑=-i i X X ，则≤-= ≤-=≤=≤∑∑==8325.12)(5665.25)()5665.2()5665.2(261226122222σσσσi ii i X X P X X P s P s P 查2χ分布表得=≤)5665.2(22σs P≤-∑=8325.12)(2612σi i X X P =1-α=1-0.0248=0.9752 三．设总体X 的概率密度为f(x)= (1),(01) 0a x x α?+<，其他，其中α>0，求参数α的矩估计和极⼤似然估计量。

考研数学数理统计基础知识点总结在准备考研数学的过程中，掌握数理统计基础知识是非常重要的。

本文将为您总结一些常见的数理统计基础知识点，帮助您更好地备考。

一、概率论基础知识1. 事件与样本空间：事件是指样本空间中的某个子集，样本空间则是指随机试验的所有可能结果的集合。

2. 概率的定义：概率是指事件发生的可能性大小，其取值范围在0到1之间。

3. 概率的运算：包括加法公式和乘法公式。

加法公式适用于互斥事件的概率计算，乘法公式则适用于独立事件的概率计算。

4. 条件概率：指在已知某一事件发生的条件下，另一事件发生的概率。

5. 贝叶斯定理：用于计算事件的后验概率，在已经得到一些信息的情况下，通过先验概率和条件概率计算出事件的后验概率。

二、随机变量与概率分布1. 随机变量的概念：随机变量是指随机试验结果的某个函数，可以是离散的或连续的。

2. 概率质量函数与概率密度函数：对于离散型随机变量，其概率可以通过概率质量函数来描述；对于连续型随机变量，则需要使用概率密度函数。

3. 常见的离散型随机变量：包括伯努利分布、二项分布、泊松分布等。

4. 常见的连续型随机变量：包括均匀分布、正态分布、指数分布等。

三、统计推断1. 抽样与抽样分布：抽样是指从总体中选取一部分个体进行研究，抽样分布则是指统计量在大量抽样下的分布情况。

2. 参数估计：根据样本数据对总体的某个参数进行估计，可以使用点估计和区间估计两种方法。

3. 假设检验：对总体参数的某个假设进行检验，包括设置原假设和备择假设，以及计算检验统计量和判断拒绝域。

4. 方差分析：一种用于比较两个或多个总体均值是否有显著差异的统计方法，适用于独立样本、配对样本和重复测量样本。

四、相关与回归分析1. 相关分析：用于判断两个变量之间的相关性强弱，包括计算相关系数和进行假设检验。

2. 简单线性回归分析：用于建立一个自变量与因变量之间的线性关系模型，通过最小二乘法来估计回归系数。

3. 多元线性回归分析：在简单线性回归的基础上，将多个自变量引入回归模型中进行分析，以探究多个变量对因变量的影响。

《概率论与数理统计》考试重点说明：我们将知识点按考查几率及重要性分为三个等级，即一级重点、二级重点、三级重点，其中，一级重点为必考点，本次考试考查频率高；二级重点为次重点，考查频率较高；三级重点为预测考点，考查频率一般，但有可能考查的知识点。

第一章 随机事件与概率1．随机事件的关系与计算 （一级重点）填空、简答事件的包含与相等、和事件、积事件、互不相容、对立事件的概念2．古典概型中概率的计算 （二级重点）选择、填空、计算记住古典概型事件概率的计算公式3. 利用概率的性质计算概率 （一级重点）选择、填空)()()()(AB P B P A P B A P -+=⋃,)()()(AB P B P A B P -=-（考得多）等，要能灵活运用。

4. 条件概率的定义 （一级重点）选择、填空 记住条件概率的定义和公式：)()(B P AB P = 5. 全概率公式与贝叶斯公式 （二级重点）计算记住全概率公式和贝叶斯公式，并能够运用它们。

一般说来，如果若干因素（也就是事件）对某个事件的发生产生了影响，求这个事件发生的概率时要用到全概率公式；如果这个事件发生了，要去追究原因，即求另一个事件发生的概率时，要用到贝叶斯公式，这个公式也叫逆概公式。

6. 事件的独立性（概念与性质） （一级重点）选择、填空定义：若)()()(B P A P AB P =，则称A 与B 相互独立。

结论：若A 与B 相互独立，则A 与B ，A 与B ，A 与B 都相互独立。

7. n 重贝努利试验中事件A 恰好发生k 次的概率公式 （一级重点）选择、填空在n 重贝努利试验中，设每次试验中事件A 的概率为p （10 p ），则事件A 恰好发生k 次的概率n k p p C k P k n k k n n ,,2,1,0,)1()( =-=-。

第二章 随机变量的分布及其数字特征8．离散型随机变量的分布律及相关的概率计算 （一级重点）选择、填空、计算、综合。

数理统计考试点汇总第一章数理统计的基本概念统计的基本概念、基本思想；常见统计量；经验分布函数；三大分布，定义会判别；正态总体下的抽样分布。

第二章参数估计概念、涵义；点估计、矩估计、极大似然估计（会求）；无偏性、有效性、一致性；最小偏差无偏估计量（会证明）；区间估计的含义。

第三章假设检验基本原理：小概率事件在一次试验中不发生；基本概念：原假设、备责假设；假设检验中易犯的两类错误、含义；正态总体下的···检验，非参数假设检验，差方和优度检验，秩和检验（了解），卡方列联表检验，总之是一大波各种公式，不过还是要记。

（1）假设检验，重点看单个正态总体，方差已知的U检验；如假设检验，你只需记住U检验公式就可以了，其它的不用记其它：1. 至少要回双因素方差分析2. 方差分析的假设条件方差分析只看有交互作用的双因素方差分析，其它的不用正交设计肯定考极差分析，非常简单的计算（2）方差分析，考核有交互作用的双因素方差分析；（3）正交设计，极差分析法；（4）列联表计算；（5）回归分析（要考不知道怎么考）（6）参数估计会证明最小方差无偏估计量；注：没有听清楚老师对正交实验设计和回归分析说了什么。

题型：选择、填空、计算、证明（最小偏差无偏估计），不能用计算器。

Excel表题目的考点：1. 指出因变量和自变量；2. 写出回归方程；3. 分析回归方程的拟合优度；4. 对回归线性模型进行显著性检验，方差分析。

貌似有一个题是和这个excel表有关（大题）每一章都会出一个大题老师可能会抠掉表格里的内容让我们填还有什么经验分布公式还有证明题，好像是最小方差无偏估计选择，填空，计算，证明数理统计重点：1、每章都有大题。

2、我根据老师讲的和自己领会的大题有：（1）假设检验，重点看单个正态总体，方差已知的U检验；（2）方差分析，考核有交互作用的双因素方差分析；（3）正交设计，极差分析法；（4）列联表计算；（5）回归分析（要考不知道怎么考）（6）参数估计会证明最小方差无偏估计量；我知道的就这些了，题型，填空、选择、证明计算；还有就是树立统计老师不会让学生不过的！如假设检验，你只需记住U检验公式就可以了，其它的不用记方差分析只看有交互作用的双因素方差分析，其它的不用正交设计肯定考极差分析，非常简单的计算。

概率论与数理统计例题和知识点总结概率论与数理统计是一门研究随机现象统计规律的学科，它在自然科学、工程技术、经济管理、社会科学等众多领域都有着广泛的应用。

下面将通过一些例题来帮助大家理解和掌握这门学科的重要知识点。

一、随机事件与概率随机事件是指在一定条件下，可能出现也可能不出现的事件。

概率则是衡量随机事件发生可能性大小的数值。

例 1：抛掷一枚均匀的硬币，求正面朝上的概率。

解：因为硬币只有正反两面，且质地均匀，所以正面朝上的概率为1/2。

知识点：古典概型中，事件 A 的概率 P(A) ＝ A 包含的基本事件数／基本事件总数。

例 2：一个袋子里有 5 个红球和 3 个白球，从中随机取出一个球，求取出红球的概率。

解：袋子里一共有 8 个球，其中 5 个是红球，所以取出红球的概率为 5/8。

知识点：概率的性质：0 ≤ P(A) ≤ 1；P(Ω) ＝ 1，P(∅）＝ 0。

二、条件概率与乘法公式条件概率是指在已知某一事件发生的条件下，另一事件发生的概率。

例 3：已知在某疾病的检测中，阳性结果中真正患病的概率为 09，而总体人群中患病的概率为 001。

如果一个人的检测结果为阳性，求他真正患病的概率。

解：设 A 表示患病，B 表示检测结果为阳性。

则 P(A) ＝ 001，P(B|A) ＝ 09，P(B|A'）＝ 1 P(B|A) ＝ 01。

根据全概率公式：P(B) ＝P(A)×P(B|A) ＋ P(A'）×P(B|A'）＝ 001×09 ＋099×01 ≈ 0108。

再根据贝叶斯公式：P(A|B) ＝ P(A)×P(B|A) ／ P(B) ＝ 001×09 ／0108 ≈ 0083。

知识点：条件概率公式：P(B|A) ＝ P(AB) ／ P(A)；乘法公式：P(AB) ＝ P(A)×P(B|A)。

三、独立性如果两个事件的发生与否互不影响，那么称它们是相互独立的事件。