概率论与数理统计期中试卷(1-4章)附答案及详解

第一章 随机事件及其概率练习： 1. 判断正误（1）必然事件在一次试验中一定发生，小概率事件在一次试验中一定不发生。

（B ）（2）事件的发生与否取决于它所包含的全部样本点是否同时出现。

（B ）（3）事件的对立与互不相容是等价的。

（B ） （4）若()0,P A = 则A =∅。

（B ）（5）()0.4,()0.5,()0.2P A P B P AB ===若则。

（B ） （6）A,B,C 三个事件至少发生两个可表示为AB BC AC ⋃⋃（A ） （7）考察有两个孩子的家庭孩子的性别，{()Ω=两个男孩（，两个女孩),(一个男孩，}一个女孩)，则P{}1=3两个女孩。

（B ）（8）若P(A)P(B)≤，则⊂A B 。

（B ） （9）n 个事件若满足,,()()()i j i j i j P A A P A P A ∀=，则n 个事件相互独立。

（B ）（10）只有当A B ⊂时，有P(B-A)=P(B)-P(A)。

（A ） 2. 选择题（1）设A, B 两事件满足P(AB)=0，则©A. A 与B 互斥B. AB 是不可能事件C. AB 未必是不可能事件D. P(A)=0 或 P(B)=0 （2）设A, B 为两事件，则P(A-B)等于(C)A. P(A)-P(B)B. P(A)-P(B)+P(AB)C. P(A)-P(AB)D. P(A)+P(B)-P(AB) （3）以A 表示事件“甲种产品畅销，乙种产品滞销”，则其对立事件A 为(D)A. “甲种产品滞销，乙种产品畅销”B. “甲乙两种产品均畅销”C. “甲种产品滞销”D. “甲种产品滞销或乙种产品畅销”（4）若A, B 为两随机事件，且B A ⊂，则下列式子正确的是(A) A. P(A ∪B)=P(A) B. P(AB)=P(A) C. P(B|A)=P(B) D. P(B-A)=P(B)-P(A) （5）设(),(),()P A B a P A b P B c ⋃===，则()P AB 等于(B)A. ()a c c + B . 1a c +-C.a b c +- D. (1)b c -（6）假设事件A 和B 满足P(B|A)=1, 则(B)A. A 是必然事件 B . (|)0P B A = C. A B ⊃ D. A B ⊂ （7）设0<P(A)<1，0<P(B)<1, (|)(|)1P A B P A B += 则(D)A. 事件A, B 互不相容B. 事件A 和B 互相对立C. 事件A, B 互不独立 D . 事件A, B 互相独立8.,,.,,.D ,,.,,.,,1419.(),(),(),(),()37514131433.,.,.,.,37351535105A B A AB A B B AB A B C AB A B D AB A B P B A P B A P AB P A P B A B C φφφφ≠=≠====对于任意两个事件必有（C ）若则一定独立；若则一定独立；若则有可能独立；若则一定不独立；已知则的值分别为：(D)三解答题1.(),(),(),(),(),(),().P A p P B q P AB r P A B P AB P A B P AB ===设求下列事件的概率：解：由德摩根律有____()()1()1;P A B P AB P AB r ⋃==-=-()()()();P AB P B AB P B P AB q r =-=-=-()()()()(1)()1;P A B P A P B P AB p q q r r p ⋃=+-=-+--=+-________()()1[()()()]1().P AB P A B P A P B P AB p q r =⋃=-+-=-+-2.甲乙两人独立地对同一目标射击一次，命中率分别是0.6和0.5，现已知目标被命中，求它是甲射击命中的概率。

一、填空题：(每题4分，共24分)1．已知事件A 与B 相互独立，()0.4P A =，()0.7P A B +=，则概率()P B A 为 。

2．某次考试中有4个单选选择题，每题有4个答案，某考生完全不懂，只能在4个选项中随机选择1个答案，则该考生至少能答对两题的概率为 ， 3．若有 ξ～(0,1)N ，η=21ξ-，则η～N （ ， ）4．若随机变量X 服从参数为λ的泊松分布，且DX EX -=4,则参数λ＝5．设连续型随机变量ξ的概率密度为2(1)01()0x x f x -<<⎧=⎨⎩其他，且2ηξ=，则η的概率密度为 。

6．设总体2~(,)X N μσ的分布，当μ已知，12,,n X X X 为来自总体的样本，则统计量∑=-ni i X 12)(σμ服从 分布。

二、选择题：(每小题4分，共20分)1. 设事件,,A B C 是三个事件，作为恒等式，正确的是（ ） A.()ABC AB CB = B.A BC A B C =C.()A B A B -=D.()()()A B C AC BC =2.n 张奖券有m 张有奖的，k 个人购买，每人一张，其中至少有一人中奖的概率是（ ）。

A.11k m n mknC C C -- B. k n m C C. k n k mn C C --1 D. 1r nm k r nC C =∑3. 设EX μ=，2DX σ=，则由切比雪夫不等式知(4)P X μσ-≤≥（ ） A.1416 B. 1516 C. 15 D. 16154. 如果随机向量),(ηξ的联合分布表为：则协方差),cov(ηξ=（ ）A.-0.2B. –0.1C.0D. 0.1 5. 设总体 ξ～2(,)N μσ ，（12,,n X X X ）是 ξ 的简单随机样本，则为使1211ˆ()n i i i C XX θ-+==-∑为2σ的无偏估计，常数C 应为( )A.1n B. 11n - C. 12(1)n - D. 12n -三、计算题：待用数据（0.9750.9750.950.95(35) 2.0301,(36) 2.0281,(35) 1.6896,(36) 1.6883t t t t ====，8413.0)1(=Φ,9772.0)2(=Φ975.0)96.1(=Φ,95.0)645.1(=Φ）1．三个人同时射击树上的一只鸟，设他们各自射中的概率分别为0.5，0.6，0.7。

20 21
2
2 第十页，共十四页。
26(.1)设有4个独立工作的元件1,2,3,4.它们的可靠 性分别为p1,p2,p3,p4,将它们按右图的方式(fāngshì)
联接(称为并串联系统);
2
3
1
4
(2)设有5个独立工作的元件1,2,3,4,5.它们的可 靠性均为p,将它们按右图的方式联接(称为(chēnɡ wéi)桥式系统);试分别求这两个系统的可靠性.
7
6
5 P171
第四页，共十四页。
14. 已知P(A)=1/4,P(B|A)1/3,P(A|B)=1/2,求P(A∪B).
解 P(A∪B)=P(A)+P(B)-P(AB)
P(AB)=P(A)P(B|A)=P(B)P(A|B)
故 P( AB) 1 1 1 P(B) P( AB) 1 12 1
第五页，共十四页。
16. 据以往资料(zīliào)表明,某一3口之家,患某种传染病的概率有以下规律:
P{孩子得病(dé bìnɡ)}=0.6, P{母亲得病|孩子得病}=0.5,
P{父亲得病|母亲(mǔ qīn)及孩子得 求病母}=亲0.及4,孩子得病但父亲未得病的概率.
解 设事件A={孩子得病},B={母亲得病},C={父亲得病}
(1)求恰有90个次品的概率;(2)求至少有2个次品的概率.
解 基本事件是从1500个产品中取200个,
基本事件总数n= 1250000
(1)从400个次品中取90个, 1100个正品中取110个的事件总数
n(1)
49000
1100 110
故恰有90个次品的概率
p(1)
n(1)
/
n
49000

概率论与数理统计试题及答案概率论与数理统计是数学领域中的一个重要分支，它在科学研究、工程技术、经济管理等多个领域都有着广泛的应用。

以下是一套概率论与数理统计的试题及答案，供学习者参考。

一、选择题1. 假设随机变量X服从正态分布N(μ, σ²)，下列哪个选项是正确的？A. X的均值是σB. X的中位数是μC. X的众数是σD. X的方差是μ答案：B2. 某事件的概率P(A)为0.3，其补事件的概率P(A')是多少？A. 0.7B. 1.0C. 0.3D. 不能确定答案：A二、填空题1. 假设随机变量X和Y的协方差是-2，X的方差是4，Y的方差是9，那么X和Y的相关系数ρ(X,Y)等于______。

答案：-1/32. 某随机试验中，事件A和事件B是互斥的，且P(A)=0.4，P(B)=0.3，那么P(A∪B)等于______。

答案：0.7三、简答题1. 什么是大数定律？请简述其主要内容。

答案：大数定律是概率论中的一个重要概念，它描述了随着试验次数的增加，随机变量的样本均值会越来越接近其期望值。

具体来说，如果随机变量X1, X2, ..., Xn是独立同分布的，那么随着n的增大，样本均值(ΣXi/n)趋于X的期望值E(X)。

2. 什么是中心极限定理？它在实际应用中有何意义？答案：中心极限定理是概率论中的另一个重要定理，它指出在一定条件下，大量相互独立的随机变量之和经过标准化后趋近于正态分布，无论这些随机变量本身是否服从正态分布。

这一定理在统计推断、质量控制、风险管理等领域有着重要的应用价值。

四、计算题1. 假设随机变量X服从参数为λ的泊松分布，求P(X=3)。

答案：P(X=3) = e^(-λ) * λ^3 / 3!2. 某工厂生产的零件长度服从均值为50，标准差为2的正态分布。

求长度在48到52之间的零件所占的比例。

答案：使用标准正态分布表或计算器，求Z分数为(48-50)/2和(52-50)/2的正态分布累积分布函数，然后求差值。

概率论与数理统计期中试题（一）《概率论与数理统计》期中试题（一）姓名班级学号成绩一、填空题（每小题4分，共12分）1．设事件仅发生一个的概率为0.3，且，则至少有一个不发生的概率为__________.2．设随机变量服从泊松分布，且，则______.3．设随机变量在区间上服从均匀分布，则随机变量在区间内的概率密度为_________.二、单项选择题（每小题4分，共16分）1．设为三个事件，且相互独立，则以下结论中不正确的是（A）若，则与也独立. （B）若，则与也独立.（C）若，则与也独立.（D）若，则与也独立. （）2．设随机变量的分布函数为，则的值为（A）. （B）. （C）. （D）. （）3．设随机变量和不相关，则下列结论中正确的是（A）与独立. （B）.（C）. （D）.4．设离散型随机变量和的联合概率分布为若独立，则的值为（A）. （A）. （C）（D）. （）三、（12分）已知一批产品中90%是合格品，检查时，一个合格品被误认为是次品的概率为0.05，一个次品被误认为是合格品的概率为0.02，求（1）一个产品经检查后被认为是合格品的概率；（2）一个经检查后被认为是合格品的产品确是合格品的概率.四、（12分）从学校乘汽车到火车站的途中有3个交通岗，假设在各个交通岗遇到红灯的事件是相互独立的，并且概率都是2/5. 设为途中遇到红灯的次数，求的分布列、分布函数、数学期望和方差.五、（12分）设二维随机变量在区域上服从均匀分布. 求关于的边缘概率密度；六、（12分）向一目标射击，目标中心为坐标原点，已知命中点的横坐标和纵坐标相互独立，且均服从分布. 求（1）命中环形区域的概率；（2）命中点到目标中心距离的数学期望.七、（12分）设, 求的概率密度.Y X0200.10.2010.30.050.120.1500.1八、（12分）已知离散型随机向量的概率分布为求.。

《概率论与数理统计》习题及答案__第一章解析-1 ?《概率论与数理统计》习题及答案第一章1 .写出下列随机试验的样本空间及下列事件中的样本点：（1）掷一颗骰子，记录出现的点数 ? A 二’出现奇数点’；（2）将一颗骰子掷两次，记录出现点数? A ='两次点数之和为10', B 二’第一次的点数，比第二次的点数大2（3）一个口袋中有5只外形完全相同的球，编号分别为 123,4,5 ;从中同时取出3只球，观察其结果， A='球的最小号码为1';（4）将a,b 两个球，随机地放入到甲、乙、丙三个盒子中去，观察放球情况， A='甲盒中至少有一球’；（5）记录在一段时间内，通过某桥的汽车流量，A ='通过汽车不足 5台’，B 二’通过的汽车不少于 3台’。

解（1）S ={0,62,03?, €56}其中e = ‘出现 i 点’i =1211 丨,6，A ={e 1 ,e 3,65}。

S 二｛(1,1), (1,2), (1,3),( ：1,5),( 1,6) (2,1), (2,2), (2,3), (2, 4), (2,5), (2,6)(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)(4,1),(4, 2), (4,3), (4, 4), (4,5), (4,6)(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)(6,1), (6, 2), (6,3), (6, 4), (6,5), (6,6) ｝；A = ｛(4,6), (5,5), (6, 4)｝ ;B 二｛(3,1), (4, 2), (5,3), (6, 4)｝。

(3) S =｛(1,2,3), (2,3,4), (3,4,5), (1,3,4), (1,4,5), (1,2,4), (1,2,5)(2,3,5), (2,4,5), (1,3,5)｝A 二｛(1,2,3), (1,2,4), (1,2,5), (1,3,4), (1,3,5), (1,4,5)｝(4) S =｛(ab,-,-)，(-, ab,-)，(-，-,ab), (a,b,-), (a,-,b), (b, a,-),(b, -a), (-a, b,), (-,b,a)｝，其中’-’表示空盒； A 二｛(ab,-,-)，(a,b,-)，(a, -, b), (b,a,-)，(b,-, a)｝。

. 200 www 14．由长期统计资料得知，某一地区在 4 月份下雨（记作事件 A ）的概率为
4/15，刮风（记作事件 B ）的概率为 7/15，刮风又下雨（记作事件 C ）的概率为
网 1/10。求 P( A | B) ， P(B | A) ， P( A ∪ B) 。
案 提示与答案： P(A | B) = 3 ， P(B | A) = 3 ， P(A ∪ B) = 19 。
6．已知事件 A 、 B 满足 P( AB) = P( A ∩ B ) 且 P( A) = 1/ 3 ，求 P(B) 。
解法一：由性质（5）知
m P(B) = P( A ∪ B) − P( A) + P( AB)
（性质 5）
co =1− P( A∪ B) − P( A) + P( AB)
（性质 3）
球，也可能是黑球），并且也只有这两种可能。因此若把这两种可能看成两个事
件，这两个事件的和事件便构成了一个必然事件。
若设 A 表示：“由甲袋取出的球是白球”； B 表示：“由甲袋取出的球是黑 球”； C 表示：“从乙袋取出的球是白球”。则 P(C) = 5 /12 。
18．设有一箱同类产品是由三家工厂生产的，其中 1 是第一家工厂生产的， 2
16．一机床有 1/3 的时间加工零件 A ，其余时间加工零件 B ，加工零件 A 时， 停机的概率是 3/10，加工零件 B 时，停机的概率是 4/10，求这台机床停机的概 率。
提示与答案：依题意，这是一全概率问题。若设 A 事件表示：“加工零件 A ”； B 事件表示：“加工零件 B ； C 事件表示：“机床停机”。 则 P(C) = 11/ 30 。
相同”； B 表示事件：“这 n 个人至少有两个人生日在同一天”。

20、袋中有n只球，记有号码 ，求下列事件的概率：（1）任意取出两球，号码为1,2；（2）任意取出3球，没有号码1；（30任意取出5球，号码1,2,3,中至少出现一个。
21、袋中装有 号的球各一只，采用（1）有放回；（1）不放回方式摸球，试求在第k次摸球时首次摸到1号球的概率。
24、从52张扑克牌中任意抽取13张来，问有5张黑桃，3张红心，3张方块，2张草花的概率。
.
14、解：若取出的号码是按严格上升次序排列，则n个号码必然全不相同， 。N个不同号码可产生 种不同的排列，其中只有一个是按严格上升次序的排列，也就是说，一种组合对应一种严格上升排列，所以共有 种按严格上升次序的排列。总可能场合数为 ，故题中欲求的概率为 .
16、解：因为不放回，所以n个数不重复。从 中取出m-1个数，从 中取出 个数，数M一定取出，把这n个数按大小次序重新排列，则必有 。故 。当 或 时，概率 .
28、解：设x，y分别为此二人到达时间，则yF N E
。显然，此二人到达时间8
与由上述条件决定的正方形CDEF内和M H
点是一一对应的(如图)。7D
设A表事件“其中一人必须等另外一人的C G
时间1/2小时以上“，则A发生意味着满足如下0 7 8 x
不等式 。由几何概率得，
事件A的概率等于ΔGDH及ΔFMN的面积之和与正方形CDEF的面积之比，所以
18、解：有利场合是，先从6双中取出一双，其两只全取出；再从剩下的5双中取出两双，从其每双中取出一只。所以欲求的概率为
19、解：（1）有利场合是，先从n双中取出2r双，再从每双中取出一只。
（2）有利场合是，先从n双中取出一双，其两只全取出，再从剩下的 双中取出 双，从鞭每双中取出一只。
.
（3） .

《概率论与数理统计》期中试题（二）解答姓名 班级 学号 成绩一、填空题（每小题4分，共13分）（1） 设()0.5P A =,()0.6P B =,(|)0.8P B A =，则,A B 至少发生一个的概率为_________.（2） 设X 服从泊松分布，若26EX =，则(1)P X >=___________. （3） 元件的寿命服从参数为1100的指数分布，由5个这种元件串联而组成的系统，能够正常工作100小时以上的概率为_____________.解：（1）()()()0.8(|)1()0.5P BA P B P AB P B A P A -===- 得 ()0.2P AB = ()()()() 1.10.20.9P A B P A P B P AB =+-=-= . （2）222~(),6()X P EX DX EX λλλ==+=+ 故 2λ=. (1)1(1)1(0)(1)P X P X P X P X >=-≤=-=-=2221213e e e ---=--=-. （3）设第i 件元件的寿命为i X ，则1~(),1,2,3,4,5100i X E i =. 系统的寿命为Y ，所求概率为125(100)(100,100,,100)P Y P X X X >=>>> 51551[(100)][11].P X e e --=>=-+=二、单项选择题（每小题4分，共16分）（1）,,A B C 是任意事件，在下列各式中，不成立的是 （A ）()A B B A B -= .（B ）()A B A B -= .（C ）()A B AB AB AB -= .（D ）()()()A B C A C B C =-- . （ ）（2）设12,X X 是随机变量，其分布函数分别为12(),()F x F x ，为使12()()()F x aF x bF x =+是某一随机变量的分布函数，在下列给定的各组数值中应取（A ）32,55a b ==-. （B ）22,33a b ==. （C ）13,22a b =-=. （D ）13,22a b ==. （ ）（3）设随机变量X 的分布函数为()X F x ，则35Y X =-的分布函数为()Y F y =（A ）(53)X F y -. （B ）5()3X F y -.（C ）3()5X y F +. （D ）31()5X yF --. （ ） （4）设随机变量12,X X 的概率分布为101111424i X P- 1,2i =. 且满足12(0)1P X X ==，则12,X X 的相关系数为12X X ρ=（A ）0. （B ）14. （C ）12. （D ）1-. （ ） 解：（1）（A ）：成立，（B ）：()A B A B A B -=-≠ 应选（B ）（2）()1F a b +∞==+. 应选（C ） （3）()()(35)((3)/5)Y F y P Y y P X y P X y =≤=-≤=>- 331()1()55X y yP X F --=-≥=- 应选（D ） （4）12(,)X X 的分布为12120,0,0EX EX EX X ===，所以12cov(,)0X X =， 于是 120X X ρ=. 应选（A ）三、（12分）在一天中进入某超市的顾客人数服从参数为λ的泊松分布，而进入超市的每一个人购买A 种商品的概率为p ，若顾客购买商品是相互独立的， 求一天中恰有k 个顾客购买A 种商品的概率。

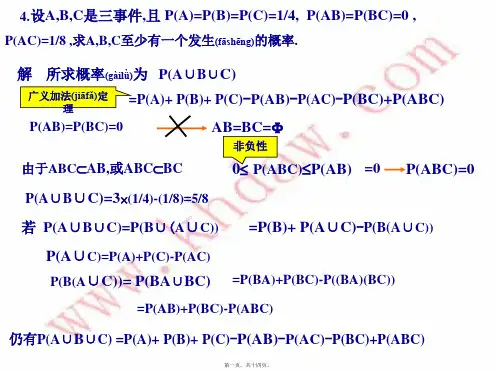
概率论与数理统计习题及答案习题 一1.写出下列随机试验的样本空间及下列事件包含的样本点. （1） 掷一颗骰子，出现奇数点. （2） 掷二颗骰子，A =“出现点数之和为奇数，且恰好其中有一个1点.”B =“出现点数之和为偶数，但没有一颗骰子出现1点.” （3）将一枚硬币抛两次， A =“第一次出现正面.” B =“至少有一次出现正面.” C =“两次出现同一面.” 【解】{}{}1123456135A Ω==（），，，，，，，，；{}{}{}{}{}(2)(,)|,1,2,,6,(12),(14),(16),(2,1),(4,1),(6,1),(22),(24),(26),(3,3),(3,5),(4,2),(4,4),(4,6),(5,3),(5,5),(6,2),(6,4),(6,6);(3)(,),(,),(,),(,),(,),(,),(,),(,),(i j i j A B A B ΩΩ=======，，，，，，正反正正反正反反正正正反正正正反反{}{},),(,),(,),C =正正正反反2.设A ，B ，C 为三个事件，试用A ，B ，C（1） A 发生，B ，C 都不发生； （2） A 与B 发生，C （3） A ，B ，C 都发生； （4） A ，B ，C （5） A ，B ，C 都不发生； （6） A ，B ，C（7） A ，B ，C 至多有2个发生； （8） A ，B ，C 至少有2个发生. 【解】（1） A BC （2） AB C （3） ABC（4） A ∪B ∪C =AB C ∪A B C ∪A BC ∪A BC ∪A B C ∪AB C ∪ABC =ABC(5) ABC=A B C (6) ABC(7) A BC∪A B C∪AB C∪AB C∪A BC∪A B C∪ABC=ABC=A∪B∪C(8) AB∪BC∪CA=AB C∪A B C∪A BC∪ABC3.指出下列等式命题是否成立，并说明理由:(1) A∪B=(AB)∪B；(2) A B=A∪B；A∩C=AB C；(3) B(4) (AB)( AB)= ∅；(5) 若A⊂B，则A=AB；(6) 若AB=∅，且C⊂A，则BC=∅；(7) 若A⊂B，则B⊃A；(8) 若B⊂A,则A∪B=A.【解】(1)不成立.特例：若Α∩B=φ，则ΑB∪B=B.所以，事件Α发生，事件B必不发生，即Α∪B发生，ΑB∪B不发生.故不成立.(2)不成立.若事件Α发生，则A不发生，Α∪B发生，所以A B不发生，从而不成立.A，AB画文氏图如下:(3)不成立.B所以,若Α-B发生,则AB发生, A B不发生,故不成立.(4)成立.因为ΑB与AB为互斥事件.(5)成立.若事件Α发生,则事件B发生,所以ΑB发生.若事件ΑB发生,则事件Α发生,事件B发生.故成立.(6)成立.若事件C发生,则事件Α发生,所以事件B不发生,故BC=φ.⊂.(7)不成立.画文氏图,可知B A(8)成立.若事件Α发生,由()A AB ⊂,则事件Α∪B 发生.若事件Α∪B 发生,则事件Α,事件B 发生. 若事件Α发生,则成立.若事件B 发生,由B A ⊂,则事件Α发生.4.设A ，B 为随机事件，且P （A ）=0.7,P (A B )=0.3，求P （AB ）. 【解】 P （AB ）=1P （AB ）=1[P (A )P (AB )]=1[0.70.3]=0.65.设A ，B 是两事件，且P （A ）=0.6,P (B )=0.7, （1） 在什么条件下P （AB（2） 在什么条件下P （AB【解】（1） 当AB =A 时，P （AB ）取到最大值为0.6.（2） 当A ∪B =Ω时，P （AB ）取到最小值为0.3.6.设A ，B ，C 为三事件，且P （A ）=P （B ）=1/4，P （C ）=1/3且P （AB ）=P （BC ）=0P（AC ）=1/12，求A ，B ，C 至少有一事件发生的概率.【解】 P （A ∪B ∪C ）=P (A )+P (B )+P (C )P (AB )P (BC )P (AC )+P (ABC )=14+14+13112=347.52张扑克牌中任意取出13张，问有5张黑桃，3张红心，3张方块，2张梅花的概率是多少？【解】 p =5332131313131352C C C C /C8. （1） 求五个人的生日都在星期日的概率； （2） 求五个人的生日都不在星期日的概率； （3） 求五个人的生日不都在星期日的概率.【解】（1） 设A 1={五个人的生日都在星期日}，基本事件总数为75，有利事件仅1个，故 P （A 1）=517=（17）5（亦可用独立性求解，下同） （2） 设A 2={五个人生日都不在星期日}，有利事件数为65，故P （A 2）=5567=(67)5(3) 设A 3={五个人的生日不都在星期日}P （A 3）=1P (A 1)=1(17)59. 从一批由45件正品，5件次品组成的产品中任取3件，求其中恰有一件次品的概率.【解】与次序无关,是组合问题.从50个产品中取3个,有350C 种取法.因只有一件次品,所以从45个正品中取2个,共245C 种取法;从5个次品中取1个,共15C 种取法,由乘法原理,恰有一件次品的取法为245C 15C种,所以所求概率为21455350C C P C =.10.一批产品共N 件，其中M 件正品.从中随机地取出n 件（n <N ）.试求其中恰有m 件（m ≤M ）正品（记为A ）的概率. （1） n 件是同时取出的； （2）n （3） n 件是有放回逐件取出的.【解】（1） P （A ）=C C /C m n m nM N M N --(2) 由于是无放回逐件取出，可用排列法计算.样本点总数有P nN 种，n 次抽取中有m次为正品的组合数为C m n 种.对于固定的一种正品与次品的抽取次序，从M 件正品中取m 件的排列数有P mM 种，从NM 件次品中取nm 件的排列数为P n mN M --种，故P （A ）=C P P P m m n mn M N MnN-- 由于无放回逐渐抽取也可以看成一次取出，故上述概率也可写成P （A ）=C C C m n mM N Mn N--可以看出，用第二种方法简便得多.（3） 由于是有放回的抽取，每次都有N 种取法，故所有可能的取法总数为N n种，n 次抽取中有m 次为正品的组合数为C m n 种，对于固定的一种正、次品的抽取次序，m 次取得正品，都有M 种取法，共有M m 种取法，n m 次取得次品，每次都有N M 种取法，共有（N M ）n m 种取法，故()C ()/m m n m nnP A M N M N -=- 此题也可用贝努里概型，共做了n 重贝努里试验，每次取得正品的概率为MN，则取得m 件正品的概率为()C 1m n mm n M M P A N N -⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭11. 在电话号码簿中任取一电话号码，求后面4个数全不相同的概率(设后面4个数中的每一个数都是等可能地取自0，1，…，9).【解】这是又重复排列问题.个数有10种选择,4个数共有104种选择.4个数全不相同,是排列问题.用10个数去排4个位置,有410P 种排法,故所求概率为4410/10P P =.12. 50只铆钉随机地取来用在10个部件上，每个部件用3只铆钉.其中有3个铆钉强度太弱.若将3只强度太弱的铆钉都装在一个部件上，则这个部件强度就太弱.求发生一个部件强度太弱的概率是多少？ 【解】设A ={发生一个部件强度太弱}133103501()C C /C 1960P A ==13.7个球，其中4个是白球，3个是黑球，从中一次抽取3个，计算至少有两个是白球的概率. 【解】 设A i ={恰有i 个白球}（i =2,3），显然A 2与A 3互斥.213434233377C C C 184(),()C 35C 35P A P A ====故 232322()()()35P A A P A P A =+=14.有甲、乙两批种子，发芽率分别为0.8和0.7，在两批种子中各随机取一粒，求：（1） 两粒都发芽的概率； （2） 至少有一粒发芽的概率； （3） 恰有一粒发芽的概率.【解】设A i ={第i 批种子中的一粒发芽}，（i =1,2）(1) 1212()()()0.70.80.56P A A P A P A ==⨯= (2) 12()0.70.80.70.80.94P A A =+-⨯=(3) 2112()0.80.30.20.70.38P A A A A =⨯+⨯=15.3次正面才停止.（1） 问正好在第6次停止的概率；（2） 问正好在第6次停止的情况下，第5次也是出现正面的概率.【解】（1） 223151115()()22232p C == (2) 1342111C ()()22245/325p == *16.0.7及0.6，每人各投了3次，求二人进球数相等的概率.【解】 设A i ={甲进i 球}，i =0,1,2,3,B i ={乙进i 球},i =0,1,2,3,则3331212330()(0.3)(0.4)C 0.7(0.3)C 0.6(0.4)i i i P A B ==+⨯⨯+22223333C (0.7)0.3C (0.6)0.4+(0.7)(0.6)⨯=0.32076*17．从5双不同的鞋子中任取4只，求这4只鞋子中至少有两只鞋子配成一双的概率.【解】 4111152222410C C C C C 131C 21p =-= 18.0.3，下雨的概率为0.5，既下雪又下雨的概率为0.1,求：（1）在下雨条件下下雪的概率；（2）这天下雨或下雪的概率. 【解】 设A ={下雨}，B ={下雪}.（1） ()0.1()0.2()0.5P AB p B A P A === （2） ()()()()0.30.50.10.7p A B P A P B P AB =+-=+-=？19.已知一个家庭有3个小孩，且其中一个为女孩，求至少有一个男孩的概率（小孩为男为女是等可能的）.【解】 设A ={其中一个为女孩}，B ={至少有一个男孩}，样本点总数为23=8，故()6/86()()7/87P AB P B A P A ===或在缩减样本空间中求，此时样本点总数为7.6()7P B A =20.5%的男人和0.25%的女人是色盲，现随机地挑选一人，此人恰为色盲，问此人是男人的概率（假设男人和女人各占人数的一半）.【解】 设A ={此人是男人}，B ={此人是色盲}，则由贝叶斯公式()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.50.05200.50.050.50.002521⨯==⨯+⨯21.两人约定上午9∶00~10∶00在公园会面，求一人要等另一人半小时以上的概率.题21图【解】设两人到达时刻为x,y ,则0≤x ,y ≤60.事件“一人要等另一人半小时以上”等价于|xy |>30.如图阴影部分所示.22301604P ==22.0，1）中随机地取两个数，求：（1） 两个数之和小于65的概率； （2） 两个数之积小于14的概率.【解】 设两数为x ,y ，则0<x ,y <1.（1） x +y <65. 11441725510.68125p =-==(2) xy =<14.1111244111d d ln 242x p x y ⎛⎫=-=+⎪⎝⎭⎰⎰ 题22图23.P （A ）=0.3,P (B )=0.4,P (A B )=0.5，求P （B ｜A ∪B ）【解】 ()()()()()()()()P AB P A P AB P B A B P A B P A P B P AB -==+- 0.70.510.70.60.54-==+-24.15个乒乓球，其中有9个新球，在第一次比赛中任意取出3个球，比赛后放回原盒中；第二次比赛同样任意取出3个球，求第二次取出的3个球均为新球的概率.【解】 设A i ={第一次取出的3个球中有i 个新球}，i =0,1,2,3.B ={第二次取出的3球均为新球}由全概率公式，有3()()()i i i P B P B A P A ==∑33123213336996896796333333331515151515151515C C C C C C C C C C C C C C C C C C =∙+∙+∙+∙0.089=25. 按以往概率论考试结果分析，努力学习的学生有90%的可能考试及格，不努力学习的学生有90%的可能考试不及格.据调查，学生中有80%的人是努力学习的，试问： （1）考试及格的学生有多大可能是不努力学习的人？ （2）考试不及格的学生有多大可能是努力学习的人？ 【解】设A ={被调查学生是努力学习的}，则A ={被调查学生是不努力学习的}.由题意知P（A ）=0.8，P （A ）=0.2，又设B ={被调查学生考试及格}.由题意知P （B |A ）=0.9，P （B |A ）=0.9，故由贝叶斯公式知（1）()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.20.110.027020.80.90.20.137⨯===⨯+⨯即考试及格的学生中不努力学习的学生仅占2.702% (2) ()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+ 0.80.140.30770.80.10.20.913⨯===⨯+⨯即考试不及格的学生中努力学习的学生占30.77%.26. 将两信息分别编码为A 和B 传递出来，接收站收到时，A 被误收作B 的概率为0.02，而B 被误收作A 的概率为0.01.信息A 与B 传递的频繁程度为2∶1.若接收站收到的信息是A ，试问原发信息是A 的概率是多少？【解】 设A ={原发信息是A }，则={原发信息是B }C ={收到信息是A }，则={收到信息是B } 由贝叶斯公式，得()()()()()()()P A P C A P A C P A P C A P A P C A =+2/30.980.994922/30.981/30.01⨯==⨯+⨯27.在已有两个球的箱子中再放一白球，然后任意取出一球，若发现这球为白球，试求箱子【解】设A i ={箱中原有i 个白球}（i =0,1,2），由题设条件知P （A i ）=13,i =0,1,2.又设B ={抽出一球为白球}.由贝叶斯公式知11112()()()()()()()i i i P B A P A P A B P A B P B P B A P A ===∑ 2/31/311/31/32/31/311/33⨯==⨯+⨯+⨯28.96%是合格品，检查产品时，一个合格品被误认为是次品的概率为0.02，一个次品被误认为是合格品的概率为0.05，求在被检查后认为是合格品产品确是合格品的概率.【解】 设A ={产品确为合格品}，B ={产品被认为是合格品}由贝叶斯公式得()()()()()()()()()P A P B A P AB P A B P B P A P B A P A P B A ==+0.960.980.9980.960.980.040.05⨯==⨯+⨯29.某保险公司把被保险人分为三类：“谨慎的”，“一般的”，“冒失的”.统计资料表明，上述三种人在一年内发生事故的概率依次为0.05,0.15和0.30；如果“谨慎的”被保险人占20%，“一般的”占50%，“冒失的”占30%，现知某被保险人在一年内出了事故，则他是“谨慎的”的概率是多少？【解】 设A ={该客户是“谨慎的”}，B ={该客户是“一般的”}，C ={该客户是“冒失的”}，D ={该客户在一年内出了事故} 则由贝叶斯公式得()()(|)(|)()()(|)()(|)()(|)P AD P A P D A P A D P D P A P D A P B P D B P C P D C ==++0.20.050.0570.20.050.50.150.30.3⨯==⨯+⨯+⨯30.次品率分别为0.02,0.03,0.05,0.03，假定各道工序是相互独立的，求加工出来的零件的次品率. 【解】设A i ={第i 道工序出次品}（i =1,2,3,4）.412341()1()i i P A P A A A A ==-12341()()()()P A P A P A P A =-10.980.970.950.970.124=-⨯⨯⨯=31.设每次射击的命中率为0.2，问至少必须进行多少次独立射击才能使至少击中一次的概率不小于0.9? 【解】设必须进行n 次独立射击.则1(0.8)0.9n-≥即为 (0.8)0.1n ≤ 故n ≥1lg8=11.07，至少必须进行11次独立射击. 32.证明：若P （A ｜B ）=P (A ｜B )，则A ，B 相互独立.【证】 (|)(|)P A B P A B =即()()()()P AB P AB P B P B =亦()()()()P AB P B P AB P B =，即()[1()][()()]()P AB P B P A P AB P B -=- 因此 ()()()P AB P A P B =,故A 与B 相互独立. 33.三人独立地破译一个密码，他们能破译的概率分别为151314，求将此密码破译出的概率. 【解】 设A i ={第i 人能破译}（i =1,2,3），则31231231()1()1()()()i i P A P A A A P A P A P A ==-=-42310.6534=-⨯⨯=34.甲、乙、丙三人独立地向同一飞机射击，设击中的概率分别是0.4,0.5,0.7，若只有一人击中，则飞机被击落的概率为0.2；若有两人击中，则飞机被击落的概率为0.6；若三人都击中，则飞机一定被击落，求：飞机被击落的概率. 【解】设A ={飞机被击落}，B i ={恰有i 人击中飞机}，i =0,1,2,3由全概率公式，得3()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)×0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)×0.6+0.4×0.5×0.7×1=0.458。

概率。
2.设的联合概率密度为,求（1）系数A；（2）落在以（0,0）、（0,1）、（1,0）、（1,1）为顶点的正方形内的概率；（3）判断X和Y是否独立。
3.对于一个学生而言,来参加家长会的家长人数是一个随机变量。设一个学生无家长、1名家长.2名家长来参加会议的概率分别为0.05.0.8、0.15。若学校共有400名学生,设各学生参加会议的家长数相互独立,且服从同一分布,求参加会议的家长数X超过450的概率。（）
4.将n个人随机地分配到N（n<N）个房间,每个房间容纳的人数不限,某一指定的房间中恰有k人的概率.______________________。
5.设连续型随机变量，为取自总体的样本，则统计量.服从_____________________分布。
6.设随机变量X的分布未知，，则根据切比雪夫不等式_____________________________。
lnL=nln(2) =nln(2) 5分
令 6分
8分
的极大似然 10分
四、证明题：（每题6分,共12分）
得分
评阅人
1.证明:因为X~, Y~
所以, 2分
因为X与Y相互独立
所以
4分
即得证X+Y~ 。6分
2.证明:设的联合概率密度函数为,的概率密度函数和分布函数分别为
和,则有
2分
4分
6分
(2) 4分
(3) 6分
8分
有f(x,y)=fX(x)fY(y),故X与Y独立10分
3.解：设表示第k个学生来参加会议的家长数，则的分布律为
0
1
2
0.05
0.8
0.15
3分
易知 4分
态分布, 6分

第1章 概率论的基本概念§1 .8 随机事件的独立性1. 电路如图，其中A,B,C,D 为开关。

设各开关闭合与否相互独立，且每一开关闭合的概率均为p,求L 与R 为通路（用T 表示）的概率。

A B L R C D1. 甲，乙,丙三人向同一目标各射击一次，命中率分别为0.4,0.5和0.6，是否命中，相互独立， 求下列概率: (1) 恰好命中一次,(2) 至少命中一次。

第1章作业答案§1 .8. 1： 用A,B,C,D 表示开关闭合，于是 T = AB ∪CD, 从而，由概率的性质及A,B,C,D 的相互独立性P(T) = P(AB) + P(CD) - P(ABCD)= P(A)P(B) + P(C)P(D) – P(A)P(B)P(C)P(D)424222p p p p p -=-+=2： (1) 0.4(1-0.5)(1-0.6)+(1-0.4)0.5(1-0.6)+(1-0.4)(1-0.5)0.6=0.38； (2) 1-(1-0.4)(1-0.5)(1-0.6)=0.88.第2章 随机变量及其分布§2.2 10-分布和泊松分布1 某程控交换机在一分钟内接到用户的呼叫次数X 是服从λ=4的泊松分布，求(1)每分钟恰有1次呼叫的概率；(2)每分钟只少有1次呼叫的概率； (3)每分钟最多有1次呼叫的概率；2 设随机变量X 有分布律： X 23 , Y ～π(X), 试求： p 0.4 0.6（1）P(X=2,Y ≤2)； (2)P(Y ≤2)； (3) 已知 Y ≤2, 求X=2 的概率。

§2.3 贝努里分布2 设每次射击命中率为0.2，问至少必须进行多少次独立射击，才能使至少击中一次的概率不小于0.9 ？§2.6 均匀分布和指数分布2 假设打一次电话所用时间（单位：分）X 服从2.0=α的指数分布，如某人正好在你前面走进电话亭，试求你等待：（1）超过10分钟的概率；（2）10分钟 到20分钟的概率。

《概率论与数理统计》分章复习题答案第一章 随机事件与概率一、 选择题1、D2、C3、A4、B5、 D6、D 7、D 8、B 9、B 10、C 11、D 12、A 13、B 14、B 15、A 16、D 17、C 18、D 19、C 20、B 21、B 22、C 23、C 24、C 25、A 26、A 27、C 28、B 29、B 30、B 31、B 32、C 33、D 34、C 35、C 36、B 37、B 二、 填空题1、A B ⋃2、133、134、0.9925、0.646、07.7、238、 0.79、 0.7 10、q p --1 11、0.2 12、 0.5 13、 0.88 14、p -115、 92 16、 7517、511）（p --18、18519、 7039 20、0.496 21、106.01）（- 22、 89 23、 116 24、3961925、84.840.7⨯ 26、23 27、127 28、13“取出的2球中至少有1个黑球”.(1) 1146210248().4515C C P A C === (2)112464210302().453C C C P B C +===7、设A =“取出的2球恰好是1黑1白球”，B =“取出的2球中至少有1个黑球”. (1)1146210248().4515C C P A C ===(2)1124662103913().4515C C C P B C +===8、 （1）作不放回抽样设 A={两只都是红球}，323()8728P A ⨯==⨯ （2）作放回抽样 设B={两只都是红球}，339()8864P B ⨯==⨯ 9、设 (1,2,3)iB i = 为第一次取出的 3 只球恰好有i只新的，A 为第二次取出的 3 只球全是没有用过的, 则由全概率公式，得33339393301212()()(|)0.1458.i i i iii i C CC P A P B P A B CC --====⋅=∑∑10、（1）设{}A =恰有两位同学不及格，1{}B =甲考试及格，2{}B =乙考试及格，3{}B=丙考试及格.则()0.29P A = （2）215()29P B A =11、设A 为被查后认为是合格品的事件，B 为抽查的产品为合格品的事件..998.09428.0/9408.0)(/)()()(===A P B A P B P A B P 12、 解 (1) 设A={选到的人患有色盲}，1B ={选到的人是男人}，2B ＝{选到的人是女人}，则12121122()()()()()()()()P A P AB AB P AB P AB P B P A B P B P A B =⋃=+=+0.50.060.50.0020.031=⨯+⨯=（2） 1111()()()30()()()31P B P A B P AB P BA P A P A ===13、 (1)设1A 表示从甲箱取得的产品是次品，2A 表示从乙箱取得的产品是次品，3A 表示从丙箱取得的产品是次品，B 表示取得的产品是次品;则取得的一件是次品的概率为3111111129()()(|).210315620360i i i P B P A P B A ===⨯+⨯+⨯=∑(2)若已知取得的一件是次品，所取得的产品是由丙车床生产的概率为3333()()(|)1/61/203(|).()()29/36029P A B P A P B A P A B P B P B ⨯====14、 解：设A={取到的产品是次品}，B={取到的产品是由甲床生产的}，C={取到的产品是由乙床生产的}，D ＝{取到的产品是由丙床生产的}，则()()()()()P A P AB AC AD P AB P AC P AD =⋃⋃=++()()()()()()P B P A B P C P A C P D P A D =++=513121210101015102025⨯+⨯+⨯=()()()1()()()4P C P A C P AC P C A P A P A ===15、解：设事件A={取得一件产品是正品}，=1B {取得一箱是甲厂产品}，=2B {取得一箱是乙厂产品},=3B {取得一箱是丙厂产品}。

概率论与数理统计期中测试答案一、 单项选择题1．当事件A 、B 同时发生时，事件C 必发生，则( B )(A) ()()()1-+≤B P A P C P (B) ()()()1-+≥B P A P C P (C) ()()AB P C P = (D) ()()B A P C P ⋃=2．设随机变量X 的概率密度是()x f ，则下列函数中一定可以作为概率密度的是( )(A) ()x f 2 (B) ()x f 2 (C) ()x f - (D) ()x f 3.设1{0,0}5P X Y ≥≥=,2{0}{0}5P X P Y ≥=≥=,则{max{,}0}P X Y ≥=( )(A)15 (B) 25 (C) 35 (D) 454．设,X Y 相互独立，X 服从()0,2上的均匀分布，Y 的概率密度函数为,0()0,0y Y e y f y y -⎧≥=⎨<⎩，则{}1P X Y +≥=( )(A) 11e -- (B) 21e -- (C) 212e -- (D) 110.5e -- 二 填空题1 设随机变量X 服从参数为λ的指数分布, 则=>}{DX X P 1/e .2 设和ξη是两个相互独立且均服从正态分布N （0，21）的随机变量，则=-|)(|ηξE3 设随机变量X 和Y 的数学期望分别为-2和2，方差分别为1和4，而相关系数为-0.5，则根据切比雪夫不等式有≤≥+}6|{|Y X P 1/12.4 设平面区域D 由曲线所围成及直线2,1,01e x x y xy ====，二维随机变量（X ，Y ）在区域D 上服从均匀分布，则（X ，Y ）关于X 的边缘概率密度在x =2处的值为1/4。

三 计算题1、自动包装机把白色和淡黄色的乒乓球混装入盒子，每盒装12只，已知每盒内装有的白球的个数是等可能的。

为检查某一盒子内装有白球的数量，从盒中任取一球发现是白球，求此盒中装的全是白球的概率。

第 4 章随机变量的数字特征一、填空题1、设X为北方人的身高，Y 为南方人的身高，则“北方人比南方人高”相当于E( X ) E(Y)2、设X为今年任一时刻天津的气温，Y 为今年任一时刻北京的气温，则今年天津的气温变化比北京的大，相当于D(X) D(Y) .3、已知随机变量X 服从二项分布，且E(X ) 2.4, D(X) 1.44 ，则二项分布的参数n= 6 , p= .4、已知X服从(x ) 1 e x2 2x 1，则 . E(X)=1 , D(X)=1/2.5、设X的分布律为X 1 0 1 2P 1 1 1 1 8 4 2 8则 E(2X 1) 9/4 .6、设X ,Y相互独立，则协方差cov( X ,Y ) 0 .这时， X ,Y 之间的相关系数XY 0 .7 、若XY是随机变量 (X,Y)的相关系数，则 | XY| 1的充要条件是P Y aX b 1 .8、XY是随机变量 ( X ,Y ) 的相关系数，当XY 0时，X与Y 不相关，当| XY | 1 时，X 与 Y 几乎线性相关 .9、若D(X) 8, D(Y ) 4 ，且X ,Y相互独立，则 D (2X Y ) 36 .10、若a, b为常数，则D (aX b) a2 D ( X ) .11、若X ,Y相互独立，E( X ) 0, E(Y) 2 ，则 E(XY ) 0 .12、若随机变量X 服从[0,2 ]上的均匀分布，则E( X )π.13、若D(X) 25, D(Y ) 36, XY 0.4 ，则 cov( X ,Y ) 12 ， D(X Y) 85，D ( X Y ) 37 .14、已知E( X ) 3，D(X) 5，则E(X 2)2 30 .15、若随机变量X 的概率密度为e x x 0，(x)x，则 E(2X ) 20 0E (e 2 X ) 1/3 .二、计算题1、五个零件中有 1 个次品，进行不放回地检查，每次取 1 个，直到查到次品为止。

《概率论与数理统计》第一章习题及答案习题1.11. 将一枚匀整的硬币抛两次，事务C,分别表示“第一次出现A,B正面”，“两次出现同一面”，“至少有一次出现正面”。

试写出样本空间及事务C,中的样本点。

A,B解：{=Ω(正，正)，〔正，反〕，〔反，正〕，〔反，反〕} {=A(正，正)，〔正，反〕}；{=B〔正，正〕，〔反，反〕} {=C(正，正)，〔正，反〕，〔反，正〕}2. 在掷两颗骰子的试验中，事务D,,分别表示“点数之和为A,BC偶数”，“点数之和小于5”，“点数相等”，“至少有一颗骰子的点数为3”。

试写出样本空间及事务D-+,-,,中AB-,ABCABCBCA的样本点。

解：{})6,6(,=Ω；),2,6(),1,6(,),2,1(),1,1(),6,2(,),2,2(),1,2(),6,1(,{})1,3(),2,2(),3,1(),1,1(AB；={})1,2(),2,1(),6,6(),4,6(),2,6(,+BA；=),5,1(),3,1(),1,1(A；C=Φ{})2,2(),1,1(BC；={})4,6(),2,6(),1,5(),6,4(),2,4(),6,2(),4,2(),5,1(BA-DC-=-3. 以C,分别表示某城市居民订阅日报、晚报和体育报。

试用A,B,表示以下事务：A,BC〔1〕只订阅日报；〔2〕只订日报和晚报；〔3〕只订一种报； 〔4〕正好订两种报； 〔5〕至少订阅一种报； 〔6〕不订阅任何报； 〔7〕至多订阅一种报； 〔8〕三种报纸都订阅； 〔9〕三种报纸不全订阅。

解：〔1〕C B A ； 〔2〕C AB ；〔3〕C B A C B A C B A ++； 〔4〕BC A C B A C AB ++;〔5〕C B A ++； 〔6〕C B A ；〔7〕C B A C B A C B A C B A +++或C B C A B A ++ 〔8〕ABC ； 〔9〕C B A ++4. 甲、乙、丙三人各射击一次，事务321,,A A A 分别表示甲、乙、丙射中。

概率论与数理统计习题 第四章 随机变量的数字特征习题4-1 某产品的次品率为，检验员每天检验 4次，每次随机地取 10件产品进行检验，如发现其中的次品数多于1个，就去调整设备，以 X 表示一天中调整设备的次数，试求E(X)(设诸产品是否为次品是相互独立的)解：设表示一次抽检的 10件产品的次品数为1 —=.从而E ( X )=np =4X =的数学期望不存在. 解:3j—)不绝对收敛，由数学期望的定义知， X 的数学期望不存在.J求 E(X), E(X 2), E(3X 25).解 E (X )=(-2) +0 +2习题4-3 设随机变量 X 的分布律为P =P (调整设备)=P ( E >1)=1 — P ( E W 1)= 1 -[P ( E =0)+ P ( E =1)］查二项分布表因此X 表示一天调整设备的次数时4P ( X =1)= XX =, P ( X =2)=1 4P ( X =3)= XX =, P ( X =4)=X 〜巳4,. 4XX =2 4XX =P ( X =0)=XX习题4-2 设随机变量 X 的分布律为P X23j ，1,2,,说明X由于.13j (1)j 勺一P(X j(1)j1-)-，而级数2 j 1 j• 1 3j- 1)j1- P(X ( 1)j由关于随机变量函数的数学期望的定理，知E(X2)=(-2) 2小2 小2+0 +2E(3X2+5)=[32 2 2(-2) +5] +[3 0 +5] +[3 2+5]如利用数学期望的性质, 则有E(3X2+5)=3E(X2)+5=3 +5=E(X)2 E(X ) E(3X22 0.4 020.3 0.30.2,习题求（1）Y22(2) 0.4 225) 3E(X ) 54-4 设随机变量2X; (2)Y e 2X0.3 2.8,13.4X的概率密度为f（X）的数学期望.(I)E( Y) E(2X) 2xf(x)dx2( 0dx2( xe 0 e x dx) 2e(II )E(Y) E(e 2X) 2x x .e e dx3x dx习题4-5 设（X,Y）的概率密度为f(x,y)求 E(X), E(Y), E(XY), E(X2 Y2).解各数学期望均可按照E[g（X, Y）]在有限区域G:｛（x,y）|0E(X)E(Y) 0,xe3xx 0,x 0dx)12y2, 0,y x 1, 其它g(x, y) f (x, y)dxdy 计算。