一维随机变量函数的概率分布

一维随机变量的分布函数
一维随机变量的分布函数是指在实数轴上，对于任意实数x，随机变量X小于等于x的概率，即F(x)=P(X<=x)，其中P为概率。

分布函数具有以下性质：
1. F(x)是一个单调不减的函数，即随着x的增大，F(x)也会增大或不变。

2. F(x)的取值范围是[0,1]，因为概率的取值范围也是[0,1]。

3. F(x)是右连续的，即对于任意x，F(x)的左右极限相等，且F(x)在x处连续。

4. 若X是一个连续型随机变量，则F(x)可以表示为X的概率密度函数f(x)的积分，即F(x)=∫f(t)dt，其中积分下限为负无穷，上限为x。

5. 若X是一个离散型随机变量，则F(x)可以表示为X的概率质量函数p(x)的累加和，即F(x)=∑p(t)，其中t取遍所有小于等于x 的离散值。

分布函数是描述随机变量的一个重要工具，可以用来求解各种概率问题，例如求解随机变量X落在某个区间内的概率，或者求解X的统计特征值等。

- 1 -。

第二章一维随机变量及其分布考试内容随机变量随机变量分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布考试要求1．理解随机变量的概念，理解分布函数的概念及性质，会计算与随机变量相联系的事件的概率。

2．理解离散型随机变量及其概率分布的概念，掌握0—1分布、二项分布B （n,p）、几何分布、超几何分布、泊松（Poisson）分布P（）及其应用。

3．了解泊松定理的结论和应用条件，会用泊松分布近似表示二项分布。

4．理解连续型随机变量及其概率密度的概念，掌握均匀分布U（a,b）、正态分布N（）、指数分布及其应用，其中参数为的指数分布E（）的概率密度为会求随机变量函数的分布。

本章导读本章的核心内容是8大分布函数及其对应的模型；如何根据定义求的函数分布一般方法。

介绍了作者用于分布函数求一维分布的直角分割法秘技。

分布函数的定义历来是使读者感到迷茫的知识点，如为什么要求分布函数必须右连续等问题？目前的教材和参考书的讲法都不清晰，作者系统地揭开了这一神秘数学面纱。

一、随机变量1概念随机试验的每一个可能的结果（即每一基本事件），对应样本间的集合中每一元素，我们都可以设令一个实数来表示该元素，显然，为实值单值函数，称为随机变量。

对，我们试验前无法确定，也就无法事先确定的值，只有在试验后才会知道的值，但取值一定服从某种确定的分布。

随机变量与普通函数区别有三，第一，随机变量定义域为样本空间的基本事件；第二，随机变量取值是随机的，只有它取每一个可能值有确定的概率；第三，随即变量是随机事件的人为数量化，而且这种数值只是一种符号表示。

比如：将一枚硬币抛三次，以表示三次投掷中出现正面的总次数，那么，对于样本空间中的每一个样本点，都有一个值与之对应，即二、随机变量的分布函数2.1 随机变量的分布函数（适合任何类型的随即变量）陈氏第2技随机变量的分布函数的全新揭秘。

● 分布函数定义形式的渊源一般情况下，人们只对某个区间内的概率感兴趣，即研究下列四种可能的区间的概率由于当所以，我们只须定义一个形式就可以了，其他区间形式都可以用它表示出来。

连续参数离散型随机过程的一维及二维的分布函数
连续参数离散型随机过程指的是一种由一维或二维连续参数随机过程构成、离散性实现的随机过程系统。

此类随机过程通常用于模拟和分析复杂的系统。

有关连续参数离散型随机过程的分布函数，本文将具体探讨一维和二维的分布函数。

一、一维分布函数
一维分布函数是指一维随机变量的概率密度的数学表达。

给定一个随机变量X，它的概率密度函数可以表示为X的概率分布，即P(X)。

一般情况下，随机变量X的概率分布函数可以表示为：
P(X)=f (X)
其中f (X)是X的概率密度函数。

一维分布函数描述了X可能出现的所有概率，对于离散型随机过程，一维分布函数可以表示为： P(X=x_i)=f (x_i)
其中x_i是离散型随机过程的状态值，f (x_i)是x_i出现的概率。

二、二维分布函数
二维分布函数是指二维随机变量的概率密度的数学表达。

给定两个随机变量X和Y，它们的概率密度函数可以表示为：
P(X,Y)=f (X,Y)
其中f (X,Y)是X和Y的概率密度函数。

二维分布函数描述了X 和Y可能出现的概率，对于离散型随机过程，二维分布函数可以表示为：
P(X=x_i, Y=y_i)=f (x_i, y_i)
其中x_i和y_i是离散型随机过程的状态值，f (x_i, y_i)是X 和Y在x_i和y_i状态下出现的概率。

综上，本文介绍了连续参数离散型随机过程的一维及二维的分布函数的基本原理，为了更好地描述此类过程，应用程序可以利用一维及二维分布函数来表征和分析相关模型。

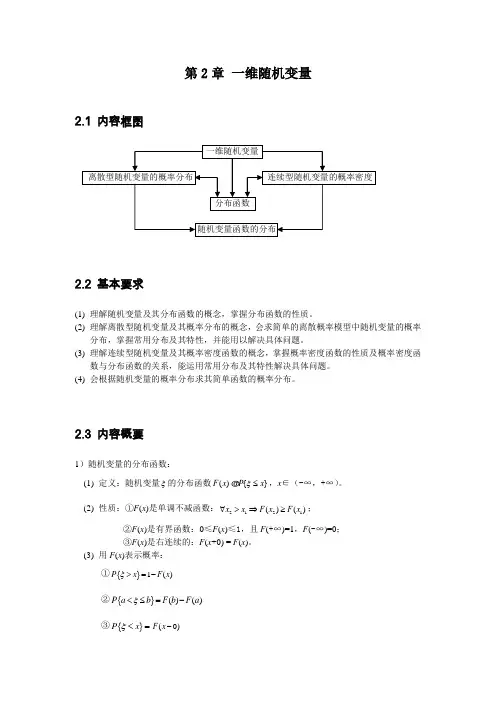
第2章 一维随机变量2.1 内容框图2.2 基本要求(1) 理解随机变量及其分布函数的概念，掌握分布函数的性质。

(2) 理解离散型随机变量及其概率分布的概念，会求简单的离散概率模型中随机变量的概率分布，掌握常用分布及其特性，并能用以解决具体问题。

(3) 理解连续型随机变量及其概率密度函数的概念，掌握概率密度函数的性质及概率密度函数与分布函数的关系，能运用常用分布及其特性解决具体问题。

(4) 会根据随机变量的概率分布求其简单函数的概率分布。

2.3 内容概要1）随机变量的分布函数：(1) 定义：随机变量ξ的分布函数(){}F x P x ξ≤@，x ∈（-∞，+∞）。

(2) 性质：①F (x )是单调不减函数：2121()()x x F x F x ∀>⇒≥； ②F (x )是有界函数：0≤F (x )≤1，且F (+∞)=1，F (-∞)=0； ③F (x )是右连续的：F (x +0) = F (x )。

(3) 用F (x )表示概率：①{}1()P x F x ξ>=- ②{}()()P a b F b F a ξ<≤=- ③{}P x ξ<=(0)F x -④{}()(0)P x F x F x ξ==--2）离散型随机变量：(1) 定义：所有可能取值为有限多个或可列无穷多个的随机变量称为离散型随机变量。

(2) 概率分布： {}i i P x p ξ==（i =1,2,…）或表示为：1212{}n i n x x x P x p p p ξξ=L L LL满足：① p i ≥0（i =1,2,…）； ②1ni i p =∑=1。

(3) 分布函数F (x ) =i ix xp ≤∑。

注 离散型随机变量ξ的分布函数F (x )是阶梯状的，ξ的每个可能取值点都是F (x )的跳跃间断点，而在其他点处F (x )连续。

3）连续型随机变量(1) 定义：设随机变量ξ的分布函数为F (x )，若存在非负函数φ(x )，使对一切实数x 成立 F (x )=()xx dx ϕ-∞⎰则称ξ为连续型随机变量，φ(x ) 称为ξ的概率密度函数。

一维的分布函数
一维分布函数是用来描述一个一维随机变量的概率分布的函数。

它可以用于描述连续型和离散型一维随机变量的概率分布情况。

对于连续型随机变量，一维分布函数通常被称为累积分布函数（Cumulative Distribution Function，CDF）。

CDF表示了随机变量取值小于等于给定值的概率。

对于一个随机变量X，其CDF 函数可以表示为F(x) = P(X <= x)。

对于离散型随机变量，一维分布函数通常被称为概率质量函数（Probability Mass Function，PMF）。

PMF表示了随机变量取某个特定值的概率。

对于一个离散型随机变量X，其PMF函数可以表示为f(x) = P(X = x)。

例如，考虑一个连续型随机变量X，表示某种产品的寿命。

我们可以用CDF函数描述该产品的寿命小于等于给定值的概率。

如果我们有一个具体的值x，可以通过计算CDF函数F(x)来得到寿命小于等于x的概率。

另一个例子是一个离散型随机变量Y，表示一个骰子的面数。

我们可以用PMF函数来描述抛掷该骰子得到某个特定面数的概率。

如果我们有一个具体的值y，可以通过计算PMF函数f(y)来得到抛掷骰子得到该面数的概率。

一维分布函数在统计学和概率论中是非常常用的工具，它提供了对随机变量的概率分布进行描述、计算和分析的方法。

通过了解一维分布函数，我们可以更好地理解和分析随机变量的概率特征和统计规律。

第二章一维随机变量及其分布第一节随机变量及其分布函数一、内容精要（一）随机变量1.随机变量的引入的背景2.随机变量的严格定义（二）分布函数1.分布函数的定义2.分布函数的性质3.分布函数表示的概率计算公式二、 常考题型分析（一） 与分布函数有关的性质1. 判定给定函数是否为分布函数例1 ()下列函数中，可以做随机变量的分布函数的是()()21.1A F x x =+ ()()31arctan .42B F x x π=+ ()()0,0,,0.1x C F x xx x≤⎧⎪=⎨>⎪+⎩ ()()2arctan 1.D F x x π=+2. 含参数的分布函数形式已知，求未知参数例2 ()()1212F x F x X X 设与分别为随机变量和的分布函数.为使 ()()()12=F x aF x bF x -()是某一随机变量的分布函数，在下列给定的各组值中应取()32,.55A a b ==- ()22,.33B a b == ()13,.22C a b =-= ()13,.22D a b ==-例3 ()()0,1,11,11,84,11,1,1,x x X F x P X ax b x x <-⎧⎪⎪=-⎪===⎨⎪+-<<⎪≥⎪⎩设随机变量的分布函数且,.a b 求未知参数3. 分布函数的连续性例4 ()000X x P X x ==设随机变量对于任意实数有的充要条件为()A X 为离散随机变量. ()B X 不是离散随机变量.()()C X F x 的分布函数为连续函数.()()D X f x 的概率密度为连续函数.例5 ()()()()1221F x X P x X x F x F x <<=-设为随机变量的分布函数，则()()F x 成立的充要条件是在()1A x 处连续. ()2B x 处连续. ()12C x x 和至少一处连续. ()12D x x 和都不连续.例6 ()()1F x F x --设为某个随机变量的分布函数，讨论函数是否为分布.函数（二） 已知分布函数求区间或某点的概率例7 ()()()00,1=01,121,1,xx F x x P X e x <⎧⎪⎪≤<=⎨⎪-≥⎪⎩，设随机变量的分布函数，则为()0.A ()1.2B ()11.2C e -- ()11.D e --例8 3164一个边长为的正立方体容器盛有的液体，假设一个小孔出现在容器 个表面的任何一个部位是等可能的，现在表面出现了一个小孔，液体经此小孔流出，试求()X F x （1）容器中剩余液体液面的高度的分布函数； 3().4P X =（2）例9 ()=()X x R F x P X x ∈<设为随机变量，对于任意，定义函数，且00,1()=01,21,1,x x F x x e x -≤⎧⎪⎪<≤⎨⎪->⎪⎩，，(1)_____________.P X ==则第二节一维随机变量及其分布一、内容精要（一）一维离散型随机变量及其分布1.分布律和性质2.分布函数3.常见分布（二）一维连续型随机变量及其分布1.概率密度及其性质2.分布函数的性质3.常见分布二、 常考题型分析（一） 与概率分布的性质相关的问题1. 判断函数是否为概率密度例1 12()()F x F x 设，为分别两个随机变量的分布函数，其相应的概率密度()12()()f x f x 分别为，，这两个函数均是连续函数，则必为概率密度的是()12()()A f x f x ()21()()B f x F x()12()()C f x F x ()1221()()()()D f x F x f x F x +2. 概率分布已知，求分布中的位置参数 例2 X 设随机变量的概率分布为()()()11,2,,,n kk kn P X k A C p p k n -==⋅-=,01___________.n Z p A +∈<<=其中为已知，则例3 ()1()1,2,2k kP X k k X θ-==⋅= 设为随机变量的分布律的充要条件 为__________.例4 []12()()1,3f x f x -设为标准正态分布的概率密度，为上均匀分布的()()12(),0,()0,0,(),0,af x x f x a b a b bf x x ≤⎧=>>⎨>⎩概率密度，若为概率密度，则应满足例5 2,0,()______.0,0,x ax e x X f x a x -⎧>==⎨≤⎩设随机变量的概率密度函数为则例6 22(),______.x xX f x ae a -+==设随机变量的概率密度函数为则（二） 已知随机试验中的随机变量，求分布律和分布函数例7 413设有三个盒子，第一盒子有个红球，个黑球；第二个盒子装有个红 223球，个黑球；第三盒子装有个红球，个黑球，现在从三个盒子中任取一盒，然后从中任取3个球，试求所取到的红球个数的分布律与分布函数.例8 ()01,p p <<某人向同一目标独立重复射击，每次射击命中概率为2X 记随机变量为第次射中目标所进行的射击的次数.求X 得分布律.（三） 已知分布函数求分布律或已知概率密度函数求分布函数1. 已知分布函数求分布律例9 X 设随机变量的分布函数为()0,1,0.4,11,0.8,13,1,3,x x F x x x <-⎧⎪-≤<⎪=⎨≤<⎪⎪≥⎩ .X 试求的分布律例10 X 已知随机变量的概率分布律为()()22123211X P θθθθ--()()32.4P X X F x θ≥=且，求未知参数及的分布函数2. 已知概率密度函数求分布函数例11 X 设连续型随机变量的密度函数为()12,0,211,1,2332,1,20,,x x x f x x x ⎧≤<⎪⎪⎪<≤⎪=⎨⎪-<≤⎪⎪⎪⎩其它 ().X F x 试求的分布函数（四） 与常见分布有关的概率问题1. 离散型常见分布例12 ()()12~,,X P p p X λ设分别为随机变量取偶数和奇数的概率，则()12.A p p = ()12.B p p < ()12C p p > ()12,D p p 大小关系不定.例13 X 设随机变量的概率密度函数为()()+1,01,0,k k x x f x ⎧<<=⎨⎩其它， 137264Y X A X ⎛⎫=≤ ⎪⎝⎭以表示对的三次独立的重复观察中，事件至少发生一次的概率为，,95%n A X 试求常数使得事件至少发生的一次的概率超过，对至少要做多少次独立重 .复的观察例14 ()01,p p <<某人向同一目标独立重复射击，每次射击命中概率为.X X 直至射中目标为止，记随机变量为射击的次数.求为偶数的概率例15 ()(),,.X B n p k P X k =设随机变量服从二项分布当取何值时，最大2. 连续型常见分布例16 ()()()~,0,0,X E s t P X s t X sλ>>>+>设则对于任意则().A t s 与无关，随的增大而增大 ().B t s 与无关，随的增大而减少 ().C s t 与无关，随的增大而增大 ().D st 与无关，随的增大而减少例17 ()()()2~,1X N P X μσμ<+设，则().A μ随的增大而增大 ().B μ随的增大而减少 ().C σ随的增大而不变 ().D σ随的增大而减少例18 ()211,X N Y μσ设随机变量服从正态分布，随机变量服从正态分布()12.A σσ< ()12.B σσ> ()12.C μμ< ()12.D μμ>例19 ()()21,0,0,03X Y N P X Y σ≤>设随机变量均服从，若概率=， ()0,0______.P X Y ><则=例20 1009010有个零件，其中个一等品，个二等品，随机地取两个，安装在 ()20,1,2i i =一台设备上，若个零件中有个二等品，则该设备的使用寿命服从参数 =1i λ+为的指数分布，试求()11设备寿命超过的概率；()212.若已知该设备寿命超过，则安装在该设备上的个零件均为一等品的概率第三节 一维随机变量函数的分布一、 内容精要（一） 一维离散型随机变量函数的分布律（二） 一维连续型随机变量函数分布求解二、 常考题型分析（一） 求可列无穷多取值的离散型随机变量函数的分布律例1 ()1,1,2,,sin .22n X P X n n Y X π⎛⎫==== ⎪⎝⎭设的分布律为求的分布律（二） 已知连续型随机变量的概率密度，求非单调函数的概率密度例2 X 设随机变量的概率密度为()1,10,21,02,40,.X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩其它2.Y X Y =令，求的概率密度函数例3 ()20,423X Y X X Y =--设服从区间上的均匀分布，随机变量，试求的 .密度函数例4 1X =max ,.Z X X λ⎛⎫ ⎪⎝⎭设随机变量服从参数为指数分布，求的分布函数（三） 抽象的随机变量函数的分布例5 ()(),,X F x Y F x =设连续型随机变量的分布函数为令求随机变量函数 .Y 的概率分布例6 (),1__________.X F x Y X =-随机变量的分布函数为则的分布函数为。