§1-2 条件分布与条件数学期望
- 格式:ppt
- 大小:842.00 KB
- 文档页数:22






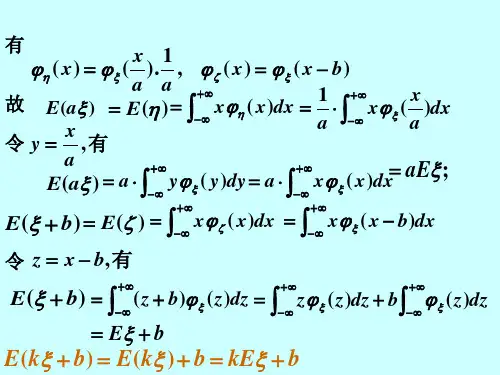




概率论中的条件期望计算方法概率论是数学中的一个重要分支,它研究随机现象的规律性和不确定性。
而条件期望是概率论中一个重要的概念,它描述了在给定某些条件下的随机变量的平均值。
在实际应用中,计算条件期望是非常常见的,因此学习条件期望的计算方法对于理解概率论的核心思想和解决实际问题非常重要。
条件期望的计算方法有多种,下面将介绍其中的两种常见方法:条件概率法和条件分布法。
首先,我们来看看条件概率法。
条件概率法是一种直观的计算条件期望的方法,它利用了条件概率的定义。
条件概率是指在某个条件下事件发生的概率。
对于一个随机变量X和一个条件Y,条件概率P(X|Y)表示在给定Y发生的条件下X发生的概率。
条件期望的计算方法可以通过条件概率来实现。
假设我们有两个随机变量X和Y,我们想要计算在给定Y的条件下X的期望。
首先,我们需要计算在给定Y的条件下X的取值的概率分布。
然后,我们将X的每个取值乘以对应的概率,并将结果相加即可得到条件期望。
举个例子来说明。
假设X表示一个硬币的正面朝上的次数,Y表示掷硬币的次数。
我们想要计算在给定掷硬币10次的条件下硬币正面朝上的次数的期望。
首先,我们需要计算在给定掷硬币10次的条件下硬币正面朝上的次数的概率分布。
然后,我们将硬币正面朝上的次数乘以对应的概率,并将结果相加即可得到条件期望。
接下来,我们来看看条件分布法。
条件分布法是一种更加抽象的计算条件期望的方法,它利用了条件概率的性质和条件分布的定义。
条件分布是指在某个条件下随机变量的概率分布。
对于一个随机变量X和一个条件Y,条件分布P(X|Y)表示在给定Y的条件下X的概率分布。
条件期望的计算方法可以通过条件分布来实现。
假设我们有两个随机变量X和Y,我们想要计算在给定Y的条件下X的期望。
首先,我们需要计算在给定Y的条件下X的概率分布。
然后,我们将X的每个取值乘以对应的概率,并将结果相加即可得到条件期望。
举个例子来说明。
假设X表示一个学生的考试成绩,Y表示学生的学习时间。
第22卷第4期2019年7月高等数学研究STUDIES IN COLLEGE MATHEMATICSVol.22,No.4July,2019doi:10.3969/j.issn.1008-1399.2019.04.024条件数学期望的定义归纳及其应用冯明勇(天津财经大学珠江学院,天津301811)摘要给出条件数学期望的一般定义、经典定义6及随机变量关于一般5代数的条件数学期望的几何定义,并举例说明条件数学期望在均值回归中的应用.关键词条件数学期望&最佳预测;最佳均方逼近中图分类号O211文献标识码A文章编号1008-1399(2019)04-0091-02Definition and Application of Conditional ExpectationFENG Mingyong(Pearl River College,Tianjin University of Finance and Economics,Tianjin301811)Abstract This paper discusses the general definition,classic definition,and geometric definition of the conditional expectation.Two examples are given for the application of the conditional expectation in the mean reversion.Keywords conditional expectation,optimum prediction,square approximation1条件数学期望的定义定义1设X是一随机变量,事件A有P(A) >0,称E)A*-#4,P(X=(;)6(,-1,2,…为一维离散型随机变量X在条件(下的条件数学期望•称E[X A*-j—4f4|A)dz为一维连续型随机变量X在条件(下的条件数学期望•其中f4\A)为随机变量X在条件(之下的条件分布概率密度•当这里的随机事件(变成另一随机变量Y时,条件数学期望就变成以下便于计算的定义方式•定义2称E(X|Y=y)=#4i P(.X-4i Y=7为一维离散型随机变量x'y==条件下的条件数学期望•称ELX\Y==*-收稿日期:2018-12-15修改日期:2019-01-08作者简介:冯明勇0981—),女,山东聊城人,硕士,讲师,研究方向:应用数学,Email:tjfengmingyong@ £4*x\y4|=)dz连续型随机变量X'Y==条件下的条件数学期望.其中f x\Y4|=)为随机变量X 在条件Y==之下的条件分布密度函数•下面给出随机变量关于一般.代数的条件数学期望的几何定义:定义3设随机变量(fx|Y(4=)可测函数)Y "L2(0,F,P),F1是F的一子.代数,用E f—(•)表示L z(n,F,P)到闭子空间L z(n,F,P|f t)上的正交投影算子,称E f$(•)为Y关于子.代数F t的条件数学期.定义3中,LJ(O,F,P|f t)与L⑵0,F,P)都是Hilbert空间,前者为后者的闭子空间,Hilbert空间上的正交投影定理保证E f:(•)的存在唯一性[1].2条件数学期望在回归分析中的应用条件数学期望主要应用在回归分析的最优估计或者预测中,应用比较广泛的结论为“均方误差最小”定理,其表述形式及如何应用解决估计或者预测问题,本文以下面两种形式展开讨论•命题1设有随机变量X与Y,g(,4)是Borel函92高等数学研究2019年7月数,则E)Y—gU)y*X E)Y—E(Y\X)y*.命题1说明,在均方意义下,随机变量X已知条件下,E(Y X)是Y的最佳预测.即若能观察变量X 的取值4则E(Y|X=4是所有对Y的估计值中均方误差最小的一个,一般称函数*4)D E(Y|X=4)是Y对X的回归函数(均值回归).例1设顾客到达银行某一窗口等待服务的人数为服从参数2的泊松过程,问题(1):在时间段(0,t]内,已经到达顾客等待的所有时间和的平均值;问题(2):假设每分钟有3个顾客到达该银行,该窗口每8分钟有一名顾客被接待服务,求一天银行工作时间(9小时)内在银行该窗口由于等待服务而浪费的平均时间和.解设Xt表示在(0,t*内到达银行窗口的顾客数,则{X(t),t>00为参数入的泊松过程.W,是第2个顾客到达的时刻,T,是第2个顾客等待的时间,则T,-t—W,.(1)在X(t)-n的条件下,”个顾客的到达时刻W1,…,w”的联合密度函数等于”个独立的[0,t*均匀分布的随机变量的顺序统计量的概率密度⑵.即XtE[#(t—W,)]2=18X(-#E[#(t—W,)\X(t)-n]P(X()-n) n=12=1-E(#W,)P(X()-n)n=12=1-tt—2]E[X()-t2(2)由题意,知A=3人/分钟,从而一天8/)、时工作时间客等服务浪费的均时间和是X60X9-6480(分钟).28一般化的回归问题:设随机变量Y与X1,X2,…X,有一定的相关关系,但不是确定的关系,一■般称Y被解释变量,X1,X2,-X t为解释变量.给定X1, X2,--X t的取值分别为41,4,-4,借助条件数学期望的几何定义,有下列“最优均方逼近”的结论.命题2设随机变量X1,X,-X t"L2(Q,F,P),Y"L2(Q,F,P),且F1=.(X1,X2,-X t)是F的一子.代数,则Y关于.代数F1-.(X1,X,…X t)的条件数学期望E(Y|F1)满足E [E(Y|F1)—Y*&E(Z—Y),其中%"L2(0,F,P|f1)且等号当且仅当Z-E(Y|F1-.(X1,X1,…X t))时即*(X1,X1,…,X t)-E(Y|F1=.(X1,X1,…,X t)是Y在LU0,F,P|f1)中的最优均方逼近例2从《中国统计年鉴》中取得外汇管理体制改革后的1994&2011年中国出口货物总额Y(亿元)、工业增加值X1(亿元)、人民币对美元的汇率X2(100美元)等数据作为样本.已知Y与其相关的X1X!的关为Y=—18231.58+0.135474X]+18.85348X Z+s 且4〜N(0,.])-N(0,533821.067S),求在工业和人汇率为(00000615)时口货总的佳解利用Y与其相关的影响因素X1,X的关系及命题2,可知在工业增加值X1和人民币对美元的汇率X2为X-(200000,615)时,出口货物总额的佳为E(Y|X)-E(—18231.58+0.135474X1+18.85348X Z+s|X) =—$823$58+0$35474X200000+18.85348X615+E(|X)-2(45&11+E(s)=20458$$求得的条件期望函数为E(Y\X)=—18231.58+0.135474X1+1&85348X,,也就是预测方程.该方程又是在给出随机变量Y, X—(X1,X z,…,X2一系列数据(y41,…,4), (2=12,•••")的情形下,可利用最小二乘法确定与所给数据相容的回归方程AY=E(Y)=—18231.58+0.135474X:+1&85348X,,其中回归系数0-(Z'Z)-1Z=及误差方差.2的无偏估计.2-—都可相应求出.本例中若给出n—2—$1994-2011年中国出口货物总额等相关数据,就可得到预测方程⑷.参考文献于林.条件数学期望概念教学的若干问题探讨中国电力教育2010(30):75-77刘嘉银,王公恕•应用随机过程[M*科学出版社,2004.严士键,王隽釀,刘秀芳•概率论基础[M*.北京:科学出版社1999.曾五一,肖红叶•统计学导论[M*.科学出版社2013.。
条 件 数 学 期 望我们曾经引进条件分布函数的概念,现在介绍条件数学期望的概念。
为了方便起见,我们讨论两个随机变量ξ与η的场合,假定它们具有密度函数(),p x y ,并以()|p y x 记已知x ξ=的条件下,η的条件密度函数,以()1p x 记ξ的密度函数。
定义 在x ξ=的条件下,η的条件数学期望定义为{}()||E x yp y x dy ηξ∞-∞==⎰例 : 某射击手进行射击,每次射击击中目标的概率为P(0<P<1),射击进行到击中目标两次时停止.令ξ表示每一次击中目标时的射击次数, η表示每二次击中目标时的射击次数,试求联合分布列ij p ,条件分布列i j j i p p ||,及数学期望}|{j E =ηξ解 据题意知),(j i p p ij ===ηξ,3,21,22=<≤=-j i q p i其中q=1-p,又∑∑∞+=-∞+=⋅==1221i j j i j iji q ppp,2,1,1112==-=--i pq q q p i i ∑∑-=--=⋅==112211j i j j i ij j q p p p3,2,)1(22=--j q p j j于是条件分布列为3,21,11)1(2222|=<≤-=-==--⋅j i j q p j q p p p p j j j ijj i 2,1,,1122|=>===----⋅i i j pq pqq p p p p i j i j i iji j 这时∑-===11|}|{n i n i ip n E ηξ21111nn i n i =-⋅=∑-= 在这个例子中,条件期望}|{n E =ηξ的意义都很直观的。
如果已知第二次击中发生在第n 次射击,那么第一次击中可能发生在第1,,1-n 次,并且发生在第i 次的概率都是11-n ,因为11|-=n p n i ,也就是说已知n =η的条件下,ξ取值为1,,1-n 是等可能的,从而它的均值为2n.条件期望具有与普通数学期望相类似的性质,例如有 (1)若b a ≤≤ξ则}|{j b E =ηξ存在,具有a ≤}|{j b E =ηξ≤b;特别,当C 是常数时, }|{j b E =ηξ=C; (2)若21,k k 是两个常数,又}|{1j b E =ηξ,}|{2j b E =ηξ存在,则}|{2211j b k k E =+ηξξ}|{}|{2211j j b E k b E k =+==ηξηξ这是在固定j b =η的条件下考察条件期望性质,由条件期望的定义可知,当给定ξ时,对于η的每一个可能的取值)2,1( =j b j 就有一个确定的实数}|{j b E =ηξ与之对应.因而}|{j b E =ηξ是η单值函数,当j b =η时,这个函数的值就等于}|{j b E =ηξ,∑∞====1)(}|{})|({j j j b p b E E ηηξηξ而∑∑∞=∞=⋅===11|}|{i i jij ij i i j p p a p a b E ηξ把它代入前面的式子中,即可得到∑∑∑∑∞=∞=⋅∞=∞=⋅==1111})|{(j ij i i j j i jij ip a p p p a E E ηξξE p a i i i ==∑∞=⋅1由此可见,随机变量ξ对η求条件期望后再求期望,等于对这个随机变量直接求期望.这是条件期望的一个重要的基本性质. 下面在随机变量是连续情况下也略作证明: 因为 ()()2E yp y dy η∞-∞=⎰(),y p x y dxdy ∞∞-∞-∞=⎰⎰(),yp x y dxdy ∞∞-∞-∞=⎰⎰而 ()()||E yp y x dy ηξ∞-∞=⎰()()1,p x y ydy p x ∞-∞=⎰ (){}()()()11,|p x y E E ydy p x dx p x ηξ∞∞-∞-∞=⎰⎰(),yp x y dxdy ∞∞-∞-∞=⎰⎰ 证毕。