当前位置：文档之家 › 条件数学期望例题ppt课件

条件数学期望例题ppt课件

  • 格式：ppt
  • 大小：717.00 KB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

3.6 条件分布与条件期望--概率论课件

3.6 条件分布与条件期望--概率论课件
=
-r
r x
2 2
r 2 x2
x r


r x r x
2
2
2
2
0,
1 dy, 2 r
r xr
其他
r xr 其他
2 r 2 x 2 , 2 r 0,
同理，
fY ( y ) f ( x, y )dx
2 r y , r y r 2 r 0, 其他
1 2 2 F | ( x | y ) 为 N a1 ( y a2 ), 1 (1 ) 分布 2
2 2 2 F| ( y | x) 为 N a2 ( x a1 ), 2 (1 ) 分布 1
注意
FX Y ( x y ), f X Y ( x y ) 仅是 x 的函数,
y是常数, 对每一 fY (y) >0 的 y 处, 只要
符合定义的条件, 都能定义相应的函数. FY X ( y x), fY X ( y x) 相仿论述. 类似于乘法公式：
f ( x, y ) f X ( x ) f Y X ( y x ) fY ( y ) f X Y ( x y )
( x a1 )( y a2 )
1 2
( y a2 ) 2 2 2
1 e 2 2
( y a2 )2 2 2 2
1 ( x a1 )2 ( x a1 )( x a2 ) 2 ( y a2 )2 exp 2 2 2 2 2 1 2 2 21 1 2(1 ) 1 1
2 x a1 1 1 y a2 exp 2 2 2(1 ) 1 2 2 1 1

《数学期望》课件

《数学期望》课件
注意事项
在计算过程中需要注意积分的上下 限以及概率密度函数的取值范围。
连续型随机变量的数学期望的性质
01
02
03
非负性
E(X) ≥ 0，即数学期望的 值总是非负的。
可加性
如果X和Y是两个独立的随 机变量，那么E(X+Y) = E(X) + E(Y)。
线性性质
如果a和b是常数，那么 E(aX+b) = aE(X)+b。
方差是数学期望的度量，表示随机变量取值 与数学期望的偏离程度。
04
CATALOGUE
连续型随机变量的数学期望
连续型随机变量的定义
连续型随机变量
如果一个随机变量X的所有可能 取值是实数轴上的一个区间变量。
概率密度函数
描述连续型随机变量X在各个点 上取值的概率分布情况，其数学
《数学期望》PPT课件
CATALOGUE
目 录
• 引言 • 数学期望的基本性质 • 离散型随机变量的数学期望 • 连续型随机变量的数学期望 • 数学期望的应用 • 总结与展望
01
CATALOGUE
引言
数学期望的定义
数学期望是概率论和统计学中的 一个重要概念，它表示随机变量
取值的平均数或加权平均数。
数学期望的定义基于概率论的基 本原理，通过将每个可能的结果 与其对应的概率相乘，然后将这
些乘积相加得到。
数学期望具有一些重要的性质， 如线性性质、期望值不变性质等 ，这些性质在概率论和统计学中
有着广泛的应用。
数学期望的起源和历史
数学期望的起源可以追溯到17世纪，当时的一些数学家开始研究概率论和统计学中 的一些基本概念。
通过计算投资组合的数学期望， 我们可以了解投资组合的预期收 益，从而制定更加合理的投资策

数学期望E(x)D(x).ppt

数学期望E(x)D(x).ppt
绝对收敛，则有
E(Y ) E[g( X )] g( x) f ( x)dx
注释
A.在计算随机变量的函数Y=g(X)的期望时，我们可以先 确定Y=g(X)的分布进而计算函数Y的期望E(Y)。但由 前两章的讨论可以看出，确定Y=g(X)的分布并不容易。 因此在计算随机变量函数的期望时，我们一般利用定 理的结论去计算。定理的重要意义在于当我们求E(Y) 时，不必知道Y的分布而只需知道X的分布就可以了。
B.在计算一些分布较复杂甚至难以确定的随机变量的期 望时，如能将X表示成有限个简单随机变量之和，那 么利用期望的性质计算就可大大简化我们的问题。这
也是计算期望的一个技巧。
C.上述定理还可以推广到二个或二个以上随机变量的函 数情况。例如，设Z是随机变量X，Y的函数Z=g(X， Y)(g是连续函数)，那么，Z也是一个随机变量，若二
1
x 2
e 2 2 dx
2
令 x t，
E(X) 1
t2
t e 2 dt
t2
e 2 dt .
2
2
特别地，若XN(0,1)，则E(X)=0。
(1) 几个常见连续型随机变量的数学期望 i.若XU(a,b),则E(X)=(a+b)/2. 证：X的概率密度为
f
(
x)
b
Y 8 2 9 5 10 3 9.1 10
结果：甲平均击中的环数9.3, 乙平均击中的环 数9.1,甲水平较高。
根据概率的统计定义作分析：击中次数N 与N的比值，是这 i
N次试验中射中环数的频率，按概率的统计定义，当N很大时, N /N接近于射中环数的概率。
i
1. 离散型随机变量的数学期望
维随机变量(X，Y)的概率密度为f(x，y)则有

4.1-数学期望PPT课件

4.1-数学期望PPT课件

1
1
84
1
.
13
例4.5 Xe(), 求EX?
f
(
x)
1
x
e
,
0,
x0 x0
E X x f(x )d x 1 x e xd x0x d (e x)
0
xex0 0exdx 0exd(x)ex0
(10)
提示: limxex x
lim x
x
x
0
e
.
14
三、随机变量函数的数学期望
0 x ,y 1 ,E (X Y )?
e lse
11
E ( X Y ) g ( x ,y ) f( x ,y ) d x d xx y ( x y ) d y
- -
设X表示掷一次骰子的得分, 则X的分布律为
X
x1
x2
x3
pk
1/6
3/6
2/6
求掷了N次的平均得分?
.
3
平 均 分 总 总 次 分 数 x 1 n 1 x 2 N n 2 x 3 n 3 x 1n N 1 x 2n N 2 x 3n N 3
nN1 f1当 N p116
平 均 分 x 1p 1 x 2p 2 x 3p 3
由此得出离散型随机变量的数学期望的定义
.
4
定义4.1 设离散型随机变量X, 它的分布律为
X x1 x2 … xn …
pk p1 p2 … pn …
若级数 xkpk绝对收敛, k1
则称其为X的数学期望(期望、均值),记为E(X),EX. 即
EXE(X) xkpk k1
.
5
注:
①EX是X在各次试验中的观察值的算数平均值的近似值

《数学期望》PPT课件

《数学期望》PPT课件
于X 和Y 的二元函数，则同样可定义随机变量 Z 的数学期望如下：
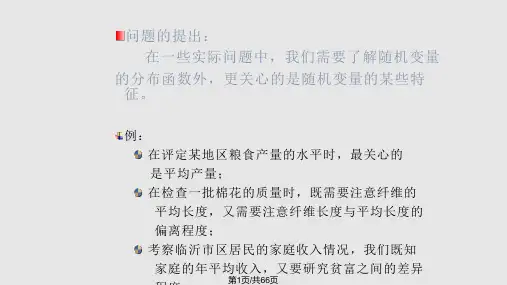
24
(1)c(rX,Y)已{知 pij},
则 ZgX,Y的数学期望为
E Z E gX ,Y gx i,yj p i.j i, 1j 1
(2)c(tX,Y)已f知 (x,y),
则 ZgX,Y的数学期望为
P { X x } p k 1 , 2 , , kk
若级数 gxk收 敛pk，则 k1 E (Y )E g X gxk pk k1
16
例1 设离散型随机变量X 的分布列为
X
-1
0
2
3
1131
P k
8
4
8
4
试计算：E X , E X 2和 E 2 X 1 。
17
解 由数学期望的定义可得
E X 1 10123311;1
8 4 8 48
E X 2 1 2 1 0 2 1 2 2 3 3 2 1 3;1 8 4 8 48
E 2 X 1 3 1 1 1 3 3 5 1
84 8 4
7. 4
18
例2 设 X 服从参数为 的泊松分布，试
Ex
x
fxd
x
9
反之，如果积分
x
发f 散x，d则x
称随机变量 X 的数学期望不存在。
例4 设 X 服从 (a,b)区间上的均匀分布， 求 X 的数学期望。
10
解 已知 X 的概率密度为
1
f
x
b
ቤተ መጻሕፍቲ ባይዱ
a
0
, xa,b，
从而
, 其它。
E x xx fd x b ax b 1 a d x 1 2 a b
14

4-1数学期望 ppt课件

4-1数学期望 ppt课件

若级数 xk pk 绝对收敛，则称此级数的和为随 i 1
机变量 X 的数学期望。记作 :EX.

既有 EX xk pk i 1
数学期望简称期望，又称均值.
PPT课件
4
数学期望
例1 甲、乙两人射击，他们射击水平由下表给出：
X:甲击中的环数
Y:乙击中的环数
X
8
9 10
Y
P
0.1 0.3 0.6

5

1 ex 0
4 e x
EM xfM (x)dx
x0 x0
0 x 5 1 ex 4 exdx
137 1
160
PPT课件
10
数学期望
2. 令：N=min{X1, X2, X3, X4, X5}, X1, X2, X3, X4, X5是 独立同分布的,于是 利用第三章第五节P99;5.8式
P
试问哪一个人的射击水平高?
解:甲、乙的平均环数为:
8
9
10
0.2 0.5 0.3
EX 8 0.1 9 0.3 10 0.6 9.5
EY 8 0.2 9 0.5 10 0.3 9.1
甲的射击水平比乙的高.
从平均环数上看
PPT课件
5
数学期望
2. 连续型
第四章 随机变量的数字特征
§1 数学期望 §2 方差 §3 协方差及相关系数 §4 矩
PPT课件
1
数学期望
§4.1 数学期望
数学期望的概念
随机变量函数的数学期望
数学期望的性质
PPT课件
2
数学期望
例1： 某班有N人参加 考试，其中有ni个人为ai ,i=1,2,…

概率论与数理统计-数学期望_图文

概率论与数理统计-数学期望_图文

因每个球落入每个盒子是等可能的均为1/M, 所以，对第i 个盒子，一个球不落入这个盒子 内的概率为(1-1/M)。故N个球都不落入这个 盒子内的概率为(1-1/M)n ，即
最常用的数字特征是：期望和方差。
第四章 数字特征
§4.1 数学期望
4.1.1 离散型随机变量的数学期望 概念引入：
某车间对工人生产情况进行考察，车工 小张每天生产的废品数 X 是一个随机变量 。如何定义 X 的平均值？
若统计了100天小张生产产品的情况，发现 ： 32天没有出废品；30天每天出一件废品； 17天每天出两件废品；21天每天出三件废品。
可以得到这n天中，每天的平均废品数为
这是以频率为 权的加权平均
由频率与概率的关系，
不难想到：求废品数X的平 均值时，用概率替代频率， 得平均值为：
这样，就得到一个确定的数
这是以概率为 权的加权平均
——随机变量X的期望(均值) 。
定义1: 设X是离散型随机变量, 概率分布为 P{X=xk}=pk , k=1,2, …。
解：设组织货源 t 吨。显然，应要求
2000≤t ≤4000。国家收益Y(单位:万元)是X
的函数Y=g(X)。表达式为
由已知条件, 知X的概率密度函为
可算得当 t = 3500 时， E(Y)=-2t2 + 14000t-8000000
达到最大值 1.55×106。 因此，应组织3500吨货源。
概率论与数理统计-数学期望_图文.ppt
前面讨论了随机变量及其分布。 如果我 们知道了随机变量 X 的概率分布，那么，关 于 X 的全部概率特征也就知道了。
然而，在实际问题中，概率分布是较难 确定的。且有时在实际应用中，我们并不需 要知道随机变量的所有性质，只要知道其一 些数字特征就够了。

3.5条件数学期望ppt课件

3.5条件数学期望ppt课件
算出罪犯的身高. 这个公式是如何推 导出来的？
25
设一个人身高为 X ,脚印长度为Y .
显然，两者之间是有统计关系的，故
应作为二维随机变量 (X ,Y )来研究. 由于影响人类身高与脚印的随机
因素是大量的、相互独立的，且各因 素的影响又是微小的,可以叠加的. 故
由中心极限定理知 (X ,Y )可以近似看
3.5 条件数学期望
条件分布 条件数学期望 条件数学期望的性质
1
回顾上节课知识点
• 1、n维随机变量函数的数学期望及求解 • 2、最值数学期望的求解 • 3、 n维随机变量函数的数学期望的性质
及应用 • 4、相关系数及性质
2
1、n维随机变量函数的数学期望及求解
3
2、最值数学期望的求解
4
3、 n维随机变量函数的 数学期望的性质及应用
可得出以脚印长度作自变量的身高近似公式.
思考：例3.5.2
28
连续型与离散型条件数学期望性质
定义
E ( X
|Y
y)
i
xi P( X xi | Y y)
xp(x | y)dx
29
注意点
E(X| Y=y) 是 y 的函数.
所以记 g(y) = E(X| Y=y). 进一步记 g(Y) = E(X| Y).
5
4、相关系数及性质回顾
6
相关矩阵
7
相关系数的性质
8
习题讲解
9
10
11
回顾条件分布
对二维随机变量(X, Y), ➢ 在给定Y取某个值的条件下, X的分布; ➢ 在给定X取某个值的条件下, Y的分布.
12
13
一、回顾条件分布
（1）、事件

第一节--数学期望省公开课获奖课件市赛课比赛一等奖课件

第一节--数学期望省公开课获奖课件市赛课比赛一等奖课件

ab 2
2）指数分布
设随机变量X 服从参数为 的指数分布．
密度函数为
f
x
e
x
x0
0 x0
则X旳数学期望为E(X)=1/
证明：E( X )
xf ( x)dx
xe- x dx
-
0
0
xde-x [ xe-x ]0
e-xdx
0
0
1
e-x
0
1
3）正态分布
X ~ N ， 2 X的密度函数为
Y= X 2 求E(Y)
3
解：E(Y ) x2k pk k 1 0 0.1 12 0.2 22 0.7 3
例6、 设一汽车沿一街道行驶， 需经过三个均设 有红绿信号灯旳路口，每盏信号灯以 1/2 旳概率 允许或禁止汽车经过.信号灯旳工作是相互独立旳. 以 表达汽车首次停下时，它已经过旳路口数， 求 (1)E() (2)E(1/1+ )
例 11
设在国际市场上每年对我国某种出口商品旳 需求量是随机变量X（吨)，它在[2023,4000] 上服从均匀分布，又设每售出这种商品一吨， 可为国家挣得外汇3万元，但假如销售不出而 囤积在仓库，则每吨需花费保养费1万元。问 需要组织多少货源，才干使国家收益最大。
解：设y为预备出口旳该商品旳数量，这个数 量可只 介于2023与4000之间， 用Y表达国家旳收益（万元）
f x
1
e
x 2
2 2
2
x
则X旳数学期望为E(X)=
证明：E( X ) -
[ (x - )] -
x
1
e dx -
（x-）2 2 2
2
1
e dx -（x2-）2 2

概率论与数理统计数学期望与方差专项PPT课件

概率论与数理统计数学期望与方差专项PPT课件

9
第9页/共66页
定理：设Y是随机变量X的函数：Y g(X )g是连续函数,
X 是离散型随机变量，它的分布律为：
P( X xk ) pk , k 1, 2,
若 g(xk )pk绝对收敛，则有E(Y ) E[g( X )] g(度为f (x)
服
从
同
一
指
数
分
布，
其
概
率密
度
为
： f (x)
1
e
x
x0
0
若将这2个电子装置串联联接
0
x0
组成整机，求整机寿命N(以小时计)的数学期望。 是
解 ：X k
(k
1,
2)
的分布函数F ( x)
1
e
x
x0
0
x0
串联情况下，N min X1, X2 ,故N的分布函数为：
指 数 分 布 的
密
Fmin (x)
dx
1
x
1 x
2
3 x4
y3
dy
1
3 2x4
[
1 2y2
] |x1
x
dx
3 4
(
1
1 x6
1 x2
)dx
3 4
(
1 5
1)
3 5
考虑：先求E(Y )
yfY
(
y)dy，这里
你算对了吗？哪个更容易呢? 第14页/共66页
fY
(
y)
1 y
y
3 2x3 y2
3 2x3 y2
dx dx
0
2
2
2
sin (0 1) 0.25 sin (11) 0.2 sin (0 2) 0.15

《数学数学期望》课件

《数学数学期望》课件
《数学数学期望》ppt课 件
CATALOGUE
目 录
• 数学期望的基本概念 • 数学期望的性质与定理 • 数学期望的应用 • 特殊随机变量的数学期望 • 数学期望的扩展与展望
01
CATALOGUE
数学期望的基本概念
定义与性质
定义
数学期望是随机试验在大量重复 下出现的频率的稳定值。
性质
数学期望具有可加性、可数性、 线性性质等。
分位数与分位数函数
分位数
分位数是概率论中的一个概念，用于描述数据分布的位置特征。常见的分位数包括中位 数、四分位数等。分位数的计算和应用对于统计分析、数据挖掘等领域具有重要意义。
分位数函数
分位数函数是描述分位数与概率之间关系的函数。通过分位数函数，可以更方便地理解 和应用分位数的概念，从而更好地分析数据的分布特征。
通过计算投资组合的数学期望， 投资者可以了解投资组合的预期
收益，并据此做出投资决策。
数学期望在金融学中还用于资产 定价、风险管理、资本预算和股
票期权定价等领域。
在决策理论中的应用
在决策理论中，数学期望被用来评估 不同决策方案的预期结果。
数学期望在决策理论中还用于风险决 策、不确定性决策和多目标决策等领 域，以帮助我们做出更加科学和合理 的决策。
大数定律与中心极限定理
大数定律
当试验次数趋于无穷时，随机事件的频率趋于该事件 发生的概率。即 limn→∞P(|En−E)/n→0P(|En−E)/n→0limn→∞P(|En −E)/n→0=1。
中心极限定理
无论随机变量X1,X2,…,XnnX_1, X_2, ldots, X_{nn}Xi1,Xi2,…,Xinn的分布如何，当它们的数量趋于 无穷时，它们的平均值的分布趋于正态分布。即 limn→∞P(|En−μ)/σ≤z)=1−12z2lim_{n to infty} P(|En−μ)/σ≤z|)=1−12z2limn→∞P(|En−μ)/σ≤z|)=1 −12z2，其中En=1n∑i=1nXiEn = frac{1}{n} sum_{i=1}^{n} X_iEn=n1∑i=1nXi，μ是随机变量的均 值，σ是标准差，z是正态分布的分位数。

4 第 一节 数学期望精品PPT课件

4 第 一节 数学期望精品PPT课件

它的数学期望不存在
例3
按规定,某车站每天8 : 00 ~ 9 : 00 , 9 : 00 ~
10 : 00都恰有一辆客车到站 , 但到站的时刻是随机
的, 且两者到站的时间相互 独立 ,其规律为
8 : 10
到站时刻 9 : 10
8 : 30 9 : 30
8 : 50 9 : 50
概率 1
3
2
6
6
6
(1) 一旅客8：00到车站,求他候车时间的数学期 望
在这些数字特征中，最常用的是 期望、方差和协方差
第四章 随机变量的数字特征
数学期望 方差 协方差与相关系数
数学期望的引例
例如：某7人的高数成绩为90，85，85，80，80，
75，60，则他们的平均成绩为
90 85 2 80 2 75 60
7
90 1 85 2 80 2 75 1 60 1
例5 已知 X 服从0,2 上的均匀分布，求
Y sin X 的数学期望。
解
EY
E sin
X
sin
x
f
x
dx
因为
f
x
1
2
,
0 x 2；
0,
其它。
所以 E sin X 2 1 sin xdx 0
0 2
例6 设相互独立的随机变量X，Y的密度函数分别为
2x, (0 x 1) f1(x) 0, 其它
如何计算随机变量函数的数学期望? 一种方法是，因为g(X)也是随机变量，
故应有概率分布，它的分布可以由已知的X 的分布求出来. 一旦我们知道了g(X)的分布， 就可以按照期望的定义把E[g(X)]计算出来.
使用这种方法必须先求出随机变量函数 g(X)的分布，一般是比较复杂的 .

14讲数学期望48页PPT

14讲数学期望48页PPT

24.12.2019
24
当X为连续型的随机变量时, 用前面的 办法，假设进行了n次试验, 取值xk的有 nk个, 则从对g(X)进行试验的观点看即取 值为g(xk)的有nk个, 则
E[g(X)]k-g(xk)nnk

g(xk)f
k-
(xk)dx

d x 0 g(x)f(x)dx
解: 产品产值X是一个随机变量, 其分布如下表:
X 6 5.4 5 4 0
P 0.7 0.1 0.1 0.06 0.04
因此,
E(X)=60.7+5.40.1+50.1+40.06+00.04
=5.48(元)
24.12.2019
14
连续型随机变量
24.12.2019
15
假设连续型的随机变量X的概率
绝对收敛, 则称这级数为X的数学
期望, 简称期望或均值, 记为E(X),
即

E(X) xk pk
k1
24.12.2019
9
例1 若X服从0-1分布, 其概率函数
为P{X=k}=pk(1-p)1-k (k=0,1), 求
E(X)。
解 E(X)=0(1-p)+1p=p
“平均” 的含义
1-p
密度为f(x),
P{xk≤X≤xk+1}近 似P{X=xk}
f(xk)dx
...
...
dx
xk-2 xk-1 xk xk+1 xk+2
24.12.2019
17
在这种情况下我们计算X的数学期
望, 可得

E ( X ) x k f ( x k )d x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ERn n ．
这个结果是正确的，现在给出一个归纳性证明．
由 于 显 然 有 ER1 1 ， 假 定 对 于 k 1, , n 1 ， 有 ERk k ．
24
为了计算 ERn ，我们先对第一轮中的匹配
数 Yn 取条件．它给出
ERn EERn Yn
n
PYn
i
ERn
Yn
i．
i0
25
现在，给定最初一轮的全部匹配数 i ，需 要的轮数将等于1加上余下的 ni 个人 匹配他们的帽子需要的匹配轮数．
5
解：
以 N 记事故次数，以 X i 记在第 i 次事故中的受伤人
数 ， i 1, 2, ， 那 么 伤 者 总 数 可 以 表 示 为
N
X i ．现在
i 1
E
N i 1
Xi
E
E
N i 1
Xi
N
．
6
但是
N
n
E i1 Xi N n E i1 Xi N n
n
E Xi i1
记 X 表示该读者遇到的印刷错误
数．令
1 Y 2
如果读者选取数学书 ， 如果读者选取历史书
3
则由全期望公式，得
EX EEX Y PY 1EX Y 1 PY 2EX Y 2
12 15 7 ． 222
4
例 2（随机变量的随机数量和的期望） 假定一工 厂设备每周出现事故次数的期望为 4．又假定在每次 事故中受伤工人数是具有相同均值 2 的独立随机变 量．再假定在每次事故中受伤工人数与每周发生的 事故数目相互独立．每周受伤人数的期望是多少？
条件数学期望例题
1
例 1 某人准备读一章数学书或者一章历史 书．如果他在读一章数学书中印刷错误数是服从 均值为 2 的 Poisson 分布，而他在读一章历史 书中的印刷错误数是服从均值为 5 的 Poisson 分布．假设该读者选取哪一本书是等可能时，求 该读者遇到的印刷错误数的期望是多少？
2
解：
EX 10 ．
18
例 5 在一次聚会上，N 个人将自己戴的 帽子扔到屋子中央．将这些帽子充分混合 后，每人随机选取一顶．求取到自己的帽子 的人数的期望数．
19
解：
以 X 记取到自己的帽子的人数．再设
1 Xi 0
第 i 个人取到自己的帽子， 其它情形
i
1,
2,
,
N ，
N
则有 X X i ． i 1
26
所以，
n
ERn PYn i 1 ERn i i0 n 1 ERn PYn 0 PYn i ERni i 1 n 1 ERn PYn 0 n iPYn i （由归纳假设） i 1 1 ERn PYn 0 n1 PYn 0 EYn ERn PYn 0 n1 PYn 0 27
22
例 6（匹配轮数问题） 假设在上面的例题中， 取到自己的帽子的人离开，而其余人（没有匹配 到的那些人）将他们取的帽子放到房间中央，混 杂后重新取．假定这个过程连续进行到每个人都 取到自己的帽子为止．假定 Rn 是开始时有 n 个人
出席的轮数．求 ERn ．
23
解： ⑴ 由上例推出，不论留在那里的人有多少，平均每轮有一 次匹配．这就使人想到
果矿工选取第 2 个门，那么 3 小时后他将回到他的矿井．但是，一旦他回到
矿井，问题就和以前一样了，而直到他到达安全地的附加时间的期望正是
EX ．因此，
EX Y 2 3 EX ．
在方程（3.7）中其它等式后面的推理是相似的．
17
因此，
EX 1 2 3 EX 5 EX ，
3 解方程，得
定相继的抛掷是独立的，这就推出在第一次出现反面直到正面首次
出现时的附加抛掷次数的期望是 EN ．
13
因此，
EN Y 11．
将式（3.6）代入方程（3.5），推出
EN p 1 p1 EN ，
解方程，得
EN 1 ．
p
14
例 4 某矿工身陷有三个门的矿井之中．经第 1 个门的通道行进 2 小时后，他将到达安全地；经第 2 个门的通道前进 3 小时后，他将回到矿井原地； 经第 3 个门的通道前进 5 小时后，他又将回到矿井 原地．假定这个矿工每次都等可能地任意一个门， 问直到他到达安全地所需时间的期望是多少？
（由 N 与 X i 相互独立）
nEX1， （由随机变量序列Xi独立同分布）
7
由它导出
E N Xi N N EX1
i1
因此，
E
N i 1
Xi
E E
N i 1
Xi
N
EN EX1
EN EX1．
8
所以，在上面的例子中，在一周中受伤人
数的期望值为
E
N
X
i
EN
E
X1
4
2
8
．
i1
9
例 3（几何分布的期望） 连续抛 掷一枚出现正面的概率为 p 的硬币直 至出现正面为止．问需要抛掷的次数的 期望多少？
10
解：
以 N 记需要抛掷的次数，而令
1 Y 0
如果第一次抛掷的结果是正面 ． 如果第一次抛掷的结果是反面
11
现在
EN EEN Y
PY 1 EN Y 1 PY 0 EN Y 0
15
解： 令 X 记矿工到达安全地所需的时间，以Y 记他 最初选取的门．现在
EX EEX Y ຫໍສະໝຸດ 3P Yi
EX
Y
i
i 1
3 1 E X Y i ， i1 3 16
然而
EX Y 1 2 ， EX Y 2 3 EX ， EX Y 3 5 EX ． （3.7） 为了理解为什么这是正确的，我们以 EX Y 2为例，给出其如下推理．如
20
现在，因为第 i 个人等可能地在 N 个帽子中取一个，
这就推出
PXi
1
P第 i
个人取到自己的帽子
1 N
，
随之，
EXi 1 PXi 1 0 PXi 0 1 ， i 1, 2, , N ．
N
21
将上式代入上面的方程，得
EX
E
N
X
i
i1
N
EXi i 1
N
1
i1 N
1．
因此，无论聚会上有多少人，平均总有一人取到自己的帽子．
其中最后一个等式用了上例中建立的结果
EYn 1．由前面的方程推出 ERn n ．
28
p EN Y 1 1 p EN Y 0．
（3.5）
12
然而
EN Y 11， EN Y 01 EN．
（3.6）
为了明白为什么式（3.6）是正确的，我们考察 EN Y 1，由于Y 1，
我们知道第一次抛掷结果是正面，所以，需要抛掷的次数的期望是
1．另一方面，如果Y 0 ，第一次抛掷结果是反面．然而，由于假