11条件数学期望(北大)

数学期望与方差的计算引言数学期望与方差是统计学中两个重要的概念。

它们是描述一个随机变量分布特征的常用指标，对于理解和分析数据具有重要意义。

本文将介绍数学期望与方差的概念、计算方法以及它们的应用。

数学期望数学期望又称平均值，是描述一个随机变量的平均水平的指标。

对于离散型随机变量，数学期望的计算公式为：$$ E(X)=\\sum_{i=1}^n x_i p_i $$其中，X为随机变量，x i为随机变量可能取的值，p i为随机变量取每个值的概率。

对于连续型随机变量，数学期望的计算公式为：$$ E(X)=\\int_{-\\infty}^{+\\infty} x f(x) dx $$其中，f(x)为随机变量的概率密度函数。

数学期望可以理解为在大量重复实验中，随机变量平均取值的水平。

方差方差是描述一个随机变量分散程度的统计指标。

方差越大，随机变量的取值越分散；方差越小，随机变量的取值越集中。

方差的计算公式为：Var(X)=E[(X−E(X))2]方差可以理解为每个随机变量与其期望的偏差的平方的加权平均。

数学期望与方差的计算方法离散型随机变量对于离散型随机变量，计算数学期望的方法如下：1.计算每个随机变量取值对应的概率。

2.将随机变量取值与对应的概率相乘。

3.将所有结果相加，得到数学期望。

计算方差可以使用以下方法：1.计算数学期望。

2.将每个随机变量取值与数学期望的差值的平方相乘。

3.将所有结果相加，得到方差。

连续型随机变量对于连续型随机变量，计算数学期望的方法如下：1.计算随机变量的概率密度函数。

2.将随机变量的取值与概率密度函数相乘。

3.对结果进行积分，得到数学期望。

计算方差可以使用以下方法：1.计算数学期望。

2.将随机变量的取值与数学期望的差值的平方与概率密度函数相乘。

3.对结果进行积分，得到方差。

数学期望与方差的应用数学期望与方差作为描述随机变量特征的指标，在统计学和概率论中有重要的应用。

数学期望在实际问题中可以用于计算平均值，如统计学中的样本均值就是数学期望的一种估计。

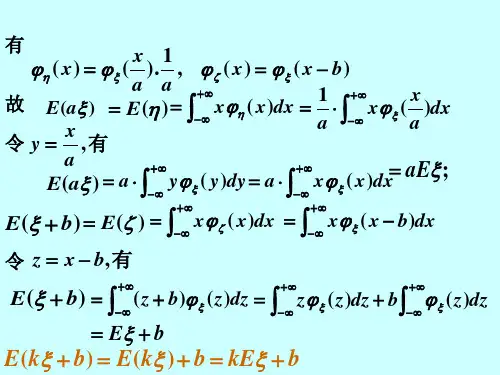
【关键字】素材充分条件与必要条件教材点拨一、充分条件命题的条件和结论是构成命题的两个部分，并且条件和结论可以互相转化。

当一个命题为假命题时，可以说条件不能推出结论；而当命题为真命题时，可以说由此条件能推出结论。

所以一个命题从条件和结论的角度看，条件与结论有着一定的关系，即：由条件能否推出结论？如果由命题的条件能推出结论，那么命题就是真命题，此时条件就叫结论的充分条件。

物理模型的直观解释：如图电路图，当开关A紧闭时，灯泡B亮，而当灯泡B亮时，开关A却不一定是紧闭的；即要使灯泡B亮，只要开关A紧闭着一个条件就够了，我们就称“开关A紧闭”是“灯泡B亮”的充分条件。

一般地，“若，则”是一个真命题，是指由通过推理可以得出，即由可推出，记作，那么，就称条件是结论的充分条件（sufficient condition）。

“若，则”是一个真命题，是指由通过推理可以得出，即由可推出，记作，那么，就称是的充分条件（sufficient condition）。

例如：①，那么，“”是“”成立的充分条件；②，那么，“”是“”成立的充分条件；③三边对应相等的两个三角形全等：“三边对应相等”是“两个三角形全等”的充分条件；④“”是函数为幂函数的充分条件；警示：充分条件就是某一个结论成立应该具备的条件，当命题具备此条件时，就可以得出此结论，或者要是此结论成立，只要具备此条件就够了，而当命题不具备此条件时，结论也有可能成立。

例如，当时，成立，但是，当时，也可以成立，即时，也成立，所以，是成立的充分条件，也是成立的充分条件。

【例】仿照示例改写下列命题，并判断条件是否为充分条件：示例：若，则，可以改写成：；是充分条件；（1）个位数字是0的自然数能被5整除；（2）对角线相等的四边形是矩形；（3）与同一平面所成的角相等的两条直线平行；（4）若定义域为的函数为奇函数，则解：（1）个位数字是0的自然数这个自然数能被5整除；是充分条件；（2）四边形的对角线相等这个四边形是矩形；不是充分条件；（3）两条直线与同一平面所成的角相等这两条直线平行；不是充分条件；（4）定义域为的函数为奇函数；是充分条件。

条件数学期望及其应用The ways of finding the inverse matrix and it ’s applicationAbstract ：The passage lists the ways of calculating the first type of curvilinear integral,and discusses it ’s application in geometry and in physical.Keywords ：Curvilinear integral;Continuous;Integrable; Lateral area.0前言在曲线积分中，被积函数可以是标量函数或向量函数.积分的值是路径各点上的函数值乘上相应的权重（一般是弧长，在积分函数是向量函数时，一般是函数值与曲线微元向量的标量积）后的黎曼和.带有权重是曲线积分与一般区间上的积分的主要不同点.物理学中的许多公式在推广之后都是以曲线积分的形式出现.曲线积分是物理学中重要的工具.1条件数学期望1.1条件数学期望的定义定义1 设X 是一个离散型随机变量，取值为},,{21 x x ，分布列为},,{21 p p .又事件A 有0)(>A P ，这时为在事件A 发生条件下X 的条件分布列.如果有 则称A i ii p x A X E |]|[∑=．为随机变量X 在条件A 下的条件数学期望（简称条件期望）．定义2 设X 是一个连续型随机变量，事件A 有0)(>A P ，且X 在条件A 之下的条件分布密度函数为)|(A x f ．若⎰∞∞-∞<dx A X xf )|(称为随机变量X 在条件A 下的条件数学期望．定义3 设),(Y X 是离散型二维随机变量，其取值全体为 },2,1,),,{( =j i y x i i ， 联合分布列为,2,1,),,(====j i y Y x X P p i i ij ，在i y Y =的条件下X 的条件分布列为 ,2,1),|(|====i y Y x X P p i i j i 若 ∞<∑j i iip x|，则为随机变量X 在i y Y =条件下的条件数学期望．定义 4 设),(Y X 是连续型二维随机变量，随机变量X 在y Y =的条件下的条件密度函数为)|(|y x p Y X ，若∞<⎰∞∞-dx y x p x Y X )|(|，则称为随机变量X 在}{y Y =条件下的条件数学期望． 1.2条件数学期望的性质定理1 条件期望具有下面的性质：（1） )|()|()|(G bE G aE G b a E ηξηξ+=+， 其中R b a ∈,，且假定)|(G b a E ηξ+存在；（2） )()]|([ξξE G E E =；（3） 如果ξ为G 可测，则ξξ=)|(G E ； （4） 如果ξ与σ代数G 独立，则ξξE G E =)|(;（5） 如果1G 是σ代数G 的子σ代数，则)|(]|))|([(11G E G G E E ξξ=； （6） )(不等式Jensen 如果f 是R 上的下凸函数，则)|)(())|((G f E G E f ξξ=；定理2 条件期望的极限定理：（1）单调收敛定理：若s a n ..ξξ↑，则在})|({-∞>G E ξ上，则)|(lim )|(G E G E n n ξξ∞→=．（2）Fatou 引理：若s a Y n .,≤ξ，则在})|({-∞>G E ξ上，则)|(sup lim )|sup (lim G E G E n n ξξ=．（3） 控制收敛定理：若Y s a Y n ,.,≤ξ可积，且P s a n 或.,ξξ→，则0)|(lim =-∞→G E n n ξξ．1.3条件数学期望的求法在现代概率论体系中，条件期望的概念只是一种理论上的工具，在其定义中没有包含算法，所以求条件期望概率往往很难，需要技巧．本文对两种不同情形下的条件期望的求法做出讨论．方法一：利用问题本身所具有的某种对称性求解．例1设n ξξξ,,,21 时独立同分布随机变量．∞<ξE ，记∑==nk k S 1ξ，求n k S E k ,,2,1,|( =ξ．解 易证j i S E S E j i ≠=),|()|(ξξ．则 即方法二：利用线性变换将随机变量分解为关于作为条件的σ域可测或独立的随机变量之和，利用条件期望的性质求和．例 2 设有正态样本n X X ,,1 ),0(2σN ，统计量∑==ni k X T 1，求)|(2T X E k ．解 令∑==nk k X S 12，则)|(1)|(2T S E n T X E k =．作正交变换：⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n X X X C Y Y Y Y 2121，其中C 为正交阵，第一行为)1,,1(nn ，则有n TI CC Y X Cov EY ===),(,0，即∑=nk k Y T 22与独立，k Yn k N ,,2),,0(2=σ，从而∑∑∑===+===nk k nk knk kY n T Y X S 2221212，2T 关于)(T σ可测，所以 由以上例题可以看出，条件期望的求法是一个复杂的问题，我们必须从问题本身出发化简，将其转化为可测或独立于σ代数的随机变量，然后运用条件期望的性质求解． 1.4全期望公式设事件n B B B ,,,21 是一完备事件组，即n B B B ,,,21 互不相交，n k B P k ≤≤>1,0)(，且Ω=⋃=k nk B 1，由全概率公式有这时若∞<X E ,则有如同全概率公式一样，上式可称为全期望公式．若n B B B ,,,21 是一个完备事件组，则也有全期望公式 （注意，X 的密度有公式))()|()(1k nk k B P B x f x f ∑==．2条件数学期望的应用2.1条件数学期望在实际问题中的应用条件数学期望在概率论与数理统计中有重要的作用，在实际问题中也有大量应用．例如人们常说体育要从娃娃抓起．某少体校要在小学中选拔一批小学生进行重点培养，为我国篮球，排球运动准备后备力量．对一个运动员来说，他（她）的身高显然是一个非常重要的因素．于是问题产生了，在一大群各项素质（包括目前的身高）都差不多的七八岁的小朋友中，用什么办法来选拔一批将来（十年以后）身材会比较高的幼苗进行重点培养呢？科学工作者发现了小孩的足长与他（她）长大后的身高之间有密切的关系．我国的体育科研人员对16个省市的几万名青少年儿童进行了观测，建立了下述预测公式：成年身高=⨯k （少儿当年足长） （单位：cm ）其中系数k 对不同性别，不同年龄组的儿童有不同的数值，其具体数值如下表：你大概很想知道上述预测公式是如何建立的？理论依据是什么？其实这正是现在所讨论的条件数学期望，对n （n 取定）岁的少年儿童来说，成年后的身高为X ，当年足长为Y 则),(Y X 是一个二维随机变量．一般认为他们的联合分布是正态分布．如果我们已知Y 的值，可以近似地以Y 的条件下X 的条件数学期望来估计X 的值，即用]|[Y X E 作X 的预测值．这时]|[Y X E 是Y 的线性函数，这就是成年身高的预测公式．例3 一全自动流水线正常生产时，产品中的一等品率为1p ，二等品率为2p ，等外品（即次品）率为3p ，1321=++p p p ．为保证产品质量，厂方规定当生产出一件等外品时，该流水线即停工检修一次．已知首次检修之前共生产了n 件产品，求n 件产品中一等品件数的数学期望．解 设X 表示前n 件产品中一等品的件数，令}{件产品首次出现等外品第n A =．据题意是要求]|[A X E ．因为在条件A 下，前1-n 件产品中没有等外品，这时1-n 件产品中的一等品率是211p p p +，而二等品率是212p p p +，因此这是参数为),1(211p p p n +-的二项分布．即2111|)1(]|[p p p n kp A X E n k A k +-==∑-=．实际上我们认为在条件A 下，前1-n 次试验是1-n 重贝努里试验，试验成功（取到一等品）的概率是211/p p p +．从直观意义看这是明显的，这也正是直接讨论条件分布的简捷之处． 2.2全期望公式的应用例4 在贝努里试验中，每次试验成功的概率为p ，试验进行到出现首次成功时停止．求平均需试验多少次？解 设X 为首次成功需做试验的次数，问题是求EX ．定义 由全期望公式)0(]0|[)1(]1|[==+===Y P Y X E Y P Y X E EX ，已知p Y P p Y P -====1)0(,)1(，在1=Y ，即首次试验成功的条件下，自然有1=X ，因此1]1|[==Y X E ．在0=Y 即首次首次实验失败的条件下，从第二次实验开始可以看作重新开始，因此，EX Y X E +==1]0|[．第一项的1是已经试验了一次，以后的情况与从头开始一样．所以 )1)(1(EX p p EX +-+=， pEX 1=． 原来求数学期望需要知道分布，但在上例的做法中可以不必知道分布，充分利用了随机变量的特性，并借助全期望公式，简化了计算，这是真正有概率特点的做法．例5 设电力公司每月可以供应某电厂的电力服从]30,10[（单位：万度）上的均匀分布，而该工厂每月实际生产所需要的电力服从]20,10[上的均匀分布．如果工厂能从电力公司得到足够的电力，则每一万度电可以创造30万元利润，若工厂从电力公司得不到足够的电力，则不足部分由工厂通过其他途径自行解决，每一万度电只有10万元利润．问该厂每月的平均利润为多大？解 设电力公司每月供应电厂的电力为X （万度），工厂每月实际需要的电力为Y （万度），工厂每月的利润为T （万元）．由题设条件知 于是当3020≤≤x 时，有 由式所以该工厂平均每月的利润为433万元． 2.3预测与回归对于二维随机变量),(Y X ，如果已知其中一个随机变量Y 的值，要根据这一信息对另一个随机变量X 的取值作出预测，这样的问题在人们的实践中可以说是比比皆是，常称它们为“预测问题”．前面我们提议用]|[Y X E 作为X 的预测值，这样做的依据是什么呢？一般地，我们可以选取Y 的一个函数)(Y g 作为X 的预测值．这时预测的误差是)(Y g X -，由于绝对值运算在数学上处理不方便，我们用2)]([Y g X -代替它．自然应该使误差尽可能地小，但2)]([Y g X -是一个随机变量，因此很自然的要求它的平均值2)]([Y g X E -尽可能地小．这样的准则就称为均方误差最小准则．假设),(Y X 为连续型二维随机变量，密度函数为),(y x f ，则对每个y ，当]|[)(y Y X E y g ==时，能使dx y x f y g x Y X )|()]([|2⎰∞∞--达到最小．因此取]|[)(Y X E Y g =时，2)]([Y g X E -达到最小，这就证明了，按照均方误差最小准则，]|[Y X E 是X 的最佳预测．这就是选取条件数学期望作X 的预测值的理论依据．对离散型情形也可用相同的方法论证上述结论．函数]|[)(Y X E Y g =称为X 关于Y 的回归函数．一般情况下，求)(y g 是比较困难的．因此，把预测问题简化，选取Y 的线性函数b aY +作为X 的预测值．同样采用均方误差最小准则，选取常数b a ,使得取最小值．我们早已知道，若a 固定，时，2][b aY X E --取最小值][aY X D -.我们只需求a ，使DX Y X a DY a aY X D +-=-),cov(2)(2 达到最小值，即a 应取为DYY X a ),cov(=， 我们称为X 关于Y 的回归直线．参考文献:[1] 中山大学数学系.概率论与数理统计[M].高等教育出版社.2002. [2] 周概容.概率论与数理统计[M].高等教育出版社.1984.[3] 茆试松.程依明.濮晓龙.概率论与数理统计教程[M].高等教育出版社.2004. [4] 孙荣恒.应用概率论[M].科学出版社.2001.[5] 何声武.概率论与数理统计[M].经济科学出版社.1992.。