叠加定理的验证

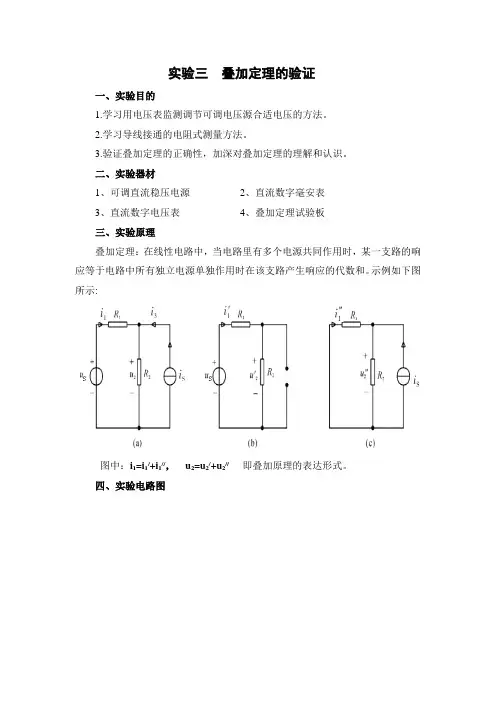
实验三叠加定理的验证一、实验目的1.学习用电压表监测调节可调电压源合适电压的方法。

2.学习导线接通的电阻式测量方法。

3.验证叠加定理的正确性，加深对叠加定理的理解和认识。

二、实验器材1、可调直流稳压电源2、直流数字毫安表3、直流数字电压表4、叠加定理试验板三、实验原理叠加定理：在线性电路中，当电路里有多个电源共同作用时，某一支路的响应等于电路中所有独立电源单独作用时在该支路产生响应的代数和。

示例如下图所示:图中：i1=i1/+i1//，u2=u2/+u2// 即叠加原理的表达形式。

四、实验电路图图3-1验证基尔霍夫定律和叠加定理的原理图五、实验过程实验准备：将可调电源中的两路“0～30V可调输出”直流可调稳压电源的输出调至最小（调节旋钮轻轻逆时针旋到底），并将恒流源的输出粗调旋钮拨到200mA档，输出细调旋钮调至最小。

将试验台最下方的电源挂箱的总控开关向上合上。

将电源转接箱和其下方的“AC220V输出”通过所带的插头连接线连接电源插孔，并将电源转接箱电源插孔通过红、蓝粗线和可调电源及测量仪表一的电源插孔相连（L与L用红线连接，N与N用蓝线连接）。

验证叠加定理的操作过程实验步骤：(1) 将测量仪表一中的直流电压表并接在可调电源两端，打开电源开关，分别调节两路可调电源的输出旋钮，用直流电压表监测使两路可调电源的输出分别为E1=6V、E2=12V，然后断开电源开关。

(2)从电路基础试验箱（一）中找到“基尔霍夫定理/叠加原理”图，并将图中的开关K1、K2向内置于短路位置。

(3)再按照实验原理图3-1用导线将已调节好输出电压值的两路直流稳压源E1、E2分别引到原理图中的U1、U2口。

(4)将电流插头插入实验电路板中三条支路电流的I3测量插孔中，（插孔中未插入电流插头时插孔两边的导线连通，插入电流插头后两边导线只能通过电流插头的两根出线连通。

）把数字多用表档位选择开关转到“蜂鸣”档位（在200ΩA”插孔中，黑表笔插入和二极管符号中间），并将多用表的红表笔插入““COM”插孔中。

叠加定理的验证实验报告叠加定理是物理学中非常重要的一个定理，它可以用来计算复杂系统的总体性质。

在本次实验中，我们将通过验证叠加定理来探究其应用。

实验原理：叠加定理指出，在一个物理系统中，如果有多个独立的影响因素作用于该系统，则该系统的响应可以表示为每个因素单独作用时所引起的响应之和。

这意味着，如果我们知道每个因素单独作用时所引起的响应，就可以计算出整个系统的响应。

这个原理在电路分析、声学、光学等领域都有广泛应用。

实验步骤：1. 准备材料：一个小球、一面平板、一支弹簧、一个振动器。

2. 实验一：小球在平板上滑行将小球放在平板上，并给予它一个初速度。

记录下小球滑行到不同位置时所需时间，并计算出此时小球的速度。

3. 实验二：弹簧振动将弹簧固定在桌子上，并给予它一个初速度。

记录下弹簧振动到不同位置时所需时间，并计算出此时弹簧的速度。

4. 实验三：振动器将振动器放在桌子上，并给予它一个初速度。

记录下振动器振动到不同位置时所需时间，并计算出此时振动器的速度。

5. 实验四：叠加定理验证将小球、弹簧和振动器放在同一平面上，并让它们同时开始运动。

记录下这三个物体在不同位置时所需时间，并计算出此时它们的速度之和。

与实验一、二、三的结果进行比较，验证叠加定理是否成立。

实验结果：1. 实验一：小球在平板上滑行小球滑行到不同位置所需时间如下表所示：位置（cm）时间（s）速度（cm/s）10 1.2 8.3320 2.3 8.7030 3.5 8.5740 4.6 8.702. 实验二：弹簧振动弹簧振动到不同位置所需时间如下表所示：位置（cm）时间（s）速度（cm/s）10 0.6 16.6720 1.1 18.1830 1.7 17.6540 2.3 17.393. 实验三：振动器振动器振动到不同位置所需时间如下表所示：位置（cm）时间（s）速度（cm/s）10 0.5 20.0020 1.0 20.0030 1.5 20.0040 2.0 20.004. 实验四：叠加定理验证小球、弹簧和振动器在同一平面上运动时，它们的速度之和如下表所示：位置（cm）总速度（cm/s）10 45.0020 46.8830 46.2240 46.09结论：通过实验结果可以看出，当小球、弹簧和振动器同时运动时，它们的速度之和等于每个物体单独运动时的速度之和。

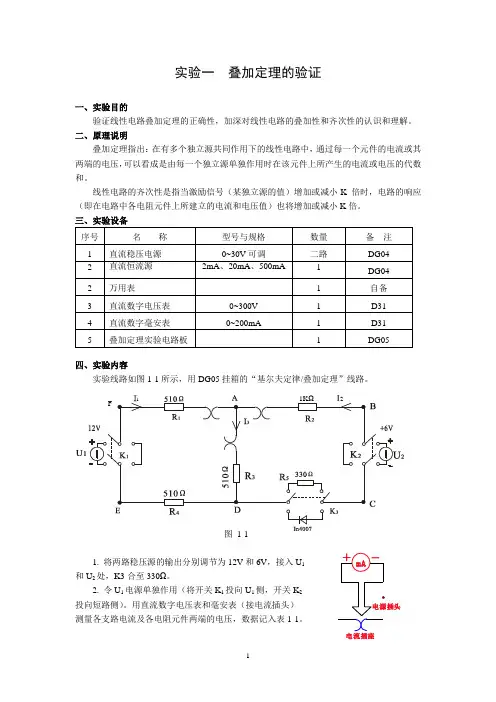
实验一 叠加定理的验证一、实验目的验证线性电路叠加定理的正确性，加深对线性电路的叠加性和齐次性的认识和理解。

二、原理说明叠加定理指出：在有多个独立源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，可以看成是由每一个独立源单独作用时在该元件上所产生的电流或电压的代数和。

线性电路的齐次性是指当激励信号（某独立源的值）增加或减小K 倍时，电路的响应（即在电路中各电阻元件上所建立的电流和电压值）也将增加或减小K 倍。

四、实验内容实验线路如图1-1所示，用DG05挂箱的“基尔夫定律/叠加定理”线路。

图 1-11. 将两路稳压源的输出分别调节为12V 和6V ，接入U 1和U 2处，K3合至330Ω。

2. 令U 1电源单独作用（将开关K 1投向U 1侧，开关K 2投向短路侧）。

用直流数字电压表和毫安表（接电流插头） 测量各支路电流及各电阻元件两端的电压，数据记入表1-1。

电流插座3. 令U2电源单独作用（将开关K1投向短路侧，开关K2投向U2侧），重复实验步骤2的测量和记录，数据记入表1-1。

4. 令U1和U2共同作用（开关K1和K2分别投向U1和U2侧），重复上述的测量和记录，数据记入表1-1。

5. 将R5（330Ω）换成二极管1N4007（即将开关K3投向二极管IN4007侧），重复1～4的测量过程，数据记入表1-2。

表1-2五、实验注意事项1. 用电流插头测量各支路电流时，或者用电压表测量电压降时，应注意仪表的极性，正确判断测得值的＋、－号后，记入数据表格。

2. 注意仪表量程的及时更换。

六、预习思考题1. 在叠加定理实验中，要令U1、U2分别单独作用，应如何操作？可否直接将不作用的电源（U1或U2）短接置零？2. 实验电路中，若有一个电阻器改为二极管，试问叠加定理的迭加性还成立吗？为什么？七、实验报告1. 根据实验数据表格，进行分析、比较，归纳、总结实验结论，即验证线性电路的叠加性。

2. 各电阻器所消耗的功率能否用叠加定理计算得出？试用上述实验数据，进行计算并作结论。

叠加定理的验证叠加定理是数学中常用的方法之一，它在各个领域中都具有广泛的应用。

本文将从几个实际问题入手，通过验证叠加定理来说明其在解决问题中的作用。

一、电路问题电路问题是叠加定理应用最广泛的领域之一。

在电路中，我们经常需要计算电流和电压的分布情况。

而叠加定理可以简化我们的计算过程。

以一个简单的电路为例，如果有多个电源供电，叠加定理告诉我们可以将每个电源的贡献单独计算，然后将结果叠加起来。

这样便可以得到整个电路的电流和电压分布情况。

为了验证叠加定理在电路问题中的应用，我们可以选取一个具体的电路，并利用计算工具进行计算。

首先，我们计算每个电源独立供电时的电流和电压，然后将其叠加起来。

最后，与直接求解整个电路的电流和电压进行比较，如果结果一致，那么就验证了叠加定理在该电路问题中的有效性。

二、力学问题力学问题是另一个可以验证叠加定理的领域。

在力学中，我们常常需要求解物体在各个方向上受力情况。

而叠加定理可以帮助我们将复杂的力分解为简单的分力进行计算。

例如，当一个物体受到多个力的作用时，叠加定理告诉我们可以将每个力的贡献分别计算，然后将其叠加起来。

这样便可以得到整个物体在各个方向上受力的情况。

为了验证叠加定理在力学问题中的应用，我们可以选取一个具体的力学系统，并进行实验。

首先，我们测量每个力的作用效果，然后将其叠加起来。

最后，与直接求解整个物体在各个方向上受力的情况进行比较，如果结果一致，那么就验证了叠加定理在该力学问题中的有效性。

三、声学问题声学问题也是叠加定理的一个重要应用领域。

在声学中，我们常常需要计算声波传播、声场分布等问题。

而叠加定理可以帮助我们简化这些计算过程。

以声波传播为例，当一个区域内存在多个声源时，叠加定理告诉我们可以将每个声源的贡献单独计算，然后将结果叠加起来。

这样便可以得到整个区域内的声波传播情况。

为了验证叠加定理在声学问题中的应用，我们可以选取一个具体的声学系统，并进行实验。

首先，我们测量每个声源单独发出的声波情况，然后将其叠加起来。

1实验一__叠加原理的验证实验一叠加定理的验证一、实验目的1．验证叠加定理。

2．加深对电路的电流、电压参考方向的理解。

3．学习通用电工学实验XX的使用方法。

4．学习万用表、电压表、电流表的使用方法。

二、实验仪器及元件1．通用电学实验XX1XX2．数字万用表UT61 1块3．电阻100Ω1支220Ω1支330Ω1支三、实验电路叠加原理指出：在有几个独立电源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，可以看成是由每一个独立电源单独作用时在该元件上所产生的电流或电压的代数和。

具体方法是：一个电源单独作用时，其他的电源必须置为零（电压源短路，电流源开路）；在求电流或电压的代数和时，当电源单独作用时电流或电压的参考方向与共同作用时的参考方向一致时，符号取正，否则取负。

叠加原理反映了线性电路的叠加性，叠加性只适用于求解线性电路中的电流、电压。

对于非线性电路，叠加性不再适用。

在本实验中，用直流稳压电源来近似模拟理想电压源，由其产生的误差可忽略不计，这是因为直流稳压电源的等效内阻很小。

+ U -+U2-图1—1 验证叠加定理电路四、实验方法1．首先粗调好直流稳压电源，使其两路输出U1、U2均在10V以下，最大不得超过14V。

2．按照实验电路图1—1接线，经过老师检查无误后，方可开始实验。

3．测量U1、U2两个电源共同作用下的电路响应：●将电路中ef、gh、jk三处分别用短接线短接；●用万用表测量电源U1、U2的准确电压值；1●用万用表测量k、m两点之间的电压值，即R3支路的电压响应U km；●断开ef间的短接线，在ef之间接入直流电流表测量R1支路的电流响应I1；●同样方法，再次测量R2、R3支路的电流响应I2和I3；●将实验数据记录入表1—1中。

4. 测量电源U1单独作用下的电路响应：●将电路中ef、gh、jk三处分别用短接线短接；●断开电源U2，将c、d两点用短接线短接；●用万用表测量k、m两点之间的电压值，即R3支路的电压响应U km；●断开ef间的短接线，在ef之间接入直流电流表测量R1支路的电流响应I1；●同样方法，再次测量R2、R3支路的电流响应I2和I3；●将实验数据记录入表1—1中。

叠加定理的验证原理与内容叠加定理是数学中一个重要的定理，它在各个数学领域中都有广泛的应用，如微积分，线性代数和物理学等，是数学中的基本工具之一。

叠加定理主要用于将复杂的问题分解为简单的部分，并通过叠加这些简单的部分来解决整个问题。

下面我将详细介绍叠加定理的验证原理和内容。

叠加定理的验证原理是基于线性性质的。

线性性质是指在某个数学对象中，如果满足特定的条件，它的求和或求积等运算可以分解为若干个部分的求和或求积。

这种分解使得我们可以将原问题分解为多个简单的子问题，并最终将它们叠加起来得到原问题的解。

对于叠加定理来说，它的线性性质是指对于任意两个满足特定条件的函数，它们的线性组合的求和等于这两个函数分别求和的结果的线性组合。

对于叠加定理的内容，我们首先需要明确它的应用范围。

叠加定理适用于满足线性微分方程的函数，具体可以分为两种情况：齐次线性微分方程和非齐次线性微分方程。

对于齐次线性微分方程，叠加定理告诉我们，如果给定两个满足齐次线性微分方程的解函数f(x)和g(x)，那么它们的线性组合a*f(x) + b*g(x)也是这个方程的解函数，其中a和b是常数。

换句话说，对于齐次线性微分方程，解的线性组合仍然是方程的解。

对于非齐次线性微分方程，叠加定理告诉我们，如果给定了方程的一个特解函数p(x)和它的对应齐次方程的通解函数h(x)，那么方程的一般解可以表示为p(x) + h(x)，其中p(x)是方程的特解，h(x)是方程的齐次方程的通解。

换句话说，对于非齐次线性微分方程，一般解可以表示为特解和通解的线性组合。

叠加定理的验证原理可以通过数学推导来证明。

对于齐次线性微分方程，我们可以将求和后的函数代入方程中，利用线性微分方程的性质，将方程分解为两个部分，然后再验证这两个部分分别满足方程，最终证明线性组合是方程的解。

对于非齐次线性微分方程，我们可以通过将方程的一般解代入方程中，然后利用线性微分方程的性质将方程分解为一个特解和一个齐次方程的解，最终证明一般解是方程的解。

叠加定理的验证叠加定理的验证实验⽬的：1.验证线性电路叠加定理的正确性；2.加深对线性电路的叠加性和齐次性的认识和理解；3.理解线性电路的叠加性和齐次性。

实验原理：叠加定理描述了线性电路的可加性或叠加性，其内容是:在有多个独⽴源共同作⽤下的线性电路中，任--电压或电流都是电路中各个独⽴电源单独作⽤时，在该处产⽣的电压或电流的叠加。

通过每-个元件的电流或其两端的电压，可以看成是由每-⼀个独⽴源单独作⽤时在该元件上所产⽣的电流或电压的代数和。

齐性定理的内容是:在线性电路中，当所有激励(电压源和电流源)都同时增⼤或缩⼩K倍(K为实常数)时，响应(电压或电流)也将同时增⼤或缩⼩K 倍。

这是线性电路的齐性定理。

这⾥所说的激励指的是独⽴电源，并且必须全部激励同时增加或缩⼩K倍，否则将导致错误的结果。

显然，当电路中只有⼀个激励时,响应必与激励成正⽐。

使⽤叠加定理时应注意以下⼏点:1)叠加定理适⽤于线性电路，不适⽤于⾮线性电路;2)在叠加的各分电路中，不作⽤的电压源置零，在电压源处⽤短路代替; 不作⽤的电流源置零，在电流源处⽤开路代替。

电路中的所有电阻都不予更动, 受控源则保留在分电路中;3)叠加时各分电路中的电压和电流的参考⽅向可以取为与原电路中的相同。

取和时，应注意各分量前的“”“-"号;4)原电路的功率不等于按各分电路计算所得功率的叠加，这是因为功率是电压和电流的乘积。

实验设备:序号名称型号与规格数量1 直流电压源6V 12 直流电压源12V 13直流数字电压表 14 直流数字电流表 15 电阻510 36 电阻330 17 电阻1K 1实验电路图：共同作⽤：6V单独作⽤：12V单独作⽤：注意事项：1.仿真实验电路必须有接地点；2.连接电源表和电流表注意极性；思考题:1.在叠加定理实验中，要令电压源，电流源分别单独作⽤，应如何操作？答：其中以电源单独作⽤，其余的电压源短路，电流源开路。

2.在线性电路中，可否⽤叠加定理来计算电阻消耗的功率？为什么？答：不可以。

叠加定理的验证汇总叠加定理是数学中的一个重要定理，它在各个领域都有广泛的应用。

简而言之，叠加定理指出，对于一个线性系统，当输入是两个或多个信号时，系统的响应等于每个输入信号分别作用时的响应之和。

以下将对叠加定理的验证进行汇总，包含不同领域的应用。

1.电路理论中的验证：在电路理论中，叠加定理被广泛应用于求解复杂电路系统的问题。

通过将电路中的每个电源或电流源分别激励，然后将各个响应叠加即可得到系统的总响应。

这种方法对于电路的线性分析非常重要，可以简化计算和分析的复杂度。

2.信号处理中的验证：信号处理是一个典型的应用叠加定理的领域。

在信号处理中，叠加定理可以用于分析复杂信号的频谱特性以及信号的传递过程。

通过将系统的输入信号进行分解，然后分别分析每个分量的频谱特性和传递特性，最后通过叠加得到整体的响应结果。

3.声学中的验证：声学是研究声音的物理学科，也可以应用叠加定理。

在声学中，叠加定理用于分析不同声源产生的声波在空间中的相互叠加效应。

当有多个声源同时存在时，可以将每个声源的声压场分别计算，然后将它们进行叠加，得到最终的声压场分布。

4.结构力学中的验证：在结构力学中，叠加定理可以用于分析复杂结构的应力、应变等问题。

通过将结构的外载分解为各个单独作用的载荷，然后分别计算每个载荷作用下的应力和应变分布，最后将它们叠加得到整体结构的应力应变分布。

5.统计学中的验证：在统计学中，叠加定理可以用于估计总体参数。

通过将总体数据分解为不同的子集，对每个子集进行独立估计，然后将估计结果进行叠加，可以得到总体参数的估计结果。

这在大数据分析和样本调查等领域有广泛的应用。

综上所述，叠加定理在电路理论、信号处理、声学、结构力学和统计学等领域都有广泛的应用。

通过将复杂系统分解为简单的部分，然后将各个部分的响应进行叠加，可以得到整体系统的响应结果。

这种分而治之的思想在分析和计算复杂问题时非常重要，能够简化计算和分析的复杂度，从而提高工作效率。

验证叠加定理引言叠加定理是电学中的一个重要定理，它能够帮助我们简化复杂电路的分析与计算。

在本文中，我们将详细探讨叠加定理的基本原理，并通过实例验证其有效性。

本文将按照以下结构展开：1.叠加定理的定义与原理2.叠加定理的应用与意义3.实例分析：验证叠加定理4.总结与展望叠加定理的定义与原理叠加定理是电学中的一种电路分析方法，它允许我们将一个复杂的电路分析问题转化为多个简单的电路分析问题，从而简化计算过程。

其基本原理可以概括为：在一个线性电路中，若有多个电源同时作用于电路中，那么在计算特定电路参数时，可以分别计算每个电源对该参数的影响，并将其叠加得到最终结果。

叠加定理的应用与意义叠加定理在电路分析中有着广泛的应用，主要体现在以下几个方面：1.线性电路分析：对于复杂的线性电路，叠加定理能够将分析问题转化为多个简单的电路分析问题，大大降低了计算的难度。

2.电路参数计算：叠加定理可以应用于电路中各个元件的电流、电压、功率等参数的计算，使得整个过程更加简化与直观。

3.电路设计与优化：通过合理运用叠加定理，我们可以更加灵活地进行电路设计与优化，提高电路性能与效率。

实例分析：验证叠加定理实例背景我们考虑一个简单的直流电路，其电路图如下所示：其中，V1和V2为两个电源，R1、R2和R3为电阻。

我们将使用叠加定理验证节点A处的电压。

实验步骤根据叠加定理的原理，我们可以通过以下步骤验证节点A处的电压：1.关闭电源V2，计算节点A处的电压，记为V_A1。

2.关闭电源V1，打开电源V2，计算节点A处的电压，记为V_A2。

3.将V_A1和V_A2相加得到最终的节点A处电压。

结果分析在实验中，我们选择了以下电路参数：•V1 = 10V•V2 = 5V•R1 = 2Ω•R2 = 4Ω•R3 = 6Ω通过计算，我们得到了以下结果：1.关闭电源V2时，节点A处的电压V_A1 = 3.33V。

2.关闭电源V1时，节点A处的电压V_A2 = 6.67V。