新苏教版数学六年级奥数流水行船问题一对一教案
- 格式:docx
- 大小:96.62 KB
- 文档页数:5
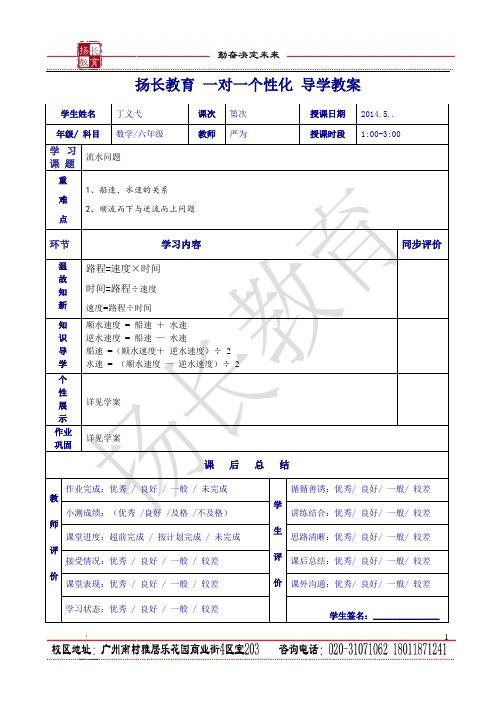
扬长教育一对一个性化导学教案学生姓名丁义弋课次第次授课日期2014.5..年级/ 科目数学/六年级教师严为授课时段1:00-3:00学习课题流水问题重难点1、船速,水速的关系2、顺流而下与逆流而上问题环节学习内容同步评价温故知新路程=速度×时间时间=路程÷速度速度=路程÷时间知识导学顺水速度= 船速+水速逆水速度= 船速—水速船速=(顺水速度+逆水速度)÷ 2 水速= (顺水速度—逆水速度)÷2个性展示详见学案作业巩固详见学案课后总结教师评价作业完成:优秀 / 良好 / 一般 / 未完成学生评价循循善诱:优秀/ 良好/ 一般/ 较差小测成绩:(优秀 /良好 /及格 /不及格)讲练结合:优秀/ 良好/ 一般/ 较差课堂进度:超前完成 / 按计划完成 / 未完成思路清晰:优秀/ 良好/ 一般/ 较差接受情况:优秀 / 良好 / 一般 / 较差课后总结:优秀/ 良好/ 一般/ 较差课堂表现:优秀 / 良好 / 一般 / 较差课外沟通:优秀/ 良好/ 一般/ 较差学习状态:优秀 / 良好 / 一般 / 较差学生签名:_______________教研组长签名:行 船 问 题一. 几个数量关系:顺水速度 = 船速 + 水速 逆水速度 = 船速 — 水速船速 =(顺水速度+ 逆水速度)÷ 2 水速 = (顺水速度 — 逆水速度)÷ 2二.例题:例1. 甲乙两港间的水路长252千米,一只船从甲港开往乙港,顺水9小时可以到达,从乙港返回甲港,逆水14小时到达,求船在静水中的速度和水流速度。
例2. 轮船在静水中的速度是每小时21千米,轮船自甲港逆水航行8小时,到达相距144千米的乙港,再从乙港返回甲港需要几小时?例3. 一膄轮船从甲港开往乙港,顺水而行每小时行28千米,返回甲港时逆顺而行用了6小时,已知水速是每小时4千米,甲乙两港相距多少千米?________________________________________________________________________________________________________________________________________________________________________________教师签名:________________家 长 反 馈________________________________________________________________________________________________________________________________________家长签名:_______________例4. 一条大河,河中间(主航道)水的流速为每小时8千米,沿岸边水的流速为每小时6千米,一条船在河中间顺流而下,13小时行驶520千米,求这条船沿岸边返回原地,需要多少小时?例5. 甲乙两个码头相距112千米,一只船从乙码头逆水而上行了8小时到达甲码头,已知船速是水速的15倍,求这只船从甲码头返回乙码头需要多少小时?例6. 一只轮船往返于相距240千米的甲乙两港之间,逆水速度是每小时18千米,顺水速度是每小时26千米,一膄汽艇的速度是每小时20千米,这膄汽艇往返于两港之间共需要多少小时?课后练习:1.一只船在静水中的速度是每小时18千米,水流速度是每小时2千米,这只船从甲港到乙港需要5小时,甲乙两港的距离是多少千米?2.一只船在水中航行,水速为每小时2千米,它在静水中航行每小时行8千米,问这只船顺水航行50千米需要几小时?3.一膄轮船在静水中的速度是每小时行15千米,它逆水航行11小时走了88千米,问这膄船返回原地需要几小时?4.一只船往返于一段长120千米的航道之间,上行时行了10小时,下行时行了6小时,求船在静水中的速度和水流速度。

第36讲流水行船问题一、知识要点当你逆风骑自行车时有什么感觉?是的,逆风时需用很大力气,因为面对的是迎面吹来的风。
当顺风时,借着风力,相对而言用里较少。
在你的生活中是否也遇到过类似的如流水行船问题。
解答这类题的要素有下列几点:水速、流速、划速、距离,解答这类题与和差问题相似。
划速相当于和差问题中的大数,水速相当于小数,顺流速相当于和数,逆流速相当于差速。
划速=(顺流船速+逆流船速)÷2;水速=(顺流船速—逆流船速)÷2;顺流船速=划速+水速;逆流船速=划速—水速;顺流船速=逆流船速+水速×2;逆流船速=逆流船速—水速×2。
二、精讲精练【例题1】一条轮船往返于A、B两地之间,由A地到B地是顺水航行,由B地到A地是逆水航行。
已知船在静水中的速度是每小时20千米,由A地到B地用了6小时,由B地到A地所用的时间是由A地到B地所用时间的1.5倍,求水流速度。
在这个问题中,不论船是逆水航行,还是顺水航行,其行驶的路程相等,都等于A、B两地之间的路程;而船顺水航行时,其形式的速度为船在静水中的速度加上水流速度,而船在怒水航行时的行驶速度是船在静水中的速度与水流速度的差。
解:设水流速度为每小时x千米,则船由A地到B地行驶的路程为[(20+x)×6]千米,船由B地到A地行驶的路程为[(20—x)×6×1.5]千米。
列方程为(20+x)×6=(20—x)×6×1.5x=4答:水流速度为每小时4千米。
练习1:1、水流速度是每小时15千米。
现在有船顺水而行,8小时行320千米。
若逆水行320千米需几小时?2、水流速度每小时5千米。
现在有一船逆水在120千米的河中航行需6小时,顺水航行需几小时?3、一船从A地顺流到B地,航行速度是每小时32千米,水流速度是每小时4千米,212天可以到达。
次船从B地返回到A地需多少小时?【例题2】有一船行驶于120千米长的河中,逆行需10小时,顺行要6小时,求船速和水速。

小学奥数流水行程问题教学设计集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-流水行程问题教学设计本课分为两课时,第一课时为例题讲解、答疑激趣、归纳算理、布置课后作业;第二课时为习题讲解,反思总结。
一、教学目标:1、知识与技能:掌握行船、流水问题的基本规律,能理清水速、船速之间的关系2、过程与方法:经历应用问题的解决,掌握流水行程问题的基本解决方法和步骤,学会用画图等方法解决问题3、情感态度价值观:经历问题解决的步骤,加强逻辑能力和思维水平,增加学生思维的挑战,引发学生的兴趣。
二、教学重点:船速、水速和顺水、逆水的等量关系式教学难点:理解问题的解决方法三、教学过程(一)展示例题,指出关键已知一艘轮船顺水行48千米需4小时,逆水行48千米需6小时.现在轮船从上游A港到下游B港.已知两港间的水路长为72千米,开船时一旅客从窗口扔到水里一块木板,问船到B港时,木块离B港还有多远1、理解信息。
请学生从中找出关键词和所了解到的信息,说说如何理解2、集思广益。
根据你了解到的信息,如何解决现在的问题3、教师展示思路:分析:顺水行速度为:48÷4=12(千米),逆水行速度为:48÷6=8(千米).因为顺水速度是比船的速度多了水的速度,而逆水速度是船的速度再减去水的速度,因此顺水速度和逆水速度之间相差的是“两个水的速度”,因此可求出水的速度为:(12-8)÷2=2(千米).现条件为到下游,因此是顺水行驶,从A到B所用时间为:72÷12=6(小时).木板从开始到结束所用时间与船相同,木板随水而飘,所以行驶的速度就是水的速度,可求出6小时木板的路程为:6×2=12(千米);与船所到达的B地距离还差:72-12=60(千米).解:顺水行速度为:48÷4=12(千米),逆水行速度为:48÷6=8(千米),水的速度为:(12-8)÷2=2(千米),从A到B所用时间为:72÷12=6(小时),6小时木板的路程为:6×2=12(千米),与船所到达的B地距离还差:72-12=60(千米).答:船到B港时,木块离B港还有60米.此题运用了关系式:(顺水速度-逆水速度)÷2=水速(二)训练拓展,巩固思维根据学生所学到的关系式进行进一步推理。

「拓展数学」流水行船问题第1讲:认识流水行船问题流水行船问题,是行程问题的一种,我们在认识流水行船问题之前,先将行程问题的三个量(即路程、速度、时间)之间的等量关系进行回顾:速度×时间=路程路程÷时间=速度路程÷速度=时间下面,我们来说流水行船问题。
我们知道,我们生活中的水存在着两种状态,一种是不流动的状态,我们称之为静止状态,叫静水。
如水塘、湖泊中的水是静止的,就是静水。
一种是流动状态,叫流水。
如江水、河水、海水都是流动的,就是流水。
一艘船在流水中行驶产生的行程问题,就是流水行船问题,简称“流水问题”。
一艘船在水中行驶会出现怎样的情况呢?第一种,船在湖泊中行驶,也就是在静水中行驶。
这时候,如果没有摇桨或者开动发动机,那么船就会漂泊在湖面上不动,即不能行驶。
船要在静水中行驶,必须要摇桨或开动发动机。
第二种,船在流动的江面上行驶,也就是在流水中行驶。
船在流水中,如果不摇桨或者不开动发动机能不能行驶呢?当然可以。
因为水本身在流动,即使不摇桨或者不开动发动机,船也会随着水流的方向行驶。
现在,我们进行假设:假设船要从西到东去A地,而水是从东往西流动的,要想使船到达目的地,不摇桨或者不开动发动机行不行?显然是不行的。
因为如果不开动发动机或者不摇桨,船会随着水流到西边去了。
我们进一步假设:在前一个假设的前提下,水的流速是5千米/时,要想使船到达A地,船开始摇桨或者开动发动机产生了4千米/时的速度。
这种情况下,船能不能到达A地?显然也不能。
因为船本身的速度是4千米/时,小于水的流速5千米/时,这时候水阻碍着船前进,船依旧会随着水流方向到西边去了。
我们再进一步假设:在第一个假设的前提下,水的流速是5千米/时,要想使船到达A地,船开始摇桨或者开动发动机产生了5千米/时的速度。
这种情况下,船能不能到达A地?显然也不能。
因为船本身的速度是5千米/时,刚好等于水的流速5千米/时,这时候水虽然阻碍着船的前进,但却不能促使船随着水流到西边去,这时候船会在原地不动,给人的感觉是静止的。

(六年级)备课教员:第9讲流水行船问题一、教学目标: 1. 在实际情境中理解顺水速度、逆水速度、静水速度及水速等数量的含义,掌握各数量间的关系。
2.掌握流水行船问题的解题方法,提高解题能力和思维的灵活性。
3. 初步养成独立思考、自主探究、合作交流的学习方式。
二、教学重点:顺水速度、逆水速度、静水速度及水速等数量间的关系,流水行船问题的解题方法。
三、教学难点:顺水速度、逆水速度、静水速度及水速等数量间的关系。
四、教学准备:PPT五、教学过程:第一课时(50分钟)一、导入(5分)师:这是龙舟比赛中的情景。
如果他们划船的速度一样,一个在顺水中划,一个在逆水中划,哪个会更快一点?生:在顺水中。
师:是的。
相信同学们应该看过。
我们知道池塘里面的水是不流动的,如果把船放在池塘里,船会动吗?生:不会。
师:是的。
这个时候要我们去划,船才会动,这时候船的速度我们称为船在静水中的速度。
也称为船速(划速)。
但如果把一条船放在流水中,那么船是不是就会顺着水流动。
其实这时候船的速度就是水流的速度。
这个时候如果我们再去划动的话,船会行的更快一点,这时候船的速度就等于水流的速度加上船在静水中的速度。
同样的道理,船在逆水中的速度等于什么?生:……师:是的,这类问题也是我们数学路程问题中的一类,今天我们就来学习这方面的知识。
板书:流水行船问题二、探索发现授课(40分)(一)例题一:(13分)一只渔船顺水行30千米,用了5小时,水流的速度是每小时1千米。
此船在静水中的速度是多少?师:同学们先看题目,题目中要我们求什么?生:船在静水中的速度。
师:前面我们推导了一些公式,船在静水中的速度可以怎么求?生:……师:很好,题目中告诉我们船是顺水行驶,那么船在静水中的速度等于什么呢?生:……师:题目中告诉我们渔船顺水行30千米,用了5小时,那么我们可以求出什么?生:……师:是的,根据速度=路程÷时间,我们求出速度,而这个速度是什么速度?生:……师:是的,顺水时的速度求出来了,题目中又告诉我们水流的速度,接下来同学们会做了吗?生:会了。
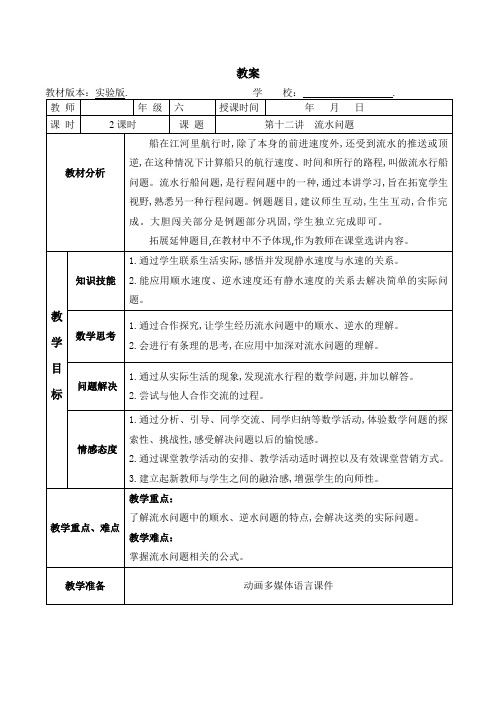
学科教师辅导讲义学员编号:年级:六年级课时数:3学员姓名:辅导科目:奥数学科教师:授课主题第25讲——流水行船问题授课类型T同步课堂P实战演练S归纳总结教学目标①掌握流水行船的基本概念;②能够准确处理流水行船中相遇和追及的速度关系。
授课日期及时段T(Textbook-Based)——同步课堂一、参考系速度通常我们所接触的行程问题可以称作为“参考系速度为0”的行程问题,例如当我们研究甲乙两人在一段公路上行走相遇时,这里的参考系便是公路,而公路本身是没有速度的,所以我们只需要考虑人本身的速度即可。
二、参考系速度——“水速”但是在流水行船问题中,我们的参考系将不再是速度为0的参考系,因为水本身也是在流动的,所以这里我们必须考虑水流速度对船只速度的影响,具体为:①水速度=船速+水速;②逆水速度=船速-水速。
(可理解为和差问题)由上述两个式子我们不难得出一个有用的结论:船速=(顺水速度+逆水速度)÷2;水速=(顺水速度-逆水速度)÷2此外,对于河流中的漂浮物,我们还会经常用到一个常识性性质,即:漂浮物速度=流水速度。
三、流水行船问题中的相遇与追及①两只船在河流中相遇问题,当甲、乙两船(甲在上游、乙在下游)在江河里相向开出:甲船顺水速度+乙船逆水速度=(甲船速+水速)+(乙船速-水速)=甲船船速+乙船船速②同样道理,如果两只船,同向运动,一只船追上另一只船所用的时间,与水速无关.知识梳理甲船顺水速度-乙船顺水速度=(甲船速+水速)-(乙船速+水速)=甲船速-乙船速也有:甲船逆水速度-乙船逆水速度=(甲船速-水速)-(乙船速-水速)=甲船速-乙船速.说明:两船在水中的相遇与追及问题同静水中的及两车在陆地上的相遇与追及问题一样,与水速没有关系。
典例分析考点一:基本的流水行船问题例1、甲、乙两港间的水路长208千米,一只船从甲港开往乙港,顺水8小时到达,从乙港返回甲港,逆水13小时到达,求船在静水中的速度和水流速度。
流水行船教案模板(共5篇)第1篇:行船问题教案课题名称:行船问题教学重点与难点:1:理解水流速度,船速,顺水速度,逆水速度的概念2:掌握水流速度,船速,顺水速度,逆水速度之间的数量关系教学内容:知识点1:基本概念(一)船在静水中的速度叫(二)船从上游顺水而行的速度叫(三)江河流动的速度叫做(四)船从下游逆水而行的速度叫做知识点2:基本公式顺流速度=船速+水速逆水速度=船速-水速变形公式:通过两个方程,把它们相加减借着两个方程组成的方程组可得:船速=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2例题1:甲乙两码头相距360千米,一艘汽艇从甲码头顺水而行到乙码头需要9小时,返回时所用的时间比去时多用1/3,求水流速度是多少千米/时?(基本行船问题求速度)练习:1、甲乙两港间的水路长208千米,一只船从甲港开往乙港,顺水8小时到达,从乙港返回甲港,逆水13小时到达,求船在静水中的速度和水流速度?2、甲乙两港间水路长252千米,一只船从甲港开往乙港,顺水9小时到达,从乙港返回甲港,逆水14小时到达,求船在静水中的速度和水流速度?3、一只船在河中航行,顺流而行时每小时20千米,已知此船顺水航行3小时和逆水航行5小时所行的路程相等,则船速和水速各是多少?4、一只船在河中航行,水速为每小时2千米,它在静水中航行12千米,则顺水航行每小时航行多少千米?逆水每小时航行多少千米?顺水航行140千米用多少小时?5、甲乙两港相距208千米,一艘船从甲港开往乙港,顺水8小时到达,从乙港返回甲港,逆水13小时到达,问船在静水中的速度和水流速度各是多少?6、一艘轮船顺流80千米,逆流45千米共用9小时;顺流60千米、逆流90千米共用13小时。
求轮船在静水中的速度?例题2:一艘小船逆水而行,到A地时随身带的一个重要的水壶掉入水中随波而下。
半小时后船行到B地,发现丢失了水壶,立即返回寻找,终于在距离A地5千米的地方追上水壶,然后又用了10分钟返回到A地。
教学内容火车过桥问题、流水问题
教学目标1、知道火车过桥问题所行使路程
2、会求火车过桥时间、速度等
3、人与车、车与车相遇、追击问题
教学重、难点重点:人与车、车与车相遇、追击问题相关公式难点:运用行程基本公式解决实际问题
1、一列客车经过南京长江大桥,大桥长6700米,这列客车长100米,每分钟行400米,这列客车经过长江大
桥需要多少分钟?
2、一列火车长160米,全车通过440米的桥需要30秒钟。
这列火车每秒行多少米?
3、某列火车通过360米的第一个隧道用了24秒钟,接着通过第二个长216米的隧道用了16秒钟,这列火车的
长度是多少米?
4、某列火车通过342米的隧道用了23秒,接着通过234米的隧道用了17秒,这列火车与另一列长88米、速
度为每秒22米的列车错车而过,问需要几秒钟?
5、一列火车全长265米,每秒行驶25米,全车要通过一座985米长的大桥,问需要多少秒钟?
变式:快车长182米,每秒行20米,慢车长134米,每秒18米,两车同向并行,当快车车尾接慢车车尾时,求快车穿过慢车的时间?
例6、一列火车长600米,它以每秒10米的速度穿过200米的隧道,从车头进入隧道到车尾离开隧道共需多长时间?
1、一列火车通过530米的桥需要40秒,以同样的速度穿过380米的隧道需要30秒。
这列火车的速度和车身长各是多少?
2、两列火车,一列长120米,每秒行20米;另一列长160米,每秒行15米,两车相向而行,从车头相遇到车尾离开需要几秒钟?。
海豚教育个性化简案学生姓名:年级:科目:授课日期:月日上课时间:时分------ 时分合计:小时教学目标1. 培养学生的观察能力及逻辑思维能力。
.2. 初步了解“流水行船”。
重难点导航1. 了解掌握奥数阶梯思维.2. 把奥数思维带入解决应用题中.教学简案:一、个性化教案二、错题汇编三、个性化作业授课教师评价:□ 准时上课:无迟到和早退现象(今日学生课堂表□ 今天所学知识点全部掌握:教师任意抽查一知识点,学生能完全掌握现符合共项)□ 上课态度认真:上课期间认真听讲,无任何不配合老师的情况(大写)□ 海豚作业完成达标:全部按时按量完成所布置的作业,无少做漏做现象审核人签字:学生签字:教师签字:备注:请交至行政前台处登记、存档保留,隔日无效(可另附教案内页)大写:壹贰叁肆签章:海豚教育个性化教案奥数讲解五题型:流水行船【知识要点】1. 船在流水中航行的问题叫做行船问题。
行船问题是行程问题中比较特殊的类型,它除了具备行程问题中路程、速度和时间之间的基本数量关系,同时还涉及到水流的问题,因船在江、河里航行时,除了它本身的前进速度外,还会受到流水的顺推或逆阻。
2. 行船问题中常用的概念有:船速、水速、顺水速度和逆水速度。
船在静水中航行的速度叫船速;江河水流动的速度叫水速;船从上游向下游顺水而行的速度叫顺水速度;船从下游往上游逆水而行的速度叫逆水速度。
3. 除了行程问题中路程、速度和时间之间的基本数量关系在这里要反复用到外,行船问题还有几个基本公式要用到。
①顺水速度=船速+水速;②逆水速度=船速-水速4. 如果已知顺水速度和逆水速度,由和差问题的解题方法,我们可以求出船速和水速。
①船速=(顺水速度+逆水速度)÷2 ;②水速=(顺水速度-逆水速度)÷2例1:船在静水中的速度为每小时13千米,水流的速度为每小时3千米,船从甲港顺流而下到达乙港用了15小时,从乙港返回甲港需要多少小时?练习1:一只船在静水中每小时行12千米,在一段河中逆水航行4小时行了36千米。