当前位置：文档之家 › 绕x轴旋转体的体积 PPT

绕x轴旋转体的体积 PPT

  • 格式：ppt
  • 大小：1.24 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

北师大版数学高二课件 4.3.2 简单几何体的体积

北师大版数学高二课件 4.3.2 简单几何体的体积

梯形绕x轴旋转一周而成的几何体，则该旋转体的体积为V＝
bπ[
a
f(x)]
2dx
.
答案
返回
题型探究
重点突破
题型一 简单旋转几何体的体积
例1 求由y＝x3，y＝0，x＝2所围图形绕x轴旋转的旋转体的体积.
解
Vx＝2πy2dx＝2πx6dx＝
0
0
πx72
7
0
＝1278π.
反思与感悟
解析答案
跟踪训练1 求由曲线y＝x2，x＝y2围成的图形绕y轴旋转形成的几何体的 体积. 解 x1＝ y，x2＝y2,0≤y≤1，
解析答案
课堂小结 1.简单旋转几何体可以看成一个平面图形绕平面内一条直线旋转而成. 2.利用定积分求体积要合理确定被积函数，然后根据图像确定积分上、 下限，要理解其中蕴含的定积分思想.
返回
本课结束
的几何体.如图所示：
因此 V＝a A(x)dx
－a
＝πab22a (a2－x2)dx＝43πab2. －a
反思与感悟
解析答案
跟踪训练2 连接坐标原点O及点P(h，r)的直线、直线x＝h及x轴围成一个 直角三角形.将它绕x轴旋转构成一个底半径为r、高为h的圆锥体.计算这个 圆锥体的体积. 解 直角三角形斜边的直线方程为 y＝hrx. 所以所求圆锥体的体积为
第四章 §3 定积分的简单应用
4.3.2 简单几何体的体积
学习 目标
1.通过实例，进一步理解定积分的思想. 2.了解定积分在求旋转体的体积方面的简单应用.
栏目 索引

知识梳理 题型探究 当堂检测
自主学习 重点突破 自查自纠
知识梳理
自主学习
知识点 用定积分表示旋转体的体积 旋转体可以看作是由连续曲线y＝f(x)、直线x＝a、x＝b及x轴所围成的曲边

《经济数学-微积分》旋转体的体积

《经济数学-微积分》旋转体的体积

旋转体定义
一个平面图形绕着它所在的平面 内的一条定直线旋转所形成的曲 面围成的几何体称为旋转体。
旋转体分类
根据旋转轴的不同，旋转体可以 分为绕x轴旋转的旋转体和绕y轴 旋转的旋转体。
体积计算公式推导
01
圆柱体体积公式推导
02
圆锥体体积公式推导
03
圆球体体积公式推导
圆柱体可以看作是一个矩形绕其一边 旋转而成的，因此其体积可以通过矩 形的面积与旋转的高度的乘积来计算 。
多重积分概念与性质
了解多重积分的概念和性质，如二重积分、三重积分等。
在旋转体体积求解中应用
对于复杂形状的旋转体，可以通过多重积分进行求解，如球体、椭 球体等。
求解步骤与技巧
掌握多重积分的求解步骤和技巧，如选择合适的坐标系、确定积分 顺序等。
数值近似解法介绍
01
数值近似解法概念
当无法直接通过积分公式求解旋 转体体积时，可以采用数值近似 解法进行估算。
04 积分法在求解旋转体体积 中应用
定积分求解旋转体体积基本原理
旋转体体积的定积分表示
通过截面面积函数对定区间进行积分，得到旋转体体积的公式。
几何意义与物理应用
定积分求解旋转体体积的方法在几何和物理领域有广泛应用，如计 算圆柱、圆锥等体积。
求解步骤与技巧
掌握定积分的求解步骤和技巧，如确定积分区间、选择合适的积分 变量等。
物理应用
旋转体体积的计算公式在物理学中也 有广泛应用，例如在计算物体的质量 、密度、浮力等方面都需要用到体积 的计算公式。
常见问题及解决方法
问题1
如何判断一个几何体是否为旋转体？
解决方法
观察几何体的形状和特征，看其是否符合旋转体的定义和 性质。

定积分求旋转体的体积

定积分求旋转体的体积
高等数学之——
7.1.3 定积分求旋转体的体积
第七章 定积分的应用
第一节 定积分在几何上的应用
第三讲 定积分求旋转体的体积
主要内容： 一、旋转体的概念
二、平面图形绕 x 轴旋转所得旋转体的体积
三、平面图形绕 y 轴旋转所得旋转体的体积
四、小结
引入：
一、旋转体：由一个平面图形绕这平面内一条直线旋转一周而
2
1
1 e4 e2 2
V b[ f (x)]2 dx a
y
y ex
1
o x=1 x=2 x
练习 求由抛物线 y x2、直线 x 2 及 x 轴所围成平面图形绕 x
轴旋转一周所得旋转体的体积.
A: 32
5
B: 16
5
C: 8
5
解 选A
D: 64
（3）V
Байду номын сангаас
b
[
f
(x)]2 dx

b y2dx
a
a
xx x dx
例1 求由曲线 y ex，直线 x 1, x 2以及 x 轴所围成的平面图
形绕 x 轴旋转一周所得旋转体的体积.
解
V

2

1

f
x2dx

2

ex
2
dx
1
1 e2x 2
D: 1 e2 1 2
解 选C
四、小结
1. 平面图形绕 x轴旋转所得旋转体的体积
V b [ f (x)]2 dx b y2dx
a
a
2. 平面图形绕 y轴旋转所得旋转体的体积

§定积分应用之简单旋转体的体积

§定积分应用之简单旋转体的体积

§定积分应⽤之简单旋转体的体积§3.2定积分应⽤之简单旋转体的体积【学习⽬标】1、利⽤定积分的意义和积分公式，求⼀些简单旋转⼏何体体积。

2、数学模型的建⽴及被积函数的确定。

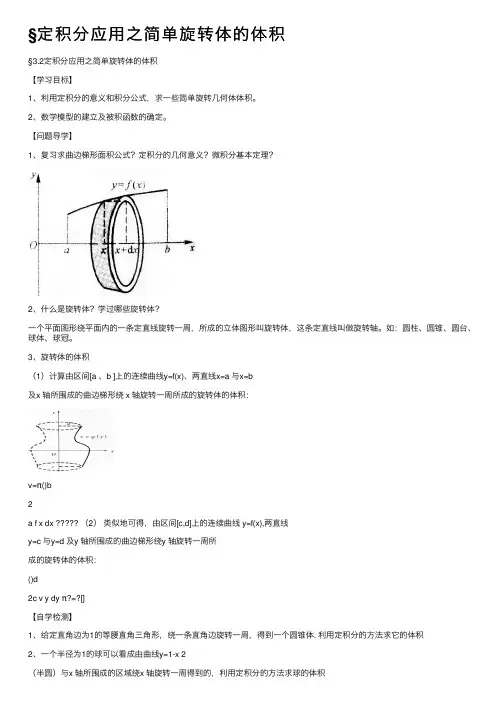
【问题导学】1、复习求曲边梯形⾯积公式？定积分的⼏何意义？微积分基本定理？2、什么是旋转体？学过哪些旋转体？⼀个平⾯图形绕平⾯内的⼀条定直线旋转⼀周，所成的⽴体图形叫旋转体，这条定直线叫做旋转轴。

如：圆柱、圆锥、圆台、球体、球冠。

3、旋转体的体积（1）计算由区间[a 、b ]上的连续曲线y=f(x)、两直线x=a 与x=b及x 轴所围成的曲边梯形绕 x 轴旋转⼀周所成的旋转体的体积：v=π()b2a f x dx （2）类似地可得，由区间[c,d]上的连续曲线 y=f(x),两直线y=c 与y=d 及y 轴所围成的曲边梯形绕y 轴旋转⼀周所成的旋转体的体积：()d2c v y dy π?=?[]【⾃学检测】1、给定直⾓边为1的等腰直⾓三⾓形，绕⼀条直⾓边旋转⼀周，得到⼀个圆锥体. 利⽤定积分的⽅法求它的体积2、⼀个半径为1的球可以看成由曲线y=1-x 2（半圆）与x 轴所围成的区域绕x 轴旋转⼀周得到的，利⽤定积分的⽅法求球的体积3、求曲线y=e x 、x=0、x=12与x 轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积【当堂训练】4、求 y = x 2 与 y 2 = x 所围图形绕 x 轴旋转所成的旋转体体积5、将第⼀象限内由x 轴和曲线y 2=6x 与直线x=6所围成的平⾯图形绕x 轴旋转⼀周所得旋转体的体积等于6、求曲线x 轴、y 轴及直线x=1围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积7、求曲线y=1x、x=1、x=2 与x 轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积8、求曲线x=1与坐标轴围成的平⾯图形绕x 轴旋转⼀周所得旋转体体积§3.2定积分应⽤之简单旋转体的体积1、3π2、43π3、(1)2e π-4、310π5、108π6、32π7、2π8、2π。

用二重积分计算旋转体的体积

用二重积分计算旋转体的体积
6.2 定积分的几何应用 15
6.2 定积分的几何应用
如果
16
D {(x, y) | 0 a x b, g(x) y f (x)}
则D绕 y轴旋转的旋转体体积为：
Vy 2 xd D
b
f (x)
2 xdx dy
a
g(x)
b
a 2 x[ f (x) g(x)]dx
b
Vy 2
6.2 定积分的几何应用 23
D L
设直线L的方程为 ax+by+c=0。
在区域D的(x,y)处取一个面积元素
d
它到直线L的距离是 ：
ax by c d
a2 b2
该面积元素绕L旋转而成的旋转体的体积约为：
dV 2d d
于是整个区域D绕直线L旋转而成的旋转体的体积为：
V dV 2 dd
D
2 r3( ) sin d 3
r r( )
2
Vx 3
r3( ) sin d
D
我们用命题1来推导一个有关区域D的形心 (质心)和旋转体体积之间的关系的定理：
古尔丁定理
6.2 定积分的几何应用 19
Paul Guldin（古尔丁） 1577 – 1643 Swiss mathematician who wrote on volumes and centres of gravity.
6.2 定积分的几何应用 26
例1 求由y=2x和y=x2所围区域D绕直线 y=2x旋转的旋转体体积V。
6.2 定积分的几何应用 3
设D是上半平面内的一个有界闭区域。 将D绕x轴旋转一周得一旋转体，求该旋转体的体积Vx。 我们用元素法来建立旋转体体积的二重积分公式。
D

《旋转体的体积》课件

《旋转体的体积》课件

示例演练
通过实例来加深对旋转体体 积计算方法的理解，同时提 供练习题来巩固所学知识。
学习方法
理论与实践相结合，多做练 习题，加深对旋转体体积计 算方法的掌握。
实例演练
通过实例来加深我们对旋转体体积的理解： 1. 利用定积分求解半径为4cm的圆形面积绕y轴旋转一周所得到的旋转体的体积。 2. 利用定积分求解x轴在[0,4]上面积为2-x^2的曲线绕y轴旋转一周所得到的旋转体的体积。
总结
旋转体数在一定区间内的取值进 行求和。
《旋转体的体积》PPT课 件
在本节课中，我们将探索旋转体的体积概念，并学习如何计算旋转体的体积。
旋转体的概念
根据定义，旋转体是由平面图形绕轴线旋转一周所得到的立体图形。例如圆锥、圆柱和球体就是旋转体的常见 示例。
计算方法
为了计算旋转体的体积，我们需要使用积分求解。定积分是一种通过极限法 求和的方法，用于计算连续函数在一定区间内的取值。

第六章 体积


4 b2 2 2 2 V1 2 a x dx ab 3 a a
②与上同理 椭球体也可以看成由半个椭圆
a
a 2 x b y2 b 及 y 轴围成的平面图形绕 y 轴旋转而成的立体
a2 2 4 2 2 V2 2 b y dy a b b 3 b
特别当 a = b 时 旋转体成为球体
2 3
2 3
2 3
四、求摆线 x a ( t sin t ) ， y a ( 1 cos t ) 的一拱， y 0 ，绕直线 y 2a 旋转所成旋转体的体积.
五、 求 x 2 y 2 a 2 绕 x b ( b a 0) 旋转所成旋转 体的体积 . 六、 设有一截锥体，其上，下底均为椭圆，椭圆的轴长 分别为2 A , 2 B 和 2a , 2b ,高为 h ，求这截锥体的体 积 . 七、 设直线 y ax b 与直线x 0 ，x 1 及 y 0 所围 成梯形面积等于A ，试求a , b 使这个梯形 绕 y 轴 旋转所得体积最小 .
r ( z ) | MQ | z 2 (1 z )2 1 2z 2z 2
截面面积 S ( z ) r 2 ( z ) (1 2 z 2 z 2 ) 1 2 立体体积 V S ( z )dz 3 0
例8 已知点A（1,0,1), B(0,1,0) ，线段AB绕 z 轴旋转一周所成的旋转曲面为S，求由S和 两平面 z = 0,z = 1所围立体的体积
y
y f ( x)
o
x
x dx
x
取以dx 为底的窄边梯形绕x 轴旋转而成的薄 dV [ f ( x )]2 dx 片的体积为体积元素，
旋转体的体积为

绕x轴旋转体积公式

绕x轴旋转体积公式在几何学中，我们经常遇到需要计算旋转体积的问题。

当一个二维图形绕某个轴旋转时，它所形成的三维图形就被称为旋转体。

而绕x轴旋转体积公式就是用来计算绕x轴旋转体的体积的公式。

绕x轴旋转体积公式可以表示为V = ∫[a,b] πf(x)^2 dx，其中V表示旋转体的体积，a和b表示x轴上的范围，f(x)表示二维图形在x 轴上的函数。

为了更好地理解绕x轴旋转体积公式，我们可以通过一个例子来说明。

假设我们有一个函数f(x) = x^2，我们希望计算将该函数绕x 轴旋转一周所形成的旋转体的体积。

我们需要确定x轴上的范围。

假设我们希望计算的范围为x = 0到x = 1。

接下来，我们需要计算函数f(x)在该范围内的面积。

由于函数f(x) = x^2是一个二次函数，它的图像是一个开口向上的抛物线。

在范围x = 0到x = 1内，该抛物线位于x轴的上方，因此我们需要计算该范围内抛物线与x轴之间的面积。

根据基本几何知识，我们知道一个矩形的面积可以通过宽度乘以高度来计算。

在这里，我们可以将抛物线与x轴之间的面积近似看作是无数个无穷小矩形的面积之和。

为了计算每个无穷小矩形的面积，我们需要知道矩形的宽度和高度。

在这里，矩形的宽度是dx，它表示无穷小区间[x, x+dx]的长度。

而矩形的高度是f(x)，它表示抛物线在x点的高度。

我们可以将绕x轴旋转体积公式改写为V = ∫[0,1] π(x^2)^2 dx。

通过计算这个积分，我们可以得到绕x轴旋转体的体积。

在这个例子中，我们可以通过计算得到V = ∫[0,1] πx^4 dx。

为了求解这个积分，我们可以使用积分的基本性质和技巧，例如换元法或分部积分法。

通过计算，我们可以得到V = π/5。

因此，将函数f(x) = x^2绕x 轴旋转一周所形成的旋转体的体积为π/5。

通过这个例子，我们可以看到绕x轴旋转体积公式的应用。

无论是计算简单的函数还是复杂的曲线，我们都可以通过这个公式来计算绕x轴旋转体的体积。

极坐标绕x轴旋转体体积公式

极坐标绕x轴旋转体体积公式
极坐标绕x轴旋转体，是指在极坐标系中，以x轴为中心，将一定厚度的圆柱体或圆锥体等旋转体沿x轴正方向旋转一周所形成的立体。

这种旋转体在实际应用中具有广泛的意义，如在物理学、工程学等领域。

为了更好地理解和研究这种旋转体，我们先来推导其体积公式。

设极坐标绕x轴旋转体的半径为r，高度为h。

根据极坐标系的定义，我们可以知道，旋转体的底面圆的半径为r，圆心与x轴的距离也为r。

现在，我们来推导极坐标绕x轴旋转体的体积公式。

旋转体的体积可以表示为：V = πrh
这里，我们采用极坐标系下的面积元素来计算。

在极坐标系中，圆的面积元素为：dA = θrdr
那么，旋转体的底面圆的面积为：A = πr
接下来，我们需要计算旋转体侧面的面积。

在极坐标系中，侧面沿x轴的正方向，其长度为2πr，高度为h。

因此，侧面的面积为：A" = 2πrh 现在，我们可以计算旋转体的体积了。

将底面圆的面积和侧面的面积相加，得到旋转体的总表面积：A总= A + A" = πr + 2πrh
根据立体体积的定义，体积V与表面积A总和高度h的关系为：V = h * A总
将A总代入，得到：V = h * (πr + 2πrh)
化简后，得到极坐标绕x轴旋转体的体积公式：V = πrh + 2πrh
此公式即为极坐标绕x轴旋转体的体积公式。

在实际应用中，我们可以根
据具体问题，将半径r、高度h和旋转角度θ代入公式，计算出相应旋转体的体积。

总之，我们通过推导得出了极坐标绕x轴旋转体的体积公式，这对于研究此类旋转体在实际问题中的应用具有重要意义。

小结旋转体的体积绕x轴旋转绕y轴旋转二


OP 的直线方程为： y r x
y
h
于是所求圆锥体的体积为：
V
h


r
0 h
x 2 dx

r 2
h2
x3

3
h

0

r 2h
3
O
x
P(h,r)
r
h
x
当然这个题可以用元素法来解。 3
例2
计算由椭圆
x2 y2 1
a2 b2
所围成的图形绕x轴旋转而成的旋转体
-R
X
O
xR
则底圆的方程为： x2 y2 R2
过 x轴上的点 x 作垂直于 x 轴的平面，截正劈锥体得等腰三角形。
这截面的面积为： A( x) h y h R2 x 2
于是所求正劈锥体得体积为：
R
R
V A( x)dx h
R2 x 2 dx
R
R
2R 2h
a 2 1 4 2 ln 2 1 4 2 2
15
小结
一、旋转体的体积
绕x轴旋
转
V
b

f ( x) 2 dx利用曲线参数方程时 b y 2dx
a
a
绕y轴旋转
按照x (t)换限
V
d

( y)
dy 2 利用曲线参数方程时
于是所求弧长为 s b 1 y'2 dx a
10
例1Biblioteka 计算曲线 y2
3
x2
上相应于
x
从
a
到
b的一段弧的长度。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如何用定积分表示体积 ? 提示:
A( y) 2x y tan
2 tan y R2 y2
V 2 tan
R
y
R2 y2 dy
0
y
o
R (x, y) x
练习题
1.求y sin x, y 0,0 x 绕 x轴和 y轴旋转一周的旋转体
的体积.
解：由公式有
Vx
sin 2 xdx
所围图形绕 x 轴旋转而
转而成的椭球体的体积.
y
解: 方法1 利用直角坐标方程
b
y b a2 x2 (a x a) a
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(aBiblioteka 2x2)dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
机动 目录 上页 下页 返回 结束
0
2
(1 cos 2x)dx 2
0
2
例20. 求由星形线x a cos 3 t , y a sin3 t 0 t
绕 x 轴旋转 一周所得的旋转体的体积. 解: 利用公式有
V a2 sin7 t 3a cos2 tdt 0
6 a3
2
(sin7 t sin9 t)dt
方法2 利用椭圆参数方程
x a cos t
y
b
sin
t
则
V 2 a y2 dx 2
2 ab2 sin3t d t
0
0
2 ab2 2 1
3
4 ab2
3
特别当b
=
a
时,
就得半径为a
的球体的体积
4
3
a3
.
机动 目录 上页 下页 返回 结束
例2. 求由曲线 y , 直x 线 及 x轴所1 围x成的平面图形 绕 轴旋转x一周所生成的旋转体的体积.
y
o
a 2 a x
2 a2 (1 cos t)2 a(1 cost) d t 0
利用对称性
2
a3 0
(1 cos t)3 d t
16
a3 sin6 0
t 2
dt
(令 u
t) 2
32
a3
2
0
sin 6
u
du
32
a3
5 6
3 4
1 2
2
5 2a3
1应用平行截面函数求旋转体体积 设所给立体垂直于x 轴的截面面积为A(x),
32
a3
0
105
o
取以dx 为底的窄边梯形绕 x轴
x
x x dx
旋转而成的薄片的体积为体积微元，
dV [ f (x)]2 dx
V b [ f ( x)]2 dx b y2dx
a
a
类似的当考虑连续曲线段 绕y 轴旋转一周所形成的立体体积为
V
d
[
(
y)]2
d
y
c
y
d y x (y) c
ox
例1 由曲线
x2 y2 R2
垂直于x 轴 的截面是直角三角形, 其面积为
A(x) 1 (R2 x2 ) tan (R x R)
2
利用对称性
V 2 R 1 (R2 x2 ) tan d x
02
2 tan R2x 1 x3 R
30
y
ox
R x
机动 目录 上页 下页 返回 结束
思考: 可否选择 y 作积分变量 ? 此时截面面积函数是什么 ?
上连续, 则对应于小区间
dV A(x) d x
的体积元素为
y
y f (x)
因此所求立体体积为
b
V a A(x) d x
oa
bx
机动 目录 上页 下页 返回 结束
例4 一平面经过半径为R的圆柱体的底圆中心，并
与底面交成 角, 计算该平面截圆柱体所得立体的体积 .
解: 如图所示取坐标系, 则圆的方程为
解：选为积分变量，由旋转体的体积公 式，得到
Vx
1
(
0
x )2 dx
1
xdx
0
x2
2
1 0
2
例3 求由曲线 x2 4 y，直线y 1及 y 轴所围成的图形
分别绕 x 轴，y 轴旋转一周所生成的旋转体的体积
y
y
x x
解：绕 x 轴旋转体的体积
Vx 12 2
2 ( x 2 )2 dx 04
第八章
第五节 定积分的应用
求旋转体的体积
一 旋转体的体积
圆柱
圆锥
圆台
如果旋转体是由连续曲线 y f ( x)、直线 x a、 x b及 x轴所围成的曲边梯形绕 x轴旋
转一周而成的立体，体积为多少？
在[a,b]上任取小区间[x, x dx] 取积分变量为 x x [a,b]
y f (x)
2
16
2 x4dy
0
2 x5 2 8
16 5
5
y
0
绕 y 轴旋转体的体积
Vy
1
(
0
4 y )2 dy
1
4 ydy
0
4
y2
1
2
2 0
例3 计算摆线
的一拱与 y＝0
所围成的图形分别绕 x 轴 旋转而成的立体体积 .
解: 绕 x 轴旋转而成的体积为
y
Vx
2 a y2 dx
0