干涉法测微小量(已批阅)教学文案
- 格式:doc
- 大小:250.00 KB
- 文档页数:9

(实验报告)干涉法测微小量(已批阅).
干涉法测微小量是物理、化学等多种领域常用的测量技术,可广泛应用于检测微小量的物理、化学物质的构成成分及大小等特性。
本实验以物理学仪器—干涉仪,以了解其相关原理及测量方法,详细研究并妥善操作干涉仪,实现对微小量的准确测量。
实验现场,我们装备了多种仪器设备,其中有半导体激光、光纤、波导、干涉物镜、计算机等,?表示所测实验样品的长度,?表示该物体的物理实验现象及测量结果。
所测样品经过精确调整,激光整体成像稳定、清晰。
依据干涉仪的原理,在激光学范畴,当灰度图像准确拍摄完毕,即可无缝连接计算机,把模拟航班仪及其相关接口的输入端全部接受,真实表示所测实验样品的物理偏移量。
在量测的过程中,根据实验要求,逐渐变化激光的数量,由而伴随波数的变化,随时记录模拟仪和相关输入端的变化,把变化偏移量输入计算机,由计算机将接受的数据按照原理预定义好的算法进行分析,由此根据分析结果,乘以放大系数,便可计算出微小物体的长度?。
本实验让我清楚地认识了干涉仪的基本原理,熟悉了具体的操作过程,详细了解了对微小量的测量原理,以及量测实验样品物理偏移量的处理过程,进而求出实验物体的长度?。
另外,本实验也锻炼了我们熟练操作干涉仪及相关仪器设备、形成有效数据、熟练处理数据的实际能力,积累了大量经验,掌握了实用的实验技术。

干涉法测微小量(已批阅)随着科技的进步,人们的观测能力也变得越来越强大。
凭借单位时间内观测到的频繁信息量提高,以及测量仪器的普及,我们正在探索小规模功能的信息,以及精细而完整的模型。
然而,当测量物理量的规模极小时,由于量的偏差、技术的局限或其他原因,测量准确度是我们不得不面对的挑战。
为了应对这种情况,干涉法实验测微小量发挥着重要作用。
干涉测量,也称为干涉仪器,是利用干涉实验结果来确定物理量,实现测量的一种技术。
其基本原理是利用一个物理量与它的规模连续变化时,另一个量(如光线,声波等)以某种特定方式实现其递变的原理。
换句话说,就是当一个定量变化时,另一个量的变化率会因此而变化,然后依据干涉定律来分析,以确定一个物理量的数值大小。
简而言之,干涉测量是一种利用变量两个量关系推断得到物理量的一种方法,是在原有量测精度上有所提升的方法。
干涉仪原理是基于物理原理的,以光为例:两片薄透镜或镜片之间,将激发的两个并行光束相交,通过太阳能出射量的变化,产生微小的振动,最后用收发件传输并检测光束的变化量。
在量测中,激发的光线束可以分解为两个平行的小强度的光线束向一个大的距离内传播,然后相互干涉,产生一个模拟或数字信号。
通过这种方式,经过测量者控制,最后经过数字信号处理之后,可以获得各种物理量在精度及计量上较高精度的测量结果。
干涉测量技术,它能够更准确、精细地测量物理量,可以获得诸如长度、变形、速率及光谱等物理量,比与之相比的传统测量技术能够提供更准确的测量结果,而且其成本更低。
干涉仪器的精度取决于其结构中细小元件的精度以及相关的测量参数的准确性,包括仪器本身的偏差以及元件的消耗量。
因此其准确性受多种因素的影响,由此获得的测量结果更接近实际值,而且能够满足特殊环境的需求,使实验室环境上获得更加准确、精确的测量结果,为我们提供更好的工具用以精确地观察内部活动,整个过程从数据变形到结论的发现都是一致的。
干涉法实验测微小量技术在我国的应用已经发展了许多年,特别是在机械、金属加工的行业,其应用更加广泛。

干涉法测微小量干涉法测微小量段心蕊 PB05000826 (九号台)一、实验目的:学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法。
二、实验原理:用牛顿环测平凸透镜的曲率半径如图所示,光束1、2干涉,全部光束在一起,产生牛顿环 1、2两束光的光程差为 22λδ+=∆第m 个暗环处 ...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=⇒m m又222)(m m R r R δ-+=, R m <<δRr mm 22=⇒δλδλδmR r R r m m m m m =⇒⎪⎪⎭⎪⎪⎬⎫=⋅=2222 我们可由λ求R 或由R 求λ。
但由于r m 不易测准,且实验者无法看出暗环真正所处的级数,故测直径D m , λmR D m 42= λR n m D n m )(42+=+ λn D D R mn m 422-=⇒+ 其中n 可以观察出来从而可以计算透镜的曲率半径R 。
三、实验仪器:显微镜、平凸透镜、显示器、玻璃片、钠光灯。
四、实验内容 1 观察牛顿环(1)将牛顿环仪按图所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
(2)调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
2 测牛顿环直径(1)使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。
(2)转动显微镜测微鼓轮,使显微镜筒沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第65环相切为止。
(3)反向转动鼓轮,当竖丝与第60环相切时,记录读数显微镜上的位置读数d 60,然后继续转动鼓轮,使竖丝依次与第50、40、30、20、10环相切,顺次记下读数d 50,d 40,d 30,d 20,d 10。
干涉法测微小量段心蕊 PB05000826 (九号台)一、实验目的:学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法。
二、实验原理:用牛顿环测平凸透镜的曲率半径如图所示,光束1、2干涉,全部光束在一起,产生牛顿环 1、2两束光的光程差为22λδ+=∆第m 个暗环处 ...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=⇒m m又222)(m m R r R δ-+=, R m <<δRr mm 22=⇒δλδλδmR r R r m m m m m =⇒⎪⎪⎭⎪⎪⎬⎫=⋅=2222 我们可由λ求R 或由R 求λ。
但由于r m 不易测准,且实验者无法看出暗环真正所处的级数,故测直径D m , λmR D m 42= λR n m D n m )(42+=+ λn D D R mn m 422-=⇒+ 其中n 可以观察出来从而可以计算透镜的曲率半径R 。
三、实验仪器:显微镜、平凸透镜、显示器、玻璃片、钠光灯。
四、实验内容 1 观察牛顿环(1)将牛顿环仪按图所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
(2)调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
2 测牛顿环直径(1)使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。
(2)转动显微镜测微鼓轮,使显微镜筒沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第65环相切为止。
(3)反向转动鼓轮,当竖丝与第60环相切时,记录读数显微镜上的位置读数d 60,然后继续转动鼓轮,使竖丝依次与第50、40、30、20、10环相切,顺次记下读数d 50,d 40,d 30,d 20,d 10。


干涉法测微小量【实验目的】1.了解等厚干涉的应用2.掌握移测显微镜的使用方法【实验仪器】实验仪器:牛顿环法测曲率半径实验的主要仪器有:读数显微镜、Na光源、牛顿环仪用劈尖测细丝直径实验的主要仪器有:读数显微镜、Na光源、劈尖【实验原理】实验原理:实验内容一:牛顿环法测曲率半径图1如图所示,在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB,C点为接触点,这样在ACB和DCF之间,形成一层厚度不均匀的空气薄膜,单色光从上方垂直入射到透镜上,透过透镜,近似垂直地入射于空气膜。
分别从膜的上下表面反射的两条光线来自同一条入射光线,它们满足相干条件并在膜的上表面相遇而产生干涉,干涉后的强度由相遇的两条光线的光程差决定,由图可见,二者的光程差△’等于膜厚度e的两倍,即△’ =2e此外,当光在空气膜的上表面反射时,是从光密媒质射向光疏媒质,反射光不发生相位突变,而在下表面反射时,则会发生相位突变,即在反射点处,反射光的相位与入射光的相位之间相差,与之对应的光程差为/2 ,所以相干的两条光线还具有/2的附加光程差,总的光程差为:(1)当△满足条件:(2)时,发生相长干涉,出现第K级亮纹。
而当:(3)时,发生相消干涉,出现第k级暗纹。
因为同一级条纹对应着相同的膜厚,所以干涉条纹是一组等厚度线。
可以想见,干涉条纹是一组以C点为中心的同心圆,这就是所谓的牛顿环。
如图所示,设第k级条纹的半径为rk ,对应的膜厚度为ek,则:(4)在实验中,R的大小为几米到十几米,而ek 的数量级为毫米,所以R >>ek,e k 2相对于2Rk是一个小量,可以忽略,所以上式可以简化为(5) 如果rk是第k级暗条纹的半径,由式(1)和(3)可得:(6) 代入式(5)得透镜曲率半径的计算公式(7) 对给定的装置,R为常数,暗纹半径(8) 和级数k的平方根成正比,即随着k的增大,条纹越来越细。
同理,如果rk是第k级明纹,则由式(1)和(2)得(9)代入式(5),可以算出(10)由式(8)和(10)可见,只要测出暗纹半径(或明纹半径),数出对应的级数k,即可算出R。

初中物理光的干涉教案。
一、教学目标1、了解什么是光的干涉,掌握干涉的基本概念。
2、掌握干涉条纹的产生规律,解释干涉现象。
3、掌握双缝干涉、单缝干涉等常见光学干涉实验原理、方法及结果分析。
二、教学重点难点1、光的干涉及产生的规律。
2、双缝干涉实验原理及其结果分析。
三、教学方法1、课堂讲授、黑板写作法:让学生在理解教师讲授的内容的基础上进行知识的结构和整合。
2、图例解说法:通过丰富的图例,生动地介绍干涉及其规律。
3、实验教学法:通过实验的观察和分析,进一步加深对干涉产生原因和规律的理解。
四、教学流程一、引入环节教师通过播放相关视频、图片的形式,让学生对干涉概念有一个初步的认识和了解。
二、知识讲解1、光的干涉干涉是两束或者多束波相遇而产生的相互作用现象。
波的峰和谷相加构成了干涉条纹。
所以光的干涉本质上就是光波的干涉。
2、干涉条纹的产生规律干涉条纹是两波在相遇区域产生交织影响而形成的。
光的干涉有两种形式,一种是互补干涉,也就是叠加波增强,另一种是互逆干涉,也就是叠加波相消。
当波峰叠加时,增加和;而当波峰和波谷相遇,相互抵消,叠加波不再增强。
3、双缝干涉实验原理及其结果分析双缝干涉是一种经典的光学实验。
实验中,通过两个隔板分隔一束单色光,隔板中开有两个细缝,两个光线经过两个细缝同时射向屏幕,形成波峰和波谷的干涉条纹。
分析实验结果可以知道:干涉条纹的间距与光的波长有关,隔板缝宽、光的波长和缝间距的比值确定了干涉条纹的宽度和亮暗程度。
三、实验环节教师配合实验室,进行双缝干涉、单缝干涉实验的演示和实验结果分析。
让学生观察干涉条纹的形成,感受双缝干涉、单缝干涉的量级。
四、总结环节教师对学生进行干涉概念的再解释,让学生对干涉条纹的成因和形成规律有一个更加全面、深入的理解。
五、作业和反思布置学生进行双缝干涉实验数据分析和条纹宽度的计算。
同时根据学生反馈,进行教学方式的反思和改进。
五、教学后记初中物理教学的目的是为了帮助学生了解自然现象、探索规律、学会科学思维方法。

实验报告5数学系06级 蔡园青 2007年5月25日 PB06001093 实验题目:干涉法测微小量实验目的: 通过本次实验,学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法,同时加深对光的波动性的认识。
实验原理:用牛顿环测平凸透镜的曲率半径当曲率半径很大的平凸透镜的凸面放在一平面玻璃上时,在透镜的凸面与平面之间形成一个从中心O 向四周逐渐增厚的空气层。
当单色光垂直照射下来时,从空气层上下两个表面反射的光束产生干涉。
等厚干涉条纹也是一组以O 点为中心的明暗相间的同心圆,称为牛顿环。
两束光的光程差为 22λδ+=∆ (1)式中λ为入射光的波长,δ是空气层厚度,空气折射率1≈n 。
当光程差Δ为半波长的奇数倍时为暗环,若第m 个暗环处的空气层厚度为m δ,则有2λδ⋅=m m (2)R m <<δ,可得 Rr mm 22=δ (3) 式中r m 是第m 个暗环的半径。
由式(2)和式(3)可得λmR r m =2(4)我们将式(4)作一变换,将式中半径r m 换成直径D m , 展开整理后有λn D D R mn m 422-=+ (5)可见,如果我们测得第m 个暗环及第(m+n )个暗环的直径D m 、D m+n ,就可由式(5)计算透镜的曲率半径R 。
实验器材:钠灯,牛顿环仪,读数显微镜。
实验内容:1.测平凸透镜的曲率半径 (1) 观察牛顿环 1)将牛顿环仪放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
2)调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
(2) 测牛顿环直径 1)使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。
2)转动显微镜测微鼓轮,使显微镜筒沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第65环相切为止。

姓名:;学号;班级;教师________;信箱号:______ 预约时间:第_____周、星期_____、第_____~ _____节;座位号:_______预习操作实验报告总分教师签字一、实验名称等厚干涉二、实验目的(1) 观察和研究等厚干涉的现象及其特点 .(2) 练习用干涉法测量透镜的曲率半径、微小厚度 ( 或直径 ).三、实验原理(基本原理概述、重要公式、简要推导过程、重要图形等;要求用自己的语言概括与总结,不可照抄教材)利用透明薄膜上、下两表面对入射光的依次反射,入射光的振幅将分解成有一定光程差的几个部分.这是一种获得相干光的重要途径,被多种干涉仪所采用若两束反射光在相遇时的光程差取决于产生反射光的薄膜厚度,则同一干涉条纹所对应的薄膜厚度相同.这就是所谓的等厚干涉。
(见右图)总的光程差为:(1)当△满足条件:(2)时,发生相长干涉,出现第K级亮纹。
而当:(3)时,发生相消干涉,出现第k级暗纹。
因为同一级条纹对应着相同的膜厚,所以干涉条纹是一组等厚度线。
可以想见,干涉条纹是一组以C点为中心的同心圆,这就是所谓的牛顿环。
如图所示,设第k级条纹的半径为rk,对应的膜厚度为ek ,则:(4)在实验中,R的大小为几米到十几米,而ek的数量级为毫米,所以R >>ek ,ek2相对于2Rk 是一个小量,可以忽略,所以上式可以简化为(5)如果rk是第k级暗条纹的半径,由式(1)和(3)可得:(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置,R为常数,暗纹半径(8)和级数k的平方根成正比,即随着k的增大,条纹越来越细。
由于从劈尖的上下表面反射的两条光线来自同一条入射光线,它们满足相干条件并在劈尖的上表面相遇而产生干涉,干涉后的强度由相遇的两条光线的光程差决定,由图可见,二者的光程差等于劈尖厚度的两倍,即n = 0时,,即在两玻璃片交线处为零级暗条纹。
如果在细丝处呈现n = N级条纹,则待测细丝直径为(9)四、实验内容和步骤(要求用自己的语言概括与总结,不可照抄教材)1. 观察牛顿环。

干涉法测微小量实验一、实验简介:光的干涉现象表明了光的波动的性质,干涉现象在科学研究与计量技术中有着广泛的应用。
在干涉现象中,不论何种干涉,相邻干涉条纹的光程差的改变都等于相干光的波长,可见光的波长虽然很小,但干涉条纹间的距离或干涉条纹的数目是可以计量的。
因此,通过对干涉条纹数目或条纹移动数目的计量,可以得到以光的波长为单位的光程差。
利用光的等厚干涉可以测量光的波长,检验表面的平面度,球面度,光洁度,以及精确测量长度,角度和微小形变等。
二、实验原理:实验内容一:牛顿环法测曲率半径图1如图所示,在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB,C点为接触点,这样在ACB和DCF之间,形成一层厚度不均匀的空气薄膜,单色光从上方垂直入射到透镜上,透过透镜,近似垂直地入射于空气膜。
分别从膜的上下表面反射的两条光线来自同一条入射光线,它们满足相干条件并在膜的上表面相遇而产生干涉,干涉后的强度由相遇的两条光线的光程差决定,由图可见,二者的光程差△’等于膜厚度e的两倍,即△’ =2e此外,当光在空气膜的上表面反射时,是从光密媒质射向光疏媒质,反射光不发生相位突变,而在下表面反射时,则会发生相位突变,即在反射点处,反射光的相位与入射光的相位之间相差π,与之对应的光程差为λ /2 ,所以相干的两条光线还具有λ /2的附加光程差,总的光程差为:(1) 当△满足条件:,()(2) 时,发生相长干涉,出现第K级亮纹。
而当:,()(3) 时,发生相消干涉,出现第k级暗纹。
因为同一级条纹对应着相同的膜厚,所以干涉条纹是一组等厚度线。
可以想见,干涉条纹是一组以C点为中心的同心圆,这就是所谓的牛顿环。
如图所示,设第k级条纹的半径为r k,对应的膜厚度为e k,则:(4)在实验中,R的大小为几米到十几米,而e k的数量级为毫米,所以R >>e k,e k2相对于2R k是一个小量,可以忽略,所以上式可以简化为(5)如果r k是第k级暗条纹的半径,由式(1)和(3)可得:(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置,R为常数,暗纹半径(8)和级数k的平方根成正比,即随着k的增大,条纹越来越细。
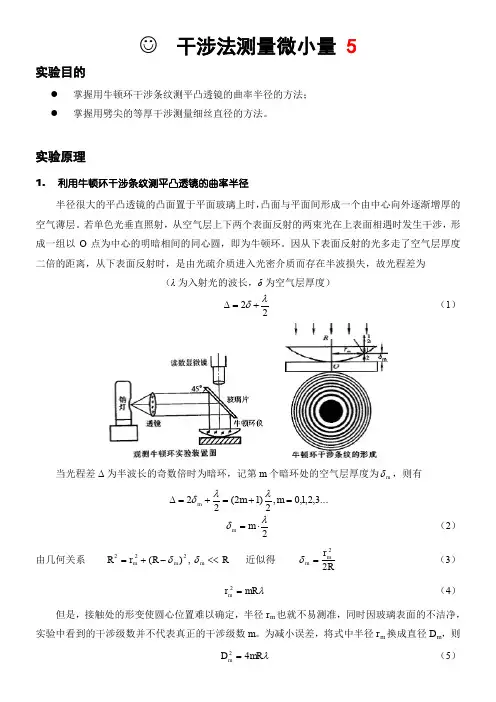
☺ 干涉法测量微小量 5实验目的● 掌握用牛顿环干涉条纹测平凸透镜的曲率半径的方法; ● 掌握用劈尖的等厚干涉测量细丝直径的方法。
实验原理1. 利用牛顿环干涉条纹测平凸透镜的曲率半径半径很大的平凸透镜的凸面置于平面玻璃上时,凸面与平面间形成一个由中心向外逐渐增厚的空气薄层。
若单色光垂直照射,从空气层上下两个表面反射的两束光在上表面相遇时发生干涉,形成一组以O 点为中心的明暗相间的同心圆,即为牛顿环。
因从下表面反射的光多走了空气层厚度二倍的距离,从下表面反射时,是由光疏介质进入光密介质而存在半波损失,故光程差为(λ为入射光的波长,δ为空气层厚度)22λδ+=∆ (1)当光程差Δ为半波长的奇数倍时为暗环,记第m 个暗环处的空气层厚度为m δ,则有...3,2,1,0,2)12(22=+=+=∆m m m λλδ2λδ⋅=m m (2)由几何关系222)(m mR r R δ-+=, R m <<δ近似得 Rr mm 22=δ(3)λmR r m =2 (4)但是,接触处的形变使圆心位置难以确定,半径r m 也就不易测准,同时因玻璃表面的不洁净,实验中看到的干涉级数并不代表真正的干涉级数m 。
为减小误差,将式中半径r m 换成直径D m ,则λmR D m 42= (5)对第m+n 个暗环有λR n m D n m )(42+=+ (6)故(7)所以,我们只需测D m 和D m+n ,就可利用上式计算曲率半径R 。
2. 劈尖的等厚干涉测细丝直径两玻璃片和细丝叠在一起如图所示,形成空气劈尖。
当用单色光垂直照射时,会产生一组明暗相间、平行于细丝的干涉条纹。
根据前面讨论知,在两玻璃片交线处,为零级暗条纹,第m 级暗纹处空气劈尖的厚度2λmd = (8)如果在细丝处呈现N 级条纹,则待测细丝直径实验室常用劈尖盒。
使用时切勿倒置木盒或将玻璃片倒出,以免细丝位置变动。
实验仪器单色光源,显微镜,牛顿环仪,待测细丝,平凸透镜。
实验题目:干涉法测微小量实验目的:学习、掌握利用光的干涉原理检验光学元件表面集合特征的方法,用劈尖的等厚干涉测量细丝直径的方法,同时加深对光的波动性的认识。
实验原理:1、用牛顿环测平凸透镜的曲率半径当曲率很大的平凸透镜的凸面放在一平面玻璃上时,会产生一组以O 为中心的明暗相间的同心圆环,称为牛顿环。
如图,1、2两束光的光程差为22λδ+=∆,式中λ为入射光的波长,δ是空气层厚度,空气折射率1≈n 。
如果第m 个暗环处空气厚度为δm ,则有...3,2,1,0,2)12(22=+=+=∆m m m λλδ 故得到:2λδ⋅=m m 。
利用几何关系有222)(m m R r R δ-+=,并根据R m <<δ,得到Rr mm 22=δ,联系以上两式,有λmR r m =2换成直径,并考虑第m+n 个环和第m 个环,有λR n m D n m )(42+=+,λmR D m 42=,故λn D D R mn m 422-=+那么测量出D m+n 和D m 就可以根据这个表达式得到R 。
2、劈尖的等厚干涉测细丝直径两片叠在一起的玻璃片,在它们的一端夹一直径待测的细丝,于是两玻璃片之间形成一空气劈尖。
当用单色光垂直照射时,会产生干涉现象。
因为程差相等的地方是平行于两玻璃片交线的直线,所以等厚干涉条纹是一组明暗相间、平行于交线的直线。
设入射光波为λ,则得第m 级暗纹处空气劈尖的厚度2λm d =。
由此可知,m=0时,d=0,即在两玻璃片交线处,为零级暗条纹。
如果在细丝处呈现m=N 级条纹,则待测细丝直径2λ⋅=N d 。
3、利用干涉条纹检验光学表面面形实验内容: 1. 测平凸透镜的曲率半径 (1) 观察牛顿环 1) 将牛顿环仪按图7.2.1-5所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
2) 调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
《散斑干涉测微小位移》【实验目的】1、通过拍摄自由空间散斑图及成像散斑图,初步了解激光散斑现象及其特点;2.擎握应用散斑干涉全息图设计方法;3、用二次曝光散斑干涉图测量物体表面的面内位移;4、设计用二次曝光散斑图测量透明固体(玻璃)的厚度及其非均匀性。
【实验原理分析与讨论】1、散斑的形成及特征激光自散射体表面漫反射或通过一个透明散射体(加毛玻璃)时,在散射体的表面和附近空间的光场中,可以观察到或用照相记录下来一种无规分布的亮暗斑纹。
这种斑纹称为激光散斑。
它是由散射体上每个面积元发出的基元光波的干涉作用造成的。
在全息术和相干光成像系统中,散斑的存在会影响分辨率,是一种令人讨厌的有害噪声。
近年来,通过研究逐渐发现了它的一些有用的特性。
在某些新的光学系统中,散斑不再是噪声因素,而是一种有用的信息载体.激光散斑.特别是散斑照相和散斑干涉,在表面粗糙度测量、图像处理、运动分析、振动分析、眼球缺陷分析和星体度量学等科技领域中有着广泛的应用,在光学小己成为一个重要的分支。
激光散斑通常可分为空间散斑和像面散斑两类:12空间散斑:如果在散射体G 的正面距离z 的地方放置全息干板记录散斑结构,其散斑的平均直径为 1.22z ds Dλ≈,其中D 是被照亮的散射面直径。
如果在侧面接收,则散斑的平均长度2()z ls Dλ≈ 像面散斑: 像面散斑的平均直径:11.22() 1.22(1+)z ds F Dλλβ≈=式中z1(像距),D (透镜的孔径)β(横向放大率)F (相对孔径的倒数)当散射面位于无限远时,成像面与后焦面重合,散斑的平均直径为1.22() 1.22f ds F Dλλ≈= f 透镜焦距。
2、散斑干涉全息图测量面内位移的光路设计空间散斑(未加成像透镜)非平行光漫反射散斑 像面散斑(放大率>1;<1)散斑干涉光路设计 平行光 空间散斑(未加成像透镜)像面散斑(加成像透镜:放大率>1;<1)空间散斑(未加成像透镜)非平行光透射散斑 像面散斑(放大率>1;<1)平行光 空间散斑(未加成像透镜)面散斑(加成像透镜:放大率>1;<1)3.用二次曝光散斑图测量面内位移(1)反射成像散斑:二次曝光散斑图测微小位移如图是拍摄散斑图的光路布置之一,其中S 是具有光学粗糙表面的平面物体,用扩束后的激光光束照射,L 是成像透镜,H 是全息干板.置于像平面上,成像透镜L 将s 面成像于记录平面H 上,形成成像散斑,如果对浏试物体在运动前后应用二次曝光法拍摄散斑图样,并假定位移的量值大于散斑特征尺寸,那么,在同一底片上就记录了两个同样的但位置稍微错开的散斑图。
⼲涉法测微⼩量_讲义⼲涉法测微⼩量实验要求:1.预习阶段(1)认真阅读实验讲义。
(2)准备预习报告。
预习报告控制在1到2页纸内,不要原封不动照抄讲义,应融⼊⾃⼰对实验原理的理解。
2. 实验阶段(1) 维护良好的课堂秩序,在实验室内尽量保持安静。
(2) 维护整洁的实验环境,不要将⽔杯等放在试验台上,不得在实验室内吃⼝⾹糖。
(3) 爱护实验设备,轻拿轻放。
在⽼师讲解后才能动⼿操作。
并且在动⼿前应仔细阅读实验注意事项和操作说明。
(4) 如实记录实验数据,不得篡改、抄袭。
(5) 实验数据经指导⽼师签字、实验设备整理好后⽅可离开。
3. 报告撰写阶段(1) 本实验要求计算平凸透镜曲率半径R的不确定度。
注意事项:1. 爱护光学元件光学实验中使⽤的⼤部分光学元件是玻璃制成的,光学表⾯经过精⼼抛光。
使⽤时要轻拿、轻放,避免碰撞、损坏元件。
任何时候都不要⽤⼿触及光学表⾯(镀膜⽚或光在此表⾯反射或折射),只能拿磨砂⾯(光线不经过的⾯⼀般都磨成⽑⾯,如透镜的侧⾯,棱镜的上下底⾯等),不要对着光学元件表⾯说话、咳嗽、打喷嚏等。
2. 钠灯需提前预热10分钟,实验过程中不要关闭,不要震动。
若关闭,需等完全冷却下来才能再次开启。
光的⼲涉现象表明了光的波动性质,⼲涉现象在科学研究与计量技术中有着⼴泛的应⽤。
在⼲涉现象中,不论是何种⼲涉,相邻⼲涉条纹的光程差的改变都等于相⼲光的波长,可见光的波长虽然很⼩,但⼲涉条纹间的距离或⼲涉条纹的数⽬却是可以计量的。
因此,通过对⼲涉条纹数⽬或条纹移动数⽬的计量,可得到以光的波长为单位的光程差。
利⽤光的等厚⼲涉现象可以测量光的波长,检验表⾯的平⾯度、球⾯度、光洁度,精确地测量长度、⾓度,测量微⼩形变以及研究⼯件内应⼒的分布等。
通过本次实验,学习、掌握利⽤光的⼲涉原理检验光学元件表⾯⼏何特征的⽅法,⽤劈尖的等厚⼲涉测量细丝直径的⽅法,同时加深对光的波动性的认识。
实验原理1.⽤⽜顿环测平凸透镜的曲率半径当曲率半径很⼤的平凸透镜的凸⾯放在⼀平⾯玻璃上时,见图7.2.1-1,在透镜的凸⾯与平⾯之间形成⼀个从中⼼O 向四周逐渐增厚的空⽓层。
干涉法测量微小量28435实验报告 5-25系05级 鄂雁祺 2006年4月22日 PB05025003 实验题目:干涉法测微小量实验目的: 通过本次实验,学习、掌握利用光的干涉原理检验光学元件表面几何特征的方法,同时加深对光的波动性的认识。
实验原理:用牛顿环测平凸透镜的曲率半径当曲率半径很大的平凸透镜的凸面放在一平面玻璃上时,在透镜的凸面与平面之间形成一个从中心O 向四周逐渐增厚的空气层。
当单色光垂直照射下来时,从空气层上下两个表面反射的光束产生干涉。
等厚干涉条纹也是一组以O 点为中心的明暗相间的同心圆,称为牛顿环。
两束光的光程差为 22λδ+=∆ (1)式中λ为入射光的波长,δ是空气层厚度,空气折射率1≈n 。
当光程差Δ为半波长的奇数倍时为暗环,若第m 个暗环处的空气层厚度为m δ,则有2λδ⋅=m m (2)R m <<δ,可得 Rr mm 22=δ (3)式中r m 是第m 个暗环的半径。
由式(2)和式(3)可得λmR r m=2(4) 我们将式(4)作一变换,将式中半径r m 换成直径D m , 展开整理后有λn D D R mn m 422-=+ (5)可见,如果我们测得第m 个暗环及第(m+n )个暗环的直径D m 、D m+n ,就可由式(5)计算透镜的曲率半径R 。
实验器材:钠灯,牛顿环仪,读数显微镜。
实验内容:1.测平凸透镜的曲率半径(1) 观察牛顿环 1)将牛顿环仪放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
2)调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
(2) 测牛顿环直径1) 使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。
2) 转动显微镜测微鼓轮,使显微镜筒沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第65环相切为止。
《干涉法测微小量》实验报告姓名学号学院专业班级一.实验目的学习掌握利用光的干涉原理检验光学元件表面集合特征的方法,用劈尖的等厚干涉测量细丝直径的方法,同时加深对光的波动性的认识二.实验仪器读数显微镜、钠光灯及电源、牛顿环仪、劈尖等三、实验原理1、用牛顿环测平凸透镜的曲率半径详见实验指导书2、劈尖的等厚干涉测细丝直径详见实验指导书四、实验步骤1. 观察牛顿环。
(1) 将牛顿环仪放置在读数显微镜镜筒和入射光调节架下方,调节玻璃片的角度,使通过显微镜目镜观察时视场最亮。
(2) 调节目镜,看清目镜视场的十字叉丝后,使显微镜镜筒下降到接近牛顿环仪然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度和显微镜,使条纹清晰。
2. 测牛顿环半径。
(1) 使显微镜十字叉丝交点和牛顿环中心重合,并使水平方向的叉丝和标尺平行(与显微镜移动方向平行)。
(2) 转动显微镜微调鼓轮,使显微镜沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第 45 环相切为止。
记录标尺读数。
(3) 反向转动鼓轮,当竖丝与第 40 环相切时,记录读数显微镜上的位置读数,然后继续转动鼓轮,使竖丝依次与第 35、30、25、20、15、10、5 环相切,顺次记下读数。
(4) 继续转动鼓轮,越过干涉圆环中心,记下竖丝依次与另一边的 5、10、15、20、25、30、35、40 环相切时的读数。
3.利用逐差法处理得到的数据,得到牛顿环半径 R。
4. 观察劈尖干涉条纹。
(1) 将劈尖放置在读数显微镜镜筒和入射光调节架下方,调节玻璃片的角度,使通过显微镜目镜观察时视场最亮。
(2) 调节目镜,看清目镜视场的十字叉丝后,使显微镜镜筒下降到接近劈尖然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度和显微镜,使条纹清晰。
5. 测量。
(1) 使显微镜的十字叉丝交点与劈尖中心重合,并使其与显微镜镜筒移动方向平行。
(2) 在劈尖玻璃面的三个不同部分,测出 20 条暗纹的总长度,测 3 个求平均值。
干涉法测微小量(已批阅)实验题目:干涉法测微小量实验目的:学习、掌握利用光的干涉原理检验光学元件表面集合特征的方法,用劈尖的等厚干涉测量细丝直径的方法,同时加深对光的波动性的认识。
实验原理:1、用牛顿环测平凸透镜的曲率半径当曲率很大的平凸透镜的凸面放在一平面玻璃上时,会产 生一组以O 为中心的明暗相间的同心圆环,称为牛顿环。
如图,1、2两束光的光程差为22λδ+=∆,式中λ为入射光 的波长,δ是空气层厚度,空气折射率1≈n 。
如果第m 个暗环处空气厚度为δm ,则有...3,2,1,0,2)12(22=+=+=∆m m m λλδ 故得到:2λδ⋅=m m 。
利用几何关系有222)(m mR r R δ-+=,并根据R m <<δ,得到Rr mm 22=δ,联系以上两式,有λmR r m =2换成直径,并考虑第m+n 个环和第m 个环,有λR n m D n m )(42+=+,λmR D m42=,故λn D D R mn m 422-=+ 那么测量出D m+n 和D m 就可以根据这个表达式得到R 。
2、劈尖的等厚干涉测细丝直径两片叠在一起的玻璃片,在它们的一端夹一直径待测的细丝,于 是两玻璃片之间形成一空气劈尖。
当用单色光垂直照射时,会产生干涉现象。
因为程差相等的地方是平行于两玻璃片交线的直线,所以等厚干涉条纹是一组明暗相间、平行于交线的直线。
设入射光波为λ,则得第m 级暗纹处空气劈尖的厚度2λm d =。
由此可知,m=0时,d=0,即在两玻璃片交线处,为零级暗条纹。
如果在细丝处呈现m=N 级条纹,则待测细丝直径2λ⋅=N d 。
3、利用干涉条纹检验光学表面面形实验内容: 1.测平凸透镜的曲率半径(1) 观察牛顿环 1)将牛顿环仪按图7.2.1-5所示放置在读数显微镜镜筒和入射光调节木架的玻璃片的下方,木架上的透镜要正对着钠光灯窗口,调节玻璃片角度,使通过显微镜目镜观察时视场最亮。
2)调节目镜,看清目镜视场的十字叉丝后,使显微镜筒下降到接近玻璃片,然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度及显微镜,使条纹更清楚。
(2) 测牛顿环直径 1)使显微镜的十字叉丝交点与牛顿环中心重合,并使水平方向的叉丝与标尺平行(与显微镜筒移动方向平行)。
2) 转动显微镜测微鼓轮,使显微镜筒沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第35环相切为止。
3) 反向转动鼓轮,当竖丝与第30环相切时,记录读数显微镜上的位置读数d 30,然后继续转动鼓轮,使竖丝依次与第25、20、15、10、5环相切,顺次记下读数d 25,d 20,d 15,d 10,d 5。
4) 继续转动鼓轮,越过干涉圆环中心,记下竖丝依次与另一边的5、10、15、20、25、30环相切时的读数5'd 、10'd 、15'd 、20'd 、25'd 、30'd 。
重复测量两次,共测两组数据。
(3) 用逐差法处理数据第30环的直径303030'd d D -=,同理,可求出D 25、D 20…D 5,式(7)中,取n=15,求出2215m m D D -+,代入式(7)计算R 和R 的标准差。
2. 测细丝直径(1) 观察干涉条纹将劈尖盒放在曾放置牛顿环的位置,同前法调节,观察到干涉条纹,使条纹最清晰。
(2) 测量 1)调整显微镜及劈尖盒的位置,当转动测微鼓轮使镜筒移动时,十字叉丝的竖丝要保持与条纹平行。
2)在劈尖玻璃面的三个不同部分,测出20条暗纹的总长度l ∆,测三次求其平均值及单位长度的干涉条纹数ln ∆=20。
3) 测劈尖两玻璃片交线处到夹细线处的总长度L ,测三次,求平均值。
4)由公式,求细丝直径22022λλλ⋅∆⋅=⋅=⋅=l L nL N d实验数据:1、测平凸透镜曲率半径(表格中数据单位为mm )表一:原始数据和直接计算得到的数据(注:此表格中1D 2D 3D 是通过计算(相减)得到的,由于计算简单直接,故写在表格中)光波长589.3nm2、测细丝直径光波长589.3nm 劈尖长度L=39.043mm20条暗纹长度(三次测量,mm ):17.590---20.531 20.682---23.607 23.776---26.752数据处理:1、测平凸透镜曲率半径 以下均取P=0.95:mm mm D 188.83188.8183.8193.830=++=mm mm 005.013)188.8188.8()188.8183.8()188.8193.8(22230=--+-+-=σ展伸不确定度mm mm C k t U B pp D 013.0)3005.096.1()3005.030.4()()3(22223030=⨯+⨯=∆+=σ mm mm D 577.73583.7575.7574.725=++=mm mm 005.013)577.7583.7()577.7575.7()577.7574.7(22225=--+-+-=σ展伸不确定度mm mm C k t U B pp D 013.0)3005.096.1()3005.030.4()()3(22222525=⨯+⨯=∆+=σ mm mm D 809.63812.6803.6812.620=++=mm mm 005.013)809.6812.6()809.6803.6()809.6812.6(22220=--+-+-=σ展伸不确定度mm mm C k t U B pp D 013.0)3005.096.1()3005.030.4()()3(22222020=⨯+⨯=∆+=σ mm mm D 006.63003.6007.6009.615=++=mm mm 003.013)006.6003.6()006.6007.6()006.6009.6(22215=--+-+-=σ展伸不确定度mm mm C k t U B pp D 008.0)3005.096.1()3003.030.4()()3(22221515=⨯+⨯=∆+=σ mm mm D 070.53071.5067.5072.510=++=mm mm 003.013)070.5071.5()070.5067.5()070.5072.5(22210=--+-+-=σ展伸不确定度mm mm C k t U B pp D 008.0)3005.096.1()3003.030.4()()3(22221010=⨯+⨯=∆+=σ mm mm D 991.33889.3886.3899.35=++=mm mm 007.013)991.3889.3()991.3886.3()991.3899.3(2225=--+-+-=σ展伸不确定度mm mm C k t U B ppD 018.0)3005.096.1()3007.030.4()()3(2222510=⨯+⨯=∆+=σ 利用逐差法处理上述数据。
根据前述公式λn D D R mn m 422-=+,则不确定度的传递公式应该是2222)4(2)4(2λλn UD n U D U m m n m n m R +=++那么:mmnm mm mm n D D R 9.8753.589154)006.6()188.8(4222152301=⨯⨯-=-=λmm n U D n U D U R 26226221515221515151521)103.589154008.0006.6(2)103.589154013.0188.8(2)4(2)4(2--++⨯⨯⨯⨯+⨯⨯⨯⨯=+=λλ =6.6mmmmnm mm mm n D D R 7.8963.589154)070.5()577.7(4222102252=⨯⨯-=-=λmm n U D n U D U R 26226221010221510151022)103.589154008.0070.5(2)103.589154013.0577.7(2)4(2)4(2--++⨯⨯⨯⨯+⨯⨯⨯⨯=+=λλ =6.0mmmmnm mm mm n D D R 8.8603.589154)991.3()809.6(422252203=⨯⨯-=-=λmm n U D n U D U R 2622622552215515523)103.589154018.0991.3(2)103.589154013.0809.6(2)4(2)4(2--++⨯⨯⨯⨯+⨯⨯⨯⨯=+=λλ=6.4mm对以上值取平均:mm mm R R R R 8.877)8.8607.8969.875(31)(31321=++⨯=++=同时mm mm U U U U R R R R 6.34.60.66.63131222232221=++⨯=++= R 不要分开求,先求总的D12-D22的平均值,求不确定度的时候也是,上式平方和的关系从何而来?故最终结果表示成:95.0,)6.38.877(=±=±=P mm U R R R 2、测细丝直径 以下均取P=0.95:三次测量的长度分别为2.941mm 、2.925mm 、2.976mm平均值mm mm l 947.23976.2925.2941.2=++=mm mm l 024.013)947.2976.2()941.2925.2()947.2941.2(222=--+-+-=σ展伸不确定度 mm mm C k t U B plpl 060.0)3005.096.1()3024.030.4()()3(2222=⨯+⨯=∆+=σ 此处由于L 值(39.043mm )直接从劈尖贴纸上读出,认为是一个确定值(不知道可以这样处理不?)。
可以当常数也可以当一次测量量那么mm mm l L d 078.02103.589947.2043.39202206=⨯⨯⨯=⨯=-λ这个有效数字不对 mm mm d lU U l d 002.0078.0947.2060.0=⨯==于是最终结果写成95=P=±Udd±mm,.0)002078.0.0(=d实验小结:1、本实验实验原理比较简单,实验操作也不复杂,但是数牛顿环和条纹时容易数错,考验细心和耐心;2、实验中应特别注意回程差的影响,测量时一旦开始向某个方向转动读数显微镜,就一定要保证本次测量绝对不能向反方向转;3、本实验数据处理比较繁琐,需要特别注意;4、在牛顿环实验中,个人认为直接从读数显微镜中操作更简单方便,而用摄像头的话,应考虑不清晰的图象的影响。