哈工大通信专业真题803信号与系统和数字逻辑电路(2014)
- 格式:pdf
- 大小:7.51 MB
- 文档页数:6
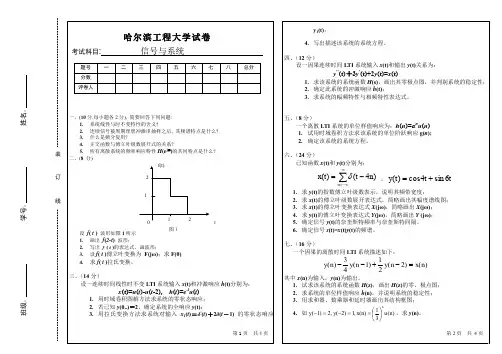
第2页 共 4页y 1(t);4. 写出描述该系统的系统方程。
四、(12分)设一因果连续时间LTI 系统输入x (t)和输出y (t)关系为:y ''(t)+3y '(t)+2y (t)=x (t)1. 求该系统的系统函数H (s),画出其零极点图,并判别系统的稳定性;2. 确定此系统的冲激响应h (t);3. 求系统的幅频特性与相频特性表达式。
五、(8分)一个离散LTI 系统的单位样值响应为:h (n )=αnu (n )1. 试用时域卷积方法求该系统的单位阶跃响应g(n );2. 确定该系统的系统方程。
六、(24分)已知函数x (t)和y (t)分别为:∑∞-∞=-=n n t t x )4()(δ ,t t t y 6sin 4cos )(+=1. 求y (t)的指数傅立叶级数表示,说明其频带宽度;2. 求x (t)的傅立叶级数展开表达式,简略画出其幅度谱线图;3. 求x (t)的傅立叶变换表达式X (j ω),简略画出X (j ω);4. 求y (t)的傅立叶变换表达式Y (j ω),简略画出Y (j ω);5. 确定信号y (t)的奈奎斯特频率与奈奎斯特间隔。
6.确定信号s (t)=x (t)y (t)的频谱。
七、(16分)一个因果的离散时间LTI 系统描述如下:)()2(21)1(43)(n x n y n y n y =-+--其中x (n)为输入,y (n)为输出。
1. 试求该系统的系统函数H (z),画出H (z)的零、极点图;2. 求系统的单位样值响应h (n),并说明系统的稳定性;3. 用求和器、数乘器和延时器画出其结构框图;4. 如)(31)(,1)2(,2)1(n u n x y y n⎪⎭⎫⎝⎛==-=-,求y (n)。
第3页 共4页 第4页 共 4页八、(8分)假设x (t)的傅立叶变换X (j ω)=0,|ω| >ωm ,而信号g(t )可表示成)}sin (]cos )({[cos )()(ttt t x t t x t g c c c πωωω*-= 式中*记做卷积,而ωc >ωm 。

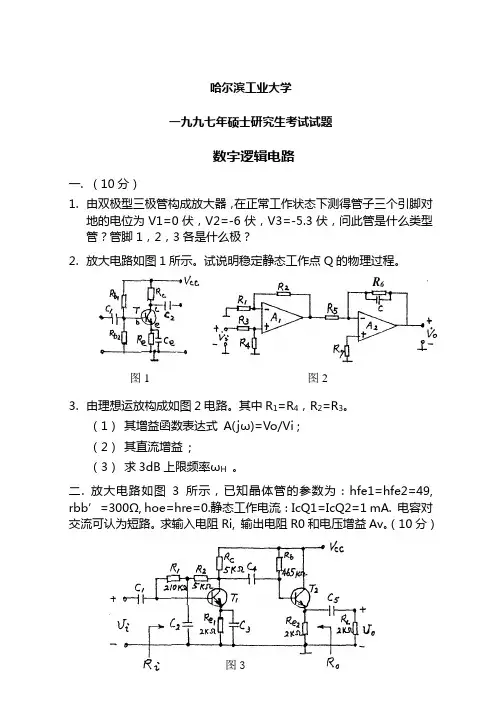
哈尔滨工业大学一九九七年硕士研究生考试试题数字逻辑电路一. (10分)1. 由双极型三极管构成放大器,在正常工作状态下测得管子三个引脚对地的电位为V1=0伏,V2=-6伏,V3=-5.3伏,问此管是什么类型管?管脚1,2,3各是什么极?2. 放大电路如图1所示。
试说明稳定静态工作点Q 的物理过程。
3. 由理想运放构成如图2电路。
其中R 1=R 4,R 2=R 3。
(1) 其增益函数表达式 A(j ω)=Vo/Vi ; (2) 其直流增益 ;(3) 求3dB 上限频率ωH 。
二. 放大电路如图3所示,已知晶体管的参数为:hfe1=hfe2=49, rbb ’=300Ω, hoe=hre=0.静态工作电流:IcQ1=IcQ2=1 mA. 电容对交流可认为短路。
求输入电阻Ri, 输出电阻R0和电压增益Av 。
(10分)R 6图1 图2三.回答下列各题(20分)1. 在下图所示电路中,M1为TTL 与非门,VoH=3.6V, 最大拉电流Ilmax=13mA, 要实现Rb 应 > ( ) Rb 应 < ( )2. 在下图所示电路中M1,M2,M3为TTL OC 门,M4为TTL 与非门,V1,V2为二只20k Ω/V 的电压表,问:S1断开 V1=( ) V2=( )S1合上 A1A2, B1B2, C1C2全为低 V1=( ) V2=( ) S1合上 A1A2为高,B1B2, C1C2为低 V1=( ) V2=( ) 3. 写出下面电路真值表及逻辑表达式。
4. 设计一个序列信号检测器用以及检测0101。
当检测到此码组时输出为1,否则输出为0。
只画出状态转换图。
F1=AB ,F2=AB四.试分别用八选一数据选择器、PLA 设计下列函数。
( 10分) F =)14,13,11,9,7,6,5,4,3(4m五.试用最少数目的与非门将下图(a),(b),(c)所示各电路合并成一个多输出端的组合网络,要求输入变量仅以原变量出现。

信号与系统试题第1页(共8页)课程代码:座位号:2013-2014学年一学期通信原理期末考试试卷(B 卷)《通信原理》试卷姓名:学号:专业:学院:信息科学与工程学院班级:2014年1月一、选择题(10小题,共20分) 1、某二元码序列传信率为2400b/s,若改用八元码序列传送消息,则码元传输速率为[ ]。
A .1200B B.800B C.600B D.300B2、产生频率选择性衰落的原因是[ ]。
A .幅频畸变 B.相频畸变 C .多径传播 D.瑞利衰落3、在模拟调制当中,属于非线性调制的是[ ]。
a 、DSBb 、AMc 、FMd 、SSB4.一个信号x (t ) = 2cos 400πt + 6cos 40πt ,用f s =500Hz 的抽样频率对它理想抽样,若抽样后的信号经过一个截止频率为400Hz 的理想低通滤波器,则输出端有以下频率[ ]。
a 、20Hz200Hz400Hz b 、 20Hz180Hz3800Hz c 、20Hz200Hz300Hz d 、180Hz220Hz380Hz5.采用13 折线A 率对信号进行非均匀量化编码,通常编码输出的二进制数的位数为[ ]。
a 、6b 、7c 、8d 、96.通过抽样可以使模拟信号实现[ ]。
A.时间和幅值的离散 B.幅值上的离散 C.时间上的离散 D.频谱上的离散7、为了解决连0 码而无法提取位同步信号的问题,人们设计了[ ]。
a、AMI 码b、多进值码c、HDB3 码d、差分码8、右图采用的是什么键控法产生什么信号[ ]。
A. 相移 2FSKB. 频移 2ASKC. 相移 2PSKD. 频移 2FSK9、当采用同步解调或相干检测时,接收端需要提供一个与发射端调制载波同频同相的相干载波,而这个相干载波的获取就称为[ ]。
A. 位同步B. 群同步C. 码元同步D. 载波同步10、下图中,a信号为未调制数字信号,b为已调信号,请问要得到b图信号需经过什么调制[ ]。

第2页 共 2页Figure 1 Figure 22. (12 points)series coefficients:X [k ] = -j δ[k - 2] + j δ[k +2] + 2δ[k - 3] + 2δ[k + 3], ω0 = π(2) Determine the discrete-time Fourier series (DTFS) coefficients of the periodic signals depicted in Fig.3.Figure 3 Figure 46. (10 points)Determine and draw sketches of the Fourier series and Fourier transform representation of the square wave depicted in Fig.47. (8 points)(1) Compute the discrete-time Fourier transform (DTFT) of the signal depicted in Fig.5.Figure 5 Figure 6(2) Draw the Fourier transform of a impulse-train sampled version of the continuous-time signal having the Fourier transform depicted in Fig.6 for (a) T = 1/2(s) and (b) T = 2(s), where T is sampling period.8. (6 points)Shown in Fig.7 is the frequency response H (j ω) of a continuous-time filter. For each of the input signals x (t ) below, determine the filtered output signal y (t ).(1) x (t ) = cos(2πt +θ) (2) x (t ) = cos(4πt +θ)第3页 共4页 第4页 共 4页Figure 79. (8 points)Find the inverse Fourier transform of the following spectra: (1) X (j ω) = 2δ(ω - 4) (2) X (e j ω) = 2cos(2ω)(3) X (j ω) = ⎩⎨⎧><πωπωω,0,cos 2(4) X (e j ω) = ⎩⎨⎧<<-otherw ise02 4,/,πωπωj e , on -π < ω < π10. (16 points)Consider a continuous-time LTI system for which the input x (t ) and output y (t ) are related by the differential equationy" (t ) - y' (t ) - 6y (t ) = x' (t ) + x (t )(1) Determine the frequency response H (j ω) of the system.(2) Determine the system function H (s) of the system. Sketch the pole-zero plot of H (s )(3) Determine the system impulse response h (t ) for each of the following cases:(a) The system is stable; (b) The system is causal.(4) Let x (t ) = e -2t u (t ). Find the output y (t ) of the causal system.11. (6 points)Consider a message signal m (t ) with the spectrum shown in Fig.8. The message bandwith ωm = 2π×103 rad/s. The signal is applied to a product modulator, together with a carrier wave A c cos(ωc t ), producing the modulated signal s (t ). The modulated signal is next applied to a synchronous demodulator (shown in Fig.9).(1) Determine the spectrum of the demodulator output when (a) the carrier frequency ωc = 2.5π×103 rad/s and (b) the carrier frequency ωc = 1.5π×103 rad/s.(2) What is the lowest carrier frequency for which each component of the modulated signal s (t ) is uniquely determined by m (t ).Figure 8 Figure 912. (6 points)(1) Draw a sketch of the spectrum ofx (t ) = cos(50πt )sin(700πt )Label the frequencies and complex amplitudes of each component.(2) Determine the minimum sampling frequency that can be used to sample x (t ) without aliasing for any of the components.。

第一章(绪论)习题及其答案【题1-1】设英文字母E 出现的概率为0.105,x 出现的概率为0.002。
试求E 及x 的信息量。
【答案1-1】字母E 出现的概率()0.105p E =,由信息量公式,可知其信息量为:2211log log () 3.25()0.105E I bit p E === 字母x 出现的概率为()0.002p x =,由信息量公式,可知其信息量为:2211log log ()8.97()0.002x I bit p x ===【题1-2】某信息源的符号集由A,B,C,D 和E 组成,设每一符号独立出现,其出现概率分别为1/4,1/8,1/8,3/16和5/16。
试求该信息源符号的平均信息量。
【答案1-2】直接利用公式21()()log ()ni i i H x p x p x ==-∑( bit/符号),将()1/4p A =,()1/8p B =,()1/8p C =,()3/16p D =,()5/16p E =代入求解,有2122222()()log ()1111113355log log log log log 448888161616162.23/ni i i H x p x p x bit ==-=-----=∑符号【题1-3】设有4个消息A 、B 、C 和D 分别以概率1111,,,4882A B C D p p p p ====传输,每个消息的出现是相互独立的,试计算其平均消息量。
【答案1-3】22222111111111()()log ()log log log log 44888822 1.75/ni i i H x p x p x bit ==-=----=∑符号【题1-4】一个由字母A,B,C,D 组成的字,对于传输的每一个字母用二进制脉冲编码,00代替A,01代替B,10代替C,11代替D,每个脉冲宽度为5ms :1)不同的字母是等可能出现时,试计算传输的平均信息速率;2)若每个字母出现的可能性分别为1113,,,54410A B C D p p p p ====,试计算传输的平均信息速率。


2010年硕士研究生入学考试大纲考试科目名称:信号与系统+数字逻辑电路考试科目代码:[803]一、考试要求:要求考生全面、系统地掌握《信号与系统》和《数字电路》课程的基本概念、原理、方法与应用,具有较强的分析、设计和解决问题的能力。
二、考试内容:(一)《信号与系统》部分1)信号分析的理论基础a:信号的基本概念和典型信号b:信号的时域分解与变换,卷积2)傅里叶变换a:傅里叶级数,傅里叶变换,傅里叶变换的性质b:周期信号的傅里叶变换,抽样信号的频谱3)拉普拉斯变换a:拉普拉斯变换与反变换b:拉普拉斯变换的性质4)Z变换a:Z变换及其收敛域,Z变换的性质,Z反变换,b:Z变换与拉普拉斯变换的关系5)连续系统的时域分析a:连续系统的经典解法b:零输入响应,冲激响应与阶跃响应,零状态响应6)连续系统的频域分析a:傅里叶变换分析法b:无失真传输条件c:理想低通滤波器7)连续系统的复频域分析a:拉普拉斯变换分析法b:系统函数,极零点分布与时域响应特性,极零点分布与系统频率特性c:线性系统的模拟8)离散系统的时域分析a:离散系统的描述和模拟b:差分方程的经典解法,零输入响应和零状态响应9)离散系统的Z域分析a:离散系统的Z变换分析法b:离散系统的系统函数及频率响应10)系统的状态变量分析法a:状态方程的建立b:连续系统和离散系统的状态方程解法(二) 《数字逻辑电路》部分1)数制与编码a:数制和编码的基本概念,不同数制之间的转换b:二进制数的运算2)逻辑代数基础a:逻辑代数基本概念,逻辑函数的表示方法b:逻辑函数的化简及实现3)门电路a:TTL门电路工作原理与输入输出特性b:OC门、三态门(TS)原理与应用,MOS门电路4)组合电路a:组合逻辑电路的分析与设计方法b:典型中、小规模集成组合电路原理与应用5)触发器a:触发器基本原理与应用b:不同触发器类型之间的转换6)时序逻辑电路a:时序逻辑电路的概念b:同步时序电路的分析与设计c:集成计数器和移位寄存器的设计与应用d:异步时序电路的基本概念7)算术运算电路a:数值比较器、加法电路、乘法电路原理与应用8)存储器与可编程逻辑器件a:RAM、ROM的基本原理和扩展b:可编程逻辑器件的基本原理和应用9)模数和数模转换a:A/D、D/A转换的基本概念、基本原理与典型转换的方法三、试卷结构:a)考试时间:180分钟,满分:150分b)题型结构a:概念题(20~30分)b:简答题(30~40分)c:计算题(40~50分)d:分析与设计题(40~50分)c)内容结构a:信号与系统(75分)c:数字逻辑电路(75分)四、参考书目a:王宝祥,信号与系统,哈尔滨工业大学出版社b:郑君里等,信号与系统,高等教育出版社c:龚之春,数字电路,电子科技大学出版社《难得的是有份清闲时光,难得的是有种知途迷返,知之为知之,不知为不知,知你冷暖,懂你悲欢,把你放在了心头上的人。
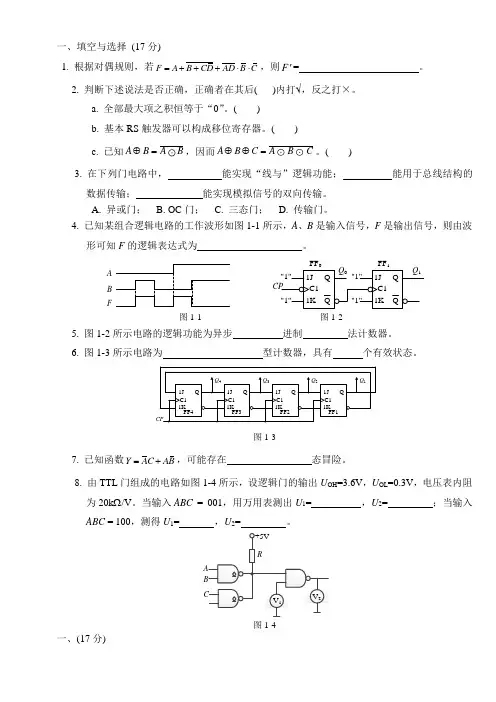
一、填空与选择 (17分)1. 根据对偶规则,若F A B CD AD B C =+++⋅⋅,则F '= 。
2. 判断下述说法是否正确,正确者在其后( )内打√,反之打×。
a. 全部最大项之积恒等于“0”。
( )b. 基本RS 触发器可以构成移位寄存器。
( )c. 已知A B AB ⊕=,因而A BC ABC ⊕⊕=。
( )3. 在下列门电路中, 能实现“线与”逻辑功能; 能用于总线结构的数据传输; 能实现模拟信号的双向传输。
A. 异或门; B. OC 门; C. 三态门; D. 传输门。
4. 已知某组合逻辑电路的工作波形如图1-1所示,A 、B 是输入信号,F 是输出信号,则由波 形可知F 的逻辑表达式为 。
B AF1J Q QC11K 1J Q QC11K CP Q 0Q 1FF 0FF 1"1""1""1""1"图1-1 图1-25. 图1-2所示电路的逻辑功能为异步 进制 法计数器。
6. 图1-3所示电路为 型计数器,具有 个有效状态。
图1-37. 已知函数Y AC AB =+,可能存在 态冒险。
8. 由TTL 门组成的电路如图1-4所示,设逻辑门的输出U OH =3.6V ,U OL =0.3V ,电压表内阻为20k Ω/V 。
当输入ABC = 001,用万用表测出U 1= ,U 2= ;当输入ABC = 100,测得U 1= ,U 2= 。
图1-4一、(17分)1. ()()F A B C D A D B C =⋅⋅+++++=()()A B C D A D B C AB ACD⋅⋅+⋅+++=+2. √,×,×3. B ,C ,D4. A B ⊕5. 二位二进制(四进制),减法6. 扭环,8个7. 08.0.3V , 3.6V; 1.4V , 0.3V;二、简答题:(8分)1. 电路如图2-1(a)所示,设各触发器的初态为“0”。