SPSS 统计描述

统计描述符合正态分布或近似正态分布资料的统计描述统计量：（一）描述平均水平的常用统计量——算术均数（二）描述变异水平（离散程度）的常用统计量——离均差平方和（SS）、平均方差（方差：MS）、标准差（SD）（三）描述抽样误差大小的统计量——标准误（SE）。

SPSS操作：对某1变量（如time）进行统计描述：正态性检验：Analyze→nonparametric tests→1-sample K-S→调入某变量和激活Nomal→OK。

正态的统计描述：analyze→descriptive statistics→descriptives→调入某变量，点击option…→点击mean、SE、SD→OK。

分析结果：表descriptive statistics（可看N、min、max、mean、SD）；Z=0.649；P=0.794＞0.05.说明time服从近似正态分布。

对某一变量分组进行统计描述（如按男、女分别做time的统计描述）：文件分割：data→split file；注意：计算机有记忆功能，文件分割后需要把它还原，才不会影响后续操作。

统计描述（操作同上）：analyze→descriptive statistics→descriptives→调入某变量，点击option…→点击mean、SE、SD→OK。

非正态资料的统计描述统计量：（一）描述集中位置——中位数（二）描述变异水平（离散程度）——四分位数间距=P75-P25。

SPSS操作：对某1变量（红血球体积hct）进行统计描述：正态性检验（同上）：Analyze→nonparametric tests→1-sample K-S→调入某变量和激活Nomal→OK。

非正态的统计描述：analyze→descriptive statistics→frequencies→调入某变量，点击statistics…→点击median和quartiles。

编制频数分布表和绘制频数分布直方图一、对数据进行重新编码（recod e）SPSS操作：统计描述：Recode：Transform→recode into different variables…（表示recode后存入新的变量名中，原始数据还在）→调入变量进入“input→output”中，在右侧output框中输入新的变量名，可label→点击change→点击框下的old and new values…→根据手工分组，确定组距后：lowest：1→range→higest:最后一组→OK。

SPSS统计分析数据特征的描述统计分析SPSS（Statistical Package for the Social Sciences）是一种常用的统计分析软件，用于对数据进行描述统计分析。

描述统计分析旨在帮助研究人员对数据进行简单的整理、描述和总结，以便更好地理解数据的特征和趋势。

下面将说明几种常用的描述统计分析方法。

1.频数统计频数统计是指对数据中各个变量的不同取值进行计数。

通过统计每个取值出现的次数，可以了解数据的分布情况和变量的特点。

SPSS提供了多种方式来进行频数统计，包括直方图、饼图等。

通过这些图表，可以清晰地看到变量的取值分布。

2.中心趋势测量中心趋势测量是描述数据集合中心位置的统计方法，常用的测量指标包括平均数、中位数和众数。

平均数是所有数据的算术平均值，中位数是将数据按大小排列后处于中间位置的数值，众数是出现次数最多的数值。

SPSS提供了计算这些测量指标的功能，以便更好地了解数据的中心位置。

3.离散程度测量离散程度测量是描述数据变异程度的方法，常用的度量指标包括标准差、方差和极差。

标准差是数据与平均数之间的平均偏差，方差是标准差的平方，表示数据的离散程度，极差是最大值与最小值之间的差异。

通过这些指标，可以判断数据的离散程度，以及是否存在异常值等问题。

4.偏度和峰度测量偏度和峰度是描述数据分布形态的指标。

偏度测量的是数据分布的偏斜程度，正偏斜表示分布右侧的极端值较多，负偏斜表示分布左侧的极端值较多。

峰度测量的是数据分布的尖峰程度，正峰度表示尖峰较高且尾巴较短，负峰度表示尖峰较低且尾巴较长。

通过偏度和峰度的测量，可以判断数据的分布形态是否符合正态分布。

5.相关分析相关分析旨在研究两个或多个变量之间的关系。

相关系数是用来衡量变量之间线性相关程度的指标，取值范围从-1到+1、接近-1的相关系数表示负相关，接近+1的相关系数表示正相关，接近0的相关系数表示无相关。

通过相关分析，可以了解不同变量之间的关系，以及它们对研究问题的影响程度。

SPSS数据分析—描述性统计分析描述性统计分析是一种针对数据本身的分析方法，通过使用统计学指标来描述数据的特征。

这种分析方法看似简单，但实际上却是许多高级分析的基础工作。

很多高级分析方法都对数据有一定的假设和适用条件，这些可以通过描述性统计分析来判断。

我们也会发现，许多分析方法的结果中都会穿插一些描述性分析的结果。

描述性统计主要关注数据的三个方面：集中趋势、离散趋势和数据分布情况。

描述集中趋势的指标包括均值、众数和中位数，其中均值包括截尾均值、几何均值和调和均值等。

描述离散趋势的指标包括频数、相对数、方差、标准差、标准误、全距、四分位间距、四分位数、百分位数和变异系数等。

需要注意的是，连续型变量和离散型变量的指标有所不同。

由于许多统计分析都有一个正态分布的假设，因此我们经常关注数据的分布特征。

常用峰度系数和偏度系数来描述数据偏离正态分布的程度。

也可以使用Bootstrap方法计算出结果与经典统计学方法计算出的结果进行对比，如果差异明显，则说明原数据呈偏态分布或存在极值。

SPSS用于描述性统计分析的过程大部分都在分析-描述统计菜单中，另有一个在比较均值-均值菜单。

虽然这几个过程用途不同，但基本上都可以输出常用的指标结果。

分析-描述统计-频率过程可以输出连续型变量集中趋势和离散趋势的主要指标，还可以输出判断分布的直方图、峰度值和偏度值。

此外，该过程最主要的作用是输出频数表。

分析-描述统计-描述过程输出的内容并不多，也没有统计图可以调用，唯一特别的是该过程可以对数据进行标准化变换，并保存为新变量。

分析-描述统计-探索过程是在原有数据进行描述性统计的基础上，更进一步的描述数据。

与前两种过程相比，它能提供更详细的结果。

分析-描述统计-比率过程主要用于对两个连续变量间的比率进行描述分析。

输出的结果比较简单，只是指标的汇总表格。

分析-描述统计-交叉表过程主要用于分类变量的描述性统计。

它可以完成频数分布和构成比的分析，也经常被用来做列联表的推断分析。

描述性统计分析是针对数据本身而言，用统计学指标描述其特征的分析方法，这种描述看似简单，实际上却是很多高级分析的基础工作，很多高级分析方法对于数据都有一定的假设和适用条件，这些都可以通过描述性统计分析加以判断，我们也会发现，很多分析方法的结果中，或多或少都会穿插一些描述性分析的结果。

描述性统计主要关注数据的三大内容：1.集中趋势2.离散趋势3.数据分布情况描述集中趋势的指标有均值、众数、中位数，其中均值包括截尾均值、几何均值、调和均值等。

描述离散趋势的指标有频数、相对数、方差、标准差、标准误、全距、四分位间距、四分位数、百分位数、变异系数等。

注意：连续型变量和离散型变量的指标有所不同。

由于很多统计分析都有一个正态分布的假设，因此我们经常也会关注数据的分布特征，常用峰度系数和偏度系数来描述数据偏离正态分布的程度，也可以使用Bootstrap方法计算出结果与经典统计学方法计算出的结果进行对比，如果差异明显，则说明原数据呈偏态分布或存在极值SPSS用于描述性统计分析的过程大部分都在分析—描述统计菜单中，另有一个在比较均值—均值菜单，虽然这几个过程用途不同，但是基本上都可以输出常用的指标结果。

一、分析—描述统计—频率此过程可以输出连续型变量集中趋势和离散趋势的主要指标，还可以输出判断分布的直方图、峰度值和偏度值，此外，该过程最主要的作用是输出频数表，结果举例如下：二、分析—描述统计—描述看起来似乎这个过程才是正统的描述统计分析过程，实际上该过程输出的内容并不多，也没有统计图可以调用，唯一特别的是该过程可以对数据进行标准化变换，并保存为新变量。

三、分析—描述统计—探索探索性分析是对原有数据进行描述性统计的基础上，更进一步的描述数据，和前两种过程相比，它能提供更详细的结果。

四、分析—描述统计—比率该过程主要用于对两个连续变量间的比率进行描述分析输出的结果比较简单，只是指标的汇总表格，在此略去五、分析—描述统计—交叉表分类变量的描述性统计比较简单，主要就是看频数分布和构成比，基本用交叉表一个过程就可以完成，该过程虽然放在描述统计中，但是由于功能丰富，也经常被用来做列联表的推断分析。

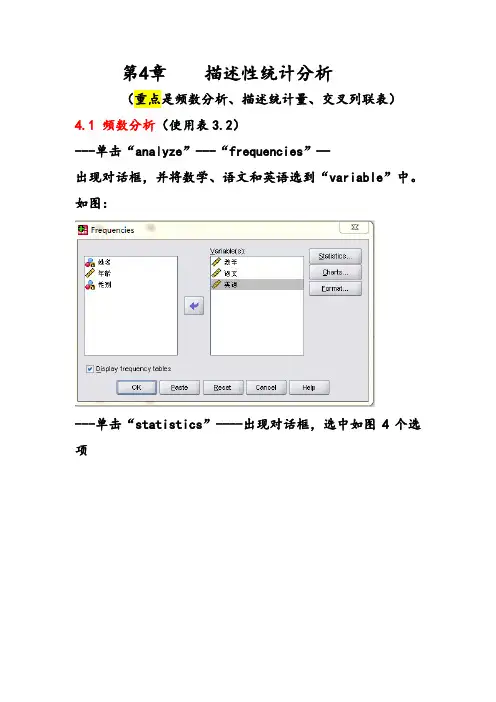
第4章描述性统计分析（重点是频数分析、描述统计量、交叉列联表）4.1 频数分析（使用表3.2）---单击“analyze”---“frequencies”—出现对话框，并将数学、语文和英语选到“variable”中。

如图：---单击“statistics”----出现对话框，选中如图4个选项-----单击“continue”回到前一对话框----单击“OK”结果如表4.1-----如图，重新选择语文---单击“charts”---得到一个对话框，如图选中2个选项----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.24.2 基本描述统计量（使用表3.2）---单击“analyze”---“descriptive statistics”—“Descriptives”---得到对话框，并将数据进行如图选入：-----单击“options”—得到对话框，并选中如图6个选项：----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.34.3 探索性分析（使用表3.2）---单击“analyze”---“descriptive statistics”—“Explore”---得到对话框，并将数据进行如图选入：----单击“Plots”—得到对话框，并选中如图4个选项：----单击“continue”----回到前一对话框---单击“OK”。

结果如表4.6（与书有不同）4.4交叉列联表分析（使用表化环0708）（1）T ransform（修改）----Recode into Different variable----选定身高------点击“向右箭头”------在“name”下写个名字：eg：T1-------change-------（此处T1和T2是已经做好的分组）点击-----old and new values对其分组---例：Range LOWEST through values :160 new values :1Rang :160 through :170 2Range HIGHEST through values :170 3 点击continue-----回到前一个对话框点击------OK同样的方法做好T2---------点击“analyze(分析)”-----“Descriptive Statistics(描述性统计)”------“Crosstabs（交叉列联表）”选中行列------点击“Exat….“则弹出“exct tests（精确检测）对话框”点“Statistics…”则弹出“Crosstabs：statistics（交叉表统计）对话框”-------点击“Chi—square（卡方检验）”----“continue”点“Cells…”则弹出“Crosstabs：Cells display（交叉表统计）对话框”-------选择“Counts”中的“Observed”和“Expected”为期望频数，-------选择“Percentages”中的“Row”“Column”“Total”选项，分别计算“频数”“列频数”“总频数”-------选择“Residuals”中的“Standardized”分别计算单元格的非标准化残差、标准化残差、调整后的残差----“continue”回到前一页点----“OK”4.5比率分析（课本71页）不需要掌握英语未写完作业：1-10，11-25，26-30。

spss描述统计实验报告SPSS描述统计实验报告引言SPSS（Statistical Package for the Social Sciences）是一种用于数据分析和统计建模的软件工具。

它可以帮助研究人员对数据进行描述统计分析，从而得出结论并做出预测。

本实验旨在利用SPSS软件对实验数据进行描述统计分析，以探究数据的特征和规律。

实验设计本实验选取了一组包括性别、年龄、身高和体重等信息的样本数据，共计100个样本。

通过SPSS软件对这组数据进行描述统计分析，包括均值、标准差、频数分布等指标，以便对样本数据进行全面的了解。

结果分析首先，我们对样本数据中的性别进行了频数分布分析。

结果显示，样本中有55%的男性和45%的女性，性别分布相对均衡。

接着，我们对年龄、身高和体重等连续变量进行了均值和标准差的分析。

结果显示，样本的平均年龄为30岁，标准差为5岁；平均身高为170厘米，标准差为8厘米；平均体重为65公斤，标准差为10公斤。

这些数据表明样本中的年龄、身高和体重分布较为集中，且具有一定的变异性。

结论通过对样本数据的描述统计分析，我们得出了对样本特征和规律的初步认识。

样本中男女比例相对均衡，年龄、身高和体重分布较为集中且具有一定的变异性。

这些结果为我们进一步的数据分析和研究提供了重要参考。

总结SPSS软件作为一种强大的数据分析工具，可以帮助研究人员对数据进行描述统计分析，从而深入了解数据的特征和规律。

本实验利用SPSS对样本数据进行了描述统计分析，得出了对样本特征和规律的初步认识，为后续的研究工作奠定了基础。

希望本实验能够对SPSS软件的应用和描述统计分析方法有所启发，为相关研究工作提供参考。

利⽤SPSS进⾏统计描述第三节利⽤SPSS进⾏统计描述⼀、统计描述⽅法在教育技术研究过程中收集到⼤量的资料数据，但从这些杂乱⽆章的资料中，很难对其总体⽔平与分布状况做出评价判断。

因此，必须采⽤⼀些适当的⽅法对这些资料进⾏处理，使之简约化、分类化、系统化，从中发现它们的分布规律，掌握总体的特征，以便对其⽔平做出客观的评价。

统计描述⽅法，是研究简缩数据并描述这些数据的统计⽅法。

将搜集来的⼤量数据资料，加以整理、归纳和分组，简缩成易于处理和便于理解的形式，并计算所得数据的各种统计量，如平均数、标准差、以及描述有关事物或现象的分布情况、波动范围和相关程度等，以揭⽰其特点和规律。

（⼀）数据资料的整理和表⽰在教育技术研究中，我们⽤各种⽅法搜集来的资料，⼀般是零散的，它只反映个别现象的个别特征，必须经过整理加⼯，使之系统化，才能计算统计指标，进⾏统计分析，为进⼀步研究提供有⽤的信息，⾸先要进⾏的是统计整理，它包含以下⼏部分内容：1．数据检查主要检查数据的完整性与正确性。

统计资料完整性的检查，就是要根据调查项⽬检查是否填写齐全，避免遗漏，删去重复。

正确性检查，就是检查搜集的资料是否真实可靠。

特别是统计数字的真实性是统计⼯作的⽣命，统计资料的检查整理必须抓紧这⼀环。

数据检查可分为逻辑检查和计算检查两种⽅法。

逻辑检查，是从理论和⼀般常识上来检查资料内容是否合理，指标之间是否⽭盾。

计算检查是检查统计数字在计算⽅法和计算结果上有否错误。

2．数据分类数据分类就是把搜集来的数据进⾏分组归类。

数据分类要做到既不重复、不遗漏，⼜不混淆，⼀般⼜可分为品质分类和数量分类。

品质分类：是按事物性质划分为不同的组别、种类。

如以性别为标志可分为男与⼥；按“理解能⼒”、“学习态度”等为标志，⼜可分为好、较好、⼀般、差等⼏种⽔平，每种⽔平可看成类，每⼀类可给以相当的数量。

可以通过各类所包含的数据再进⾏数量化的⽐较和分析。

数量分类：是按数量的属性分类。

SPSS论文描述性统计分析概述描述性统计，是指运用制表和分类，图形以及计算概括性数据来描述数据特征的各项活动。

描述性统计分析要对调查总体所有变量的有关数据进行统计性描述，主要包括数据的频数分析、集中趋势分析、离散程度分析、分布以及一些基本的统计图形。

①数据的频数分析。

比如问卷数据或病例数据中人群的基本情况，性别、职业、学历等，在数据的预处理部分，利用频数分析和交叉频数分析可以检验异常值。

②数据的集中趋势分析。

用来反映数据的一般水平，常用的指标有平均值、中位数和众数等。

③数据的离散程度分析。

主要是用来反映数据之间的差异程度，常用的指标有方差和标准差。

④数据的分布。

在统计分析中，通常要假设样本所属总体的分布属于正态分布。

⑤绘制统计图。

用图形的形式来表达数据，比用文字表达更清晰、更简明。

在SPSS软件里，可以很容易地绘制各个变量的统计图形，包括条形图、饼图和折线图等。

案例实操现有服用两组不同降血压药物（A药和B药）的患者的性别、年龄、收缩压的数据，请统计描述服用两组不同降血压药物（A药和B药）的患者的性别、年龄、收缩压。

案例分析及统计策略分析该案例数据为研究论文中常见的数据，有定量数据和定性数据，定量数据有正态分布的，也有非正态分布的，采用的一般是均数、标准差（正态分布数据）和中位数、四分位数（非正态分布数据）；定性数据，一般采用率和构成比（百分比）描述。

同时，在论文中，还会采用差异性比较的方法来探讨不同组间有无统计学差异（这个在后期课程会进一步论述）。

论文中描述性统计分析的结果会呈现在第一张表格中，同时包含了数据的差异性结果。

论述研究对象基本特征及其组间差异性。

如下表：SPSS实际操作（源数据sav，可在公众号扣1获取）描述性统计操作：（一）定量资料（收缩压、心率）①分析—描述统计—探索。

因变量列表放入需要观察的指标“收缩压”、“心率”，因子列表放入分组变量“药物类型”。

②点击统计“统计”选项，勾选“百分位数”（一）定性资料（性别、药物类型）：①分析—描述统计—交叉表。

均值（平均值、平均数）:表示的是某变量所有取值的集中趋势或平均水平。

例如，学生某门学科的平均成绩、公司员工的平均收入、某班级学生的平均身高等。

计算公式如下。

中位数：定义：把一组数据按递增或递减的顺序排列，处于中间位置上的变量值就是中位数。

它是一种位置代表值，所以不会受到极端数值的影响，具有较高的稳健性计算公式：一个大小为的数列，要求其中位数，首先应把该数列按大小顺序排列好，如果为奇数，那么该数列的中位数就是位置上的数；如果N为偶数，中位数则是该数列中第与第+1位置上两个数值的平均数众数：定义：众数是指一组数据中，出现次数最多的那个变量值。

众数在描述数据集中趋势方面有一定的意义。

例如，制鞋厂可以根据消费者所需鞋的尺码的众数来安排生产。

计算公式：手工计算众数比较麻烦，需要统计数据的次数分布。

全距：定义：全距也称为极差，是数据的最大值与最小值之间的绝对差。

在相同样本容量情况下的两组数据，全距大的一组数据要比全距小的一组数据更为分散。

计算公式：最大值－最小值。

方差（Variance）和标准差（Standard Deviation）：定义：方差是所有变量值与平均数偏差平方的平均值，它表示了一组数据分布的离散程度的平均值。

标准差是方差的平方根，它表示了一组数据关于平均数的平均离散程度。

方差和标准差越大，说明变量值之间的差异越大，距离平均数这个“中心”的离散趋势越大。

频数（Frequency）：定义：频数就是一个变量在各个变量值上取值的个案数。

如要了解学生某次考试的成绩情况，需要计算出学生所有分数取值，以及每个分数取值有多少个人，这就需要用到频数分析。

变量的频数分析正是实现上述分析的最好手段，它可以使人们非常清楚地了解变量取值的分布情况。

峰度（Kurtosis）：定义：峰度是描述某变量所有取值分布形态陡缓程度的统计量。

这个统计量是与正态分布相比较的量，峰度为0表示其数据分布与正态分布的陡缓程度相同；峰度大于0表示比正态分布高峰要更加陡峭，为尖顶峰；峰度小于0表示比正态分布平顶峰。

SPSS 描述性统计分析SPSS描述性统计分析,集中在Descriptive Statistics菜单中,最常用的是列在最前面的四个过程：Frequencies过程：产生频数表和百分位数；Descriptives过程：进行一般性的统计描述,用于服从正态分布的资料，计算产生均数、标准差等；Explore过程：用于对数据概况不清时的探索性分析；Crosstabs过程：完成计数资料和等级资料的统计描述和一般的统计检验，我们常用的X2检验也在其中完成。

1 频数分布分析（Frequencies过程）频数分布表是描述性统计中最常用的方法之一,Frequencies过程就是专门为产生频数表而设计的。

它不仅可以产生详细的频数表,还可以按要求给出某百分位点的数值，以及常用的条图,圆图等统计图.注：SPSS给出详细频数表,即并不按某种要求确定组段数和组距,而是按照数值精确列表。

Frequencies界面说明Frequencies对话框的界面如下所示：以下介绍各部分的功能：1、【Display frequency tables复选框】确定是否在结果中输出频数表.2、【Statistics钮】单击后弹出Statistics对话框如下，用于定义需要计算的其他描述统计量.现将各部分解释如下：1、Percentile Values复选框组: 定义需要输出的百分位数,可计算四分位数（Quartiles）、每隔指定百分位输出当前百分位数（Cut points for equal groups）、或直接指定某个百分位数（Percentiles），如直接指定输出P2.5和P97.5。

2、Central tendency复选框组用于定义描述集中趋势的一组指标：均数（Mean）、中位数(Median)、众数(Mode)、总和（Sum).3、Dispersion复选框组用于定义描述离散趋势的一组指标：标准差(Std.deviation）、方差(Variance）、全距（Range)、最小值(Minimum)、最大值(Maximum）、标准误(S。