机械的效率及自锁
- 格式:ppt
- 大小:3.46 MB
- 文档页数:61






§5 机械的效率和自锁填空题:1.设机器中的实际驱动力为rP ,在同样的工作阻力和不考虑摩擦时的理想驱动力为r P 0,则机器效率的计算式是η = r P 0/rP 。
2.设机器中的实际生产阻力为rQ ,在同样的驱动力作用下不考虑摩擦时能克服的理 想生产阻力为r Q 0,则机器效率的计算式是 η= r Q /rQ 0 。
3.假设某机器由两个机构串联而成,其传动效率分别为1η和2η,则该机器的传动效率为 1η*2η 。
4.假设某机器由两个机构并联而成,其传动效率分别为1η和2η,则该机器的传动效率为 (P 1*η1+ P 2*η2)/(P 1+P 2) 。
5. 从受力观点分析,移动副的自锁条件是 外力的作用线与运动方向法线的夹角小于等于摩擦角 ;转动副的自锁条件是 外力的作用线与摩擦圆相切或相割 ;从效率观点来分析,机械自锁的条件是 效率小于等于零 。
综合题1:某滑块受力如图所示,已知滑块与地面间摩擦系数f ,试求F 与Q 分别为驱动力时的机构运动效率。
F 为驱动力:f tg1-=ϕ于是由正弦定理:)90sin()90sin(00ϕθϕ--+=Q F 令0=ϕ,得)90sin(00θ-=QF 因此,其效率为)90sin()90sin()90sin(00θϕϕθη-+--==F F 当Q 为驱动力,F 变为阻力,取ϕ-代替上式中的ϕθ-)90sin()90sin(90sin(000ϕθϕθη+---==)F F 第四章习题中,综合题5,要求计算该机构效率。
(可直接利用前面的计算结果)0153077.8==-f tg ϕ由正弦定理:)90sin()2180sin(0210ϕβγϕ-=--+R P 和)90sin()2sin(012ϕϕβ+=-R Q 于是Q P *-+*---+=)2sin()90sin()90sin()2180sin(00ϕβϕϕβγϕ代入各值得:N P 7007.1430=取上式中的00=ϕ,可得N P 10000=于是6990.00==PP η综合题2:图 示 为 由 A 、B 、C 、D 四 台 机 器 组 成 的 机 械 系统,设 各 单 机 效 率 分 别 为ηA 、ηB 、ηC 、ηD , 机 器B 、D 的 输 出 功 率 分 别 为N B 和N D 。


第五章机械的效率和自锁研究内容:1 机械的效率2 机械的自锁第1讲机械的效率5.1.1 机械效率的概念5.1.2机械效率的计算5.1.3机组效率的计算机械效率的概念及意义:(1) 概念: 机械效率 η 机械损失率 ξ η=W r W d 摩擦损失是不可避免的,总有 ξ >0 和 η < 1;机械效率反映了输入功在机械中的有效利用的程度。
(2) 意义: 降耗节能是国民经济可持续发展的重要任务之一。
机械效率的高低是机械中的一个主要性能指标。
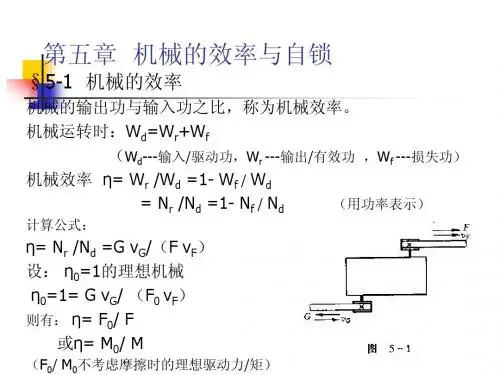
—— 机械的输出功(W r )与输入功(W d )之比—— 机械的损失功(W f )与输入功(W d )之比=1−Wf W d =1−ξ机械效率的计算:1) 以功表示的计算公式 η=W r W d =1−W f W d2) 以功率表示的计算公式 η=P r P d =1−P f P d 3) 以力或力矩表示的计算公式η=F 0F =M 0M实际机械装置 ηF 0v F机械传动装置 Gv Gη=P r P d =Gv G Fv F η0=Gv G F 0v F =1即 η=理想驱动力实际驱动力=理想驱动力矩实际驱动力矩机组 ——由若干个机器组成的机械系统整机 ——由若干个机构组成的整台机器 已知机组各机器的效率,便可计算该机组的总效率。
1. 串联机组1) 功率传动特点: 前一机器的输出功率即为后一机器的输入功率。
2) 总机械效率:η=P r P d =P 1P d P 2P 1…P k P k−1=η1η2…ηn⋯1 2kP dP 1P 2P k -1P k串联机组模型结论:串联机组中任一机器效率很低,整个机械效率就会极低;且串联机器的数目越多,机械效率也越低。
2.并联机组1)传动功率特点:机组的输入功率为各机器的输入功率之和,而输出功率为各机器的输出功率之和。
2) 总机械效率:η=P riP di=P1η1+P2η2+⋯+P kηkP1 +P2 +⋯+P kη1 η2 ηkP1η1P1 P2 P kP dP2η2Pkηk结论:⏹并联机组的总效率与各机器的效率和传动功率大小均有关;⏹其总效率主要取决于传动功率大的机器的效率;⏹要提高并联机组的总效率,应着重提高传动功率大的路线的效率。

第五章 机械的效率和自锁§5-1 机械的效率正常运转时:输入功 = 输出功 + 损失功 即:fr d W W W += (5—1)一.机械效率的一般表达形式 机械在一个运动循环内,输出功和输入功的比值称为机械效率,反映了输入功在机械中有效利用的程度,通常以η表示:d f d f d f r rd r W W W W W W W W W W -=-=+==1η (5—2)式(5—1)、(5—2)除以做功的时间,则得d f d r N N N N -==1η (5—2’) 式中N d 、N r 和N f 分别为输入功率、输出功率和损耗功率。
因w f (或N f )>0,由上式可知1<η,且w f (或N f )越大,η越低。
为了使机械具有较高的机械效率,应尽量减少机械中的损耗功,而机械中的损耗主要是摩擦损耗,因此在设计机械时应尽量简化机械传动系统,减少运动副的数目和设法减少运动副中的摩擦 机械损失系数(损失率)ξdf d f N N W W //==ξ (5—3)二.机械效率以力或力矩的形式表达机械效率还可以用力或力矩的比值形式来表达。
图5-1所示为一机械传动示意图,设F 为实际驱动力,G 为相应的实际生产阻力;v F 和v G 分别为F 和G 的作用点沿该力作用线方向的速度,根据式(5—2’)可得F Gd r Fv Gv N N ==η (a )如设该机械系统不存在摩擦力(称为理想机械),因而N f =0,其效率η0必等于1。
对于理想机械,为了克服同样生产阻力G 所需的驱动力称为理想驱动力F 0 ,它必定小于实际驱动力F 。
由理想机械的定义可得F G v F Gv 0= (b ) 将式(b )代入式(a )得F F Fv v F Fv Gv F F FG 00===η (c )此式说明,机械效率也等于在克服同样生产阻力G 的情况下,理想驱动力F 0与实际驱动力F 的比值。
同理,如设M 和M 0各为实际的和理想的驱动力矩,可得:M M 0=η (d ) 所以:实际驱动力矩理想驱动力矩实际驱动力理想驱动力==η (5—4) 举例:①斜面机构正行程:αtan 0G F =反行程:(此时G 为驱动力) ②螺旋机构同理:拧紧时:)tan(/tan /0v M M ϕααη+==拧松时:αϕαηtan /)tan(v -= 机械效率的确定 计算方法 实验方法 常用机构的机械效率见表5-1 三、机器机组效率的确定①串联(只要其中任一个环节的效率很低,整个机组的效率就很低) 如图5-2所示 ②并联输入总功率:k d P P P PP ++++= 321 输出总功率:'++'+'+'=k rP P P P P 321 此式表明:并联机组的总效率不仅与各机器的效率有关,还 与各机器传递功率的大小有关。