纯电阻电感电容电路

单相交流电路概述在直流电路中，电路的参数只有电阻R 。

而在交流电路中，电路的参数除了电阻R 以外，还有电感L 和电容C 。

它们不仅对电流有影响，而且还影响了电压与电流的相位关系。

因此，研究交流电路时，在确定电路中数量关系的同时，必须考虑电流与电压的相位关系，这是交流电路与直流电路的主要区别。

本节只简单介绍纯电阻、纯电感、纯电容电路。

一、纯电阻电路纯电阻电路是只有电阻而没有电感、电容的交流电路。

如白炽灯、电烙铁、电阻炉组成的交流电路都可以近似看成是纯电阻电路，如图3—7所示。

在这种电路中对电流起阻碍作用的主要是负载电阻。

加在电阻两端的正弦交流电压为u ，在电路中产生了交流电流i ，在纯电阻电路中，龟压和电流瞬时值之间的关系，符合欧姆定律，即：/i u R =由于电阻值不随时间变化，则电流与电压的变化是一致的。

就是说，电压为最大值时，电流也同时达到最大值；电压变化到零时，电流也变化到零。

如图3—8所示。

纯电阻电路中，电流与电压的这种关系称为“同相”。

通过电阻的电流有效值为：/I U R =公式3—14是纯电阻电路的有效值。

在纯电阻电路中，电流通过电阻所做的功与直流电路的计算方法相同，即：22P UI I R U R ===二、纯电感电路纯电感电路是只有电感而没有电阻和电容的电路。

如由电匪很小的电感线圈组成的交流电路，都可近似看成是纯电感电路，如图3—9所示。

在如图3—9所示的纯电感电路中；如果线圈两端加上正弦交流电压，则通过线圈的电流i 也要按正弦规律变化。

由于线圈中电流发生变化，在线圈中就产生自感电动势，它必然阻碍线圈电流变化。

经过理论分析证明，由于线圈中自感电动势的存在，使电流达到最大值的时间，要比电压滞后90︒，即四分之一周期。

也就是说，在纯电感电路中，虽然电压和电流都按正弦规律变化，但两者不是同相的，如图3—10所示，正弦电流比线圈两端正弦电压滞后90︒，或者说，电压超前电流90︒。

理论证明，纯电感电路中线圈端电压的有效值U ，与线圈通过电流的有效值之间的关系是：L //I U L U X ω==L ω是电感线圈对角频率为叫的交流电所呈现的阻力，称为感抗，用L X 表示，即： L 2X L fL ωπ==式中 L X ——感抗(Ω)；f ——频率(Hz)；L ——电感(H)。

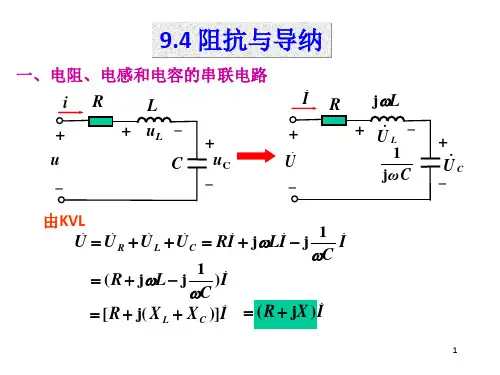
第二节电阻、电感、电容在交流电路中的特性在直流稳态电路中，电感元件可视为短路，电容元件可视为开路。

但在交流电路中，由于电压、电流随时间变化，电感元件中的磁场不断变化，引起感生电动势；电容极板间的电压不断变化，引起电荷在与电容极板相连的导线中移动形成电流。

因此，电阻R、电感L、及电容C对交流电路中的电压、电流都会产生影响。

电压和电流的波形及相量图如图2-10b、c所示。

电阻R两端的电压和流经R的电流同相，且其瞬时值、幅值及有效值均符合欧姆定律。

电阻元件R的瞬时功率为：电阻功率波形如图2-10d。

任一瞬间，p≥0，说明电阻都在消耗电能。

电阻是耗能元件，将从电源取得的电能转化为热能。

电路中通常所说的功率是指一个周期内瞬时功率的平均值，称平均功率，又称有功功率，用大写字母P表示，单位为瓦（W）。

（2-13）式中，U、I 分别为正弦电压、电流的有效值。

例2 －4有一电灯，加在其上的电压u=311sin314t V，电灯电阻R=100Ω，求电流I、电流有效值I和功率P。

若电压角频率由314rad/s变为3140rad/s，对电流有效值及功率有何影响？解：由欧姆定律可知因电阻阻值与频率无关,所以当频率变化时,电流有效值及功率不变。

2．电感元件当电感线圈中通过一交变电流i时，如图2-11a，在线圈中引起自感电动势e L，设电流（2-14）电感电压（2-15）用相量表示：即（2-16）同理，有效值相量（2-17）令则式2-18为电感元件的伏安特性，其中XL称为电感抗，简称感抗，单位欧姆（Ω）。

感抗XL表示电感对交流电流的阻碍能力，与电阻元件的电阻R类似；但与电阻不同，XL 不仅与电感元件本身的自感系数L有关，还与正弦电流的角频率ω有关，ω越大，感抗越大。

对于直流电路，ω=0，XL=0，电感可视为短路。

电感元件的瞬时功率为：（2-21）其平均值为：（2-22）电感的瞬时功率波形图见图2-11d。

在第一和第三个1/4周期，电感元件处于受电状态，它从电源取得电能并转化为磁场能，功率为正，电感元件所储存的磁场能（2-23）电流的绝对值从0增加到最大值Im，磁场建立并逐渐增强，磁场能由0增加到最大值1/2LIm2；在第二和第四个1/4周期，电感元件处于供电状态，它把磁场能转化为电能返回给电路，功率为负，电流由最大值减小到0，磁场消失，磁场能变为0。

有功功率：在交流电路中，凡是消耗在电阻元件上，功率不可逆转换的那部分功率（如转变为热能，光能，或机械能），称为有功功率；无功功率：电路中，电感元件建立磁场，电容元件建立电场消耗的功率称为无功率，这个功率是随交流电的周期，与电源不断的进行能量转换，而并不消耗能量；视在功率：交流电源所能提供的总功率，称为视在功率，在数值上即是，电压与电流的乘积，单位VA,视在功率即是交流电源的容量；阻性负载:即和电源相比当负载电流负载电压没有相位差时负载为阻性(如负载为白帜灯、电炉等）通俗一点的讲，仅是通过电阻类的元件进行工作的纯阻性负载称为阻性负载。

感性负载通常情况下，一般把负载带电感参数的负载，即符合和电源相比负载电流滞后负载电压一个相位差的特性的负载为感性(如负载为电动机;变压器;)。

通俗地说，即应用电磁感应原理制作的大功率电器产品，如电动机、压缩机、继电器、日光灯等等。

这类产品在启动时需要一个比维持正常运转所需电流大得多（大约在3-7倍）的启动电流。

例如，一台在正常运转时耗电150瓦左右的电冰箱，其启动功率可高达1000瓦以上。

此外，由于感性负载在接通电源或者断开电源的一瞬间，会产生反电动势电压，这种电压的峰值远远大于车载交流供电器所能承受的电压值，很容易引起车用逆变器的瞬时超载，影响逆变器的使用寿命。

因此，这类电器对供电波形的要求较高。

容性负载电路中类似电容的负载，可以使负载电流超前负载电压一个相位差（和电源相比），降低电路功率因数。

一般把负载带电容参数的负载，即符合电压滞后电流特性的负载成为容性负载。

充放电时，电压不能突变。

其对应的功率因为为负值。

对应的感性负载的功率因数为正值。

一般电源控制类产品，所给出的负载，如未加说明则是给出的是视在功率；即总容量功率；它既包括有功功率，也包括无功功率；而一般感性负载说明中给出的往往是有功功率的大小，例如荧光灯，标注为15~40瓦的荧光灯，镇流器消耗功率约为8瓦，实际在考虑用定时器，感应开关在控制它时，则要加上这8瓦；具体不同的产品感性部分，即无功功率的大小，可以通过其给出的功率因数来计算。

课题4－2纯电阻电路课型新课授课班级授课时数1教学目标1．掌握纯电阻电路中电流与电压的数量关系及相位关系；2．理解纯电阻电路的功率；3．会分析纯电阻电路的电流与电压的关系；4．会分析计算纯电阻电路的相关物理量。

教学重点1．纯电阻电路的电压、电流的大小和相位关系。

2．纯电阻电路瞬时功率、有功功率、无功功率的计算。

教学难点纯电阻电路瞬时功率、有功功率、无功功率的计算。

教学后记1.提出问题，引导学生思考电方面知识，引起兴趣。

2.结合前面学过的知识，让学生自主探究，让他们由“机械接受”向“主动探究”发展，从而落实了新课程理念：突出以学生为主体，让学生在活动中发展。

3.总结结论，引导学生自己得出结论，养成良好的自主学习能力。

引入新课【复习提问】1、正弦交流电的三要素是什么2、正弦交流电有哪些方法表示【课题引入】：我们在是日常生活中用到的白炽灯、电炉、电烙铁等都属于电阻性负载，它们与交流电源联接组成纯电阻电路，那么它们在交流电路中工作时，电压和电流间的关系是否也符合欧姆定律呢纯电阻电路的定义只有交流电源和纯电阻元件组成的电路叫做纯电阻电路。

第一节纯电阻电路一、电路1．纯电阻电路：交流电路中若只有电阻，这种电路叫纯电阻电路。

如含有白炽灯、电炉、电烙铁等的电路。

2．电阻元件对交流电的阻碍作用，单位二、电流与电压间的关系1．大小关系电阻与电压、电流的瞬时值之间的关系服从欧姆定律。

设在纯电阻电路中，加在电阻R上的交流电压u U m sin t,则通过电阻R的电流的瞬时值为：i =Ru=RtUsinm Im sintI mRUmI =2m I RU 2m =RU IRU：纯电阻电路中欧姆定律的表达式，式中：U 、I 为交流电路中电压、电流的有效值。

这说明，正弦交流电压和电流的最大值、有效值之间也满足欧姆定律。

2．相位关系（1）在纯电阻电路中，电压、电流同相。

（2）表示：电阻的两端电压 u 与通过它的电流 i 同相，其波形图和相量图如图1所示。

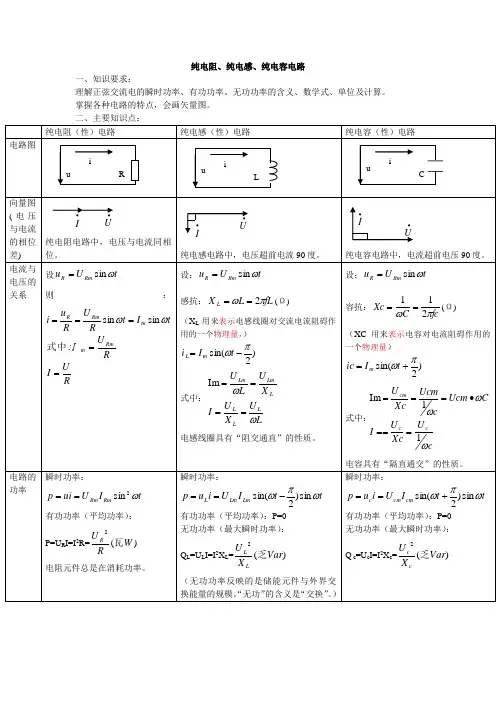
纯电阻、纯电感、纯电容电路一、知识要求：理解正弦交流电的瞬时功率、有功功率、无功功率的含义、数学式、单位及计算。

掌握各种电路的特点，会画矢量图。

三、例题：1.已知电阻R=10Ω，其两端电压V t t u R )30314sin(100)(︒+=，求电流i R(t ).、电路消耗的功率。

解：由于电压与电流同相位，所以 i R(t )=10)(=Rt u R )30314sin(︒+t A 电路消耗的功率P=U R I=W X Um 5002101002Im 2==• 2、已知电感L=0.5H ，其两端电压V t t u L )301000sin(100)(︒+=，求电流i L(t ). 解：L X L ω==1000X0.5=500Ω由于纯电感电路中，电流滞后电压90°，所以：A t t X t i LL )601000sin(2.0)90301000sin(100)(︒-=︒-︒+=3.已知电容C=10μF ，其两端电压V t t u c )301000sin(100)(︒+=，求电流i c (t ).. 解： Ω===-10010101000116X X C X c ω 由于电流超前电压90°，所以：A t t Xct i c )1201000sin()90301000sin(100)(︒+=︒+︒+=四、练习题： （一）、填空题1、平均功率是指（ ），平均功率又称为（ ）。

2、纯电阻正弦交流电路中，电压有效值与电流有效值之间的关系为（ ），电压与电流在相位上的关系为（ ）。

纯电感正弦交流电路中，电压有效值与电流有效值之间的关系为（ ），电压与电流在相位上的关系为（ ）。

纯电容正弦交流电路中，电压有效值与电流有效值之间的关系为（ ），电压与电流在相位上的关系为（ ）。

3、在纯电阻电路中，已知端电压V t u )30314sin(311︒+=，其中R=1000Ω，那么电流i=（ ）,电压与电流的相位差=（ ），电阻上消耗的功率P=（ ）。

纯电阻电路和非纯电阻电路公式1. 什么是电路？大家好，今天我们要聊聊电路，特别是纯电阻电路和非纯电阻电路。

这听起来可能有点儿复杂，但其实就像说吃饭一样，简单又实用。

首先呢，我们得明白，电路就是电流走的路。

电流就像咱们在街上走来走去的人，而电路里的电阻就像是路上的各种障碍物，有的挡路，有的让人走得轻松。

1.1 纯电阻电路的基本概念在纯电阻电路里，所有的电阻都是简单的电阻，没有其他复杂的东西。

这就像你在马路上走，只有平坦的道路，没有坑坑洼洼的地方。

这种电路的好处是，电流流动非常顺畅。

咱们通常用欧姆定律来描述它，公式就是 ( I = frac{U{R )。

这里的 ( I ) 是电流，( U ) 是电压，( R ) 是电阻。

听起来是不是很简单？就像买东西时知道价格，直接拿出钱来就行了。

1.2 纯电阻电路的应用这种电路在生活中无处不在，比如你家的灯泡。

灯泡亮起来，就是电流通过了电阻，发出光来。

想想看，冬天的时候，暖气就是个好例子，电流通过电阻器，变成热量，暖和了我们的身体。

不过呢，纯电阻电路并不总是适用，因为很多设备不光需要电阻，还有其他的电子元件，比如电容和电感，这就引出了我们的下一个话题。

2. 非纯电阻电路的魅力非纯电阻电路，就是说里面有电阻，还有电容和电感。

就像一个热闹的市场，不光有卖水果的，还有卖衣服的和理发的。

电容器能存储电能，而电感器则能产生磁场。

它们一起工作，让电路更复杂，但也更有趣。

这种电路常常用于交流电中，比如咱们家里的冰箱和空调。

就像一场精彩的表演，每个演员都有自己的角色。

2.1 非纯电阻电路的公式对于非纯电阻电路，咱们的公式就得多花点心思了。

这里常用的一个公式是基尔霍夫定律。

简单说，就是“电压相加等于零，电流相加也等于零”。

这就像我们的人生，无论如何都得平衡。

再加上交流电的频率、相位等因素，这些都让电路的表现变得更复杂。

哎，有点像我们生活中的种种挑战，得有耐心才能搞定。

2.2 非纯电阻电路的应用那么，这些非纯电阻电路在生活中有什么用呢？想象一下你正在看电视，里面有各种复杂的电子元件在运作。

第二节 纯电阻、纯电感与纯电容电路教学内容：主要讲三个问题：1.纯电路电流与电压的相位关系2..纯电路电流与电压的数量关系3.纯电路的功率关系教学方法：采用作图分析法教学课时：2×45 min 。

目的要求：使学生了解各种纯电路电流、电压的相位关系及功率关系。

重点难点：重点：三大关系；难点：纯电感电路电流与电压的相位关系。

时间分配：复习提问：5~10min ；讲课：45~50min ；课堂小结：5~10min ；作业练习：25~30min 。

上节内容提问：1.交流电的三要素是什么？2.什么是交流电初相角与相位差？3.如何用矢量图来表正弦交流电？一、纯电阻电路白炽灯、电烙铁、电炉等。

如图1所示。

1.电流与电压的相位关系 设加在电阻两端的电压为t U u m ωsin = （1）根据欧姆定律可知，通过电阻的电流为t I t RU R u i m mωωsin sin ===（2） 比较（1）、（2）两式可以看出，电流与电压是同相位的，其波形图与矢量图如图（2）所示。

2.电流与电压的数量关系 从（2）式可得：RU I mm =两边都除以2：RUI =单位：A=V/Ω （3） 可见其数量关系符合欧姆定律。

3.功率关系纯电阻电路的瞬时功率可表示为：t IU IU t U I t U I iu p mm m m ωωω2cos )2cos 1(2sin 2-=-=== 即 t IU IU p ω2cos -= （4）其波形图如图（2）所示。

其实从电流电压同相位这一点，就能得到功率的波形图。

由图可知，每一瞬时的功率都为正，说明电阻元件始终从电源索取能量用来作功，是个耗能元件。

我们用一个周期内功率的平均值作为纯电阻电路的平均功率，也叫有功功率：RU R I IU P 22=== （W ） （5）“有功”的本质含义是消耗。

例：有一220V 、60W 的电灯，接在220V 的电源上，试求通过电灯的电流和电灯的电阻。

欧姆定律适用范围欧姆定律适用范围是：纯电阻电路（电能转化为内能的电路）. 对于电感电路或电容电路不能适用。

欧姆定律所代表的就是，在相同的电路里面，然后通过某段电流和这段导体两端电压成正比，跟它的电阻却是成反比，这个定律是欧姆在1826年的论文中提出来的。

一、欧姆定律简述欧姆定律的简述是：在同一电路中，通过某段导体的电流跟这段导体两端的电压成正比，跟这段导体的电阻成反比。

该定律是由德国物理学家乔治·西蒙·欧姆1826年4月发表的《金属导电定律的测定》论文提出的。

随研究电路工作的进展，人们逐渐认识到欧姆定律的重要性，欧姆本人的声誉也大大提高。

为了纪念欧姆对电磁学的贡献，物理学界将电阻的单位命名为欧姆，以符号Ω表示。

二、欧姆定律适用条件1.在通常温度或温度不太低的情况下，对于电子导电的导体（如金属），欧姆定律是一个很准确的定律。

当温度低到某一温度时，金属导体可能从正常态进入超导态。

处于超导态的导体电阻消失了，不加电压也可以有电流。

对于这种情况，欧姆定律当然不再适用了。

2.在通常温度或温度变化范围不太大时，像电解液（酸、碱、盐的水溶液）这样离子导电的导体，欧姆定律也适用。

而对于气体电离条件下，所呈现的导电状态，和一些导电器件，如电子管、晶体管等，欧姆定律不成立。

3.欧姆定律成立时，以导体两端电压为横坐标，导体中的电流I为纵坐标，所做出的曲线，称为伏安特性曲线。

这是一条通过坐标原点的直线，它的斜率为电阻的倒数。

具有这种性质的电器元件叫线性元件，其电阻叫线性电阻或欧姆电阻。

4.欧姆定律不成立时，伏安特性曲线不是过原点的直线，而是不同形状的曲线。

把具有这种性质的电器元件，叫作非线性元件。

初中物理中，纯电阻电路是一个重要的概念。

纯电阻电路是指电路中只有纯电阻元件的电路，也就是说，在这个电路中电能只转化为热能，如电灯、电烙铁、熨斗等都是纯电阻元件。

在纯电阻电路中，电压和电流是同相位，也就是说，电压和电流同时达到最大值或最小值。

同时，欧姆定律和焦耳定律都成立。

纯电阻电路的一个特点是，电能全部转化为内能，不对外做功。

在实际应用中，电动机和电容补偿器等设备虽然不是纯电阻元件，但在某些情况下也可以看作是纯电阻电路。

另外，有电动机存在的电路中，电能被转化成动能，经电容补偿后可以使相位平衡，功率因数可以为1。

此外，有纯电感线圈存在的电路中，由于没有欧姆电阻，因此该线圈也就不存在热量损耗。

总之，初中物理中的纯电阻电路是一个重要的概念，掌握其特点和应用是学好物理的基础。

纯电阻、纯电感、纯电容电路的功率及功率因数一、纯电阻电路纯电阻电路就是既没有电感，又没有电容，只包含有线性电阻的电路。

在实际生活中，由白炽灯、电烙铁、电阻炉或电阻器组成的交流电路都可以近似地看成是纯电阻交流电路。

1、纯电阻电路的功率在任一瞬间，电阻中的电流瞬时值与同一瞬间电阻两端电压的瞬时值的乘积，称为电阻获取的瞬时功率，用PR表示，即:PR=uRi=(URmsinωt)2/R由于瞬时功率时刻变动，不便计算，因而通常都是计算一个周期内取用功率的平均值，即平均功率。

平均功率又称有功功率，用P表示。

电流、电压用有效值表示时，其功率P的计算与直流电路相同，即:P=URI=I2R=UR2/R2、纯电阻电路的功率因数在交流电路中，电压与电流之间的相位差(φ)的余弦叫做功率因数，用符号cosφ表示。

负载为纯电阻时,电流和电压同相位，它们之间没有相位差, 即φ=0°因此纯电阻电路的功率因数cosφ=cos0°=1。

二、纯电感电路由电阻很小的电感线圈组成的交流电路，都可近似地看成是纯电感电路。

1、纯电感电路的功率纯电感线圈时而“吞进”功率，时而“吐出”功率，在一个周期内的平均功率为零，平均功率不能反映线圈能量交换的规模，因而就用瞬时功率的最大值来反映这种能量交换的规模，并把它叫做电路的无功功率。

无功功率用字母QL表示。

QL的大小为：QL=ULI=I2XL=UL2/XL为与有功功率相区别，无功功率的单位是乏。

在上式中，当各物理量的单位分别用伏特、安培、欧姆时，无功功率的单位是乏（var）。

必须指出，“无功”的含义是“交换”而不是“消耗”，它是相对“有功”而言的，绝不能理解为“无用”。

2、纯电感电路的功率因数在数值上，功率因数是有功功率和视在功率的比值，即cosφ=P/S。

纯电感通过交流电时，只有无功功率QL，有功功率为零，即P=0。

因此纯电感电路的功率因数cosφ=P/S=0/S=0。

三、纯电容电路由介质损耗很小，绝缘电阻很大的电容器组成的交流电路，可近似看成纯电容电路。