【精准解析】2021新高考数学二轮(山东)：主观题专练 解析几何(9)

山东省青岛市2021届新高考数学第二次调研试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．连接双曲线22122:1x y C a b -=及22222:1y x C b a-=的4个顶点的四边形面积为1S ，连接4个焦点的四边形的面积为2S ，则当12S S 取得最大值时，双曲线1C 的离心率为（ ） AB．2CD【答案】D 【解析】 【分析】先求出四个顶点、四个焦点的坐标，四个顶点构成一个菱形，求出菱形的面积，四个焦点构成正方形，求出其面积，利用重要不等式求得12S S 取得最大值时有a b =，从而求得其离心率.【详解】双曲线22221x y a b-=与22221y x b a -=互为共轭双曲线，四个顶点的坐标为(,0),(0,)a b ±±，四个焦点的坐标为(,0),(0,)c c ±±，四个顶点形成的四边形的面积112222S a b ab =⨯⨯=， 四个焦点连线形成的四边形的面积2212222S c c c =⨯⨯=，所以1222221222S ab ab ab S c a b ab ==≤=+， 当12S S 取得最大值时有a b =，c =，离心率c e a== 故选：D. 【点睛】该题考查的是有关双曲线的离心率的问题，涉及到的知识点有共轭双曲线的顶点，焦点，菱形面积公式，重要不等式求最值，等轴双曲线的离心率，属于简单题目.2．已知集合A ＝{x ∈N|x 2＜8x}，B ＝{2，3，6}，C ＝{2，3，7}，则()A B C ⋃ð＝（ ） A ．{2，3，4，5} B ．{2，3，4，5，6} C ．{1，2，3，4，5，6}D ．{1，3，4，5，6，7}【答案】C 【解析】 【分析】根据集合的并集、补集的概念，可得结果. 【详解】集合A ＝{x ∈N|x 2＜8x}＝{x ∈N|0＜x ＜8}， 所以集合A ＝{1，2，3，4，5，6，7} B ＝{2，3，6}，C ＝{2，3，7}， 故A C ð＝{1，4，5，6}，所以()A B C ⋃ð＝{1，2，3，4，5，6}. 故选：C. 【点睛】本题考查的是集合并集，补集的概念，属基础题.3．已知等差数列{}n a 的前n 项和为n S ，且282,10a a =-=，则9S =（ ） A ．45 B ．42C ．25D ．36【答案】D 【解析】 【分析】由等差数列的性质可知1928a a a a +=+,进而代入等差数列的前n 项和的公式即可. 【详解】 由题,192899()9()9(210)36222a a a a S ++⨯-+====. 故选:D 【点睛】本题考查等差数列的性质,考查等差数列的前n 项和.4．在棱长均相等的正三棱柱111ABC A B C =中，D 为1BB 的中点，F 在1AC 上，且1DF AC ⊥，则下述结论：①1AC BC ⊥；②1AF FC =；③平面1DAC ⊥平面11ACC A ：④异面直线1AC 与CD 所成角为60︒其中正确命题的个数为( )A ．1B ．2C ．3D ．4【答案】B 【解析】 【分析】设出棱长，通过直线与直线的垂直判断直线与直线的平行，推出①的正误；判断F 是1AC 的中点推出②正的误；利用直线与平面垂直推出平面与平面垂直推出③正的误；建立空间直角坐标系求出异面直线1AC 与CD 所成角判断④的正误．【详解】解：不妨设棱长为：2，对于①连结1AB ，则1122AB AC ==1190AC B ∴∠≠︒即1AC 与11B C 不垂直，又11//BC B C ，∴①不正确；对于②，连结AD ，1DC ，在1ADC ∆中，15AD DC ==而1DF AC ⊥，F ∴是1AC 的中点，所以1AF FC =，∴②正确；对于③由②可知，在1ADC ∆中，3DF =，连结CF ，易知2CF =Rt CBD ∆中，5CD =，222DF CF CD ∴+=，即DF CF ⊥，又1DF AC ⊥，DF ⊥∴面11ACC A ，∴平面1DAC ⊥平面11ACC A ，∴③正确； 以1A 为坐标原点，平面111A B C 上过1A 点垂直于11A C 的直线为x 轴，11A C 所在的直线为y 轴，1A A 所在的直线为z 轴，建立如图所示的直角坐标系；()10,0,0A ， )13,1,0B ，()10,2,0C ， ()0,0,2A ， ()0,2,2C ， )3,1,1D；()10,2,2AC =-u u u u r， )3,1,1CD =--u u u r ；异面直线1AC 与CD 所成角为θ，11cos 0||||AC CD AC CD θ==u u u u r u u u r g u u u ur u u u r ，故90θ=︒．④不正确． 故选：B ．【点睛】本题考查命题的真假的判断，棱锥的结构特征，直线与平面垂直，直线与直线的位置关系的应用，考查空间想象能力以及逻辑推理能力．5．如图，正方形网格纸中的实线图形是一个多面体的三视图，则该多面体各表面所在平面互相垂直的有（）A．2对B．3对C．4对D．5对【答案】C【解析】【分析】-，易证平面PAD⊥平面ABCD，平面PCD⊥平面PAD，平面PAB⊥画出该几何体的直观图P ABCD平面PAD，平面PAB⊥平面PCD，从而可选出答案．【详解】该几何体是一个四棱锥，直观图如下图所示，易知平面PAD⊥平面ABCD，作PO⊥AD于O，则有PO⊥平面ABCD，PO⊥CD，又AD⊥CD，所以，CD⊥平面PAD，所以平面PCD⊥平面PAD，同理可证：平面PAB⊥平面PAD，由三视图可知：PO＝AO＝OD，所以，AP⊥PD，又AP⊥CD，所以，AP⊥平面PCD，所以，平面PAB⊥平面PCD，所以该多面体各表面所在平面互相垂直的有4对．【点睛】本题考查了空间几何体的三视图，考查了四棱锥的结构特征，考查了面面垂直的证明，属于中档题． 6．已知函数()()cos 0,02f x x πωϕωϕ⎛⎫=+><<⎪⎝⎭的最小正周期为π，且满足()()f x f x ϕϕ+=-，则要得到函数()f x 的图像，可将函数()sin g x x ω=的图像（ ） A ．向左平移12π个单位长度 B ．向右平移12π个单位长度C ．向左平移512π个单位长度 D ．向右平移512π个单位长度 【答案】C 【解析】 【分析】依题意可得2ω=，且x ϕ=是()f x 的一条对称轴，即可求出ϕ的值，再根据三角函数的平移规则计算可得； 【详解】解：由已知得2ω=，x ϕ=是()f x 的一条对称轴，且使()f x 取得最值，则3πk ϕ=，π3ϕ=，π5ππ()cos 2cos 23122f x x x ⎡⎤⎛⎫⎛⎫=+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，π()sin 2cos 22g x x x ⎛⎫==- ⎪⎝⎭，故选：C. 【点睛】本题考查三角函数的性质以及三角函数的变换规则，属于基础题.7．我国著名数学家陈景润在哥德巴赫猜想的研究中取得了世界瞩目的成就，哥德巴赫猜想内容是“每个大于2的偶数可以表示为两个素数的和”（ 注：如果一个大于1的整数除了1和自身外无其他正因数，则称这个整数为素数），在不超过15的素数中，随机选取2个不同的素数a 、b ，则3a b -<的概率是（ ） A ．15B ．415C ．13D ．25【答案】B【解析】 【分析】先列举出不超过15的素数，并列举出所有的基本事件以及事件“在不超过15的素数中，随机选取2个不同的素数a 、b ，满足3a b -<”所包含的基本事件，利用古典概型的概率公式可求得所求事件的概率. 【详解】不超过15的素数有：2、3、5、7、11、13，在不超过15的素数中，随机选取2个不同的素数，所有的基本事件有：()2,3、()2,5、()2,7、12()()f x f x -、()2,13、()3,5、()3,7、()3,11、()3,13、()5,7、()5,11、()5,13、()7,11、()7,13、()11,13，共15种情况，其中，事件“在不超过15的素数中，随机选取2个不同的素数a 、b ，且3a b -<”包含的基本事件有：()2,3、()3,5、()5,7、()11,13，共4种情况，因此，所求事件的概率为415P =. 故选：B. 【点睛】本题考查古典概型概率的计算，一般利用列举法列举出基本事件，考查计算能力，属于基础题.8．若函数()y f x =的定义域为M ＝{x|－2≤x≤2}，值域为N ＝{y|0≤y≤2},则函数()y f x =的图像可能是（ ）A ．B ．C ．D ．【答案】B 【解析】因为对A 不符合定义域当中的每一个元素都有象，即可排除； 对B 满足函数定义，故符合；对C 出现了定义域当中的一个元素对应值域当中的两个元素的情况，不符合函数的定义，从而可以否定； 对D 因为值域当中有的元素没有原象，故可否定． 故选B ．9．如图所示，正方体ABCD-A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E 、F 且EF=22，则下列结论中错误的是（ ）A ．AC ⊥BEB ．EF //平面ABCDC ．三棱锥A-BEF 的体积为定值D ．异面直线AE,BF 所成的角为定值【答案】D 【解析】 【分析】A ．通过线面的垂直关系可证真假；B ．根据线面平行可证真假；C ．根据三棱锥的体积计算的公式可证真假；D ．根据列举特殊情况可证真假. 【详解】A ．因为11,,AC BD AC DD DD BD D ⊥⊥=I ，所以AC ⊥平面11BDDB ， 又因为BE ⊂平面11BDD B ，所以AC BE ⊥，故正确；B ．因为11//D B DB ，所以//EF DB ，且EF ⊂/平面ABCD ，DB ⊂平面ABCD ， 所以//EF 平面ABCD ，故正确；C ．因为11224BEF S EF BB =⨯⨯=V 为定值，A 到平面11BDD B 的距离为1222h AC ==， 所以11312A BEF BEF V S h -=⋅⋅=V 为定值，故正确； D ．当1111AC B D E =I ，AC BD G ⋂=，取F 为1B ，如下图所示：因为//BF EG ，所以异面直线,AE BF 所成角为AEG ∠，且222tan12AGAEGGE∠===，当1111AC B D F=I，AC BD G⋂=，取E为1D，如下图所示：因为11//,D F GB D F GB=，所以四边形1D GBF是平行四边形，所以1//BF D G，所以异面直线,AE BF所成角为AEG∠，且2232tan212AGAEGGE∠===⎛⎫+ ⎪⎝⎭由此可知：异面直线,AE BF所成角不是定值，故错误.故选：D.【点睛】本题考查立体几何中的综合应用，涉及到线面垂直与线面平行的证明、异面直线所成角以及三棱锥体积的计算，难度较难.注意求解异面直线所成角时，将直线平移至同一平面内.10．在ABCV中，角、、A B C的对边分别为,,a b c，若tan2sin()a Bb B C=+．则角B的大小为() A．π3B．π6C．π2D．π4【答案】A【解析】【分析】由正弦定理化简已知等式可得sin tan2sin sinA B B A=，结合sin0A>，可得tan2sinB B=，结合范围()0,Bπ∈，可得sin0B>，可得1cos2B=，即可得解B的值．【详解】解：∵()tan2sin2sina Bb B C b A=+=，∴由正弦定理可得：sin tan2sin sinA B B A=，∵sin0A>，∴tan2sinB B=，∵()0,B π∈，sin 0B >， ∴1cos 2B =， ∴3B π=．故选A ． 【点睛】本题主要考查了正弦定理在解三角形中的应用，考查了计算能力和转化思想，属于基础题．11．赵爽是我国古代数学家、天文学家，大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的）.类比“赵爽弦图”.可类似地构造如下图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成一个大等边三角形.设22DF AF ==，若在大等边三角形中随机取一点，则此点取自小等边三角形（阴影部分）的概率是（ ）A ．413B ．21313C ．926D ．31326【答案】A 【解析】 【分析】根据几何概率计算公式，求出中间小三角形区域的面积与大三角形面积的比值即可． 【详解】在ABD ∆中，3AD =，1BD =，120ADB ∠=︒，由余弦定理，得222cos12013AB AD BD AD BD =+-⋅︒所以13DF AB =. 所以所求概率为24=1313DEF ABC S S ∆∆=. 故选A. 【点睛】本题考查了几何概型的概率计算问题，是基础题．12．设0.50.82a =，sin1b =，lg 3c =，则a ，b ，c 三数的大小关系是 A ．a c b << B ．a b c << C ．c b a << D ．b c a <<【答案】C 【解析】 【分析】利用对数函数，指数函数以及正弦函数的性质和计算公式，将a ，b ，c 12比较即可. 【详解】由0.50.50.820.8a =>1sin1sin 23b π<=<==<11lg3lg1022c =<==，所以有c b a <<.选C. 【点睛】本题考查对数值，指数值和正弦值大小的比较，是基础题，解题时选择合适的中间值比较是关键，注意合理地进行等价转化.二、填空题：本题共4小题，每小题5分，共20分。

姓名，年级：时间：应试技巧必备巧用5招秒杀选择题、填空题妙招1 特值（例)法特值（例）法是根据题设和各选项的具体情况和特点,选取满足条件的特殊的数值、特殊的点、特殊的例子、特殊的图形、特殊的位置、特殊的函数、特殊的方程、特殊的数列等，针对各选项进行代入对照，从而得到正确答案的方法．(1）使用前提：满足当一般性结论成立时，对符合条件的特殊情况也一定成立．（2)使用技巧：找到满足条件的合适的特殊例子，有时甚至需要两个或两个以上的特殊例子才可以确定结论．(3）常见问题：求范围,比较大小,含字母求值或区间,恒成立问题,任意性问题等．真题示例技法应用(2020·全国卷Ⅱ）若α为第四象限角，则（）A．cos 2α＞0 B．cos 2α＜0 C．sin 2α＞0 D．sin 2α＜0当α＝－错误!时，cos 2α＝0,sin 2α＝－1，排除A，B，C,故选D．（2019·全国卷Ⅰ)已知三棱锥P。

ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体如图所示,构造边长为错误!的正方体PBJA.CDHG,显然满足题设的一切条件，则球O就是该正方体的外接球,从而体积为错误!π。

选D积为( )A．8错误!πB．4错误!πC．2错误!πD．错误!π（2017·全国卷Ⅰ)已知α∈错误!，tan α＝2,则cos错误!＝________.结合三角函数的定义,取角α终边上的特殊点(1,2），求出sin α＝错误!，cos α＝错误!，代入计算．答案：错误!（2017·山东高考）若a〉b〉0，且ab＝1，则下列不等式成立的是( )A．a＋错误!<错误!<log2（a＋b) B．错误!<log2(a＋b)〈a＋错误! C．a＋错误!〈log2（a＋b)〈错误!D．log2（a＋b)<a＋1b<错误!根据条件不妨对a,b选取特殊值验证，如a＝2，b＝12时，选项A，C,D对应的不等式不成立．选B(2016·全国卷Ⅱ)函数y＝A sin （ωx＋φ)的部分图象如图所示,则( )A．y＝2sin错误! B．y＝2sin错误! C．y＝2sin错误!结合图象，分别取x＝0和x＝错误!验证．选A（2020·全国卷Ⅱ）设函数f （x ）＝ln|2x ＋1|－ln|2x －1|，则f (x )( )A ．是偶函数，且在错误!，＋∞单调递增B ．是奇函数，且在－错误!，错误!单调递减C ．是偶函数，且在－∞，－12单调递增D ．是奇函数，且在－∞，－12单调递减由错误!得函数f (x )的定义域为错误!∪错误!∪错误!，其关于原点对称，因为f (－x ）＝ln ｜2（－x )＋1｜－ln|2（－x ）－1｜＝ln|2x －1|－ln ｜2x ＋1|＝－f (x )，所以函数f (x )为奇函数，排除A ，C ．当x ∈错误!时，f （x )＝ln （2x＋1）－ln(1－2x )，易知函数f (x ）单调递增，排除B ．当x ∈－∞,－错误!时，f （x ）＝ln(－2x －1）－ln （1－2x )＝ln 错误!＝ln 错误!,易知函数f （x )单调递减，故选D（2019·全国卷Ⅲ)函数y ＝错误!在［－6，6]的图象大致为（ ）由函数解析式易知函数为奇函数，故可排除C ，再取特殊值x ＝4，可排除D ，取特殊值x ＝6，可排除A ．选B验证法是把选项代入题干中进行检验，或反过来从题干中找合适的验证条件，代入各选项中进行检验,从而可否定错误选项，得到正确选项的方法．（1）使用前提：选项中存在唯一正确的答案．(2019·全国卷Ⅰ)古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是错误!错误!，著名的“断臂维纳斯”便是如此．此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是错误!.若某人满足上述两个黄金分割比例，且腿长为105 cm ，头顶至脖子下端的长度为26 cm ，则其身高可能是（ ）A ．165 cmB ．175 cmC ．185 cmD ．190 cm头顶至脖子下端的长度为26 cm,可得咽喉至肚脐的长度小于42 cm ，肚脐至足底的长度小于110 cm ，则该人的身高小于178 cm 。

2021年山东省济南市高考数学二模试卷一、单选题（本大题共8小题，共40.0分）1. 已知全集U =R ，集合A ={x|x ≥2}，B ={x|log 2(x −1)<1}，则(∁U A)∩B =( )A. (−∞,2)B. (−∞,2]C. (1,2)D. (1,3)2. 已知(2−i)⋅z =i ，i 为虚数单位，则|z|=( )A. √55B. 1C. 2D. √53. “直线l 垂直于平面α内的无数条直线”是“l ⊥α”的一个( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 已知随机变量X 服从正态分布N(1,σ2)，若P(X ≤0)=0.2，则P(X <2)=( )A. 0.2B. 0.4C. 0.6D. 0.85. 已知椭圆C ：x 24+y 23=1，过点P(1,12)的直线交椭圆C 于A 、B 两点，若P 为AB 的中点，则直线AB的方程为( )A. 3x −2y −2=0B. 3x +2y −4=0C. 3x +4y −5=0D. 3x −4y −1=06. 在平面直角坐标系xOy 中，O 为坐标原点，已知点M(√3,−1)和点N(0,1).若点P 在∠MON 的角平分线上，且|OP ⃗⃗⃗⃗⃗ |=4，则OP ⃗⃗⃗⃗⃗ ⋅MN⃗⃗⃗⃗⃗⃗⃗ =( ) A. −2 B. −6 C. 2 D. 67. 已知函数f(x)={−1+2lnx,x >11−2lnx,0<x ≤1，若f(a)=f(b)，则a +b 的最小值是( )A. 2√eB. eC. 1+eD. 2e8. “曼哈顿距离”是由赫尔曼⋅闵可夫斯基所创的词汇，是一种使用在几何度量空间的几何学用语，例如在平面直角坐标系中，点P(x 1,y 1)、Q(x 2,y 2)的曼哈顿距离为：L PQ =|x 1−x 2|+|y 1−y 2|.若点P(1,2)，点Q 为圆C ：x 2+y 2=4上一动点，则L PQ 的最大值为( )A. 1+√2B. 1+2√2C. 3+√2D. 3+2√2二、多选题（本大题共4小题，共20.0分）9. 已知a >b >0，c ∈R ，下列不等式恒成立的有( )A. (13)a <(13)b B. ac 2>bc 2C. log 21a >log 21bD. (a+b 2)2<a 2+b 2210. 函数f(x)=2cos(2x −π6)+1(x ∈R)，则下列说法正确的是( )A. 若f(x 1)=f(x 2)=3，则x 1−x 2=kπ(k ∈Z)B. 函数f(x)在[−π6,π3]上为增函数 C. 函数f(x)的图象关于点(π3,1)对称D. 函数f(x)的图象可以由g(x)=2sin(2x −π3)+1(x ∈R)的图象向左平移π12个单位长度得到11. 已知f(x)是定义在R 上的偶函数，f(1−x)=−f(1+x)，且当x ∈[0,1]时，f(x)=x 2+x −2，则下列说法正确的是( )A. f(x)是以4为周期的周期函数B. f(2018)+f(2021)=−2C. 函数y =log 2(x +1)的图象与函数f(x)的图象有且仅有3个交点D. 当x ∈[3,4]时，f(x)=x 2−9x +1812. 如图，直四棱柱ABCD −A 1B 1C 1D 1中，底面ABCD 为平行四边形，AB =AA 1=12AD =1，∠BAD =60°，点P 是半圆弧A 1D 1⏜上的动点(不包括端点)，点Q 是半圆弧BC ⏜上的动点(不包括端点)，则下列说法正确的是( )A. 四面体PBCQ 的体积是定值B. AD ⃗⃗⃗⃗⃗⃗ ⋅A 1P ⃗⃗⃗⃗⃗⃗⃗ 的取值范围是(0,4)C. 若C 1Q 与平面ABCD 所成的角为θ，则tanθ>12D. 若三棱锥P −BCQ 的外接球表面积为S ，则S ∈[4π,13π)三、单空题（本大题共4小题，共20.0分）13. 已知(x −2x )n 的展开式中各项的二项式系数的和为128，则这个展开式中x 3项的系数是______． 14. 已知tan(π4−α)=12，则cos2α=______． 15. 设双曲线x 2a 2−y 2b 2=1(a >0,b >0)的左右焦点分别为F 1，F 2，过F 1的直线分别交双曲线左、右两支于点M ，N.若以MN 为直径的圆经过点F 2且|MF 2|=|NF 2|，则双曲线的离心率为______．16. 设函数f(x)=e x −cosx −2a ，g(x)=x ，若存在x 1，x 2∈[0,π]使得f(x 1)=g(x 2)成立，则x 2−x 1的最小值为1时，实数a =______． 四、解答题（本大题共6小题，共70.0分）17. 在①(sinB −sinC)2=sin 2A −sinBsinC ；②2asinC =ctanA ；③2cos 2B+C 2=cos2A +1；三个条件中任选一个，补充在下面问题中，并作答．问题：已知△ABC 的内角A ，B ，C 所对应的边分别为a ，b ，c ，若b =√2，___． (1)求A 的值；(2)若sinB =√2sinC ，求△ABC 的面积．18. 已知数列{a n }是正项等比数列，满足a 3是2a 1，3a 2的等差中项，a 4=16．(1)求数列{a n }的通项公式；(2)若b n =(−1)n log 2a 2n+1，求数列{b n }的前n 项和T n ．19. 甲、乙两人进行“抗击新冠疫情”知识竞赛，比赛采取五局三胜制．约定先胜三局者获胜，比赛结束．假设在每局比赛中，甲获胜的概率为23，乙获胜的概率为13，各局比赛相互独立． (1)求甲获胜的概率；(2)设比赛结束时甲和乙共进行了X 局比赛，求随机变量X 的分布列及数学期望．20.如图，四边形ABEF是矩形，平面ABC⊥平面ABEF，D为BC中点，∠CAB=120°，AB=AC=4，AF=√6．(1)证明：平面ADF⊥平面BCF；(2)求二面角F−AD−E的余弦值．21.已知抛物线C：x2=2py(p>0)，过点T(0,p)作两条互相垂直的直线l1和l2，l1交抛物线C于A、B两．点，l2交抛物线C于E、F两点，当点A的横坐标为1时，抛物线C在点A处的切线斜率为12(1)求抛物线C的标准方程；(2)已知O为坐标原点，线段AB的中点为M，线段EF的中点为N，求△OMN面积的最小值．22.已知函数f(x)=xlnx−ax2+x，g(x)=(1−a)xlnx−e x−1，a>0．(1)当a=e时，判断函数f(x)在定义域内的单调性；2(2)若f(x)≥g(x)+x恒成立，求实数a的取值范围．答案和解析1.【答案】C【解析】解：因为B ={x|log 2(x −1)<1}={x|1<x <3}， 又集合A ={x|x ≥2}，全集U =R ， 所以(∁U A ={x|x <2}, 所以(∁U A)∩B =(1,2)． 故选：C ．先利用对数不等式求出集合B ，然后由补集的定义和交集的定义求解即可．本题考查了集合的运算，涉及了对数不等式的解法，补集的定义以及交集定义的理解和应用，属于基础题．2.【答案】A【解析】解：由已知可得： z =i2−i =i(2+i)(2−i)(2+i)=−1+2i 5，所以|z|=√(−15)2+(25)2=√55，故选：A ．由已知求出z ，进而可以求解．本题考查了复数的运算性质，涉及到模的求解，属于基础题．3.【答案】B【解析】解：直线l 垂直于平面α内的无数条直线，若无数条直线是平行线，则l 与α不一定平行， 如果l ⊥α，根据线面垂直的性质可知直线l 垂直于平面α内的无数条直线． 故“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的必要不充分条件． 故选：B ．直线l 垂直于平面α内的无数条直线，若无数条直线是平行线，则l 与α不一定平行，如果l ⊥α，根据线面垂直的性质可知直线l 垂直于平面α内的无数条直线，最后根据“若p ⇒q 为假命题且q ⇒p 为真命题，则命题p 是命题q 的必要不充分条件”可得结论．本题主要考查了直线与平面垂直的判定，以及必要条件、充分条件与充要条件的判断，同时考查了化归与转化的数学思想方法，以及空间想象能力、推理论证能力，属于基础题．4.【答案】D【解析】解：随机变量X服从正态分布N(1,σ2)，P(X≤0)=0.2，∴P(0≤X≤1)=0.5−0.2=0.3，∴P(1≤X≤2)=P(0≤X≤1)=0.3．所以P(X<2)=0.5+0.3=0.8．故选：D．先求出P(0≤X≤1)，再计算P(1≤X≤2)，然后求解P(X<2)．本题考查了正态分布的对称性，属于基础题．5.【答案】B【解析】解：设A(x1,y1)，B(x2,y2)，则3x12+4y12=12，3x22+4y22=12，∴3(x1+x2)(x1−x2)+4(y1+y2)(y1−y2)=0．∵P(1,1)恰为线段AB的中点，即有x1+x2=2，y1+y2=1，∴3(x1−x2)+2(y1−y2)=0，∴直线AB的斜率为k=y1−y2x1−x2=−32，∴直线AB的方程为y−12=−32(x−1)，即3x+2y−4=0．由于P在椭圆内，故成立．故选：B．利用“点差法”、线段中点坐标公式、斜率计算公式即可得出．本题考查了“点差法”、线段中点坐标公式、斜率计算公式，属于中档题．6.【答案】A【解析】解：点M(√3,−1)可知OM 与x 轴正方向所角为30°，如图点M(√3,−1)和点N(0,1)那么ON =1，MO =2，余弦定理可得∠MON =120°， 点P 在∠MON 的角平分线上，且|OP ⃗⃗⃗⃗⃗ |=4， 那么∠MOP =∠NOP =60°， 可得P 的坐标为(2√3,2)，∴OP ⃗⃗⃗⃗⃗ ⋅MN ⃗⃗⃗⃗⃗⃗⃗ =(2√3,2)⋅(−√3,2)=−6+4=−2； 故选：A ．根据点M(√3,−1)可知OM 与x 轴正方向所角为30°，点M(√3,−1)和点N(0,1)所成夹角∠MON =120°，然后求出P 的坐标，结合向量的坐标运算，即可求解OP ⃗⃗⃗⃗⃗ ⋅MN ⃗⃗⃗⃗⃗⃗⃗ 的值． 本题考查了向量的坐标运算和余弦定理的应用，属于基础题．7.【答案】C【解析】解：∵函数f(x)={−1+2lnx,x >11−2lnx,0<x ≤1，设b >1≥a >0，由f(a)=f(b)可得−1+2lnb =1−2lna ，即lna +lnb =1，即ab =e ， ∴a +b =a +ea ≥2√a ⋅ea =2√e ，当且仅当a =√e 时，等号成立，但0<a ≤1时，即y =a +ea 在(0,1]上单调递减， 故y =a +ea 在(0,1]上的最小值为：1+e1=1+e ， 故选：C ．根据函数的性质可得ab =e ，再根据基本不等式以及函数的单调性，再代值计算即可 本题主要考查函数的性质以及基本不等式的应用，意在考查学生的逻辑推理能力．8.【答案】D【解析】解：由题意设P(2cosθ,2sinθ)(0≤θ<2π)， 则L PQ =|1−2cosθ|+|2−2sinθ|， 当cosθ≥12时，即当θ∈[0,π3]∪[5π3,2π)时， L PQ =2cosθ−1+2−2sinθ=1+2√2cos(θ+π4)， ∵θ∈[0,π3]∪[5π3,2π)，∴θ+π4∈[π4,7π12]∪[23π12,94π)， 则当θ+π4=2π时，L PQ 的最大值为1+2√2； 当cosθ<12时，即当θ∈(π3,5π3)时，L PQ =1−2cosθ+2−2sinθ=3−2√2cos(θ+π4)， ∵θ∈(π3,5π3)∴θ+π4∈(7π12,23π12)，则当θ+π4=32π时，L PQ 的最大值为3+2√2． 综上所述，L PQ 的最大值为3+2√2． 故选：D ．由题意设P(2cosθ,2sinθ)(0≤θ<2π)，则L PQ =|1−2cosθ|+|2−2sinθ|，然后对θ分段去绝对值，再由三角函数求最值．本题考查点与圆的位置关系，考查新定义下的两点间的距离公式的应用，训练了利用三角函数求最值，是中档题．9.【答案】AD【解析】解：对于A ：由于a >b >0，函数y =(13)x 为减函数，故(13)a <(13)b ；故A 正确； 对于B ：当c =0时，ac 2=bc 2；故B 错误；对于C ：当a >b >0时，1b >1a >0，由于y =log 2x 在(0,+∞)单调递增，所以log 21b >log 21a ，故C 错误； 对于D ：根据不等式的性质，(a+b 2)2<a 2+b 22恒成立，故D 正确；故选：AD ．直接利用指数函数和对数函数的单调性的应用和基本不等式的应用确定A 、B 、C 、D 的结论．本题考查的知识要点：指数函数和对数函数的单调性，基本不等式的应用，主要考查学生的运算能力和数学思维能力，属于基础题．10.【答案】AC【解析】解：对于函数f(x)=2cos(2x−π6)+1(x∈R)，若f(x1)=f(x2)=3，则x1−x2=kT=kπ(k∈Z)，故A正确；在[−π6,π3]上，2x+π6∈[−π6,5π6]，函数f(x)没有单调性，故B错误；令x=π3，求得f(x)=1，可得函数f(x)的图象关于点(π3,1)对称；把g(x)=2sin(2x−π3)+1(x∈R)的图象向左平移π12个单位长度得到y=2sin(2x+π6−π3)+1=2sin(2x−π6)+1(x∈R)的图象，故D错误，故选：AC．由题意利用函数y=Asin(ωx+φ)的图象变换规律，正弦函数的图象和性质，得出结论．本题主要考查函数y=Asin(ωx+φ)的图象变换规律，正弦函数的图象和性质，属于中档题．11.【答案】ACD【解析】解：根据题意，依次分析选项：对于A，f(x)满足f(1−x)=−f(1+x)，即f(−x)=−f(2+x)，又由f(x)为偶函数，则f(2+x)=−f(x)，则有f(x+4)=−f(x+2)=f(x)，则f(x)是周期为4的周期函数，A正确；对于B，f(x)是周期为4的周期函数，则f(2018)=f(2)=−f(0)=−(−2)=2，f(2021)=f(1)=0，则f(2018)+f(2021)=2，B错误；对于C，根据题意，作出函数y=log2(x+1)的图象与函数f(x)的图象，结合图象可得两个函数有3个交点，C正确；对于D，当x∈[3,4]时，则4−x∈[0,1]，则f(4−x)=(4−x)2+(4−x)−2=x2−9x+18，又由f(x)为周期为4的周期函数且f(x)是偶函数，则f(x)=f(x−4)=f(4−x)=x2−9x+18，D正确；根据题意，依次分析选项是否正确，即可得答案．本题考查函数奇偶性的性质以及应用，涉及函数周期性的判断，属于中档题．12.【答案】BCD【解析】解：对A ：在四棱柱ABCD −A 1B 1C 1D 1中，点P 到面ABCD 的距离为1，则V P−BCQ =13d ×12BC ×ℎ=13ℎ，由于h 不为定值，故V P−BCQ 不为定值，故A 错误；对B ：在Rt △A 1PD 1中，cos∠D 1A 1P =A 1PA 1D 1，所以AD ⃗⃗⃗⃗⃗⃗ ⋅A 1P ⃗⃗⃗⃗⃗⃗⃗ =A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⋅A 1P ⃗⃗⃗⃗⃗⃗⃗ =|A 1D 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |⋅|A 1P ⃗⃗⃗⃗⃗⃗⃗ |cos∠D 1A 1P =4cos²∠D 1A 1P ，因为∠D 1A 1P ∈(0,π2)，所以cos∠D 1A 1P ∈(0,1)， 所以AD ⃗⃗⃗⃗⃗⃗ ⋅A 1P ⃗⃗⃗⃗⃗⃗⃗ 的取值范围是(0,4)，故B 正确；对C ：由于CC 1⊥面ABCD ，所以C 1Q 与面ABCD 所成的角为∠C 1QC ， 所以tanθ=C 1C CQ=1CQ ，因为CQ ∈(0,2)，所以tanθ>12，故C 正确；对D ：以D 为坐标原点，DB 、DC 、DD 1所在直线分别为x ，y ，z 轴建立如图所示坐标系， 则B(√3,0，0)，C(0,1，0)，A 1(√3,−1,1)，D 1(0,0，1)， 线段BC 的中点M(√32,12,0)，线段A 1D 1的中点N(√32,−12,1)，设球心O(√32,12,t)，点P(x,y ，1)，则(x −√32)²+(y +12)²=1，由|OP ⃗⃗⃗⃗⃗ |=|OB⃗⃗⃗⃗⃗⃗ |，可得(x −√32)²+(y +12)²+(1−t)²=1+t²， 整理可得2t =(x −√32)²+(y −12)²=1−(y +12)²+(y −12)²=1−2y ，则t =12−y ，因为−1<y ≤12，则t =12−y ∈[0,32)，|OB ⃗⃗⃗⃗⃗⃗ |=√1+t 2∈[1,√132)， 所以S =4π|OB⃗⃗⃗⃗⃗⃗ |²∈[4π,13π)，故D 正确；利用椎体的体积公式可判断A；利用空间向量数量积的定义可判断B；利用线面角的定义可判断C；利用建系的方法计算出三棱锥P−BCQ的外接球半径的取值范围，结合球体的表面积公式可判断D．本题考查了命题真假判断，涉及空间位置关系及其判断、简易逻辑的判定方法，考查了了推理能力与计算能力，属于中档题．13.【答案】84【解析】解：∵2n=128，∴n=7，∴(x−2x )7的展开式中的通项T r+1=C7r⋅(−2x)r⋅x7−r=(−2)r⋅C7r⋅x7−2r，令7−2r=3，得r=2，∴(x−2x)7的展开式中x3项的系数为：4C72=84，故答案为：84．利用二项式系数的性质可求得n=7，再利用(x−2x)7的展开式中的通项公式可求得答案．本题考查二项式定理及其通项公式的应用，考查运算求解能力，属于中档题．14.【答案】45【解析】解：因为tan(π4−α)=1−tanα1+tanα=12，则tanα=13，cos2α=cos2α−sin2αcos2α+sin2α=1−tan2α1+tan2α=45．故答案为：45．由已知结合两角差的正切公式可求tanα，然后结合同角基本关系即可求解．本题主要考查了两角差的正切公式及同角基本关系，属于基础题．15.【答案】√3【解析】解：由MN为直径的圆经过点F2则可得：MF2⊥NF2，且|MF2|=|NF2|，所以△MNF2为等腰直角三角形，所以∠F1NF2=45°如图所示；设|NF2|=t，则|MF2|=t，由双曲线的定义可得：|MF1|=t−2a，|NF1|=t+2a所以|MN|=|NF1|−|MF1|=4a=√2t，解得t=2√2a，所以|NF1|=t+2a=(2√2+2)a，在△F1NF2，由余弦定理可得：|F2F2|2=|NF1|2+|NF2|2−2|NF1||NF2|cos45°，即4c2=(2√2+2)2a2+ 8a2−8(1+√2)a2，可得e2=3，所以离心率为√3；故答案为：√3．由MN为直径的圆经过点F2则可得：MF2⊥NF2，且|MF2|=|NF2|，所以△MNF2为等腰直角三角形，设一个焦半径，可以求出其他线段的长度，在三角形中由余弦定理求出a，c的关系，进而求出双曲线的离心率．考查双曲线的性质，属于中档题．16.【答案】−12【解析】解：令F(x)=f(x)−g(x)=e x−cosx−x−2a，由f(x1)=g(x2)得x2=e x1−cosx1−2a，则x2−x1=e x1−cosx1−x1−2a，则x2−x1的最小值即求F(x)在[0,π]上的最小值，F′(x)=e x+sinx−1≥0恒成立，x∈[0,π]，∴F(x)在[0,π]上单调递增，∴F(x)min=F(0)=−2a=(x2−x1)min=1，∴a=−1，2故答案为：−1．2令F(x)=f(x)−g(x)，x2−x1的最小值即求F(x)在[0,π]上的最小值，求出函数的导数，根据函数的单调性求出F(x)的最小值，得到关于a的方程，解出即可．本题考查了函数的单调性，最值问题，考查导数的应用以及转化思想，是中档题．17.【答案】解：(1)若选①：∵(sinB−sinC)2=sin2A−sinBsinC，∴由正弦定理得(b−c)2=a2−bc，整理得b2+c2−a2=bc，∴cosA=b2+c2−a22bc =12，且0<A<π，∴A=π3；若选②：∵2asinC=ctanA，∴根据正弦定理得2sinAsinC=sinC⋅sinAcosA，且sinA>0，sinC>0，∴cosA=12，且0<A<π，∴A=π3；若选③：∵2cos2B+C2=cos2A+1，∴cos(B+C)+1=2cos2A−1+1，∴2cos2A+cosA−1=0，解得cosA=12或cosA=−1，且0<A<π，∴A=π3；(2)∵sinB=√2sinC，∴由正弦定理得b=√2c，且b=√2，∴c=1，∴S△ABC=12bcsinA=12×√2×1×√32=√64．【解析】(1)若选择条件①：根据正弦定理可得出b2+c2−a2=bc，然后根据余弦定理即可求出cosA=12，从而求出A=π3；若选择条件②：根据正弦定理即可求出cosA=12，从而求出A=π3；若选择条件③：根据二倍角的余弦公式即可得出2cos2A+cosA−1=0，然后可求出cosA=12，进而解出A=π3；(2)根据正弦定理可得出b=√2c，从而求出c=1，然后根据三角形的面积公式即可求出△ABC的面积．本题考查了正余弦定理，二倍角的余弦公式，弦化切公式，三角形的面积公式，考查了计算能力，属于中档题．18.【答案】解：(1)数列{a n}是正项等比数列，满足a3是2a1，3a2的等差中项，a4=16，设数列的公比为q，则2a1q2=2a1⋅3a1q，由于a 1≠0，故2q 2−3q −2=0，解得q =2或−12． 由于数列为正项数列， 所以q =2． 则a n =2n ．(2)由(1)知：a 2n+1=22n+1，所以b n =(−1)n log 2a 2n+1=(−1)n ⋅(2n +1)，当n 为偶数时，则T n =(−3+5)+(−7+9)+...+[−(2n −1)+(2n +1)]=2×n2=n ， 当n 为奇数时，则T n =(−3+5)+(−7+9)+...+[−(2n −1)+(2n +1)]=2×n−12−(2n +1)=−n −2．故T n ={n (n 为偶数)−n −2(n 为奇数)．【解析】(1)直接利用已知条件求出数列的通项公式； (2)利用分组法的应用求出数列的和．本题考查的知识要点：数列的通项公式的求法和应用，分组法在求和中的应用，主要考查学生的运算能力和数学思维能力，属于基础题．19.【答案】解：(1)由已知可得，比赛三局且甲获胜的概率为P 1=(23)3=827，比赛四局且甲获胜的概率为P 2=C 32(23)2×(1−23)×23=827， 比赛五局且甲获胜的概率为P 3=C 42(23)2×(1−23)2×23=1681， 所以甲获胜的概率为P =P 1+P 2+P 3=827+827+1681=6481； (2)随机变量X 的取值为3，4，5， 则P(X =3)=(23)3+(13)3=13，P(X =4)=C 32(23)2×13×23+C 32(13)2×23×13=827+227=1027，P(X =5)=C 42(23)2×(13)2×23+C 42×(13)2×(23)2×13=827，所以随机变量X 的分布列为：X 3 4 5 P131027827则随机变量X 的数学期望为E(X)=3×13+4×1027+5×827=10727．【解析】(1)甲获胜分为三种情况：比赛三局且甲获胜，比赛四局且甲获胜，比赛五局且甲获胜，分别求解概率，然后由分类计数原理求解即可．(2)先求出随机变量X 的可能取值，然后求出其对应的概率，列出分布列，由数学期望的计算公式求解即可．本题考查了概率问题的求解，离散型随机变量及其分布列和离散型随机变量期望的求解与应用，考查了逻辑推理能力与化简运算能力，属于中档题．20.【答案】解：(1)证明：∵AB =AC ，D 为BC 中点，∴AD ⊥BC ，∵ABEF 是矩形，∴FA ⊥AB ，∵平面ABC ⊥平面ABEF ，平面ABC ∩平面ABEF =AB ， AF ⊂平面ABEF ，∴AF ⊥平面ABC ， ∵BC ⊂平面ABC ，∴AF ⊥BC ，∵BC ⊥AF ，AD ⊂平面ADF ，AF ∩AD =A ，∴BC ⊥平面ADF ， 又BC ⊂平面BCF ，∴平面ADF ⊥平面BCF ． (2)由(1)知AF ⊥平面ABC ，∴以A 为原点，在平面ABC 中过A 作AB 的垂线为x 轴，AB 为y 轴，AF 为z 轴，建立空间直角坐标系， 则A(0,0，0)，F(0,0，√6)，B(0,4，0)，C(2√3,−2,0)，E(0,4，√6)， ∴D(√3,1，0)，AD ⃗⃗⃗⃗⃗⃗ =(√3,1，0)，AF ⃗⃗⃗⃗⃗ =(0,0，√6)，BC ⃗⃗⃗⃗⃗ =(2√3,−6,0)， 由(1)知BC ⃗⃗⃗⃗⃗ =(2√3,−6,0)是平面ADF 的一个法向量， 设平面ADE 的一个法向量n⃗ =(x,y ，z)， 则{n ⃗ ⋅AD⃗⃗⃗⃗⃗⃗ =√3x +y =0n ⃗ ⋅AE ⃗⃗⃗⃗⃗ =4y +√6x =0，取x =1，得n ⃗ =(1,−√3,2√2)， ∴cos <n ⃗ ,BC ⃗⃗⃗⃗⃗ >=n⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ |n ⃗⃗ |⋅|BC⃗⃗⃗⃗⃗ |=8√32√3⋅4√3=√33， ∵二面角F −AD −E 是平面角是锐角， ∴二面角F −AD −E 的余弦值为√33．【解析】(1)推导出AD ⊥BC ，FA ⊥AB ，从而AF ⊥平面ABC ，进而AF ⊥BC ，BC ⊥平面ADF ，由此能证明平面ADF ⊥平面BCF ．(2)由AF ⊥平面ABC ，以A 为原点，在平面ABC 中过A 作AB 的垂线为x 轴，AB 为y 轴，AF 为z 轴，建立空间直角坐标系，利用向量法能求出二面角F −AD −E 的余弦值．本题考查面面垂直的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力、推理论证能力等数学核心素养，是中档题．21.【答案】解：(1)因为x 2=2py(p >0)可化为y =x 22p ，所以y′=xp ，因为当A 点的横坐标为1时，抛物线C 在点A 处的切线斜率为12，所以1p =12， 所以p =2，所以抛物线C 的标准方程为x 2=4y ． (2)由(1)知点T 的坐标为(0,2)，由题意可知，直线l 1和l 2斜率都存在且均不为0， 设直线l 1的方程为y =kx +2，由{y =kx +2x 2=4y ，联立消去y 并整理可得x 2−4kx −8=0， 所以△=(−4k)2+32=16k 2=32>0，设A(x 1,y 1)，B(x 2,y 2)，则x 1+x 2=4k ，x 1x 2=−8， 所以y 1+y 2=k(x 1+x 2)+4=4k 2+4， 因为M 为AB 的中点，所以M(2k,2k 2+2)， 因为l 1⊥l 2，N 为EF 中点，所以N(−2k ,2k 2+2)， 所以直线MN 的方程为y −(2k 2+2)=2k 2+2−(2k 2+2)2k+2k⋅(x −2k)=(k −1k)⋅(x −2k)，整理可得y =(k −1k )x +4， 所以直线MN 恒过定点(0,4)，所以△OMN 的面积S =12×4×|2k −(−2k )|=4|k +1k |≥8， 当且仅当k =1k ，即k =±1时，△OMN 面积取得最小值为8．【解析】(1)将抛物线方程化为y =x22p ，求导得y′=x p ，由导数的几何意义可得1p =12，解得p ，进而可得抛物线C 的标准方程．(2)由(1)知点T 的坐标为(0,2)，设A(x 1,y 1)，B(x 2,y 2)，直线l 1的方程为y =kx +2，联立抛物线的方程，结合韦达定理可得x 1+x 2，x 1x 2，进而可得y 1+y 2，由中点坐标公式可得M(2k,2k 2+2)，N(−2k ,2k 2+2)，写出直线MN 的方程，得y =(k −1k )x +4，即可得出直线MN 恒过定点(0,4)，再计算△OMN 的面积S =4|k +1k|，由基本不等式，即可得出答案．本题考查直线与抛物线相交问题，解题中需要一定的计算能力，属于中档题．22.【答案】解：(1)当a =e 2时，f(x)=xlnx −e2x 2+x ，所以f′(x)=lnx −ex +2，令p(x)=lnx −ex +2，则p′(x)=1x −e =1−ex x，若p′(x)>0，则0<x <1e ，若p′(x)<0，则x >1e ， 所以p(x)在(0,1e )上为增函数，在(1e ,+∞)上为减函数， 则p(x)≤p(1e )=0，即f′(x)≤0，仅在x =1e 时，f′(x)=0， 所以函数f(x)在(0,+∞)内单调递减．(2)因为f(x)=xlnx −ax 2+x ，g(x)=(1−a)xlnx −e x−1，a >0， 若f(x)≥g(x)+x 恒成立，即对任意x >0，e x−1−ax(x −lnx)≥0恒成立， 即对任意的x >0，e x−1x−a(x −lnx)≥0恒成立，即e x−lnx−1≥a(x −lnx)，令t =t(x)=x −lnx ，则t(x)′=1−1x =x−1x，所以当x ∈(0,1)时，t′(x)<0，t(x)单调递减， 当x ∈(1,+∞)时，t′(x)>0，t(x)单调递增， 所以t =t(x)≥t(1)=1，若e x−lnx−1≥a(x −lnx)对任意x >0恒成立， 则a ≤e x−lnx−1x−lnx =e t−1t恒成立，设g(t)=e t−1t，t ≥1，则g′(t)=e t−1(t−1)t 2≥0，所以当t ∈[1,+∞)时，g(t)单调递增，所以g(t)≥g(1)=1，所以a≤1，所以若f(x)≥g(x)+x恒成立，则实数a的取值范围是(−∞,1]．【解析】(1)对f(x)求导，利用导数即可判断函数的单调性；(2)不等式恒成立转化为e x−lnx−1≥a(x−lnx)，令t=x−lnx，利用导数可求得t≥1，则不等式进一步转化为a≤e t−1t 恒成立，令g(t)=e t−1t，利用导数求出g(t)的最小值，从而可求得a的取值范围．本题主要考查利用导数研究函数的单调性与最值，考查转化思想与运算求解能力，属于难题．。

山东省济南市2021届新高考数学二月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知复数168i z =-，2i z =-，则12z z =（ ） A ．86i -B ．86i +C ．86i -+D ．86i --【答案】B【解析】 分析：利用21i =-的恒等式，将分子、分母同时乘以i ，化简整理得1286z i z =+ 详解：2122686886z i i i i z i i --===+-- ，故选B 点睛：复数问题是高考数学中的常考问题，属于得分题，主要考查的方面有：复数的分类、复数的几何意义、复数的模、共轭复数以及复数的乘除运算，在运算时注意21i =-符号的正、负问题.2．已知集合{2,0,1,3}A =-，{B x x =<<，则集合A B 子集的个数为（ ） A ．4B ．8C ．16D ．32 【答案】B【解析】【分析】首先求出A B ，再根据含有n 个元素的集合有2n 个子集，计算可得. 【详解】解：{2,0,1,3}A =-，{B x x =<<，{2,0,1}A B ∴=-，A B ∴子集的个数为328=.故选：B .【点睛】考查列举法、描述法的定义，以及交集的运算，集合子集个数的计算公式，属于基础题．3．已知甲盒子中有m 个红球，n 个蓝球，乙盒子中有1m -个红球，+1n 个蓝球(3,3)m n ≥≥，同时从甲乙两个盒子中取出(1,2)i i =个球进行交换，（a ）交换后，从甲盒子中取1个球是红球的概率记为(1,2)i p i =.（b ）交换后，乙盒子中含有红球的个数记为(1,2)i i ξ=.则（ ）A ．1212,()()p p E E ξξ><B ．1212,()()p p E E ξξC ．1212,()()p p E E ξξ>>D ．1212,()()p pE E ξξ<<【答案】A【解析】 分析：首先需要去分析交换后甲盒中的红球的个数，对应的事件有哪些结果，从而得到对应的概率的大小，再者就是对随机变量的值要分清，对应的概率要算对，利用公式求得其期望.详解：根据题意有，如果交换一个球，有交换的都是红球、交换的都是蓝球、甲盒的红球换的乙盒的蓝球、甲盒的蓝球交换的乙盒的红球， 红球的个数就会出现,1,1m m m -+三种情况；如果交换的是两个球，有红球换红球、蓝球换蓝球、一蓝一红换一蓝一红、红换蓝、蓝换红、一蓝一红换两红、一蓝一红换亮蓝，对应的红球的个数就是2,1,,1,2m m m m m --++五种情况，所以分析可以求得1212,()()p p E E ξξ><，故选A.点睛：该题考查的是有关随机事件的概率以及对应的期望的问题，在解题的过程中，需要对其对应的事件弄明白，对应的概率会算，以及变量的可取值会分析是多少，利用期望公式求得结果.4．设双曲线221x y a b+=的一条渐近线为2y x =-，且一个焦点与抛物线24x y =的焦点相同，则此双曲线的方程为（ ）A ．225514x y -=B ．225514y x -=C ．225514y x -=D ．225514x y -= 【答案】C【解析】【分析】求得抛物线的焦点坐标，可得双曲线方程221y x b a-=-的渐近线方程为y =，由题意可得4b a =-，又21c =，即1b a -=，解得a ，b ，即可得到所求双曲线的方程.【详解】解：抛物线24x y =的焦点为0,1 可得双曲线()2210,0x y b a a b+=><即为221y x b a-=-的渐近线方程为y =由题意可得2b a =-，即4b a =- 又21c =，即1b a -=解得15a =-，45b =. 即双曲线的方程为225514y x -=. 故选：C【点睛】本题主要考查了求双曲线的方程，属于中档题.5．执行如下的程序框图，则输出的S 是（ ）A ．36B ．45C ．36-D ．45-【答案】A【解析】【分析】 列出每一步算法循环，可得出输出结果S 的值.【详解】18i =≤满足，执行第一次循环，()120111S =+-⨯=-，112i =+=；28i =≤成立，执行第二次循环，()221123S =-+-⨯=，213i =+=；38i =≤成立，执行第三次循环，()323136S =+-⨯=-，314i =+=；48i =≤成立，执行第四次循环，()4261410S =-+-⨯=，415i =+=；58i =≤成立，执行第五次循环，()52101515S =+-⨯=-，516i =+=；68i =≤成立，执行第六次循环，()62151621S =-+-⨯=，617i =+=；78i =≤成立，执行第七次循环，()72211728S =+-⨯=-，718i =+=；88i =≤成立，执行第八次循环，()82281836S =-+-⨯=，819i =+=；98i =≤不成立，跳出循环体，输出S 的值为36，故选：A.【点睛】本题考查算法与程序框图的计算，解题时要根据算法框图计算出算法的每一步，考查分析问题和计算能力，属于中等题.6．△ABC 的内角A ，B ，C 的对边分别为,,a b c ，已知1,30a b B ===，则A 为( ) A ．60B ．120C ．60或150D ．60或120【答案】D【解析】【分析】由正弦定理可求得sin 2A =，再由角A 的范围可求得角A. 【详解】由正弦定理可知sin sin a b A B =1sin 30=，解得sin A =，又0180A <<，且>a b ，所以60A ︒=或120︒。

山东省聊城市2021届新高考数学第二次调研试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知定义在[)1,+∞上的函数()f x 满足()()33f x f x =，且当13x ≤≤时，()12f x x =--，则方程()()2019f x f =的最小实根的值为（ ） A ．168 B ．249C ．411D ．561【答案】C 【解析】 【分析】先确定解析式求出(2019)f 的函数值，然后判断出方程()()2019f x f =的最小实根的范围结合此时的5()3f x x =-，通过计算即可得到答案.【详解】当1x ≥时，()()33f x f x =，所以22()3()3()33x x f x f f ===L 3()3n n x f =，故当 +133n n x ≤≤时，[1,3]3n x ∈，所以()13,233(12)33,23n n nn n nx x x f x x x +⎧-≥⋅=--=⎨-<⋅⎩，而 672019[3,3]∈，所以662019(2019)3(12)3f =--=732109168-=，又当13x ≤≤时， ()f x 的极大值为1，所以当+133n n x ≤≤时，()f x 的极大值为3n ，设方程()168f x =的最小实根为t ，45168[3,3]∈，则56533(3,)2t +∈，即(243,468)t ∈，此时5()3f x x =-令5()3168f x x =-=，得243168411t =+=，所以最小实根为411. 故选：C. 【点睛】本题考查函数与方程的根的最小值问题，涉及函数极大值、函数解析式的求法等知识，本题有一定的难度及高度，是一道有较好区分度的压轴选这题.2．如图所示，网格纸上小正方形的边长为1，粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为A ．72B ．64C ．48D ．32【答案】B 【解析】 【分析】由三视图可知该几何体是一个底面边长为4的正方形，高为5的正四棱柱，挖去一个底面边长为4，高为3的正四棱锥，利用体积公式，即可求解。

山东省济南市2021届新高考数学二模试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

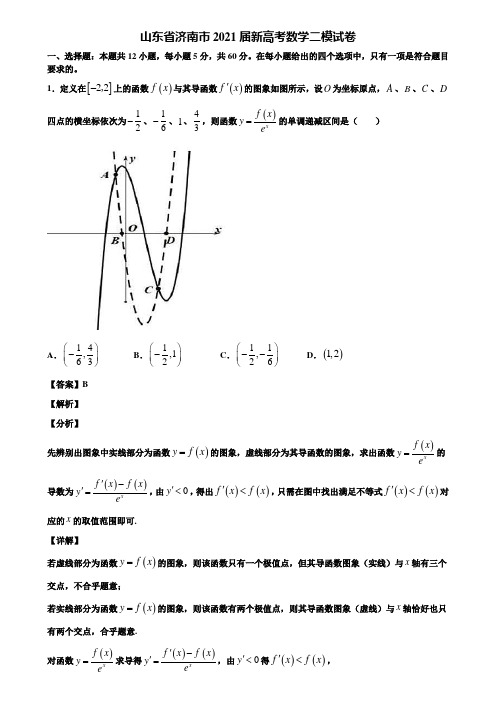
1．定义在[]22-,上的函数()f x 与其导函数()f x '的图象如图所示，设O 为坐标原点，A 、B 、C 、D 四点的横坐标依次为12-、16-、1、43，则函数()xf x y e=的单调递减区间是（ ）A ．14,63⎛⎫-⎪⎝⎭B ．1,12⎛⎫-⎪⎝⎭C ．11,26--⎛⎫⎪⎝⎭D ．()1,2【答案】B 【解析】 【分析】先辨别出图象中实线部分为函数()y f x =的图象，虚线部分为其导函数的图象，求出函数()xf x y e =的导数为()()xf x f x y e'='-，由0y '<，得出()()f x f x '<，只需在图中找出满足不等式()()f x f x '<对应的x 的取值范围即可. 【详解】若虚线部分为函数()y f x =的图象，则该函数只有一个极值点，但其导函数图象（实线）与x 轴有三个交点，不合乎题意；若实线部分为函数()y f x =的图象，则该函数有两个极值点，则其导函数图象（虚线）与x 轴恰好也只有两个交点，合乎题意. 对函数()xf x y e=求导得()()xf x f x y e'='-，由0y '<得()()f x f x '<，由图象可知，满足不等式()()f x f x '<的x 的取值范围是1,12⎛⎫-⎪⎝⎭， 因此，函数()xf x y e =的单调递减区间为1,12⎛⎫-⎪⎝⎭. 故选：B. 【点睛】本题考查利用图象求函数的单调区间，同时也考查了利用图象辨别函数与其导函数的图象，考查推理能力，属于中等题.2．已知复数z 满足1z =，则2z i +-的最大值为（ ）A ．23+B ．1+C ．2+D ．6【答案】B 【解析】 【分析】设i,,z a b a b R =+∈，2z i +-=，利用复数几何意义计算. 【详解】设i,,z a b a b R =+∈，由已知，221a b +=，所以点(,)a b 在单位圆上，而2i |(2)(1)i |=z a b +-=++-(,)a b到(2,1)-的距离，故21z i +-≤+=1. 故选：B. 【点睛】本题考查求复数模的最大值，其实本题可以利用不等式|2||||2|z i z i +-≤+-来解决.3．20世纪产生了著名的“31x +”猜想：任给一个正整数x ，如果x 是偶数，就将它减半；如果x 是奇数，则将它乘3加1，不断重复这样的运算，经过有限步后，一定可以得到1.如图是验证“31x +”猜想的一个程序框图，若输入正整数m 的值为40，则输出的n 的值是（ ）A ．8B ．9C ．10D ．11【答案】C 【解析】 【分析】列出循环的每一步，可得出输出的n 的值. 【详解】1n =，输入40m =，112n =+=，1m =不成立，m 是偶数成立，则40202m ==； 213n =+=，1m =不成立，m 是偶数成立，则20102m ==； 314n =+=，1m =不成立，m 是偶数成立，则1052m ==；415n =+=，1m =不成立，m 是偶数不成立，则35116m =⨯+=；516n =+=，1m =不成立，m 是偶数成立，则1682m ==； 617n =+=，1m =不成立，m 是偶数成立，则842m ==；718=+=n ，1m =不成立，m 是偶数成立，则224m ==；819n =+=，1m =不成立，m 是偶数成立，则212m ==；9110n =+=，1m =成立，跳出循环，输出n 的值为10.故选：C. 【点睛】本题考查利用程序框图计算输出结果，考查计算能力，属于基础题. 4．已知复数为纯虚数(为虚数单位)，则实数（ ） A ．-1 B ．1C ．0D ．2【答案】B 【解析】 【分析】 化简得到，根据纯虚数概念计算得到答案.【详解】为纯虚数，故且，即.故选：. 【点睛】本题考查了根据复数类型求参数，意在考查学生的计算能力. 5．复数2iz i=-（i 是虚数单位）在复平面内对应的点在（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】B 【解析】 【分析】利用复数的四则运算以及几何意义即可求解. 【详解】 解：()()()21212222555i i i i z i i i i +-+====-+--+， 则复数2i z i =-（i 是虚数单位）在复平面内对应的点的坐标为：12,55⎛⎫- ⎪⎝⎭， 位于第二象限. 故选：B. 【点睛】本题考查了复数的四则运算以及复数的几何意义，属于基础题.6．已知ABC ∆的内角,,A B C 的对边分别是,,,a b c 且444222222a b c a b ca b +++=+，若c 为最大边，则a b c +的取值范围是（ ）A ．231⎛ ⎝⎭,B ．(3C ．231⎛ ⎝⎦,D ．3]【答案】C 【解析】 【分析】由444222222a b c a b c a b+++=+，化简得到cos C 的值，根据余弦定理和基本不等式，即可求解. 【详解】由444222222a b c a b c a b +++=+，可得222422222(2)a b c a b c a b ++-=+， 可得22222222222()c a b c a b a b c a b+-++-=+， 通分得2222222222()()0a b c c a b a b a b+---+=+， 整理得222222()a b c a b +-=，所以22221()24a b c ab +-=，因为C 为三角形的最大角，所以1cos 2C =-， 又由余弦定理2222222cos ()c a b ab C a b ab a b ab =+-=++=+-2223()()()24a b a b a b +≥+-=+，当且仅当a b =时，等号成立，所以)2c a b >+，即3a b c +≤， 又由a b c +>，所以a b c +的取值范围是(1,]3. 故选：C. 【点睛】本题主要考查了代数式的化简，余弦定理，以及基本不等式的综合应用，试题难度较大，属于中档试题，着重考查了推理与运算能力.7．已知集合{lgsin A x y x ==，则()cos22sin f x x x x A =+∈，的值域为（ ）A ．31,2⎡⎤⎢⎥⎣⎦B ．31,2⎛⎤ ⎥⎝⎦C ．11,2⎛⎤- ⎥⎝⎦D ．2⎫⎪⎪⎝⎭【答案】A 【解析】 【分析】先求出集合(]0,3A =，化简()f x =22sin 2sin 1x x -++，令sin x t =(]0,1∈，得()2221g t t t =-++由二次函数的性质即可得值域. 【详解】由2sin 00390x x x >⎧⇒<≤⎨-≥⎩，得(]0,3A = ，()cos22sin f x x x =+=-22sin 2sin 1x x ++，令sin x t =， (]0,3x ∈，(]0,1t ∴∈，所以得()2221g t t t =-++ ，()g t 在10,2⎛⎫ ⎪⎝⎭ 上递增，在1,12⎛⎫⎪⎝⎭上递减，()1311,22g g ⎛⎫== ⎪⎝⎭ ，所以()31,2g t ⎡⎤∈⎢⎥⎣⎦，即 ()f x 的值域为31,2⎡⎤⎢⎥⎣⎦故选A 【点睛】本题考查了二次不等式的解法、二次函数最值的求法，换元法要注意新变量的范围，属于中档题 8．如图是来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC 的斜边BC ，直角边,AB AC .已知以直角边,AC AB 为直径的半圆的面积之比为14，记ABC α∠=，则sin 2α=（ ）A ．925B ．1225C ．35D ．45【答案】D 【解析】 【分析】由半圆面积之比，可求出两个直角边,AB AC 的长度之比，从而可知1tan 2AC AB α==，结合同角三角函数的基本关系，即可求出sin ,cos αα，由二倍角公式即可求出sin 2α. 【详解】解：由题意知0,2πα⎛⎫∈ ⎪⎝⎭ ，以AB 为直径的半圆面积21122AB S π⎛⎫= ⎪⎝⎭， 以AC 为直径的半圆面积22122AC S π⎛⎫= ⎪⎝⎭，则222114S AC S AB ==，即1tan 2AC AB α==.由22sin cos 1sin 1tan cos 2ααααα⎧+=⎪⎨==⎪⎩，得sin cos αα⎧=⎪⎪⎨⎪=⎪⎩，所以4sin 22sin cos 25ααα===. 故选:D. 【点睛】本题考查了同角三角函数的基本关系，考查了二倍角公式.本题的关键是由面积比求出角的正切值. 9．将函数()cos f x x =的图象先向右平移56π个单位长度，在把所得函数图象的横坐标变为原来的1ω(0)>ω倍，纵坐标不变，得到函数()g x 的图象，若函数()g x 在3(,)22ππ上没有零点，则ω的取值范围是（ ）A ．228(0,][,]939B ．2(0,]9C ．28(0,][,1]99D ．(0,1]【答案】A 【解析】 【分析】根据y=Acos （ωx+φ）的图象变换规律，求得g （x ）的解析式，根据定义域求出56x πω-的范围，再利用余弦函数的图象和性质，求得ω的取值范围． 【详解】函数()cos f x x =的图象先向右平移56π个单位长度， 可得5cos 6y x π⎛⎫=-⎪⎝⎭的图象， 再将图象上每个点的横坐标变为原来的1ω(0)>ω倍(纵坐标不变)，得到函数5()cos 6g x x πω⎛⎫=- ⎪⎝⎭的图象， ∴周期2T πω=，若函数()g x 在3(,)22ππ上没有零点，∴ 553526626x ωπππωππω-<-<-， ∴ 35526262T ωππωπππω⎛⎫⎛⎫---≤=⎪⎪⎝⎭⎝⎭， 21ω∴≤，解得01ω<≤，又522635226k k πωππππωπππ⎧-+≤-⎪⎪⎨⎪+≥-⎪⎩，解得3412323k ωω-≤≤-， 当k=0时，解2839ω≤≤， 当k=-1时，01ω<≤，可得209ω<≤， ω∴∈228(0,][,]939.故答案为：A. 【点睛】本题考查函数y=Acos （ωx+φ）的图象变换及零点问题，此类问题通常采用数形结合思想，构建不等关系式，求解可得，属于较难题. 10．已知1sin 243απ⎛⎫+= ⎪⎝⎭，则sin α的值等于（ ） A ．79-B ．29-C ．29D ．79【答案】A 【解析】 【分析】由余弦公式的二倍角可得，27cos()12sin 2249παπα⎛⎫+=-+= ⎪⎝⎭，再由诱导公式有 cos()sin 2παα+=-，所以7sin 9α=-【详解】 ∵1sin 243απ⎛⎫+=⎪⎝⎭ ∴由余弦公式的二倍角展开式有27cos()12sin 2249παπα⎛⎫+=-+= ⎪⎝⎭又∵cos()sin 2παα+=-∴7sin 9α=- 故选：A 【点睛】本题考查了学生对二倍角公式的应用，要求学生熟练掌握三角函数中的诱导公式，属于简单题11．已知集合{}21|A x log x =<，集合{}|2B y y x ==-，则A B =（ ）A ．(),2-∞B ．(],2-∞C ．()0,2D ．[)0,+∞【答案】D 【解析】 【分析】可求出集合A ，B ，然后进行并集的运算即可． 【详解】解：{}|02A x x =<<，{}|0B y y =≥；∴[)0,A B =+∞．故选D ． 【点睛】考查描述法、区间的定义，对数函数的单调性，以及并集的运算．12．如图，正方体的底面与正四面体的底面在同一平面α上，且//AB CD ，若正方体的六个面所在的平面与直线CE EF ，相交的平面个数分别记为m n ，，则下列结论正确的是（ ）A ．m n =B ．2m n =+C ．m n <D ．8m n +<【答案】A 【解析】 【分析】根据题意，画出几何位置图形，由图形的位置关系分别求得,m n 的值，即可比较各选项. 【详解】如下图所示，CE ⊂平面ABPQ ，从而//CE 平面1111A B PQ ，易知CE 与正方体的其余四个面所在平面均相交， ∴4m =，∵//EF 平面11BPPB ，//EF 平面11AQQ A ，且EF 与正方体的其余四个面所在平面均相交， ∴4n =，∴结合四个选项可知，只有m n =正确. 故选：A. 【点睛】本题考查了空间几何体中直线与平面位置关系的判断与综合应用，对空间想象能力要求较高，属于中档题. 二、填空题：本题共4小题，每小题5分，共20分。

山东省济南市2021届新高考二诊数学试题一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知l，m是两条不同的直线，m⊥平面α，则“//lα”是“l⊥m”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】【分析】根据充分条件和必要条件的定义，结合线面垂直的性质进行判断即可.【详解】当m⊥平面α时，若l∥α”则“l⊥m”成立，即充分性成立，若l⊥m，则l∥α或l⊂α，即必要性不成立，则“l∥α”是“l⊥m”充分不必要条件，故选：A.【点睛】本题主要考查充分条件和必要条件的判断，结合线面垂直的性质和定义是解决本题的关键.难度不大，属于基础题2．“纹样”是中国艺术宝库的瑰宝，“火纹”是常见的一种传统纹样.为了测算某火纹纹样（如图阴影部分所示）的面积，作一个边长为3的正方形将其包含在内，并向该正方形内随机投掷200个点，己知恰有80个点落在阴影部分据此可估计阴影部分的面积是（）A．165B．325C．10 D．185【答案】D【解析】【分析】直接根据几何概型公式计算得到答案. 【详解】根据几何概型：809200Sp==，故185S=.本题考查了根据几何概型求面积，意在考查学生的计算能力和应用能力.3．2-31ii =+（ ） A ．15-22i B ．15--22iC ．15+22i D ．15-+22i 【答案】B 【解析】 【分析】利用复数代数形式的乘除运算化简得答案． 【详解】()()()()231231515111222i i i i z i i i i -----====--++-． 故选B ． 【点睛】本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．4．在直角ABC ∆中，2C π∠=，4AB =，2AC =，若32AD AB =，则CD CB ⋅=u u u r u u u r （ ）A ．18-B ．63-C ．18D ．63【答案】C 【解析】 【分析】在直角三角形ABC 中，求得12AC cos CAB AB ∠== ，再由向量的加减运算，运用平面向量基本定理，结合向量数量积的定义和性质：向量的平方即为模的平方，化简计算即可得到所求值． 【详解】在直角ABC ∆中，2C π∠=，4AB =，2AC =，，12AC cos CAB AB ∠==， 若32AD AB =u u u v u u u v ，则2CD CB AD AC AB AC AD AB AD AC AC AB AC ⋅=-⋅-=⋅-⋅-⋅+u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v （）（）223322AB AB AC AC AB AC =-⋅-⋅+u u u v u u u v u u u v u u u v u u u v u u u v 3511642418222=⨯-⨯⨯⨯+=．本题考查向量的加减运算和数量积的定义和性质，主要是向量的平方即为模的平方，考查运算能力，属于中档题．5．已知复数为纯虚数(为虚数单位)，则实数（）A．-1 B．1 C．0 D．2【答案】B【解析】【分析】化简得到，根据纯虚数概念计算得到答案.【详解】为纯虚数，故且，即.故选：.【点睛】本题考查了根据复数类型求参数，意在考查学生的计算能力.6．执行如图所示的程序框图，则输出的n的值为（）A．1B．2C．3D．4【答案】B【解析】【分析】列出循环的每一步，进而可求得输出的n值.根据程序框图，执行循环前：0a =，0b =，0n =，执行第一次循环时：1a =，2b =，所以：229840+≤不成立． 继续进行循环，…，当4a =，8b =时，226240+=成立，1n =， 由于5a ≥不成立，执行下一次循环，5a =，10b =，225040+≤成立，2n =，5a ≥成立，输出的n 的值为2.故选：B ． 【点睛】本题考查的知识要点：程序框图的循环结构和条件结构的应用，主要考查学生的运算能力和转换能力，属于基础题型．7．在明代程大位所著的《算法统宗》中有这样一首歌谣，“放牧人粗心大意，三畜偷偷吃苗青，苗主扣住牛马羊，要求赔偿五斗粮，三畜户主愿赔偿，牛马羊吃得异样．马吃了牛的一半，羊吃了马的一半．”请问各畜赔多少？它的大意是放牧人放牧时粗心大意，牛、马、羊偷吃青苗，青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食（1斗=10升），三畜的主人同意赔偿，但牛、马、羊吃的青苗量各不相同．马吃的青苗是牛的一半，羊吃的青苗是马的一半．问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食？（ ） A ．2550100,,777B ．252550,,1477C ．100200400,,777 D ．50100200,,777【答案】D 【解析】 【分析】设羊户赔粮1a 升,马户赔粮2a 升,牛户赔粮3a 升,易知123,,a a a 成等比数列,1232,50q a a a =++=,结合等比数列的性质可求出答案. 【详解】设羊户赔粮1a 升,马户赔粮2a 升,牛户赔粮3a 升,则123,,a a a 成等比数列,且公比1232,50q a a a =++=,则1(1a q +)250q +=,故1250501227a ==++,2110027a a ==,23120027a a ==. 故选:D. 【点睛】本题考查数列与数学文化,考查了等比数列的性质,考查了学生的运算求解能力,属于基础题. 8．正项等比数列{}n a 中的1a 、4039a 是函数()3214633f x x x x =-+-的极值点，则2020a =（ ）A ．1-B ．1C ．2D ．2【答案】B 【解析】 【分析】根据可导函数在极值点处的导数值为0，得出140396a a =，再由等比数列的性质可得. 【详解】解：依题意1a 、4039a 是函数()3214633f x x x x =-+-的极值点，也就是()2860f x x x '=-+=的两个根∴140396a a =又{}n a 是正项等比数列，所以2020140396a a a =⋅= ∴202066loglog61a ==.故选：B 【点睛】本题主要考查了等比数列下标和性质以应用，属于中档题.9．函数()2xx e f x x=的图像大致为（ ）A ．B ．C ．D ．【答案】A 【解析】 【分析】根据()0f x >排除C ，D ，利用极限思想进行排除即可． 【详解】解：函数的定义域为{|0}x x ≠，()0f x >恒成立，排除C ，D ，当0x >时，2()xx x e f x xe x ==，当0x →，()0f x →，排除B ， 故选：A ．本题主要考查函数图象的识别和判断，利用函数值的符号以及极限思想是解决本题的关键，属于基础题．10．正项等差数列{}n a 的前n 和为n S ，已知2375150a a a +-+=，则9S =（ ）A ．35B ．36C ．45D ．54【答案】C 【解析】 【分析】由等差数列{}n a 通项公式得2375150a a a +-+=，求出5a ，再利用等差数列前n 项和公式能求出9S .【详解】Q 正项等差数列{}n a 的前n 项和n S ，2375150a a a +-+=，2552150a a ∴--=，解得55a =或53a =-（舍），()91959995452S a a a ∴=+==⨯=，故选C. 【点睛】本题主要考查等差数列的性质与求和公式，属于中档题. 解等差数列问题要注意应用等差数列的性质2p q m n r a a a a a +=+=（2p q m n r +=+=）与前n 项和的关系.11．在正方体1111ABCD A B C D -中，球1O 同时与以A 为公共顶点的三个面相切，球2O 同时与以1C 为公共顶点的三个面相切，且两球相切于点F .若以F 为焦点，1AB 为准线的抛物线经过12O O ，，设球12O O ，的半径分别为12r r ，，则12r r =（ ） AB．C．12-D．2【答案】D 【解析】 【分析】由题先画出立体图，再画出平面11AB C D 处的截面图，由抛物线第一定义可知，点2O 到点F 的距离即半径2r ，也即点2O 到面11CDD C 的距离，点2O 到直线1AB 的距离即点2O 到面11ABB A 的距离因此球2O 内切于正方体，设21r =，两球球心和公切点都在体对角线1AC 上，通过几何关系可转化出1r ，进而求解根据抛物线的定义，点2O 到点F 的距离与到直线1AB 的距离相等，其中点2O 到点F 的距离即半径2r ，也即点2O 到面11CDD C 的距离，点2O 到直线1AB 的距离即点2O 到面11ABB A 的距离，因此球2O 内切于正方体，不妨设21r =，两个球心12O O ，和两球的切点F 均在体对角线1AC 上，两个球在平面11AB C D 处的截面如图所示，则1222132AC O F r AO ====，，所以2231AF AO O F =-=-.又因为11113AF AO O F r r =+=+，因此()13131r +=-，得123r =-，所以1223rr =-.故选：D 【点睛】本题考查立体图与平面图的转化，抛物线几何性质的使用，内切球的性质，数形结合思想，转化思想，直观想象与数学运算的核心素养12．若集合{}10A x x =-≤≤，01xB x x ⎧⎫=<⎨⎬-⎩⎭，则A B =U （ ）A ．[)1,1-B ．(]1,1-C ．()1,1-D ．[]1,1-【答案】A 【解析】 【分析】用转化的思想求出B 中不等式的解集，再利用并集的定义求解即可． 【详解】解：由集合01x B x x ⎧⎫=<⎨⎬-⎩⎭，解得{|01}B x x =<<，则{}{}{}[)|10|01|111,1A B x x x x x x =-<<=-<=-U U 剟? 故选：A ． 【点睛】本题考查了并集及其运算，分式不等式的解法，熟练掌握并集的定义是解本题的关键．属于基础题． 二、填空题：本题共4小题，每小题5分，共20分。

山东省临沂市2021届新高考数学二模考试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知七人排成一排拍照，其中甲、乙、丙三人两两不相邻，甲、丁两人必须相邻，则满足要求的排队方法数为（ ）. A ．432 B ．576 C ．696 D ．960【答案】B 【解析】 【分析】先把没有要求的3人排好，再分如下两种情况讨论：1.甲、丁两者一起，与乙、丙都不相邻，2.甲、丁一起与乙、丙二者之一相邻. 【详解】首先将除甲、乙、丙、丁外的其余3人排好，共有33A 种不同排列方式，甲、丁排在一起共有22A 种不同方式；若甲、丁一起与乙、丙都不相邻，插入余下三人产生的空档中，共有34A 种不同方式； 若甲、丁一起与乙、丙二者之一相邻，插入余下三人产生的空档中，共有1224C A 种不同方式；根据分类加法、分步乘法原理，得满足要求的排队方法数为33A 22A 34(A +1224)576C A =种.故选：B. 【点睛】本题考查排列组合的综合应用，在分类时，要注意不重不漏的原则，本题是一道中档题. 2．复数z 满足()11i z i +=-，则z =（ ）A ．1i -B ．1i +C ．22- D ．22+ 【答案】C 【解析】 【分析】利用复数模与除法运算即可得到结果. 【详解】解: )()())1111112ii i z i i i ---=====++-， 故选：C 【点睛】本题考查复数除法运算，考查复数的模，考查计算能力，属于基础题.3．已知12,F F 是双曲线222:1(0)x C y a a-=>的两个焦点，过点1F 且垂直于x 轴的直线与C 相交于,A B 两点，若2AB =，则2ABF ∆的内切圆半径为（ ）A ．23 B ．33C ．323D ．233【答案】B 【解析】 【分析】 首先由2AB =求得双曲线的方程，进而求得三角形的面积，再由三角形的面积等于周长乘以内切圆的半径即可求解. 【详解】由题意1b =将x c =-代入双曲线C 的方程,得1y a =±则22,2,3a c a===,由2121222AF AF BF BF a -=-==,得2ABF ∆的周长为2211||22||42||62AF BF AB a AF a BF AB a AB ++=++++=+=,设2ABF ∆的内切圆的半径为r ,则11362232,223r r ⨯=⨯⨯=, 故选：B【点睛】本题考查双曲线的定义、方程和性质，考查三角形的内心的概念，考查了转化的思想，属于中档题. 4．己知全集为实数集R ，集合A={x|x 2 +2x-8>0}，B={x|log 2x<1}，则()RA B ⋂等于（ ）A ．[-4,2]B ．[-4,2)C ．(-4,2)D ．(0,2)【答案】D 【解析】 【分析】求解一元二次不等式化简A ，求解对数不等式化简B ，然后利用补集与交集的运算得答案. 【详解】解：由x 2 +2x-8>0，得x ＜-4或x ＞2， ∴A={x|x 2 +2x-8>0}＝{x| x ＜-4或x ＞2}， 由log 2x<1，x ＞0，得0＜x ＜2， ∴B={x|log 2x<1}＝{ x |0＜x ＜2}， 则{}|42RA x x =-≤≤， ∴()()0,2RA B =.故选：D. 【点睛】本题考查了交、并、补集的混合运算，考查了对数不等式，二次不等式的求法，是基础题. 5．已知函数()()sin 06f x A x a a A ωπ⎛⎫=+-<< ⎪⎝⎭在区间70,3ωπ⎡⎤⎢⎥⎣⎦有三个零点1x ，2x ，3x ，且123x x x <<，若123523x x x π++=，则()f x 的最小正周期为（ ） A ．2πB ．23πC ．πD ．43π【答案】C 【解析】 【分析】根据题意，知当7π3x ω=时，π5π62x ω+=，由对称轴的性质可知122π3x x ω+=和238π3x x ω+=，即可求出w ，即可求出()f x 的最小正周期. 【详解】解：由于()()sin 06f x A x a a A ωπ⎛⎫=+-<< ⎪⎝⎭在区间70,3ωπ⎡⎤⎢⎥⎣⎦有三个零点1x ，2x ，3x ， 当7π3x ω=时，π5π62x ω+=， ∴由对称轴可知1x ，2x 满足12πππ2662x x ωω+++=⨯， 即122π3x x ω+=. 同理2x ，3x 满足23ππ3π2662x x ωω+++=⨯，即238π3x x ω+=， ∴12310π5π233x x x ω++==，2ω=，所以最小正周期为：2ππ2T ==. 故选：C. 【点睛】本题考查正弦型函数的最小正周期，涉及函数的对称性的应用，考查计算能力. 6．设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 【答案】B 【解析】 【分析】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断． 【详解】由面面平行的判定定理知：α内两条相交直线都与β平行是//αβ的充分条件，由面面平行性质定理知，若//αβ，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是//αβ的必要条件，故选B ． 【点睛】面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,//a b a b αβ⊂⊂，则//αβ”此类的错误．7．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（ ）A ．2-3B ．3-2C ．52D ．25【答案】C根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案.【详解】由题意，3,15a n ==， 第1次循环，2,23a n =-=，满足判断条件；第2次循环，5,32a n ==，满足判断条件；第3次循环，3,45a n ==，满足判断条件；可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =. 故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.8．已知函数()xf x e b =+的一条切线为(1)y a x =+，则ab 的最小值为（ ） A ．12e-B ．14e-C ．1e-D ．2e-【答案】A 【解析】 【分析】求导得到'()xf x e =，根据切线方程得到ln b a a =，故2ln ab a a =，设()2ln g x x x =，求导得到函数在120,e -⎛⎫ ⎪⎝⎭上单调递减，在12e ,-⎛⎫+∞ ⎪⎝⎭上单调递增，故()12min g x g e -⎛⎫= ⎪⎝⎭，计算得到答案. 【详解】()x f x e b =+，则'()x f x e =，取0x e a =，()0a >，故0ln x a =，()0f x a b =+.故(ln 1)a b a a +=+，故ln b a a =，2ln ab a a =.设()2ln g x x x =，()()'2ln 2ln 1g x x x x x x =+=+，取()'0g x =，解得12x e -=.故函数在120,e -⎛⎫ ⎪⎝⎭上单调递减，在12e ,-⎛⎫+∞ ⎪⎝⎭上单调递增，故()12min 12g x g e e -⎛⎫==- ⎪⎝⎭.本题考查函数的切线问题，利用导数求最值，意在考查学生的计算能力和综合应用能力. 9．执行如图所示的程序框图，当输出的2S =时，则输入的S 的值为( )A ．-2B ．-1C ．12-D ．12【答案】B 【解析】若输入2S =-，则执行循环得1313,2;,3;2,4;,5;,6;3232S k S k S k S k S k =====-===== 132,7;,8;,9;32S k S k S k =-=====结束循环，输出32S =，与题意输出的2S =矛盾；若输入1S =-，则执行循环得11,2;2,3;1,4;,5;2,6;22S k S k S k S k S k =====-=====11,7;,8;2,9;2S k S k S k =-=====结束循环，输出2S =，符合题意；若输入12S =-，则执行循环得212,2;3,3;,4;,5;3,6;323S k S k S k S k S k =====-=====12,7;,8;3,9;23S k S k S k =-=====结束循环，输出3S =，与题意输出的2S =矛盾；若输入12S =，则执行循环得12,2;1,3;,4;2,5;1,6;2S k S k S k S k S k ===-======-=1,7;2,8;1,9;2S k S k S k =====-=结束循环，输出1S =-，与题意输出的2S =矛盾；综上选B.10．△ABC 的内角A ，B ，C 的对边分别为,,a b c ，已知3,1,30a b B ===，则A 为( )A ．60B ．120C ．60或150D ．60或120【答案】D 【解析】由正弦定理可求得sin 2A =，再由角A 的范围可求得角A. 【详解】由正弦定理可知sin sin a b A B =1sin 30=，解得sin A =，又0180A <<，且>a b ，所以60A ︒=或120︒。