第10讲_传输线方程及其解
- 格式:pdf
- 大小:867.17 KB
- 文档页数:21

传输线方程是一种非常重要的物理学公式,用于描述电路中传输线的特性。
它可以用来计算某一电路中传输线的电压、电流、功率和电阻等参数。
传输线方程是电路中传输线特性的重要公式。
它可以用来计算某一电路中传输线的参数,包括电压、电流、功率和电阻等。
传输线方程的定义如下:
传输线方程由两部分组成,即传输线的电压和电流。
传输线的电压是指传输线上的电压,它由两个部分组成,一部分是电压的幅度,另一部分是电压的相位。
电流是指传输线上的电流,它也由两个部分组成,一部分是电流的幅度,另一部分是电流的相位。
通过传输线方程,可以计算出传输线的功率和电阻等参数。
电功率是指传输线上传输电能的能量,它取决于传输线的电阻和电流。
电阻是指传输线上电能损失的程度,它决定了传输线上电流的大小。
传输线方程是电路中传输线特性的重要公式,它可以用来计算某一电路中传输线的电压、电流、功率和电阻等参数,从而帮助我们更好地了解传输线的特性,提高电路的可靠性。




均匀传输线方程还存在一些难以解决的问题,因此对传输线方程通过拉氏变换在复频域内求解成为了一个研究方向。
为了便于计算,假设线上电压、电流都为零初始条件,则对方程(1)、(2)两端分别取拉氏变换可得如下的形式一一dU_(x,s):(风+sLo)I(x,s)(6)a,x—a—I(_x,s):(G。
+sCo)U(x,s)(7)ax其中U(x,J)和舡声)分别为u(x,0和如,f)的象函数。
联立方程(6)、(7)可解得线上电压电流的复频域通解为u(x,J)=Fs(s)e一7‘’n+E0)P+7‘。
n(8)m,班赤k∽州小一哪矿巾¨】(9)上两式中r(s)为均匀传输线的传播常数,其定义为y(s)=.,/—(Ro+SL—o)(Go+—sC—o)(10)z。
(s)为均匀传输线的特性阻抗,其定义为Zc(s)=F10)、F2(s)均为。
的定。
在式(8)、(9)中,分别令x----O并分别代2,至tJ式(12)、(t3)t扣,可得关于Fl(s)、,20)的方程组E(J)+R(s)=u,(s)一丽1m)一删m)(14’Fl(s)e‘7‘5’。
+E(J)e7‘’’‘。
去k∽e州叫一哪矽∽7m)(15)联立方程04)、(15)将求解所得的Fl(s)、F2(s)分别代入式(8)、(9)可得均匀传输线在给定边界条件下吣,)和J0,s)的解为U(x∽=筹箫琊m),s)2≥而≤老嚣F七(s)(,s(5)(16)怖)=蒂鞴k(S)Us∽如印2亩‘蒜黹而。
’(17)其中n。
(J)、n20)分别为传输线始端和终端的反oF==i=;r。
图1长度为l传输线的复频域模型图1所示为一段均匀传输线的复频域模型,该传输线的长度为,,假设其始端接有内阻为zo(s)的电压源己‘O),终端接入一任意负载Z施),则始端和终端边界条件的复频域形式分别为u(o,s)=Us(s)一I(o,s)zo(s)(12)u(1,5)=,(,,s)ZL(s)(13)08)州加揣∽,㈣=丽z丽As)而(20)如果给出激励源“O)的具体形式.那么对式(t4)、(15)分别求取拉氏反变换则可获得线上电压、电流在给定边界条件下的解析解,但是从现有的文献州中还找不到可以描述线上行波多次反射过程的拉氏变换对,因此只能求取某些特定情形下的解析解。





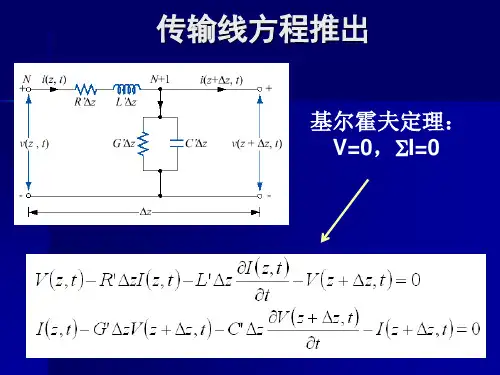
传输线基本公式1、电报方程对于一段均匀传输线,在有关书上可查到,等效电路如下图所示。
Z i V1V2Z2等效电路根据线的微分参数可列出经典的电报方程,解出的结果为:V1=21(V2+I2Z0)eγχ+21(V2-I2Z0)e-γχI1=Z21(V2+I2Z0)eγχ-Z21(V2-I2Z0) e-γχ式中,x是传输线上距离的坐标,它由负载端起算,即负载端的x为0。
γ为传输线的传输系统,γ=α+jβ,α为衰减常数,β为相移常数。
无耗时γ=jβ。
一般情况下常用无耗线来进行分析,这样公式简单一些,也明确一些,或者说理想化一些。
而这样做实际上是可行的,真要计算衰减时,再把衰减常数加上。
Z0为传输线的特性阻抗。
Z i为源的输出阻抗(或源内阻),通常假定亦为Z0;若不是Z0,其数值仅影响线上电压的幅度大小,并不影响其分布曲线形状。
上述两式中,前一项x 越大值越大,相位也越领先,即为入射波。
后一项x 越大值越小,相位也越落后,即为反射波。
由于一般只对线上的电压、电流的空间分布感兴趣,因此上式中没有写时间因子e j ωt (下同)。
2、无耗线上的电压电流分布上面式(1.1)和式(1.2)中,下标2为负载端,下标1为源端,而x 可为任意值,那么V 1、I 1可以泛指线上任意一点的电压与电流,因此下面将V 1、I 1的下标1字省掉。
V=21(V 2+I 2Z 0)e j βχ +21(V 2-I 2Z 0) e -j βχ =21(V 2+I 2Z 0)e j βχ{1+Γe -j (2βχ-ψ)} I=21{ (V 2+I 2Z 0)/ Z 0}e j βχ{1-Γe -j (2βχ-ψ)} 式中,发射系数Γ=Γ∠ψ=022022Z I V Z I V +-=0202Z Z Z Z +- Γ≤1,要想反射为零,只要Z 2 =Z 0即成。
上式中,首项不是x 的函数,而e jβχ为相位因子,不影响幅度。
只是末项影响幅度分布。