(优选)第二讲传输线方程及解
- 格式：ppt
- 大小：1.01 MB
- 文档页数：13
下载文档原格式
合集下载
传输线方程及解
k 特征阻抗为入射电压波与入射电流波之比：
Zc V i I i 1/ Yc
电流波解：
特征导纳Yc
反射电压波与反射电流波在相位上相差180º
传输线纵向V(z)、I(z)分布与终端负载阻抗ZL有关
不同的ZL
有耗传输线方程的解
传输线有损耗，即R’=0，G’=0
传输线方程为：
有耗线的传播常数和特征阻抗 解
传输线方程推出
基尔霍夫定理： V=0，I=0
传输线方程推出I
V (z,t) V (z z,t) V (z,t)
z
z
这就是传输线上电压、电流要满足的方程－传输线方程
方程的复数形式
时谐量与其复数形式的关系是： 把它们代入方程中，即
得到方程的复数形式：
无耗传输线方程的解
如果传输线无损耗
R’＝0，G’＝0
传输线方程简化为：
dV/dz=-jL’I, dI/dz=-jC’V
d 2V dz2
2L'C'V
k 2V
d 2V dz2
k 2V
0
该方程的解为：
无耗传输线方程的解I
定义本征阻抗和导纳：
电流为 注意：这里得到的电压、电流波均为复数形式！
由时谐量与复数表示的对应关系，可得到：
注意：Zc, k 均为复数!!
有耗传输线方程的解I
传播常数k为
方程的解：
传输线上衰减波
把复数传播常数代入，得到：
有耗传输线方程的解II
传播常数的虚部ki>0, 称为波的衰减因 子或衰减常数，表示波的衰减。
传播常数的实部kr>0, 称为相位常数， 表示波的传播。
从解V, I 表达式中可知：传输线上电压、 电流波的传播可唯一地由两个特征参数 k, Zc（或Yc）。
传输线方程
egz
V + = A1e-
gz
表示向+z方向传播的波，即自源到 1 + I = A e 1 负载方向的入射波，用V+或I +表示. Z0
V - = A2 e g z
gz
表示向-z方向传播的波，即自负载 到源方向的反射波，用V-或I -表示。 I - = - 1 A e g z 2 Z0 电压电流解为
j wt j y v ( z ) j wt 轾 v( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 V e e = Re V ( z ) e 0 犏 犏 臌 臌 j wt j y I ( z ) j wt 轾 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾 I e e = Re I ( z ) e 0 犏 犏 臌 臌
③TEM波传输线的长度为10cm，当信号频率为 10GHz （ λ
=3cm)时。
l /λ ①短线(0.00167)；②长线(3.33)；③长线(3.33)。
2. 传输线的分布参数 (Distributed parameter)
低频传输线在低频电路中只起连接线的作用，因频率低， 其本身分布参数所引起的效应可以忽略不计，所以在低频电路 中只考虑时间因子而忽略空间效应，因而把传输线当作集总参 数电路来处理是允许的。 而对于微波传输线，因为频率很高，此时分布参数效应不 能再忽视了，传输线不能仅当作连接线，它将形成分布参数电 路，参与整个电路的工作。因而传输线在电路中所引起的效应 必须用传输线理论来研究。 亦即，在微波传输线上处处存在分布电阻、分布电感，线 间处处存在分布电容和漏电电导。用R1、L1、G1、C1分别表 示传输线单位长度的电阻、电感、电导和电容，它们的数值 与传输线截面尺寸、导体材料、填充介质以及工作频率有关。
V + = A1e-
gz
表示向+z方向传播的波，即自源到 1 + I = A e 1 负载方向的入射波，用V+或I +表示. Z0
V - = A2 e g z
gz
表示向-z方向传播的波，即自负载 到源方向的反射波，用V-或I -表示。 I - = - 1 A e g z 2 Z0 电压电流解为
j wt j y v ( z ) j wt 轾 v( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 V e e = Re V ( z ) e 0 犏 犏 臌 臌 j wt j y I ( z ) j wt 轾 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾 I e e = Re I ( z ) e 0 犏 犏 臌 臌
③TEM波传输线的长度为10cm，当信号频率为 10GHz （ λ
=3cm)时。
l /λ ①短线(0.00167)；②长线(3.33)；③长线(3.33)。
2. 传输线的分布参数 (Distributed parameter)
低频传输线在低频电路中只起连接线的作用，因频率低， 其本身分布参数所引起的效应可以忽略不计，所以在低频电路 中只考虑时间因子而忽略空间效应，因而把传输线当作集总参 数电路来处理是允许的。 而对于微波传输线，因为频率很高，此时分布参数效应不 能再忽视了，传输线不能仅当作连接线，它将形成分布参数电 路，参与整个电路的工作。因而传输线在电路中所引起的效应 必须用传输线理论来研究。 亦即，在微波传输线上处处存在分布电阻、分布电感，线 间处处存在分布电容和漏电电导。用R1、L1、G1、C1分别表 示传输线单位长度的电阻、电感、电导和电容，它们的数值 与传输线截面尺寸、导体材料、填充介质以及工作频率有关。
传输线方程及其解
对于无耗传输线 ， 0 ，此时 j
LC
无耗传输线传播常数为纯虚数 对于损耗很小的传输线 R L G C ，其传播常数为
( R jL) /(G jC ) j LC (1 R / jL)(1 G / jC )
j LC (1 R / 2 jL)(1 G / 2 jC ) j LC (1 R / 2 jL G / 2 jC R C G L R G j LC j LC 2 L 2 C 2 Z 0 2Y0 R G 2 Z 0 2Y0
d 2U ( z ) 2U ( z ) 0 2 2 ZY dz 其中 d 2 I ( z) ( R jL)(G jC ) 2 I ( z) 0 dz 2
入射波 反射波
通解
U z A1ez A2 e z U U I z A1e A2 e
什么叫色散？均匀无耗传输线上的导行波为无色散波，
有耗线的波为色散波，为何？重点掌握四个物理量的意义
微波工程基础
17
微波工程基础
10
第一章 均匀传输线理论之•均匀传输线方程及其解
i ( z, t ) u ( z z, t ) u ( z, t ) Rzi ( z, t ) Lz t u ( z z, t ) i( z z, t ) i ( z, t ) Gzu ( z z, t ) Cz t 将上式整理，并忽略高阶小量，可得： u ( z, t ) i( z, t ) Ri( z, t ) L z t i( z, t ) u ( z, t ) Gu ( z, t ) C z t 对于角频率为 的正弦电源，传输线方程 为
第2讲2011传输线方程及其解
γ 2 = Z 0Y0
电子与信息学院
解得:
South China University of Technology
－ U ( z ) = U 0+ e −γ z + U 0 eγ z 1 － I ( z) = (U 0+ e −γ z − U 0 eγ z ) Zc
Zc =
Z0 Y0
Z0 R0 + jω L0 L0 1 Zc = = = = Y0 G0 + jωC0 C0 2π
µ b µr b ln = 60 ln ε a εr a
电子与信息学院
γ = Z 0Y0 = ( R0 + jω L0 )(G0 + jωC0 ) = jω L0C0
South China University of Technology
传输线特性阻抗。
γ = Z 0Y0 = α + j β 传输线的传播常数。
－ U 0+ , U 0
待定系数
β
0
I
U
U+ U−
Zc
ZL
z
电子与信息学院
l
物理意义：
－ U ( z ) = U 0+ e −γ z + U 0 eγ z 1 － I ( z) = (U 0+ e −γ z − U 0 eγ z ) Zc
South China University of Technology
U e
+ −γ z 0
1 + −γ z U0 e Zc 1 − γz − U0 e Zc
I
U+ U−
正向传输的波 e−γ z = e−α z − jβ z 反向传输的波
第2讲 传输线方程及其解
如果我们着重研究时谐(正弦或余弦)的变化情况，有
u ( z, t ) Re U ( z )e jt jt i ( z, t ) Re I ( z )e
式中，U(z)、I(z)只与z有关，表示在传输线z处的电 压或电流的复值。
dU ( R j L) I ZI dz dI (G jC )U YU dz
当典型Δz→0时，有 i( z, t ) u ( z z, t ) u ( z, t ) Ri ( z , t ) L t z i ( z z , t ) i ( z , t ) Gu ( z , t ) C u ( z , t ) z t 式(2-3)是均匀传输线方程或电报方程。
J 传 输 空 间
D
H S E
d
J
二 长线与分布参数电路
1. 长线与短线 L 时，传输线为长线 L 时，传输线为短线
例： 电源与负载间的铜导线长1.5CM L 1 短线 若 f1 1MHZ，则 1 94.86m 若 f 2 10GHZ，则 2 0.949cm L 1.52 长线
Z 0 Zl j 2 l A1 e A2 0 Z 0 Zl
构成线性方程组
A1 A2 g Eg Z 0 Z0 0
其中 g 最后得到
Z g Z0 Z g Z0
, l
很易得到
C j z j z I ( z) ( A1e A2e ) ( A1e j z A2e j z ) L L
1 j z j z ( A1e A2e ) z0
其中，特性阻抗 Z
0
传输线方程式
假想多段傳輸線問題解答：步驟7
Y ( z3 ) = Y ′ + Y pa ≈ 0.01533 j 0.00373
( )
正規化導納 (對第二段傳輸線而言)
0.7665 j 0.1865
對應之正規化阻抗
1.23 + j 0.30 (C點)
1- 106
106
電磁波
傳輸線(電路觀點) 第1章 傳輸線(電路觀點)
電磁波
傳輸線(電路觀點) 第1章 傳輸線(電路觀點)
z = z2
假想多段傳輸線問題解答：步驟9
處的阻抗為
Z se 和 Z ′ 串聯
z2 = 2 3
Z ( z2 ) = Z ′ + Z se ≈ 40.0 + j15.0
() 對第一段傳輸線的正規化阻抗 0.53 + j 0.20 (E點)
1- 108
1- 100
100
電磁波
傳輸線(電路觀點) 第1章 傳輸線(電路觀點)
假想多段傳輸線問題解答：步驟2
各段傳輸線均無耗損故傳到
Z ( z1 ) 的功率亦必傳到 z = z 2
+ 送到 Z ( z 2 ) 的功率佔送到
z = z2
z = z2 處的等效電路
+
處功率的比例為
e2 =
Re{Z se + Z ( z 2 + )} Re{Z ( z 2 + )}
(A點 ) 連接O點和A點，其距離移至 駐波比標尺即得電壓駐波比為2.4
1- 93
93
電磁波
傳輸線(電路觀點) 第1章 傳輸線(電路觀點)
Smith圖使用例解答：步驟2
延長 OA 與波長標尺相交，讀值 mo = 0.192 距負載端3.87波長處應位於 波長標尺上
SJ 2012 第02讲 传输线方程及解(1)
1.
一维波动方程： U z ZI ( z ) U z ZI ( z ) I z YU ( z ) I z YU ( z )
2 ZY R j L G jC 令：
U ( z ) A1e A2e
z
z
2.2.2 均匀传输线方程的解
2.
电压和电流通解：
U ( z ) A1e A2e
1 dU z I ( z) Z dz
z
z
Z 1 z z ( A1e A2e ) Z0
( A1e z A2e z )
2 2
4.
无耗时：
j
2
j L jC
LC
1 vp LC
2.2.2 均匀传输线方程的解
4.
根据边界条件确定待定系数：
U 0 U L 已知： I 0 I L
Vg
Z in z
Ii
IL
Z0 ,
Vi
VL
ZL
真空、空气电容率：
1 9 单位：F/m 0 10 36
一般物质：
0 r r 1
补充材料:材料的参数
真空、空气磁导率：
非磁性材料： 磁性材料：
0 4 10
7
单位：H/m
0 4 10
7
0 r
2.2.1 均匀传输线方程
2.2.1 均匀传输线方程
传输线方程（或电报方程）
i z , t u z , t Ri z , t L z t i z , t Gu z , t C u z , t t z
一维波动方程： U z ZI ( z ) U z ZI ( z ) I z YU ( z ) I z YU ( z )
2 ZY R j L G jC 令：
U ( z ) A1e A2e
z
z
2.2.2 均匀传输线方程的解
2.
电压和电流通解：
U ( z ) A1e A2e
1 dU z I ( z) Z dz
z
z
Z 1 z z ( A1e A2e ) Z0
( A1e z A2e z )
2 2
4.
无耗时：
j
2
j L jC
LC
1 vp LC
2.2.2 均匀传输线方程的解
4.
根据边界条件确定待定系数：
U 0 U L 已知： I 0 I L
Vg
Z in z
Ii
IL
Z0 ,
Vi
VL
ZL
真空、空气电容率：
1 9 单位：F/m 0 10 36
一般物质：
0 r r 1
补充材料:材料的参数
真空、空气磁导率：
非磁性材料： 磁性材料：
0 4 10
7
单位：H/m
0 4 10
7
0 r
2.2.1 均匀传输线方程
2.2.1 均匀传输线方程
传输线方程（或电报方程）
i z , t u z , t Ri z , t L z t i z , t Gu z , t C u z , t t z
电磁场课件第二章传输线的基本理论
1正弦时变条件下传输线方程
令信源角频率已知 ，线上的电压、电流皆为正弦时变规律（或称为谐变），这样具有普遍性意义。
2 方程的通解
典型波动方程的解 传播常数和波阻抗
3 已知信源端电压和电流时的解
求待定系数
边界条件
解的具体形式
用到的数学公式
4 已知负载端电压和电流时的解
边界条件 求待定系数
信号各频率成分的幅值传输过程中无变化（衰减常数）。
均匀无损耗传输线无频率失真，即为无色散系统。
一般情况，衰减常数及相移常数与频率关系复杂，是色散系统。
均匀无损耗传输特性
行波，没有反射波
驻波，反射波和入射波振幅相同
混合波
相向两列行波叠加结果
3 传输线上任一位置处的输入阻抗
传输线上任一位置处的输入阻抗定义为该点电压和电流的比值。
传输线是用以传输电磁波信息和能量的各种形式的传输系统的总称。
微波传输线是用以传输微波信息和能量的各种形式的传输系统的总称，它的作用是引导电磁波沿一定方向传输, 因此又称为导波系统, 其所导引的电磁波被称为导行波。
一、传输线的概念
1
一般将截面尺寸、形状、媒质分布、材料及边界条件均不变的导波系统称为规则导波系统, 又称为均匀传输线。
考察点位置，实际上和传输线长度有关，
在线电磁波的频率，
外接负载阻抗的阻抗，
传输线的波阻抗（特征阻抗）。
输入阻抗决定因素
输入阻抗和传输线相对长度关系
四分之一波长线：阻抗变换性 二分之一波长线：阻抗不变性 是无损耗传输线的一个重要特性
例2–1 均匀无损耗传输线的波阻抗75Ω，终端接50Ω纯阻负载，求距负载端0.25λ、0.5λ位置处的输入阻抗。若信源频率分别为50MHz、100MHz，求计算输入阻抗点的具体位置。
微波技术 1章传输线方程及其解
V ( z)＝VL ch z Z c I L sh z VL I ( z )＝I L ch z sh z Zc
（1.45）
传输线方程及其解
传输线方程解举例
(2)、已知传输线始端电压V0,始端电流I0。
设始端距负载l,将z=l时V(l)＝V0,I（l）＝I0代入(1.39)式，得 1 I0 ( A1e l A2e l ) V ( z) A ez A e z V0 Ae l A2e l 1 1 2 Zc 1 I ( z) ( A1e z A2 e z ) 对上两式联立求解得 Zc 1 1 l l A1 (V0 I 0 Z c )e A2 (V0 I 0 Z c )e 2 2 将A1，A2代回（1.39）式中，有
where LC
()
velocity_ of _ propagatio phase_ velocity: n vp
1 1 LC
(m / s )
传输线方程及其解
长线及分布参数概念
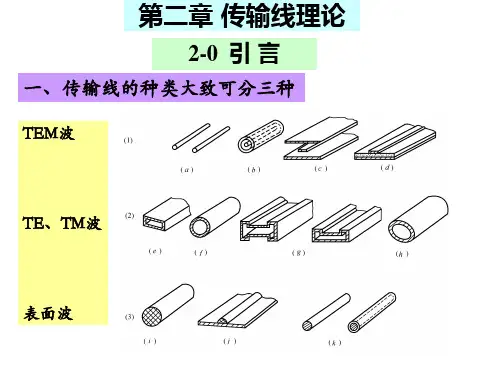
两个非常重要的概念，即“长线”和“分布参数电路”。 一、长线 引入“电长度”概念,电长度定义传输线的长度与其上所传输的电 l l l 波波长之比 。若 ≥1，称之为“长线”。若 1，称之为“短线”
i(z) u(z) z L z i(z+ z) u(z+ z) z+ z R z
C
z
G
z
传输线方程及其解
一般传输线方程的解
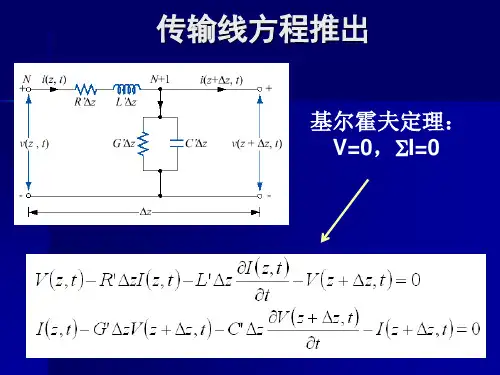
对于传输线Z处的小线元△Z设其两端的电压电流分别为v(z,t) i(z,t) v(z＋△z,t) i(z＋△z,t)，根据克希霍夫定律利用 Kirchhoff 定律，有
i( z, t ) v( z z, t ) v( z, t ) v( z, t ) R1z i ( z, t ) L1z t v( z, t ) i( z z, t ) i( z, t ) i( z, t ) G1z v( z , t ) C1z t
传输线方程及其解ppt课件
化为只含一个待求函数的方程。
d2U (z) dd2zI2(z)
dz 2
ZYU (z) 0 ZYI(z) 0
一维齐次波动方程
令 2 ZY (R0 jL0 )(G0 jC0 ) ，解式为
U (z)
I(
z)
A1e z B1e z
A2ez B2ez
式中积分常数A1, A2, B1, B2须由传输线始端或终端的电压、
传输线上任意点处的电压，都是这一点上入射波电压与反 射波电压的叠加；传输线上任意点处的电流，也是该点处入射 波电流与反射波电流的叠加。
电磁场、微波技术与天线
2-2 传输线方程及其解
12
霍夫电路定律可写出Δz端口上的电压、电流关系：
u(
z,
t
)
u(
z
z,
t
)
R0zi(
z,
t)ຫໍສະໝຸດ L0zi(z, t
t
)
i(
z,
t
)
i(
z
z,
t
)
G0
zu(
z
z,
t
)
C0
z
u(
z
z, t
t)
电磁场、微波技术与天线
2-2 传输线方程及其解
4
2 传输线电报方程（2/2）
上式可整理为：
u ( z, t )
1 2
ZL Z0
1ILe d
电磁场、微波技术与天线
2-2 传输线方程及其解
10
4 对传输线方程解的讨论（1/2）
为方便分析而假定式中Z0, ZL都为纯阻，代入 =α+jβ，相应
的瞬时值表达式
u(d, t) Re U (d )e jt
第二传输线的基本理论PPT学习教案
Ae j z
e j z 2L A
e j z 2
L Ae j z
Ae jz 1 L 2LAcos z
I z 1 ( Ae j z Be j z )
Zc
1 Zc
[ Ae j z
1 L
j2L Asin z]
混合
波
第25页/共73页
U z Ae jz Be jz Ae jz (1 Le j2z ) Ae jz (1 L e jLe j2z )
第二传输线的基本理论
会计学
1
TEM或准TEM 传输线
双导线、同轴 线、带状线、
微带线等
分 类
封闭金属波导
矩形、圆形 、脊形、椭
圆形等
表面波波导 （开波导）
介质波导、 介质镜像线 、单根线等
第1页/共73页
分析方法
电、磁场（麦克
场
斯韦方程组）
路
电压、电流（基尔
霍夫定律）
短线
集中参数电
(Short Line) 路
第28页/共73页
例：已知某同轴线的特性阻抗50欧姆，线上驻 波系数1.5，第一电压波节点离终端10mm， 相邻节点间距离50mm，求负载阻抗。
L 2 z (2n 1)
zmin
L 4
2n 1
4
第29页/共73页
2.4 史密斯圆图
阻抗圆图（等反射系数圆+归一化电阻、电抗
圆）
等反射系数圆
得：d
2U ( z ) dz2
2U ( z )
dI (z) dz
Y1U (z)
同理：d 2I(z) dz 2
2I(z)
其中： Z1Y1 R1 j L1 G1 jC1 j
2_传输线方程及其解
对于给定激励、给定的传输线，其状态主要由终端负载决定。 Z ( z) Zc ( z ) 因为 u Z ( z) Zc Z Zc 所以 u (0) L | u (0) | e j (0) ZL Zc
2 ZL Zc ( RL Z c ) 2 X L | u (0) | 1 2 2 ZL Zc ( RL Z c ) X L
YL jYc tan kl Y ( z l ) Yc Yc jYL tan kl
13
11120010 · 电磁场与电磁波 · 郑史烈
反射系数沿传输线变换的图示
ZL Zc | u (0) | e j (0) u (0) ZL Zc
2 ZL Zc ( RL Z c ) 2 X L 1 | u (0) | 2 2 ZL Zc ( RL Z c ) X L
11120010 · 电磁场与电磁波 · 郑史烈
无耗传输线方程解的初步解释
i j t kz r j t kz u z, t U e U e
第一项表示入射波。第二项表示反射波。 k称为传播常数。 入射波与反射波的相速 波长
2π / k
有耗传输线方程的解
对于有损耗的情况，如果传播常数k与特征阻抗Zc（或导纳Yc）定义为
jk ( R ' j L ')(G ' j C ')
那么传输线方程
Zc
1 R ' j L ' Yc G ' j C '
dU z R ' j L ' I z dz
1 u 与 1 u 沿等 u
微波技术1章传输线方程及其解
从麦克斯韦方程组出发，考虑电 磁波在传输线中的传播特性，通 过求解波动方程得到传输线方程 。
02
传输线方程是描述电磁波在传输 线中传播特性的偏微分方程，包 含了电场和磁场分量以及时间和 空间变量。
传输线方程的形式
传输线方程的一般形式为：∂E/∂t=c^2*∂^2E/∂x^2+σE，其中E为电场强度，t为时间，x为空间变量，c 为光速，σ为电导率。
数值解的概念
数值解是通过数值计算方法求解方程的方法。数值解可以提供精确的结果，但需要使用 数值计算软件或算法。
数值解的求解过程
数值解通常采用迭代方法、有限差分法、有限元法等数值计算技术来求解方程。在传输 线方程中，数值解可以通过离散化传输线并使用数值算法来求解。
数值解的应用场景
数值解适用于大规模复杂系统和实际工程应用。通过数值计算软件或算法，可以高效地 处理复杂的传输线问题，并提供精确的结果。
05 结论
本章总结
传输线方程是描述微波传输线中电磁波传播的基本方 程，通过求解该方程可以得到微波信号在传输线中的
传播特性。
输标02入题
本章介绍了传输线方程的基本形式和求解方法，包括 时域和频域的求解方法。
01
03
传输线方程的求解方法在实际应用中具有广泛的应用， 如微波测量、微波通信、雷达系统等领域。
04 传输线的应用
微波传输系统
微波传输系统概述
微波传输系统是利用微波波段电磁波进行信息传输的系统，广泛 应用于通信、广播、电视等领域。
微波传输系统的组成
微波传输系统主要由发射机、传输线路、接收机三部分组成，其中 传输线路是实现信号传输的关键部分。
微波传输系统的特点
微波传输系统具有频带宽、容量大、抗干扰能力强等优点，但也存 在传输损耗大、传输距离短等局限性。
02
传输线方程是描述电磁波在传输 线中传播特性的偏微分方程，包 含了电场和磁场分量以及时间和 空间变量。
传输线方程的形式
传输线方程的一般形式为：∂E/∂t=c^2*∂^2E/∂x^2+σE，其中E为电场强度，t为时间，x为空间变量，c 为光速，σ为电导率。
数值解的概念
数值解是通过数值计算方法求解方程的方法。数值解可以提供精确的结果，但需要使用 数值计算软件或算法。
数值解的求解过程
数值解通常采用迭代方法、有限差分法、有限元法等数值计算技术来求解方程。在传输 线方程中，数值解可以通过离散化传输线并使用数值算法来求解。
数值解的应用场景
数值解适用于大规模复杂系统和实际工程应用。通过数值计算软件或算法，可以高效地 处理复杂的传输线问题，并提供精确的结果。
05 结论
本章总结
传输线方程是描述微波传输线中电磁波传播的基本方 程，通过求解该方程可以得到微波信号在传输线中的
传播特性。
输标02入题
本章介绍了传输线方程的基本形式和求解方法，包括 时域和频域的求解方法。
01
03
传输线方程的求解方法在实际应用中具有广泛的应用， 如微波测量、微波通信、雷达系统等领域。
04 传输线的应用
微波传输系统
微波传输系统概述
微波传输系统是利用微波波段电磁波进行信息传输的系统，广泛 应用于通信、广播、电视等领域。
微波传输系统的组成
微波传输系统主要由发射机、传输线路、接收机三部分组成，其中 传输线路是实现信号传输的关键部分。
微波传输系统的特点
微波传输系统具有频带宽、容量大、抗干扰能力强等优点，但也存 在传输损耗大、传输距离短等局限性。
2-传输线理论(第2讲)_第二部分
由于此刻负载开路，即ZL→∞，则：
Z& i ∞
=
Z& L Z& C
+ +
jZ& C tgβl jZ& L tgβl
⋅ Z& C
= − jZ& Cctgβl
上式表明无损耗开路线的输入阻抗是纯电抗。
ctgβl既可为正，也可为负，即开路线输入阻抗
可能呈容性或者感性。
2013-9-26
东南大学电磁兼容研究室
+
U& L Z& C
Z&CshΓ& d shΓ& d
⎫ ⎪ ⎬ ⎪ ⎭
I&(x)
=20eZ1&−Γ3C& x-9(-U2& 6S
+ I&S 2
Z&C
)
−
eΓ& x Z&C
(U& S
− I&SZ&C东) 南大学电磁兼容研究室 2
3
传输线的输入阻抗
输入阻抗
– 传输线上任意一点的 电压和电流之比定义 为传输线在该点处的 输入阻抗，也就是从 该位置向负载看去的 等效阻抗。
ρ& L
=
B& e Γ& l A& e − Γ& l
B& = A& ρ& e −2 Γ&l L
Zi
(x)
=
ZC
1+ 1−
ρ& ρ&
(x) (x)
ρ&
(
x)＝
Z&i(x)－Z&C Z&i (x) + Z&C
总复习传输线方程及其解
散化的解。
04 传输线方程的应用
长线理论
1 2
描述长距离信号传输的特性
长线理论主要研究长距离信号传输过程中信号的 衰减、延迟和畸变等特性，为通信系统设计提供 理论基础。
传输线方程的推导
基于电磁场理论和分布参数电路理论，推导出传 输线方程，用于描述传输线上电压和电流的分布。
3
传输线参数的确定
通过测量传输线的阻抗、电感和电容等参数，可 以进一步分析信号在传输线上的传播特性。
法等。
时变传输线方程
要点一
总结词
时变传输线方程考虑了时间变量的影响，能够描述传输线 参数随时间变化的动态过程。
要点二
详细描述
时变传输线方程是在传统的传输线方程基础上引入时间变 量，以描述传输线参数随时间变化的动态过程。这种动态 过程可能是由于环境因素、温度变化或机械振动等因素引 起的。求解时变传输线方程需要采用数值方法，如有限差 分法、有限元法等，同时还需要考虑时间步长的选择和稳 定性问题。
有限元法
总结词
有限元法是一种基于变分原理的数值求解偏 微分方程的方法，通过将连续的空间离散化 为有限个小的单元，将偏微分方程转化为有 限元方程进行求解。
详细描述
有限元法的核心是将连续的空间离散化为有 限个小的单元，每个单元选择一个基函数进 行近似，通过变分原理将原方程转化为有限 元方程。在传输线方程的求解中，有限元法 可以用来求解二维或三维波动方程，得到离
有限差分法
总结词
有限差分法是一种数值求解偏微分方程的方 法，通过将连续的空间离散化，用差分近似 代替微分，将偏微分方程转化为差分方程进 行求解。
详细描述
有限差分法的核心是将偏微分方程中的微分 项用离散的差分近似表示，从而将原方程转 化为离散的差分方程。在传输线方程的求解 中，有限差分法可以用来求解一维波动方程， 得到离散化的解。
04 传输线方程的应用
长线理论
1 2
描述长距离信号传输的特性
长线理论主要研究长距离信号传输过程中信号的 衰减、延迟和畸变等特性，为通信系统设计提供 理论基础。
传输线方程的推导
基于电磁场理论和分布参数电路理论，推导出传 输线方程，用于描述传输线上电压和电流的分布。
3
传输线参数的确定
通过测量传输线的阻抗、电感和电容等参数，可 以进一步分析信号在传输线上的传播特性。
法等。
时变传输线方程
要点一
总结词
时变传输线方程考虑了时间变量的影响，能够描述传输线 参数随时间变化的动态过程。
要点二
详细描述
时变传输线方程是在传统的传输线方程基础上引入时间变 量，以描述传输线参数随时间变化的动态过程。这种动态 过程可能是由于环境因素、温度变化或机械振动等因素引 起的。求解时变传输线方程需要采用数值方法，如有限差 分法、有限元法等，同时还需要考虑时间步长的选择和稳 定性问题。
有限元法
总结词
有限元法是一种基于变分原理的数值求解偏 微分方程的方法，通过将连续的空间离散化 为有限个小的单元，将偏微分方程转化为有 限元方程进行求解。
详细描述
有限元法的核心是将连续的空间离散化为有 限个小的单元，每个单元选择一个基函数进 行近似，通过变分原理将原方程转化为有限 元方程。在传输线方程的求解中，有限元法 可以用来求解二维或三维波动方程，得到离
有限差分法
总结词
有限差分法是一种数值求解偏微分方程的方 法，通过将连续的空间离散化，用差分近似 代替微分，将偏微分方程转化为差分方程进 行求解。
详细描述
有限差分法的核心是将偏微分方程中的微分 项用离散的差分近似表示，从而将原方程转 化为离散的差分方程。在传输线方程的求解 中，有限差分法可以用来求解一维波动方程， 得到离散化的解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（优选）第二讲传输线方程 及解
传输线方程推出I
V (z,t) V (z z,t) V (z,t)
z
z
这就是传输线上电压、电流要满足的方程－传输线方程
方程的复数形式
时谐量与其复数形式的关系是： 把它们代入方程中，即
得到方程的复数形式：无耗传来自线方程的解如果传输线无损耗
R’＝0，G’＝0
传输线方程简化为：
将传输线分成N段后，只要每一段长度l << ，基尔
霍夫定理仍适用。
传输线方程及其解：传输线的特征参数为传播常数k与 特征阻抗Zc（或特征导纳Yc = 1/Zc）。k的实部kr表示 波的传播，虚部ki表示波的衰减，传输线上电压、电 流与位置z有关，可分解为入射波与反射波之和。电压 入射波与电流入射波之比为特征阻抗Zc，电压反射波 与电流反射波相位相差180°。
传输线上衰减波
把复数传播常数代入，得到：
有耗传输线方程的解II
传播常数的虚部ki>0, 称为波的衰减因 子或衰减常数，表示波的衰减。
传播常数的实部kr>0, 称为相位常数， 表示波的传播。
从解V, I 表达式中可知：传输线上电压、 电流波的传播可唯一地由两个特征参数 k, Zc（或Yc）。
复习要点
入射波
反射波
入射波的相速：vi = dz/dt = /k (+z方向) 反射波的相速：vr = dz/dt = -/k （-z方向）
无损耗传传输播线速上度波就的是传填播充速介度质为中：的光速
v p1/ L'C' 1/
无耗解的初步解释I
波长： 2
k 特征阻抗为入射电压波与入射电流波之比：
Zc V i I i 1/ Yc
电流波解：
特征导纳Yc
反射电压波与反射电流波在相位上相差180º
传输线纵向V(z)、I(z)分布与终端负载阻抗ZL有关
不同的ZL
有耗传输线方程的解
传输线有损耗，即R’=0，G’=0
传输线方程为：
有耗线的传播常数和特征阻抗 解
注意：Zc, k 均为复数!!
有耗传输线方程的解I
传播常数k为
方程的解：
dV/dz=-jL’I, dI/dz=-jC’V
d 2V dz2
2L'C'V
k 2V
d 2V dz2
k 2V
0
该方程的解为：
无耗传输线方程的解I
定义本征阻抗和导纳：
电流为 注意：这里得到的电压、电流波均为复数形式！
由时谐量与复数表示的对应关系，可得到：
无耗解的初步解释
讨论电压波情况：
传播常数
传输线方程推出I
V (z,t) V (z z,t) V (z,t)
z
z
这就是传输线上电压、电流要满足的方程－传输线方程
方程的复数形式
时谐量与其复数形式的关系是： 把它们代入方程中，即
得到方程的复数形式：无耗传来自线方程的解如果传输线无损耗
R’＝0，G’＝0
传输线方程简化为：
将传输线分成N段后，只要每一段长度l << ，基尔
霍夫定理仍适用。
传输线方程及其解：传输线的特征参数为传播常数k与 特征阻抗Zc（或特征导纳Yc = 1/Zc）。k的实部kr表示 波的传播，虚部ki表示波的衰减，传输线上电压、电 流与位置z有关，可分解为入射波与反射波之和。电压 入射波与电流入射波之比为特征阻抗Zc，电压反射波 与电流反射波相位相差180°。
传输线上衰减波
把复数传播常数代入，得到：
有耗传输线方程的解II
传播常数的虚部ki>0, 称为波的衰减因 子或衰减常数，表示波的衰减。
传播常数的实部kr>0, 称为相位常数， 表示波的传播。
从解V, I 表达式中可知：传输线上电压、 电流波的传播可唯一地由两个特征参数 k, Zc（或Yc）。
复习要点
入射波
反射波
入射波的相速：vi = dz/dt = /k (+z方向) 反射波的相速：vr = dz/dt = -/k （-z方向）
无损耗传传输播线速上度波就的是传填播充速介度质为中：的光速
v p1/ L'C' 1/
无耗解的初步解释I
波长： 2
k 特征阻抗为入射电压波与入射电流波之比：
Zc V i I i 1/ Yc
电流波解：
特征导纳Yc
反射电压波与反射电流波在相位上相差180º
传输线纵向V(z)、I(z)分布与终端负载阻抗ZL有关
不同的ZL
有耗传输线方程的解
传输线有损耗，即R’=0，G’=0
传输线方程为：
有耗线的传播常数和特征阻抗 解
注意：Zc, k 均为复数!!
有耗传输线方程的解I
传播常数k为
方程的解：
dV/dz=-jL’I, dI/dz=-jC’V
d 2V dz2
2L'C'V
k 2V
d 2V dz2
k 2V
0
该方程的解为：
无耗传输线方程的解I
定义本征阻抗和导纳：
电流为 注意：这里得到的电压、电流波均为复数形式！
由时谐量与复数表示的对应关系，可得到：
无耗解的初步解释
讨论电压波情况：
传播常数