列分式方程解应用题的方法——列表分析法

巧用列表法列分式方程解应用题
郭娇玲
【期刊名称】《基础教育论坛（综合版）》
【年(卷),期】2016(000)013
【摘要】列分式方程解应用题是初中数学代数教学中的一个难点.这类应用题往往题目长,涉及到的知识点多,数量关系复杂,因此很多学生对列分式方程解应用题常怀畏惧心理,常感束手无策.列分式方程解应用题时,如果能借助表格,将题目所反映的基本量和所给条件用表格呈现,便可理清复杂的数量关系,轻松列出分式方程,大大降低解题难度.
【总页数】3页(P25-27)
【作者】郭娇玲
【作者单位】浙江省临海市永丰镇中学
【正文语种】中文
【相关文献】
1.列分式方程解应用题 [J], 孙慧
2.巧用列表法列分式方程解应用题 [J], 郭娇玲;
3.列分式方程解应用题 [J], 孙慧
4.列分式方程解应用题 [J], 孙慧
5.精准建模，正确解题——例谈列分式方程解应用题 [J], 万方红;
因版权原因，仅展示原文概要，查看原文内容请购买。

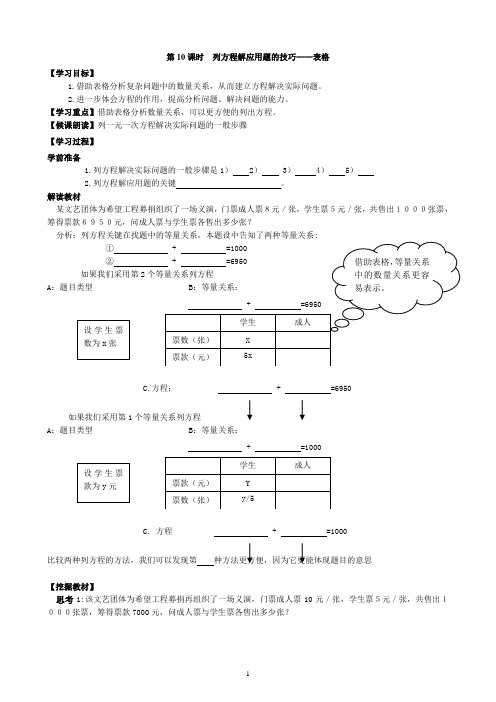
第10课时 列方程解应用题的技巧——表格【学习目标】1.借助表格分析复杂问题中的数量关系，从而建立方程解决实际问题。

2.进一步体会方程的作用，提高分析问题、解决问题的能力。

【学习重点】借助表格分析数量关系，可以更方便的列出方程。

【候课朗读】列一元一次方程解决实际问题的一般步骤 【学习过程】 学前准备1.列方程解决实际问题的一般步骤是1） 2） 3） 4） 5）2.列方程解应用题的关键 。

解读教材某文艺团体为希望工程募捐组织了一场义演，门票成人票８元／张，学生票５元／张，共售出１０００张票，筹得票款６９５０元，问成人票与学生票各售出多少张？分析：列方程关键在找题中的等量关系，本题设中告知了两种等量关系:A如果我们采用第1A ：题目类型 B ：等量关系：【挖掘教材】思考1:该文艺团体为希望工程募捐再组织了一场义演，门票成人票10元／张，学生票５元／张，共售出１０００张票，筹得票款7000元，问成人票与学生票各售出多少张？思考2: 在上面问题中,如果票价不变,那么售出1000张票所得票款可能是6930元吗?可能是6932元吗?说出理由.【反思总结】1.在寻找复杂应用题中的数量关系时,我们借助了 ,使得题设中数量关系更简单、明了.2.灵活地设置未知数，合理选择等量关系，可给解题带来便捷。

3.解出方程后应注意检验求出的值是不是方程的解,是否符合实际【达标检测】1.小兵用172元买了两种书，共10本,单价分别是18元、10元。

每种书小兵各买了多少本？2.一份希望小学的数学竞赛初赛试卷只有25道选择题，选对一道得4分，选错或少选一题倒扣1分，某同学得了90分，他作对的题数是多少？3.学校决定对数学竞赛优胜者进行奖励，获胜者共25人，其中获省里奖的每人奖励价值为200元的奖品，获得市里奖的每人奖励价值50元的奖品，共花去2000元，那么你知道获得省、市奖的学生各有多少人？4.甲队有32人，乙队有28人，如果要使甲队人数是乙队人数的2倍，设从乙队抽调x人到甲队.（完成下表的填空）5.某车间28名工人生产螺栓和螺母，螺栓与螺母个数1∶2，每人每天平均生产螺栓12个或螺母18个，刚好配套.求多少人生产螺栓？6.一项工程,甲独做需要40天完成,乙独做需要30天完成,丙独做需要24天完成,甲、乙、丙三人合作了3天后，乙、丙二人因事离开工地几天，乙比丙后返回工地3天，结果，前后共用14天完成这项工程，问途中乙丙各离开多少天？。

“列表分析法”搭台“分式方程应用”唱戏作者：康海芯来源：《初中生世界·八年级读写版》2014年第06期分式方程应用题是本章的重要内容，由于它涉及的知识点多，数量关系复杂，因此很多同学对列分式方程解应用题有畏惧心理. 解分式方程应用题时，如果能借助表格，分析、挖掘其中的等量关系，往往可以化难为易，化繁为简，起到事半功倍的效果. 本文将结合2013年各地中考题，谈谈列表分析法在解答分式方程应用题的运用，供同学们参考.一、行程问题例1 （湖南湘西）吉首城区某中学组织学生到距学校20 km的德夯苗寨参加社会实践活动，一部分学生沿“谷韵绿道”骑自行车先走，半小时后，其余学生沿319国道乘汽车前往，结果他们同时到达（两条道路路程相同），已知汽车速度是自行车速度的2倍，求骑自行车学生的速度.【分析】行程问题涉及三个基本量：路程、速度和时间，它们之间的基本关系是：路程=速度×时间，在这三个基本量中，已知两个可以求出第三个. 本题中涉及两种交通方式，包含的等量关系有：①速度关系：汽车的速度=自行车速度的2倍；②时间关系：坐汽车所用的时间=骑自行车的时间-半小时.如果以②等量关系列分式方程，则需要设速度为未知数，即设骑自行车学生的速度为每小时x千米，可以设计4行3列的表格，把题目中有关的量填入表格如下：本题还可以以①为等量关系列分式方程，则需要设时间为未知数，同学们可以试一试.解：设骑自行车学生的速度为x km/h，则汽车的速度为2x km/h，根据题意得：=-.解得：x=20. 经检验，x=20是原方程的解.答：骑自行车学生的速度为20 km/h.二、销售问题例2 （湖北仙桃）某文化用品商店用1 000元购进一批“晨光”套尺，很快销售一空；商店又用1 500元购进第二批该款套尺，购进时单价是第一批的倍，所购数量比第一批多100套.求第一批套尺购进时单价是多少？【分析】销售问题涉及三个基本量：总价、单价和数量，它们之间的基本关系是：总价=单价×数量，在这三个基本量中，已知两个可以求出第三个. 本题中涉及两个批次的进货，包含的等量关系有：①单价关系：第二批套尺购进单价=第一批套尺购进单价的倍；②数量关系：第二批所购数量=第一批所购数量+100套.如果以②等量关系列分式方程，则需要设单价为未知数，即设第一批套尺购进单价为x 元，可以设计4行3列的表格，把题目中有关的量填入表格如下：本题还可以以①为等量关系列分式方程，则需要设数量为未知数，同学们可以试一试.解：（1）设第一批套尺购进时单价是x元/套.由题意得：-=100，即-=100，解得：x=2.经检验：x=2是所列方程的解.答：第一批套尺购进时单价是2元/套.三、工程问题例3 （2013·四川德阳）一项工程，甲队单独做需40天完成，若乙队先做30天后，甲、乙两队一起合做20天恰好完成任务，请问乙队单独做需要多少天才能完成任务？【分析】本题是虚拟类工程问题，工作总量通常看作单位1，工程问题涉及三个基本量：工作总量、工作效率和工作时间，它们之间的基本关系是：工作总量=工作效率×工作时间，在这三个基本量中，已知两个可以求出第三个. 本题中涉及两个人工作，涉及工作总量的等量关系为：甲的工作总量+乙的工作总量=1.如果以工作总量为等量关系列分式方程，则需要设乙的工作时间为未知数，即设乙队单独做需要x天才能完成任务，可以设计4行3列的表格，把题目中有关的量填入表格如下：解：设乙单独做需要x天完成，由题意得×20+×（20+30）=1解得x=100.经检验x=100是原方程的解，答：乙单独做需要100天完成.综上所述，用列表分析法解分式方程应用题时，主要包括三个步骤：第一，要确定问题的类型（如工程问题，行程问题等），以及它涉及的哪些量，基本关系是什么？第二，根据题意，写出问题中所有的等量关系，确定列分式方程的那个等量关系，并选择合适的量设未知数，然后借助表格来理清这些量之间的关系，把其他量用含未知数的代数式表示出来；第三，根据选择好的基本等量关系就可以列出分式方程，从而求解.（作者单位：江西省赣县江口中学）。

巧用列表法解分式方程应用题摘要：列分式方程解应用题是人教版初中二年级数学教学的一个重点,也是难点。

之所以难，因为初中的应用题与实际结合比较紧密,有些学生缺乏生活、生产经验,解题有些困难，产生了畏惧心理；另一方面题目长，经常看到后面忘记了前面的，数量多且关系复杂，看完题目头脑一片混乱。

应用题对学生的分析能力、计算能力、逻辑思维能力及解决实际问题的能力都有较高要求。

关键词：分式分程列表法解应用题列表法，顾名思义就是借助于列出表格的形式进行解题的一种方法。

有些应用题的条件较多，错综复杂，不易理清脉络，我们可以根据题意画出表格，把题中的已知量、未知量、隐蔽条件和所求问题一一填入表格中，这样就很容易看出数量间的关系，找出解题的途径。

画出表格后，在排列条件时要写清事物的简称，如数、量（包括单位）及其它等量对应关系；同学们在解决实际问题中一定要能分析出各量都与哪个量之间关系多，就将此量设为未知数，其它各量用这个未知数表示出来，根据等量关系列出方程。

有很多典型的应用题，通常有三个基本关系：“ab=c”型数量关系（如：速度×时间=路程；单价×数量=总价）。

这类应用题用列表法分析很适用。

掌握了这种方法，你会发现解决这类应用题将会轻而易举，不在话下。

下面就让我们开始吧！一、行程问题分析例1：甲、乙两人分别从距目的地6千米和10千米的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20分到达目的地。

求甲、乙的速度。

分析：数量关系为“路程=速度×时间”，本题中的条件关系较多，不利于理清，因此可以采用列表法来帮助分析整理。

首先列一个三行四列的表格，然后找到三个关键量“路程”、“速度”、“时间”，将其填入第一行的后三个空格中，再找到两种分类，“甲”、“乙”填入第一列的下两个空格中，再把对应的数据填入相应的空格，根据题目设适当的未知数。

因为甲、乙的速度比是3：4，所以最好设甲的速度为3x千米/时，则乙的速度为4x千米/时。

用列表法解分式应用题
习水县桃林乡沙溪附中 任德波
分式应用题是人教版八年级下册第十六章的内容人。

由于学生刚接触分式的内容，很大程度上思维还定势在整式的模式上。

特别是列分式方程解答应用题，更让学生感到头疼。

笔者就分式应用题谈一点体会。

分式应用题一般涉及的项目有两个，而对这两个项目的几个方面的内涵均可用列表法一一对应地填上各自的量（其中包括已知量和未知量），然后根据题中告知的某两个量之间的等量关系，列出分式方程。

而且，在教学的过程中，可以用多媒体进行教学，既方便老师教学，也利于学生思考和操作。

下面结合几个个体事例展现列表法的实用之处。

例1：甲、乙两地相距150千米，一轮船从甲地逆流航行至乙地，然后从乙地返回甲地，已知水流流速为3千米/时，回来时所用的时
间是过去时的3/4，求轮船在静水中的速度。

解：设轮船在静水中的速度为x 千米/时。

列出表格如下：
从表中可知逆流所用时间为 ，顺流时间为 ，题中
150 X －3
150 X ＋3
“顺流时间是逆流所用时间的”，列出方程为： ＝ 。

对这个分式方程的解便不在话下。

3 4 150 X －3 150
X －3。

巧用表格列分式方程应用题发表时间：2018-04-09T15:30:02.803Z 来源：《中国教师》2018年3月刊作者：刘晔[导读] 列表法降低了应用题的难度，从根本上解决了学生们对列分式方程应用题的恐惧，学生能较容易的学会如何列分式方程应用题，我主要从以下几个方面进行教学。

刘晔新疆第一师一团双语中学 843000中图分类号：G623.24 文献标识码：A 文章编号：ISSN1672-2051（2018）03-175-01今年6月底我参加了中考数学网上阅卷工作，我改的第18题分式方程，分值8分，属于简单题，全师共3148份全部改完平均得分为4.3分，为什么很简单的一道应用题得分却不太高，丢分原因有以下几种情况。

1、不会列方程；2、方程列错；3、方程解错；4、分式方程不检验，失分较多是前两种情况。

纵观2010-2016年这7年的中考试卷60%机率考了分式方程应用题，考试题型以解答题为准，教师如何教会学生从实际生活问题转化到方程建模，怎么引导才能让学生见到应用题不害怕，是我一直思考的问题，我在平时的教学中借助表格，搭建一个平台让学生能容易理清题目中数量关系，列表法降低了应用题的难度，从根本上解决了学生们对列分式方程应用题的恐惧，学生能较容易的学会如何列分式方程应用题，我主要从以下几个方面进行教学。

一、审题。

1、理清楚本题到底用到了那些数量关系，一般题目常会出现以下数量关系；路程=速度*时间，总价=单价*数量，工作总量=工作效率*工作时间，逆流速度=静水中的航速-水流速度等一些常见的数量关系。

2、找题目中的等量关系，一般题目中都有一些关键的字词，如是、比、多、少等来体现题目中的一些关系。

通常题目会有2个等量关系，一个等量关系用来设未知数，另一个等量关系用来列方程，在后面例题中会具体讲用如何用这两个等量关系。

二、列表格可以画一个四行三列的表格，竖列可以填审题中找到的数量关系，横行填类型，一般题目会出现几种不同情况，如原计划和实际，骑自行和步行等。

列表法解分式方程应用题四川省凉山州冕宁县泸沽中学刘能芳用分式方程解应用题是初中阶段应用题的一个难点内容，学生不容易找到等量关系，而采用列表和等量关系相结合的方法就很容易列出分式方程，举例如下：例1：八年级（2）班学生周末乘汽车到郊区游览，郊区到学校240千米，一部分学生乘慢车先行，出发2小时后，另一部分学生乘快车前往，结果他们同时到达，已知快车速度是慢车的1.5倍，求慢车的速度分析：方法⑴：因为快车速度=慢车的速度×1.5 ，所以设慢车的速度为x,则快车的速度为1.5x,如表①，由慢车的时间=快车的时间+2，得方程：x =x5.1+2方法⑵：因为慢车的时间=快车的时间+2，所以设快车的时间为x,则慢车的时间为x+2, 如表②由快车速度=慢车的速度×1.5，得方程：x =2+x×1.5求出x 再带入2240+x 就能求出慢车的速度。

例2：、有两块面积相同的试验田，分别收获油菜800kg 和1600kg ，已知第一块试验田每亩收获油菜比第二块少300kg ，求第一块试验田每亩收获油菜多少千克．设第一块试验田每亩收获油菜xkg ，根据题意，可得方程（ ）A ．x x 1600300800=+ B ．3001600800-=x x C ．3001600800+=x x D ． xx 1600300800=-分析：因为第二块试验田每亩收获油菜=第一块+300，所 以设第一块试验田每亩收获油菜 x kg ，则第二块每亩收获油菜 （x+300）kg ，各种关系如下表：由面积相等得方程：300x +=x故选择C例3：王莉与张明共同清点一批图书，已知张明清点完600本图书所用的时间与王莉清点完400本图书所用的时间相同，且张明平均每分钟比王莉多清点10本，求王莉平均每分钟清点图书的数量．解：设王莉平均每分钟清点图书x 本，则张明平均每分钟清点 (x+10) 本， 依题意，得方程：10x 600400+=x 解得: x=20经检验 x=20是原方程的解．答：王莉平均每分钟清点图书20本．。

用“列表法”解应用题作者：游晶星来源：《知音励志·教育版》2016年第11期摘要列方程解应用题是初中数学中理论联系实际的一个重要方面，也是教学中的重点和难点，它对培养学生思维能力，分析问题和解决问题的能力有着重要的意义。

列表法顾名思义就是借助于列出表格的形式进行解题的一种方法。

当有些应用题的条件较多，错综复杂，不易理清脉络时，我们可以根据题意画出表格，把题中的已知量、未知量、隐蔽条件和所求问题一一填入表格中，这样就很容易地看出数量间的关系，找出解题的途径。

本文就列表法在行程问题、工程问题、价格问题、百分数问题、形积问题和新型应用问题等几个方面的应用，分类举例说明。

【关键词】初中数学；应用题；解题；列表法列方程解应用题是初中数学中理论联系实际的一个重要方面，也是教学中的重点和难点，它对培养学生思维能力，分析问题和解决问题的能力有着重要的意义。

而列方程（组）解应用题贯穿七年级到九年级课本的始终。

由于应用题与实际结合比较紧密，有些学生缺乏生活、生产经验，解题有些困难，产生畏惧心理；另一方面应用题对学生的分析能力、计算能力、逻辑思维能力及解决实际问题的能力都有较高要求。

据笔者观察，许多初中学生的数学成绩就是从解应用题开始滑坡的。

“教学有方，教无定法”，经过多年的教学实践，对列方程（组）解应用题这一教学难点，我发现用“列表法”处理，对提高学生解应用题能力，提高数学素养有裨益，特别是对初学列方程解应用题的同学，效果尤其显著。

当应用题的数量关系较为隐蔽，所求的问题较复杂时，可以采用列表法来分析思考。

列表法顾名思义就是借助于列出表格的形式进行解题的一种方法。

有些应用题的条件较多，错综复杂，不易理清脉络，我们可以根据题意画出表格，把题中的已知量、未知量、隐蔽条件和所求问题一一填入表格中，这样就很容易地看出数量间的关系，找出解题的途径。

画出表格后，在排列条件时，要写清事物的简称，如数、量（包括单位）及其它等对应关系；有的可写一个字或一个符号来代替。

列分式方程解应用题的方法——列表分析法作者：张慧梅来源：《科技创新导报》 2013年第20期列分式方程解应用题的方法----列表分析法张慧梅（山东省济宁市第八中学山东省济宁市 272100）摘要：初中数学知识中，列分式方程解应用题一直是教学的重点，也是学生学习的难点。

学生每每学到这些知识就感到困惑，迷茫，审题不清楚，找不准等量关系，无法正确地列出方程，视为难点。

而此教学点也一直是教师们比较头痛的问题，而通过归类把方程分成几种不同的形式（例行程问题，工程问题，销售问题等），一道一道的研究等量关系，从学生学习的效果来看，并不理想。

关键词列分式方程解应用题的方法列表分析法中图分类号:G633 文献标识码: A文章编号：1674-098X(2013)07(b)-0000-00怎样能使学生们比较快地理解并掌握这一难点，通过十多年的教学研究和实践，我采用列表分析法进行教学，学生们较易接受和掌握，效果不错。

在实际教学中，我发现在应用题的题目本身结构中一般会有两个共同之处：①三个量；②两种情况。

所谓三个量：不管什么类型的题目都是三个量之间的关系。

例如：行程问题中是速度、路程、时间；工程问题中是工作时间、工作效率、工作总量；销售问题中是单价、数量、总价；等等；所谓两种情况：不管什么题目都会有甲、乙两人，或两个工程队，或今年、明（去）年，或计划、实际等。

所以，在解应用题时可以先列个表格，具体方法如下：例题1：某化肥厂计划在规定日期内生产化肥120吨，由于采用了新技术，每天多生产化肥3吨，实际生产180吨与原计划生产120吨的时间相等，求计划每天生产多少吨化肥？(1)三个量：工作时间、工作效率、工作总量；(2)两种情况：计划、实际；(3)列表：工作总量工作效率工作时间计划实际(4)设未知数：计划每天生产x吨化肥。

(5)用已知条件及含有未知数的代数式表示各数量关系。

先填已知数据，如：120吨，180吨；再填未知数x;最后填由已知和未知表示的数据如：120/x天，（x+3）吨，180/(x+3)天，即工作总量工作效率工作时间计划120吨x吨120/x天实际180吨（x+3）吨180/(x+3)天(6)找出计划、实际两种情况下某一量之间的关系的语句：实际生产180吨与原计划生产120吨的时间相等。