信号与系统-22-冲激响应求解举例2

格式：pptx
大小：52.00 KB
文档页数：2

下载文档原格式

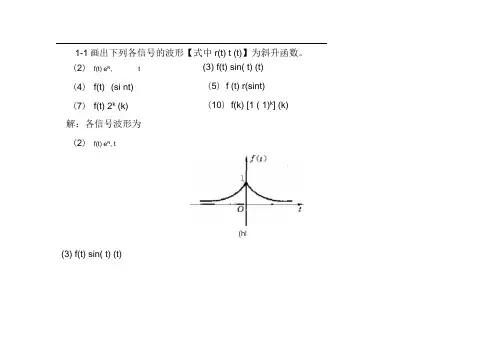
信号与线性系统分析吴大正习题答案1_2

1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。

(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解：各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数］。

(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解：各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为：(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。

信号与系统题库(完整版)

信号与系统题目部分，(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中，若h '（0）=1，且该系统为稳定的因果系统，则该系统的冲激响应()h t 为。

A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示，则x[n]的偶分量[]e x n 是。

[3]波形如图示，通过一截止角频率为50rad sπ，通带内传输值为1，相移为零的理想低通滤波器，则输出的频率分量为（） A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ，其中2TπΩ=；又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭；则()f t 的傅里叶变换为________。

A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+，则该系统是________系统。

A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为（23kk --+）u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。

第二章第2讲_冲激响应与阶跃响应

信号与系统同济大学汽车学院魏学哲 weixzh@
2
将r(t)=h(t)及e(t)=(t)代入给定微分方程
(k1 k2 ) (t ) (3k1 k2 ) (t ) (t ) 2 (t )
k1 k2 1 3k1 k 2 2
将h(t)、h’(t)和(t)代入微分方程两端
ke (t ) ke u(t ) ke u(t ) (t )
k e (t ) (t )
t
t
duc (t ) uc (t ) e(t ) dt
t
t
h (t ) e u (t ) rzs (t ) uczs (t ) e(t ) h(t )
d h (t ) t 3t t 3t ( k1e k2e ) (t ) (k1e 9k2e )u(t ) 2 dt t 3t ( k1e 3k2e ) (t )
(k1 k2 ) (t ) ( k1 3k2 ) (t ) (k1et 9k2e3t )u(t )
当n＝m时， h ( t )
ki e
i 1
i t
u (t ) kn 1 (t )
当n<m时，h(t)中还应包含(t)的导数
信号与系统同济大学汽车学院魏学哲 weixzh@
三、确定h(t)中的系数ki 将h(t)及其各阶导数代入系统方程左端，(t)及其各级导数代入方程右端，令对应项系数相等。
k 0
n
2、系统的零状态响应
( t ) h ( t )
对于线性时不变系统 n
k (t t0 ) kh(t t0 )
rzs (t )
k 0
e ( k t ) t h ( t k t )

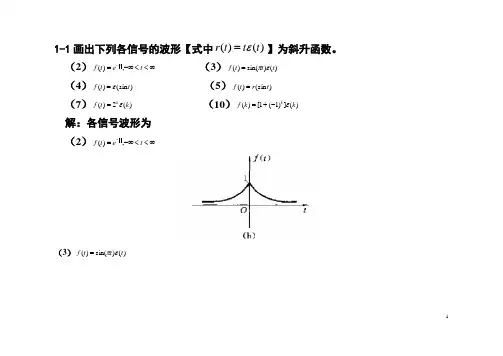
信号与线性系统分析吴大正习题答案2

11-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为（2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fε=t)(sin(t（5）)tf=r(t)(sin2（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1()1[341-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε56（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε71-3 写出图1-3所示各波形的表达式。

81-4 写出图1-4所示各序列的闭合形式表达式。

91-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）) 63cos()443cos()(2ππππ+++=kkkf（5）)sin(2cos3)(5tttfπ+=解：10111-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

信号与系统复习题(答案全)

1、若系统的输入f (t)、输出y (t) 满足()3()4t y t e ft -=，则系统为线性的（线性的、非线性的）、时变的（时变的、时不变）、稳定的（稳定的、非稳定的）。

2、非周期、连续时间信号具有连续、非周期频谱；周期、连续时间信号具有离散、非周期频谱；非周期、离散时间信号具有连续、周期频谱；周期、离散时间信号具有离散、周期频谱。

3、信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10-5 s . 4、 )100()(2t Sa t f =是能量信号（功率信号、能量信号、既非功率亦非能量信号）。

5、 ()2cos()f t t =+是功率信号（功率信号、能量信号、既非功率亦非能量信号）。

6、连续信号f(t)=sint 的周期T 0= 2π ,若对f(t)以fs=1Hz 进行取样，所得离散序列f(k)=sin(k) ,该离散序列是周期序列？否。

7、周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑，此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。

8、 f (t) 的周期为0.1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。

试写出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。

9、 f (k) 为周期N=5的实数序列，若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、则F 5 (3 )= ()54512πjeF +=- 、F 5 (4 )= ()52511πj eF +=- 、F 5 (5 )= 2 ；f(k) =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。

信号与系统(吴大正)-完整版答案-纠错修改后版本精选全文完整版

可编辑修改精选全文完整版第一章信号与系统1-1画出以下各信号的波形【式中)()(t t t r ε=】为斜升函数。

〔2〕∞<<-∞=-t et f t,)( 〔3〕)()sin()(t t t f επ=〔4〕)(sin )(t t f ε= 〔5〕)(sin )(t r t f = 〔7〕)(2)(k t f kε= 〔10〕)(])1(1[)(k k f kε-+=解：各信号波形为〔2〕∞<<-∞=-t e t f t,)(〔3〕)()sin()(t t t f επ=〔4〕)=tfε)(sin(t 〔5〕)rtf=(t(sin)〔7〕)f kεt=2()(k〔10〕)(])1(1[)(k k f k ε-+=1-2 画出以下各信号的波形[式中)()(t t t r ε=为斜升函数]。

〔1〕)2()1(3)1(2)(-+--+=t t t t f εεε 〔2〕)2()1(2)()(-+--=t r t r t r t f 〔5〕)2()2()(t t r t f -=ε 〔8〕)]5()([)(--=k k k k f εε 〔11〕)]7()()[6sin()(--=k k k k f εεπ 〔12〕)]()3([2)(k k k f k---=εε解：各信号波形为〔1〕)2()1(3)1(2)(-+--+=t t t t f εεε〔2〕)2()1(2)()(-+--=t r t r t r t f〔5〕)2()2()(t t r t f -=ε〔8〕)]5()([)(--=k k k k f εε〔11〕)]7()()[6sin()(--=k k k k f εεπ〔12〕)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别以下各序列是否为周期性的。

如果是，确定其周期。

信号与系统冲激响应和阶跃响应

r t
t2
t
t
a t a t
b
bu
t t
c
u
t
rt aut
h 0 1 ,h '0 2
代入h(t),得
hh'00A A113AA2212
h(t)1ete3t u(t)
A A121212
2
X
12
第
用奇异函数项相平衡法求待定系数页
h ( t ) A 1 e t A 2 e 3 tu ( t )
RC (t)A (t)
1 RCA1 A
RC
X
波形
htvC(t)R 1C eR 1C tu(t)
vC (t) h(t) 1 RC
iC(t)
CdvC(t) dt
O
注意！
iC (t)
R12CeR1Ctu(t)
1 (t)
R
1
O R
电容器的电流在
t =0时有一冲激，这就是电容电压突
1 R 2C
变的原因。
•当nm时， ht中应包 t含；
•当nm时， ht应包含 t及其各阶导数。 X
10
第
例2-5-2 页
求系统 d d 2r t(2 t)4d d r(tt)3 r(t)的冲d d e 激(tt响) 应2 e 。(t) 解：
将e(t)→(t)， r(t)→h(t)
d 2 d h t( 2 t) 4d d h (tt)3 h (t)d d ( tt)2 (t)
CtR1CeR1Ctut
X
6
方法2：奇异函数项相平衡原理
第页
已知方程冲激响应求导代入原方程
RC dvdCt(t)vC(t)(t) t vC(t)Ae RCu(t)

各种响应的解法

uS
解:系统转移算子为: 系统转移算子为: u2 1 p +1 1 1 1 H( p) = = = = + p us 2 p +1 2 4 p + 1 2 1+ 1+ p 电路的微分方程为: 电路的微分方程为: 2u′ (t) + u2 (t) = u′ (t) + us (t) 2 s 冲激响应为: 冲激响应为:
16
2.4
卷积积分
卷积积分的意义卷积积分的图解计算卷积积分的性质
17
卷积积分的意义
用δ(t)表示任意信号 t)表示表示任意信号
f (t) = ∫
∞ ∞
f (τ )δ (t τ )dτ
即任意信号 f (t)可以分解为无穷多个不同强度的冲激函数之和. (t)可以分解为无穷多个不同强度的冲激函数之和可以分解为无穷多个不同强度的冲激函数之和. 来表示. 也就是任意信号可以用函数 δ(t) 来表示.
+ (C1 2C2 )δ (t)+ (C1et + 4C2e2 t )ε (t)
10
例 2.8
方法一:用直接求解法方法一:
将上述三个等式及f (t) = δ (t) 代入原微分方程,经整理代入原微分方程,
此例说明了用直接法的步骤: 此例说明了用直接法的步骤: 比较方程两边系数,解得: 比较方程两边系数,解得: 确定冲激响应的形式; 确定冲激响应的形式; 将冲激响应代入原方程, 3 将冲激响应代入原方程, B1 = 1 B0 = 1 C1 = 2 C2 = 用待定系数法确定其系数. 用待定系数法确定其系数. 系统的冲激响应为: 故,系统的冲激响应为:
对于任意信号为输入信号的零状态响应: 对于任意信号为输入信号的零状态响应:

2.4系统的单位冲激响应与单位样值响应

1 连续系统的单位冲激响应的确定一．冲激响应
1．定义
系统在单位冲激信号 (作t) 用下产生的零状态响应，称
为单位冲激响应，简称冲激响应，一般用h(t)表示。
(t)
h(t )
H
2．一阶系统的冲激响应 3．n阶系统的冲激响应
例1 一阶系统的冲激响应
求下图RC电路的冲激响应. （条件：vc 0 0）
特征根 1
RC
t
vC (t) Ae RC u(t)
t 0时的解
下面的问题是确定系数A。
方法：奇异函数项相平衡法，定系数A。
A=1/RC
vC
(t)
1 RC
1t
e RC u(t)
即:
h(t)
1
1t
e RC u(t)
RC
波形
波形
ht
vC (t)
1 RC
1t
e RC u(t )
vc (t ) h(t ) 1 RC
统特性不同，冲激响应可以衡量系统的特性。冲激响应的求解至关重要。用变换域(拉氏变换)方法求冲激响应和阶跃响应会简捷方便，但时域求解方法直观、物理概念明确。
2 离散系统单位样值响应的确定
一．单位样值响应
(n)
h(n)
系统
即 n作用下，系统的零状态响应，表示为 h n
h k 0 k 1,2,3,N
的) 冲d e激(t响) 应2e。(t)
dt
解：
将e(t)→(t)， r(t)→h(t)
d2 h(t dt2
)
4
d h(t) dt
3h(t )
d (t)
dt
2
(t)
求特征根 2 4 3 0 1 1,2 3

2-2冲激响应和阶跃响应

d 3t 3t [ Ae ( t )] 3 Ae ( t ) 2y(0t )) y(0 ) ( 、 dt 3t 3t 3t Ae ( t ) 3 Ae ( t ) 3 Ae ( t ) 2 ( t )

A ( t ) 2 ( t )
b0 (t ) a0

上的特征根λi(i=1，2，…，n)均为单根，则系统的阶跃响应的一般形式(n≥m)为
g( t ) ( ci e
i 1
n
i t
b0 ) ( t ) a0
信号的时域分解
一、信号分解为冲激信号的叠加：在信号分析与系统分析时，常常需要将信号分解为基本信号的形式。这样，对信号与系统的分析就变为对基本信号的分析，从而将复杂问题简单化，且可以使信号与系统分析的物理过程更加清晰。号分解为冲激信号序列就是其中的一个实例。
y(t ) 5 y(t ) 6 y(t ) f (t ) 2 f (t ) 3 f (t )
h(t ) (3e
2t
6e ) (t ) (t )
3t
2.2.2

阶跃响应
一线性非时变系统，当其初始状态为零时，输入为单位阶跃函数所引起的响应称为单位阶跃响应，简称阶跃响应，用g(t)表示。阶跃响应是激励为单位阶跃函数u(t)时，系统的零状态响应，如图2.17 所示。
y x (0 ) y(0 ) yx (0 ) y(0 )
零状态响应：令初始状态为零，即
y(0 ) y(0 ) 0
零状态响应 = 齐次解+特解
由系数匹配法定
y(0 )、y(0 )
§２.2 冲激响应和阶跃响应
主要内容：一、冲激响应的概念及求解二、阶跃响应的概念及求解重点：

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。