直角三角形的性质习题
- 格式:doc
- 大小:198.50 KB
- 文档页数:6

直角三角形的性质练习题一、选择题1. 在直角三角形ABC中,角A为90°,且满足AB = 3,AC = 4,BC = 5,那么∠B的度数是:A) 30°B) 45°C) 60°D) 90°2. 直角三角形PQR中,∠P = 90°,PR = 5,RQ = 12,那么∠Q的度数是:A) 30°B) 45°C) 60°D) 90°3. 若一个直角三角形的一个锐角的度数是30°,那么另一个锐角的度数是:A) 30°B) 45°C) 60°D) 90°4. 若三角形ABC是直角三角形,其中∠A = 90°,AB = 8,AC = 15,则BC的长度为:A) 7B) 9C) 17D) 245. 直角三角形XYZ中,∠X = 90°,XY = 5,YZ = 12,则∠Y的正弦值是:A) 5/12B) 12/13C) 5/13D) 12/5二、填空题1. 直角三角形ABC中,∠C = 90°,AC = 7,BC = 24,则AB的长度为 ________。
2. 设直角三角形XYZ中,∠Y = 90°,XY = 6,则YZ的长度为________。
3. 直角三角形PQR中,PR = 5,RQ = 12,则∠P的度数为________。
4. 若直角三角形ABC中,∠B = 90°,AB = 14,则AC的长度为________。
5. 若直角三角形XYZ中,∠Y = 90°,XY = 9,则∠Z的度数为________。
三、解答题1. 已知直角三角形ABC,其中∠A = 90°,AB = 5,AC = 12,求BC的长度。
解析:根据直角三角形的性质,可使用勾股定理求解。
根据勾股定理,若AC、BC、AB分别表示直角三角形ABC的三条边的长度,则有AC² = AB² + BC²。

解直角三角形知识点及跟踪习题 考点一、直角三角形的性质1、直角三角形的两个锐角互余可表示如下:∠C=90°⇒∠A+∠B=90°2、在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30° 可表示如下: ⇒BC=21AB ∠C=90°3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下: ⇒CD=21AB=BD=AD D 为AB 的中点 知识点二.三角函数对于锐角A 的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的. 因此这几个比值都是锐角∠A 的函数,记作sin A 、cos A 、tan A 、cot A ,即sin A =斜边的对边A ∠, cos A =斜边的邻边A ∠, tan A =的邻边的对边A A ∠∠, cot A = 的对边的邻边A A ∠∠分别叫做锐角∠A 的正弦、余弦、正切、余切,统称为锐角∠A 的三角函数.知识点三。
锐角三角函数的特征与性质:(1)锐角三角函数的值都是正实数,并且0<sin A <1,0<cos A <1 (2)tan A •cot A =1(3)补充:sin tan cos AAA,cos cot sin AA A (视情况定) (4)补充:已知锐角∠A ,则22sin cos 1AA(视情况定)(5)锐角三角函数的增减性当角度在0°~90°之间变化时,①.正弦值随着角度的增大(或减小)而增大(或减小) ②.余弦值随着角度的增大(或减小)而减小(或增大) ③.正切值随着角度的增大(或减小)而增大(或减小) ④.余切值随着角度的增大(或减小)而减小(或增大 知识点四、一些特殊角的三角函数值三角函数 0° 30°45°60°90° sinα 0 21 22 23 1 cos α 1 23 22 21 0 tan α 0 33 1 3不存在 cot α不存在3133 0︒15020米30米从上往下看,视线与水平线的夹角叫做俯角.(2在修路、挖河、开渠和筑坝时,设计纸上都要注明斜坡的倾斜程度. 如图19.4.5,坡面的铅垂高度(h )和水平长度(l )的比叫做坡面坡度 (或坡比).记作i ,即i =lh . 坡度通常写成1∶m 的形式,如i =1∶6. 坡面与水平面的夹角叫做坡角,记作a ,有i =lh=tan a 显然,坡度越大,坡角a 就越大,坡面就越陡. 知识点六.1.解直角三角形:在直角三角形中,除一个直角外,还有2个角和3条边共5个元素,由已知元素求出未知元素 的过程,叫做解直角三角形。

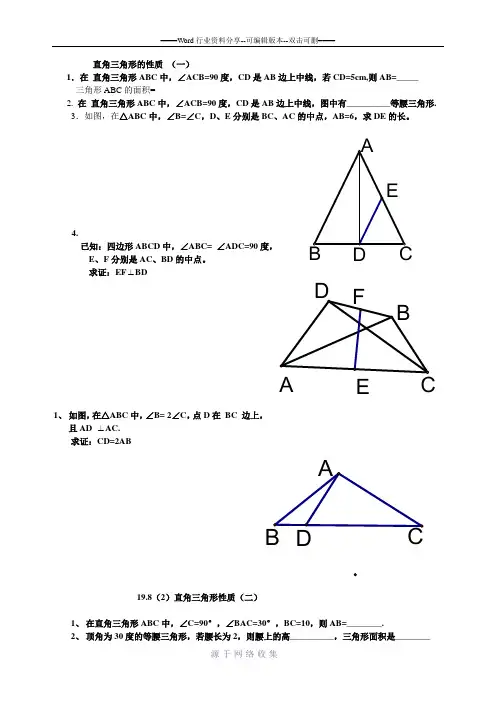
直角三角形的性质 (一)1.在 直角三角形ABC 中,∠ACB=90度,CD 是AB 边上中线,若CD=5cm,则AB=_____ 三角形ABC 的面积=____________2. 在 直角三角形ABC 中,∠ACB=90度,CD 是AB 边上中线,图中有__________等腰三角形. 3.如图,在△ABC 中,∠B=∠C ,D 、E 分别是BC 、AC 的中点,AB=6,求DE 的长。
4.已知:四边形ABCD 中,∠ABC= ∠ADC=90度, E 、F 分别是AC 、BD 的中点。
求证:EF ⊥BD1、 如图,在△ABC 中,∠B= 2∠C ,点D 在 BC 边上,且AD ⊥AC.求证:CD=2AB19.8(2)直角三角形性质(二)1、 在直角三角形ABC 中,∠C=90°,∠BAC=30°,BC=10,则AB=________.2、 顶角为30度的等腰三角形,若腰长为2,则腰上的高__________,三角形面积是________E3、 等腰三角形顶角为120°,底边上的高为3,则腰长为_________4、 三角形ABC 中,AB=AC=6,∠B=30°,则BC 边上的高AD=_______________5、 Rt △ABC 中,∠C=90°,∠A=15°,AB 的垂直平分线交AC 于D,AB 于E,求证AD=2BC.6、 已知:△ABC 中,AB=AC ,∠B=30°,AD ⊥AB ,求证:2DC=BD7.如图,△ABC 中,∠C=90°,∠A=60 °,EF 是AB 的垂直平分线,判断CE 与BE 之间的关系19.8(3)直角三角形的性质(三)1.在直角三角形中,有一个锐角为52度,那么另一个锐角度数为 ;2、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.3、在△ABC 中, ∠ACB=90 °,CE 是AB 边上的中线,那么与CE 相等的线段有_________,与∠A 相等的角有_________,若∠A=35°,那么∠ECB= _________.DACBADEFCBA4、已知:∠ABC=∠ADC=90 度,E 是AC 中点。

直角三角形练习题及答案一、选择题1. 直角三角形中,直角边长分别为3厘米和4厘米,斜边长是多少?A. 5厘米B. 6厘米C. 7厘米D. 8厘米2. 在直角三角形ABC中,∠C=90°,AC=5,BC=12,求AB的长度。
A. 13B. 15C. 20D. 263. 直角三角形的两条直角边分别为a和b,斜边为c,根据勾股定理,正确的表达式是:A. a² + b² = cB. a² + b² = c²C. a² - b² = cD. a² + c² = b二、填空题4. 直角三角形的斜边长为13,一条直角边长为5,另一条直角边的长度是________。
5. 如果直角三角形的一条直角边长为x,另一条直角边长为2x,斜边长为3x,那么x的值是________。
三、解答题6. 已知直角三角形的两条直角边分别为6厘米和8厘米,求斜边的长度。
7. 一个直角三角形的斜边长为10厘米,一条直角边长为6厘米,求另一条直角边的长度。
8. 直角三角形的高为4厘米,底为6厘米,求斜边的长度。
答案:一、选择题1. A2. B3. B二、填空题4. 12厘米5. 3三、解答题6. 根据勾股定理,斜边长度为√(6²+8²)=√(36+64)=√100=10厘米。
7. 根据勾股定理,另一条直角边的长度为√(10²-6²)=√(100-36)=√64=8厘米。
8. 根据勾股定理,斜边长度为√(4²+6²)=√(16+36)=√52厘米。
以上练习题及答案旨在帮助学生加深对直角三角形及其性质的理解,通过实际计算来掌握勾股定理的应用。


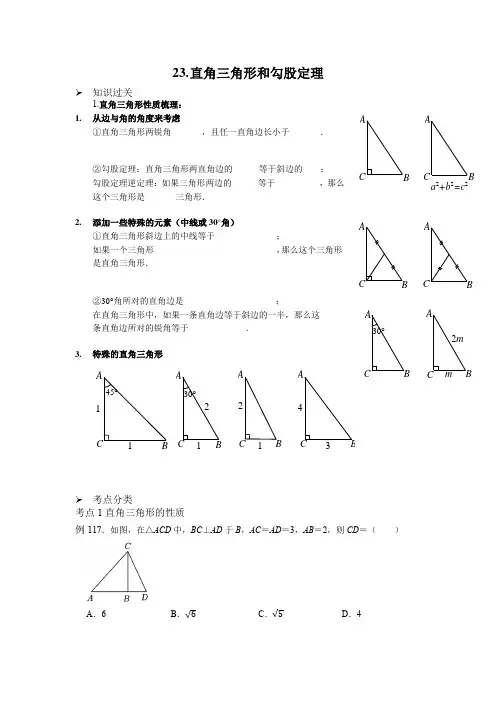
23. 直角三角形和勾股定理➢ 知识过关1.直角三角形性质梳理: 1. 从边与角的角度来考虑①直角三角形两锐角_______,且任一直角边长小于_______.②勾股定理:直角三角形两直角边的______等于斜边的____; 勾股定理逆定理:如果三角形两边的______等于__________,那么这个三角形是_______三角形.2. 添加一些特殊的元素(中线或30°角)①直角三角形斜边上的中线等于______________;如果一个三角形____________________________,那么这个三角形是直角三角形.②30°角所对的直角边是_____________________;在直角三角形中,如果一条直角边等于斜边的一半,那么这 条直角边所对的锐角等于_____________.3. 特殊的直角三角形➢ 考点分类考点1直角三角形的性质例117.如图,在△ACD 中,BC ⊥AD 于B ,AC =AD =3,AB =2,则CD =( )A .6B .√6C .√5D .4ACB 45°1130°234211BCABCA BCAa 2+b 2=c2CBAC B A A BC ABC C BA2mm AB C 30°考点2勾股定理及其逆定理例2如图,在△ABC 中,AB =6,AC =9,AD ⊥BC 于D ,M 为AD 上任一点,则MC 2﹣MB 2等于( )A .29B .32C .36D .45例3等面积法例3若直角三角形两条直角边的长分别为7和24,在这个三角形内有一点P 到各边的距离都相等,则这个距离是( )A .4B .3C .2D .1➢ 真题演练1.如图,在边长为1的正方形网格中,A 、B 、C 均在正方形格点上,则C 点到AB 的距离为( )A .3√1010B .2√105C .5√104D .4√1052.如图,AB =AC =13,BP ⊥CP ,BP =8,CP =6,则四边形ABPC 的面积为( )A .48B .60C .36D .723.如图,在Rt △ABC 中,∠ACB =90°,AB =6,若以AC 边和BC 边向外作等腰直角三角形AFC 和等腰直角三角形BEC .若△BEC 的面积为S 1,△AFC 的面积为S 2,则S 1+S 2=( )A .36B .18C .9D .44.如图,在△ABC 中,∠ACB =90°,AC =6,BC =8,点D 在边AB 上,AD =AC ,AE ⊥CD ,垂足为F ,与BC 交于点E ,则BE 的长是( )A .3B .5C .163D .65.如图,△ABC 的顶点A ,B ,C 在边长为1的正方形网格的格点上,则BC 边长的高为( )A .√302B .85√5 C .45√5 D .√1326.如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE =5,AB =13,则EF 的值是( )A .7B .2√3C .√13D .7√27.如图,∠ABC =∠ADB =90°,DA =DB ,AB 与CD 交于点E ,若BC =2,AB =4,则点D 到AC 的距离是( )A.5√56B .6√55C .4√55D .5√548.如图,将一副直角三角尺重叠摆放,使得60°角的顶点与等腰直角三角形的直角顶点重合,且DE⊥AB于点D,与BC交于点F,则∠FCE的度数为()A.60°B.65°C.75°D.85°9.如图,AC=AB=BD,∠ABD=90°,BC=8,则△BCD的面积为()A.8B.12C.14D.1610.如图,四边形ABCD中,连接BD,O为BD中点,∠BAD=∠BCD=90°,∠BDA=30°,∠BDC=45°,则∠CAO=()A.15°B.18°C.22.5°D.30°➢课后练习1.如图,等边△ABD和等边△BCE中,A、B、C三点共线,AE和CD相交于点F,下列结论中正确的个数是()①△ABE≌△DBC②BF平分∠AFC③AF=DF+BF④∠AFD=60°A.1B.2C.3D.42.如图,△ABC中,∠ACB=60°,AG平分∠BAC交BC于点G,BD平分∠ABC交AC 于点D,AG、BD相交于点F,BE⊥AG交AG的延长线于点E,连接CE,下列结论中正确的有()①若∠BAD=70°,则∠EBC=5°;②BF=2EF;③BE=CE;④AB=BG+AD;⑤S△BFGS△AFD =BFAF.A.5个B.4个C.3个D.2个3.在△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于E、F,给出以下四个结论:当∠EPF在△ABC内绕P旋转时(点E不与A、B重合),①AE=CF;②EF=AP;③△EPF是等腰直角三角形;④S四边形AEPF= 12S△ABC;⑤EF的最小值为√2;⑥BE2+CF2=EF2.则正确结论有()A.2个B.3个C.4个D.5个4.如图,O是正△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为8;③∠AOB=150°;④四边形AOBO′的面积是24+16√3;⑤S△AOC+S△AOB=24+9√3 4.其中正确结论有()个.A.5B.4C.3D.25.如图,Rt△ACB中,∠ACB=90°,△ACB的角平分线AD,BE相交于点P,过P作PF ⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②AD=PF+PH;③DH平分∠CDE;④S四边形ABDE=74S△ABP;⑤S△APH=S△ADE,其中正确的结论是()A.①②③B.②③④C.①②④⑤D.①②⑤6.如图,O为△ABC内的一点,D为AB边上的一点,OD=OB,OA=OC,∠AOC=∠BOD =90°,连接CD.下列结论:①AB=CD;②AB⊥CD;③∠AOD+∠OCD=45°;④S △BOC=S△AOD.其中所有正确结论的序号是()A.①②B.①③C.①②③D.①②③④➢冲击A+如图1,AB为圆O的直径,C为圆O上一点,连接CB,过C作CD⊥AB于点D,过点C 作∠BCE,使∠BCE=∠BCD,其中CE交AB的延长线于点E.(1)求证:CE是圆O的切线;(2)如图2,点F在圆O上,且满足∠FCE=2∠ABC,连接AF并延长交EC的延长线于点G.①求证:CF=2CD;②若CD=4,BD=2,求线段FG的长.。

1.2.1直角三角形的性质与判定练习题一、选择题1.如图,带阴影的矩形面积是()平方厘米.A.9 B.24 C.45 D.512、已知直角三角形两边的长为3和4,则此三角形的周长为().A.12B.7+7C.12或7+7D.以上都不对3.等腰三角形的腰长为10,底长为12,则其底边上的高为()A.13 B.8 C.25 D.644.如果一个直角三角形的两条直角边分别为n2﹣1,2n(n>1),那么它的斜边长是()A.2n B.n+1 C.n2﹣1 D.n2+15.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是()A.25 B.7 C.5和7 D.25或76.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为h cm,则h的取值范围是().A.h≤17cm B.h≥8cmC.15cm≤h≤16cm D.7cm≤h≤16cm7.如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6cm2 B.8cm2 C.10cm2 D.12cm2二、填空题8.在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .9.如图,△ABC中,AC=6,AB=BC=5,则BC边上的高AD=______.10.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,阴影部分的面积是.11.直角三角形的三边长为连续偶数,则其周长为 cm.12.如图,△ABC中,∠C=90°,AB垂直平分线交BC于D.若BC=8,AD=5,则AC等于.三、解答题13.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和是多少?14. 如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.15.去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?(3≈1.732)答案:1. C分析:根据勾股定理先求出直角边的长度,再根据长方形的面积公式求出带阴影的矩形面积.解:∵=15厘米,∴带阴影的矩形面积=15×3=45平方厘米.故选C.2.C(提示:因直角三角形的斜边不明确,结合勾股定理可求得第三边的长为5或7,所以直角三角形的周长为3+4+5=12或3+4+7=7+7)故选C;3. B分析:先作底边上的高,由等腰三角形的性质和勾股定理即可求出此高的长度.解:作底边上的高并设此高的长度为x,根据勾股定理得:62+x2=102,解得:x=8.故选B.4. D分析:根据勾股定理直接解答即可.解:两条直角边与斜边满足勾股定理,则斜边长是:===n2+1.故选D.5. D分析:分两种情况:①当3和4为直角边长时;②4为斜边长时;由勾股定理求出第三边长的平方即可.解:分两种情况:①当3和4为直角边长时,由勾股定理得:第三边长的平方,即斜边长的平方=32+42=25;②4为斜边长时,由勾股定理得:第三边长的平方=42﹣32=7;综上所述:第三边长的平方是25或7;故选:D .6. D (提示:筷子在杯中的最大长度为22815+=17cm ,最短长度为8cm ,则筷子露在杯子外面的长度为24-17≤h ≤24-8,即7cm ≤h ≤16cm ,)故选D .7. A分析:首先根据翻折的性质得到ED=BE ,再设出未知数,分别表示出线段AE ,ED ,BE 的长度,然后在Rt △ABE 中利用勾股定理求出AE 的长度,进而求出AE 的长度,就可以利用面积公式求得△ABE 的面积了.解:∵长方形折叠,使点B 与点D 重合,∴ED=BE ,设AE=xcm ,则ED=BE=(9﹣x )cm ,在Rt △ABE 中,AB 2+AE 2=BE 2,∴32+x 2=(9﹣x )2,解得:x=4,∴△ABE 的面积为:3×4×=6(cm 2).故选:A .8.分析:由三角形ABC 为直角三角形,利用勾股定理根据斜边AB 的长,可得出AB 的平方及两直角边的平方和,然后将所求式子的后两项结合,将各自的值代入即可求出值. 解:∵△ABC 为直角三角形,AB 为斜边,∴AC 2+BC 2=AB 2,又AB=2,∴AC 2+BC 2=AB 2=4,则AB 2+BC 2+CA 2=AB 2+(BC 2+CA 2)=4+4=8.故答案为:89. 3.6(提示:设DC =x ,则BD =5-x .在Rt △ABD 中,AD 2=52-(5-x )2,在Rt △ADC 中,AD 2=62-x 2,∴52-(5-x )2=62-x 2,x =3.6.故AD =226.36-=4.8);10. 分析:在直角三角形ABE 中,由AE 与BE 的长,利用勾股定理求出AB 的长,由正方形面积减去直角三角形面积求出阴影部分面积即可.解:∵AE⊥BE,∴∠AEB=90°,在Rt△ABE中,AE=3,BE=4,根据勾股定理得:AB==5,则S阴影=S正方形﹣S△ABE=52﹣×3×4=25﹣6=19,故答案为:19.11.分析:设直角三角形的三边边长分别为2n﹣2,2n,2n+2,由勾股定理得:两直角边的平方和等于斜边的平方,据此列出关于n的方程,求出符合题意n的值,即求出了直角三角形的三边长,之后求出周长即可.解:设直角三角形的三边边长分别为2n﹣2,2n,2n+2.由勾股定理得:(2n﹣2)2+(2n)2=(2n+2)2,解得:n1=4,n2=0(不合题意舍去),即:该直角三角形的三边边长分别为6cm,8cm,10cm.所以,其周长为6+8+10=24cm.12.分析:根据线段垂直平分线的性质可求得BD的长,从而求得CD的长,再根据勾股定理即可求得AC的长.解:∵AB垂直平分线交BC于D,AD=5,∴BD=AD=5,∵BC=8,∴CD=BC﹣BD=3,∴AC==4,故答案是:4.13.分析:根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积.解:由图形可知四个小正方形的面积和等于最大正方形的面积,故正方形A ,B ,C ,D 的面积之和=49cm 2.故答案为:49cm 2. 14.解:.∵在Rt △ABC 中,∠C=90°,∠A=30°,BD 是∠ABC 的平分线,∴∠ABD=∠CBD=30°.∴AD=DB.又∵Rt △CBD 中,CD=5 cm ,∴BD=10 cm.∴BC=22BD CD -=22105-=53(cm).∴AB=2BC=103 cm.15. 解 如图所示,过点C 作CD ⊥AB ,垂足为点D ,由题意可得∠CAB =30°,∠CBA =45°,在Rt △CDB 中,∠BCD =45°,∴∠CBA =∠BCD ,∴BD =CD .在Rt △ACD 中,∠CAB =30°,∴AC =2CD .设CD =DB =x ,∴AC =2x .由勾股定理得AD =22CD AC -=224x x -=3x .∵AD +DB =2.732,∴3x +x =2.732,∴x ≈1.即CD ≈1>0.7,∴计划修筑的这条公路不会穿过公园.。
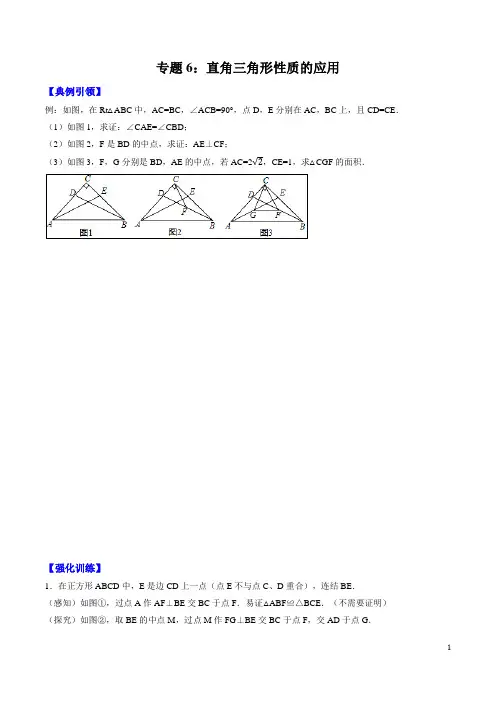
专题6:直角三角形性质的应用【典例引领】例:如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2√2,CE=1,求△CGF的面积.【强化训练】1.在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.(1)求证:BE=FG.(2)连结CM,若CM=1,则FG的长为.(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为.2.综合与实践:如图1,将一个等腰直角三角尺ABC的顶点C放置在直线l上,∠ABC=90°,AB=BC,过点A作AD⊥l于点D,过点B作BE⊥l于点E.观察发现:(1)如图1.当A,B两点均在直线l的上方时,①猜测线段AD,CE与BE的数量关系,并说明理由;②直接写出线段DC,AD与BE的数量关系;操作证明:(2)将等腰直角三角尺ABC绕着点C逆时针旋转至图2位置时,线段DC,AD与BE又有怎样的数量关系,请写出你的猜想,并写出证明过程;拓广探索:(3)将等腰直角三用尺ABC绕着点C继续旋转至图3位置时,AD与BC交于点H,若CD=3,AD=9,请直接写出DH的长度.3.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.4.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.5.如图,在△ABC中,∠ABC=90°,AB=BC,点E是直线BC上一点,连接AE,过点C作CF⊥AE于点F,连接BF.如图①,当点E在BC上时,易证AF﹣CF=√2BF(不需证明),点E在CB的延长线上,如图②:点E在BC的延长线上,如图③,线段AF,CF,BF之间又有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.专题6:直角三角形性质的应用【典例引领】例:如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)如图1,求证:∠CAE=∠CBD;(2)如图2,F是BD的中点,求证:AE⊥CF;(3)如图3,F,G分别是BD,AE的中点,若AC=2√2,CE=1,求△CGF的面积.【答案】(1)证明见解析;(2)证明见解析;(3)S△CFG=78.【解析】(1)直接判断出△ACE≌△BCD即可得出结论;(2)先判断出∠BCF=∠CBF,进而得出∠BCF=∠CAE,即可得出结论;(3)先求出BD=3,进而求出CF=32,同理:EG=32,再利用等面积法求出ME,进而求出GM,最后用面积公式即可得出结论.【解答】(1)在△ACE和△BCD中,{AC=BC∠ACB=∠ACB=90°CE=CD,∴△ACE≌△BCD,∴∠CAE=∠CBD;(2)如图2,在Rt△BCD中,点F是BD的中点,∴CF=BF,∴∠BCF=∠CBF,由(1)知,∠CAE=∠CBD,∴∠BCF=∠CAE,∴∠CAE+∠ACF=∠BCF+∠ACF=∠BAC=90°,∴∠AMC=90°, ∴AE ⊥CF ; (3)如图3,∵AC=2√2, ∴BC=AC=2√2, ∵CE=1, ∴CD=CE=1,在Rt △BCD 中,根据勾股定理得,BD=√CD 2+BC 2=3, ∵点F 是BD 中点, ∴CF=DF=12BD=32,同理:EG=12AE=32,连接EF ,过点F 作FH ⊥BC , ∵∠ACB=90°,点F 是BD 的中点, ∴FH=12CD=12,∴S △CEF =12CE•FH=12×1×12=14,由(2)知,AE ⊥CF ,∴S △CEF =12CF•ME=12×32ME=34ME ,∴34ME=14, ∴ME=13,∴GM=EG-ME=32-13=76, ∴S △CFG =12CF•GM=12×32×76=78.【强化训练】1.在正方形ABCD 中,E 是边CD 上一点(点E 不与点C 、D 重合),连结BE . (感知)如图①,过点A 作AF ⊥BE 交BC 于点F .易证△ABF ≌△BCE .(不需要证明) (探究)如图②,取BE 的中点M ,过点M 作FG ⊥BE 交BC 于点F ,交AD 于点G . (1)求证:BE=FG .(2)连结CM ,若CM=1,则FG 的长为 .(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为.【答案】(1)证明见解析;(2)2,9.【解析】【分析】感知:利用同角的余角相等判断出∠BAF=∠CBE,即可得出结论;探究:(1)判断出PG=BC,同感知的方法判断出△PGF≌CBE,即可得出结论;(2)利用直角三角形的斜边的中线是斜边的一半,应用:借助感知得出结论和直角三角形斜边的中线是斜边的一半即可得出结论.【解答】感知:∵四边形ABCD是正方形,∴AB=BC,∠BCE=∠ABC=90°,∴∠ABE+∠CBE=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠BAF=∠CBE,在△ABF和△BCE中,{∠BAF=∠CBEAB=BC∠ABC=∠BCE=90°,∴△ABF≌△BCE(ASA);探究:(1)如图②,过点G作GP⊥BC于P,∵四边形ABCD是正方形,∴AB=BC,∠A=∠ABC=90°,∴四边形ABPG是矩形,∴PG=AB ,∴PG=BC ,同感知的方法得,∠PGF=∠CBE , 在△PGF 和△CBE 中, {∠PQF =∠CBEPQ =BC∠PFG =∠ECB =90° , ∴△PGF ≌△CBE (ASA ), ∴BE=FG ;(2)由(1)知,FG=BE , 连接CM ,∵∠BCE=90°,点M 是BE 的中点, ∴BE=2CM=2, ∴FG=2, 故答案为:2.应用:同探究(2)得,BE=2ME=2CM=6, ∴ME=3,同探究(1)得,CG=BE=6, ∵BE ⊥CG ,∴S 四边形CEGM =12CG×ME=12×6×3=9,故答案为:9.2.综合与实践:如图1,将一个等腰直角三角尺ABC 的顶点C 放置在直线l 上,∠ABC =90°,AB =BC ,过点A 作AD ⊥l 于点D ,过点B 作BE ⊥l 于点E . 观察发现:(1)如图1.当A ,B 两点均在直线l 的上方时, ①猜测线段AD ,CE 与BE 的数量关系,并说明理由; ②直接写出线段DC ,AD 与BE 的数量关系; 操作证明:(2)将等腰直角三角尺ABC 绕着点C 逆时针旋转至图2位置时,线段DC ,AD 与BE 又有怎样的数量关系,请写出你的猜想,并写出证明过程; 拓广探索:(3)将等腰直角三用尺ABC 绕着点C 继续旋转至图3位置时,AD 与BC 交于点H ,若CD =3,AD =9,请直接写出DH 的长度.【答案】(1)①AD+CE=BE.理由见解析;②DC+AD=2BE;(2)CD−AD=2BE;证明见解析;(3)DH的长度为32.【分析】(1)过点B作BF⊥AD,根据已知条件结合直角三角形性质证明ΔCBE≅ΔABF,从而得到四边形DEBF为正方形,最后得出①AD+CE=BE,直接写出②DC+AD=2BE(2)过点B作BG⊥AD,先证明ΔBCE≅ΔBAG,证明四边形DEBG为正方形,根据正方形的性质求解(3)过点B作BF⊥AD,证明ΔBAF≅ΔBCE,四边形DEBF为正方形,再求解.【解答】解:(1)①AD+CE=BE.理由如下:如图,过点B作BF⊥AD,交DA的延长线于点F,∵BE⊥l,BF⊥AD,∴∠BEC=∠F=90°.又∵AD⊥l∴∠FDE=90°∴四边形DEBF为矩形.∴∠FBE=90°.又∵∠ABC=90°,∴∠ABC−∠ABE=∠FBE−∠ABE.即∠CBE=∠ABF.在ΔCBE和ΔABF中,{∠CBE=∠ABF,∠CEB=∠AFB=90°,CB=AB,∴ΔCBE≅ΔABF(AAS).∴CE=AF,BE=BF.又∵四边形DEBF为矩形,∴四边形DEBF为正方形.∴BE=DE=FD=FB.∴AD+CE=AD+AF=FD=BE.②DC+AD=2BE.(2)如图,过点B作BG⊥AD,交AD延长线于点G,∵BE⊥l,BG⊥AD,∴∠BEC=∠G=90°.又∵AD⊥l,∴∠GDE=90°.∴四边形DEBF为矩形.∴∠GBE=90°.又∵∠ABC=90°,∴∠ABC−∠ABE=∠GBE−∠ABE,即∠CBE=∠ABG.在ΔBCE和ΔBAG中,{∠CBE=∠ABG,∠CEG=∠AGB=90°,CB=AB,∴ΔBCE≅ΔBAG(AAS).∴CE=AG,BE=BG.又∵四边形DEBG为矩形,∴四边形DEBG为正方形.∴DE=BE=GB=DG.∵CD=CE+DE,∴CD=AG+BE=AD+DG+BE=AD+2BE.∴CD−AD=2BE.(3)如图,过点B作BF⊥AD,交DA于点F,同理可证,ΔBAF≅ΔBCE,四边形DEBF为正方形.∴CE=AF,ED=BE=DF.∵CD=CE−ED,∴CD=AF−BE=AD−DF−BE=AD−2BE.∴AD−CD=2BE.∵CD=3,AD=9,∴BE=ED=3,CE=CD+ED=6.∵DH∥EB,∴DHEB =CDCE.∴DH3=36.∴DH=32.3.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.【答案】(1)AF=√2AE;(2)AF=√2AE,证明详见解析;(3)结论不变,AF=√2AE,理由详见解析.【分析】(1)如图①中,结论:AF=√2AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=√2AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=√2AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF 是等腰直角三角形即可.【解答】(1)如图①中,结论:AF=√2AE.理由:∵四边形ABFD是平行四边形,∴AB=DF,∵AB=AC,∴AC=DF,∵DE=EC,∴AE=EF,∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形,∴AF=√2AE.(2)如图②中,结论:AF=√2AE.理由:连接EF,DF交BC于K.∵四边形ABFD是平行四边形,∴AB∥DF,∴∠DKE=∠ABC=45°,∴EKF=180°﹣∠DKE=135°,∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE,∵∠DKC=∠C,∴DK=DC,∵DF=AB=AC,∴KF=AD,在△EKF和△EDA中,{EK=DK∠EKF=∠ADEKF=AD,∴△EKF≌△EDA,∴EF=EA,∠KEF=∠AED,∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=√2AE.(3)如图③中,结论不变,AF=√2AE.理由:连接EF,延长FD交AC于K.∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,∴∠EDF=∠ACE,∵DF=AB,AB=AC,∴DF=AC在△EDF和△ECA中,{DF=AC∠EDF=∠ACEDE=CE,∴△EDF≌△ECA,∴EF=EA,∠FED=∠AEC,∴∠FEA=∠DEC=90°,∴△AEF是等腰直角三角形,4.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.【答案】(1)PM=PN,PM⊥PN,理由见解析;(2)理由见解析;(3)PM=kPN;理由见解析【分析】(1)由等腰直角三角形的性质易证△ACE≌△BCD,由此可得AE=BD,再根据三角形中位线定理即可得到PM=PN,由平行线的性质可得PM⊥PN;(2)(1)中的结论仍旧成立,由(1)中的证明思路即可证明;(3)PM=kPN,由已知条件可证明△BCD∽△ACE,所以可得BD=kAE,因为点P、M、N分别为AD、AB、DE的中点,所以PM=BD,PN=AE,进而可证明PM=kPN.【解答】(1)PM=PN,PM⊥PN,理由如下:∵△ACB和△ECD是等腰直角三角形,∴AC=BC,EC=CD,∠ACB=∠ECD=90°.在△ACE和△BCD中,∴△ACE≌△BCD(SAS),∴AE=BD,∠EAC=∠CBD,∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,∴PM=BD,PN=AE,∴PM=PM,∵∠NPD=∠EAC,∠MPN=∠BDC,∠EAC+∠BDC=90°,∴∠MPA+∠NPC=90°,∴∠MPN=90°,即PM⊥PN;(2)∵△ACB和△ECD是等腰直角三角形,∴AC=BC,EC=CD,∠ACB=∠ECD=90°.∴∠ACB+∠BCE=∠ECD+∠BCE.∴∠ACE=∠BCD.∴△ACE≌△BCD.∴AE=BD,∠CAE=∠CBD.又∵∠AOC=∠BOE,∠CAE=∠CBD,∴∠BHO=∠ACO=90°.∵点P、M、N分别为AD、AB、DE的中点,∴PM=BD,PM∥BD;PN=AE,PN∥AE.∴PM=PN.∴∠MGE+∠BHA=180°.∴∠MGE=90°.∴∠MPN=90°.∴PM⊥PN.(3)PM=kPN∵△ACB和△ECD是直角三角形,∴∠ACB=∠ECD=90°.∴∠ACB+∠BCE=∠ECD+∠BCE.∴∠ACE=∠BCD.∵BC=kAC,CD=kCE,∴=k.∴△BCD∽△ACE.∴BD=kAE.∵点P、M、N分别为AD、AB、DE的中点,∴PM=BD,PN=AE.∴PM=kPN.5.如图,在△ABC中,∠ABC=90°,AB=BC,点E是直线BC上一点,连接AE,过点C作CF⊥AE于点F,连接BF.如图①,当点E在BC上时,易证AF﹣CF=√2BF(不需证明),点E在CB的延长线上,如图②:点E在BC的延长线上,如图③,线段AF,CF,BF之间又有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.【答案】证明AF=CF+√2BF.如图②中,结论:CF﹣AF=√2BF.理由见解析;②如图③中,结论:CF+AF=√2BF.理由见解析.【分析】如图①中,作BH⊥BF交AF于H.只要证明△BAH≌△BCF,即可解决问题.①如图②中,结论:CF-AF=√2BF.作BH⊥BF交AF于H.只要证明△BAH≌△BCF,即可解決问題.②如图③中,结论:CF+AF=√2BF,只要证明△BAH≌△BCF,即可解決问题.【解答】证明:如图①中,作BH⊥BF交AF于H.∵∠ABC=∠FBH,∴∠FBC=∠ABH,∵∠EFC=∠EBA=90°,∠CEF=∠AEB,∴∠ECF=∠EAB,在△BAH和△BCF中,,∴△BAH≌△BCF,∴AH=CF,BH=BF,∵∠FBH=90°,∴△BFH是等腰直角三角形,∴FH=BF,∵FH=AF﹣AH=AF﹣CF,∴AF﹣CF=BF,∴AF=CF+BF.①如图②中,结论:CF﹣AF=BF.理由:作BH⊥BF交AF于H.∵∠ABC=∠FBH,∴∠FBC=∠ABH,∵∠AFC=∠ABC=90°,∴∠CEF+∠FCB=90°,∠AEB+∠BAH=90°∴∠ECF=∠EAB,在△BAH和△BCF中,,∴△BAH≌△BCF,∴AH=CF,BH=BF,∵∠FBH=90°,∴△BFH是等腰直角三角形,∴FH=BF,∵FH=AH﹣AF=CF﹣AF,∴CF﹣AF=BF.②如图③中,结论:CF+AF=BF.理由:作BH⊥BF交AF于H.∵∠ABC=∠FBH,∴∠FBC=∠ABH,∵∠AFC=∠ABC=90°,∴∠BCF+∠BAF=180°,∵∠BAF+∠BAH=180°∴∠BCF=∠BAH,在△BAH和△BCF中,,∴△BAH≌△BCF,∴AH=CF,BH=BF,∵∠FBH=90°,∴△BFH是等腰直角三角形,∴FH=BF,∵FH=AH+AF=CF+AF,∴CF+AF=BF.。
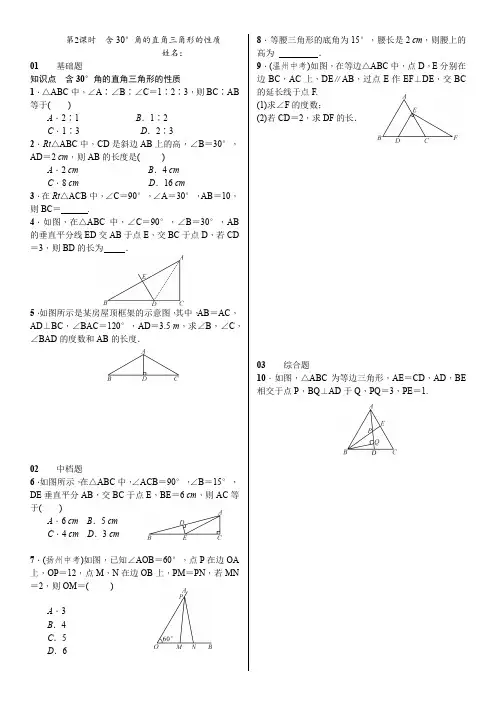
第2课时 含30°角的直角三角形的性质姓名:01 基础题知识点 含30°角的直角三角形的性质1.△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,则BC ∶AB 等于( )A .2∶1B .1∶2C .1∶3D .2∶32.Rt △ABC 中,CD 是斜边AB 上的高,∠B =30°,AD =2 cm ,则AB 的长度是( )A .2 cmB .4 cmC .8 cmD .16 cm 3.在Rt △ACB 中,∠C =90°,∠A =30°,AB =10,则BC = .4.如图,在△ABC 中,∠C =90°,∠B =30°,AB 的垂直平分线ED 交AB 于点E ,交BC 于点D ,若CD =3,则BD 的长为 .5.如图所示是某房屋顶框架的示意图,其中,AB =AC ,AD ⊥BC ,∠BAC =120°,AD =3.5 m ,求∠B ,∠C ,∠BAD 的度数和AB 的长度.02 中档题 6.如图所示,在△ABC 中,∠ACB =90°,∠B =15°,DE 垂直平分AB ,交BC 于点E ,BE =6 cm ,则AC 等于( )A .6 cmB .5 cmC .4 cmD .3 cm7.(扬州中考)如图,已知∠AOB =60°,点P 在边OA 上,OP =12,点M ,N 在边OB 上,PM =PN ,若MN =2,则OM =( )A .3B .4C .5D .68.等腰三角形的底角为15°,腰长是2 cm ,则腰上的高为 .9.(温州中考)如图,在等边△ABC 中,点D ,E 分别在边BC ,AC 上,DE ∥AB ,过点E 作EF ⊥DE ,交BC 的延长线于点F. (1)求∠F 的度数;(2)若CD =2,求DF 的长.03 综合题10.如图,△ABC 为等边三角形,AE =CD ,AD ,BE 相交于点P ,BQ ⊥AD 于Q ,PQ =3,PE =1.。
八上数学每日一练:直角三角形的性质练习题及答案_2020年解答题版答案解析答案解析答案解析答案解析2020年八上数学:图形的性质_三角形_直角三角形的性质练习题1.(2019双台子.八上期末) 如图,在△ABC 中,∠BAC =90°,AD ⊥BC 于点D ,BE 交AD 于点F ,交AC 于点E ,若BE平分∠ABC ,试判断△AEF 的形状,并说明理由.考点: 角的平分线;直角三角形的性质;等腰三角形的判定;2.(2019榆树.八上期末) 如图所示,一辆卡车装满货物后,高4m , 宽3m , 这辆卡车能通过横截面积如图(上方为半圆)的隧道吗?为什么?考点: 直角三角形的性质;勾股定理;3.(2018长春.八上期末) 已知直角三角形的斜边为2,周长为 ,求这个直角三角形的面积.考点: 直角三角形的性质;勾股定理;4.(2018长春.八上期末) 如图,在Rt △ABC 中,∠ABC =90°,AB =8,BC =6,点D 为AC 边上的动点,点D 从点C 出发,沿边CA 向点A运动,当运动到点A 时停止,若设点D 运动的时间为t 秒.点D 运动的速度为每秒1个单位长度.(1) 当t =2时,CD = , AD = ;(2) 求当t 为何值时,△CBD 是直角三角形,说明理由;(3) 求当t 为何值时,△CBD 是以BD 或CD 为底的等腰三角形?并说明理由.考点: 直角三角形的性质;等腰三角形的判定与性质;勾股定理;5.(2018云南.八上期末)如图,以等腰直角三角形ABC 的斜边AB 为边作等边,连接DC ,以DC 当边作等边、 E 在C 、D 的同侧,若 ,求BE 的长.考点:直角三角形的性质;全等三角形的判定与性质;等边三角形的性质;答案解析2020年八上数学:图形的性质_三角形_直角三角形的性质练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
1.2.2直角三角形的性质与判定练习题一、选择题1.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以到达该建筑物的最大高度是( )A.12米B.13米C.14米D.15米2.如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米.则小明到达的终止点与原出发点的距离是( )A.90米B.100米C.120米D.150米3.在长、宽、高分别为12 cm、4 cm、3 cm的木箱中,放一根木棒,能放进去的木棒的最大长度为( )A.5 cmB.12 cmC.13 cmD.153 cm4.如图,一个高1.5米,宽3.6米的大门,需要在相对的顶点间用一条木板加固,则这条木板的长度是( )A.3.8米B.3.9米C.4米D.4.4米5.如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是()A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤156.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刘搬来一架高2.5米的木梯,准备把拉花挂到2.4米高的墙上,则梯脚与墙角距离应为()A.0.7米B.0.8米C.0.9米D.1.0米7.一根旗杆在离地面12米处断裂,旗杆顶部落在离旗杆底部5米处.旗杆折断之前有米.A.23米B.15米C.25米D.22米8.如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是()尺.A.3.5 B.4 C.4.5 D.5二、填空题9.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200 m,结果他在水中实际游了520 m,该河流的宽度为__________m.10.如图,长方体的底面边长分别为2cm和4cm,高为5cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为________cm.11.如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长则不超过米。
(完整版)三角形的性质和判定练习题一、三角形的性质1. 三条边的关系- 三角形的任意两条边之和必须大于第三条边。
2. 三个角的关系- 三个角的和等于180度。
3. 顶角和底角的关系- 顶角和底角互补,其和等于180度。
4. 等腰三角形- 两边相等的三角形称为等腰三角形。
- 等腰三角形的顶角相等,底角相等。
5. 直角三角形- 有一个角等于90度的三角形称为直角三角形。
- 直角三角形的两条边相互垂直。
二、三角形的判定练题1. 判断下列三组边是否能构成三角形:- a) 3cm, 4cm, 9cm- b) 5cm, 7cm, 10cm- c) 6cm, 6cm, 10cm2. 判断下列三角形是何种三角形,并给出理由:- a) 6cm, 8cm, 10cm- b) 4cm, 4cm, 4cm- c) 5cm, 12cm, 13cm3. 判断下列三角形是否为直角三角形,并给出理由:- a) 3cm, 4cm, 5cm- b) 6cm, 8cm, 10cm- c) 7cm, 24cm, 25cm4. 如果一个三角形的两边长分别为7cm和10cm,那么第三边的可能长度有哪些?5. 如果一个三角形的三个角分别为30度、60度和90度,那么它的形状是什么?三、答案与解析1. 判断下列三组边是否能构成三角形:- a) 3cm, 4cm, 9cm* 不能构成三角形,因为任意两边之和小于第三边。
- b) 5cm, 7cm, 10cm* 可以构成三角形,因为任意两边之和大于第三边。
- c) 6cm, 6cm, 10cm* 可以构成三角形,因为任意两边之和大于第三边。
2. 判断下列三角形是何种三角形,并给出理由:- a) 6cm, 8cm, 10cm* 这是一个直角三角形,因为边长符合勾股定理的条件(8^2 + 6^2 = 10^2)。
- b) 4cm, 4cm, 4cm* 这是一个等边三角形,因为三条边都相等。
- c) 5cm, 12cm, 13cm* 这是一个直角三角形,因为边长符合勾股定理的条件(5^2 + 12^2 = 13^2)。
直角三角形练习题一、选择题1. 在直角三角形中,若直角边长分别为3和4,则斜边长为:A. 5B. 7C. 8D. 92. 直角三角形的两条直角边分别为6和8,其面积为:A. 24B. 30C. 48D. 603. 如果一个直角三角形的斜边长为10,一条直角边长为6,则另一条直角边长为:A. 4B. 8C. 14D. 无法确定4. 直角三角形的周长是60,斜边长为25,一条直角边长为15,则另一条直角边长为:A. 15B. 20C. 25D. 无法确定5. 一个直角三角形的两条直角边的比为1:2,如果斜边长为5,则较短的直角边长为:A. 1B. 2C. 5D. 10二、填空题6. 直角三角形的斜边长为13,如果一条直角边长为5,则另一条直角边长为________。
7. 直角三角形的面积公式为________,其中a和b分别为两条直角边长。
8. 如果直角三角形的两条直角边长分别为x和y,斜边长为z,则根据勾股定理,有________。
9. 直角三角形的内角和为________度。
10. 若直角三角形的两条直角边长分别为7和24,则其周长为________。
三、计算题11. 已知直角三角形的两条直角边长分别为9和12,求其面积和周长。
12. 一个直角三角形的斜边长为17,一条直角边长为8,求另一条直角边长。
13. 一个直角三角形的周长为40,斜边长为15,如果一条直角边长为11,求另一条直角边长。
14. 已知直角三角形的斜边长为20,一条直角边长为16,求其面积。
15. 一个直角三角形的两条直角边长分别为a和b,斜边长为c。
如果a:b=3:4,c=10,求a和b的具体数值。
四、解答题16. 一个直角三角形的斜边长为26,一条直角边长为10,求该三角形的高。
17. 一个直角三角形的两条直角边长分别为15和20,求该三角形的内切圆半径。
18. 一个直角三角形的两条直角边长分别为x和y,斜边长为z。
如果x+y+z=60,且x^2+y^2=z^2,求x,y和z的具体数值。
直角三角形的性质与判定练习题一、填空题1在Rt △ABC 中,∠C=90°,a=1,①∠A=30°,b=__,c=__. ②∠A=45°,b=__,c=__。
2.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米。
如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )A. 9分米B. 15分米C. 5分米D. 8分米 3.已知等边三角形的边长为2cm ,则它的高为,面积为。
4.△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( )A .42B .32C .42 或 32D .37 或 335.有一只小鸟在一棵高4m 的小树梢上捉虫子,它的伙伴在离该树12m ,高20m 的一棵大树的树梢上发出友好的叫声,它立刻以4m/s 的速度飞向大树树梢,那么这只小鸟至少秒才可能到达大树和伙伴在一起? 6.有一个角为30度的等腰三角形,若腰长为2,则腰上的高__________,三角形面积是________ 7.在△ABC 中,若a 2=b 2-c 2,则△ABC 是三角形,是直角;8.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为,此三角形的形状为。
9.在Rt △ABC 中,∠C=90°①若a=3,c=5,则b=___________;②若a=5,b=12,则c=___________; ③若c=25,b=7,则a=__________;④a=8,b=15,则c=。
10已知一个Rt △的两边长分别为3和4,则第三边长是11. 已知等腰三角形腰长是10,底边长是16,则这个等腰三角形面积为 。
12.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
13.如图,某会展中心在会展期间准备将高5m ,长13m,宽2m 的楼道上铺地毯,已知地毯每平方米18元,请你计算一下最少费用是多少?14.已知△ABC 的三边长分别为1,2,则△ABC 是三角形. 15.等腰三角形的腰长为10,底边上的高为6,则底边的长为. 16如图,小方格都是边长为1的正方形,则四边形ABCD 的周长是. 17.在直角三角形中,两锐角之比为2:1,则两锐角的度数分别为.18.如图,以Rt △ABC 的三边向外作正方形,其面积分别为1S ,2S ,3S 且14S =,28S =,则3S =;以Rt ∆ABC 的三边向外作等边三角形,其面积分别为1S ,2S ,3S , 则1S ,2S ,3S 三者之间的关系为.19.如图,△ABC 中,∠C =90°,点D 在BC 上,DE ⊥AB 于E ,且AE=EB ,DE=DC ,BAFEDCBA的度数为.20.如图,△ABC 中,∠C =90°,AC=BC ,AD 平分∠BAC ,BD =3.5,BC =6,则△ABC 的周长是.21.如图,在△ABC 中,∠A =90,BD 是角平分线,若AD =m ,BC =n ,则△BDC 的面积为.22. 如图,将一根长24cm 的筷子,置于底面直径为5cm ,高为12cm 的圆柱形茶杯中,设筷子露在杯子外面的长为acm (茶杯装满水),则a 的取值X 围是。
列举直角三角形有哪些性质?
1两个锐角:2含30度角3斜边上的中线4面积
测试题:
1.在直角三角形ABC中,∠ACB=90度,CD是AB边上中线,若CD=5cm,则AB=_____ 三角形ABC的面积=____________
2. 在直角三角形ABC中,∠ACB=90度,CD是AB边上中线,图中有__________等腰三
角形.
3.如图,在△ABC中,∠B=∠C,D、E分别是BC、AC的中点,AB=6,求DE的长。
4.已知:四边形ABCD中,∠ABC= ∠ADC=90度,E、F分别是AC、BD的中点。
求证:EF⊥BD
5.如图,在△ABC中,∠B= 2∠C,点D在BC 边上,且AD ⊥AC.
求证:CD=2AB
再练习:
1、在直角三角形ABC中,∠C=90°,∠BAC=30°,BC=10,则AB=________.
2、顶角为30度的等腰三角形,若腰长为2,则腰上的高__________,三角形面积是
________
3、等腰三角形顶角为120°,底边上的高为3,则腰长为_________
4、三角形ABC中,AB=AC=6,∠B=30°,则BC边上的高AD=_______________
5、Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线交AC于D,AB于E,
求证AD=2BC.
M
F
E D C B A
6、 已知:△ABC 中,AB=AC ,∠B=30°,AD ⊥AB ,
求证:2DC=BD
7.如图,△ABC 中,∠C=90°,∠A=60 °,EF 是AB 的垂直平分线,判断CE 与BE 之间的关系
1.在直角三角形中,有一个锐角为52度,那么另一个锐角度数为 ;
2、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.
3、在△ABC 中, ∠ACB=90 °,CE 是AB 边上的中线,那么与CE 相等的线段有_________,与∠A 相等的角有_________,若∠A=35°,那么∠ECB= _________.
4、已知:∠ABC=∠ADC=90度,E 是AC 中点。
求证:(1)ED=EB (2)图中有哪些等腰三角形?
5、如图,AB 、CD 交与点O,且BD=BO ,CA=CO ,E 、F 、M 分别是OD 、OA 、BC 的中点。
求证:ME=MF.
6、在等边三角形ABC 中,点D 、EF 分别在AB 、AC 边上,AD=CE ,CD 与BE 交与F, DG ⊥BE 。
求证:(1)BE=CD;(2)DF=2GF
C
B
A
E F C
B
A G E F D
C
B
A
D 2、如图所示,BD 、C
E 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点 求证:MN ⊥DE
4、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何?证明你的猜想。
练一练
1.△ABC 中,∠BAC=2
∠B ,AB=2AC ,AE 平分∠CAB 。
求证:AE=2CE 。
2.已知,Rt △ABC 中,∠ACB=90°,CD ⊥AB
,CE 为AB 边上的中线,且∠BCD=3∠DCA 。
求证:DE=DC 。
3.如图:AB=AC ,AD ⊥BC 于D ,AF=FD ,AE
∥BC 且交BF 的延长线于E ,若AD=9,BC=12,求BE 的长。
2.如图,ABC △中,90ACB =∠,AC BC =,CO 为中线.现将一直角三角板的直角顶点放在点O 上并绕点O 旋转,若三角板的两直角边分别交AC CB ,的延长线于点
G H ,.
(1)试写出图中除AC BC OA OB OC ===,外其他所有相等的线段; (2)请任选一组你写出的相等线段给予证明. 我选择证明 = .
证明:
3.如图,在△ABC
中,AB
=AC ,D 是BC 边上的一点,
DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,添加一个条件,使DE = DF ,并说明理由. 解: 需添加条件是 . 理由是:
4.将一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆放成如下右图的形式,使点B 、F 、C 、D 在同一条直线上. (1)求证:AB ED ⊥;
(2)若PB BC =,请找出图中与此条件有关的一对..全等三角形,并给予证明.
A
B
C D
H
G
D
B
D
5.已知:如图,△ABC 是边长3cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 方向匀速移动,它们的速度都是1cm/s ,当点P 到达点B 时,P 、Q 两
点停止运动.设点P 的运动时间为t (s ),解答下面的问题: 当t 为何值时,△PBQ 是直角三角形?
6.如图,P 是等边三角形ABC 内的一点,
连结PA PB PC ,,,以BP 为边作60PBQ ∠=,且BQ BP =,连结CQ .
(1)观察并猜想AP 与CQ 之间的大小关系,并证明你的结论.
(2)若::3:4:5PA PB PC =,连结PQ ,试判断PQC △的形状,并说明理由.
17、小明站在高为20米的楼上C 处,测得一条河边一点A 的俯角为30°,河对岸一点B
的俯角为15°,问河宽约多少米?
18、在△ABC 中,∠BAC=90°,AC=5cm ,AD 是高,AE 是斜边上的中线,且DC=2
1
AC ,求∠
B 的度数及AE 的长。
Q
C
P A
B
A B C
19、如图,在矩形ABCD 中,AB=8,BC=4,将矩形 对角线AC
求重叠部分△A FC 的面积.
22、如图,△ABC 中,AD 是高,CE 是中线,DC =BE ,DG ⊥CE 于G 。
(1)求证:G 是CE 的中点; (2)∠B =2∠BCE 。
23、如图,等腰梯形ABCD 中,AD ∥BC ,腰长为8cm ,AC 、BD 相交于O 点,且∠AOD =600,设E 、F 分别为CO 、AB 的中点,则EF = 。
B A 第 22
G E
D 题图 第7题图
F
E
O D C
B
A。