当前位置：文档之家 › 高考数学一轮总复习 第八章 第6节 直线与圆锥曲线的位置关系课件

高考数学一轮总复习 第八章 第6节 直线与圆锥曲线的位置关系课件

  • 格式：ppt
  • 大小：1.16 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

高中数学一轮复习课件：直线与圆锥曲线的位置关系

高中数学一轮复习课件：直线与圆锥曲线的位置关系

第十三页，编辑于星期日：二十三点 七分。
数学
高考总复习人教A版 ·(理)
由中点坐标公式得x1＋2 x2＝x，y1＋2 y2＝y， 即 x1＋x2＝2x，y1＋y2＝2y.⑤ 把④⑤代入到③中得 x＝－4y ∴直线方程为 x＋4y＝0，
由x42＋y2＝1， x＋4y＝0，
得 x2＝156.
∴x1＝－4
数学
高考总复习人教A版 ·(理)
变式迁移 1 抛物线 y＝ax2＋1 与直线 y＝x 相切，
则 a 等于
()
1 A.8
1 B.4
1 C.2
D．1
解法一：抛物线 y＝ax2＋1 与直线 y＝x 相切等价于 方程组yy＝ ＝axx2＋1， 有惟一实数解，即方程 ax2－x＋1 ＝0 有两等实根．∴判别式 Δ＝(－1)2－4a＝0，∴a＝14.
答案：D
第八模块 平面解析几何
第十一页，编辑于星期日：二十三点 七分。
数学
高考总复习人教A版 ·(理)
3．直线y＝kx－2与抛物线y2＝8x交于A、B不同两点，
且AB的中点横坐标为2，则k的值是__________．
解析：设 A(x1，y1)、B(x2，y2) 由yy＝2＝k8xx－，2， 消去 y 得 k2x2－4(k＋2)x＋4＝0， 由题意得
第八模块 平面解析几何
第五页，编辑于星期日：二十三点 七分。
数学
高考总复习人教A版 ·(理)
第八模块 平面解析几何
第六页，编辑于星期日：二十三点 七分。
数学
高考总复习人教A版 ·(理)
(1)将端点坐标代入方程：ax212＋by212＝1，ax222＋by222＝1. (2)两等式对应相减：ax212－ax222＋by212－by222＝0.

直线与圆锥曲线的位置关系 课件(62张)

直线与圆锥曲线的位置关系 课件(62张)
由直线 l 与双曲线交于不同的两点得
1-3 2 ≠ 0,
= (-6 2k)2 + 36(1-3 2 ) = 36(1- 2 ) > 0,
1
3
故 k2≠ 且 k 2<1.①
6 2k
-9
1-3
1-32
设 A(x1,y1),B(x2,y2),则 x1+x2=
2,x1x2=
.
由·>2 得 x1x2+y1y2>2.
直线与圆锥曲线的位置关系
目录
退出
1.直线与圆锥曲线位置关系的判断方法
(1)代数法,把圆锥曲线方程与直线方程联立消去 y,整理得出关于 x 的
方程 Ax2+Bx+C=0,若圆锥曲线是双曲线或是抛物线,当 A=0 时,表示直线与
双曲线的渐近线或抛物线的轴平行;当 A≠0 时,记该一元二次方程根的判
别式为 Δ.(ⅰ)若 Δ>0 时,直线与圆锥曲线相交;(ⅱ)若 Δ=0 时,直线与圆锥曲
截的线段的中点坐标时,设出直线和圆锥曲线的两个交点坐标,代入圆锥曲
线的方程并作差,从而求出直线的斜率,然后利用中点求出直线方程.“点差
法”的常见题型有:求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直
平分线问题.必须提醒的是“点差法”具有不等价性,即要考虑判别式 Δ 是否
为正数.
4.圆锥曲线的定值、最值、存在性问题很大一部分是利用等价转化思
B. -∞,-
2
2
∪
2
,+
2
∞
C.(-∞,-2 2)∪(2 2,+∞)
D.(-∞,- 2)∪( 2,+∞)
)
【答案】D
4

2015高考数学一轮总复习课件：8.8直线与圆锥曲线的位置关系

2015高考数学一轮总复习课件：8.8直线与圆锥曲线的位置关系
C．[－1，1]
B．[－2，2] D．[－4，4]
由位置关系求字母参数时，用代数法转化为 方程的根或不等式解集，也可以数形结合， 求出边界位置，再考虑其它情况．
第二十页，编辑于星期五：十二点 四十五分。
C 聚焦考向透析 考 向 二 根据直线与圆锥曲线的位置求参数
变式训练
2．(2014·沈阳模拟)若直线 y＝kx＋2 与
F（x，y）＝0，
第五页，编辑于星期五：十二点 四十五分。
C 基础知识梳理
基础知识系统化
(1)当 a≠0 时，设一元二次方程 ax2＋bx＋c＝0 的判别式为 Δ，则 Δ＞0⇔直线与圆锥曲线 C 相交； Δ＝0⇔直线与圆锥曲线 C 相切； Δ＜0⇔直线与圆锥曲线 C 相离．
(2)当 a＝0，b≠0 时，即得到一个一次方程，则直线 l 与圆锥曲线 C 相交，且只有一个交点， 此时，若 C 为双曲线，则直线 l 与双曲线的渐近线的位置关系是平行；若 C 为抛物线，则直 线 l 与抛物线的对称轴的位置关系是平行．
第十九页，编辑于星期五：十二点 四十五分。
C 聚焦考向透析
考 向 二 根据直线与圆锥曲线的位置求参数
例题精编
审题视点 典例精讲 类题通法 变式训练
(2014·合肥模拟)设抛物线 y2＝8x
的准线与 x 轴交于点 Q，若过点 Q 的直线 l 与
抛物线有公共点，则直线 l 的斜率的取值范围是
()
1 1 A.－2，2
10 x1x2＝－1－k2＞0，
直线与双曲线右支有两个不同交点，解得－ 315＜k＜－1.
第二十一页，编辑于星期五：十二点 四十五分。
C 聚焦考向透析
考 向 三 弦长问题
例题精编
x2 y2 过双曲线 3 － 6 ＝1 的右焦点 F2，倾

[精]高三第一轮复习全套课件8圆锥曲线方程：直线与圆锥曲线的位置关系共16页文档

[精]高三第一轮复习全套课件8圆锥曲线方程：直线与圆锥曲线的位置关系共16页文档
的方程为__x_2___y_2___1 _ 25 75
5.双曲线 x2 y2 1的左焦点F,P为双曲线在第
三象限内的任一点,则直线PF的斜率k的取值范围是
__k<__0_或__k>__1
3
6.过抛物线 y 2 4 x 的焦点,且倾斜角为 4 的直线
交抛物线于P,Q两点,则三角形OPQ的面积是
____2___2 ____
直线与双曲线的 渐进线平行
相交（一个交点）
得到一元二次方程 计算判别式
>0 =0 <0 相交 相切 相离
直线与抛物线 把直线方程代入抛物线方程
得到一元一次方程 得到一元二别式大于 0，相交 判别式等于 0，相切 判别式小于 0，相离
判断直线与曲线位置关系的操作程序 把直线方程代入曲线方程
例题一
已知椭圆C的一个顶点为A(0,-1),焦点在x轴 上,且其右焦点到直线x-y+2 2 =0的距离是3.
(1) 求椭圆C的方程.
(2) 试问能否找到一条斜率为k(k≠0)的直线l, 使得l与椭圆交于两个不同点M,N且使AM与AN 的长度相等,并指出k的取值范围.
x2 y2 1 3
-1<k<1(k≠0)时存在 满足条件的直线l
[精]高三第一轮复习全套课件8圆锥曲 线方程：直线与圆锥曲线的位置关系
服从真理，就能征服一切事物
【复习目标】
1.在计算直线与圆锥曲线相交弦长或弦中点等相 关问题时,能够运用一元二次方程根与系数的关 系简化运算,如在计算相交弦长可运用弦长公式
A B 1k2 x1x224x1x2 或
AB 1k12y1y224y1y2
不存在,说明理由.
0k2 或 2k4
6x2 2y2 1

高考数学(文科,大纲)一轮复习配套课件：8.4直线与圆锥曲线的位置关系

高考数学(文科,大纲)一轮复习配套课件：8.4直线与圆锥曲线的位置关系

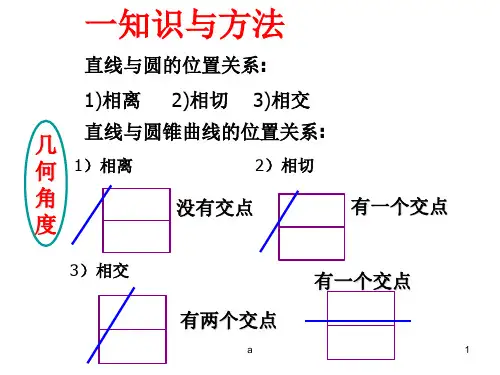
§8.4直线与圆锥曲线的位置关系本节目录知能演练轻松闯关考向瞭望把脉高考 考点探究讲练互动 教材回顾夯实双基基础梳理1.直线与圆锥曲线的位置关系：相交、相切、相离三种情况.一般通过它们的方程来研究:设直线Z： Ar+By + C=O,二次曲线C： /(x,刃=0.联立方程[Ax+By + C=Q组仁,)=0 '消却或谕到一个关于欢或刃的方程ax2+^x+c=0(或aj2+^j+c=0).⑴当G HO时,®A>0,则方程有两个不同的解，直线与圆锥曲线有两个公共点，直线与圆锥曲线相交；②A = O,则方程有两个相同的解，直线与圆锥曲线有一个公共点, 直线与圆锥曲线相切③AVO,则方程无解，直线与圆锥曲线无公共点，直线与圆锥曲线⑵当“=0时, 方程为一次方程，若心0,方程有一个解，直线与圆锥曲线2.弦长公式：设弦4B的端点坐标为（兀“丿1）,（兀2，丿2），直线有一个公共点，直线与圆锥曲线41交的斜率为匕则\AB I=^/（x2—Ji）2=y]l+k2\x2—x! I =-^ 1 + ! + X2)2 - 4x !X2 = J +齊1 + pV 01 + J2)2— 4J1J 2-思考探究直线与圆锥曲线只有一个公共点的几何意义是什么?有一个公共点时，它们是相切.对于耳E物线）直线与圆锥曲线只有一个公共点，它们可能是相切，也可能是相交.平行于双曲线的渐近线，平行于抛物线的对称轴的直线，它们分别与双曲线、抛物线只有一个公共点.提示：课前热身1.（教材改编）直线与双曲线*2_y —4没有公共点，贝狀的取值范围为（A. (-14)B. [-M1D. (—oo, —1] U [1, +oo) C・（一1,+oo）2.已知抛物线y2=lp X(p>^的经过焦点的弦的两端点坐标分别为A(x lf Ji), B(x2f y2)f贝!尸宁的值一定等于()A・ 4 B. -4答案：BC. p 2答案：B答案：D A. 4x —j —3=0C ・ 4x+j —5=01内的点为中点的弦所在直线的方程B. X—4y+3=0 D・ x+4y—5=0答案：34.已知抛物线*2=_12y的切线＜垂直于直线”+y=°，则'的方程为_________ -答案：y=x+35.过双曲线的右焦点作直线》，交双曲线于A、B两点，若14〃1 = 4,则这样的直线的条数为____________考点1直线与圆锥曲线的位置关系判断它们的位置关系或者利用它们的位置关系，方程的思想与数形结合思想要结合起来•答案：3越A 已知双曲线C：2x2-y2=2与点P(l，2),求过点P(l, 2)的直线2的斜率的取值范围，使2与C分别有一个交点，两个交点，没有交点.【思路分析】将直线方程与双曲线方程联立，组成方程组, 消去丿，利用一元二次方程根的判别式求解.【解】⑴当2垂直兀轴时，此时直线与双曲线相切•⑵当I不与X轴垂直时，设直线I的方程为y-2=k(x-l)代入双曲线C的方程中，并整理得(2—疋＞?+2伙2-2Qx-X+4氐一6=0, (*)当疋=2,即k=±^时，(*)为一次方程，显然只有一解; 当疋工2时，A=4(A:2—2k)2—4(2—k2)(—k2^r4k—6)=48—32k.3令A=0，可解得k=q；3令A>0，即48—32氐>0，此时衣〒考点2直线与圆锥曲线相交时的中点弦类型：（1）求中点弦所在直线方程问题；（2）求弦中点的轨迹方程问题；（3）弦长为定值时，弦的中点坐标问题，其解法有代点相减法，设而不求法，参数法，待定系数法及中心对称变换法等，最常用的是代点相减法和设而不求的方法.I：丿=兀+加对称，且吋2=—£，求实数加的值.【思路分析】【解】法一：如图所示，・・・4、B 两点关于直线Z 对称，:.AB 丄人 且4B 中点Mg ）,旳）在直线？上・ 可设仃亦y=—x+n 9J=—x + n,y=2x 2f .••兀1+ 兀2= —2* n 亠X 1X 2=—y 由兀 1兀2 =—得"=1・ _xi+x 2 乂 X Q —即点M 为（一£, |）,得 2x 2+x —n = 0, 由点M 在直线/上，得扌 + 3一2- 0 x1法二：TA、B两点在抛物线J=2X2±,Jji = 2xtr 2 -Jl-J2=2（X1+X2）（X1 —X2）•（J2 = 2X2，设AB中点M（x Of jo）,则XI+X2=2X0代入可得, 1 y\~yikAB =即M（_t，/«—£）,=4兀0・Xi~X2又AB丄Z, /. k^B =— 1，从而兀0=—彳即y = _x+/n_£,代入1 r_ 1 ,•••xi兀2=—一y"=—刁【思维总结］设参数，再消参数，可简化运算•:.AB的方程是歹一（加一玄）=跟踪训练1.在本例中，设AB 与2的交点为M,求过M 的弦的中点0的轨 迹方程.y=2?相交的弦所在直线『斜率一定存在.设卩与抛物线的交点为C 、D.C （X3,丿3），D （兀4’丿4），CD 的中点0为（兀‘丿）且兀3工兀4・ :.y3=2xj f ①y 4 = 2xt ②解：由以上解答可知, 当加=号时，M （—|）,过M 与抛物线「 V 4 4y —5 4j —5又•:k CD =k QM =—~^^^i A 4^+1=4X , 兀十4.•.j=4x 2+x+|®t 是点Q 的轨迹方程.kcD = 丿3一丁4=4x. ：• y 3—y 4 = 4x (x 3 —x 4),利用公式Ixi —x 2l = b 2—4ac \a\ 求得. 考点3直线与圆锥曲线相交时的弦长问题 求圆锥曲线的弦长问题的一般思路是：将直线方程代入圆锥曲 线方程，消去刃或兀）后，得到关于兀（或丿）的一元二次方程处彳+&r+c=O(或 ay 2+by+c=Q)9 再由弦长公式IAB^^/1+Plx! —X 2I= \/1+右1力一力1，求出其弦长.在求Ixi —对时，可直接线人j=x+2±, SAB//I.当ZABC=90。

高考数学总复习(一轮)(人教A)教学课件第八章 平面解析几何第8节 直线与圆锥曲线的位置关系

高考数学总复习(一轮)(人教A)教学课件第八章 平面解析几何第8节 直线与圆锥曲线的位置关系

P1F1P2F2的面积.

(2)解:由已知得


- = ,
2
2
解得 a =2,b =1,
+ = ,

2
所以双曲线方程为 -y =1.



根据(1)的结论直线 P1P2 的斜率为 ÷=,

所以直线 P1P2 的方程为 y-1=(x-2),即 x=3y-1,
判断直线与圆锥曲线的位置关系的方法
(1)代数法:直线与圆锥曲线方程联立,利用判别式求解;
(2)几何法:直线过定点时,若定点在圆锥曲线内部,则直线一定与
圆锥曲线相交;
若定点在圆锥曲线上,则直线与圆锥曲线相交或相切;
若定点在圆锥曲线外部,则直线与圆锥曲线相交、相切或相离.
[针对训练] 直线y=kx(k>0)与双曲线
+
等式两边同除以(x1+x2)(x1-x2),得
+
·
-
-




· =0,即 k1k2= .
(2)若双曲线的焦点分别为 F1(- ,0),F2( ,0) ,点P1 的坐标为

(2,1), 直 线 OM 的 斜 率 为 , 求 由 四 点 P1,F1,P2,F2 所 围 成 四 边 形


代入双曲线方程可解得 P2(- ,-),注意到 P1,P2 在直线 F1F2 的两侧,




所以四边形 P1F1P2F2 的面积为 |F1F2|·|y1-y2|= × =

.
解决圆锥曲线“中点弦”问题的思路
(1)根与系数的关系法:联立直线和圆锥曲线的方程得到方程组,消元

直线与圆锥曲线的位置关系总结归纳ppt课件

a283Fra bibliotek或k＜－
3 3 .(*)
25
设 A、B 两点的坐标是 A(x1，y1)，B(x2，y2)， 则 x1＋x2＝－1＋369k2，x1·x2＝1＋279k2.
由于以 AB 为直径的圆过原点，∴x1x2＋y1y2＝0， 即 x1x2＋(kx1＋2)(kx2＋2)＝0.
∴(1＋k2)x1x2＋2k(x1＋x2)＋4＝0， 即271(＋1＋9kk22)－17＋2k92k2＋4＝0，解得 k＝± 331，满足(*)式．
|AB|＝ 1＋k2|x1－x2|＝ (1＋k2)[(x1＋x2)2－4x1x2]
＝ 1＋k12|y1－y2|＝ (1＋k12)[(y1＋y2)2－4y1y2].
a
13
1.直线y=kx-k+1与椭圆 x2 y2 1 的位置关系为( A )
(A) 相交 (B) 相切 9 (C)4相离
(D) 不确定
的右焦点为
F，若过点
F
的直线
与双曲线的右支有且只有一个交点，则此直线斜率的取值范围
(
33 )A．(－ 3 ， 3 )
B．(－
3，
3)C.－
33，
33D．[－
3， 3]
x2 y2
又由双曲线方程12－ 4 ＝1，有双曲线的渐近线方程为
y＝±
33x，
∴有－ 33≤k≤ 33.
• 答案：C
a
15
• 【例1】 已知直线y＝(a＋1)x－1与曲线y2＝ax恰有一 个公共点，求实数a的值．
1
,
1 2
P A 2）若 P 是椭圆上的动点，求线段 中点 M . 的轨迹方程；
（3）过原点O 的直线交椭圆于点 B , C

2015高考数学(文)一轮总复习课件：8.8 直线与圆锥曲线的位置关系


化简得（ a2 ＋ b2 ） x2 ＋ 2a2cx ＋ a2 （ c2 － b2 ）＝ 0 ，则 x1 ＋ x2 ＝ a2（c2－b2） a2＋b2
－2a2c a2＋b2
， x1x2 ＝
.（4 分）
∵直线 AB 的斜率为 1， ∴|AB|＝ 2|x1－x2|＝ 2[（x1＋x2）2－4x1x2]，
5.（2013·银川质检）已知点 A（1，2）是抛物线 C：y2＝2px 与直线 l：y＝k（x ＋1）的一个交点，则抛物线 C 的焦点到直线 l 的距离是 2
解析：将点（1，2）代入 y2＝2px 中，可得 p＝2，即得抛物线 y2＝4x，其焦点 坐标为（1，0） ，将点（1，2）代入 y＝k（x＋1）中，可得 k＝1，即得直线 x |1－0＋1| －y＋1＝0，∴抛物线 C 的焦点到直线 l 的距离 d＝ ＝ 2 2
思路点拨： （1）求出点 P，Q 坐标，利用向量数量积求解.（2）分类讨论直线斜率 的情况，联立方程组利用根与系数的关系证明.
x2 规范解答： （1 ） 当 PQ⊥x 轴时， 将 x＝m 代入方程 ＋y2＝1， 得 Pm， 4 Qm，－ m2 1－ .（2 分） 4 m2 1－ ·m－2，－ 4 m2 1－ ＝ 4 m2 1－ ， 4
2× b2＝
（x1＋x2）2－4x1x2 ＝
15 87 15 ， ， 时， 可分别得|AB| 4 16 16
＝2，1，3，此时对应的直线 l 有 6 条.
题型2 ·圆锥曲线的弦长及弦中点问题
例 2（2013·南京模拟）已知椭圆的两个焦点分别为 F1（0，－2 2） ，F2 2 2 （0，2 2） ，离心率为 e＝ . 3 （1）求椭圆方程； （2）一条不与坐标轴平行的直线 l 与椭圆交于不同的两点 M，N，且线 1 段 MN 中点的横坐标为－ ，求直线 l 的倾斜角的取值范围. 2

2024届高考一轮复习数学课件(新教材人教A版)：两条直线的位置关系


√A.4
B.－4
C.1
D.－1
因为直线 2x＋my＋1＝0 与直线 3x＋6y－1＝0 平行，所以23＝m6 ≠－11， 解得 m＝4.
教材改编题
3.直线x－2y－3＝0关于x轴对称的直线方程为_x_＋__2_y_－__3_＝__0_.
直线 x－2y－3＝0 的斜率为 k＝12且与 x 轴交于点(3,0)， 故所求直线的斜率为－12，且过点(3,0)， 其方程为 y＝－12(x－3)， 即x＋2y－3＝0.
跟踪训练1 (1)(2023·襄阳模拟)设a，b，c分别为△ABC中角A，B，C所对
边的边长，则直线xsin A＋ay＋c＝0与bx－ysin B＋sin C＝0的位置关系是
A.相交但不垂直 C.平行
√B.垂直
D.重合
由题意可知，直线 xsin A＋ay＋c＝0 与 bx－ysin B＋sin C＝0 的斜率 分别为－sina A，sinb B， 又在△ABC 中，sina A＝sinb B， 所以－sina A·sinb B＝－1， 所以两条直线垂直.
(2)(2022·桂林模拟)已知直线l1：ax＋(a－1)y＋3＝0，l2：2x＋ay－1＝0，
若l1⊥l2，则实数a的值是
√A.0或－1
B.－1或1
C.－1
D.1
由题意可知l1⊥l2，故2a＋a(a－1)＝0， 解得a＝0或a＝－1，经验证，符合题意.
思维升华
判断两条直线位置关系的注意点 (1)斜率不存在的特殊情况. (2)可直接利用直线方程系数间的关系得出结论.
命题点1 点关于点的对称问题
例 3 直线 3x－2y＝0 关于点13，0对称的直线方程为
A.2x－3y＝0 C.x－y＝0

高考数学一轮复习直线与圆锥曲线的位置关系课件理


4．椭圆 ax2＋by2＝1 与直线 y＝1－x 交于 A、B 两点，若
过原点与线段 AB 中点的直线的倾斜角为 30°，则ab的值为( )
3
3
A. 4 B. 3
3 C. 2 D. 3
解析：设 AB 的中点为 M(x0，y0)，A(x1，y1)，B(x2, y2)，
由点差法得yx11－ －yx22＝－abxy00＝－1，
解析：方法 1：设以 Q 为中点的弦 AB 端点坐标为 A(x1， y1)，B(x2，y2)，则有 y12＝8x1，y22＝8x2，
两式相减，得(y1－y2)(y1＋y2)＝8(x1－x2)． 又 x1＋x2＝8，y1＋y2＝2， 则 k＝xy22－－xy11＝y1＋8 y2＝4，
∴所求直线 AB 的方程为 y－1＝4(x－4)， 即 4x－y－15＝0. 方法 2：设弦 AB 所在的直线方程为 y＝k(x－4)＋1，
由yy＝ 2＝k8xx－4＋1， 消去 x 整理，得 ky2－8y－32k＋8＝0. 设 A(x1，y1)，B(x2，y2)，
由韦达定理得 y1＋y2＝8k. 又∵Q 是 AB 中点，∴y1＋2 y2＝1，
∴8k＝2，∴k＝4. ∴弦 AB 所在直线方程为 4x－y－15＝0.
点评：有关弦中点轨迹、中点弦所在直线的方程，中点坐 标的问题，有时采用“平方差”法，可优化解题方法，简化运 算．
＝2 5m＋20.
(3)设线段 AB 中点坐标为(x，y)，则 x＝x1＋2 x2＝－2， y＝y1＋2 y2＝2x1＋2 x2＝－4. ∴AB 中点坐标为(－2，－4).
题型三 圆锥曲线的中点弦问题 例 3 过点 Q(4,1)作抛物线 y2＝8x 的弦 AB，恰被 Q 所平分， 求 AB 所在直线的方程．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八章 平面解析几何
第6节 直线与圆锥曲线的位置关系
1．掌握解决直线与椭圆、抛物线的位置关系的思想方 法．
2．了解圆锥曲线的简单应用． 3．理解数形结合的思想．
[要点梳理] 1．直线与圆锥曲线的位置关系的判定 (1)代数法：把圆锥曲线方程与直线方程联立消去y，整理 得到关于x的方程ax2＋bx＋c＝0.
(2)因为双曲线 C 与直线 l 相交于两个不同的点，故知方程 组ax22－y2＝1， 有两组不同的实数解，消去 y 并整理，得(1－
4．(2015·雅安模拟)已知斜率为 1 的直线过椭圆x42＋y2＝1 的右焦点交椭圆于 A，B 两点，则弦 AB 的长为______________．
[解析] 右焦点( 3，0)，直线 AB 的方程为 y＝x－ 3.
y＝x－ 3， 由x42＋y2＝1
得 5x2－8 3x＋8＝0.
设 A(x1，y1)，B(x2，y2)，则 x1＋x2＝853，x1x2＝85，
1＋k12 y1＋y22－4y1·y2.
[基础自测] 1．给出下列命题： ①直线l与椭圆C相切的充要条件是：直线l与椭圆C只有一 个公共点． ②直线l与双曲线C相切的充要条件是：直线l与双曲线C只 有一个公共点． ③直线l与抛物线C相切的充要条件是：直线l与抛物线C只 有一个公共点．
④如果直线 x＝ty＋a 与圆锥曲线相交于 A(x1，y1)，B(x2，
b]2＝1，
Δ＝4k2(2k－b)2＋4(1－k2)[(2k－b)2＋1]
＝4(1－k2)＋4(2k－b)2＝4(3k2－4bk＋b2＋1)
＝43k2－43bk＋49b2－b32＋1
＝43k－23b2－b32＋1， 不论 k 取何值，Δ≥0，则 1－b32≥0， 所以b32≤1，所以 b2≤3，则－ 3≤b≤ 3.故选 B. [答案] B
|AB|＝
1＋1285 32－4×85＝85.
[答案]
8 5
5. (2015·沈阳模拟)已知点 A(－ 2，0)，点 B( 2，0)，且动 点 P 满足|PA|－|PB|＝2，则动点 P 的轨迹与直线 y＝k(x－2)有 两个交点的充要条件为 k∈________.
[解析] 由已知得动点 P 的轨迹为一双曲线的右支且 2a＝ 2，c＝ 2，则 b＝ c2－a2＝1，
a＝0 a≠0
方程ax2＋bx＋c＝0的解 b＝0 无解(含l是双曲线的渐近线)
l与C1的交点 _无__公__共__点__
b≠0
Δ＞0 Δ＝0
有一解(含l与抛物线的对称轴平行 或与双曲线的渐近线平行) 两个不等的解 两个相等的解
_一__个__交__点__
_两__个__交__点__ _一__个__交__点__
C．3条
D．4条
[解析] 与抛物线相切有2条，与对称轴平行有1条，共3
条. 故选C.
[答案] C
3．若不论 k 为何值，直线 y＝k(x－2)＋b 与曲线 x2－y2＝1
总有公共点，则 b 的取值范围是( )
A．(－ 3， 3)
B．[－ 3， 3]
C．(－2,2)
D．[－2,2]
[解析] 把 y＝k(x－2)＋b 代入 x2－y2＝1 得 x2－[k(x－2)＋
t2y1－y22＋y1－y22＝ 1＋t2|y1－y2|.⑤错误，应是以 l 为垂直 平分线的线段 AB 所在的直线 l′与抛物线方程联立，消元后所 得一元二次方程的判别式 Δ＞0. 故选 C.
[答案] C
2．过点(0,1)作直线，使它与抛物线y2＝4x仅有一个公共
点，这样的直线有( )
A．1条
B．2条
y2)两点，则弦长|AB|＝ 1＋t2|y1－y2|. ⑤若抛物线 C 上存在关于直线 l 对称的两点，则需满足直
线 l 与抛物线 C 的方程联立消元得到的一元二次方程的判别式
Δ＞0.
其中正确的是( )
A．①②
B．②③
C．①④
D．①④⑤
[解析] ①正确，直线 l 与椭圆 C 只有一个公共点，则直 线 l 与椭圆 C 相切，反之亦成立．
②错误，因为直线 l 与双曲线 C 的渐近线平行时，也只有 一个公共点，是相交，但并不相切．
③错误，因为直线 l 与抛物线 C 的对称轴平行时，也只有 一个公共点，是相交，但不相切．
④正确，|AB|＝ x1－x22＋y1－y22，又 x1＝ty1＋a，x2＝ty2 ＋ a ， 所 以 |AB| ＝ [ty1＋a－ty2＋a]2＋y1－y22 ＝
∴P 点的轨迹方程为 x2－y2＝1(x＞0)，其一条渐近线方程 为 y＝x.若 P 点的轨迹与直线 y＝k(x－2)有两个交点，则需 k∈ (－∞，－1)∪(1，＋∞)．
[答案] (－∞，－1)∪(1，＋∞)
[典例透析]
考向一 根据直线与圆锥曲线的位置求参数
例 1 (1)(2015·合肥模拟)设抛物线 y2＝8x 的准线与 x 轴交
Δ＜0 无实数解
_无__交__点__
(2)几何法：在同一直角坐标系中画出圆锥曲线和直线，利 用图像和性质可判定直线与圆锥曲线的位置关系．
2．直线与圆锥曲线的相交弦长问题 设斜率为 k(k≠0)的直线 l 与圆锥曲线 C 相交于 A，B 两点， A(x1 ， y1) ， B(x2 ， y2) ， 则 |AB| ＝ 1＋k2 |x1 － x2| ＝ 1＋k2 x1＋x22－4x1·x2＝ 1＋k12|y1－y2|＝
思路点拨 (1)设直线 l 的方程，将其与抛物线方程联立， 利用 Δ≥0 解得．(2)联立方程组，利用 P、A、B 坐标之间的关 系，建立 a 的方程．
[解析] (1)由题意得 Q(－2,0)．设 l 的方程为 y＝k(x＋2)， 代入 y2＝8x 得 k2x2＋4(k2－2)x＋4k2＝0，
∴当 k＝0 时，直线 l 与抛物线恒有一个交点；当 k≠0 时， Δ＝16(k2－2)2－16k4≥0，即 k2≤1，∴－1≤k≤1，且 k≠0，综 上－1≤k≤1.故选 C.
于点 Q，若过点.－12，12 C．[－1,1]
B．[－2,2] D．[－4,4]
(2)已知双曲线 C：ax22－y2＝1(a＞0)与 l：x＋y＝1 相交于两 个不同的点 A、B，与 y 轴交于点 P，若P→A＝152P→B，则 a＝________.