高等数学 及其教学软件. 上册3版(;上海交通大学,集美大学编)思维导图

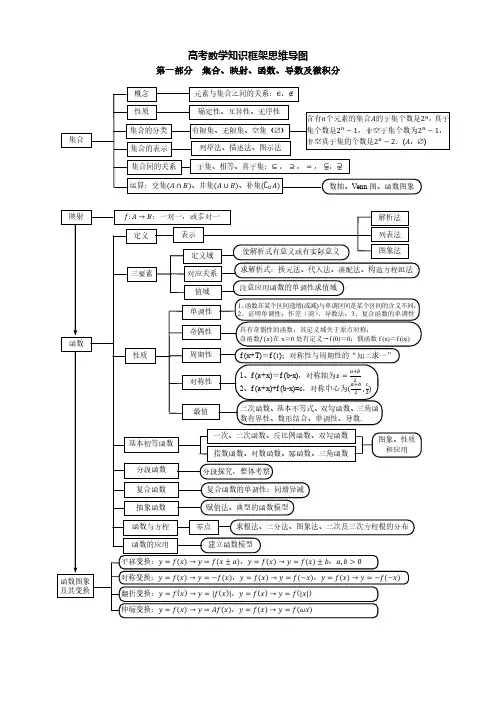
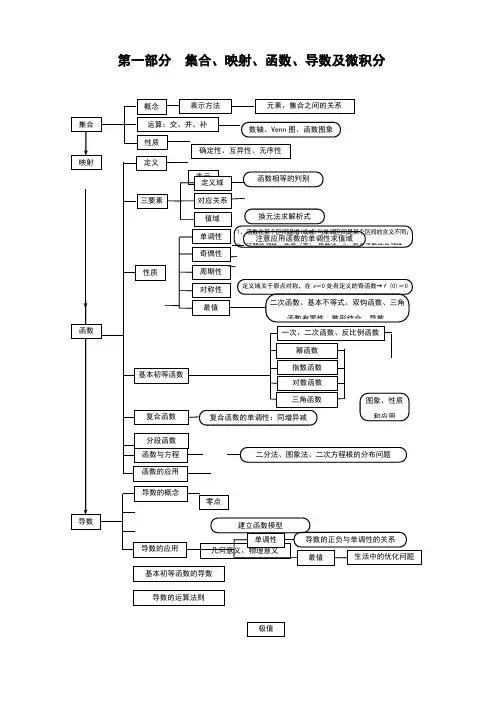
第一部分集合、映射、函数、导数及微积分第二部分 三角函数与平面向量对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x 轴的直线，对称中心是正余弦函数图象的零点，正切函数的对y ＝A sin(x ＋)＋①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②图象也可以用五点作图法；③用整体代换求单调区间（注意的符号）；2a →∥b →b →＝a → x 1y 2－x 2y 1=0 a →⊥b →b →·a →＝0x 1x 2＋y 1y 2=0b →在a →方向上的投影为|b →|cos ＝a →·b→设a →与b →夹角，则cos＝a →·b →——|a →|·|b →|第三部分数列与不等式＜0，或d＞r ＝0，或d＝r ＞0，或d＜r范围：(0，90]范围：[0，90]范围：[0，180]第六部分统计与概率P(A)＝1－P(A)第七部分其他部分内容等价关系否命题：若p则q逆命题：若q则p或：p q且：p q非：p高中数学各章内容必修1：第一章集合与函数概念；第二章基本初等函数(1)；第三章函数的应用必修2：第一章空间几何体；第二章点、直线、平面之间的位置关系；第三章直线与方程；第四章圆与方程必修3：第一章算法初步；第二章统计；第三章概率必修4：第一章三角函数；第二章平面向量；第三章三角恒等变换必修5：第一章解三角形；第二章数列；第三章不等式选修1-1：第一章常用逻辑用语；第二章圆锥曲线与方程；第三章导数及其应用选修1-2：第一章统计案例；第二章推理与证明；第三章数系的扩充与复数的引入4-4坐标系与参数方程：第一讲坐标系；第二讲参数方程请各位同学们将此资料保留到高三毕业。

高中数学知识点关联图谱与思维导图数学作为一门抽象的学科，往往给学生带来许多困惑和挑战。

为了更好地掌握高中数学知识，提高数学学习的效果，数学知识点关联图谱与思维导图成为了学生们经常使用的工具。

本文将介绍这两种工具的定义、特点以及如何使用它们来提升数学学习的效果。

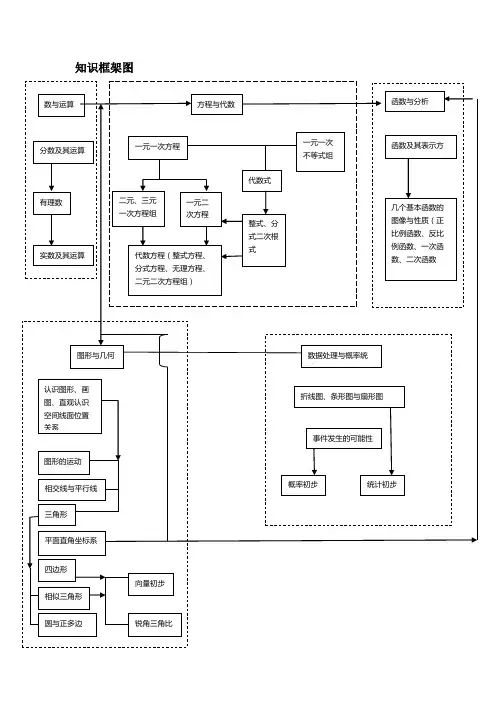
一、数学知识点关联图谱的定义和特点数学知识点关联图谱是将数学知识点之间的联系呈现在图形上的一种工具。

它可以清晰地展示数学知识点之间的逻辑关系、先后顺序以及各个知识点的核心概念。

数学知识点关联图谱的特点如下：1.整体性：数学知识点关联图谱能够将数学知识点的内容整合起来，呈现出一个整体的结构。

通过观察整体结构，学生可以快速了解数学知识的脉络和重点。

2.层次性：数学知识点关联图谱通常采用层级结构，将知识点按照一定的层次进行分类和归纳。

这样做可以帮助学生理清各个知识点之间的关系，避免知识之间的孤立和零散。

3.多样性：数学知识点关联图谱可以根据学生的需要和不同的主题进行定制。

学生可以根据自己的情况，绘制出适合自己的图谱，有助于更好地理解和记忆数学知识。

二、思维导图的定义和特点思维导图是一种以中心思考点为核心，通过分支展开的方式呈现思维的工具。

它可以帮助学生将零散的知识点整合成一个有机的结构，拓展学生的思维广度和深度。

思维导图的特点如下：1.自由性：思维导图的分支展开方式非常自由，学生可以根据自己的理解和记忆方式进行创造性的构建。

这种自由性可以激发学生的创造力和思维能力。

2.关联性：思维导图通过分支的方式将各个知识点进行关联，有助于学生理清知识之间的内在联系。

通过思维导图，学生可以更好地理解数学知识的逻辑和内涵。

3.可视性：思维导图以图形化的方式展示，具有很强的可视性。

学生通过观察思维导图，可以直观地捕捉到各个知识点的关系，提高学习的效果。

三、如何使用关联图谱和思维导图提升数学学习效果1.构建关联图谱：学生可以根据教材或者课堂笔记，将相关的数学知识点整合成一个关联图谱。

思维导图在中高职贯通《数学》课程教学中的应用发表时间：2014-11-12T10:12:05.013Z 来源：《职业技术教育》2014年第8期供稿作者：徐冰[导读] 从2010年起，上海市4所中等职业学校和3所高职院校首次试点中高职贯通培养模式。

徐冰（上海食品科技学校201599）摘要：思维导图是一种图像式思维的工具，也是一种利用图像式思考来表达思维的工具。

据权威统计：使用思维导图可以提高学习工作效率20%，在中高职贯通《数学》课程教学中引入思维导图，对教师能突破传统教学手段，革新教学设计、教学实施和教学评价，提高教学效果；对学生能调动学习的主动性和积极性，提高学习效率。

关键词：思维导图中高职贯通《数学》课程教学应用从2010年起，上海市4所中等职业学校和3所高职院校首次试点中高职贯通培养模式，意味着学生在完成3年中职阶段学习后可直接进入相关高职院校继续深造2年，获得高职毕业文凭。

至2014年，上海市的中高职贯通已扩大到56所职业院校。

《数学》课程作为五年制中高职贯通教育的一门文化基础公共必修课程，对于学生认识数学与自然界、数学与人类社会的关系，认识数学的科学价值、文化价值、应用价值、思维价值，提高提出问题、分析问题、解决问题的能力，形成理性思维具有基础性的作用，对于学生学习专业课程以及职业生涯的终身发展，具有十分重要的意义。

但在传统的课堂教学中，教师只是简单地、照本宣科地讲授知识，教育手段比较落后，加之本课程内容横跨初等数学和高等数学，尤其是高等数学内容复杂抽象，中高职贯通班学生知识基础普遍不理想等客观原因，教学效果始终困扰着教师，日积月累造成学生缺乏学习的积极性，学习过程中依然处于被动接受状态，参与性较弱，教学质量低下，短时间内也无法改变学生知识基础薄弱的现状。

因此，在教学过程中引进先进的教学方法就显得尤为重要，思维导图的引入，不仅有效地提高了课程的教学效果，也为中高职贯通班学生提供了一种高效的学习方法，提高了学习效率，为实现中职向高职顺利转段夯实基础，从教和学两方面提高了教学质量。