(完整)上海交通大学_2007-2008学年_高等数学(高数)_期末考试_解答

……………………………… 密 ……………………………… 封 ………………………………… 线 ………………………………安 徽 工 业 大 学 工 商 学 院 试 题 纸（一）2007 ~ 2008学年第二学期期末考试《 高等数学A2》试卷(A 卷)一、选择题(共4分×6)(将结果填入下表中: ) 1、函数),(y x f z =在),(y x 点有偏导数是它在该点连续的( ).(A)充分而非必要条件； （B ）必要而非充分条件；(C)充分必要条件； （D ）既非充分又非必要条件.2、设),2ln(),(xy x y x f += 则=)0,1(y f ( ）.(A) 21-； (B)21； (C) 0； (D) 1.3、函数3121x cx y -=(c 为任意常数)是微分方程222x dxy d -=的（ ).(A)解,但既非通解又非特解； (B)通解;(C)特解; (D)不是解.4、函数y x xy y x z 84222-+++-=的驻点是（ ）. （A ）(-1,3); （B ）(3,-1); （C ）(3, 1); （D ）(-1,-3).5、二阶线性非齐次方程xe x y y y )1(2-=+'-''的特解形式是（ ）.(A)x e b ax )(+; （B ）xe bx ax )(2+; (C)xe bx ax )(23+; （D ）xe bx ax )(3+.6、设级数∑∞=1)1(!3n nn nn 与级数∑∞=1)2(!2n nnnn , 则成立（ ）.(A)级数(1)、(2)均收敛; (B)级数(1)、(2)均发散.; (C)级数(1)收敛, 级数(2)发散; (D)级数(1)发散, 级数(2)收敛二、填空题(共4分×6)1、设),(v u f 有连续偏导数,且),(yxe ef z =, 则=dz __________________.2、级数∑∞=+1623n nnn 的和是__________.3、)(x f 在某区域内有连续导数, 若积分⎰+Ly dy x f xdx e ])([2与路径无关, 则.____________________)(=x f4、设一个二阶常系数线性齐次微分方程的特征方程有两个特征根,为-2和3,则此微分方程是________________________, 其通解为___________________________.5、设Ω是由光滑闭曲面∑围成的空间区域,其体积是V , 则沿∑内侧的曲面积分⎰⎰∑=-+-+-.______________)2()3()(dxdy y z dzdx x y dydz z x6、设平面上力j xy i y F 32+-=, 在力F 的作用下, 质点沿曲线L 运动, 则力F 所做的功用曲线积分表示为__________________________.三、解答题(共47分) 1、[5分]求曲面1232=+z xy 在点(1,-2,2)处的切平面与法线方程.2、[5分]计算积分: ⎰⎰ππydx xx dy sin 0.3、[5分]求微分方程满足初始条件的特解: ⎪⎩⎪⎨⎧==+1)0(y ey dx dy x .高数试卷A2(A 卷)（第1页）……………………………… 密……………………………… 封 ………………………………… 线 ………………………………安 徽 工 业 大 学 工 商 学 院 试 题 纸（二）4、[5分]用重积分算出半球体0,2222≥≤++z a z y x 的体积V .(用其它方法不给分)5、[5分]),(v u f 可微, 且32),(x x x f =, 422),(x x x x f u -=,求 ),(2x x f v .6、 [5分]设L 是圆周x y x 222=+的正向曲线,计算第二类曲线积分dy y xydx y x x I L⎰-+-=)()(3223. (注:163cossin204204πππ⎰⎰==xdx xdx )7、[6分]求幂级数∑∞=-1)3(n nnx 的收敛域(含端点讨论).8、[6分]求幂级数∑∞=-11n n nx 在(-1,1)上的和函数.9、[5分]设222),,(z y x z y x f ++= ，求函数在点M （1，1，0）沿方向)1,2,1(=l的方向导数lf ∂∂.四、[5分]计算二重积分：,)1ln(2dxdy y y x I D⎰⎰++=其中D 由x y 3-=，24x y -=，x = 1 所围成的闭区域.五、附加题 [6分]设微分分方程0)4(32='++''y ey y(1)若把x 看成未知函数，y 看成自变量，则方程化成什么形式； (2)求此方程的通解.高数试卷A2(A 卷)（第2页）。

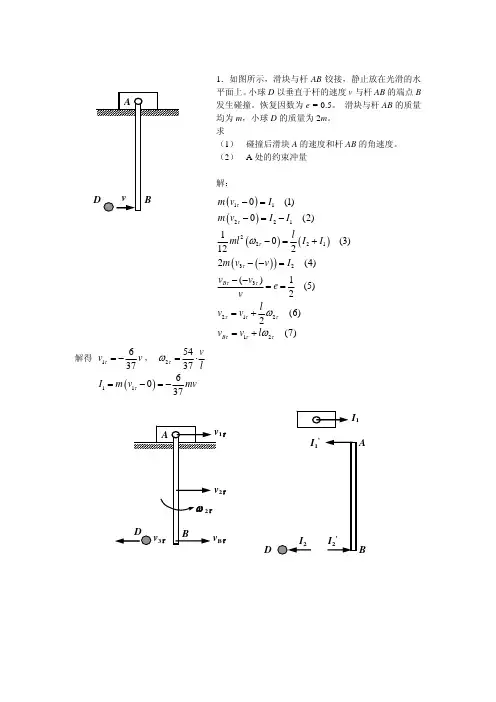
1．如图所示，滑块与杆AB 铰接，静止放在光滑的水平面上。

小球D 以垂直于杆的速度v 与杆AB 的端点B 发生碰撞。

恢复因数为e = 0.5。

滑块与杆AB 的质量均为m ，小球D 的质量为2m 。

求（1） 碰撞后滑块A 的速度和杆AB 的角速度。

（2） A 处的约束冲量 解：()()()()()()112212221323212120(1)0(2)10(3)1222(4)()1(5)2(6)2(7)B B m v I m v I I lml I I m v v I v v e v lv v v v l ττττττττττττωωω−=−=−−=+−−=−−===+=+ 解得 1637v v τ=−， 25437v lτω=⋅ ()116037I m v mv τ=−=−ABDI 1I 1’1τ2ττ2．如图所示，半径为r 的圆盘与匀质折杆OAB在B 处铰接，2OA AB r ==。

设圆盘的质量为m ，折杆OAB 的质量为2m ，图示位置AB 水平，BC水平。

用达朗贝尔原理求系统在图示位置无初速开始运动时折杆OAB 的角加速度和B 端作用于圆盘的约束力。

11113311,4242D x D y a l r a l r αααα====eCX CY B Cα+=+a a a a ，2eC r αα=a,12B =a得到1122,2CX CY a r a r r ααα==+**111123,2x D x y D y F ma mr F ma mr αα====()**212122,2x C x y F ma mr F m r r ααα===+222222222552052031221241233O ml ml l ml ml ml ml J m l mr ⎡⎤⎛⎞=+++=+===⎢⎥⎜⎟⎝⎠⎢⎥⎣⎦*2111203O M J mr αα==, *222212C M J mr αα==取系统为对象，对O 点取矩****1222232302x y r M M r r mg mg r +++−⋅−⋅=F F()221211220122324032mr mr r mr mr r r mgr ααααα++⋅++−= 即22125074032mr mr mgr αα+−= （1） 取圆盘为对象，对B 点取矩**220y M r mgr +−=F()22121202mr mr r r mgr ααα++−= 即22123202mr mr mgr αα+−= （2）得到： 212433g r αα=− （3）将（3）代入（1），解得：1536g r α=，21327grα= 取圆盘为对象*215218B x x F F mr mg α=−=−=−()*2125134********y F m r r m g g mg αα⎛⎞=+=+=⎜⎟⎝⎠*241135454B y y F mg F mg mg mg =−=−=*3． 凸轮机构在图示位置处于平衡。

第11章 级数1．写出下列级数的前5项：(1) 11(1)3n nn -∞=-∑；(2) 113(21)242n n n ∞=⨯-⨯∑；(3) 21(ln )nn n ∞=∑；(4) 1!n n n n ∞=∑ 解答：(1)23451111133333-+-+-； (2) 1131351357135792242462468246810••••••••••+++++••••••••••；(3) 2345611111(ln 2)(ln 3)(ln 4)(ln 5)(ln 6)+++++； (4)234511212312341234512345••••••••••+++++。

所属章节：第十一章第一节 难度：一级2．写出下列级数的通项：(1) 2341357++++；(2)2-+；(3)2242468x x ++++⨯⨯⨯⨯解答：(1) 21nn -； (2) 1(1)(1)n n n --+；(3)2242n xn•。

所属章节：第十一章第一节 难度：一级3．已知级数的部分和S n ，写出该级数，并求和：(1) 1n n S n+=；(2) 212n n n S -=；解答：(1) 一般项为111121u S +===，111,2,3,1(1)n n n n n u S S n n n n n -+-=-=-==--，故该级数为212(1)n n n∞=--∑，该级数的和为1lim lim 1n n n n S n →∞→∞+==；(2) 一般项为1112u S ==，11121211,2,3,222n n n n n n n n u S S n -----=-=-==，故该级数为112n n ∞=∑，该级数的和为21lim lim 12n n n n n S →∞→∞-== 。

所属章节：第十一章第一节难度：一级4．根据定义求出下列级数的和：(1) 1326n nnn ∞=+∑；(2) 11(2)n n n ∞=+∑；(3) 1(1)(2)(3)n nn n n ∞=+++∑；(4) 1n ∞=∑解答：(1) 111113211332()()1162321123nnn n n n n n ∞∞∞===+=+=+=--∑∑∑； (2) 1111111111113()(1)(2)222324354n n n n nn ∞∞===-=-+-+-+=++∑∑； (3) 111123111111[()]()()2(1)(2)(3)2122322334n n nn n n n n n∞∞===-+-⋅=-++⨯=++++++∑∑； (4)11n n∞∞==-=-∑∑1n ∞==∑1==-所属章节：第十一章第一节难度：一级5．证明下列级数发散： (1)121n nn ∞=+∑；(2) 12nn n ∞=∑；(3) 11nn n n ∞=⎛⎫⎪+⎝⎭∑；(4)111n nnn nn n +∞=⎛⎫+ ⎪⎝⎭∑解答：(1) 由于10212n n u n =→≠+，所以级数121n n n ∞=+∑发散；(2) 由于20nn u n =→+∞≠，所以级数12n n n∞=∑发散；(3) 由于1()01n n n u n e =→≠+，所以级数11nn n n ∞=⎛⎫⎪+⎝⎭∑发散； (4) 由于1111011(1)()(1)n n nn nn n n n nn n u n e n n n ++=≥=→≠+++，所以级数111n nn n n n n +∞=⎛⎫+ ⎪⎝⎭∑发散。

1. 利用定积分定义计算由直线y =x +1,直线x =a ，x =b （a<b ）及x 轴所围成的图形的面积. 解 因y =x +1在[a,b ]上连续,所以x +1在[a,b ]上可积,从而可特殊地将[a,b ]n 等分,并取,,()()1i i i b a b a b aa i x f a i n n nξξ---=+==++Δ, 于是111()[()1]1()(1)11()[(1)(1)()]2nni i i i ni b a b af x a i n nb a b a a i n n b a n a n b a n ξ===--=++-=-++=-+++-⋅∑∑∑Δ 故面积 2111(1)lim ()()(1)22nbi i an i b a S x x f x b a a b a n ξ→∞=-=+==-+++-∑⎰d Δ 1()(2)2b a a b =-++2. 利用定积分的几何意义求定积分： (1)102d x x ⎰;(2) 0ax ⎰（a ＞0）.解 (1)根据定然积分的几何意义知, 102d x x ⎰表示由直线y =2x ,x =0,x =1及x 轴所围的三角形的面积,而此三角形面积为1,所以12d x x ⎰=1.(2) 根据定积分的几何意义知,0ax ⎰表示由曲线0,y x x a ===及x 轴所围成的14圆的面积,而此14圆面积为214πa ,所以2014πx a =⎰.3. 根据定积分的性质，比较积分值的大小： (1)120d x x ⎰与130d x x ⎰； (2)1e d x x ⎰与1(1)d x x +⎰.解 (1)∵当[0,1]x ∈时,232(1)0x x x x -=-≥,即23x x ≥,又2x3x ,所以11230d d x x x x >⎰⎰.(2)令()1,()1e e x xf x x f x '=--=-,因01x ≤≤,所以()0f x '>, 从而()(0)0f x f ≥=,说明1e xx ≥+,又e x1+x .所以11(1)e d d xx x x >+⎰⎰.4. 估计下列各积分值的范围： (1)421(1)d x x +⎰；(2) arctan d x x ;(3)2e d ax ax --⎰（a ＞0)； (4)22e d xxx -⎰.解 (1)在区间[1,4]上,函数2()1f x x =+是增函数,故在[1,4]上的最大值(4)17M f ==,最小值(1)2m f ==,所以4212(41)(1)17(41)d x x -≤+≤-⎰, 即 4216(1)51d x x ≤+≤⎰.(2)令()arctan f x x x =,则2()arctan 1xf x x x '=++,当x ∈时,()0f x '>,从而()f x在上是增函数,从而f (x )在上的最大值M f ==,最小值πm f ==所以2arctan 93ππππd x x =≤≤= 即2arctan 93ππd x x x ≤≤.(3)令2()e x f x -=,则2()2e x f x x -'=-,令()0f x '=得驻点x =0,又(0)1f =，2()()ea f a f a -=-=,a >0时, 21ea -<,故()f x 在[-a,a ]上的最大值M =1,最小值2ea m -=,所以2222ee d aa x aa x a ---≤≤⎰.(4)令2()e xxf x -=,则2()(21)e xxf x x -'=-,令()0f x '=得驻点12x =,又(0)1,f = 1241(),(2)2e ef f -==,从而()f x 在[0,2]上的最大值2e M =,最小值14e m -=,所以 212242ee d e x x x --≤≤⎰,而2222ed e d x xx x x x --=-⎰⎰,故 21024222e ed ex xx ---≤≤-⎰.5. 设f (x )及g (x )在[a , b ]上连续, 证明:(1)若在[a , b ]上, f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0; (2)若在[a , b ]上, f (x )≥0, 且f (x )≢0, 则0)(>⎰ba dx x f ;(3)若在[a , b ]上, f (x )≤g (x ), 且⎰⎰=b a ba dx x g dx x f )()(, 则在[a ,b ]上f (x )≡g (x ).证明 (1)假如f (x )≢0, 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是0)(2)()()()()()(0>-≥≥++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd d c c a b a . 这与条件0)(=⎰ba dx x f 相矛盾. 因此在[a ,b ]上f (x )≡0.(2)证法一 因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是⎰⎰>-≥≥badcc d x f dx x f dx x f 0)(2)()()(0. 证法二 因为f (x )≥0, 所以0)(≥⎰ba dx x f . 假如0)(>⎰ba dx x f 不成立. 则只有0)(=⎰ba dx x f , 根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰ba dx x f .(3)令F (x )=g (x )-f (x ), 则在[a , b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba b a b a b a dx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).1. 求下列导数：(1) 20d d x t x ⎰; (2) 53ln 2d e d d x t t t x -⎰；(3) cos 2sin cos()d xxt t '⎡⎤π⎢⎥⎣⎦⎰; (4) 22dsin d d xtt xtπ⎰(x ＞0). 解220(1)()2d d x t x x'==⎰5353ln 2(2)d e d e d x tx t t x x --=⎰cos cos sin 222sin 00cos sin 220022222(3)cos()cos()cos()cos()cos()cos(cos )(cos )cos(sin )(sin )cos(cos )sin cos(sin )cos cos(sin )sin πd πd πd πd πd πππππx x xx xx t t t t t t t t t tx x x x x x x x x x ''⎡⎤⎡⎤=-⎣⎦⎣⎦''⎡⎤⎡⎤=-⎣⎦⎣⎦''=⋅-⋅=--=-⎰⎰⎰⎰⎰22cos(sin )cos (sin cos )cos(sin )ππx x x x x =-2222sin sin sin (4)cos sin sin cos .ππd d d d d d d d d d xx t t x t t xt x x x t x x x x x x x x x⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭--=-=⎰⎰2. 求下列极限：(1) 02arctan d limxx t t x→⎰; (2) 2030sin 3d lime d x xx tt t t t→-⎰⎰; (3)()22220e d lime d x t xx t t t t→⎰⎰.解 ()002200021arctan arctan arctan 11(1)limlim lim lim 222d d x xx x x x t t t t x x x x x →→→→'⎡⎤--⎣⎦+====-'⎰⎰2220030003300222200sin 3sin 3sin 32(2)lim lim lim 2sin 3sin 3lim lim 663d d e e d e d e e x x x x x x x t xt x xx x t t t t x x x t tt t x x x x-→→→--→→'⎡⎤⋅⎢⎥⎣⎦=='⎡⎤⎣⎦=⋅=⋅⋅=⎰⎰⎰⎰ ()()[]222222222222222200002000022000200022(3)lim lim lim lim 222lim lim lim 2122e d e d e d e e d e e e d e d e d e e e e xxx x t t t x tx x x x x x x t x t x t x x x x x x x t t t t x x t tt t t x x x x →→→→→→→'⎡⎤⋅⎢⎥⎣⎦==='⎡⎤⎣⎦'⎡⎤⎣⎦====+'+⋅⎰⎰⎰⎰⎰⎰⎰ 3. 求由方程e d cos d 0yxt t t t +=⎰⎰所确定的隐函数y =y (x )的导数.解 方程两边对x 求导数得:cos 0e y y x '⋅+=, cos e yxy '∴=-. 又由已知方程有000sin e y xtt +=,即1sin sin 00e y x -+-=即1sin e yx =-,于是有cos cos sin 1e yx xy x '=-=-.4. 当x 为何值时，I (x )=2e d xt t t -⎰有极值?解 2()e x I x x -'=,令()0I x '=得驻点0x =,又22()(12),(0)10e x I x x I -''''=-=>, 所以当x =0时,I (x )有极小值,且极小值为I (0)=0.5. 计算下列定积分：(1)3x ⎰; (2)221d x x x --⎰;(3)()d f x x π⎰,其中,0,2()sin ,2x x f x x x π⎧≤≤⎪⎪=⎨π⎪≤≤π;⎪⎩ (4){}222max 1,d x x -⎰.解433322233222(1)(43)(8333x x ⎛⎫==-=- ⎪⎝⎭⎰21222221101(2)()()()d d d d x x x x x x x x x x x x --=-+-+--⎰⎰⎰⎰012322332101111111116322332x x x x x x -⎛⎫⎛⎫⎛⎫=++=--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()22220022(3)()sin 1cos 82ππππππππd d d xf x x x x x x x =+=+=+-⎰⎰⎰(4)由于22221()max{1,}11112x x f x x x x x ⎧-≤<-⎪==-≤<⎨⎪≤≤⎩,于是 21121212223312122111120max{1,}333d d 1d d x x x x x x x x x x -------=++=++=⎰⎰⎰⎰6. 已知f (x )连续，且f (2)=3,求2222()d d lim(2)xt x f u u t x →⎡⎤⎢⎥⎣⎦-⎰⎰.解 []222222222222()()()()limlim lim lim(2)2(2)2(2)(2)x xt t x xx x x x t f u u t f u u f u u f u u x x x x →→→→''⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦===--''-⎡⎤-⎣⎦⎰⎰⎰⎰⎰⎰d d d d d d 22()113lim lim ()(2)2222x x f x f x f →→-==-=-=-.7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ;(2)⎰-=ππ0sin kxdx ;(3)⎰-=πππkxdx 2cos ;(4)⎰-=πππkxdx 2sin.证明 (1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2))(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k kk k x k k kxdx0cos 1cos 1=+-=ππk k k k .(3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx .8. 设k 及l 为正整数, 且k ≠l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ;(2)⎰-=ππ0cos cos lxdx kx ;(3)⎰-=ππ0sin sin lxdx kx .证明 (1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos 0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k .(2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos 0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k .(3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin .0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k .9. 设⎩⎨⎧∈∈=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论ϕ(x )在(0,2)内的连续性.解 当0≤x ≤1时, 302031)()(x dt t dt t f x xx===⎰⎰ϕ; 当1<x ≤2时, 6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x x xϕ.因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ.因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ,316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ,所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.10. 设⎪⎩⎪⎨⎧><≤≤=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.解 当x <0时, 00)()(0===⎰⎰xxdt dt t f x ϕ;当0≤x ≤π时, 21cos 21|cos 21sin 21)()(00+-=-===⎰⎰x t tdt dt t f x xxxϕ; 当x >π时, πππϕ00|cos 210sin 21)()(t dt tdt dt t f x x x-=+==⎰⎰⎰10cos 21cos 21=+-=π. 因此 ⎪⎩⎪⎨⎧≥≤≤-<=ππϕx x x x x 10 )cos 1(210 0)(.11. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0, ⎰-=xa dt t f ax x F )(1)(. 证明在(a , b )内有F '(x )≤0.证明 根据积分中值定理, 存在ξ∈[a , x ], 使))(()(a x f dt t f xa-=⎰ξ. 于是有)(1)()(1)(2x f ax dt t f a x x F xa-+--='⎰))(()(1)(12a x f a x x f a x ----=ξ)]()([1ξf x f ax --=. 由f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内,x -a >0, 所以在(a , b )内 0)]()([1)(≤--='ξf x f ax x F .。

1上海交通大学《高等数学》2006-2007 学年期末考试及答案一、 单项选择题 （每小题3分， 共 15分） 1. 设 xoy 平面上区域D ={(x , y )| x 2+y2≤1, y ≥ x }， D 1 是D 在第一象限的部分， 则∫∫(xy 3 +sin 2 x sin y )dxdy 等于 （ ）D（A ） 2 ∫∫ sin 2 x sin ydxdy ； D （C ） 4 ∫∫ (xy 3 + sin 2 x sin y )dxdy ；D 解 ∫∫(xy 3 + sin 2 x sin y )dxdyD= ∫∫ xy 3dxdy + ∫∫ sin 2x s in y dxdyD D= 2 ∫∫ sin 2x sin ydxdyD 答案： A（B ） 2 ∫∫ xy 3dxdy ；D （D ） 0 .2. 设 Ω ={(x , y , z ) | x 2+ y 2+ z2≤ 1}， 则三重积分∫∫∫e xdv = （ ）Ω（A ） ； （B ） π； （C ）； （D ） 2π .解 1 e xdv >dv = π， 排除答案 A 、 B ； 猜： C 或 De |x | : 1 → 2.718， 3π/ 4π = 1.125， 2π/ 4π= 1.52 3 3答案： D解 2 ∫∫∫ e xdv = ∫1 dx ∫∫ e xdydzΩ y 2 +z 2 ≤1−x 2= ∫1πe x (1 − x 2 )dx = 2π∫01e x (1 − x 2 )dx= −2π+4π∫01xe x dx= −2π+4πe − 4π(e − 1) = 2π答案： D解 3 ∫∫∫e xdv = ∫∫∫e zdv = ∫02πd θ∫0ππππd ϕ∫01eρcos ϕρ2sin ϕd ρΩ Ω= 2π∫0ππππd ϕ∫01eρcos ϕρ2sin ϕd ρD 1111π= 2π∫1d ρ[∫02 e ρcos ϕρ2 sin ϕd ϕ+∫ππππππππe −ρcos ϕρ2sin ϕd ϕ] 2= 2π∫01d ρ[ −ρe ρcos ϕ02 +ρe −ρcos ϕ|ϕϕ=ππππππππ] 2= 4π∫01ρ(e ρ − 1)d ρ= 2π答案： D3. 设 F = y i + zj + x k ,则 rot F = （ ）（A ）i + j + k ； （B ）−( i + j + k )； （C ）i − j + k ； （D ）−i + j − k .解 rot F = ∂ ∂ ∂( −1, −1, −1)答案： B4. 幂级数x n 在收敛域[ −1,1) 上的和函数s (x ) = （ ）（A ）ln(1 − x )； （B ）− ln(1 − x )； （C ）− ； （D ）−x ln(1 − x ) .解x n = xx n −1 = x ∫0x(x n −2 )dx= x ∫0x()dx = −x ln(1 − x )答案： D1,π 0 ≤ x <2≤ x ≤π展开成正弦级数， 其和函数s (x ) =b n sin nx ， 则s (−) =（A ） −1； （B ） −2；（C ） 1；（ ）（D ） 2 .解 s (− 9π) = s (−π) = −s (π) = − 1 + 3= −22 2 2 2 答案： B二、 填空题 （每小题3分， 共 15分） 6. 设 u = z +,则div (grad u ) = .∂x ∂y ∂zϕ=π5. 设函数f (x ) = 45 − x , π解 div (grad u ) = div (x , y,1)x 2 + y 2 x 2 + y 2x 2 + y 2 − x ⋅ x x 2 + y 2 − y ⋅y= ( x 2 + y 2 ) + ( x 2 + y 2 ) + 0y 2 + x 2 1= =7. 设 f (x ) 是连续函数，F (t ) = ∫∫∫ f (x 2 + y 2 + z 2 )dv ，F ′(t ) = .x 2 +y 2 +z 2 ≤t 2解 F (t ) = 2π⋅ 2 ⋅ ∫0tf (ρ2 )ρ2d ρ， F ′(t ) = 4πt 2 f (t 2)8. 设 C 为曲线x = e t cos t , y = e t sin t , z = e t 上对应于t 从0 变到2 的这段弧， 则曲线积分ds = .解 该积分 = ∫02dt= ∫02dt =(1 − e −2)9. 全微分方程(x +y − 1)dx +(e y +x )dy = 0 的通解为 .解 1 (x + y − 1)dx + (e y + x )dy = 0⇒ (x − 1)dx +(ydx +xdy )+e y dy = 0⇒ d () +d (xy )+d (e y ) = 0⇒ 通解：+xy +e y = C解 2 u = ∫(x + y − 1)dx + (e y + x )dy= ∫0x(x − 1)dx + ∫0y(e y+x )dy=+ xy +e y − 1⇒ 通解：+xy +e y − 1 = Cx 2 + y 2 x 2 + y 2(x 2 + y 2 ) x 2 + y 2 x 2 + y 210. 级数 的敛散性为 .解 un +1 == n + 1 = 1， 收敛u n n ! (2n + 1)(2n + 2) 2(2n )!三、计算下列各题 （第 1小题6分， 第2 小题8分, 共 14分） 11. 设 z 是方程x +y − z = e z所确定的x , y 的隐函数， 求∂2z解 ∂z = − 1 = 1 ∂z = − 1 =1 ∂x −1 − e z 1 + e z，∂y −1 − e z 1 +e z= () y = −= − = −12. 计算曲面z = y 2 − x 2 夹在圆柱面x 2 +y 2 = 1 和x 2 +y 2 = 9 之间部分 的面积.解 1 +2+ 2=， 则所求面积I = ∫∫dxdy1≤x 2 +y 2 ≤9 = ∫02πd θ∫13rdr= 2π⋅ (1 + 4r 2 ) |13 = (37 − 5)四、计算下列各题 （每小题 10分， 共30分）13. 计算曲线积分(x +e sin y )dy − (y − )dx ， 其中C 是位于第一象限中的直线x +y = 1 与位于第二象限中的圆弧x 2 +y 2 = 1 构成的曲线， 方向从A (1, 0) 经过B (0,1)， 再到C (−1, 0) .解 L ： y = 0， 方向从(−1, 0) 到(1, 0)， 并记C + L 所围区域为D ， 则所求曲线积分I = −∫C +L L= 2dxdy − ∫−1 2dx∂x ∂y .1 1π π2 214. 试求参数λ， 使当曲线C 落在区域D ={(x , y )| y > 0}时， 曲线积分(x 2 +y 2 )λdx −(x 2 +y 2 )λdy 与路径无关， 并求u (x , y ) = ∫(x 2 + y 2 )λdx −(x 2 + y 2 )λdy .解 记P =(x 2 + y 2)λ， Q = −(x 2 + y 2)λ， 则∂P2λxy 2 (x 2 + y 2)λ−1− x (x 2 + y 2)λ=∂Q 2x (x 2 + y2)λ+ 2λx 3 (x 2 + y 2)λ−1= −= ⇒ 2λxy 2 + x (x 2 + y 2 ) + 2λx 3 = 0⇒λ= −解 1 = ⇒ u =+ϕ(y )= −及 u (0,1) = 0 ⇒ u =− 1解 2 u (x , y ) = ∫dx −dy= ∫1y0dy + ∫0xdxx 2 + y 2y15. 求 ∫∫2xzdydz + yzdzdx − z 2dxdy ， 其中Σ 为Σz = 与 z = 所围立体表面的外侧.解 记Σ 所围立体为Ω， 则∫∫ 2xzdydz + yzdzdx − z 2dxdy = ∫∫∫ zdxdydzΣ Ω∂x y 2∂P ∂Q∂y ∂x ∂y y 2= − 1= + 1 − 1 == zdz dxdy +∫ 22 2zdz dxdyx 2 +y 2 ≤z 2 x 2 +y 2 ≤8 −z 2= ∫02z ⋅πz 2dz + 2z ⋅π(8 − z 2 )dz = 8π 五、（本题 10 分） 16. 将函数f (x ) =展开为x − 1 的幂级数.解 f (x ) =4x − 3 = 2 +12 1 1= ⋅ −3 1 +1 − (x − 1)= −n(x − 1)n −(x − 1)n=( −1)nn +1− 1 (x − 1)n， 0 < x < 2六、（本题8 分） 17. 设 f (x ) =(x − 1)n ， 求f (n ) (1) .解 f (x ) = (x − 1)nf (k ) (1) =， (k = 0,1, 2, )f (n ) (1) == e −1七、（本题8 分）18. 设 f (x ) 在(−1,1) 内具有三阶连续导数， 且f ′′′(0) ≠ 0， 证明： 级数∞ 1 1绝对收敛.(2x +1)(x − 2) 2x +1 x − 22 1 2(x − 1) +3 (x − 1) − 1 = + 证明 lim x →∑ {n [f ( ) − f ( − )] − 2f ′(0)}n =1 n n( )( ) = lim = > 0→ lim n f n 1 − f − n 1− 2f ' 0= f ''' 0 > 0f (x ) − f ( −x ) − 2xf '(0) f ′(x ) + f ′( −x ) − 2f '(0) f ′′(x ) − f ′′( −x ) ( ) ( )x →0 6 3( ) n →∞ 1 32故由级数收敛， 可知级数∞ 1 1n lim 3 x →0 xlim 2 ∑ {n [f ( ) − f ( − )] − 2f ′(0)}n =1 n n绝对收敛.x →0 3x limx →0 6x ===f ′′′ x + f ′′′ −x f ''' 0。

2007-2008学年第一学期2007级电气、电子、工程管理、机制、教技、土木工程、计算机、农机、网络工程、物理专业高等数学Ⅰ 试卷A 参考答案一、填空题(填对每空得2分，填错或不填每空得0分，计20分) 1．982442424++++x x x x ．2．3-e．3． 3 ． 4． 3 ． 5． （ 0 ，-1 ）． 6．21．7．0144=++y x ．8．51．9． 0 ． 10．14．二、选择题（选对每题得2分，不选、选错或多选每题得0分，计10分） 1．（ D ） 2．（ B ） 3．（ C ） 4．（ A ） 5．（ B ）三、计算题（每小题5分，计20分）1．解： xx x x x x x x sin )sin 21(1lim sin 2cos 1lim 200--=-→→…………………………2分xx xx sin sin 2lim 20→= …………………………………3分 x xx sin 2lim0→=..........................................4分 2=． (5)分2．解：应用洛必达法则得xxx xtd t t x xx 2arctan limarctan lim20-=∞-→∞-→⎰………………………3分x x a r c t a nlim 21∞-→-= ………………………4分 4)2(21ππ=-⨯-=. ………………………5分3．解： ⎰dx xx2sin ⎰-=x xd cot ……………………………………1分 ⎰+-=xdx x x cot cot ， …………………………2分 ⎰+-=dx x x x x sin cos cot ……………………………3分 ⎰+-=x d x x x s i n s i n1c o t ………………………4分c x x x ++-=|s i n |ln cot ．………………………5分4．解： ⎰-+1021xx dx ⎰+=20cos sin cos sin πtt tdt tx ……………………………1分⎰++=202)cos (sin )cos (sin cos πt t dt t t t (2)分⎰+++=202sin 112cos 2sin 21πdttt t……………………3分⎰⎪⎭⎫ ⎝⎛++=202sin 12cos 121πdt t t ………………………4分 4)2sin 1ln(212120ππ=⎥⎦⎤⎢⎣⎡++=t t ．………………5分四、解答题（每小题5分，计20分） 1．解：)sin ()cos 1(t t ad t ad dxdy --= (1)分ttcos 1sin -=． …………………………………………2分)sin (cos 1sin 22t t ad t t d dxy d -⎪⎭⎫ ⎝⎛-= ………………………………………3分)cos 1()cos 1(sin )cos 1(cos 22t a t t t t ----=……………………………4分23)cos 1(1)cos 1(1cos t a t a t --=--=． …………………5分 2．解： 方程两边同时微分得)()(y x e d xy d += ………………………1分即 )(dy dx e xdy ydx y x +=++ ……………………3分 整理得 ydx dx e dy e xdy y x y x -=-++， …………………4分 从而得 dx ex yedy yx yx ++--=．……………………………5分3．解：令u e x=可得u x ln =，代入已知式得 ……………………………1分 u u f ln )(='， c u u u udu +-=⎰ln ln …………………2分 从而有 0ln )(c u u u u f +-= ……………………………………3分 由0)1(=f 得 10=c ……………………………………………4分 因此 1ln )(+-=x x x x f ． ……………………………………5分4．解：设所求平面的法线向量为0),,(≠=C B A n ，两个已知平面的法线向量分别为)4,2,1(,)2,5,3(21-=-=n n， ……………………………………1分则有n n n n⊥⊥21, 即有 ⎩⎨⎧=+-=-+0420253C B A C B A ………………………2分得 A C A B 1611,87-=-=，0≠A ……………………………………3分 所以所求平面的方程为 0)3(161187)2(=+---z A Ay x A ，………4分整理得所求平面的方程为 065111416=---z y x ． …………………5分五、证明题（6分×2题＝12分） 1．证明：由题设有hx f h x f x f h )()(lim)(0000-+='→，所以…………………1分hx f h x f x f h x f hh x f h x f h h )]()5([)()3(lim)5()3(lim 00000000----+=--+→→……………2分⎥⎦⎤⎢⎣⎡----+=→h x f h x f h x f h x f h )()5()()3(lim 00000…………3分hx f h x f h x f h x f h h 5)()5(lim53)()3(lim3000000---+-+=→→……5分)(8)(5)(3000x f x f x f '='+'=． (6)分2．证：设x x x x f -++=)1ln()1()(，则0)0(=f ，………………………1分 又 )1l n ()(x x f +='． ……………………………………………2分 当0>x 时， 0)(>'x f ，函数单调增加， ……………………3分当01<<-x 时， 0)(<'x f ，函数单调减少．………………………4分 从而，当01≠<-x 时有0)(>x f ，且0)0(=f ， ………………………5分因此，当1->x 时，x x x ≥++)1ln()1(． ……………………………6分六、综合应用题（6分×3题＝18分）解：由⎩⎨⎧=+-=022y x x y 得两曲线交点为)4,2(),1,1(-， …………………1分1．图形面积为 ⎰--+=212)2(dx x x A …………………………3分 29312212132=⎥⎦⎤⎢⎣⎡-+=-x x x ， …………………6分2．图形绕x 轴旋转一周所得旋转体的体积为⎰--+=21222])()2[(dx x x V x π……………………………9分 57251)2(312153ππ=⎥⎦⎤⎢⎣⎡-+=-x x ……………………12分3．曲线2x y =交y 轴于点)0,0(，直线02=+-y x 与y 交于点)2,0( ……………………………13分图形绕y 轴旋转一周所得旋转体的体积为⎰⎰--=4422)2(dy y ydy V y ππ， (15)分 316)2(32423402πππ=--=y y ； ………………………18分。

精品文档.第11章级数1．写出下列级数的前5项：(1) 11(1)3n n n -∞=-∑；(2) 113(21)242n n n ∞=⨯-⨯∑L L ；(3) 21(ln )n n n ∞=∑；(4) 1!n n n n∞=∑解答：(1)23451111133333-+-+-L ；(2)1131351357135792242462468246810••••••••••+++++••••••••••L ；(3) 2345611111(ln 2)(ln 3)(ln 4)(ln 5)(ln 6)+++++L ；(4) 234511212312341234512345••••••••••+++++L 。

所属章节：第十一章第一节难度：一级2．写出下列级数的通项：(1) 2341357++++L ；(2) 251017261220-+-+L ；(3) 22242462468x x x x x ++++⨯⨯⨯⨯⨯⨯L 解答：(1) 21n n -；(2) 211(1)(1)n n n n -+-+；(3)2242nx n•L 。

所属章节：第十一章第一节难度：一级3．已知级数的部分和S n ，写出该级数，并求和：(1) 1n n S n +=；(2) 212n n n S -=；解答：(1) 一般项为111121u S +===，111,2,3,1(1)n n n n n u S S n nn n n -+-=-=-==--L ，故该级数为212(1)n n n∞=--∑，该级数的和为1lim lim 1n n n n S n →∞→∞+==；(2) 一般项为1112u S ==，11121211,2,3,222nn n n n n n n u S S n -----=-=-==L ，故该级数为112n n ∞=∑，该级数的和为21lim lim 12nn nn n S →∞→∞-== 。

所属章节：第十一章第一节难度：一级4．根据定义求出下列级数的和：．根据定义求出下列级数的和：(1)1326nnn n ∞=+∑；(2)11(2)n n n ∞=+∑；(3)1(1)(2)(3)n n n n n ∞=+++∑；(4) 1(221)n n n n ∞=+-++∑解答：(1) 111113211332()()1162321123n nnnnn n n ∞∞∞===+=+=+=--∑∑∑；(2) 1111111111113()(1)(2)222324354n n n n n n ∞∞===-=-+-+-+=++∑∑L ； (3)111123111111[()]()()2(1)(2)(3)2122322334n n nn n n n n n ∞∞===-+-⋅=-++⨯=++++++∑∑；(4)11(221)[(21)(1)]n n n n n n n n n ∞∞==+-++=+-+-+-∑∑111()211n n n n n ∞==-+++++∑11221=-=-+ 所属章节：第十一章第一节难度：一级5．证明下列级数发散：．证明下列级数发散：(1) 121n n n ∞=+∑；(2) 12nn n ∞=∑；(3) 11nn n n ∞=⎛⎫ ⎪+⎝⎭∑；(4) 111n nn n nn n +∞=⎛⎫+ ⎪⎝⎭∑解答：(1) 由于1212nnu n =→≠+，所以级数121n nn ∞=+∑发散；发散；(2) 由于20nn u n =→+∞≠，所以级数12nn n∞=∑发散；发散；(3) 由于1()01n n n u n e =→≠+，所以级数11nn n n ∞=⎛⎫ ⎪+⎝⎭∑发散；发散； (4) 由于1111011(1)()(1)n n nnnn n nn nn nu n en n n ++=≥=→≠+++，所以级数111n nnn nn n +∞=⎛⎫+ ⎪⎝⎭∑发散。

武汉大学数学与统计学院2007—2008第一学期《高等数学B 》期末考试试题（180学时）一、（87'⨯）试解下列各题：1、计算n →∞2、计算0ln(1)lim cos 1x x xx →+--3、计算arctan d x x x ⎰4、 计算4x ⎰5、计算d x xe x +∞-⎰6、设曲线方程为sin cos 2x t y t=⎧⎨=⎩，求此曲线在点4t π=处的切线方程。

7、已知2200d cos d y x te t t t =⎰⎰，求x y d d8、设11x y x-=+，求()n y二、（15分）已知函数32(1)x y x =-求： 1、函数)(x f 的单调增加、单调减少区间，极大、极小值；2、函数图形的凸性区间、拐点、渐近线 。

三、（10分）设()g x 是[1,2]上的连续函数，0()()d x f x g t t =⎰1、用定义证明()f x 在(1,2)内可导；2、证明()f x 在1x =处右连续；四、（10分）1、设平面图形A 由抛物线2y x = ，直线8x =及x 轴所围成，求平面图形A 绕x轴旋转一周所形成的立体体积； 2、在抛物线2(08)y x x =≤≤上求一点，使得过此点所作切线与直线8x =及x 轴所围图形面积最大。

五、（9分）当0x ≥，对()f x 在[0,]b 上应用拉格朗日中值定理有： ()(0)()(0,)f b f f bb ξξ'-=∈对于函数()arcsin f x x =，求极限0lim b bξ→武汉大学数学与统计学院 B 卷2007—2008第一学期《高等数学B 》期末考试试题一、（86'⨯）试解下列各题：1、计算30arctan lim ln(12)x x x x →-+2、计算120ln(1)d (2)x x x +-⎰ 3、计算积分：21arctanxd x x +∞⎰ 4、已知两曲线()y f x =与1x yxy e++=所确定，在点(0,0)处的切线相同，写出此切线方程，并求极限2lim ()n nf n→∞5、设，2221cos cos t x t udu y t t ⎧=⎪⎨=-⎪⎩，试求：d d y x，22d |d t y x 的值。