常见晶体配位数等资料讲解

物质结构与性质高考热点归纳配位数的确定一、各种典型配合物中配位数的判断1．配位数可以等同于中心离子(或原子)与配位原子形成的配位键键数，也可以等同于配位体的数目。

如[Ag(NH3)2]NO3、[Ag(CN)2]－、[Cu(NH3)4]SO4、[Cu(H2O)4]2＋、[Zn(NH3)4]2＋、[Zn(CN)4]2－、K3[Fe(SCN)6]、[Fe(CN)6]3－、[FeF6]3－等配合物或配离子中的中心离子与配位体的数目以及配位原子形成的配位键键数均相等，其中Ag＋离子的配位数为2，Cu2＋离子与Zn2＋离子的配位数均为4，Fe3＋离子的配位数为6。

一般规律：一般配合物的配位数可以按中心离子电荷数的二倍来计算。

又如Ni(CO)4、Fe(CO)5、Cr(CO)6等羰基化合物中Ni、Fe、Cr原子的配位数分别为4、5、6。

[Co(NH3)4(H2O)2]Cl2、[CrCl(H2O)5]Cl2中Co2＋离子与Cr3＋离子的配位数均为6。

说明：羰基化合物中的中心原子呈电中性，此类配合物的配位数由化学式直接判断。

Co2＋离子与Cr3＋离子的电荷数分别为2、3，但配位数都是6。

所以，配合物的配位数不一定按中心离子(或原子)的电荷数判断。

2．当中心离子(或原子)与多基配体配合时，配位数可以等同于配位原子的数目，但不是配位体的数目。

如[Cu(EN)2]中的EN是乙二胺(NH2CH2CH2NH2)的简写，属于双基配体，每个乙二胺分子有2个N原子与Cu2＋离子配位，故Cu2＋离子的配位数是4而不是2。

3．当中心离子(或原子)同时以共价键与配位键结合时，配位数不等于配位键的键数。

如[BF4]－、[B(OH)4]－、[AlCl4]－、[Al(OH)4]－等配离子中，B、Al原子均缺电子，它们形成的化学键，既有共价键，又有配位键，配位数与配位键的键数不相等，配位数均为4。

又如Al2Cl6(如下左图所示)中Al原子的配位数为4。

配合物或晶体中配位数的判断配合物或晶体中一个微粒周围最近邻的微粒数称为配位数。

配位数这个概念存在于配位化学和晶体学中，定义有所不同。

配合物中的配位数是指直接同中心离子(或原子)配位的原子数目。

晶体学中的配位数是指晶体中一个原子周围与其等距离的最近邻的原子数目。

离子晶体中的配位数是指一个离子周围最近的异电性离子数目。

高中阶段判断配合物或晶体中配位数的方法可作如下小结。

一、各种典型配合物中配位数的判断1．配位数可以等同于中心离子(或原子)与配位原子形成的配位键键数，也可以等同于配位体的数目。

如[Ag(NH3)2]NO3、[Ag(CN)2]-、[Cu(NH3)4]SO4、[Cu(H2O)4]2+、[Zn(NH3)4]2+、[Zn(CN)4]2-、K3[Fe(SCN)6]、[Fe(CN)6]3-、[FeF6]3-等配合物或配离子中的中心离子与配位体的数目以及配位原子形成的配位键键数均相等，其中Ag+离子的配位数为2，Cu2+离子与Zn2+离子的配位数均为4，Fe3+离子的配位数为6。

一般规律：一般配合物的配位数可以按中心离子电荷数的二倍来计算。

又如Ni(CO)4、Fe(CO)5、Cr(CO)6等羰基化合物中Ni、Fe 、Cr原子的配位数分别为4、5、6。

[Co(NH3)4(H2O)2]Cl2、[CrCl(H2O)5]Cl2中Co2+离子与Cr3+离子的配位数均为6。

说明：羰基化合物中的中心原子呈电中性，此类配合物的配位数由化学式直接判断。

Co2+离子与Cr3+离子的电荷数分别为2、3，但配位数都是6。

所以，配合物的配位数不一定按中心离子(或原子)的电荷数判断。

2．当中心离子(或原子)与多基配体配合时，配位数可以等同于配位原子的数目，但不是配位体的数目。

如[Cu(en)2]中的en是乙二胺(NH2CH2CH2NH2)的简写，属于双基配体，每个乙二胺分子有2个N 原子与Cu2+离子配位，故Cu2+离子的配位数是4而不是2。

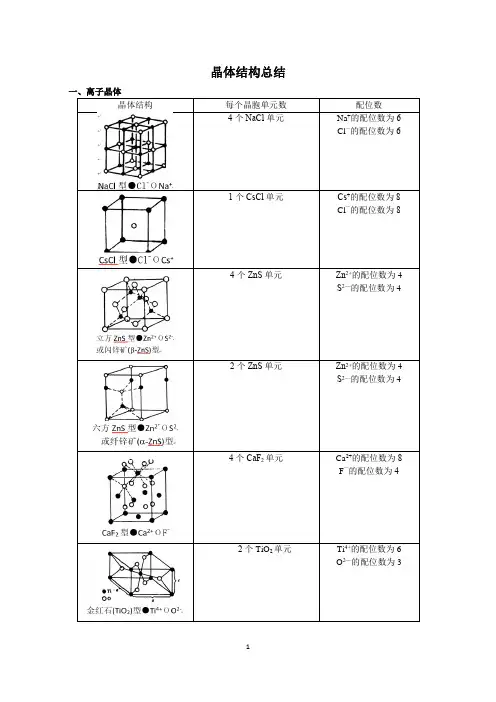
晶体结构总结一、离子晶体晶体结构离子晶体的结构类型的制约因素主要是离子的电荷比（决定数量比）和半径大小比（决定配位数），离子的电子组态在一定程度上也会影响它的晶体结构，这三个性质综合起来还会决定离子键的共价性成分，后者过分强烈时，将使离子晶体转变为原子晶体，其间存在离子晶体到原子晶体的过渡型。

离子半径比r+－与配位数和晶体构型的关系堆积方式体心立方堆积面心立方最密堆积六方最密堆积三、原子晶体1.金刚石、晶体硅的结构：金刚石的晶体结构如下图所示，每个碳原子以sp3杂化与相邻的4个碳原子形成4个共价键，把晶体内所有的C原子连结成一个整体，形成空间网状结构，这种结构使金刚石具有很大的硬度和熔沸点。

由金刚石晶胞得，在一个金刚石晶胞中，含有8个C原子。

晶体硅具有金刚石型的结构。

只需将金刚石中的C原子换成Si原子，即得到硅的结构。

2.SiO2的结构:在每个Si—Si键中插入1个O原子，即得到SiO2的晶体结构，如下图所示，每个Si原子与4个氧原子形成1个Si—O四面体，Si原子配位数为4，O原子配位数为2.四、分子晶体水凝结变成冰，冰晶体中，H2O分子之间存在范德华力和氢键，其晶体结构如下图所示：CO2晶体俗称干冰，CO2分子之间通过范德华力结合，其晶胞如下图所示：注意：在干冰晶体结构中，每个CO2分子周围与之最近且等距离CO2分子的个数有12个。

五、混合型晶体混合型晶体又称过渡型晶体，石墨是典型的混合型晶体。

晶体的微粒之间存在两种或两种以上的作用力，这样的晶体就是混合型晶体。

石墨是层状结构，C原子采用sp2杂化轨道，与相邻的三个C原子以σ键相连结。

每个C原子周围形成三个σ键，键角120°。

每个C原子还有一个2p轨道，其中有一个2p电子。

这些2p 轨道都垂直于sp2杂化轨道的平面，因此互相平行，形成了大π键。

大π键中的电子沿层面方向的活动能力很强，与金属中的自由电子具有相似之处，所以石墨具有金属光泽，并具有良好的导电和导热性。

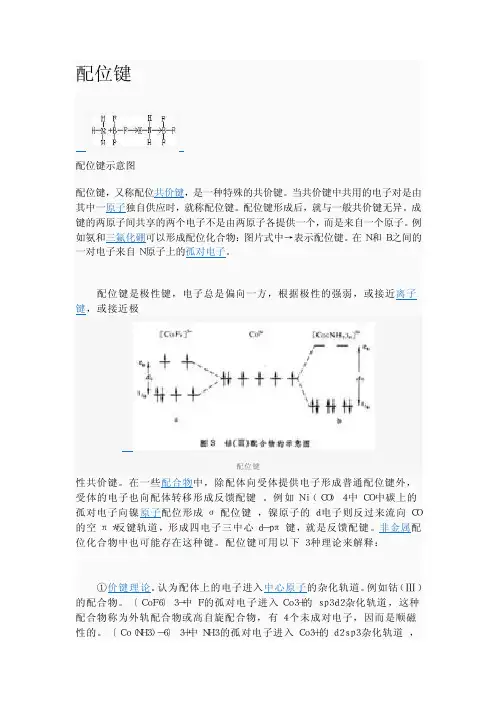
配位键　配位键示意图　配位键，又称配位共价键，是一种特殊的共价键。

当共价键中共用的电子对是由其中一原子独自供应时，就称配位键。

配位键形成后，就与一般共价键无异。

成键的两原子间共享的两个电子不是由两原子各提供一个，而是来自一个原子。

例如氨和三氟化硼可以形成配位化合物：图片式中→表示配位键。

在Ｎ和Ｂ之间的一对电子来自Ｎ原子上的孤对电子。

　 配位键是极性键，电子总是偏向一方，根据极性的强弱，或接近离子键，或接近极 配位键性共价键。

在一些配合物中，除配体向受体提供电子形成普通配位键外，受体的电子也向配体转移形成反馈配键　。

例如Ｎｉ（ＣＯ）４中ＣＯ中碳上的孤对电子向镍原子配位形成σ配位键　，镍原子的ｄ电子则反过来流向ＣＯ的空π＊反键轨道，形成四电子三中心ｄ－ｐπ键，就是反馈配键。

非金属配位化合物中也可能存在这种键。

配位键可用以下３种理论来解释： ①价键理论。

认为配体上的电子进入中心原子的杂化轨道。

例如钴（Ⅲ）的配合物。

〔ＣｏＦ６〕３－中Ｆ的孤对电子进入Ｃｏ３＋的ｓｐ３ｄ２杂化轨道，这种配合物称为外轨配合物或高自旋配合物，有４个未成对电子，因而是顺磁性的。

〔Ｃｏ（ＮＨ３）－６〕３＋中ＮＨ３的孤对电子进入Ｃｏ３＋的ｄ２ｓｐ３杂化轨道　，这种配合物称为内轨配合物或低自旋配合物，由于所有电子都已成对，因而没有顺磁性而为抗磁性。

②晶体场理论。

晶体场理论将配体看作点电荷或偶极子，同时考虑配体产生的静电场对中心原子的原子轨道能级的影响［１］。

例如，把中心原子引入位于正八面体６个顶角上的６个配体中，原来五重简并的ｄ轨道就分裂成一组二重简并的ｅｇ（－ｙ２、ｄｚ２）轨道和一组三重简并的ｔ２ｇ（ｄｘｙ、ｄｘｚ、ｄｙｚ）轨道　。

ｅｇ和ｔ２ｇ轨道的能量差　，称为分离能Δ０，Δ０≡１０Ｄｑ，Ｄｑ称为场强参量。

在上述钴（Ⅲ）配合物中，６个Ｆ－产生的场不强，Δ０较小，ｄ电子按照洪特规则排布，有四个未成对电子，因而〔ＣｏＦ６〕３－为弱场配合物或高自旋配合物　。

晶胞配位数计算技巧
晶胞配位数是晶体结构中与一个原子或离子最近邻的原子或离子的数目。

要计算晶胞配位数，可以遵循以下步骤：
1. 确定晶胞类型：不同晶胞类型的晶体结构不同，配位数也不同。

2. 确定原子或离子的最近邻原子或离子：在晶体结构中，一个原子或离子的最近邻原子或离子是与它直接相邻的原子或离子。

3. 计算配位数：一个原子或离子的配位数是与其最近邻原子或离子的数目。

例如，在面心立方晶胞中，每个原子或离子的最近邻原子或离子有8个，因此其配位数为8。

注意，以上计算的是理想情况下的配位数。

实际上，晶体结构中可能存在畸变，导致实际配位数与理想配位数有所不同。

因此，计算晶胞配位数时需要考虑晶体的畸变情况。

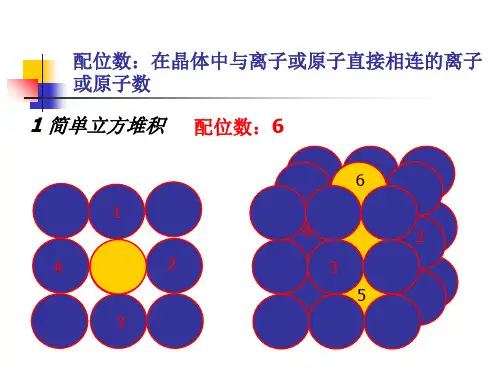
书山有路勤为径，学海无涯苦作舟矿石的晶体化学分析—配位数和配位多面体晶体结构中，原子或离子总是按一定的方式与周围的原子或离子相接触。

每个原子或离子周围最邻近的原子或异号离子的数目称为该原子或离子的配位数，以一个原子或离子为中心，将其周围与之成配位关系的原子或离子的中心连接起来所获得的多面体称为配位多面体。

例如在石盐（NaCI )的结构中（图1），每个Na＋的周围都有6 个Cl－与之相接触，Na＋的配位数为6；由Cl－所构成的配位多面体为八面体，Na＋位于八面体的中心，而Cl－则位于八面体的6 个角顶上。

配位多面体有多种形式，晶体结构常可看做是由配位多面体相互联结而成的一种体系。

图1 石盐NaCl 的晶形（a）及质点排列（b）大球Cl－；小球Na＋在等大球的最紧密堆积中，每个球周围有12 个球，配位数为12。

在离子晶体中，存在着半径不同的阴、阳离子，形成了非等大球的堆积。

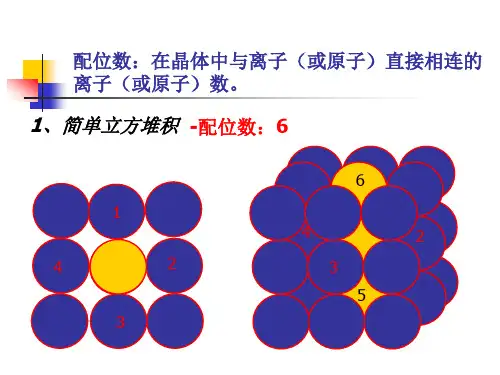
此时，只有当异号离子相互接触时才是稳定的[图2—（a）]；如果阳离子变小，使阴离子有了接触[图2—（b）]，结构仍然可以稳定，但已达稳定的极限；如果阳离子更小，使阴、阳离子脱离了接触，这样的结构就是不稳定的了，将引起配位数的改变[图2—（c）、（d）、（e）]。

配位数的大小，从几何观点看，取决于离子的相对大小。

当阴离于相同时，阳离子越小，其配位数亦越小。

即阴、阳离子大小相差悬殊，配位数愈小；大小愈接近，配位数愈大。

图2 阳离子配位稳定性图解在通常温度和压力的情况下，若离子不发生变形或变形很小时，配位数主要取决于阳离子半径RK 和阴离子半径RA 的比值，如表1 的关系。

表1 阳离子配位数与阳、阴离子半径比值RK/RA 的关系配位数稳定的界限（表1），是用几何方法计算出来的。

这种配位数的计算是纯几何学的。

在实际晶体结构中，情况要复杂得多。

离子的极化作用可使配。