四川大学信号与系统实验2(题目二)

信号与系统实验二信号与系统实验报告实验二实验名称：连续时间信号的频域分析指导老师：苏永新班级：09通信工程1班学号：2009963924姓名：王维实验二连续时间信号的频域分析一、实验目的1、掌握连续时间周期信号的傅里叶级数的物理意义和分析方法；2、观察截短傅里叶级数而产生的“Gibbs 现象”，了解其特点以及产生的原因；3、掌握连续时间傅里叶变换的分析方法及其物理意义；4、掌握各种典型的连续时间非周期信号的频谱特征以及傅里叶变换的主要性质；5、学习掌握利用MATLAB语言编写计算CTFS、CTFT和DTFT的仿真程序，并能利用这些程序对一些典型信号进行频谱分析，验证CTFT、DTFT的若干重要性质。

基本要求：掌握并深刻理傅里叶变换的物理意义，掌握信号的傅里叶变换的计算方法，掌握利用MATLAB编程完成相关的傅里叶变换的计算。

二、实验原理及方法1、连续时间周期信号的傅里叶级数CTFS分析任何一个周期为T1的正弦周期信号，只要满足狄利克利条件，就可以展开成傅里叶级数。

其中三角傅里叶级数为：∑∞=++=1000)]sin()cos([)(k k k t k b t k a a t x ωω2.1 或：∑∞=++=100)cos()(k k k t k c a t x ϕω2.2 其中12T πω=，称为信号的基本频率（Fundamentalfrequency ），kkb a a ，和，0分别是信号)(t x 的直流分量、余弦分量幅度和正弦分量幅度，kkc ϕ、为合并同频率项之后各正弦谐波分量的幅度和初相位，它们都是频率0ωk 的函数，绘制出它们与0ωk 之间的图像，称为信号的频谱图（简称“频谱”），kc －0ωk 图像为幅度谱，kϕ－0ωk 图像为相位谱。

三角形式傅里叶级数表明，如果一个周期信号x(t)，满足狄里克利条件，那么，它就可以被看作是由很多不同频率的互为谐波关系（harmonically related ）的正弦信号所组成，其中每一个不同频率的正弦信号称为正弦谐波分量 (Sinusoid component)，其幅度（amplitude ）为kc 。

实验四 振幅键控、移频键控、移相键控调制一、实验目的1． 掌握绝对码、相对码的概念以及它们之间的变换关系和变换方法。

2． 掌握用键控法产生2ASK 、2FSK 、2DPSK 信号的方法。

3． 掌握相对码波形与2PSK 信号波形之间的关系以及绝对码波形与2DPSK 信号波形之间的关系。

4． 掌握2ASK 、2FSK 、2DPSK 信号的频谱特性。

二、实验内容1． 观察绝对码和相对码的波形。

2． 观察2ASK 、2FSK 、2DPSK 信号波形。

3． 观察2ASK 、2FSK 、2DPSK 信号频谱。

三、实验器材1． 信号源模块2． 数字调制模块3． 频谱分析模块4． 20M 双踪示波器 一台5． 频率计（选用） 一台四、实验原理调制信号为二进制序列时的数字频带调制称为二进制数字调制。

由于被调载波有幅度、频率、相位三个独立的可控参量，当用二进制信号分别调制这三种参量时，就形成了二进制振幅键控(2ASK)、二进制移频键控（2FSK ）、二进制移相键控(2PSK)三种最基本的数字频带调制信号，而每种调制信号的受控参量只有两种离散变换状态。

1． 2ASK 调制原理。

在振幅键控中载波幅度是随着基带信号的变化而变化的。

使载波在二进制基带信号1或0的控制下通或断，即用载波幅度的有或无来代表信号中的“1”或“0”，这样就可以得到2ASK 信号，这种二进制振幅键控方式称为通—断键控（OOK ）。

2ASK 信号典型的时域波形如图15-1所示，其时域数学表达式为：2()cos ASK n c S t a A t ω=⋅ （15－1）式中，A 为未调载波幅度，c ω为载波角频率，n a 为符合下列关系的二进制序列的第n 个码元：⎩⎨⎧=P P a n －出现概率为出现概率为110 （15－2）综合式15－1和式15－2，令A ＝1，则2ASK 信号的一般时域表达式为：t nT t g a t S c n s n ASK ωcos )()(2⎥⎦⎤⎢⎣⎡-=∑ t t S c ωcos )(= （15－3）式中，T s 为码元间隔，()g t 为持续时间 [－T s /2，T s /2] 内任意波形形状的脉冲（分析时一般设为归一化矩形脉冲），而()S t 就是代表二进制信息的随机单极性脉冲序列。

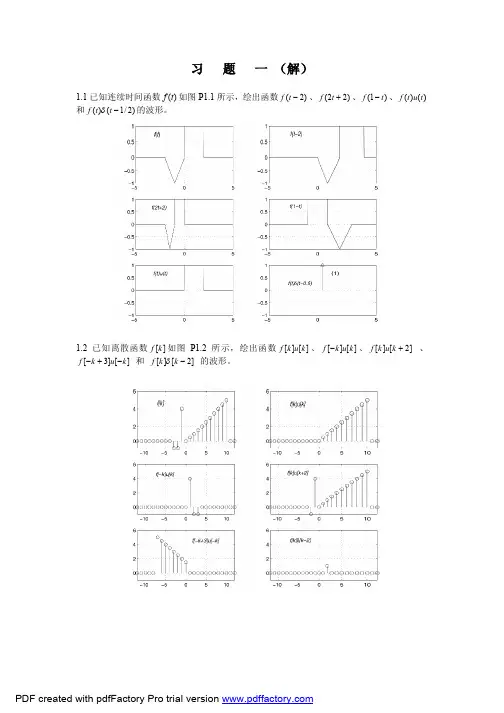
四川大学理论基础考试题参考解与评分标准考试内容：信号与系统（选自清华等七校硕士入学试题） 成 绩： 时 间：180分钟（闭卷） 姓 名： 总 分：150试题 符号说明：1，ARect （0t t τ-）表示幅度为A 、寛度为τ、中心位于0t 的矩形信号。

2，0()sin []pt t A c t π-表示中心主瓣幅度为A 、中心主瓣底部一半的寛度为p t 、中心位于0t 的辛格sin xx信号。

3，0)(A t t δ-）表示强度为A 、位于0t 处的冲激信号。

4，0()Au t t -表0t t <其值为零，在0t t =处突变高度为A 且一直保持的阶跃信号。

5，sgn()A t 表示在当0t <幅度为－A ，当0t >幅度为A 的符号信号。

一,完成下列运算（每小题5分，本题共计25分） 1,42[()(4)](43)?u t u t t t dt δ-∞---+=⎰44[(3)(1)][(3)(1)]2t t dt t t dt δδδ-∞-∞=--=-+-=⎰⎰2,()(0.5)[(2)(3)]nf n u n u n =*+--（空电）21()(0.5)()(), 1.(0.5)(1)nz f n u n u n z z z =*↔>--0.51R e [(0.5)]R e [(1)](0.5)(1)(0.5)(1)n n z z zzs z z s z z z z z z ===-+----- 1[2()]()2nu n =- 11()(2)(3)f n f n f n =+--=21[2()](2)2n u n +=-+31[2()](3)2n u n ---- 3，一CLTI 系统的10()1H s s =+，画出(H j ω草图并给出带宽.（华南理工大）解：因系统只有一个（－1）极点，系统是稳定的，则频率响应()H j ω存在，且为 1()1H j j ωω=+(H j ω=3dB 带宽，2121,ωω+=⇒=± 即 2ω∆=4,求信号sin[(5)](5)t t π--的自相关函数.解：这个信号是持续在(,)-∞∞区间上的能量型信号，其相关函数与能量谱密度()E ω间是FT 关系。

实验报告课程名称信号与系统实验名称信号与LTI系统的时频域分析实验时间2017 年 6 月15 日学院电子信息学院指导教师周新志学生姓名班级学号学院(系) 电子信息学院专业信息安全实验报告x3=x1+x2;subplot(2,2,3),stem(n,x3),grid on;title('余弦相加信号x3[n]')xlabel('Time index n');（2）a．clear;h1=[0.0031,0.0044,-0.0031,-0.0272,-0.0346,0.0374,0.1921,0.3279,0.3279,0.1921,0.0374,-0.0346,-0. 0272,-0.0031,0.0044,0.0031];k1=0:15;n=-4:4;ylabel('y3[k]');b.clear;h2=[-0.0238,0.0562,-0.0575,-0.1302,0.5252, -0.6842,-0.3129,5.6197,5.6197, -0.3129,-0.6842,0.5252,-0.1302,-0.0575,0.0562,-0.0238];k1=0:15;n=-4:4;x1=cos(0.25*pi*n);y1=conv(h2,x1);%计算序列f1与f2的卷积和fk0=k1(1)+n(1); %计算序列f非零样值的起点位置k3=length(x1)+length(h2)-2; %计算卷积和f的非零样值的宽度k=k0:k0+k3; %确定卷积和f非零样值的序号向量subplot(2,2,1);stem(k,y1);title('x1[n]与h2[n]的卷积和y1[n]');3.(a)fs=128;t=1/fs;L=256;n=0:1:L-1;x1=cos(0.25*pi*n); x2=cos(1.25*pi*n); x3=x2+x1;N = 2^nextpow2(L); X1=fft(x1,N)/N*2; X2=fft(x2,N)/N*2; X3=fft(x3,N)/N*2; f=fs/N*(0:1:N-1); figure;plot(f,abs(X3)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2); plot(f,angle(X3)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');(b)fs=128;t=1/fs;L1=256;n=0:1:L1-1;h1=[0.0031,0.0044,-0.0031,-0.0272,-0.0346,0.0374,0.1921,0.3279,0.3279,0.1921,0.0374,-0.0346,-0. 0272,-0.0031,0.0044,0.0031];x1=cos(0.25*pi*n);subplot(2,1,1); plot(f,abs(Y13)); title('幅值频谱'); xlabel('频率(HZ)'); ylabel('幅值'); subplot(2,1,2); plot(f,angle(Y13)); title('相位频谱'); xlabel('频率(HZ)'); ylabel('相位');实验报告4）从3）（b ）（c ）h1的频谱图可知在大约40-90的范围h1幅度几乎为零，左右两边迅速升起，最后在10和120处达到最大值后趋于平缓，h1的频谱图可知在大约60-70的范围h1幅度几乎为零，左右两边迅速升起，最后在35和100处达到最大值后趋于平缓，又由（a ）中x1，x2，x3的频谱图可以看到x1，x3有两个冲击在15,110处，x2，x3有两个冲击在40-90范围内，输出信号的频谱图如（b ）（c ）发现其 幅值满足(e )(e )(e )j j j Y X H ωωω= 的模值相乘，如此比较它们的相位图，发现也存在这种关系，故可知验证输出信号的频谱与输入信号、h [n]的频谱关系（或卷积性质），即是否满足(e )(e )(e )j j j Y X H ωωω=5）输出信号及频谱不同的原因是：由4）我们知道它们满足(e )(e )(e )j j j Y X H ωωω=，故是因为在输入信号一定时，由系统冲击函数的不同造成的，它们趋于零的范围不同，达到的最大值不同，相位也不同，同理系统冲击函数一定时，由输入信号不同造成，所以输出信号及频谱不同。

实验二 利用DFT 分析离散信号频谱一、 实验目的应用离散傅里叶变换(DFT)，分析离散信号x [k ]。

深刻理解利用DFT 分析离散信号频谱的原理，掌握改善分析过程中产生的误差的方法。

二、实验原理根据信号傅里叶变换建立的时域与频域之间的对应关系，可以得到有限长序列的离散傅里叶变换(DFT)与四种确定信号傅里叶变换的之间的关系，实现由DFT 分析其频谱。

三、实验内容1. 利用FFT 分析信号的频谱； (1) 确定DFT 计算的参数；(2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。

①源代码 N=32;k=0:31; x=cos(3*pi/8*k); X=fft(x,N); subplot(2,1,1);stem(k-N/2,abs(fftshift(X))); ylabel('Magnitude'); xlabel('Frequency(rad/s)'); title('频谱图'); subplot(2,1,2);stem(k-N/2,angle(fftshift(X))); ylabel('Phase');xlabel('Frequency(rad/s)'); title('相位图'); ②运行结果31,1,0 ),8π3cos(][ ==k k kx③结果分析经计算可知：该信号的基波周期N=16，根据题意，为了显示k=0到31，所以取周期N ’=32，基波频率w 0=2πN′= π8。

对于计算值，由于在时间轴上的取值范围有限，计算时只取区间[-16,16]上的值，此时在频率轴上对应16，而理论值的区间为（-∞，+∞），经计算可知结果为一冲击信号，强度为π，二者显然不相同。

误差原因：计算响应时，所选取的区间不同。

改善方法：在条件允许范围内，应尽量多取点。

2. 利用FFT 分析信号的频谱；(1) 确定DFT 计算的参数；(2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。

现代通信技术仿真实验报告课程现代通信技术实验题目二进制数字FSK、PSK调制和解调学生姓名学号班级电子信息工程x班实验时间 2019年1月10日一、实验要求使用MATLAB软件仿真实现二进制数字调制FSK、PSK和解调，满足下列要求:1.使用随机序列产生12位二进制基带信号bn时显示基带信号域波形及频谱2.载波频率设为基带信号速率的4倍，产生两种调制信号2FSK、2PSK (FSK另一个频率设为3倍基带信号速率)并解调，并要求显示时域波形和频谱3.分析比较基带信号和已调信号的带宽二、实验目的1.通过仿真实验进一步理解掌握FSK、PSK的调制和解调原理。

2.学会使用MATLAB编写FSK、PSK的调制程序。

3.掌握数字通信的FSK、PSK的调制方式三、实验内容1. 二进制数字调制FSK的MATLAB仿真实现。

2．二进制数字调制的PSK的MATLAB仿真实现。

四、实验环境软件版本：MATLAB 2018a for windows系统版本：Windows10五、实验原理数字调制方式可以分为基带传输和载波传输。

在基带传输中，数据流以离散的PAM信号形式直接通过低通信道传输；在数字信号的载波传输中，输入数据流（数字信号）被调制到载波上并通过带通信道传输。

三种基本数字调制是幅度键控ASK、频移键控FSK、相移键控PSK。

实验一、二进制数字调制FSK的调制和解调一、实验原理1.二进制频移键控2FSKA[m(t)]=1ωc+ddtϑ[m(t)]={ωc0 当an=0ωc1 当an=1载波的幅度不变，频率随m(t)在两个频率中变化，或者说用两个不同的频率携带传递二进制数字信息，当发送1时对应于某个载波频率wc1，当发送0时对应于另一个载波频率wc0，我们把这种调制方式称之为二进制频移键控2FSK。

当二进制数字信息序列m(t)是具有逻辑电平1和0的单极性不归零码时，二进制频移键控信号可以堪称两个不同载频的二进制幅度键控信号之和，所以二进制频移键控信号的时域表达式为s2FSK=[∑a n g(t−nTb)n cosw c1t]+[∑a n̅̅̅g(t−nTb)ncosw c2t]其中an非是an的反码它的频带宽度是两倍基带信号B基带与|f c1+f c0|之和，即B2FSK=2B基带+|f c1+f c0|2.调制方法二进制频移键控信号的产生有两种(1)直接调频法按照1和0分别选择一个载波作为输出，这正是频率键控通信方式早期采用的实现方法，也是利用模拟调频法实现数字调频的方法。

川大08硕题解一，填空题（每小题3分，共21分）1，信号sin 3()t x t t ππ=的总能量E ＝2231Re ()326siin t dt ct d t πωωπππ∞∞-∞-∞==⎰⎰焦。

1()3sin (3)Re ()(3;)63p x t c t ct A t ωππ=↔== 2，5cos 2sin22ttππ-的周期T ＝411212222544;;5;225TT T T T T ππππ=→==→==是有理数。

故5cos 2sin 22t t ππ-是周期信号。

其周期T 是1,2T T 的最小公倍数，即为4。

3，CLTI 系统的输入输出满足1()()ty t e x d τττ-+-∞=⎰该系统的冲激响应()h t =11()()()()tt y t e x d e x t u t τττ-+--∞==*⎰这由图可知，是一个时变系统，时变系统的冲激响应是二元函数(,)h t τ，己超出范围。

4，DLTI 系统是稳定系统的必要充分条件是1），l i m ()0x t y n →∞=；2），()H z 的所有极点1,1,2,3,i r i <= 3），()n h n ∞=<∞∑4），()j H e ω存在。

5，周期信号的周期T ＝7，傅利（什么形式的）叶级数系数为1(1)kk a =--，则(3)x t-的第三次谐波分量的平均功率等于认为是基本形式的叶级数系数2122k p a W ==。

6，己知()x t 的FT 0100(){elsex j ωω=≠<则()()(0.5)y t x t x t =*-的理想抽样频率为(0.5)x t -比()x t 的时间展宽一倍，其频谱压缩一倍，即有100ω∆=（()x t 的200ω∆=）；()y j ω则是{}{}()()(0.5)()(0.5)y t x t x t FT x t FT x t =*-↔∙-，结果的频谱宽度由窄的100ω∆=25(50;)H H f ωπ==决定，故得抽样频率502s H f f π≥=7,()x n 的ZT 为(),2x z z <；则()x n -的ZT 为111()()()();2nn n n x n zx n X z Z Z ∞∞'--'=-∞=-∞'-==<∑∑ 二，判断题（每小题4分，共20分）1，设()(21)x t t δ=-⨯标出。