弧度制1
- 格式:doc
- 大小:204.00 KB
- 文档页数:4



1.中心角为60°的扇形,它的弧长为2π,则它的内切圆半径为()A .2B .3C .1D .232.0240的弧度数是( )A .65πB .67πC .34πD .35π3.半径为1cm ,中心角为0150的角所对的弧长为( ) A.cm 32 B.cm 32π C.cm 65 D.cm 65π4.已知扇形面积为83π,半径是1,则扇形的圆心角是()(A )163π (B )83π (C )43π (D )23π5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为 ( )A .3πB .2πC .3D .26.集合}2ππ4ππ|{Z k k k ∈+≤≤+,αα,中的角所表示的范围(阴影部分)是7.若扇形的面积为38π,半径为1,则扇形的圆心角为( ) A. 32πB. 34πC. 38πD. 316π8、若弧长为4的弧所对的圆心角是2 ,则这条弧所在的圆的半径等于( )A .8B .4C .2D .19、半径为10cm ,弧长为20cm 的扇形的圆心角为( )A.︒2B.2弧度C.π2弧度D.10弧度10、若弧长为4的弧所对的圆心角是2 ,则这条弧所在的圆的半径等于( )A .8B .4C .2D .111、若扇形的周长是16cm ,圆心角是2弧度,则扇形的面积是 (单位2cm ) A .16 B .32 C .8 D .6412、已知扇形面积为83π,半径是1,则扇形的圆心角是 ( )(A )163π (B )83π (C )43π (D )23π13、在面积为定值9的扇形中,当扇形的周长取得最小值时,扇形的半径是( )(A) 3 (B) 2 (C) 4 (D) 514、若扇形圆心角的弧度数为2,且扇形狐所对的弦长也是2,则这个扇形的面积为( ) A.21cos 1 B. 21sin 1 C. 22cos 1 D. 22sin 115、已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( ) (A) 2sin 2 (B)sin2 (C) 1sin 2(D)2sin116、若一圆弧长等于其所在圆的内接正三角形的边长,则圆弧所对圆心角的弧度数为( )A .3πB .32πC .3D .217、圆心角为1350,面积为B的扇形围成一个圆锥,若圆锥的表面积为A,则A:B等于 A.811 B. 813 C. 38 D. 81318、设扇形的周长为6,面积为2,则扇形中心角的弧度数是A. 1B. 4C. 1或4D. π19、把114π-表示成2()k k Z πθ+∈ 的形式,使θ 最小的θ的值 A. 4π B. -4π C. -34π D. 34π20、一个半径为R 的圆中,60 的圆心角所对的弧长为( )A.60RB.R 6πC.R 31D.3πR21、集合M={x|x= k 〃90°450 Z ∈k }与P={x|x=m 〃45°Z ∈m }之间的关系为( )A .M PB .P MC .M=PD .M ∩P=22、设集合M={α|α=5-2ππk ,k ∈Z},N={α|-π<α<π},则M ∩N 等于 ( )A .{-105ππ3,} B .{-510ππ4,7}C .{-5-105ππππ4,107,3,} D .{07,031-1ππ } 23、中心角为60°的扇形,它的弧长为2π,则它的内切圆半径为A .2B .3C .1D .2324、设集合M={α|α=k π±6π,k ∈Z},N={α|α=k π+(-1)k 6π,k ∈Z}那么下列结论中正确的是 ( )A .M=NB .M NC .N MD .M N 且N M25、已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是 ( )A .2B .1sin 2C .1sin 2D .2sin26、在“①160°②480°③-960°④-1600°”这四个角中,属于第二象限的角是( )A.①B.①②C.①②③D.①②③④27、 若是第三象限的角, 则是 ( )(A) 第一或第二象限的角 (B) 第一或第三象限的角(C) 第二或第三象限的角 (D) 第二或第四象限的角28、与411π-终边相同的角为( ) (A) 43π- (B) 4π- (C) 4π (D) 43π 29、已知扇形的圆心角为72°,半径为20cm ,则扇形的面积为____.30、已知扇形的半径为8cm ,圆心角为045,则扇形的面积是 2cm . 31、若扇形的周长为12cm ,圆心角为2rad ,则该扇形的面积为 cm 2.32、已知扇形的半径为10㎝,圆心角为120°,则扇形的面积为_.33、若2弧度的圆心角所对的弧长为4cm ,则这个圆心角所在的扇形面积为 cm 234、设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 ;35、若扇形OAB 的面积是21cm ,它的弧所对的圆心角是2rad ,则它的弧长________;36、已知扇形的半径为10㎝,圆心角为120°,则扇形的面积为_____________.37、一个扇形的面积为1,周长为4,则这个扇形的圆心角为______.38、半径为2cm,圆心角为23π的扇形面积为 .39、已知相互啮合的两个齿轮,大轮有48齿,小轮有20齿,当大轮转动一周时,小轮转动的角是,即rad.如果大轮的转速为180minr/(转/分),小轮的半径为10.5 cm,那么小轮周上一点每1s转过的弧长是.40、若角π|π(1)4mm mθαα⎧⎫==+-∈⎨⎬⎩⎭Z,·,则角θ所在的象限是41、已知扇形OAB的圆心角为120 ,半径长为6cm,求:(1)弧AB的长;(2)该扇形所含弓形的面积.42、把radπ53化成度43、如图,已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。

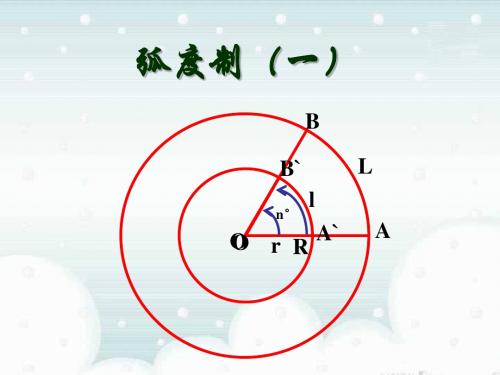
题:4.2弧度制(一)教学目的:1.理解1弧度的角、弧度制的定义.2.掌握角度与弧度的换算公式并能熟练地进行角度与弧度的换算.3.熟记特殊角的弧度数教学重点:使学生理解弧度的意义,正确地进行角度与弧度的换算.教学难点:弧度的概念及其与角度的关系.授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:讲清1弧度角的定义,使学生建立弧度的概念,理解弧度制的定义,达到突破难点之目的. 通过电教手段的直观性,使学生进一步理解弧度作为角的度量单位的可靠性、可行性.通过周角的两种单位制的度量,得到角度与弧度的换算公式. 使学生认识到角度制、弧度制都是度量角的制度,二者虽单位不同,但是互相联系的、辩证统一的.进一步加强对辩证统一思想的理解.教学过程:一、复习引入:1.角的概念的推广⑴“旋转”形成角一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB 叫做角α的终边,射线的端点O叫做角α的顶点.⑵.“正角”与“负角”“0角”我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210°,β=-150°,γ=660°,定义的?规定周角的3601作为1°的角,我们把用度做单位来度量角的制度叫做角度制,有了它,可以计算弧长,公式为180rn l π=3.探究30°、60°的圆心角,半径r 为1,2,3,4,分别计算对应的弧长l ,再计算弧长与半径的比结论:圆心角不变,则比值不变,因此比值的大小只与角的大小有关,我们可以利用这个比值来度量角,这就是另一种度量角的制度——弧度制二、讲解新课:1. 定义:长度等于半径长的弧所对的圆心角称为1弧度的角它的单位是rad读作弧度,这种用“弧度”做单位来度量角的制度叫做弧度制.如下图,依次是1rad , 2rad , 3rad ,αrad探究:⑴平角、周角的弧度数,(平角=π rad 、周角=2π rad )⑵正角的弧度数是正数,负角的弧度数是负数,零角的弧度数是0 ⑶角α的弧度数的绝对值 rl=α(l 为弧长,r 为半径) ⑷角度制、弧度制度量角的两种不同的方法,单位、进制不同,就像度量长度一样有不同的方法,千米、米、厘米与丈、尺、寸,反映了事物本身不变,改变的是不同的观察、处理方法,因此结果就有所不同⑸用角度制和弧度制来度量零角,单位不同,但数量相同(都是0) 用角度制和弧度制来度量任一非零角,单位不同,量数也不同2. 角度制与弧度制的换算:∵ 360︒=2π rad ∴180︒=π rad∴ 1︒=rad rad 01745.0180≈π'185730.571801=≈⎪⎭⎫ ⎝⎛=πrad三、讲解范例:例1 把'3067化成弧度解:⎪⎭⎫⎝⎛=2167'3067∴ rad rad ππ832167180'3067=⨯=例2 把rad π53化成度 解: 1081805353=⨯=rad π 注意几点:1.度数与弧度数的换算也可借助“计算器”进行;2.今后在具体运算时,“弧度”二字和单位符号“rad ”可以省略 如:3表示3rad , sin π表示πrad 角的正弦;3.一些特殊角的度数与弧度数的对应值应该记住:4.应确立如下的概念:角的概念推广之后,无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系任意角的集合 实数集R例3用弧度制表示:1 终边在x 轴上的角的集合2 终边在y 轴上的角的集合3 终边在坐标轴上的角的集合解:1 终边在x 轴上的角的集合 {}Z k k S ∈==,|1πββ 2 终边在y 轴上的角的集合 ⎭⎬⎫⎩⎨⎧∈+==Z k k S ,2|2ππββ 3 终边在坐标轴上的角的集合 ⎭⎬⎫⎩⎨⎧∈==Z k k S ,2|3πββ 四、课堂练习:1.下列各对角中终边相同的角是( )A.πππk 222+-和(k∈Z) B.-3π和322πC.-97π和911πD. 9122320ππ和2.若α=-3,则角α的终边在( )A.第一象限B.第二象限C.第三象限D.第四象限3.若α是第四象限角,则π-α一定在( )A.第一象限B.第二象限C.第三象限D.第四象限4.(用弧度制表示)第一象限角的集合为 ,第一或第三象限角的集合为 .5.7弧度的角在第 象限,与7弧度角终边相同的最小正角为 .6.圆弧长度等于截其圆的内接正三角形边长,则其圆心角的弧度数为 .7.求值:2cos4tan6cos6tan3tan3sinππππππ-+.8.已知集合A={α|2kπ≤α≤π+2kπ,k∈Z},B ={α|-4≤α≤4},求A ∩B .9.现在时针和分针都指向12点,试用弧度制表示15分钟后,时针和分针的夹角.参考答案: 1.C 2.C 3.C4.{α|2k π<α<2π+2k π,k ∈Z } {α|k π<α<2π+k π,k ∈Z } 5.一 7-2π 6.3 7.28.A ∩B ={α|-4≤α≤-π或0≤α≤π} 9.2411π五、小结 1.弧度制定义 2.与弧度制的互化 2.特殊角的弧度数 六、课后作业:已知α是第二象限角,试求:(1)2α角所在的象限;(2)3α角所在的象限;(3)2α角所在范围.解:(1)∵α是第二象限角,∴2π+2k π<α<π+2k π,k ∈Z ,即4π+k π<2α<2π+k π,k ∈Z .故当k =2m (m ∈Z )时,4π+2m π<2α<2π+2m π,因此,2α角是第一象限角;当k =2m +1(m ∈Z )时,45π+2m π<2α<23π+2m π,因此,2α角是第三象限角.综上可知,2α角是第一或第三象限角.(2)同理可求得:6π+32k π<3α<3π+32k π,k ∈Z .当k =3m (m ∈Z )时,ππαππm m 23326+<<+,此时,3α是第一象限角;当k =3m +1(m ∈Z )时,πππαπππ322333226++<<++m m ,即3265αππ<+m <π+2m π,此时,3α角是第二象限角; 当k =3m +2(m ∈Z )时,ππαππm m 2353223+<<+,此时,3α角是第四象限角.综上可知,3α角是第一、第二或第四象限角. (3)同理可求得2α角所在范围为:π+4k π<2α<2π+4k π,k ∈Z .评注:(1)注意某一区间内的角与象限角的区别.象限角是由无数个区间角组成的,例如0°<α<90°这个区间角,只是k =0时第一象限角的一种特殊情况.(2)要会正确运用不等式进行角的表达,同时会以k 取不同值,讨论形如θ=α+32k π(k ∈Z )所表示的角所在象限. (3)对于本例(3),不能说2α只是第一、二象限的角,因为2α也可为终边在y 轴负半轴上的角23π+4k π(k ∈Z ),而此角不属于任何象限. 七、板书设计(略)八、课后记:一般情况下,我们在研究圆中的角的弧度一般都是正数!除非题目有特别的要求!有两种方法可以解释,一是正的弧对的弧度为正,负的弧对的是负的弧度(解释稍显牵强!),二是无论是顺时针方向还是逆时针旋转的角度数值始终是正数,所以研究时弧度取正数!扇形的圆心角始终是正数!。

角度制与弧度制的换算公式
弧度制与角度制的换算公式:1度=π/180≈0.01745弧度,1弧度=180/π≈57.3度。
角的度量单位通常有两种,一种是角度制,另一种就是弧度制。
1、弧度制
用弧长与半径之比度量对应圆心角角度的方式,叫做弧度制,用符号rad表示,读作弧度。
等于半径长的圆弧所对的圆心角叫做1弧度的角。
由于圆弧长短与圆半径之比,不因为圆的大小而改变,所以弧度数也是一个与圆的半径无关的量。
角度以弧度给出时,通常不写弧度单位。
弧度制的精髓就在于统一了度量弧与角的单位,从而大大简化了有关公式及运算,尤其在高等数学中,其优点就格外明显。
2、角度制
用度(°)、分(′)、秒(″)来测量角的大小的制度叫做角度制。
角度制:规定周角的360分之一为1度的角,用度作为单位来度量角的单位制叫做角度制。
单位换算
角度制中,1°=60′,1′=60″,1′=(1/60)°,1″=(1/60)′。
角度制就是运用60进制的例子。
运算法则
两个角相加时,°与°相加,′与′相加,″与″相加,其中如果满60则进1。
两个角相减时,°与°相减,′与′相减,″与″相减,其中如果不够则从上一个单位退1当作60。
弧度制
一、复习回顾:
1、角度制规定:将一个圆周分成360份,每一份叫做1度,故一周等于360度,平角等于180度,直角等于90度等等.
2、在角度制下 360
n 180
2
r l r n S ππ=
=
扇扇
二、新课学习:
弧度制的定义
等于半径长的圆弧所对的圆心角叫做1弧度的角,用符号rad 表示,读作弧度。
用弧度作单位来度量角的制度叫做弧度制。
在这种规定下,圆周长所对的圆心角为π2rad,半圆所对的圆心角为π rad ,︒90=2
π
rad,你能继续往下推吗?
请你填写书上第6页的表格。
注:1、一般地,正角的弧度数是一个正数(正实数),负角的弧度数是一个负数(负实数),零角的弧度数是零。
这里,α的正负由角α的终边的旋转方向决定。
2、用角度制和弧度制度量零角,单位不同,数量相同;用角度制和弧度制度量任一非零角,单位不同,数量也不同。
练习:请你填下列表格。
角度
0°
15°
45°
弧度
角度 90° 270°
弧度
更进一步,我们可以得到: '
185730.57)180
(
101745.0180
1180︒=︒≈︒=≈=
︒︒
=π
π
πrad rad rad rad
利用上面的方法,我们可以把任意一个角度转换成弧度,或将任意一个弧度转化成角度。
例:按照下列要求,把67°30′化成弧度。
1)精确值; 2)精确到0.001的近似值。
例:将3.14rad 转换成角度。
练习:书上第9页1、2题。
提问:当圆心角α一定时,它所对应的弧长与半径的比值是唯一确定的,与半径的大小无关,这句话对吗?为什么?
公式1:1)如果半径为r 的圆的圆心角α所对弧长为l ,那么,角α的弧度数的绝对值是r
l =
α.
2)若求弧长,则可变形为r l α=
3)若求半径,则可变形为α
l
r =
注:1、无论采用角度制或弧度制,都能使角的集合与实数集合R 存在一一对应关系:每一个角都对应唯一的一个实数。
2、弧度制的基本思想
弧度制的基本思想是使圆半径与圆周长有同一度量单位,然后用对应的弧长与圆半径之比来度量角度,这一思想的雏型起源于印度。
印度著名数学家阿利耶毗陀﹝476?-550?﹞定圆周长为21600分,相度地定圆半径为3438分﹝即取圆周率π3.142﹞,但阿利耶毗陀没有明确提出弧度制这个概念。
严格的弧度概念是由瑞士数学家欧拉﹝1707-1783﹞于1748年引入。
欧拉与阿利耶毗陀不同,先定半径为1个单位,那么半圆的弧长为π,此时的正弦值为0,就记为sin π= 0,同理,1/4圆周的弧长为π/2,此时的正弦为1,记为sin(π/2)=1。
从而确立了用π、π/2分别表示半圆及1/4圆弧所对的中心角。
其它的角也可依此类推。
3、弧度制的精髓
弧度制的精髓就在于统一了度量弧与半径的单位,从而大大简化了有关公式及运算,尤其在高等数学中,其优点就格外明显。
三、典型例题:
例:设角1570α=-°,2750α=°,1237,5
3
βπβπ=
=-
(1)将12,αα用弧度制表示出来,并指出它们各自所在的象限;
(2)将12,ββ用角度制表示出来,并在-720°~O °之间找出与它们有相同终边的所有角. 练习:把下列各角化成0~2π间的角加上2k πk ∈Z)的形式,并指出它们是哪个象限的角.
练习:角度与弧度互化: (1)
5
3π (2)3.5 (3)252º (4)11º15¹
例:利用弧度制证明扇形面积公式:lR R
S 2
12
12
=
=α扇
练习:扇形弧长为18 cm ,半径为12 cm ,求扇形面积.
练:一条弦的长度等于半径r ,求 1)这条弦所对的劣弧长?r π31
2)这条弦和劣弧所组成的弓形的面积。
2
)4
36
(
r -
π
练习:若一扇形的周长为60cm ,那么当它的半径和圆心角各为多少时,扇形的面积最大,最大值是多少?
例:已知扇形的周长是6cm ,面积是2cm 2,试求扇形的中心角的弧度数。
rad rad l r l r lr l r 41,224122
162==∴⎩⎨⎧==⎩⎨
⎧==⇒⎪⎩⎪⎨⎧==+αα或或解: 练习:分别用角度制、弧度制下的弧长公式,计算半径为1 m 的圆中,60°的圆心角所对的
弧的长度。
例:写出终边在如图所示阴影部分的角的集合:
练习:写出终边在如图所示阴影部分的角的集合: 练习:下列说法错误的是 A .“度”与“弧度”是度量角的两种不同的度量单位 B .1°的角是周角的
1360
,1 rad 的角是周角的
12π
C .1 rad 的角比1°的角要大
D .用角度制和弧度制度量角,都与圆的半径有关 练习:若α是第二象限角,
则90°-α是第( )象限角。
例、根据条件写出α与β之间的关系式:
⑴ 两角的终边关于x 轴对称; ⑵ 两角的终边关于y 轴对称;
⑶ 两角的终边关于原点对称; ⑷ 两角的终边关于y=x 轴对称; ⑸ 两角的终边关于y= -x 轴对称。
四、基础自测
1、下列各式正确的是
A.180=π
B.14.3=π
C. rad 2
90π
=︒ D.π=rad 1
2、在不等的圆中,1rad 的圆心角所对的
A. 弦长相等
B. 弧长相等
C. 弦长等于所在圆半径
D. 弧长等于所在圆半径 3、将下列各角的弧度数化为角度数:
o
y x
π4
π3
π6
o
y
x
7π6
5π6
o
y
x
(1)=-
6
7π 度; (2)=-
3
8π 度 (3)1.4 = 度;
4、若扇形的半径为1,周长为π,则扇形的面积是
A. 2-π
B. 12
-π C. 1-π D. 2
π
5、集合⎭⎬⎫⎩
⎨⎧∈+=
=Z k k A ,2ππ
αα与⎭
⎬⎫⎩⎨⎧∈+±==Z k k B ,22ππ
αα的关系是 A.A=B B.B A ⊆ C.B A ⊇ D. 以上都不对
6、若Z k k ∈+=,3
ππ
α,则α是第 象限角。
7、把4
11π-
表示成πθk 2+(k ∈Z )的形式,使θ最小的θ值是 .
8、已知一半径为R 的扇形,它的周长等于所在圆的周长,那么扇形的圆心角是多少弧度?合多少度?扇形的面积是多少?
9、已知{}Z k k k A ∈+≤≤=,)12(2παπα,{}44≤≤-=ααB ,则.____=⋂B A A.φ B. {}44≤≤-αα C. {}παα≤≤0 D. {}παα-≤≤-4{}πα≤≤⋃0∪ 10. 钟表分针长5cm ,经过20分钟,分针端点转过的弧长是( )
A.
cm 3
5π B.10cm C.cm 310
D. cm 3
10π 11、如图,用弧度制表示下列终边落在阴影部分的角的集合(不包括边界).
12、角α的终边落在区间(-3π,-5
2
π)内,则角α所在象限是 ( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 13.将时钟的分针拨慢十分钟,则分针转过的弧度数为( ) .
3
A π .3
B π-
.
5
C π .5
D π-
14、与角4
35π-终边相同的最小正角是 .
15、若6
-=α
,则α为第几象限角?。