2018-2019学年度最新北师大版必修2课下能力提升：(十八)Word版含解析

——教学资料参考参考范本——2019-2020学年度北师大版必修2课下能力提升：（二十四）Word版含解析______年______月______日____________________部门一、选择题1．有下列叙述：①在空间直角坐标系中，在x轴上的点的坐标一定可记为(0，b,0)；②在空间直角坐标系中，在yOz平面上的点的坐标一定可记为(0，b，c)；③在空间直角坐标系中，在z轴上的点的坐标一定可记为(0,0，c)；④在空间直角坐标系中，在xOz平面上的点的坐标一定可记为(a,0，c)．其中正确叙述的个数是( )A．1 B．2C．3 D．4 2．已知点A(－3,1,4)，则点A关于原点的对称点的坐标为( )A．(1，－3，－4) B．(－4,1，－3)C．(3，－1，－4) D．(4，－1,3) 3．在空间直角坐标系中P(2,3,4)，Q(－2,3,4)两点的位置关系是( )A．关于x轴对称B．关于yOz平面对称C．关于坐标原点对称D．以上都不对4．设z为任一实数，则点(2,2，z)表示的图形是( )A．z轴B．与平面xOy平行的一直线C．平面xOyD．与平面xOy垂直的一直线5．已知点A(2,3－μ，－1＋v)关于x轴的对称点为A′(λ，7，－6)，则λ，μ，v的值为( )A．λ＝－2，μ＝－4，v＝－5B．λ＝2，μ＝－4，v＝－5C．λ＝2，μ＝10，v＝8D．λ＝2，μ＝10，v＝7二、填空题6．点A(－5,5,6)关于坐标平面yOz对称的点为A1，则点A1关于坐标平面xOy的对称点A2的坐标为________．7．点A(2,4,6)关于y轴对称的点的坐标为________．8．在空间直角坐标系中，点M(－2，4，－3)在xOz平面上的射影为M′点，则M′关于原点对称的点的坐标是________．三、解答题9．如图，棱长为a的正方体OABC­D′A′B′C′中，对角线OB′与BD′相交于点Q，顶点O为坐标原点，OA、OC分别在x轴、y轴的正半轴上，试写出点Q的坐标．10．如右图，在棱长为1的正方体ABCD­A1B1C1D1中，E，F分别是D1D，BD的中点，G在棱CD上，且CG＝CD，H为C1G的中点，试建立适当的直角坐标系，写出点E，F，G，H的坐标．答案1．解析：选C ①错误，②③④正确．2．解析：选 C 空间直角坐标系中一点关于原点对称点的坐标特点是：三个坐标都变为它的相反数．∴A(－3,1,4)关于原点对称点的坐标为(3，－1，－4)．3．解析：选B ∵P，Q两点对应的三个坐标横坐标互为相反数，∴P，Q关于yOz平面对称．4．解析：选 D (2,2，z)表示过点(2,2,0)且与z轴平行的直线，即与平面xOy垂直的直线．5．解析：选D 两个点关于x轴对称，那么这两个点的x坐标不变，y坐标与z坐标均互为相反数，故有λ＝2,7＝－(3－μ)，－6＝－(－1＋v)，∴λ＝2，μ＝10，v＝7. 6．解析：点A(－5,5,6)关于yOz对称的点A1坐标为(5,5,6)，则点A1关于坐标平面xOy的对称点A2的坐标为(5,5，－6)．答案：(5,5，－6) 7．解析：关于y轴对称的点的纵坐标不变，横坐标和竖坐标变成相反数，故A(2,4,6)关于y轴对称的点的坐标为(－2,4，－6)．答案：(－2,4，－6) 8．解析：点M在xOz上的射影为(－2,0，－3)，其关于原点对称的坐标为(2,0,3)．答案：(2,0,3)9．解：因为OB′与BD′相交于点Q，所以Q点在xOy平面内的投影应为OB与AC的交点，所以Q的坐标为.同理可知Q点在xOz平面内的投影也应为AD′与OA′的交点，所以Q点的坐标为. 10．解：以D为原点，DA所在直线为x轴，DC所在直线为y轴，DD1所在直线为z轴建立如图所示的空间直角坐标系．∵点E在z轴上，且为D1D的中点，故点E坐标为.过F作FM⊥AD，FN⊥DC，则|FM|＝|FN|＝，故点F坐标为；点G在y轴上，又|GD|＝，故点G坐标为；过H作HK⊥CG于点K，由于H为C1G的中点，故|HK|＝，|CK|＝.∴|DK|＝.故点H的坐标为.。

课下能力提升(十八)一、选择题1．直线3x －2y ＋m ＝0和(m 2＋1)x ＋3y －3m ＝0的位置关系是( )A ．平行B ．重合C ．相交D ．不确定2．直线l 过直线3x －y ＝2和x ＋y ＝6的交点，且过点(－3，－1)，则直线l 的方程为( )A ．2x －y ＋5＝0B ．x ＋y ＋4＝0C ．x －y ＋2＝0D ．3x －y －2＝03．直线(2k －1)x －(k ＋3)y －(k －11)＝0(k ∈R )所经过的定点为( )A ．(2,3)B ．(5,2)C.⎝⎛⎭⎫－12，3 D ．(5,9) 4．已知点P (－1,0)，Q (1,0)，直线y ＝－2x ＋b 与线段PQ 相交，则b 的取值范围是( )A ．[－2,2]B ．[－1,1]C.⎣⎡⎦⎤－12，12 D ．[0,2] 5．使三条直线4x ＋y ＝4，mx ＋y ＝0,2x －3my ＝4不能围成三角形的m 值最多有( )A ．1个B ．2个C ．3个D ．4个二、填空题6．已知直线ax ＋4y －2＝0和2x －5y ＋b ＝0垂直且都过点A (1，m )，则a ＝__________，b ＝________，m ＝________.7．若三条直线x －2y ＋1＝0，x ＋3y －1＝0，ax ＋2y －3＝0共有两个不同的交点，则a ＝________.8．在△ABC 中，已知B (2,1)，AC 边所在直线的方程为2x －y ＋5＝0，直线3x －2y ＋1＝0是BC 边的高线，则点C 的坐标为________．三、解答题9．求经过直线l 1：x －y ＋1＝0与l 2：x ＋2y －5＝0的交点且与直线l 3：4x ＋y ＋1＝0平行的直线l 的方程．10．已知点A 是x 轴上的动点，一条直线过点M (2,3)且垂直于MA ，交y 轴于点B ，过A ，B 分别作x ，y 轴的垂线交于点P ，求点P (x ，y )满足的关系式．答案1．解析：选C ∵k 1＝32，k 2＝－m 2＋13，∴k 1≠k 2.∴两直线相交． 2．解析：选C 由⎩⎪⎨⎪⎧3x －y ＝2，x ＋y ＝6，得直线3x －y ＝2和x ＋y ＝6的交点为(2,4)， ∵直线l 过点(2,4)和(－3，－1)两点，∴直线l 的方程为y －4－1－4＝x －2－3－2，即x －y ＋2＝0.3．解析：选A 将原方程变为k (2x －y －1)－x －3y ＋11＝0，令⎩⎪⎨⎪⎧ 2x －y －1＝0，－x －3y ＋11＝0，得⎩⎪⎨⎪⎧x ＝2，y ＝3，∴定点为(2,3)． 4．解析：选A 直线PQ 的方程为y ＝0，由⎩⎪⎨⎪⎧y ＝－2x ＋b ，y ＝0，得交点⎝⎛⎭⎫b 2，0，由－1≤b 2≤1，得－2≤b ≤2. 5．解析：选D 要使三条直线不能围成三角形，只需其中两条直线平行或三条直线共点．若4x ＋y ＝4与mx ＋y ＝0平行，则m ＝4；若4x ＋y ＝4与2x －3my ＝4平行，则m ＝－16； 若mx ＋y ＝0与2x －3my ＝4平行，则m 不存在；若4x ＋y ＝4与mx ＋y ＝0及2x －3my ＝4共点，则m ＝－1或m ＝23. 6．解析：已知两直线方程可化为l 1：y ＝－a 4x ＋12，l 2：y ＝25x ＋b 5. ∵两直线垂直，∴－a 4·25＝－1，∴a ＝10， 即直线l 1方程为10x ＋4y －2＝0.又点A (1，m )在直线l 1上，∴10×1＋4m －2＝0，∴m ＝－2，即A (1，－2)．又点A 在直线l 2上，∴2×1－5×(－2)＋b ＝0，∴b ＝－12.答案：10 －12 －27．解析：因为直线x －2y ＋1＝0与x ＋3y －1＝0相交于一点，要使三条直线共有两个不同交点，只需ax ＋2y －3＝0与以上两条直线中的一条平行即可，当ax ＋2y －3＝0与x －2y ＋1＝0平行时，有－a 2＝12，解得a ＝－1； 当ax ＋2y －3＝0与x ＋3y －1＝0平行时，有－a 2＝－13，解得a ＝23. 答案：23或－1 8．解析：设BC 的方程为2x ＋3y ＋m ＝0，将点B 的坐标代入，可得m ＝－7，∴BC 的方程为2x ＋3y －7＝0.解方程组⎩⎪⎨⎪⎧2x ＋3y －7＝0，2x －y ＋5＝0.得C (－1,3)． 答案：(－1,3)9．解：联立⎩⎪⎨⎪⎧ x －y ＋1＝0，x ＋2y －5＝0，解得⎩⎪⎨⎪⎧x ＝1，y ＝2， 即直线l 1与直线l 2的交点为(1,2)．∵l ∥l 3，∴l 3的方程可设为4x ＋y ＋b ＝0.将(1,2)代入，得b ＝－6.∴直线l 的方程为4x ＋y －6＝0.10．解：如图所示，∵P A ⊥x 轴，PB ⊥y 轴，P 点坐标为(x ，y )，∴A 点坐标为(x,0)，B 点坐标为(0，y )，由题意可知MA ⊥MB ，当x ≠2时，k MA ·k MB ＝－1，即3－02－x ·3－y 2－0＝－1(x ≠2)，化简得2x ＋3y －13＝0. 当x ＝2时，点P 与M 重合，点P (2,3)的坐标也满足方程2x ＋3y －13＝0.∴点P (x ，y )满足的关系式为2x ＋3y －13＝0.。

一、选择题1．抽查10件产品，记事件A 为“至少有2件次品”，则A 的对立事件为( ) A ．至多有2件次品 B ．至多有1件次品 C ．至多有2件正品 D ．至少有2件正品2．同时掷三枚硬币，那么互为对立事件的是( ) A ．至少有1枚正面向上和最多有1枚正面向上 B ．最多1枚正面向上和恰有2枚正面向上 C ．不多于1枚正面向上和至少有2枚正面向上 D ．至少有2枚正面向上和恰有1枚正面向上3．某产品分甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03、丙级品的概率为0.01，则对成品抽查一件，抽得正品的概率为( )A ．0.09B ．0.98C ．0.97D ．0.964．甲、乙两人下棋，甲获胜的概率为40%，甲不输的概率为90%，则甲、乙两人下成和棋的概率为( )A ．60%B ．30%C ．10%D ．50%5．如果事件A 与B 是互斥事件，则( ) A ．A ∪B 是必然事件 B.A －与B －一定是互斥事件 C.A －与B －一定不是互斥事件 D.A －∪B －是必然事件 二、填空题6．某战士射击一次中靶的概率为0.95，中靶环数大于5的概率为0.75，则中靶环数大于0且小于6的概率为________．(只考虑整数环数)7．盒中有大小、形状相同的黑球、白球和黄球，从中摸出一个球，摸出黑球的概率为0.42，摸出黄球的概率为0.18，则摸出白球的概率为________，摸出的球不是黄球的概率为________，摸出的球是黄球或黑球的概率为________．8．事件A ，B 互斥，它们都不发生的概率为25，且P (A )＝2P (B )，则P (A －)＝________.三、解答题9．某医院一天内派出医生下乡医疗，派出医生的人数及其概率如下：(1)求派出至多2名医生的概率； (2)求派出至少3名医生的概率．10．在数学考试中(满分100分)，小明的成绩在90分以上(包括90分)的概率是0.18，在80～89分的概率是0.51，在70～79分的概率是0.15，在60～69分的概率是0.09.(1)求小明在数学考试中成绩在80分以上(包括80分)的概率； (2)求小明考试不及格(低于60分)的概率．答 案1. 解析：选B 至少有2件次品包含2,3,4,5,6,7,8,9,10件．共9种结果，故它的对立事件为含有1或0件次品，即至多有1件次品．2. 答案：C3. 解析：选D 设“抽得正品”为事件A ，“抽得乙级品”为事件B ，“抽得丙级品”为事件C ，由题意，事件B 与事件C 是互斥事件，而事件A 与并事件(B ＋C )是对立事件；所以P (A )＝1－P (B ＋C )＝1－[P (B )＋P (C )]＝1－0.03－0.01＝0.96. 4. 解析：选D 甲不输，包含两个事件：甲获胜，甲、乙和棋． ∴甲、乙和棋概率P ＝90%－40%＝50%.5. 解析：选D A 、B 可以都不发生，∴选项A 错，A －、B －可以同时发生，即A 、B 可以都不发生，∴选项B 错．当A 与B 是对立事件时A －与B －是互斥事件，∴选项C 错，因为A 、B 互斥，所以A －、B －中至少有一个发生，故选项D 正确．6. 解析：因为某战士射击一次“中靶的环数大于5”事件A 与“中靶的环数大于0且小于6”事件B 是互斥事件，故P (A ＋B )＝0.95.∴P (A )＋P (B )＝0.95，∴P (B )＝0.95－0.75＝0.2. 答案：0.27. 解析：P {摸出白球}＝1－0.42－0.18＝0.4.P {摸出的球不是黄球}＝1－0.18＝0.82. P {摸出的球是黄球或黑球}＝0.42＋0.18＝0.6.答案：0.4 0.82 0.68. 解析：由题意知P (A ＋B )＝1－25，即P (A )＋P (B )＝35.又P (A )＝2P (B )，联立方程组解得P (A )＝25，P (B )＝15，故P (A －)＝1－P (A )＝35.答案：359. 解：记派出医生的人数为0,1,2,3,4,5及其以上分别为事件A 0，A 1，A 2，A 3，A 4，A 5，显然它们彼此互斥．(1)至多2名医生的概率为P (A 0＋A 1＋A 2)＝P (A 0)＋P (A 1)＋P (A 2)＝0.18＋0.25＋0.36＝0.79. (2)法一：至少3名医生的概率为P (C )＝P (A 3＋A 4＋A 5)＝P (A 3)＋P (A 4)＋P (A 5) ＝0.1＋0.1＋0.01＝0.21.法二：“至少3名医生”的反面是“至多2名医生”，故派出至少3名医生的概率为 1－P (A 0＋A 1＋A 2)＝1－0.79＝0.21.10. 解：分别记小明的考试成绩“在90分以上(包括90分)”“在80～89分”“在70～79分”“在60～69分”为事件B ，C ，D ，E .由题意知，这4个事件彼此互斥．(1)小明的考试成绩在80分以上(包括80分)的概率为P (B ＋C )＝P (B )＋P (C )＝0.18＋0.51＝0.69.(2)小明考试及格的概率，即成绩在60分以上(包括60分)的概率为P (B ＋C ＋D ＋E )＝P (B )＋P (C )＋P (D )＋P (E )＝0.18＋0.51＋0.15＋0.09＝0.93.而小明考试不及格与小明考试及格为对立事件，所以小明考试不及格(低于60分)的概率为1－P (B ＋C ＋D ＋E )＝1－0.93＝0.07.。

课下能力提升(十八)一、选择题1．直线3x －2y ＋m ＝0和(m 2＋1)x ＋3y －3m ＝0的位置关系是( )A ．平行B ．重合C ．相交D ．不确定2．直线l 过直线3x －y ＝2和x ＋y ＝6的交点，且过点(－3，－1)，则直线l 的方程为( )A ．2x －y ＋5＝0B ．x ＋y ＋4＝0C ．x －y ＋2＝0D ．3x －y －2＝03．直线(2k －1)x －(k ＋3)y －(k －11)＝0(k ∈R )所经过的定点为( )A ．(2,3)B ．(5,2)C. D ．(5,9)(－12，3)4．已知点P (－1,0)，Q (1,0)，直线y ＝－2x ＋b 与线段PQ 相交，则b 的取值范围是( )A ．[－2,2]B ．[－1,1]C. D ．[0,2][－12，12]5．使三条直线4x ＋y ＝4，mx ＋y ＝0,2x －3my ＝4不能围成三角形的m 值最多有( )A ．1个B ．2个C ．3个D ．4个二、填空题6．已知直线ax ＋4y －2＝0和2x －5y ＋b ＝0垂直且都过点A (1，m )，则a ＝__________，b ＝________，m ＝________.7．若三条直线x －2y ＋1＝0，x ＋3y －1＝0，ax ＋2y －3＝0共有两个不同的交点，则a ＝________.8．在△ABC 中，已知B (2,1)，AC 边所在直线的方程为2x －y ＋5＝0，直线3x －2y ＋1＝0是BC 边的高线，则点C 的坐标为________．三、解答题9．求经过直线l 1：x －y ＋1＝0与l 2：x ＋2y －5＝0的交点且与直线l 3：4x ＋y ＋1＝0平行的直线l 的方程．10．已知点A 是x 轴上的动点，一条直线过点M (2,3)且垂直于MA ，交y 轴于点B ，过A ，B 分别作x ，y 轴的垂线交于点P ，求点P (x ，y )满足的关系式．答案1．解析：选C ∵k 1＝，k 2＝－，∴k 1≠k 2.∴两直线相交．32m 2＋132．解析：选C 由Error!得直线3x －y ＝2和x ＋y ＝6的交点为(2,4)，∵直线l 过点(2,4)和(－3，－1)两点，∴直线l 的方程为＝，即x －y ＋2＝0.y －4－1－4x －2－3－23．解析：选A 将原方程变为k (2x －y －1)－x －3y ＋11＝0，令Error!得Error!∴定点为(2,3)．4．解析：选A 直线PQ 的方程为y ＝0，由Error!得交点，由－1≤≤1，得－2≤b ≤2.(b 2，0)b 25．解析：选D 要使三条直线不能围成三角形，只需其中两条直线平行或三条直线共点．若4x ＋y ＝4与mx ＋y ＝0平行，则m ＝4；若4x ＋y ＝4与2x －3my ＝4平行，则m ＝－；16若mx ＋y ＝0与2x －3my ＝4平行，则m 不存在；若4x ＋y ＝4与mx ＋y ＝0及2x －3my ＝4共点，则m ＝－1或m ＝.236．解析：已知两直线方程可化为l 1：y ＝－x ＋，l 2：y ＝x ＋.a 41225b 5∵两直线垂直，∴－·＝－1，∴a ＝10，a 425即直线l 1方程为10x ＋4y －2＝0.又点A (1，m )在直线l 1上，∴10×1＋4m －2＝0，∴m ＝－2，即A (1，－2)．又点A 在直线l 2上，∴2×1－5×(－2)＋b ＝0，∴b ＝－12.答案：10　－12　－27．解析：因为直线x －2y ＋1＝0与x ＋3y －1＝0相交于一点，要使三条直线共有两个不同交点，只需ax ＋2y －3＝0与以上两条直线中的一条平行即可，当ax ＋2y －3＝0与x －2y ＋1＝0平行时，有－＝，解得a ＝－1；a 212当ax ＋2y －3＝0与x ＋3y －1＝0平行时，有－＝－，解得a ＝.a 21323答案：或－1238．解析：设BC 的方程为2x ＋3y ＋m ＝0，将点B 的坐标代入，可得m ＝－7，∴BC 的方程为2x ＋3y －7＝0.解方程组Error!得C (－1,3)．答案：(－1,3)9．解：联立Error!解得Error!即直线l 1与直线l 2的交点为(1,2)．∵l ∥l 3，∴l 3的方程可设为4x ＋y ＋b ＝0.将(1,2)代入，得b ＝－6.∴直线l 的方程为4x ＋y －6＝0.10．解：如图所示，∵PA ⊥x 轴，PB ⊥y 轴，P 点坐标为(x ，y )，∴A 点坐标为(x,0)，B 点坐标为(0，y )，由题意可知MA ⊥MB ，当x ≠2时，k MA ·k MB ＝－1，即·＝－1(x ≠2)，化简得2x ＋3y －13＝0.3－02－x 3－y2－0当x＝2时，点P与M重合，点P(2,3)的坐标也满足方程2x＋3y－13＝0.∴点P(x，y)满足的关系式为2x＋3y－13＝0.。

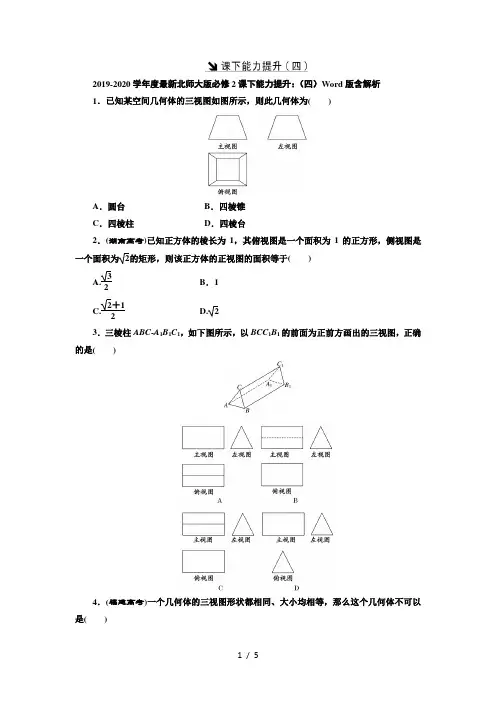
2019-2020学年度最新北师大版必修2课下能力提升：（四）Word版含解析1．已知某空间几何体的三视图如图所示，则此几何体为()A．圆台B．四棱锥C．四棱柱D．四棱台2．(湖南高考)已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于()A.32B．1C.2＋12 D. 23．三棱柱ABC-A1B1C1，如下图所示，以BCC1B1的前面为正前方画出的三视图，正确的是()4．(福建高考)一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是()A ．球B ．三棱锥C ．正方体D ．圆柱5．一个几何体的三视图如图所示，其中主视图中△ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的左视图的面积为( )A.32B.23 C ．12 D ．6 二、填空题6．如图所示，为一个简单几何体的三视图，它的上部是一个________，下部是一个________．7．用小正方体搭成一个几何体，如图是它的主视图和左视图，搭成这个几何体的小正方体的个数最多为________个．8．如图(1)，E 、F 分别为正方体的面ADD 1A 1和面BCC 1B 1的中心，则四边形BED 1F 在该正方体的面上的射影可能是图(2)中的________(要求：把可能的图的序号都填上)．三、解答题9．如图所示，图②是图①中实物的主视图和俯视图，你认为正确吗？如果不正确，请找出错误并改正，然后画出它的左视图．10．某建筑由若干个面积相同的房间组成，其三视图如下，其中每一个小矩形表示一个房间．(1)该楼有几层？共有多少个房间？(2)画出此楼的大致形状．答案1. 解析：选D由主视图和左视图可以判断一定为棱台或圆台，又由俯视图可知其一定为棱台且为四棱台．2. 解析：选D由已知，正方体的正视图与侧视图都是长为2，宽为1的矩形，所以正视图的面积等于侧视图的面积，为 2.3. 解析：选A正面是BCC1B1的矩形，故主视图为矩形，左侧为△ABC，所以左视图为三角形，俯视图为两个有一条公共边的矩形，公共边为CC1在面ABB1A1内的投影．4. 解析：选D球的三视图是三个相同的圆；当三棱锥为正三棱锥时其三视图可能是三个全等的三角形；正方体的三视图可能是三个相同的正方形；不论圆柱如何放置，其三视图形状都不会完全相同．5. 解析：选A由主视图、左视图、俯视图之间的关系可以判断该几何体是一个底面为正六边形的正六棱锥．∵主视图中△ABC是边长为2的正三角形，此三角形的高为3，∴左视图的高为 3.俯视图中正六边形的边长为1，其小正三角形的高为32，∴左视图的底为32×2＝3， ∴左视图的面积为12×3×3＝32.6. 解析：由三视图可知该几何体图示为所以，其上部是一个圆锥，下部是一个圆柱． 答案：圆锥 圆柱7. 解析：其俯视图如图所示时为小正方体个数最多情况(其中小正方形内的数字表示小正方体的个数)共需7个小正方体.答案：78. 解析：根据平行投影的理论，从正方体的上下、前后、左右三个角度分别投影，从上往下投影，选择②，从前往后投影，选择②，从左往右投影，选择③.答案：②③9. 解：图①是由两个长方体组合而成的，主视图正确，俯视图错误．俯视图应该画出不可见轮廓(用虚线表示)，左视图轮廓是一个矩形，有一条可视的交线(用实线表示)，正确画法如图所示．10. 解：(1)由主视图和左视图可知，该楼共3层，由俯视图可知，该楼一楼有5个房间，结合主视图与左视图，易知二楼和三楼分别有4个，1个房间，故共10个房间．(2)此楼的大致形状如图：。

一、选择题1．设a，b是两条直线，α，β是两个平面，若a∥α，a β，α∩β＝b，则α内与b相交的直线与a的位置关系是()A．平行B．相交C．异面D．平行或异面2．平面α∩平面β＝a，平面β∩平面γ＝b，平面γ∩平面α＝c，若a∥b，则c与a，b 的位置关系是()A．c与a，b都异面B．c与a，b都相交C．c至少与a，b中的一条相交D．c与a，b都平行3．下列说法正确的个数为()①两平面平行，夹在两平面间的平行线段相等；②两平面平行，夹在两平面间的相等的线段平行；③如果一条直线和两个平行平面中的一个平行，那么它和另一个平面也平行；④两平行直线被两平行平面截得的线段相等．A．1 B．2C．3 D．44．如图，P是△ABC所在平面外一点，平面α∥平面ABC，α分别交线段P A，PB，PC 于A′，B′，C′，若P A′∶AA′＝2∶3，则△A′B′C′与△ABC面积的比为()A．2∶5B．3∶8C．4∶9 D．4∶255．若不在同一直线上的三点A、B、C到平面α的距离相等，且A∉α，则()A．α∥平面ABCB．△ABC中至少有一边平行于αC．△ABC中至多有两边平行于αD．△ABC中只可能有一边与α相交二、填空题6．如图，正方体ABCD-A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．7．在棱长为a 的正方体ABCD -A 1B 1C 1D 1中，M ，N 分别是棱A 1B 1，B 1C 1的中点，P 是棱AD 上一点，AP ＝a 3，过P ，M ，N 的平面与棱CD 交于Q ，则PQ ＝________. 8．如图所示，直线a ∥平面α，点A 在α另一侧，点B ，C ，D ∈a .线段AB ，AC ，AD 分别交α于点E ，F ，G .若BD ＝4，CF ＝4，AF ＝5，则EG ＝________.三、解答题9．如图，棱柱ABC -A 1B 1C 1的侧面BCC 1B 1是菱形，设D 是A 1C 1上的点且A 1B ∥平面B 1CD ，求A 1D ∶DC 1的值．10．在底面是平行四边形的四棱锥P -ABCD 中，点E 在PD 上，且PE ∶ED ＝2∶1，如图，在棱PC 上是否存在一点F ，使BF ∥平面AEC ，证明你的结论．答 案1. 解析：选C a ∥α，a 与α内的直线没有公共点，所以，a 与α内的直线的位置关系是异面或平行，α内与b 平行的直线与a 平行，α内与b 相交的直线与a 异面．2. 解析：选D 如图：∵a ∥b ，且a γ，b γ，∴a ∥γ，∵a α且α∩γ＝c ，∴a ∥c ，∴b ∥c .3. 解析：选B 易知①④正确，②不正确；③若α∥β、a β，则a 与α平行，故③不正确．4. 解析：选D 由题意知，△A ′B ′C ′∽△ABC ，从而S △A ′B ′C ′S △ABC＝⎝⎛⎭⎫P A ′P A 2＝⎝⎛⎭⎫252＝425. 5. 解析：选B 若三点在平面α的同侧，则α∥平面ABC ，有三边平行于α.若一点在平面α的一侧，另两点在平面α的另一侧，则有两边与平面α相交，有一边平行于α，故 △ABC 中至少有一边平行于α.6. 解析：因为直线EF ∥平面AB 1C ，EF 平面ABCD ，且平面AB 1C ∩平面ABCD ＝AC ，所以EF ∥AC ，又因为E 是DA 的中点，所以F 是DC 的中点，由中位线定理可得：EF ＝12AC ，又因为在正方体ABCD -A 1B 1C 1D 1中，AB ＝2，所以AC ＝22，所以EF ＝ 2. 答案： 27. 解析：∵MN ∥平面AC ，PQ ＝平面PMN ∩平面AC ，∴MN ∥PQ ，易知DP ＝DQ ＝2a 3， 故PQ ＝PD 2＋DQ 2＝2DP ＝22a 3. 答案：22a 38. 解析：A ∉a ，则点A 与直线a 确定一个平面，即平面ABD .因为a ∥α，且α∩平面ABD ＝EG ，所以a ∥EG ，即BD ∥EG . 所以AF AC ＝AE AB ，又EG BD ＝AE AB ，所以AF AC ＝EG BD. 于是EG ＝AF ·BD AC ＝5×45＋4＝209. 答案：2099. 解：设BC 1交B 1C 于点E ，连接DE ，则DE是平面A1BC1与平面B1CD的交线．因为A1B∥平面B1CD，且A1B 平面A1BC1，所以A1B∥DE.又E是BC1的中点，所以D为A1C1的中点，即A1D∶DC1＝1.10. 解：当F为PC的中点时，BF∥平面AEC.证明如下：如图，取PE的中点M，连接MF、MB，则MF∥CE，∵PE∶ED＝2∶1，∴点E也是MD的中点，连接BD，设BD∩AC＝O. ∵ABCD是平行四边形，∴O是BD的中点．∴OE∥BM，而BM 平面AEC，OE 平面AEC，∴BM∥平面AEC，同理FM∥平面AEC.又BM∩FM＝M，∴平面BMF∥平面AEC.又BF 平面BMF，∴BF∥平面AEC.。

课下能力提升(二十五)一、选择题1．点B 是点A (1,2,3)在坐标平面上yOz 内的射影，则|OB |等于( ) A.14 B.13C ．2 3 D.112．点P ⎝⎛⎭⎫22，33，66到原点O 的距离是( ) A.306 B ．1 C.336 D.3563．已知点A (x,1,2)和点B (2,3,4)，且|AB |＝26，则实数x 的值是( )A ．－3或4B ．6或2C ．3或－4D ．6或－24．已知三点A (－1,0,1)，B (2,4,3)，C (5,8,5)，则A 、B 、C 三点( )A ．构成等腰三角形B ．构成直角三角形C ．构成等腰直角三角形D ．不能构成三角形5．在空间直角坐标系中，与点A (3,1,2)，B (4，－2，－2)，C (0，5,1)等距离的点的个数为( )A ．1B ．2C ．3D ．无数二、填空题6．已知正方体不在同一表面上的两顶点A (－1,2，－1)，B (3，－2,3)，则正方体的体积是________．7．点A (2，－1,2)到y 轴的距离为________．8．Rt △ABC 中，∠BAC ＝90°，A (2,1,1)，B (1,1,2)，C (x ，0,1)，则x ＝________.三、解答题9．已知正三棱锥A -BCD ，高为1，底面正三角形边长为3，建立适当坐标系写出A 、B 、C 、D 四点的坐标，并求侧棱AB 的长度．10．如图，以正方体的三条棱所在直线为坐标轴，建立空间直角坐标系O -xyz ，点P 在正方体的对角线AB 上，点Q 在正方体的棱CD 上．(1)当点P 为对角线AB 的中点，点Q 在棱CD 上运动时，探究|PQ |的最小值；(2)当点Q 为棱CD 的中点，点P 在对角线AB 上运动时，探究|PQ |的最小值．答案1．解析：选B B 点坐标为(0,2,3)，∴|OB |＝13.2．解析：选B |OP |＝ ⎝⎛⎭⎫22－02＋⎝⎛⎭⎫33－02＋⎝⎛⎭⎫66－02 ＝ 12＋13＋16＝1. 3．解析：选D 由空间两点间的距离公式得(x －2)2＋(1－3)2＋(2－4)2＝26，解得x ＝6或x ＝－2.4．解析：选D 由已知得|AB |＝(－1－2)2＋(0－4)2＋(1－3)2＝29， |AC |＝(－1－5)2＋(0－8)2＋(1－5)2＝116＝229，|BC |＝(2－5)2＋(4－8)2＋(3－5)2＝29，∴|AB |＋|BC |＝|AC |，故不能构成三角形．5．解析：选D 由两点间距离公式可得|AB |＝26，|BC |＝74，|AC |＝26，易知A 、B 、C 三点不共线，故可确定一个平面．在△ABC 所在平面内可找到一点到A 、B 、C 距离相等，而过该点与面ABC 垂直的直线上的每一点到A 、B 、C 距离均相等．6．解析：设正方体棱长为a ，则a 2＋a 2＋a 2＝|AB |＝42＋(－4)2＋42，所以a ＝4，V ＝43＝64.答案：647．解析：点A 在y 轴上的投影为(0，－1,0)，∴点A 到y 轴的距离为22＋(－1＋1)2＋22＝2 2. 答案：2 28．解析：由距离公式|AB |＝(2－1)2＋(1－1)2＋(1－2)2＝2； |AC |＝(2－x )2＋(1－0)2＋(1－1)2＝(2－x )2＋1； |BC |＝(1－x )2＋(1－0)2＋(2－1)2＝(1－x )2＋2；∵∠BAC ＝90°，∴|BC |2＝|AB |2＋|AC |2，∴(1－x )2＋2＝2＋(2－x )2＋1，解得x ＝2.答案：29．解：设O 为A 在底面BCD 上的射影，则O 为正三角形BCD 的中心．如图以OB 所在直线为x 轴，以OA 所在直线为z 轴，以过O 与CD 平行的直线为y 轴，建立空间直角坐标系，设CD 中点为E ，由BC ＝3，O 为△BCD 中心可知，|OB |＝23|BE |＝23·32|BC |＝1，|OE |＝12|OB |＝12， ∴B (1,0,0)，E ⎝⎛⎭⎫－12，0，0. 又|CE |＝|ED |＝32， ∴C ⎝⎛⎭⎫－12，32，0，D ⎝⎛⎭⎫－12，－32，0. 又∵A 在z 轴上，且|AO |＝1，∴A (0,0,1)．由两点间的距离公式|AB |＝(1－0)2＋(0－0)2＋(0－1)2＝2，∴各点坐标为A (0,0,1)，B (1,0,0)，C ⎝⎛⎭⎫－12，32，0，D ⎝⎛⎭⎫－12，－32，0，侧棱AB 长为 2.10．解：设正方体的棱长为a .(1)当点P 为对角线AB 的中点时，点P 的坐标是(a 2，a 2，a 2)．因为点Q 在线段CD 上，设Q (0，a ，z )．|PQ |＝ ⎝⎛⎭⎫a 22＋⎝⎛⎭⎫a 2－a 2＋⎝⎛⎭⎫z －a 22。

一、选择题1．已知b是平面α外的一条直线，下列条件中，可得出b∥α的是()A．b与α内的一条直线不相交B．b与α内的两条直线不相交C．b与α内的无数条直线不相交D．b与α内的所有直线不相交2．空间四边形ABCD中，E，F分别是AB和BC上的点，若AE∶EB＝CF∶FB＝1∶3，则对角线AC和平面DEF的关系是()A．平行B．相交C．在平面内D．平行或相交3．如图是正方体的平面展开图，则在这个正方体中，下列判断正确的是()A．平面BME∥平面ACNB．AF∥CNC．BM∥平面EFDD．BE与AN相交4．已知m，n表示两条直线，α，β，γ表示平面，下列结论中正确的个数是()①若α∩γ＝m，β∩γ＝n，m∥n，则α∥β；②若m，n相交且都在α，β外，且m∥α，m∥β，n∥α，n∥β，则α∥β；③若m∥α，m∥β，则α∥β；④若m∥α，n∥β，且m∥n，则α∥βA．1 B．2C．3 D．45．在正方体ABCD-A1B1C1D1中，M是棱A1D1上的动点，则直线MD与平面A1ACC1的位置关系是()A．平行B．相交C．在平面内D．相交或平行二、填空题6．点E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，则空间四边形的六条棱中与平面EFGH平行的条数是________．7．三棱锥S-ABC中，G为△ABC的重心，E在棱SA上，且AE＝2ES，则EG与平面SBC的关系为________．8．如图，在正方体ABCD-A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足________时，有MN∥平面B1BDD1.三、解答题9．已知：△ABC中，∠ACB＝90°，D，E分别为AC，AB的中点，沿DE将△ADE 折起，使A到A′的位置，M是A′B的中点，求证：ME∥平面A′CD.10．如图，在正方体ABCD-A1B1C1D1中，S是B1D1的中点，E，F，G分别是BC，DC 和SC的中点．求证：(1)EG∥平面BDD1B1；(2)平面EFG∥平面BDD1B1.答案1. 解析：选D若b与α内的所有直线不相交，即b与α无公共点，故b∥α.2. 解析：选A如图所示，在平面ABC内，因为AE∶EB＝CF∶FB＝1∶3，所以AC∥EF.又因为AC 平面DEF，EF 平面DEF，所以AC∥平面DEF.3. 解析：选A作出如图所示的正方体．易知AN∥BM，AC∥EM，且AN∩AC＝A，所以平面ACN∥平面BEM.4. 解析：选A①仅满足mα，nβ，m∥n，不能得出α∥β，不正确；②设m，n 确定平面为γ，则有α∥γ，β∥γ，从而α∥β，正确；③④均不满足两个平面平行的条件，故③④均不正确．5. 解析：选D当M与D 1重合时，∵DD1∥A1A，DD1面AA1C1C，AA1面AA1C1C，∴MD∥面AA1C1C.当M不与D1重合时，DM与AA1相交，也即DM与面AA1C1C相交．6. 解析：由线面平行的判定定理知：BD∥平面EFGH，AC∥平面EFGH.答案：27. 解析：如图，取BC中点F，连SF.∵G为△ABC的重心，∴A，G，F共线且AG＝2GF.又∵AE＝2ES，∴EG∥SF.又SF 平面SBC，EG平面SBC，∴EG∥平面SBC.答案：EG∥平面SBC8. 解析：∵HN∥BD，HF∥DD1，HN∩HF＝H，BD∩DD1＝D，∴平面NHF∥平面B1BDD1，故线段FH上任意点M与N连接，有MN∥平面B1BDD1.答案：M∈线段FH。

一、选择题1．某牛奶生产线上每隔30分钟抽取一袋进行检验，该抽样方法记为①；从某中学的30名数学爱好者中抽取3人了解学业负担情况，该抽样方法记为②.那么( )A．①是系统抽样，②是简单随机抽样B．①是简单随机抽样，②是简单随机抽样C．①是简单随机抽样，②是系统抽样D．①是系统抽样，②是系统抽样2．(四川高考)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43，则这四个社区驾驶员的总人数N为( )A．101 B．808 C．1 212 D．2 0123．(湖南高考)某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n＝( )A．9 B．10 C．12 D．134．下列抽样中不是系统抽样的是( )A．从标有1～15号的15个球中，任选3个作为样本．将15个球按从小号到大号排序，随机选i0号作为起始号码，以后选i0＋5，i0＋10(超过15则从1再数起)号入样B．工厂生产的产品，在用传送带将产品送入包装车间前，检验人员从传送带上每隔五分钟抽取一件产品进行检验C．进行某一市场调查时，规定在商场门口随机抽取一个人进行询问调查，直到调查到事先规定的调查人数为止D．在报告厅对与会听众进行调查，通知每排(每排人数相等)座位号为14的听众留下来座谈5．某学校有职工140人，其中教师91人，教辅行政人员28人，总务后勤人员21人．为了了解职工的某种情况，要从中抽取一个容量为20的样本．以下的抽样方法中，依次为简单随机抽样、系统抽样、分层抽样顺序的是( )方法1：将140人从1～140编号，然后制作出编号1～140的形状、大小相同的号签，并将号签放入同一箱子里均匀搅拌，然后从中依次抽取20个号签，编号与号签相同的20个人被选出；方法2：将140人分成20组，每组7人，并将每组7人按1～7编号，在第一组采用抽签法抽出k 号(1≤k ≤7)，其余各组k 号也被抽出，20个人被选出；方法3：按20∶140＝1∶7的比例，从教师中抽出13人，从教辅行政人员中抽出4人，从总务后勤人员中抽出3人．从各类人员中抽取所需人员时，均采用随机数法，可抽到20人．A ．方法2，方法1，方法3B ．方法2，方法3，方法1C ．方法1，方法2，方法3D ．方法3，方法1，方法2二、填空题6．(浙江高考)某个年级有男生560人，女生420人，用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，则此样本中男生人数为________．7．某学校高一、高二、高三三个年级共有学生3 500人，其中高三学生数是高一学生数的两倍，高二学生数比高一学生数多300人，现在按1100的抽样比用分层抽样的方法抽取样本，则应抽取高一学生数为________．8．一个总体中有100个个体，随机编号为0、1、2、…、99，依编号顺序平均分成10个小组，组号依次为1、2、3、…、10.现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m ，那么在第k 组中抽取的号码个位数字与m ＋k 的个位数字相同．若m ＝6，则在第7组中抽取的号码是________．三、解答题9．为了调查某路口一个月的车流量情况，交警采用系统抽样的方法，样本距为7，从每周中随机抽取一天，他正好抽取的是星期日，经过调查后做出报告．你认为交警这样的抽样方法有什么问题？应当怎样改进？如果是调查一年的车流量情况呢？10．某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加其中一组．在参加活动的职工中，青年人占42.5%，中年人占47.5%，老年人占10%.登山组的职工占参加活动总人数的14，且该组中，青年人占50%，中年人占40%，老年人占10%.为了了解各组不同的年龄层的职工对本次活动的满意程度，现用分层抽样的方法从参加活动的全体职工中抽取容量为200的样本．试求：(1)游泳组中，青年人、中年人、老年人分别所占的比例；(2)游泳组中，青年人、中年人、老年人分别应抽取的人数．答 案1. 解析：选A 对于①，因为每隔30分钟抽取一袋，是等间距抽样，故①为系统抽样；对于②，总体数量少，样本容量也小，故②为简单随机抽样．2. 解析：选B 依题意得知，甲社区驾驶员的人数占总人数的1212＋21＋25＋43＝12101，因此有96N ＝12101，解得N ＝808. 3. 解析：选D 由分层抽样可得，360＝n 260，解得n ＝13. 4. 解析：选C 分析各选项中抽样的特点，与系统抽样的概念、特点进行比较．A 、D 显然是系统抽样．B 项中，传送带的速度是恒定的，实际上是将某一段时间内生产的产品分成一组，且可以认为这些产品已经排好，又总在某一位置抽取样品，这正好符合系统抽样的概念．选项C 因事先不知道总体的个数，而且抽样时不能保证每个个体等可能入样，因此它不是系统抽样．5. 解析：选C 结合简单随机抽样、系统抽样、分层抽样的定义判断．6. 解析：由分层抽样得，此样本中男生人数为560×280560＋420＝160. 答案：1607. 解析：若设高三学生数为x ，则高一学生数为x 2，高二学生数为x 2＋300，所以有x ＋x 2＋x 2＋300＝3 500，解得x ＝1 600.故高一学生数为800，因此应抽取高一学生数为800100＝8. 答案：88. 解析：第k 组的号码为(k －1)10，(k －1)10＋1，…，(k －1)·10＋9，当m ＝6、k ＝7时，第k 组抽取的号码m ＋k 的个位数字为3，所以(7－1)×10＋3＝63.答案：639. 解：交警所统计的数据以及由此所推断出来的结论，只能代表星期日的交通流量．由于星期日是休息时间，很多人不上班，不能代表其他几天的情况．改进方法可以将所要调查的时间段的每一天先随机地编号，再用系统抽样方法来抽样，或者使用简单随机抽样来抽样亦可．如果是调查一年的交通流量，使用简单随机抽样法显然已不合适，比较简单可行的方法是把样本距改为8.。

课下能力提升(二十一)一、选择题1．若圆x 2＋y 2－2x －4y ＝0的圆心到直线x －y ＋a ＝0的距离为22，则a 的值为( ) A ．－2或2 B.12或32C ．2或0D ．－2或02．已知圆C 的半径长为2，圆心在x 轴的正半轴上，直线3x ＋4y ＋4＝0与圆C 相切，则圆C 的方程为( )A ．x 2＋y 2－2x －3＝0B ．x 2＋y 2＋4x ＝0C ．x 2＋y 2＋2x －3＝0D ．x 2＋y 2－4x ＝03．圆x 2＋y 2－2x －2y ＋1＝0上的点到直线x －y ＝2的距离的最大值是( )A ．2B ．1＋2C ．2＋22D ．1＋22 4．已知圆C ：x 2＋y 2＋mx －4＝0上存在两点关于直线x －y ＋3＝0对称，则实数m 等于( )A ．8B ．－4C ．6D ．无法确定5．圆的方程为x 2＋y 2＋kx ＋2y ＋k 2＝0，当圆面积最大时，圆心坐标为( )A ．(－1,1)B ．(1，－1)C ．(－1,0)D ．(0，－1)二、填空题6．过点(－3，－2)的直线l 经过圆x 2＋y 2－2y ＝0的圆心，则直线l 的倾斜角大小为________．7．若直线3x －4y ＋12＝0与两坐标轴交点为A ，B ，则以线段AB 为直径的圆的一般方程为________．8．若点(a ＋1，a －1)在圆x 2＋y 2－2ay －4＝0的内部(不包括边界)，则a 的取值范围是________．三、解答题9．若点A (1，－1)，B (1,4)，C (4，－2)，D (a,1)共圆，求a 的值．10．求经过A (4,2)、B (－1,3)两点，且在两坐标轴上的四个截距之和是2的圆的方程．答案1．解析：选C 由圆的方程得圆心坐标为(1,2)．再由点到直线的距离公式得|1－2＋a|2＝22，解得a ＝2或a ＝0.2．解析：选D 设圆心为(a,0)，且a ＞0，则(a,0)到直线3x ＋4y ＋4＝0的距离为2，即|3×a ＋4×0＋4|32＋42＝2⇒3a ＋4＝±10⇒a ＝2或a ＝－143(舍去)，则圆的方程为(x －2)2＋(y －0)2＝22，即x 2＋y 2－4x ＝0. 3．解析：选B 圆的方程变为(x －1)2＋(y －1)2＝1，∴圆心为(1,1)，半径为1，圆心到直线的距离d ＝|1－1－2|12＋－＝2，∴所求的最大值为1＋2.4．解析：选C 因为圆上两点A ，B 关于直线x －y ＋3＝0对称，所以直线x －y ＋3＝0过圆心⎝⎛⎭⎫－m 2，0，从而－m 2＋3＝0，即m ＝6. 5．解析：选D 方程变形为⎝⎛⎭⎫x ＋k 22＋(y ＋1)2＝1－34k 2， ∴r 2＝1－34k 2，当k ＝0时，r 有最大值．∴圆心坐标为(0，－1)． 6．解析：由x 2＋y 2－2y ＝0，得x 2＋(y －1)2＝1，∴圆心为(0,1)，∴k ＝错误!＝错误!＝错误!.∴直线的倾斜角为60°.答案：60°7．解析：依题意A (－4,0)，B (0,3)，∴AB 中点C 的坐标为⎝⎛⎭⎪⎫－2，32， 半径r ＝|AC |＝ 错误!＝错误!，∴圆的方程为(x ＋2)2＋⎝ ⎛⎭⎪⎫y －322＝⎝ ⎛⎭⎪⎫522， 即x 2＋y 2＋4x －3y ＝0.答案：x 2＋y 2＋4x －3y ＝08．解析：∵点(a ＋1，a －1)在圆x 2＋y 2－2ay －4＝0内部，∴错误!即2a ＜2，a ＜1.答案：(－∞，1)9．解：设圆的方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0，将A ，B ，C 三点坐标代入，整理得方程组⎩⎪⎨⎪⎧ D －E ＋F ＝－2，D ＋4E ＋F ＝－17，4D －2E ＋F ＝－20，解得D ＝－7，E ＝－3，F ＝2.∴圆的方程为x 2＋y 2－7x －3y ＋2＝0.又∵点D 在圆上，∴a 2＋1－7a －3＋2＝0.∴a ＝0或a ＝7.10．解：设所求圆的方程为x 2＋y 2＋Dx ＋Ey ＋F ＝0，令y ＝0得x 2＋Dx ＋F ＝0，∴圆在x 轴上的截距之和为x 1＋x 2＝－D .令x ＝0得y 2＋Ey ＋F ＝0，∴圆在y 轴的截距之和为y 1＋y 2＝－E .由题设x 1＋x 2＋y 1＋y 2＝－(D ＋E )＝2.∴D ＋E ＝－2.①又A (4,2)，B (－1,3)在圆上，∴16＋4＋4D ＋2E ＋F ＝0，②1＋9－D＋3E＋F＝0.③由①②③解得D＝－2，E＝0，F＝－12. 故所求圆的方程为x2＋y2－2x－12＝0.。

2019-2020学年度最新北师大版必修2课下能力提升：（十五）Word版含解析1．下列四个结论：①方程k＝y－2x＋1与方程y－2＝k(x＋1)可表示同一直线；②直线l过点P(x1，y1)，倾斜角为90°，则其方程是x＝x1；③直线l过点P(x1，y1)，斜率为0，则其方程是y＝y1；④所有的直线都有点斜式和斜截式方程．正确的结论有()A．1个B．2个C．3个D．4个2．直线y＝ax－1a的图像可能是()3．直线l过点(－1，－1)，(2,5)两点，点(1 005，b)在l上，则b的值为()A．2 009 B．2 010 C．2 011 D．2 0124．直线l的方程为y＝3x＋2，若直线l′与l关于y轴对称，则直线l′的方程为()A．y＝－3x＋2 B．y＝－33x＋2C．y＝3x－2 D．y＝－3x－25．在等腰△ABO中，AO＝AB，点O(0,0)，A(1,3)，而点B在x轴的正半轴上，则直线AB的方程为()A．y－1＝3(x－3) B．y－1＝－3(x－3)C．y－3＝3(x－1) D．y－3＝－3(x－1)二、填空题6．若直线y＝2x＋b与坐标轴围成的三角形的面积为9，则b＝________.7．直线l的方程为x－y－(m2－m＋1)＝0，若l在y轴上的截距为－3，则m的值为________．8．直线过点(1,2)且与直线2x＋3y－9＝0在y轴上的截距相等，则直线l的方程为________．三、解答题9．已知△ABC的三个顶点在第一象限，A(1,1)，B(5,1)，A＝45°，B＝45°，求：(1)AB 所在直线的方程；(2)AC 边和BC 边所在直线的方程．10．求过点(2,3)且与两坐标轴的交点到原点的距离相等的直线方程．答 案1. 解析：选B ①中方程k ＝y －2x ＋1表示的直线不能过(－1,2)，而y －2＝k (x ＋1)表示过(－1,2)点、斜率为k 的直线，∴二者不能表示同一直线；②③正确；④中，点斜式、斜截式不能表示平行于y 轴的直线，∴结论错误．2. 解析：选B 在B 中，直线的倾斜角为钝角，故斜率a ＜0，直线在y 轴上截距－1a ＞0，与直线和y 轴正半轴有交点，符合要求．3. 解析：选C ∵直线斜率k ＝5－(－1)2－(－1)＝2， ∴直线的点斜式方程为y －5＝2(x －2)，即y ＝2x ＋1，令x ＝1 005，得b ＝2 011.4. 解析：选A ∵l ′与l 关于y 轴对称，直线l 过定点(0,2)，∴直线l ′也过点(0,2)．直线l 的斜率为3，∴l 的倾斜角为60°，l ′的倾斜角为180°－60°＝120°.∴l ′的斜率为－ 3.∴直线l ′的方程为y ＝－3x ＋2.5. 解析：选D 由题意，OA 与OB 的倾斜角互补．k OA ＝3 ，k AB ＝－3.∴AB 的方程为y －3＝－3(x －1)．6. 解析：令x ＝0，得y ＝b ，令y ＝0，得x ＝－b 2， ∴所求的面积S ＝12|b |·⎪⎪⎪⎪－b 2＝14b 2＝9.∴b ＝±6. 答案：±67. 解析：由题知3－(m 2－m ＋1)＝0，解得：m ＝－1或2.答案：－1或28. 解析：直线2x ＋3y －9＝0在y 轴上的截距为3，即直线l 过(0,3)．∴直线l 的斜率k＝3－20－1＝－1. ∴l 的方程为y ＝－x ＋3，即x ＋y －3＝0.答案：x ＋y －3＝09. 解：根据已知条件，画出示意图如图．(1)由题意知，直线AB 平行于x 轴，由A ，B 两点的坐标知，直线AB 的方程为y ＝1.(2)由题意知，直线AC 的倾斜角等于角A ，所以k AC ＝tan 45°＝1，又点A (1,1)，所以直线AC 的方程为y －1＝1·(x －1)，即y ＝x .同理可知，直线BC 的倾斜角等于180°－B ＝135°，所以k BC ＝tan 135°＝－1，又点B (5,1)，所以直线BC 的方程为y －1＝－1·(x －5)，即y ＝－x ＋6.10. 解：由条件知该直线的斜率存在且不为0，由点斜式可设直线方程为y －3＝k (x －2)．令x ＝0得y ＝3－2k .令y ＝0得x ＝2－3k. 由|3－2k |＝|2－3k |，得k ＝－1或k ＝32，或k ＝1. 故直线方程为y ＝－x ＋5或y ＝32x 或y ＝x ＋1.。

2019-2020年高中数学课下能力提升十八北师大版一、选择题1．抽查10件产品，记事件A 为“至少有2件次品”，则A 的对立事件为( )A ．至多有2件次品B ．至多有1件次品C ．至多有2件正品D ．至少有2件正品2．同时掷三枚硬币，那么互为对立事件的是( )A ．至少有1枚正面向上和最多有1枚正面向上B ．最多1枚正面向上和恰有2枚正面向上C ．不多于1枚正面向上和至少有2枚正面向上D ．至少有2枚正面向上和恰有1枚正面向上3．某产品分甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03、丙级品的概率为0.01，则对成品抽查一件，抽得正品的概率为( )A ．0.09B ．0.98C ．0.97D ．0.964．甲、乙两人下棋，甲获胜的概率为40%，甲不输的概率为90%，则甲、乙两人下成和棋的概率为( )A ．60%B ．30%C ．10%D ．50%5．如果事件A 与B 是互斥事件，则( )A ．A ∪B 是必然事件B.A －与B －一定是互斥事件C.A －与B －一定不是互斥事件D.A －∪B －是必然事件二、填空题6．某战士射击一次中靶的概率为0.95，中靶环数大于5的概率为0.75，则中靶环数大于0且小于6的概率为________．(只考虑整数环数)7．盒中有大小、形状相同的黑球、白球和黄球，从中摸出一个球，摸出黑球的概率为0.42，摸出黄球的概率为0.18，则摸出白球的概率为________，摸出的球不是黄球的概率为________，摸出的球是黄球或黑球的概率为________．8．事件A ，B 互斥，它们都不发生的概率为25，且P (A )＝2P (B )，则P (A －)＝________. 三、解答题9．某医院一天内派出医生下乡医疗，派出医生的人数及其概率如下：(1)(2)求派出至少3名医生的概率．10．在数学考试中(满分100分)，小明的成绩在90分以上(包括90分)的概率是0.18，在80～89分的概率是0.51，在70～79分的概率是0.15，在60～69分的概率是0.09.(1)求小明在数学考试中成绩在80分以上(包括80分)的概率；(2)求小明考试不及格(低于60分)的概率．答 案1. 解析：选B 至少有2件次品包含2,3,4,5,6,7,8,9,10件．共9种结果，故它的对立事件为含有1或0件次品，即至多有1件次品．2. 答案：C3. 解析：选D 设“抽得正品”为事件A ，“抽得乙级品”为事件B ，“抽得丙级品”为事件C ，由题意，事件B 与事件C 是互斥事件，而事件A 与并事件(B ＋C )是对立事件；所以P (A )＝1－P (B ＋C )＝1－[P (B )＋P (C )]＝1－0.03－0.01＝0.96.4. 解析：选D 甲不输，包含两个事件：甲获胜，甲、乙和棋．∴甲、乙和棋概率P ＝90%－40%＝50%.5. 解析：选D A 、B 可以都不发生，∴选项A 错，A －、B －可以同时发生，即A 、B 可以都不发生，∴选项B 错．当A 与B 是对立事件时A －与B －是互斥事件，∴选项C 错，因为A 、B 互斥，所以A －、B －中至少有一个发生，故选项D 正确．6. 解析：因为某战士射击一次“中靶的环数大于5”事件A 与“中靶的环数大于0且小于6”事件B 是互斥事件，故P (A ＋B )＝0.95.∴P (A )＋P (B )＝0.95，∴P (B )＝0.95－0.75＝0.2.答案：0.27. 解析：P {摸出白球}＝1－0.42－0.18＝0.4.P {摸出的球不是黄球}＝1－0.18＝0.82.P {摸出的球是黄球或黑球}＝0.42＋0.18＝0.6.答案：0.4 0.82 0.68. 解析：由题意知P (A ＋B )＝1－25，即P (A )＋P (B )＝35.又P (A )＝2P (B )，联立方程组解得P (A )＝25，P (B )＝15，故P (A －)＝1－P (A )＝35.答案：359. 解：记派出医生的人数为0,1,2,3,4,5及其以上分别为事件A 0，A 1，A 2，A 3，A 4，A 5，显然它们彼此互斥．(1)至多2名医生的概率为P (A 0＋A 1＋A 2)＝P (A 0)＋P (A 1)＋P (A 2)＝0.18＋0.25＋0.36＝0.79.(2)法一：至少3名医生的概率为 P (C )＝P (A 3＋A 4＋A 5)＝P (A 3)＋P (A 4)＋P (A 5)＝0.1＋0.1＋0.01＝0.21.法二：“至少3名医生”的反面是“至多2名医生”，故派出至少3名医生的概率为 1－P (A 0＋A 1＋A 2)＝1－0.79＝0.21.10. 解：分别记小明的考试成绩“在90分以上(包括90分)”“在80～89分”“在70～79分”“在60～69分”为事件B ，C ，D ，E .由题意知，这4个事件彼此互斥．(1)小明的考试成绩在80分以上(包括80分)的概率为P (B ＋C )＝P (B )＋P (C )＝0.18＋0.51＝0.69.(2)小明考试及格的概率，即成绩在60分以上(包括60分)的概率为P (B ＋C ＋D ＋E )＝P (B )＋P (C )＋P (D )＋P (E )＝0.18＋0.51＋0.15＋0.09＝0.93.而小明考试不及格与小明考试及格为对立事件，所以小明考试不及格(低于60分)的概率为1－P (B ＋C ＋D ＋E )＝1－0.93＝0.07.2019-2020年高中数学课下能力提升十八新人教A 版(I)题组1 基本事件的列举问题1．同时投掷两颗大小完全相同的骰子，用(x ，y )表示结果，记A 为“所得点数之和小于5”，则事件A 包含的基本事件数是( )A ．3B ．4C ．5D ．62．做试验“从0,1,2这3个数字中，不放回地取两次，每次取一个，构成有序数对(x ，y )，x 为第1次取到的数字，y 为第2次取到的数字”．①写出这个试验的基本事件；②求出这个试验的基本事件的总数；③写出“第1次取出的数字是2”这一事件包含的基本事件．题组2 简单古典概型的计算3．下列关于古典概型的说法中正确的是( )①试验中所有可能出现的基本事件只有有限个；②每个事件出现的可能性相等；③每个基本事件出现的可能性相等；④基本事件的总数为n ，随机事件A 若包含k 个基本事件，则P (A )＝k n. A ．②④ B ．①③④ C ．①④ D ．③④4．下列试验中，属于古典概型的是( )A ．种下一粒种子，观察它是否发芽B ．从规格直径为250 mm±0.6 mm 的一批合格产品中任意抽一根，测量其直径dC ．抛掷一枚硬币，观察其出现正面或反面D ．某人射击中靶或不中靶5．设a 是掷一枚骰子得到的点数，则方程x 2＋ax ＋2＝0有两个不相等的实根的概率为( )A.23B.13C.12D.5126．一枚硬币连掷3次，有且仅有2次出现正面向上的概率为( )A.38B.23C.13D.147．袋中有6个球，其中4个白球，2个红球，从袋中任意取出两球，求下列事件的概率：(1)A ：取出的两球都是白球；(2)B ：取出的两球1个是白球，另1个是红球．题组3 较复杂的古典概型的计算8．某停车场临时停车按时段收费，收费标准如下：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元(不足1小时按1小时计算)．现有甲、乙两人在该地停车，两人停车都不超过4小时．(1)若甲停车1小时以上且不超过2小时的概率为13，停车费多于14元的概率为512，求甲的停车费为6元的概率；(2)若甲、乙两人每人停车的时长在每个时段的可能性相同，求甲、乙两人停车费之和为28元的概率．1．下列是古典概型的是( )A ．任意掷两枚骰子，所得点数之和作为基本事件时B ．求任意的一个正整数平方的个位数字是1的概率，将取出的正整数作为基本事件时C．从甲地到乙地共n条路线，求某人正好选中最短路线的概率D．抛掷一枚均匀硬币首次出现正面为止2．(xx·广东高考)已知5件产品中有2件次品，其余为合格品．现从这5件产品中任取2件，恰有一件次品的概率为( )A．0.4 B．0.6C．0.8 D．13．(xx·新课标全国卷Ⅰ)如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数．从1,2,3,4,5中任取3个不同的数，则这3个数构成一组勾股数的概率为( )A.310B.15C.110D.1204．从个位数与十位数之和为奇数的两位数中任取一个，其个位数为0的概率是( )A.49B.13C.29D.195．(xx·石家庄高一检测)一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都会随机地选择一条路径，则它能获得食物的概率为________．6．从三男三女共6名学生中任选2名(每名同学被选中的概率均相等)，则2名都是女同学的概率等于________．7．(xx·天津高考)设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛．(1)求应从这三个协会中分别抽取的运动员的人数．(2)将抽取的6名运动员进行编号，编号分别为A1，A2，A3，A4，A5，A6.现从这6名运动员中随机抽取2人参加双打比赛．①用所给编号列出所有可能的结果；②设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，求事件A发生的概率．8．(xx·山东高考)海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量(单位：件)如下表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.(1)求这6件样品中来自(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．答 案[学业水平达标练]1. 解析：选D 事件A 包含的基本事件有6个：(1,1)，(1,2)，(1,3)，(2,1)，(2,2)，(3,1)．故选D.2. 解：①这个试验的基本事件为(0,1)，(0,2)，(1,0)，(1,2)，(2,0)，(2,1)． ②基本事件的总数为6.③“第1次取出的数字是2”包含以下2个基本事件：(2,0)，(2,1)．3. 解析：选B 根据古典概型的特征与公式进行判断，①③④正确，②不正确，故选B. 4. 解析：选C 依据古典概型的特点判断，只有C 项满足：①试验中所有可能出现的基本事件只有有限个；②每个基本事件出现的可能性相同．5. 解析：选A 基本事件总数为6，若方程有两个不相等的实根则a 2－8＞0，满足上述条件的a 为3,4,5,6，故P ＝46＝23. 6. 解析：选A 所有的基本事件是(正，正，正)，(正，正，反)，(正，反，正)，(正，反，反)，(反，正，正)，(反，正，反)，(反，反，正)，(反，反，反)，共有8个，仅有2次出现正面向上的有：(正，正，反)，(正，反，正)，(反，正，正)，共3个．则所求概率为38. 7. 解：设4个白球的编号为1,2,3,4；2个红球的编号为5,6.从袋中的6个小球中任取2个球的取法有(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,3)，(2,4)，(2,5)，(2,6)，(3,4)，(3,5)，(3,6)，(4,5)，(4,6)，(5,6)，共15种． (1)从袋中的6个球中任取两个，所取的两球全是白球的取法共有6种，为(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)．∴取出的两个球全是白球的概率为P (A )＝615＝25. (2)从袋中的6个球中任取两个，其中一个是红球，而另一个是白球，其取法包括(1,5)，(1,6)，(2,5)，(2,6)，(3,5)，(3,6)，(4,5)，(4,6)共8种．∴取出的两个球一个是白球，一个是红球的概率为P (B )＝815. 8. 解：(1)记“一次停车不超过1小时”为事件A ，“一次停车1到2小时”为事件B ，“一次停车2到3小时”为事件C ，“一次停车3到4小时”为事件D .由已知得P (B )＝13，P (C ＋D )＝512. 又事件A ，B ，C ，D 互斥，所以P (A )＝1－13－512＝14. 所以甲的停车费为6元的概率为14. (2)易知甲、乙停车时间的基本事件有(1,1)，(1,2)，(1,3)，(1,4)，(2,1)，(2,2)，(2,3)，(2,4)，(3,1)，(3,2)，(3,3)，(3,4)，(4,1)，(4,2)，(4,3)，(4,4)，共16个；而“停车费之和为28元”的事件有(1,3)，(2,2)，(3,1)，共3个，所以所求概率为316. [能力提升综合练]1. 解析：选C A 项中由于点数的和出现的可能性不相等，故A 不是；B 项中的基本事件是无限的，故B 不是；C 项满足古典概型的有限性和等可能性，故C 是；D 项中基本事件可能会是无限个，故D 不是．2. 解析：选B 5件产品中有2件次品，记为a ，b ，有3件合格品，记为c ，d ，e ，从这5件产品中任取2件，有10种结果，分别是(a ，b )，(a ，c )，(a ，d )，(a ，e )，(b ，c )，(b ，d )，(b ，e )，(c ，d )，(c ，e )，(d ，e )，恰有一件次品，有6种结果，分别是(a ，c )，(a ，d )，(a ，e )，(b ，c )，(b ，d )，(b ，e )，设事件A ＝{恰有一件次品}，则P (A )＝610＝0.6，故选B.3. 解析：选C 从1,2,3,4,5中任取3个不同的数共有如下10个不同的结果：(1,2,3)，(1,2,4)，(1,2,5)，(1,3,4)，(1,3,5)，(1,4,5)，(2,3,4)，(2,3,5)，(2,4,5)，(3,4,5)，其中勾股数只有(3,4,5)，所以概率为110.故选C. 4. 解析：选D 分类讨论法求解．个位数与十位数之和为奇数，则个位数与十位数中必一个奇数一个偶数，所以可以分两类．(1)当个位为奇数时，有5×4＝20个符合条件的两位数．(2)当个位为偶数时，有5×5＝25个符合条件的两位数．因此共有20＋25＝45个符合条件的两位数，其中个位数为0的两位数有5个，所以所求概率为P ＝545＝19. 5. 解析：该树枝的树梢有6处，有2处能找到食物，所以获得食物的概率为26＝13. 答案：136. 解析：用A ，B ，C 表示三名男同学，用a ，b ，c 表示三名女同学，则从6名同学中选出2人的所有选法为：AB ，AC ，Aa ，Ab ，Ac ，BC ，Ba ，Bb ，Bc ，Ca ，Cb ，Cc ，ab ，ac ，bc,2名都是女同学的选法为：ab ，ac ，bc ，故所求的概率为315＝15. 答案：157. 解：(1)应从甲、乙、丙三个协会中抽取的运动员人数分别为3,1,2.(2)①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为{A 1，A 2}，{A 1，A 3}，{A 1，A 4}，{A 1，A 5}，{A 1，A 6}，{A 2，A 3}，{A 2，A 4}，{A 2，A 5}，{A 2，A 6}，{A 3，A 4}，{A 3，A 5}，{A 3，A 6}，{A 4，A 5}，{A 4，A 6}，{A 5，A 6}，共15种．②编号为A 5和A 6的两名运动员中至少有1人被抽到的所有可能结果为{A 1，A 5}，{A 1，A 6}，{A 2，A 5}，{A 2，A 6}，{A 3，A 5}，{A 3，A 6}，{A 4，A 5}，{A 4，A 6}，{A 5，A 6}，共9种．因此，事件A 发生的概率P (A )＝915＝35. 8. 解：(1)因为样本容量与总体中的个体数的比是650＋150＋100＝150， 所以样本中包含三个地区的个体数量分别是：50×150＝1,150×150＝3,100×150＝2. 所以A ，B ，C 三个地区的商品被选取的件数分别为1,3,2.(2)设6件来自A ，B ，C 三个地区的样品分别为：A ；B 1，B 2，B 3；C 1，C 2.则从6件样品中抽取的这2件商品构成的所有基本事件为：{A ，B 1}，{A ，B 2}，{A ，B 3}，{A ，C 1}，{A ，C 2}，{B 1，B 2}，{B 1，B 3}，{B 1，C 1}，{B 1，C 2}，{B 2，B 3}，{B 2，C 1}，{B 2，C 2}，{B 3，C 1}，{B 3，C 2}，{C 1，C 2}，共15个．每个样品被抽到的机会均等，因此这些基本事件的出现是等可能的．记事件D ：“抽取的这2件商品来自相同地区”，则事件D 包含的基本事件有： {B 1，B 2}，{B 1，B 3}，{B 2，B 3}，{C 1，C 2}，共4个．所以P (D )＝415，即这2件商品来自相同地区的概率为415.。

一、选择题1．如果直线l ，m 与平面α，β，γ满足：l ＝β∩γ，l ∥α，m α和m ⊥γ，那么必有( ) A ．α⊥γ且l ⊥m B ．α⊥γ且m ∥β C ．m ∥β且l ⊥m D ．α∥β且α⊥γ2．(浙江高考)设m ，n 是两条不同的直线，α，β是两个不同的平面( ) A ．若m ∥α，n ∥α，则m ∥n B ．若m ∥α，m ∥β，则α∥β C ．若m ∥n ，m ⊥α，则n ⊥α D ．若m ∥α，α⊥β，则m ⊥β3．在矩形ABCD 中，AB ＝3，BC ＝4，P A ⊥平面ABCD ，且P A ＝1，PE ⊥DE ，则PE 的长为( )A.292 B.135C.175D.11954．设平面α⊥平面β，且α∩β＝l ，直线a α，直线b β，且a 不与l 垂直，b 不与l垂直，那么a 与b ( )A ．可能垂直，不可能平行B ．可能平行，不可能垂直C ．可能垂直，也可能平行D ．不可能垂直，也不可能平行A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABC 二、填空题7．已知平面α⊥平面β，在α，β的交线上取线段AB ＝4 cm ，AC ，BD 分别在平面α和β内，它们都垂直于AB ，并且AC ＝3 cm ，BD ＝12 cm ，则CD 的长为________ cm.①若α⊥β，α∩β＝m ，n ⊥m ，则n ⊥α或n ⊥β； ②若α∥β，α∩γ＝m ，β∩γ＝n ，则m ∥n ；③若m 不垂直于α，则m 不可能垂直于α内的无数条直线； ④若α∩β＝m ，m ∥n ，且n α，n β，则n ∥α且n ∥β.三、解答题9．如图，A，B，C，D是空间四点，在△ABC中，AB＝2，AC＝BC＝2，等边△ADB 所在的平面以AB为轴可转动．(1)当平面ADB⊥平面ABC时，求CD的长；(2)当△ADB转动过程中，是否总有AB⊥CD？请证明你的结论．10．如图，已知四边形ABCD是矩形，P A⊥平面ABC，M，N分别是AB，PC的中点．(1)求证：MN⊥AB；(2)若P A＝AD，求证：MN⊥平面PCD.答案1. 解析：选A∵m⊥γ，mα，lγ，∴α⊥γ，m⊥l；B错，有可能mβ；C错，有可能mβ；D错，有可能α与β相交．2.解析：选C逐一判断可知，选项A中的m，n可以相交，也可以异面；选项B中的α与β可以相交；选项D中的m与β的位置关系可以平行、相交、m在β内，故选C.3.解析：选B如图所示，连接AE.∵P A⊥平面ABCD，BD平面ABCD，∴P A⊥BD.又∵BD ⊥PE ，P A ∩PE ＝P ，∴BD ⊥平面P AE ，∴BD ⊥AE .∴AE ＝3×45＝125.所以在Rt △P AE 中，由P A ＝1，AE ＝125，得PE ＝135.4. 解析：选B 当a ，b 都平行于l 时，a 与b 平行，假设a 与b 垂直，如图所示，由于b 与l 不垂直，在b 上任取一点A ，过点A 作b ′⊥l ，∵平面α⊥平面β，∴b ′⊥平面α，从而b ′⊥a ，又由假设a ⊥b 易知a ⊥平面β，从而a ⊥l ，这与已知a 不与l 垂直矛盾，∴假设不正确，a 与b 不可能垂直．5. 解析：选D 在图①中，∵∠BAD ＝90°，AD ＝AB ， ∴∠ADB ＝∠ABD ＝45°.∵AD ∥BC ，∴∠DBC ＝45°.又∵∠BCD ＝45°， ∴∠BDC ＝90°，即BD ⊥CD .在图②中，此关系仍成立．∵平面ABD ⊥平面BCD ， ∴CD ⊥平面ABD .∵BA 平面ADB ，∴CD ⊥AB . ∵BA ⊥AD ，∴BA ⊥平面ACD .∵BA 平面ABC ，∴平面ABC ⊥平面ACD .6. 解析：利用面面垂直的判定，可知①③④⇒②为真；利用面面垂直的性质，可知②③④⇒①为真．答案：若①③④，则②(或若②③④，则①) 7. 解析：如图，连接AD ，CD .在Rt △ABD 中，AB ＝4，BD ＝12， ∴AD ＝122＋42＝410 cm. 又∵α⊥β，CA ⊥AB ，CA α， ∴CA ⊥β.∴△CAD 为直角三角形．∴CD ＝CA 2＋AD 2＝32＋42×10＝169＝13(cm)．答案：13设α∩β∩γ＝m，过m上任意一点，在γ内作n⊥m，则直线n既不垂直于α，∵α∥β，∴α与β无公共点，∴直线m与直线n也无公共点．又m∈γ，n∈γ，∴m∥n.∵n∥m，mα，mβ，nα，nβ，∴必有n∥α，n∥β.∴应填②④.答案：②④9. 解：(1)设AB中点为O，连接OC、OD，则OC⊥AB，∵平面ADB⊥平面ABC，平面ADB∩平面ABC＝AB.∴OC⊥面ADB.∵OD平面ADB，∴OC⊥OD.即∠COD＝90°.在等边△ADB中，AB＝2，∴OD＝ 3.在△ABC中，AC＝BC＝2，AB＝2，∴OC＝1.在Rt△COD中，CD＝OC2＋OD2＝2.(2)当△ADB在转动过程中，总有OC⊥AB，OD⊥AB，∴AB⊥平面COD.∴AB⊥CD.当△ADB转动到与△ABC共面时，仍然有AB⊥CD.故△ADB转动过程中，总有AB⊥CD.10. 证明：(1)取CD的中点E，连接EM、EN，则CD⊥EM，且EN∥PD.∵P A⊥平面ABC，CD平面ABC，∴P A⊥CD，又CD⊥AD.∴CD⊥平面P AD.∵PD平面P AD.∴CD⊥PD.∴CD⊥EN.又CD⊥ME，∴CD⊥平面MNE，∴CD⊥MN.又CD∥AB，∴MN⊥AB.(2)在Rt△P AD中有P A＝AD，取PD的中点K，连接AK，KN，则KN 12DC AM，且AK⊥PD.∴四边形AMNK为平行四边形，从而MN∥AK.因此MN⊥PD.由(1)知MN⊥DC.又PD∩DC＝D，∴MN⊥平面PCD.。

一、选择题1．下列说法中正确的个数是()①相等的角在直观图中对应的角仍然相等②相等的线段在直观图中对应的线段仍然相等③平行的线段在直观图中对应的线段仍然平行④线段的中点在直观图中仍然是线段的中点A．1B．2C．3 D．42．利用斜二测画法画边长为1 cm的正方形的直观图，正确的是如图所示中的()3．已知一个正方形的直观图是一个平行四边形，其中有一边长为4，则此正方形的面积是()A．16B．64 C．16或64D．都不对4．如图，直观图所表示(A′C′∥O′y′，B′C′∥O′x′)的平面图形是()A．正三角形B．锐角三角形C．钝角三角形D．直角三角形5．一个平面四边形的斜二测画法的直观图是一个边长为a的正方形，则原平面四边形的面积等于()A.24a2 B.433a2C.34a2D．22a2二、填空题5．如图所示，为一个水平放置的正方形ABCO，它在直角坐标系xOy中，点B的坐标为(2,2)，则在用斜二测画法画出的正方形的直观图中，顶点B′到x′轴的距离为________．6．水平放置的△ABC的斜二测直观图如图所示，已知A′C′＝3，B′C′＝2，则AB边上的中线的实际长度为________．8．如图所示是水平放置的△ABC在直角坐标系中的直观图，其中D是AC的中点，原△ACB中，∠ACB≠30°，则原图形中与线段BD的长相等的线段有________条．三、解答题9．画出一个正三棱台的直观图(尺寸：上、下底面边长分别为1 cm、2 cm，高为2 cm)．10.用斜二测画法得到一水平放置的三角形为直角三角形ABC，AC＝1，∠ABC＝30°，如图所示，试求原图的面积．答案1. 解析：选B只有③④正确．2. 解析：选D正方形的直观图应是平行四边形，且相邻两边的边长之比为2∶1.3. 解析：选C当其中在x′轴上的边长为4时，正方形面积为16；当其中在y′轴上的边长为4时，正方形面积为64.4. 解析：选D由A′C′∥O′y′，B′C′∥O′x′，∠A′C′B′＝45°知对应的平面图形为直角三角形．5. 解析：选D由题意知，平行四边形的直观图为对应在直角坐标系下的图形为：∴平行四边形的面积为S′＝2×12×a×22a＝22a2.6. 解析：在直观图中，A′B′C′O′是有一个角为45°且长边为2，短边为1的平行四边形，∴B′到x′轴的距离为22.答案：2 27. 解析：由于直观图中，∠A′C′B′＝45°，则在原图形中∠ACB＝90°，AC＝3，BC ＝4，则斜边AB＝5，故斜边AB上的中线长为2.5.答案：2.58. 解析：先按照斜二测画法把直观图还原为真正的平面图形，然后根据平面图形的几何性质找与线段BD长度相等的线段，把△ABC还原后为直角三角形，则D为斜边AC的中点，∴AD＝DC＝BD.答案：29. 解：(1)画轴，以底面△ABC的垂心O为原点，OC所在直线为y轴，平行于AB的直线为x轴，建立平面直角坐标系，以上底面△A′B′C′的垂心O′与O的连线为z轴，建立空间坐标系．(2)画下底面，在xOy平面上画△ABC的直观图，在y轴上量取OC＝33cm，OD＝36cm.过D作AB∥x轴，且AB＝2 cm，以D为中点，连接AC、BC，则△ABC为下底面三角形的直观图．(3)画上底面，在z轴上截取OO′＝2 cm，过O′作x′轴∥x轴，y′轴∥y轴，在y′轴上量取O′C′＝36cm，O′D′＝312cm，过D′作A′B′∥x′轴，A′B′＝1 cm，。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==你认为你迫切需要提高的是哪方面的技能或素质?你计划通过什么途径和方法提高?篇一：浅谈企业应该如何提高员工的素质浅谈企业应该如何提高员工的素质在市场激烈竞争的今天，企业要生存，要发展壮大，必须提高市场竞争能力。

员工素质的高低直接影响到企业的发展，员工素质跟不上企业发展和市场竞争的需要，目前已成为制约企业做强做大的“瓶颈”，提高员工队伍的整体素质，是增强企业竞争力、促进企业发展的重要途径，更是广大员工根本利益之所在。

因此，提高员工素质显得尤为重要。

为有效地促进企业发展，现就企业如何提高员工整体素质在此谈几点个人粗浅的看法。

一、企业的发展迫切需要提高员工素质企业长久发展需要员工提高自身素质；员工为了提高工资待遇需要提高自身素质；能够胜任岗位，满足社会需要，迫切要求员工加强学习；做到与时代发展同步，不被时代淘汰，需要员工加强学习，因此提高员工素质是每个企业必须面对和要做的工作。

1、提高员工职业道德素质，是企业发展的需要。

职业道德的基本要求是向社会负责，忠于职守。

“坚忍不拔，诚实不欺，奉献不已，自强不息”既是公司的企业精神，也是全体员工的道德价值取向。

投资事业部要在激烈的市场竞争中站稳脚根并求得发展，只有依靠优质工程和优质的服务，而职工道德素质是做好这两项工作的前提。

要抓好员工道德素质的提高，公司应通过多种途径，对员工进行全方位的职业道德教育，以推动员工职业道德水平的不断提高；对员工进行有针对性的思想教育工作，广泛提倡敬业精神、团队精神和协作精神，培养良好职业道德；要让员工们清醒地意识到，只有树立良好的职业道德，与企业同舟共济，团结拼搏,企业才能在激烈的市场竞争中生存、发展，始终立于不败之地。

2、提高企业员工的劳动技能素质，是企业发展的基础。

对于一个现代企业来说，迫切需要生产一线的高素质员工，因此必须重视员工劳动技能的提高。

一、选择题
1．如果空间四点A，B，C，D不共面，那么下列判断中正确的是()
A．A，B，C，D四点中必有三点共线
B．A，B，C，D四点中不存在三点共线
C．直线AB与CD相交
D．直线AB与CD平行
2．若点A在直线b上，b在平面β内，则A，b，β之间的关系可以记作()
A．A∈b，b∈βB．A∈b，bβ
C．A b，bβD．A b，b∈β
3．如图，平面α∩平面β＝l，点A∈α，点B∈α，且点C∈β，点C∉l.又AB∩l＝R，设A，B，C三点确定的平面为γ，则β∩γ是()
A．直线AC B．直线BC
C．直线CR D．直线AR
4．平行六面体ABCD-A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为() A．3 B．4 C．5 D．6
5．在四面体ABCD的棱AB，BC，CD，DA上分别取E，F，G，H四点，如果EF与HG交于点M，则()
A．M一定在直线AC上
B．M一定在直线BD上
C．M可能在AC上，也可能在BD上
D．M不在AC上，也不在BD上
二、填空题
6．空间四点A，B，C，D，其中任何三点都不在同一直线上，它们一共可以确定平面的个数为________．
7．如图，在这个正方体中，①BM与ED平行；②CN与BM是异面直线；③CN与BE是异面直线；④DN与BM是异面直线．。

课下能力提升(十八)一、选择题．直线－＋＝和(＋)＋－＝的位置关系是( )．平行．重合．相交．不确定．直线过直线－＝和＋＝的交点，且过点(－，－)，则直线的方程为( )．－＋＝．＋＋＝．－＋＝．－－＝．直线(－)－(＋)－(－)＝(∈)所经过的定点为( )．() ．()．()．已知点(－)，()，直线＝－＋与线段相交，则的取值范围是( )．[－] ．[－]．[]．使三条直线＋＝，＋＝－＝不能围成三角形的值最多有( )．个．个．个．个二、填空题．已知直线＋－＝和－＋＝垂直且都过点(，)，则＝，＝，＝.．若三条直线－＋＝，＋－＝，＋－＝共有两个不同的交点，则＝.．在△中，已知()，边所在直线的方程为－＋＝，直线－＋＝是边的高线，则点的坐标为．三、解答题．求经过直线：－＋＝与：＋－＝的交点且与直线：＋＋＝平行的直线的方程．．已知点是轴上的动点，一条直线过点()且垂直于，交轴于点，过，分别作，轴的垂线交于点，求点(，)满足的关系式．答案．解析：选∵＝，＝－，∴≠.∴两直线相交．．解析：选由(\\(－＝，＋＝，))得直线－＝和＋＝的交点为()，∵直线过点()和(－，－)两点，∴直线的方程为＝，即－＋＝.．解析：选将原方程变为(－－)－－＋＝，令(\\(－－＝，,－－＋＝，))得(\\(＝，＝，))∴定点为()．．解析：选直线的方程为＝，由(\\(＝－＋，＝，))得交点，由－≤≤，得－≤≤.．解析：选要使三条直线不能围成三角形，只需其中两条直线平行或三条直线共点．若＋＝与＋＝平行，则＝；若＋＝与－＝平行，则＝－；若＋＝与－＝平行，则不存在；若＋＝与＋＝及－＝共点，则＝－或＝.．解析：已知两直线方程可化为：＝－＋，：＝＋.∵两直线垂直，∴－·＝－，∴＝，即直线方程为＋－＝.又点(，)在直线上，∴×＋－＝，∴＝－，即(，－)．又点在直线上，∴×－×(－)＋＝，∴＝－.答案：－－．解析：因为直线－＋＝与＋－＝相交于一点，要使三条直线共有两个不同交点，只需＋－＝与以上两条直线中的一条平行即可，当＋－＝与－＋＝平行时，有－＝，解得＝－；当＋－＝与＋－＝平行时，有－＝－，解得＝.答案：或－．解析：设的方程为＋＋＝，将点的坐标代入，可得＝－，∴的方程为＋－＝.解方程组(\\(＋－＝，－＋＝.))得(－)．答案：(－)．解：联立(\\(－＋＝，＋－＝，))解得(\\(＝，＝，))即直线与直线的交点为()．∵∥，∴的方程可设为＋＋＝.将()代入，得＝－.∴直线的方程为＋－＝.．解：如图所示，∵⊥轴，⊥轴，点坐标为(，)，∴点坐标为()，点坐标为(，)，由题意可知⊥，当≠时，。