直角三角形的性质 (3)

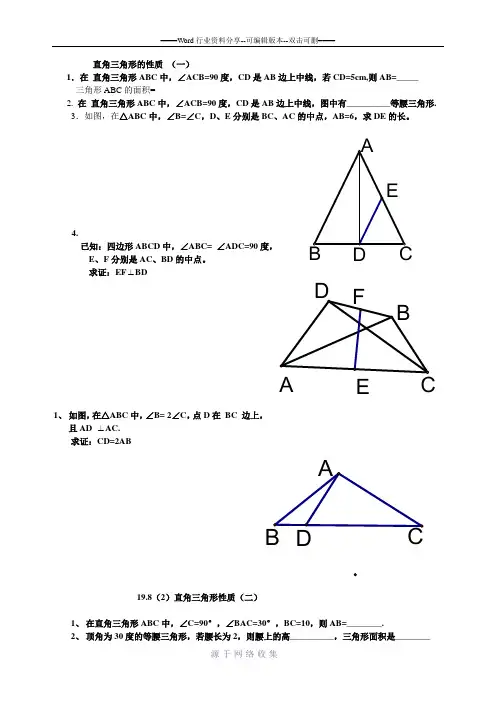
直角三角形的性质 （一）1．在 直角三角形ABC 中，∠ACB=90度，CD 是AB 边上中线，若CD=5cm,则AB=_____ 三角形ABC 的面积=____________2. 在 直角三角形ABC 中，∠ACB=90度，CD 是AB 边上中线，图中有__________等腰三角形. 3．如图，在△ABC 中，∠B=∠C ，D 、E 分别是BC 、AC 的中点，AB=6，求DE 的长。

4.已知：四边形ABCD 中，∠ABC= ∠ADC=90度， E 、F 分别是AC 、BD 的中点。

求证：EF ⊥BD1、 如图，在△ABC 中，∠B= 2∠C ，点D 在 BC 边上，且AD ⊥AC.求证：CD=2AB19.8（2）直角三角形性质（二）1、 在直角三角形ABC 中，∠C=90°，∠BAC=30°，BC=10，则AB=________.2、 顶角为30度的等腰三角形，若腰长为2，则腰上的高__________，三角形面积是________E3、 等腰三角形顶角为120°，底边上的高为3，则腰长为_________4、 三角形ABC 中，AB=AC=6，∠B=30°，则BC 边上的高AD=_______________5、 Rt △ABC 中，∠C=90°，∠A=15°，AB 的垂直平分线交AC 于D,AB 于E,求证AD=2BC.6、 已知：△ABC 中,AB=AC ，∠B=30°，AD ⊥AB ，求证：2DC=BD7.如图，△ABC 中，∠C=90°，∠A=60 °，EF 是AB 的垂直平分线，判断CE 与BE 之间的关系19.8（3）直角三角形的性质(三)1.在直角三角形中，有一个锐角为52度，那么另一个锐角度数为 ；2、在直角三角形中，斜边及其中线之和为6，那么该三角形的斜边长为________．3、在△ABC 中， ∠ACB=90 °，CE 是AB 边上的中线，那么与CE 相等的线段有_________，与∠A 相等的角有_________，若∠A=35°，那么∠ECB= _________．DACBADEFCBA4、已知：∠ABC=∠ADC=90 度，E 是AC 中点。

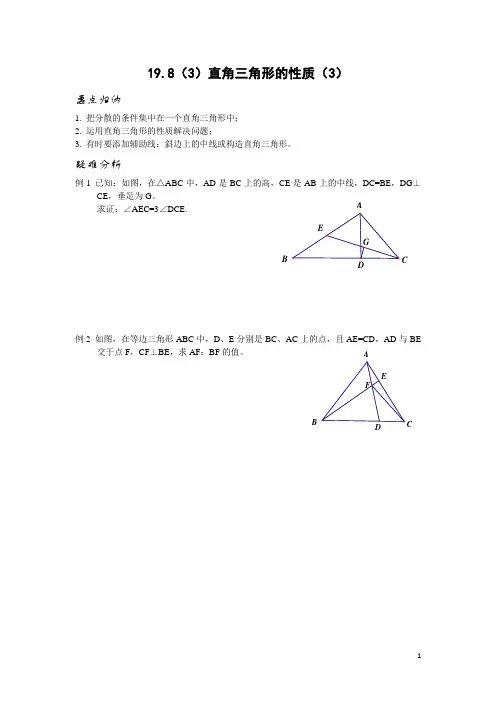
19.8（3）直角三角形的性质（3）要点归纳1. 把分散的条件集中在一个直角三角形中；2. 运用直角三角形的性质解决问题；3. 有时要添加辅助线：斜边上的中线或构造直角三角形。

疑难分析例1 已知：如图，在△ABC 中，AD 是BC 上的高，CE 是AB 上的中线，DC=BE ，DG ⊥CE ，垂足为G 。

求证：∠AEC=3∠DCE.例2 如图，在等边三角形ABC 中，D 、E 分别是BC 、AC 上的点，且AE=CD ，AD 与BE交于点F ，CF ⊥BE ，求AF ：BF 的值。

B CB C基础训练1. 等腰直角三角形底边上的中线长为8，则这个三角形的面积为＿＿＿＿；2. 在Rt △ABC 中，∠C=90°，∠A=60°，将此三角形沿斜边翻折得Rt △ABC ’，若BC ’=14厘米，则CC ’=＿＿＿＿厘米；3. 如图在Rt △ABC 中，∠ACB=90°，∠BAC 的平分线AD 交BC 于点D ，DE ∥AC ，DE 交AB 于点E ，M 为BC 中点，连接DM ，在不添加辅助线和字母的情况下，图中等腰三角形有＿＿＿＿个；（第3题） （第4题）4. 如图，在Rt △ABC 中，∠ACB=90°，如果CD 、CM 分别是斜边上的高和中线，那么下列结论中错误的是（ ）。

A.∠ACM=∠BCDB.∠ACD=∠BC.∠ACD=∠BCMD.∠ACD=∠MCDBC B5. 如图，在Rt △ABC 中，∠BAC=90°，AD ⊥BC ，BE 平分∠ABC 交AD 于点E ，EF ∥AC 交BC 于点F 。

下列结论一定成立的是（ ）A. AE=EDB. AB=BFC. AD=DCD. ∠ABE=∠DFE（第5题） （第6题） 6. 已知：如图，在△ABC 中，∠C=2∠A ，AC=2BC. 求证：△ABC 是直角三角形。

7. 已知：如图，BD 、CE 是△ABC 的高，M 、N 分别是BC 、DE 的中点。

直角三角形常考的10个易错点浅析1. 直角三角形的性质性质1：直角三角形两锐角互余.性质2：直角三角形斜边上的中线等于斜边的一半.性质3：直角三角形中30o所对的直角边等于斜边的一半.2. 直角三角形的判定判定1：有两个角互余的三角形是直角三角形.判定2：一边上的中线等于这边的一半的三角形是直角三角形.3. 直角三角形的性质勾股定理：如果直角三角形的两直角边为a 和b ，斜边为 c ，那么222c b a =+.4. 直角三角形的判定勾股定理逆定理：如果三角形三边长a 、b 、c 满足a 2+b 2=c 2，那么这个三角形是直角三角形.5. 直角三角形全等的判断：斜边和一直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边公理”或“H L ”）6. 角平分线的性质定理：角平分线上的点到角的两边的距离相等.7. 角平分线的性质定理的逆定理：角平分线性质定理： 角平分线上的点到角的两边的距离相等. 易错点1 忽略了运用直角三角形的性质的前提条件在运用直角三角形的性质时，它的前提是在直角三角形中.如果三角形不是直角三角形，那么这些性质就不存在了，所以运用时要注意前提条件。

例题1 如图，在△ABC 中，CD 是AB 边上的高，∠A =60°，则∠BCD 的度数为（ ）A .30°B .60°C .90°D .无法确定【错解】B【错因】在本题中没有指明△ABC 是直角三角形，故不能利用直角三角形的性质进行计算。

错解中想当然地认为△ABC 是直角三角形，然后利用了直角三角形的性质，进而造成错解。

【正解】D例题2 如图，在△ABC 中，∠ABC =75°，从顶点B 引射线BD 与CA 交于D 点，使∠CDB =30°，BD =AD 。

求证：AD =2BC 。

【错解】在△BCD 中，∵∠CDB =30°，∴BC =12BD 。

∵BD =AD ，∴BC =12AD ，即AD =2BC 【错因】在本题中没有指明∠C =90O，故不能直接利用直角三角形的性质进行计算。

直角三角定义直角三角形是一种特殊的三角形，它的一个角度为90度，也就是直角。

直角三角形是数学中的基本概念之一，应用广泛，并且有着重要的几何性质。

本文将探讨直角三角的定义、特性以及其在实际问题中的应用。

一、直角三角形的定义直角三角形是指一个角度为90度的三角形。

根据直角三角形的定义，直角三角形有三个边，分别为斜边、邻边和对边。

斜边位于直角的对面，邻边连接直角和斜边的两个边，对边与直角相对。

在一个直角三角形中，斜边的长度记作c，邻边记作a，对边记作b。

根据勾股定理，直角三角形的边长满足 a² + b² = c²。

这是直角三角形的重要性质，也被称为勾股定理。

二、直角三角形的性质1. 直角三角形的三个角度之和为180度。

由于直角三角形中有一个角度是90度，因此其他两个角度之和为90度。

2. 直角三角形的斜边是最长的边，邻边和对边的长度小于斜边。

3. 直角三角形可以根据边长比例划分为不同的型式，如等腰直角三角形、等边直角三角形等。

4. 直角三角形可以通过三角函数来描述其边长与角度之间的关系。

常用的三角函数有正弦、余弦和正切函数，它们在解决实际问题中具有重要的应用价值。

三、直角三角形的应用直角三角形在实际应用中有广泛的用途，以下是一些例子：1. 测量不可直接获取的物体的距离：利用直角三角形的性质，在已知一个角度和相关边长的情况下，可以使用三角函数来计算物体与测量地点之间的距离。

2. 解决倾斜问题：在工程测量和建筑设计中，直角三角形常被用于解决倾斜问题。

通过测量两个角度或边长，可以确定物体或土地的倾斜程度。

3. 导航和定位：在航海、航空和导航等领域，直角三角形常用于确定目标物体的位置和方向。

通过测量物体与观察点之间的角度，可以计算出物体相对于观察点的位置。

4. 解决真实生活中的问题：例如在建房过程中，可以通过直角三角形计算斜坡的高度和坡度，以确保建筑物的结构稳固。

总结：直角三角形作为一个基本的几何概念，具有重要的定义和性质。

三角形的基本概念与性质三角形是平面几何中最基本的图形之一，它由三条边和三个角组成。

本文将介绍三角形的基本概念和性质，包括三角形的定义、分类、元素、角度关系以及三角形的定理等。

一、三角形的定义三角形是由三条线段连接起来的图形，其中每个线段都被称为一个边，而连接两个边的点则被称为顶点。

三角形的三个顶点围成一个封闭的区域。

二、三角形的分类根据三角形的边长以及角度大小，可以将三角形分为以下几类：1. 根据边长分类(1) 等边三角形：三条边的长度均相等。

(2) 等腰三角形：两条边的长度相等。

(3) 普通三角形：三条边的长度都不相等。

2. 根据角度大小分类(1) 钝角三角形：一个角大于90°。

(2) 直角三角形：唯一一个角等于90°。

(3) 锐角三角形：三个角均小于90°。

3. 根据边长和角度大小综合分类(1) 正三角形：既是等边三角形，又是等腰三角形。

(2) 等腰直角三角形：既是等腰三角形，又是直角三角形。

三、三角形的元素三角形除了边和角之外，还有一些重要的元素：1. 顶点角：三角形的三个顶点所对应的角。

2. 底边：连接两个顶点的边。

3. 高：从底边到顶点所做的垂直线段。

四、三角形的角度关系1. 内角和定理：三角形内角的和等于180°。

2. 外角和定理：三角形的外角的和等于360°。

五、三角形的性质与定理1. 等腰三角形的性质：(1) 等腰三角形的两底角相等。

(2) 等腰三角形的高、中线、角平分线和垂心都是重合的。

2. 直角三角形的性质（勾股定理）：(1) 直角三角形的两条直角边的平方和等于斜边的平方。

(2) 根据勾股定理可以判断一个三角形是否为直角三角形。

3. 三角形的面积公式（海伦公式）：三角形的面积可以用海伦公式进行计算，公式如下：面积= √[s(s-a)(s-b)(s-c)]其中，s为三角形的半周长，a、b、c为三角形的三条边的长度。

通过了解三角形的基本概念与性质，我们可以更好地理解和分析三角形相关的问题。

直角三角形所有性质
性质1：直角三角形两直角边的平方和等于斜边的平方．
性质2：在直角三角形中，两个锐角互余．∠C=90° ∠A+∠B=90°
性质3：在直角三角形中，斜边上的中线等于斜边的一半
性质4：直角三角形的两直角边的乘积等于斜边与斜边上高的乘积，即ab=ch．
性质5：含30°的直角三角形三边之比为1：√3：2,它所对的直角边等于斜边的一半。

性质6：含45°角的直角三角形三边之比为1：1：√2
考点二、直角三角形的判定
1、有一个角是直角的三角形是直角三角形。

2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、勾股定理的逆定理
如果三角形的三边长a，b，c有：，那么这个三角形是直角三角形。

考点三、直角三角形全等的判定
斜边和直角边对应相等的两个直角三角形全等（斜边、直角边或者HL）
SAS（边角边）ASA（角边角）AAS（角角边）SSS（）
考点四、角平分线的性质
1.角的平分线上的点到角两边的距离相等。

2.角的内部到角的两边距离相等的点在角平分线上。

直角三角形的特殊性质与推论直角三角形是一种特殊的三角形，它具有一些独特的性质和推论。

在本文中，我们将详细探讨直角三角形的特点，并分析其相关的推论。

一、直角三角形的定义和基本性质直角三角形是指一个角度为90度的三角形。

根据直角三角形的定义，我们可以得出以下基本性质：1. 直角三角形的两条边与直角边的关系：直角三角形的两条边相互垂直，并与直角边存在一定的比例关系。

2. 直角三角形的斜边：直角三角形的斜边是直角边的对边，也是直角三角形中最长的一条边。

3. 直角三角形的两个锐角：直角三角形的两个锐角是互补角，即它们的和为90度。

二、勾股定理勾股定理是直角三角形中最著名的推论之一。

它指出，在直角三角形中，直角边的平方和等于斜边的平方。

勾股定理可以用数学公式表示为：c² = a² + b²，其中a和b代表直角边的长度，c代表斜边的长度。

这个定理由古希腊数学家毕达哥拉斯提出，被认为是数学中最重要的定理之一。

勾股定理的应用非常广泛。

它可以用来计算直角三角形的任意一边的长度，或者判断一个三边长度是否能够构成直角三角形。

三、特殊的直角三角形除了勾股定理，直角三角形还有一些特殊的性质和推论。

下面我们将介绍两种特殊的直角三角形。

1. 等腰直角三角形：等腰直角三角形是指两条直角边长度相等的直角三角形。

在等腰直角三角形中，两个锐角也是相等的，都为45度。

2. 30-60-90三角形：30-60-90三角形是指一个锐角为30度，一个锐角为60度的直角三角形。

在30-60-90三角形中，斜边的长度是直角边长度的两倍，而较小的锐角为30度的直角边长度是较大锐角为60度的直角边长度的一半。

这两种特殊的直角三角形在几何学和三角学中有广泛的应用。

四、直角三角形的应用直角三角形的性质和推论在实际问题中有许多应用。

以下是几个常见的应用场景：1. 测量高度：直角三角形常用于测量无法直接测量的高度。

通过测量斜边和相关的角度，可以使用三角函数来计算出高度的长度。

直角三角形的性质与特点直角三角形是一种特殊的三角形，其中一个角度为90度。

直角三角形的性质和特点包括勾股定理、特殊比例关系以及与三角函数的关系。

一、勾股定理勾股定理是直角三角形最基本的性质之一。

它指出，在一个直角三角形中，直角边的平方等于两个直角边的平方和。

即：c² = a² + b²其中，c是斜边（即直角三角形的斜边），a和b分别是直角边（即直角三角形的两条直角边）。

勾股定理是直角三角形中判断边长关系的重要方法。

二、特殊比例关系直角三角形中，两条直角边之间及直角边与斜边之间存在特殊的比例关系。

其中一个常见的比例关系是3:4:5。

如果直角边的长度为3单位，另一个直角边的长度为4单位，那么斜边的长度将会是5单位。

这种比例关系被称为“3-4-5三角形”，它是直角三角形中最简单的特殊比例关系之一。

除了3:4:5，还存在其他一些常见的特殊比例关系，如5:12:13、7:24:25等。

这些特殊比例关系在数学和实际问题中应用广泛，能够方便地计算直角三角形的边长。

三、与三角函数的关系直角三角形的另一个重要性质是与三角函数的关系。

三角函数包括正弦函数、余弦函数和正切函数。

在直角三角形中，这些函数可以用来表示角度与边长之间的关系。

正弦函数（sin）定义为直角三角形的对边与斜边的比值。

即：sinθ = a / c余弦函数（cos）定义为直角三角形的邻边与斜边的比值。

即：cosθ = b / c正切函数（tan）定义为直角三角形的对边与邻边的比值。

即：tanθ = a / b通过这些函数，我们可以利用已知的边长信息求解直角三角形的角度，或者根据已知的角度求解直角三角形的边长。

综上所述，直角三角形具有勾股定理、特殊比例关系和与三角函数的关系等性质和特点。

这些性质不仅在数学中具有重要意义，而且在实际生活中也应用广泛，例如测量直角三角形边长和角度、解决实际工程问题等。

熟悉直角三角形的性质与特点，对于理解和应用三角学有着重要的帮助。

19.8(3)直角三角形的性质一、课前练习1.填空:(1)在Rt △ABC 中,∠B=90°,∠C=30°,若AB=4,则_ __=8;(2)在Rt △ABC 中,∠B=90°,当AC=_ __时,∠A=30°.2.已知:如图,在Rt △ABC 中,CD 是斜边AB 上的高,CD=21AC,则线段AD 与BD 在数量上有什么关系?为什么?3.填空:(1)等腰三角形的顶角为150°,腰长为a,则腰上的高为___________;(2)若等腰三角形腰上的高等于腰长的一半,则等腰三角形的顶角等于___________度.二、阅读理解1.阅读教材P120.2.线段垂直平分线的性质是 角平分线的性质是3.填空:(1)直角三角形的两个锐角 .(2)直角三角形斜边上的中线等于斜边的 .(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于 .(4)在直角三角形中,如果一条直角边等于斜边的一半,那么 .4.阅读中遇到的问题有三、新课探索例题1 已知:如图,在△ABC 中,AD 平分∠BAC,BE ⊥AD,垂足为E,点F 是AB 的中点. 求证:EF ∥AC.例题2 已知:如图,在△ABC 中,∠A=30°,∠ACB=90°,M 、D 分别为AB 、MB 的中点. 求证:CD ⊥AB.四、课内练习1.已知:如图,在△ABC 中,∠C=90°,D 为直角边AC 上的一个点,BD 平分∠ABC,AD=2CD. 求证:(1)∠A=30°;(2)点D 在线段AB 的垂直平分线上.2.已知:如图,在Rt △ABC 中,∠C=90°,AD 平分∠CAB,交BC 于点D,DE 垂直平分AB,点E 为垂足.求证:(1)∠B=30°;(2)BD=2CD.3.已知:如图,在△ABC 中,∠BAC=90°,∠C=30°,EF 垂直平分AC,点D 在BA 的延长线上,AD=21EC.求证:(1)△DAF ≌△EFC;(2)DF=BE.操作 请画一个30°的角(工具不限),看谁的方法多.19.8（3）直角三角形的性质1、已知：如图，在等边三角形ABC 中，点D 、E 分别在AB 、AC 上，且BD=AE ，CD 交BE 于点O ，DF ⊥BE ，点F 为垂足 1）求证：∠ABE=∠BCD2)求证：OD=2OF2、如图，已知△ABC 中，∠C=90°，点D 、P 分别在边AC 、AB 上，且BD=AD ， PE ⊥BD ，PF ⊥AD ，垂足分别为E 、F1） 当时∠A=30°时，求证：PE+PF=BC2） 当时∠A ≠30°（∠A<∠ABC ）时，试问以上结论是否依然成立？若成立，请加以证明；若不成立，请说明理由.AB D E A BCD EF P。

直角三角形的性质和判定
性质：直角三角形两个锐角互余；直角三角形斜边上的中线等于斜边的一半；在直角三角形中，30度角所对的直角边是斜边的一半。

判定：有一个角为90°的三角形是直角三角形；一个三角形，如果这个三角形一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形。

直角三角形的性质
①直角三角形的两个锐角互为余角；
②直角三角形斜边上的中线等于斜边的一半；
③直角三角形的两直角边的平方和等于斜边的平方（勾股定理）；
④直角三角形中30度角所对的直角边等于斜边的一半；
直角三角形的判定
判定1：有一个角为90°的三角形是直角三角形。

判定2：若a²+b²=c²的平方，则以a、b、c为边的三角形是以c为斜边的直角三角形（勾股定理的逆定理）。

判定3：若一个三角形30°内角所对的边是某一边的一半，那么这个三角形是以这条长边为斜边的直角三角形。

判定四:有两个互补锐角的三角形是直角三角形。

判定5：证明直角三角形全等时可以利用HL ，两个三角形的斜边长对应相等，以及一个直角边对应相等，则两直角三角形全等。

（定理：斜边和一条直角对应相等的两个直角三角形全等。

简称为HL）
决定6:如果两条直线相交，并且它们的斜率的乘积是负倒数，那么这两条直线是垂直的。

判定7:如果三角形一边的中线等于中线所在边的一半，那么这个三角形是直角三角形。