当前位置：文档之家 › 2014.12.1正切函数图象和性质全总结

2014.12.1正切函数图象和性质全总结

  • 格式：doc
  • 大小：492.50 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

正切函数的图像和性质

正切函数的图像和性质

−
3π 2
−π
−
π
2
0
π
2
π
3π 2
x
从图中可以看出,正切曲线是由被相互平行的直线 从图中可以看出 正切曲线是由被相互平行的直线
x=
π
2
+ kπ , (k ∈ Z ) 所隔的无穷多支曲线组成的 所隔的无穷多支曲线组成的.
二:性质
你能从正切函数的图象出发,讨论它的性质吗 你能从正切函数的图象出发 讨论它的性质吗? y 1
π
(3)x ∈(kπ , kπ + ),(k ∈ Z ) 2
π
tan x≤ 3?
小结: 1.正切曲线的几何画法以及正切函数的性质 2.正切函数性质 3.用数形结合的思想理解和处理有关的问题.
性质 函数 定义域 值域 周期性 奇偶性 单调性 y=tanx π {x | x ≠ kπ + , k ∈ Z} 2 R T= π 奇函数 π π 增区间 (kπ − , kπ + )k ∈ Z 2 2
是否为周期函数 周期函数？ 2、正切函数 y = tan x 是否为周期函数？ 由诱导公式知
y tan α = ⇒ x ≠ 0 ⇒ α的终边不在y轴上 x π ∴ α ≠ kπ + (k ∈ z ) 2 思考
π
2
Q f ( x + π ) = tan ( x + π ) = tan x = f ( x ), x ∈ R, x ≠
A
x
4.10 正切函数的图像和性质
问题2 问题2、如何利用正切线画出函数 的图像？ 的图像？
y=
π π tan x，x ∈ − 2 ， 2
π
角 的终边 3 T

正切函数的性质与图像 课件

正切函数的性质与图像 课件

y tan x T π
2、奇偶性 tan( x)
tan
x,
x
R,

π
kπ, k
Z
2
正切函数是奇函数
例1、判断下列函数的奇偶性并求周期：
（1）y tan 3x
（2）y tan2x
奇函数，T
3
.
奇函数，T
2
.
（3）y
tan
x 2
3
(4) y tan( π x 3) 35
非奇非偶函数，T 2.非奇非偶函数，T 3
O
6
4
3
2
正切函数的性质:
定义域：x
x
2
k
,
k
Z
值域： R
周期性：T
奇偶性：奇函数
单在调每性一：个在开开区区间间内 都2是 单k调, 2增 函k数 k.能 Z不内能递说增 正切函数在整个定义域上单调递增？
三、例题研究
例2、求函数y tan π x π 的定义域、 2 3
周期和单调区间.
正切函数的性质和图象
一、探究
请问:研究正弦函数、余弦函数之后 你积累了那些经验？
单位圆技法 诱导公式、函数性质
平移正弦线、余弦线 五点法
画函数图象
描点法
二、正切函数的性质
新角度来研究
1、周期性 tan( x π)
T π
tan x,
x
R,
x
π
kπ, k
Z
y A tan(x ) T 2
理清: (1)换元法 (2)周期T π
ω (3)复合函数的单调性
例3、比较tan 13 π与tan 17 π的大小.
4
5

正切函数的性质及其应用

正切函数的性质及其应用

正切函数的性质及其应用正切函数是三角函数中的一种，表示一个角的正切值。

在数学和物理学中，正切函数具有一些重要的性质，并且在各种应用中扮演着关键角色。

本文将探讨正切函数的性质以及一些常见的应用。

一、正切函数的定义和图像特点正切函数的定义公式为：tan(x) = sin(x) / cos(x)，其中x为角度或弧度。

根据定义，我们可以得出正切函数的几个图像特点。

1. 定义域和值域：正切函数的定义域是所有实数除去所有使得cos(x) = 0的点，通常写作D: x ≠ (2n + 1) * π / 2，其中n为整数。

值域是整个实数集，记作R。

2. 周期性：正切函数的图像在一个周期内呈周期性变化。

周期为π，即tan(x) = tan(x + kπ)，其中k为整数。

3. 奇函数性质：正切函数具有奇函数性质，即满足tan(-x) = -tan(x)，这是由于sin(-x) = -sin(x)，cos(-x) = cos(x)。

4. 渐近线：正切函数在x = (n + 1/2) * π，其中n为整数时，有垂直渐近线。

在x = n * π，其中n为整数时，有水平渐近线。

基于这些性质，我们可以画出正切函数的图像。

图像在每个周期内呈现周期性的上升与下降，同时存在垂直和水平渐近线。

二、正切函数的应用正切函数在各个领域有着广泛的应用。

以下是一些常见的应用示例：1. 三角测量：正切函数在三角测量中扮演着重要的角色。

例如，在测量一个目标物体的高度时，可以利用正切函数来计算角度并得到正确的高度值。

2. 电工学：在电路分析中，正切函数可以用来计算交流电路中电压和电流的相位差。

相位差是指两个波形之间的时间延迟，正切函数可以帮助我们解决相关的计算问题。

3. 工程学：在工程学中，正切函数经常用于解决角度和距离的计算问题。

例如，在建筑工程中，可以利用正切函数来计算楼梯的坡度和斜面的角度。

4. 自然科学：正切函数在自然科学中也有着广泛的应用。

三角函数正切函数的性质与图像

三角函数正切函数的性质与图像

正切函数的图像向右平移π个单位，可以得 到余弦函数的图像。
左右翻转
正切函数的图像关于$y$轴对称，即$tan( - x) = tan(x)$。 正切函数的图像向左翻转后，可以得到正切函数的图像。
03
正切函数的图像绘制
利用Python绘制正切函数图像
导入matplotlib库
定义正切函数
首先需要导入matplotlib库，该库是 Python中用于绘图的常用库之一。
使用xlabel和ylabel参数可以添加x轴和y轴的标签，例如x轴 标签为“$x$”，y轴标签为“$y$”。
显示网格线
使用grid参数可以显示网格线，以便更好地观察图像的细节 。
04
三角函数的实际应用
物理中的三角函数
简谐振动
简谐振动的位移与时间的关系可以表示为正弦或余弦函数，利用三角函数性 质可以更深入地理解简谐振动的特征。
正切函数的对称性
正切函数图像无对称轴，但在$x = \frac{\pi}{2} + k\pi$ 处，函数图像呈现对称性。
正切函数的奇偶性
$tan( - x) = - tan(x)$，因此正切函数为奇函数。
正切函数的应用
正切函数在解直角三角形、求三角形的面积、研究三角恒 等式等方面具有广泛应用。
对未来研究正切函数的展望
三角函数正切函数的性质与图像
xx年xx月xx日
contents
目录
• 正切函数概述 • 正切函数的性质 • 正切函数的图像绘制 • 三角函数的实际应用 • 总结与展望
01
正切函数概述
正切函数的定义
正切函数：tan(x) = sin(x) / cos(x) 值域：(-∞，∞)
定义域：{x | x ≠ π/2 + kπ，k ∈ Z} 周期：π

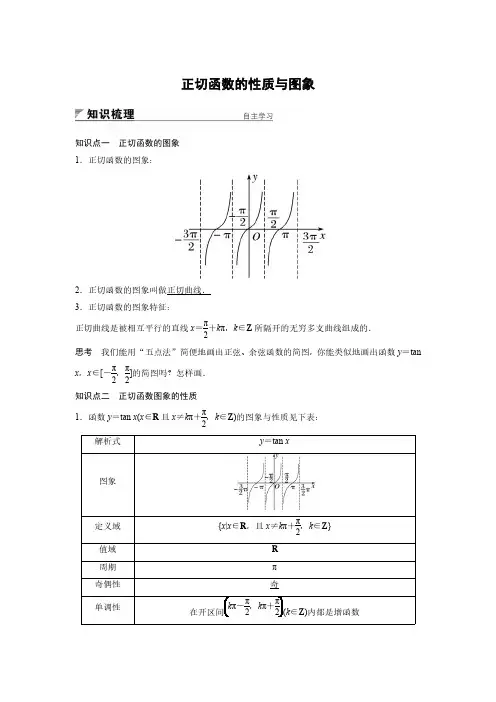
正切函数的性质与图象 课件

正切函数的性质与图象 课件
π + ,∈Z 求x 的范围,该范围就是不等式的解集.当 ω<0 时,先利
用诱导公式将 x 的系数变为正值,再进行上述步骤.
【变式训练 5】 求函数 y= tan + 1 + lg(1 − tan )的定义域
.
tan + 1 ≥ 0,
解:由题意得
即-1≤tan x<1.
1-tan > 0,
故函数的单调递增区间为
- , +
3 18 3
18
π
π
3x− ≠kπ+ (∈
3
2
即函数的定义域为 ≠
递减区间.
(∈Z),不存在单调
反思求函数y=Atan(ωx+φ),A≠0,ω>0的定义域和单调区间,可以通
过解不等式的方法去解答:把“ωx+φ(ω>0)”看作一个整体,借助正切
函数的定义域和单调区间来解决.若ω<0,则先利用诱导公式将x的
首先观察α,β是否在正切函数的同一个单调区间,若是,则直接运
用正切函数的单调性比较大小;若不是,则先利用诱导公式,将角α,β
π π
转化到正切函数的同一单调区间内,通常是转化到区间 - , 再运
内,
2 2
用正切函数的单调性比较大小.
19π
23π
与 tan
的大小.
7
8
19π
2π
2π
解:tan
= tan 3π= −tan ,
π
π
(2)由 T= , 得6π= , ∴
||
||
1
答案:(1)3π (2)±
6
1
-
3
π
+

正切曲线的性质与图像

正切曲线的性质与图像
正切函数是周期函数,T= 正切函数是奇函数 正切函数在开区间
内都是增函数
值域
k , k , k Z 2 2
正切函数的值域是实数集R
11
探究二 正切函数的图象
y
类比 正弦函数图象 的作法画出正切函数图 象.


2

3 8 4


8

8


9
探究一 正切函数的性质
周期性
奇偶性
正切函数是周期函数,T= 正切函数是奇函数 正切函数在开区间 内都是增函数
单调性
k , k , k Z 2 2
值域
正切函数的值域是实数集R
10
探究一 正切函数的性质
定义域
周期性 奇偶性 单调性
x | x k , k Z 2
19
典例分析: 例3求函数 y tan( x ) 的定义域、周期、单调区间. 2 3
解:函数的自变量
x k , k Z , 2 3 2
x 应满足
tan ( x 2) f ( x 2), 3 2
即
1 x 2k , k Z . 3
增函数增函数正方向正方向实数集实数集rr负方向负方向探究一正切函数的性质单位圆中正切线10周期性奇偶性单调性值域正切函数是周期函数t正切函数在开区间内都是增函数探究一正切函数的性质正切函数是奇函数正切函数的值域是实数集r11周期性奇偶性单调性值域正切函数是奇函数正切函数在开区间内都是增函数正切函数的值域是实数集r探究一正切函数的性质正切函数是周期函数t定义域12正弦函数图象的作法画出正切函数图探究二正切函数的图象类比13的图象如图可以根据周期性左右扩展得到其14正切函数的图象正切函数ytanxxrx的图象如图所示

正切函数的性质与图象

正切函数的性质与图象

正切函数的性质与图象知识点一正切函数的图象1．正切函数的图象：2．正切函数的图象叫做正切曲线．3．正切函数的图象特征：正切曲线是被相互平行的直线x ＝π2＋k π，k ∈Z 所隔开的无穷多支曲线组成的．思考我们能用“五点法”简便地画出正弦、余弦函数的简图，你能类似地画出函数y ＝tanx ，x ∈[－π2，π2]的简图吗？怎样画．知识点二正切函数图象的性质1．函数y ＝tan x (x ∈R 且x ≠k π＋π2，k ∈Z )的图象与性质见下表：2.函数y ＝tan ωx (ω≠0)的最小正周期是π|ω|.思考正切函数图象是否具有对称性？如果具有对称性，请指出其对称特征．题型一正切函数的定义域例1(1)函数y ＝tan(sin x )的定义域为，值域为．(2)求函数y ＝tan(2x －π4)的定义域．跟踪训练1求函数y ＝tan x ＋1＋lg(1－tan x )的定义域．题型二求正切函数的单调区间例2求函数y ＝tan －12x跟踪训练2求函数y ＝tan x 题型三正切函数图象性质的应用例3(1)函数y ＝tan(2x ＋π6)的最小正周期是()A ．πB ．2π C.π2D.π6(2)画出函数y ＝|tan x |的图象，并根据图象判断其单调区间、奇偶性、周期性．跟踪训练3(1)下列函数中，既是以π为周期的奇函数，又是(0，π2)上的增函数的是()A ．y ＝tan x B ．y ＝cos xC ．y ＝tan x 2D ．y ＝|sin x |例4当x ∈(－32π，32π)时，确定方程tan x －sin x ＝0的根的个数．1．下列说法正确的是()A ．正切函数在整个定义域内是增函数B ．正切函数在整个定义域内是减函数C ．函数y ＝3tan x 2的图象关于y 轴对称D ．若x 是第一象限角，则y ＝tan x 是增函数2．函数f (x )＝tan(x ＋π4)的单调递增区间为()A ．(k π－π2，k π＋π2)，k ∈ZB ．(k π，(k ＋1)π)，k ∈ZC ．(k π－3π4，k π＋π4)，k ∈ZD ．(k π－π4，k π＋3π4)，k ∈Z32π为周期；③是奇函数的是()A ．y ＝tan xB ．y ＝cos xC ．y ＝tan x 2D ．y ＝－tan x4．方程x ＝3在区间[0,2π)上的解的个数是()A ．5B ．4C ．3D ．25．函数y ＝3tan 的对称中心的坐标是．一、选择题1．函数y ＝x ∈R 且x ≠310π＋k π，k ∈Z 的一个对称中心是()A ．(0,0)，D ．(π，0)2．函数f (x )＝lg(tan x ＋1＋tan 2x )为()A ．奇函数B ．既是奇函数又是偶函数C ．偶函数D ．既不是奇函数又不是偶函数3．函数y ＝tan ()4．函数f (x )＝tan ωx (ω>0)的图象的相邻两支曲线截直线y ＝π4所得线段长为π4，则f 是()A ．0B ．1C ．－1 D.π45．函数y ＝lg(1＋tan x )的定义域是()A ．(k π－π2，k π＋π2)(k ∈Z )B ．(k π－π2，k π＋π4)(k ∈Z )C ．(k π－π4，k π＋π2)(k ∈Z )D ．(k π－π4，k π＋π4)(k ∈Z )6．函数y ＝tan x ＋sin x －|tan x －sin x |()二、填空题7．使函数y ＝2tan x 与y ＝cos x 同时为单调递增的区间是．8．函数y ＝3tan(ωx ＋π6)的最小正周期是π2，则ω＝.9．求函数y ＝－tan 2x ＋4tan x ＋1，x ∈－π4，π4的值域为．10．已知函数y ＝tan ωx 在(－π2，π2)是减函数，则ω的取值范围是．三、解答题11．判断函数f(x)＝lg tan x＋1tan x－1的奇偶性．12．求函数y＝tan(x2－π3)的定义域、周期、单调区间和对称中心．13．(1)求函数y＝3tan(π4－2x)的单调区间；(2)比较tan1，tan2，tan3的大小．。

2014.12.1诱导公式、三角函数图象和性质全总结

2014.12.1诱导公式、三角函数图象和性质全总结

诱导公式、三角函数的图象和性质全总结一、诱导公式 题型1：直接应用公式1、若m -=-++)sin()sin(ααπ,则)2sin(2)3sin(απαπ-++等于A ．－23 m B ．－32 m C ．23 m D ．32m2、21)cos(-=+απ，23π<α<π2,)2sin(απ-值为（ ） A. 23 B. 21 C. 23±D. —233．设角则,635πα-=)(cos )sin(sin 1)cos()cos()sin(222απαπααπαπαπ+--+++--+的值等于A ．33B ．－33C ．3D ．－3 4．.已知,1)sin(=+y x 求证：.0tan )2tan(=++y y x 5、已知sin （3π＋θ）＝41，求)cos()cos()2cos()2cos(]1)[cos(cos )cos(θθππθπθθπθθπ-+++-+-++的值.6、化简：︒+︒︒︒+790cos 250sin 430cos 290sin 21题型2：间接应用公式1、已知sin(4π+α)=23，则sin(α-43π)值为（ ）A. 21 B. —21 C. 23 D. —232、若sin （125°－α）=1213,则sin （α＋55°）= ．3、若=--=-)133cos(,2/1)137sin(0a a 则题型3：分类讨论1、若k ∈Z ，求证：])1cos[(])1sin[()cos()sin(απαπαπαπ-++++-k k k k ＝－1．2、设sin ,(0)()(1)1,(0)x x f x f x x π<⎧=⎨-+≥⎩和1cos ,()2()1(1)1,()2x x g x g x x π⎧<⎪⎪=⎨⎪-+≥⎪⎩求++)31()41(f g +)65(g )43(f 的值.二、三角函数的图象和性质正弦函数、余弦函数、正切函数的图像题型1：三角函数的图象变换例1、做出下列函数的图像（1）、x y s i n -=（2）()x y --=sin （3）x y tan -= （4）()x y --=tan例2、（2000全国，5）函数y ＝－xc os x 的部分图象是（ ）D练1、函数tan cos y x x = 的部分图象是2、函数y =－x ·cos x 的部分图象是()3、1sin [,]222y x y x x ππ==∈-函数与在内有多少个交点？ 4、sin y x y x x R ==∈函数与在内有多少个交点？ 5、方程2sin2x =x －3的解的个数为_______.题型2：三角函数的单调性例．求下列函数的单调区间：（1）y =21sin （4π－32x）；（2）y =－｜sin （x +4π）｜。

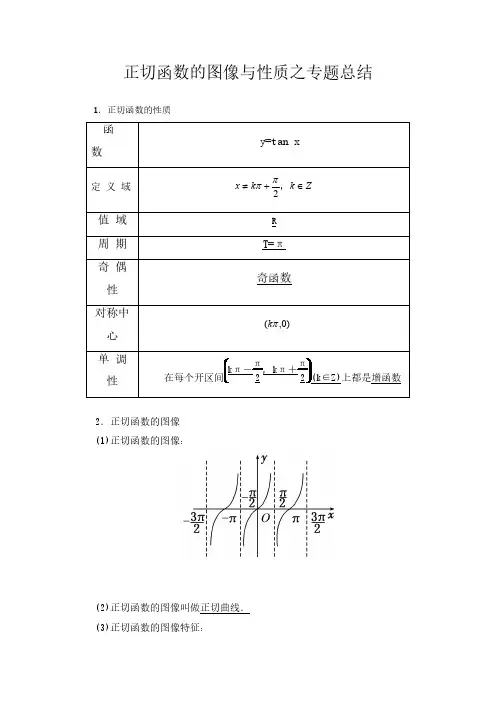
三角函数正切函数的图像与性质之专题总结

三角函数正切函数的图像与性质之专题总结

正切函数的图像与性质之专题总结1．正切函数的性质2．正切函数的图像(1)正切函数的图像：(2)正切函数的图像叫做正切曲线．(3)正切函数的图像特征：正切曲线是被的直线x ＝π2＋k π，k ∈Z 所隔开的无穷多支曲线组成的注意：a.不能说正切函数在整个定义域内是增函数b.正切函数在每个单调区间内都是增函数题型一、作正切函数的图像例1.画出函数⎪⎭⎫ ⎝⎛+=3tan πx y 的图像并讨论其性质分析：可以利用平移法，将个单位像左平移3tan πx y =例2.画出函数[]ππ,,tan -∈=x x y 的图像，并讨论其性质题型二、正切函数的定义域问题例1求函数)4tan(x y -=π的定义域.分析：)4tan()4tan(ππ--=-x x 我们已经知道了ztan 的定义域，那么)4tan(π-x 的定义域相当于令4π-=x z ，把)4tan(x -π看做4tan π-=x z z 和复合而成，此时称）4tan(π-=x y 为复合函数，即定义域为2ππ+≠k z ，Z k ∈,也就是24-πππ+≠k x Zk k x ∈+≠，43ππ例2..函数2225)tan 1(log xx y -+=的定义域变式练习： 1.求函数的定义域:1cos 2)1lg(tan -+=x x y .2.函数y ＝11＋tan x 的定义域3.求函数)42tan(π-=x y 的定义域小结：正切函数定义域方法定义域限制条件：①分母不为0②偶次根式被开方数大于等于0③对数的真数大于0④特别地，2,tan ππ+≠=k x x y ⑤复合函数的定义域需要用到换元法，令2ππβ+≠+k nx 题型三、正切函数的值域例1.已知⎥⎦⎤⎢⎣⎡-∈46ππ，x ，求函数2tan tan 2++=x x y 的最值分析：令xt tan =例2.若⎥⎦⎤⎢⎣⎡∈612ππ，x 时，求x y tan =的值域例3.求函数⎪⎭⎫ ⎝⎛<<+=40cot tan πx x x y 的值域变式练习：1.求函数3tan 2tan 2+-=x x y 值域2.求函数y ＝1tan 1tan +-x x 的值域3.当⎥⎦⎤⎢⎣⎡∈34ππ，x 时，求函数1tan tan 2++=x x y 的值域4.求函数3tan(π-=x y 的值域5.求函数)32tan(2π+=x y 的定义域和值域6.函数y ＝3tan(π＋2x )，－π4<x ≤π6的值域小结:正切函数值域求法①二次型c x b x a y ++=tan tan 2，换元令x t tan =，运用二次函数图象性质(一看对称轴,二看区间端点)②对勾函数型xbx a y tan tan +=，形如ab b a 2≥+③()ϕ+=wx y tan 型，先求ϕ+wx 的取值范围，再由x y tan =单调性求值域题型四、利用正切函数解不等式例1.解不等式3tan ≥x .分析：根据正切函数图像，在一个周期内只需23ππ≤≤x ，所以23ππππ+≤≤+k x k例2.解不等式1tan -≤x 变式练习：1.不等式tanx＞-1的解集是？2解不等式tan(2x-3π)≤1小结：解正切不等式方法①图像法，即先画出函数图像，找出符合条件的边界角，再写出符合条件的角的集合②三角函数线法，则是先在单位圆中作出角的边界值时的正切线，得到边界角的终边，在单位圆中画出符合条件的区域.要特别注意函数的定义域题型五、判断正切函数的奇偶性例1.判断函数1tan ()lg1tan xf x x+=-+的奇偶性例2..判断函数()tan f x x =的奇偶性变式练习： 1.求函数y =tan4x 的定义域、值域，并判断其奇偶性。

正切函数的性质及图像

正切函数的性质及图像

正切函数的性质及图像正切函数的性质及图像
一、正切函数的性质：
1、定义域：{x|x≠(π/2)+kπ,k∈Z}。

2、值域：实数集R。

3、奇偶性：奇函数。

二、正切函数的图像：
正切定理：
在平面三角形中，正切定理说明任意两条边的和除以第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。

正切定理：(a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2)
证明——由下式开始：
由正弦定理得出
正切函数是直角三角形中，对边与邻边的比值。

放在直角坐标系中（如图《定义图》所示）即tanθ=y/x。

也有表示为tgθ=y/x，但一般常用tanθ=y/x。

曾简写为tg，现已停用，仅在20世纪90年代以前出版的书籍中使用。

正切函数的图像及性质

正切函数的图像及性质

y = 3 tan(2 x + ) 4
π
∴周期T =
π
2
练习 1,观察三角函数图像，分别求 的范围 观察三角函数图像， 观察三角函数图像 分别求x的范围
(1) sin x < 0, (2) cos x ≥ 0, (3) tan x > 0
解 (1) x ∈(2kπ + π ,2kπ + 2π ),(k ∈ Z)
单调性 max & min
π
2
+ kπ ,

π
2
+ kπ )上单调增
无
例1
π 的定义域。 求函数 y = tan ( x + ) 的定义域。 4
π 解 ，那么函数y=tanz的定义域为 4 π z | z ∈ R, z ≠ + kπ, k ∈ Z 2 π π 即x + ≠ + kπ 4 2 π x ≠ + kπ 4 π y = tan( x + )的定义域为 所以函数 4 π x | x ∈ R, x ≠ + kπ, k ∈ Z 4
5 π π 2π π Q− < < < 2 4 5 2
5
5
函数y = tan x，x ∈ − ， ）是增函数 （ 2 2
π π
2π ∴tan( ) < tan( ) 4 5 11 13 即tan − π）< tan （ （- π） 4 5
π
例3.求下列函数的周期.
分析： 的周期为２ ， 分析：y=sinx与y=cosx的周期为２∏，则 与 的周期为 y=Asin(wx+Q)与y=Asin(wx+Q)的周期为 与 的周期为2∏/w 的周期为 y=tanx的周期为 ，则y=Atan(wx+Q)的周期为： 的周期为∏， 的周期为： 的周期为 的周期为 T=∏/w

正切函数的图象和性质

正切函数的图象和性质

(1) 900 1670 1730 1800 解：
) 上是增函数 又 y tan x 在 (900 ,2700
0 t an1670 t an173
(2) tan2 tan3 tan1.
例题讲解
例3 求函数
1 y 3 tan( x ) 的单调区间. 2 4
2
x

得 : k u k , k Z 2 2 4
:
y 3 tan(
1 x )的单调递减区间为 : 2 4
3 2k x 2k 2 2
3 2k ,2k , k z 2 2
例题讲解
例4 求下列函数的周期：
正切函数在开区间 内都是增函数。
k , k , k Z 2 2
3 2k ,2k , k z 2 2
例题讲解
x 变题(2) y 3 tan( ) 2 4 x 解 : 因为原函数可化为: y 3 tan( ); 2 4 1
由u
1 即 : k x k 2 2 4 2
(一)
我们先来作一个周期内的图象。
想一想：先作哪个区间上的图象好呢？
作法如下：
( 2 2 , )
①作直角坐标系，并在 y 轴左侧作单位圆；
②把单位圆右半圆分成8等份，分别在单位圆 中作出正切线；
③把 x 到 2 别作平移个线段; ④连线成图. 轴上


2
这一段分成8等份, 然后,分
正切函数的图像
内都是增函数。
能否说:正切函数就是单调增函数?
例题讲解
例1.观察图象，写出满足下列条件的x值的范围：

正切函数的性质

正切函数的性质

变题(2) y 3 tan( x )
24
u
24
1 x 为增函数 ;且y tan u的单调区间为
2 k 4 u k ,k Z
2
2
由u 1 x 得 :
24
k 1 x k 22 4 2
解 :因为原函数可化为 : y 3 tan( x );
:
令u
x
; 所以 y
1y、=ta作n图x 的x 基本(思路,：利)用的正图切象线，作由出正函切数函数
22
的周期性，将图象左、右扩展得到正切曲线； 2、图象特征：正切曲线是由相互平行的直线
x k (k Z ) 所隔开的无穷多支曲线
2
组成，每支曲线向上、向下可无限接近相应 的两体直线； 3、由函数y=tanx图象可变换得到函数 y=Atan(ωx+φ)的图象。
作法如下： Y
➢作直角坐标系，并在
直角坐标系y轴左侧作单
位圆。
把单位圆右半圆
中作出正切线。
X
0
2
找横坐标（把x轴上
到 这一段分成8
2
等份）
找交叉点。
➢连线。
由正切函数的周期性，把图象向左、向右扩 展，得到正切函数的图象，称为正切曲线
y
1 x
-3/2 - -/2
0 /2
3/2
-1
y=tanx x k k z
2
2
(2k ,2k 3 ) (k Z)
2
2
例4 求下列函数的周期：
(1) y 3 tan( 2x ); (2)变题y 3 tan( 1 x );
4 解 : f (x) 3 tan( 2x )
3
tan( 2 x
4

正切函数图象与性质总结

正切函数图象与性质总结

3
3
解得
掌握正切函 数的性质是 解决此类问 题的关键
因此，函数的单调递增区间是
( 5 2k, 1 2k), k . 33
题型二：求周期
例2 求函数 y tan 3 x 的周期.
解：因为 tan(3x ) tan 3x,
即tan3(x+ )=tan3x,
3
T
3
总结：正切函数的周期公式T =
w
练习：求下列函数的周期：
(1) y 5 tan x (2) y tan(4 x)
2
4
2
题型三：解不等式
例3 解 不 等 式 ：tan x 3
解：
y
3
0 x
32
由图可知：x

k

3Biblioteka ,k
2

(k

Z
)
|
x

2k

1 3
,
k

.
由于 f (x) tan( x ) tan( x )
23
23
因此函数的周期为2.

tan

2

x

2


3

由 k x k, k
2
2 32
5 2k x 1 2k, k .
kZ
(7)对称中心
( kπ,0) 2
题型一：求函数定义域、单调区间
例1.求函数 y tan( x ) 的定义域、周期和单调区间.
23
解：函数的自变量 x 应满足
x k , k , 即 x 2k 1 , k .
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

诱导公式、三角函数的图象和性质全总结正切函数的图像题型1：三角函数的图象变换例1、做出下列函数的图像（1）x y tan -= （2）()x y --=tan练、1、在区间（－π23，π23）内，函数x y tan =与函数x y sin =图象交点的个数为（ ）A ．1B ．2C ．3D ．52、函数在一个周期内的图像是（ ）题型2：三角函数的单调性例1、写出下列函数的单调区间及在此区间的增减性：(1)1tan()26y x π=-； (2)tan(2)4y x π=-．例2、作出函数y=｜tanx ｜的图像，并根据图像求其单调区间．练、1、下列命题中正确的是 ( )A ． x y tan =在第一象限单调递增．B ． 在x y tan =中，x 越大，y 也越大C ． 当x ＞0时，x tan ＞0．D ． x y tan =的图象关于原点对称 2、使函数y=tanx 和y=sinx 同时为单调递增函数的区间是．3、已知函数y =tan ωx 在(-2π,2π)内是单调减函数,则ω的取值范围是 ( ) (A)0<ω≤ 1 (B) -1≤ω<0 (C) ω≥1 (D) ω≤ -14、求下列函数y =5、观察正切曲线，满足条件1tan <x 的x 的取值范围是(其中k ∈Z) ( ) A ．(2k π-4π,2k π+4π) B ．(k π,k π+4π) C ．(k π4π-,k π+4π) D ．(k π+4π,k π+43π)6、观察正切曲线，满足条件3tan >x 的x 的取值范围是．题型3：求与正余弦函数有关的定义域问题例、求函数y=lg （tanx-3）+3cos 2+x 的定义域． 练、1、函数y =lgtan 2x的定义域是 ( ) (A){x |k π<x <k π+4π,k ∈Z} (B) {x |4k π<x <4k π+2π,k ∈Z} (C) {x |2k π<x <2k π+π,k ∈Z} (D)第一、三象限 2、函数xy tan 11-=的定义域是．3、求函数()()3tan 13tan 2-++-=x x x f 的定义域．4、若直线2π⋅=a x ()1≤a 与函数⎪⎭⎫⎝⎛+=42tan πx y 图象不相交，则=a．5、试求函数 的定义域，并作出区间上的图像．题型4：求正余弦函数的周期例．求下列函数的单调区间： （1）y =tanx ；（2）y =｜tanx+1｜练、1、直线y = a （a 为常数）与y = tan ωx （ω>0）的相邻两支的交点距离为 A ．πB ．ωπ C.ωπ2 D ．与a 有关的值 2、在下列函数中,同时满足(1)在(0,2π)上递增；(2)以2π为周期；(3)是奇函数的是 ( ) (A) y =|tanx | (B) y =cos x (C) y =tan21x (D) y =－tanx3、函数的最小正周期是____________．题型5：求正余弦函数的最值例、函数y =tan 2x -2tan x +3的最小值是 ; 练、1、函数⎥⎦⎤⎝⎛-∈=4,3,tan ππx x y 的值域是 A ．(]1,∞- B ．(]1,3- C ．()+∞∞-, D ．()+∞-,32、已知 ．求函数的值域．3、函数 的值域是__________．题型6：利用单调性，比较正余弦函数值的大小例、下列不等式中，正确的是 A ． tan 74π＞tan 73πB ． tan(-413π)＞tan(-512π) C ． tan 4＜tan3 D ． tan281°＞tan665°练1、已知a =tan1,b =tan2,c =tan3,则a 、b 、c 的大小关系是 ( ) (A) a <b <c (B) c <b <a (C) b <c <a (D) b <a <c 2、不通过求值，比较下列各式的大小 （1）tan(-5π)与tan(-37π) (2)tan(78π)与tan (16π)3、4tan ,3tan ,2tan ,1tan 由小到大排列为．4、比较大小：（1）ο125tan 与ο137tan ； （2）⎪⎭⎫ ⎝⎛-34tan π与⎪⎭⎫⎝⎛-511tan π。

题型7：求正切函数的对称轴对称中心例、求函数y=3tan （2x+3π）的对称中心的坐标．练、1、求函数y=tan （2x-3π）的单调区间．题型8：三角函数寄偶性练、1、函数y=3tan(2x +3π)的对称中心的坐标是 ．2、若函数)0(33tan ≠⎪⎭⎫⎝⎛-=a ax y π的最小正周期为2π，则=a ．3、函数的图像对称于（）A．原点B．轴C．轴D．直线题型4：三角函数的定义域、值域例5．（1）已知f （x ）的定义域为［0，1］，求f （c os x ）的定义域； （2）求函数y =lgsin （c os x ）的定义域； 分析：求函数的定义域：（1）要使0≤c os x ≤1，（2）要使sin （c os x ）＞0，这里的c os x 以它的值充当角。

解析：（1）0≤c os x ＜1⇒2k π－2π≤x ≤2k π+2π，且x ≠2k π（k ∈Z ）。

∴所求函数的定义域为{x ｜x ∈［2k π－2π，2k π+2π］且x ≠2k π，k ∈Z }。

（2）由sin （c os x ）＞0⇒2k π＜c os x ＜2k π+π（k ∈Z ）。

又∵－1≤c os x ≤1，∴0＜c os x ≤1。

故所求定义域为{x ｜x ∈（2k π－2π，2k π+2π），k ∈Z }。

点评：求三角函数的定义域，要解三角不等式，常用的方法有二：一是图象，二是三角函数线。

题型6：三角函数的奇偶性例7．（2001上海春）关于x 的函数f （x ）=sin （x +ϕ）有以下命题： ①对任意的ϕ，f （x ）都是非奇非偶函数； ②不存在ϕ，使f （x ）既是奇函数，又是偶函数； ③存在ϕ，使f （x ）是奇函数； ④对任意的ϕ，f （x ）都不是偶函数。

其中一个假命题的序号是_____.因为当ϕ=_____时，该命题的结论不成立。

答案：①，k π（k ∈Z ）；或者①，2π+k π（k ∈Z ）；或者④，2π+k π（k ∈Z ）解析：当ϕ=2k π，k ∈Z 时，f （x ）=sin x 是奇函数。

当ϕ=2（k +1）π，k ∈Z 时f （x ）=－sin x 仍是奇函数。

当ϕ=2k π+2π，k ∈Z 时，f （x ）=c os x ，或当ϕ=2k π－2π，k ∈Z 时，f （x ）=－c os x ，f （x ）都是偶函数.所以②和③都是正确的。

无论ϕ为何值都不能使f （x ）恒等于零。

所以f （x ）不能既是奇函数又是偶函数。

①和④都是假命题。

点评：本题考查三角函数的奇偶性、诱导公式以及分析问题的能力，注意k ∈Z 不能不写，否则不给分，本题的答案不惟一，两个空全答对才能得分。

题型7：三角函数的周期性例8．设)0(cos sin )(>+=ωωωx b x a x f 的周期π=T ，最大值4)12(=πf ，（1）求ω、a 、b 的值；（2）的值终边不共线，求、、的两根，为方程、、若)tan(0)(βαβαβα+=x f 。

解析：(1) )sin()(22ϕω++=x b a x f ， π=∴T ， 2=∴ω，又 )(x f Θ的最大值。

4)12(=πf Θ， 224b a +=∴ ① ，且 122cos b 122sin a 4π+π=②，由 ①、②解出 a =2 , b =3.(2) )32sin(42cos 322sin 2)(π+=+=x x x x f ， 0)()(==∴βαf f ，)32sin(4)32sin(4πβπα+=+∴， 32232πβππα++=+∴k ， 或)32(232πβπππα+-+=+k ，即 βπα+=k (βα、 共线，故舍去) ， 或 6ππβα+=+k ，33)6tan()tan(=+=+∴ππβαk )(Z k ∈。

点评：方程组的思想是解题时常用的基本思想方法；在解题时不要忘记三角函数的周期性。

题型8：三角函数的最值例9．（2000京、皖春理，10）函数y ＝xx cos sin 21++的最大值是（ ）A ．22－1 B ．22＋1 C ．1－22D ．－1－22 解析：B ；221221)4sin(221cos sin 21+=-≤+++++=πx x x y例1．比较下列各组三角函数的值的大小 （1）sin194°和cos160°；（2）)1543(π-ctg 和)1974(π-ctg （3）)83sin(sin π和)83sin(cos π；（4）tg1，tg2和tg3；例2．求下列各函数的单调区间 （1）)32cos(2π+-=x y ；（2）x x y 2cos 32sin 1+-=（减区间） （3）x x y sin sin 2+-=； （4）)43cos(log 1ππ+=x y （增区间）例3. 求下列函数最小正周期（1）)2(cos 2+=x y π；（1）T=1； （2）a x ctg a x tgy -=；（2）2||xa T =； （3）)6sin()3sin(x x y -+=ππ；（3）T=π； （4）x x y 44sin cos -=；（4）T=π； （5）xx y sin 1cos +=；（5）T=2π；（6）x tg x tg y 21222+=；（6）2π=T ； （7）y=|sin2x|；（7）2π=T ；例4.求函数)tan 1(sec )tan 1(sin 422x x x x y +-=的周期。

例5．已知函数)(3sin)(N n n x f ∈=π， 求：f(1)+f(2)+f(3)+……+f(100)的值。

例6．求下列函数的最小正周期 （1）|)32sin(|π-=x y （2）|21)32sin(|+-=πx y例7．函数)252sin(π+=x y 的图像的一条对称方程是（）。

A ．2π-=x B ．4π-=xC ．8π=xD ．π45=x例8．函数)321(π-=x tg y 在一个周期内的图象是（）例4．已知函数R x x x x y ∈++=，1cos sin 23cos 212， （1）当y 取得最大值时，求自变量x 的集合；（2）该函数的图象可由y=sinx （x ∈R ）的图象经过怎样的平移和伸缩变换得到（2000年高考，难度0.70）1．已知函数x x x x x f 4466cos sin cos sin )(+++=求（1）f （x ）的值域 （2）f （x ）的最小正周期 （3）f （x ）的单调区间. 2．判断下列函数的奇偶性。