高中数学必修4《正切函数的性质与图象》

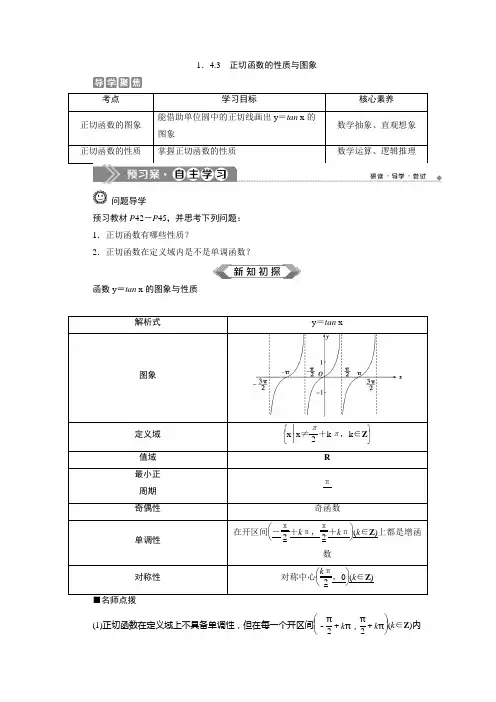
1．4.3 正切函数的性质与图象考点 学习目标核心素养 正切函数的图象 能借助单位圆中的正切线画出y ＝tan x 的图象数学抽象、直观想象 正切函数的性质掌握正切函数的性质数学运算、逻辑推理问题导学预习教材P 42－P 45，并思考下列问题： 1．正切函数有哪些性质？2．正切函数在定义域内是不是单调函数？函数y ＝tan x 的图象与性质解析式y ＝tan x图象定义域 ⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠π2＋k π，k ∈Z值域 R 最小正 周期 π 奇偶性奇函数单调性在开区间⎝⎛⎭⎫－π2＋k π，π2＋k π(k ∈Z )上都是增函数对称性对称中心⎝⎛⎭⎫k π2，0(k ∈Z )(1)正切函数在定义域上不具备单调性，但在每一个开区间⎝ ⎛⎭⎪⎫－π2＋k π，π2＋k π(k ∈Z )内是增函数．不能说函数在其定义域内是单调递增函数．(2)正切函数无单调递减区间，在每一个单调区间内都是递增的，并且每个单调区间均为开区间，不能写成闭区间．判断(正确的打“√”，错误的打“×”) (1)正切函数的定义域和值域都是R .( ) (2)正切函数在整个定义域上是增函数．( ) (3)正切函数在定义域内无最大值和最小值．( ) (4)存在某个区间，使正切函数为减函数．( ) 答案：(1)× (2)× (3)√ (4)× 函数f (x )＝tan ⎝⎛⎭⎫x ＋π6的定义域是( )A.⎩⎨⎧⎭⎬⎫x |x ∈R ，x ≠k π－π2，k ∈ZB ．{x |x ∈R ，x ≠k π，k ∈Z }C.⎩⎨⎧⎭⎬⎫x |x ∈R ，x ≠k π＋π6，k ∈ZD.⎩⎨⎧⎭⎬⎫x |x ∈R ，x ≠k π＋π3，k ∈Z答案：D函数y ＝tan ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π4的最小正周期为( )A.π2 B ．π C ．2π D ．3π答案：A函数y ＝tan ⎝⎛⎭⎫x －π4的单调递增区间是________．答案：⎝⎛⎭⎫－π4＋k π，3π4＋k π，k ∈Z正切函数的定义域求下列函数的定义域：(1)y ＝11＋tan x ；(2)y ＝lg(3－tan x )．【解】 (1)要使函数y ＝11＋tan x有意义，需使⎩⎨⎧1＋tan x ≠0，x ≠k π＋π2（k ∈Z ），所以函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x ∈R 且x ≠k π－π4，x ≠k π＋π2，k ∈Z .(2)因为3－tan x ＞0，所以tan x ＜ 3. 又因为tan x ＝3时，x ＝π3＋k π(k ∈Z )，根据正切函数图象，得k π－π2＜x ＜k π＋π3(k ∈Z )，所以函数的定义域是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |k π－π2＜x ＜k π＋π3，k ∈Z .求正切函数定义域的方法(1)求与正切函数有关的函数的定义域时，除了求函数定义域的一般要求外，还要保证正切函数y ＝tan x 有意义，即x ≠π2＋k π，k ∈Z .(2)求正切型函数y ＝A tan(ωx ＋φ)(A ≠0，ω＞0)的定义域时，要将“ωx ＋φ”视为一个“整体”．令ωx ＋φ≠k π＋π2，k ∈Z ，解得x .函数 y ＝tan(2x －π4)的定义域是________．解析：因为 2x －π4≠π2＋k π(k ∈Z )⇒x ≠3π8＋k π2(k ∈Z )，所以定义域为{x |x ≠k π2＋3π8，k∈Z }．答案：{x |x ≠k π2＋3π8，k ∈Z }正切函数的单调性及其应用(1)求y ＝tan ⎝⎛⎭⎫12x ＋π4的单调区间．(2)比较tan 65π与tan ⎝⎛⎭⎫－137π的大小． 【解】 (1)由题意，k π－π2<12x ＋π4<k π＋π2，k ∈Z ，即k π－3π4<12x <k π＋π4，k ∈Z ，所以2k π－3π2<x <2k π＋π2，k ∈Z ，故单调递增区间为⎝ ⎛⎭⎪⎫2k π－3π2，2k π＋π2(k ∈Z )．(2)tan 65π＝tan ⎝ ⎛⎭⎪⎫π＋π5＝tan π5，tan ⎝⎛⎭⎫－137π＝－tan 137π＝－tan ⎝ ⎛⎭⎪⎫2π－π7 ＝－tan ⎝ ⎛⎭⎪⎫－π7＝tan π7，因为－π2＜π7＜π5＜π2，y ＝tan x 在⎝ ⎛⎭⎪⎫－π2，π2上单调递增，所以tan π7＜tan π5，即tan 65π＞tan ⎝⎛⎭⎫－137π.(1)运用正切函数单调性比较大小的方法①运用函数的周期性或诱导公式将角化到同一单调区间内． ②运用单调性比较大小关系．(2)求函数y ＝A tan(ωx ＋φ)(A ，ω，φ都是常数)的单调区间的方法①若ω＞0，由于y ＝tan x 在每一个单调区间上都是增函数，故可用“整体代换”的思想，令k π－π2＜ωx ＋φ＜k π＋π2，k ∈Z ，解得x 的范围即可．②若ω＜0，可利用诱导公式先把y ＝A tan(ωx ＋φ)转化为y ＝A tan[－(－ωx －φ)]＝－A tan(－ωx －φ)，即把x 的系数化为正值，再利用“整体代换”的思想，求得x 的范围即可．1．函数 f (x )＝13tan ⎝⎛⎭⎫π2x ＋π4的单调递增区间为( )A.⎝⎛⎭⎫2k －32，2k ＋12，k ∈Z B.⎝⎛⎭⎫2k －12，2k ＋12，k ∈Z C.⎝⎛⎭⎫4k －12，4k ＋12，k ∈Z D.⎝⎛⎭⎫4k －32，4k ＋12，k ∈Z 解析：选 A ．由 k π－π2<π2x ＋π4<k π＋π2(k ∈Z )得 2k －32<x <2k ＋12(k ∈Z )．故 f (x )的单调递增区间为⎝⎛⎭⎫2k －32，2k ＋12(k ∈Z )． 2．函数y ＝tan ⎝⎛⎭⎫x 2＋π4，x ∈⎝⎛⎭⎫0，π6的值域是________．解析：因为x ∈⎝ ⎛⎭⎪⎫0，π6，所以x 2＋π4∈⎝ ⎛⎭⎪⎫π4，π3，所以tan ⎝ ⎛⎭⎪⎫x 2＋π4∈(1，3)．答案：(1，3)正切函数奇偶性和周期性的应用已知函数 f (x )＝sin x|cos x |.(1)求函数 f (x )的定义域； (2)用定义判断函数f (x )的奇偶性； (3)在[－π，π]上作出函数 f (x ) 的图象． 【解】 (1)由 cos x ≠0，得 x ≠k π＋π2(k ∈Z )，所以函数f (x )的定义域是{x |x ≠kπ＋π2，k ∈Z }．(2)由(1)知函数 f (x )的定义域关于原点对称．因为 f (－x )＝sin （－x ）|cos （－x ）|＝－sin x|cos x |＝－f (x )，所以 f (x )是奇函数．(3)f (x )＝⎩⎪⎨⎪⎧tan x ，－π2<x <π2，－tan x ，－π≤x <－π2或π2<x ≤π，所以 f (x )在[－π，π]上的图象如图所示．正切型函数的周期性、奇偶性问题的解题策略(1)一般地，函数y ＝A tan(ωx ＋φ)的最小正周期为T ＝π|ω|，常常利用此公式来求周期．(2)判断函数的奇偶性要先求函数的定义域，判断其是否关于原点对称．若不对称，则该函数无奇偶性，若对称，再判断f (－x )与f (x )的关系．画出 f (x )＝tan |x |的图象，并根据其图象判断其单调区间、周期性、奇偶性．解：f (x )＝tan |x |化为 f (x )＝⎩⎪⎨⎪⎧tan x ，x ≠k π＋π2，x ≥0（k ∈Z ），－tan x ，x ≠k π＋π2，x <0（k ∈Z ）， 根据 y ＝tan x 的图象，作出 f (x )＝tan |x |的图象，如图所示，由图象知，f (x )不是周期函数，是偶函数，单调增区间为⎣⎢⎡⎭⎪⎫0，π2，⎝ ⎛⎭⎪⎫k π＋π2，k π＋3π2(k ∈N )；单调减区间为⎝ ⎛⎦⎥⎤－π2，0，⎝⎛⎭⎪⎫k π－3π2，k π－π2(k ＝0，－1，－2，…)．1．函数y ＝1tan x ⎝⎛⎭⎫－π4＜x ＜π4的值域是( ) A ．(－1，1)B ．(－∞，－1)∪(1，＋∞)C ．(－∞，1)D ．(－1，＋∞)解析：选B.因为－π4＜x ＜π4，所以－1＜tan x ＜1，所以1tan x ∈(－∞，－1)∪(1，＋∞)，故选B.2．比较大小：tan13π4________tan 17π5. 解析：因为tan 13π4＝tan π4，tan 17π5＝tan 2π5，又 0<π4<2π5<π2，y ＝tan x 在⎣⎢⎡⎭⎪⎫0，π2内单调递增，所以 tan π4<tan 2π5，即 tan 13π4<tan 17π5.答案：<3．求函数 y ＝tan ⎝⎛⎭⎫－12x ＋π4的单调区间及最小正周期．解：因为 y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4＝－tan ⎝ ⎛⎭⎪⎫12x －π4，所以函数仅存在单调递减区间． 由 k π－π2<12x －π4<k π＋π2(k ∈Z )，得2k π－π2<x <2k π＋32π(k ∈Z )，所以函数 y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4的单调递减区间是⎝⎛⎭⎪⎫2k π－π2，2k π＋32π，k ∈Z ，函数 y ＝tan ⎝ ⎛⎭⎪⎫－12x ＋π4的最小正周期 T ＝π⎪⎪⎪⎪－12＝2π.[A 基础达标]1．函数f (x )＝|tan 2x |是( ) A ．周期为π的奇函数 B ．周期为π的偶函数 C ．周期为π2的奇函数D ．周期为π2的偶函数解析：选D.f (－x )＝|tan(－2x )|＝|tan 2x |＝f (x )为偶函数，T ＝π2.2．(2019·河南林州一中月考)函数 y ＝1－tan ⎝⎛⎭⎫x －π4 的定义域为( )A.⎝⎛⎦⎤k π，k π＋π4，k ∈ZB.⎝⎛⎦⎤k π，k π＋π2，k ∈ZC.⎝⎛⎦⎤k π－π4，k π＋π2，k ∈ZD.⎝⎛⎦⎤k π－π4，k π＋π4，k ∈Z解析：选 C ．由 1－tan ⎝ ⎛⎭⎪⎫x －π4≥0，得 tan ⎝ ⎛⎭⎪⎫x －π4≤1，所以 k π－π2<x －π4≤k π＋π4，k∈Z ，解得 k π－π4<x ≤k π＋π2，k ∈Z ，故所求函数的定义域为⎝ ⎛⎦⎥⎤k π－π4，k π＋π2，k ∈Z ，故选 C.3．函数y ＝tan ⎝⎛⎭⎫12x －π3在一个周期内的图象是下图中的( )解析：选A.由函数周期T ＝π12＝2π，排除选项B 、D.将x ＝23π代入函数解析式中，得tan ⎝ ⎛⎭⎪⎫12×23π－π3＝tan 0＝0，故函数图象与x 轴的一个交点为⎝⎛⎭⎫23π，0.4．与函数y ＝tan ⎝⎛⎭⎫2x ＋π4的图象不相交的一条直线是( )A ．x ＝π2B ．x ＝－π2C ．x ＝π4D ．x ＝π8解析：选D.当x ＝π2时，y ＝tan ⎝ ⎛⎭⎪⎫2x ＋π4＝tan 5π4＝1；当x ＝－π2时，y ＝tan ⎝ ⎛⎭⎪⎫2x ＋π4＝tan ⎝ ⎛⎭⎪⎫－3π4＝1；当x ＝π4时，y ＝tan ⎝ ⎛⎭⎪⎫2x ＋π4＝tan 3π4＝－1；当x ＝π8时，y ＝tan ⎝⎛⎭⎪⎫2x ＋π4＝tan π2，不存在．5．在(0，2π)内，使 tan x >1 成立的 x 的取值范围为( )A.⎝⎛⎭⎫π4，π2 B.⎝⎛⎭⎫54π，32π C.⎝⎛⎭⎫π4，π2∩⎝⎛⎭⎫54π，32π D.⎝⎛⎭⎫π4，π2∪⎝⎛⎭⎫54π，32π 解析：选 D ．因为 x ∈(0，2π)，由正切函数的图象，可得使 tan x >1 成立的 x 的取值范围为⎝ ⎛⎭⎪⎫π4，π2∪⎝⎛⎭⎫54π，32π. 6．函数y ＝3tan(π＋x )，－π4<x ≤π6的值域为________． 解析：函数y ＝3tan(π＋x )＝3tan x ，因为正切函数在⎝ ⎛⎭⎪⎫－π2，π2上是增函数， 所以－3<y ≤3，所以值域为(－3， 3 ]．答案：(－3，3]7．函数 f (x )＝tan ⎝⎛⎭⎫π4－x 的单调减区间为________． 解析：因为 f (x )＝tan ⎝ ⎛⎭⎪⎫π4－x ＝－tan ⎝ ⎛⎭⎪⎫x －π4，所以原题即求函数 y ＝tan ⎝ ⎛⎭⎪⎫x －π4的单调增区间．由 k π－π2<x － π4<k π＋π2，k ∈Z ，得 k π－π4<x <k π＋3π4，k ∈Z ，即函数 f (x )＝tan ⎝ ⎛⎭⎪⎫π4－x 的单调减区间为⎝⎛⎭⎪⎫k π－π4，k π＋3π4，k ∈Z . 答案：⎝⎛⎭⎫k π－π4，k π＋3π4，k ∈Z . 8．函数y ＝tan x 2满足下列哪些条件________(填序号)． ①在⎝⎛⎭⎫0，π2上单调递增； ②为奇函数；③以π为最小正周期；④定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠π4＋k π2，k ∈Z . 解析：令x ∈⎝ ⎛⎭⎪⎫0，π2，则x 2∈⎝ ⎛⎭⎪⎫0，π4， 所以y ＝tan x 2在⎝ ⎛⎭⎪⎫0，π2上单调递增正确；tan ⎝⎛⎭⎫－x 2＝－tan x 2，故y ＝tan x 2为奇函数； T ＝πω＝2π，所以③不正确； 由x 2≠π2＋k π，k ∈Z ，得{x |x ≠π＋2k π，k ∈Z }， 所以④不正确．答案：①②9．求函数 y ＝lg tan x ＋9－x 2的定义域．解：要使 y 有意义，则有⎩⎨⎧tan x >0，x ≠k π＋π2（k ∈Z ），9－x 2≥0，即⎩⎨⎧k π<x <k π＋π2（k ∈Z ），－3≤x ≤3 解得 －3≤x <－π2或 0<x <π2. 故所求的定义域为⎣⎢⎡⎭⎪⎫－3，－π2∪⎝ ⎛⎭⎪⎫0，π2. 10．比较下列两个正切值的大小：(1)tan 167°，tan 173°；(2)tan ⎝⎛⎭⎫－11π4，tan ⎝⎛⎭⎫－13π5. 解：(1)因为90°<167°<173°<180°，y ＝tan x 在(90°，180°)上为增函数，所以tan 167°<tan 173°.(2)因为tan ⎝ ⎛⎭⎪⎫－11π4＝tan π4， tan ⎝ ⎛⎭⎪⎫－13π5＝tan 2π5， 且0<π4<2π5<π2，y ＝tan x 在⎝ ⎛⎭⎪⎫0，π2上为增函数， 所以tan π4<tan 2π5，即tan ⎝ ⎛⎭⎪⎫－11π4<tan ⎝ ⎛⎭⎪⎫－13π5. [B 能力提升]11．已知函数y ＝tan ωx 在⎝⎛⎭⎫－π2，π2内是减函数，则 ( ) A ．0＜ω≤1 B ．－1≤ω＜0C ．ω≥1D ．ω≤－1解析：选B.因为y ＝tan ωx 在⎝ ⎛⎭⎪⎫－π2，π2内是减函数， 所以ω＜0且T ＝π|ω|≥π. 所以|ω|≤1，即－1≤ω＜0.12．已知点 M (－3，－1)，若函数 y ＝tanπ4x [x ∈(－2，2)]的图象与直线 y ＝1 交于点 A ，则|MA |＝__________．解析：令 y ＝tan π4x ＝1，解得 x ＝1＋4k ，k ∈Z ，又 x ∈(－2，2)，所以 x ＝1，所以函数 y ＝tan π4x 与直线 y ＝1 的交点为 A (1，1)，又 M (－3，－1)，所以|MA |＝（1＋3）2＋（1＋1）2＝2 5.答案：2 513．设函数 f (x )＝tan ⎝⎛⎭⎫x 2－π3. (1)求函数的定义域、最小正周期和单调区间．(2)求不等式 f (x )≤ 3 的解集．解：(1)根据函数 f (x )＝tan ⎝ ⎛⎭⎪⎫x 2－π3，可得x 2－π3≠k π＋π2，k ∈Z ，得 x ≠2k π＋5π3，k ∈Z . 故函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠2k π＋5π3，k ∈Z . 它的最小正周期为π12＝2π. 令 k π－π2<x 2－π3<k π＋π2，k ∈Z ，得 2k π－π3<x <2k π＋5π3，k ∈Z . 故函数的增区间为⎝⎛⎭⎪⎫2k π－π3，2k π＋5π3，k ∈Z . (2)求不等式 f (x )≤ 3，即 tan ⎝ ⎛⎭⎪⎫x 2－π3≤ 3， 所以 k π－π2<x 2－π3≤k π＋π3，k ∈Z ， 求得 2k π－π3<x ≤2k π＋4π3，k ∈Z ， 故不等式的解集为⎝⎛⎦⎥⎤2k π－π3，2k π＋4π3，k ∈Z . 14．(选做题)若x ∈⎣⎡⎦⎤－π3，π4，求函数y ＝1cos 2x ＋2tan x ＋1的最值及相应的x 的值． 解：y ＝1cos 2x＋2tan x ＋1 ＝cos 2x ＋sin 2x cos 2x＋2tan x ＋1 ＝tan 2x ＋2tan x ＋2＝(tan x ＋1)2＋1.因为x ∈⎣⎢⎡⎦⎥⎤－π3，π4， 所以tan x ∈[－3，1]，所以当tan x ＝－1，即x ＝－π4时，y 取最小值1，当tan x ＝1， 即x ＝π4时，y 取最大值5.。

正切函数的性质与图象［学习目标］ 1.了解正切函数图象的画法，理解掌握正切函数的性质.2。

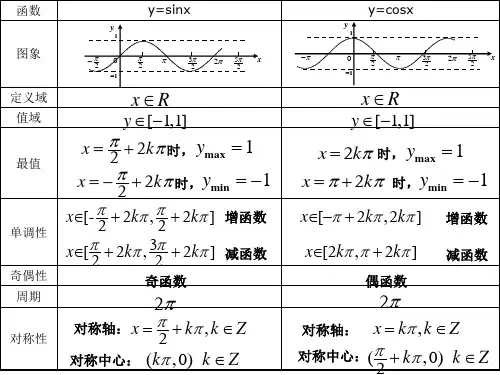
能利用正切函数的图象及性质解决有关问题．知识点一正切函数的图象1．正切函数的图象:2．正切函数的图象叫做正切曲线．3．正切函数的图象特征：正切曲线是被相互平行的直线x＝错误!＋kπ，k∈Z所隔开的无穷多支曲线组成的．思考我们能用“五点法”简便地画出正弦、余弦函数的简图,你能类似地画出函数y＝tan x，x∈［－错误!，错误!]的简图吗？怎样画．答案能．找三个关键点:(错误!，1），(0,0）,(－错误!，－1)，两条平行线：x＝错误!，x＝－错误!.知识点二正切函数图象的性质1．函数y＝tan x（x∈R且x≠kπ＋错误!,k∈Z）的图象与性质见下表：解析式y＝tan x图象定义域{x|x∈R，且x≠kπ＋错误!，k∈Z｝值域R周期π奇偶性奇单调性在开区间错误!(k∈Z)内都是增函数2.函数y＝tan ωx（ω≠0）的最小正周期是错误!。

思考正切函数图象是否具有对称性？如果具有对称性，请指出其对称特征．答案具有对称性，为中心对称，对称中心为（错误!，0），k∈Z。

题型一正切函数的定义域例1 (1）函数y＝tan(sin x)的定义域为 ,值域为．答案R[tan（－1），tan 1］解析因为－1≤sin x≤1，所以tan(－1)≤tan(sin x)≤tan 1，所以y＝tan（sin x）的定义域为R，值域为［tan（－1），tan 1]．（2）求函数y＝tan(2x－错误!）的定义域．解由2x－错误!≠错误!＋kπ,k∈Z得，x≠错误!π＋错误!kπ，所以y＝tan（2x－错误!)的定义域为｛x|x≠错误!＋错误!kπ，k∈Z｝．跟踪训练1 求函数y＝错误!＋lg（1－tan x)的定义域．解由题意得错误!即－1≤tan x〈1.在错误!内，满足上述不等式的x的取值范围是错误!.又y＝tan x的周期为π，所以所求x的范围是［kπ－错误!，kπ＋错误!)（k∈Z)即函数定义域是错误!(k∈Z）．题型二求正切函数的单调区间例2 求函数y＝tan错误!的单调区间及最小正周期．解y＝tan错误!＝－tan错误!，由kπ－错误!〈错误!x－错误!<kπ＋错误!（k∈Z），得2kπ－错误!<x<2kπ＋错误!π，k∈Z，∴函数y＝tan错误!的单调递减区间是错误!,k∈Z.周期T＝错误!＝2π。

1. 4.3正切函数的性质与图象预习课本P42〜45,思考并完成以下问题(1) 正切函数有哪些性质？(2) 正切函数在定义域内是不是单调函数?［新知初探］正切函数y= tan x的性质与图象y= tan x图象L2TV2n审^：＜7T In *1 1■ ■定义域n“xx€ R，且x M k n+ 2，k€ Z ?值域R周期最小正周期为n奇偶性奇函数单调性在开区间*n-2，k n+ 2 (k€ Z)内递增［点睛］正切函数的单调性：正切函数在每一个开区间 2 + k n -+ M/k€ Z)上，都是从一8增大到+ 故正切函数在每一个开区间一n + k n,寸+ k n (k € Z)上是增函数，但不能说函数y= tan x在定义域内是增函数.［小试身手］1. 判断下列命题是否正确. (正确的打“V”，错误的打“x”)(1) 正切函数的定义域和值域都是R.( )(2) 正切函数在整个定义域上是增函数. ()(3) 正切函数在定义域内无最大值和最小值. ()课前口左学习.基乾才能楼高(4) 正切函数的图象既是轴对称图形，也是中心对称图形. ()答案：⑴X （2）X ⑶V ⑷x2. 函数y= tan x—n的定义域是()A. lx € R x 丰 k n+ ¥，k€ Z >B. x € R x丰k n—5n，k€ Z >C . ix € R x 丰 2k n+ 孝k € Z f5 n 、厂 rD . x € R x 丰 2k n— y, k € Z ；答案：A3. 函数f(x) = tan x+ 4的单调递增区间为()A. k n—扌，k n+n , k€ ZB. (k n, (k+ 1) n,) k€ ZC. ［k n—普,k n+n ) k € ZD . k n—n，k n+ 3n , k € Z答案：C-n4. _______________________________________ 函数y= tan x, x € 0, 4的值域是. 答案：［0,1］［解］(1)由x+ k 7+寸化€ Z)得,X M k n+n，k € Z，所以函数y= tan x + ；的定义域为f n Ix x工k n+ n，k € Z r .(1)y= tan x+ ：；(2)y= 3 —tan x.⑵由 3 —tan x> 0 得，tan x< 3.结合y= tan x的图象可知，在「扌，n 上,满足tan x w 3的角x应满足—f vx wfv 2 3所以函数y= J ；3 — tan x的定义域为n n . * rlix k n—2<x w k n+ 3，k€ Z F .I 2 3丿求正切函数定义域的方法(1) 求与正切函数有关的函数的定义域时，除了求函数定义域的一般要求外，还要保证正切函数y= tan x有意义即X M n+ k n k€乙而对于构建的三角不等式，常利用三角函数的图象求解.(2) 求正切型函数y= Atan( ®x+妨(A M 0, w>0)的定义域时，要将“》+扩视为一个“整体”.令3x+严k n+ n，k € Z,解得x.［活学活用］求函数y= 1一的定义域.1 + tan x解：要使函数有意义，则有 1 + tan X M 0,/• tan X M—1 x M k n—n M X M k n+ n, k € 乙4 2ix x M k n— n且x M k n+ k € Z‘.与正切函数有关的周期性、奇偶性问题［典例］⑴求f(x)= tan 2x +才的周期；⑵判断y= sin x+ tan x的奇偶性.［解］(1) •/ tan 2x+ n+ n= tan 2x + ；, 即tan 2^+2 +秤伽丘+3)，因此，函数y=11 + tan x的定义域为••• f(x)= tan 2x +扌的周期是n(2)定义域为lx x丰k n+n, k€ Z為关于原点对称，■/ f(—x) = sin(—x) + tan( —x) = —sin x—tan x =—f(x),•它是奇函数.［活学活用］1 •函数y= tan訴+ 3的最小正周期是()A. 4B. 4 nC. 2 nD. 2解析：选D T=n= n2= 2.n n22.已知函数1 f(x)= tan x + x,tan x若f( a=5,贝y f( — a=解析：f(x)的定义域为［k n— n，k n」U ［kn, k n+n)k€ Z) •可知f(x)的定义域关于原点对称•又f(-x)=tan(-x)+taT—T = - tan x+盘=—f(x)，• f(x)为奇函数.••• f(—a=—f(a=—5.答案：—5题点一：求单调区间1.求函数y= tan —；x+ 4的单调区间. 解：y= tan 匕丁乂+ ；=一tangx—；由k n—n<2x—才“冗+訴^可,得2k n-f<x<2k讦了“ Z，•••函数y= tan —2x+才的单调递减区间是2k n—2, 2k n+丰，k€ Z.题点二：比较大小2.比较tan —宁与tan —号5的大小.解: tan —= tan —4 n+ 宁=tan3j-n=—tan^ , tan —= tan —2 n—卑(2 n 2 ntan — E =—怡肓，o<吴竺n，且y= tan x在o, n内递增，4 5 2 22 n• tan —v tan ,4 5tan n> —tan-r4 5题点三：求最值或值域解：令u= tan x,因为|x|w 3，所以u€ [ —3, 3 ],3所以函数化为y= u2—2u.对称轴为u= 1 € [—3, 3 ].所以当u= 1 时，y min= 1 2—2 X 1 = —1.当U = —-J3时，y max= 3+ 2”.；：3.所以f(x)的值域为[—1,3 + 2 3 ].2 运用单调性比较大小关系.课后艮级训练.歩步提升陡力3.已知f(x) = tan* 1 2x—2tan x |x|w 扌，求f(x)的值域.A . x =nB . x =—n层级一学业水平达标1 .函数 y =— 2+ tan ^x +n 的定义域是(r 5 n \2k n — 3 n, 2k n+ 3 , k € ZB . 2k n —n , 2k n+ 舟冗,k € Z5 n 、k n — 3n, k n+ 3 , k € Z k n —3, k n+ 3n , k € Z解析：选A 由-n+ k n< 2x +扌< 亍+山k € Z ,解得—5 n 5n +2k n < x v 3+2k n,k €乙2. f(x)= tan — 2x + 3的最小正周期为(n A —B .n解析：选B 法一：函数y = tan( 3x+$)的周期是 T =~,13直接套用公式，可得n |—2|_ n=2.法二：由诱导公式可得n ■,tan — 2x + 3 = tanf x +n =f(x),所以周期为Tn2.3.函数 f(x) = tanax — n 与函数 g(x)= sin 7— 2x 的最小正周期相同，贝U 3=(解析：选A g(x)的最小正周期为n 则^n= n ,得 3= ±.□ I4.函数 y = |tan 2x|是( )A .周期为n 的奇函数B .周期为n 的偶函数C .周期为n 的奇函数D .周期为；的偶函数解析：选 D f(— x)= |tan(— 2x)| = |tan 2x|= f(x)为偶函数，T = nn 的图象不相交的一条直线是()—2x + n = tan所以5.与函数y = tan解析：选D 当x=；时，2x +亍=扌，而2的正切值不存在，所以直线x =n与函数的图象不相交.6 .函数y= 71 —tan x的定义域是________________________________________ .解析：由1—tan x > 0即tan x< 1结合图象可解得.答案：k n—寸,k n+ 才(k€ Z)7.函数y= tan [2x + 4 /的单调递增区间是_____________________________________ . 解析：令k n—n< 2x + n v k n+n，k€ Z,8.函数y= 3tan( + x),—n<x<才的值域为.解析：函数y= 3tan( n+ x) = 3tan x，因为正切函数在一寸，寸上是增函数，所以一3<y w 3，所以值域为(—3, 3 ].答案：(—3, 3 ]9•比较下列各组中两个正切函数值的大小.(1)tan 167 ° 与tan 173 ° ;解：(1) •/ 90 ° < 167° < 173° < 180/• tan 167 ° < tan 1737tD - x=8又T y= tan x 在3n上是增函数,tan13 n又.• 0<n< 罕打，函数y= tan x，x€••• tan n< tan^r，4 513 n5 -2 4答案：号(2)tantan (-(2) ■/tan.11 n . ntan T=tan n，5 =即tan tank nv x < k计 n ，k€ Z：2k n-n v x 益k n +n ，k € Z10.已知 f(x)= tan 2x + 扌 ⑴求f(x)的最小正周期； (2)若f(x +妨是奇函数，则$应满足什么条件？并求出满足Wlv0值.解：⑴法一：■/ y = tan x 的周期是 n. ••• y = tan 2x +扌的周期是 亍即 f x + 2 = f(x). • f(x)的周期是n⑵•/ f(x +妨=tan 2x +n + 2 0是奇函数,•图象关于原点中心对称， •扌+ 2 A 齐€ Z),k n 4 冗-6(k € Z). k n 4n nn v n k € Z), 解得-f v k v 3，k € Z. • k =— 1,0,1,或 2. 从而得o=-箫，-n 协n层级1.函数y = " logman x 的定义域是(应试能力达标)B .x 2k nV x < 2k n+n 4,k € Ztan法二：由诱导公式知: =tan答案:6 n 3n\k n+ 5 , k n + 2(k € Z) 6.已知函数y = tan 在—2,2内是单调减函数，贝y3的取值范围是1解析：选C 要使函数有意义，只要log2tan x >0,即卩0v tan x w 1.由正切函数的图象n知,k nV x w k n+~ , k € 乙42.函数y = tan （cos x ）的值域是（）C . [— tan 1, tan 1] 解析：选 C 1w cosx w 1,且函数 y = tan x 在[—1,1]上为增函数，/• tan( — 1)w tanx w tan 1.即一tan 1 w tan x w tan 1.得x =拿可知函数图象与 x 轴一交点的横坐标为 ¥•故可排除C 、D.令,—中=—：,得x 3 3 2 3 2n ，或令2x —n =n ，得x =釁故排除B ,选A .tan 2x + 3 = 3在区间［0,2 n 上的解的个数是（ ）由 tan 2x += 3 得 2x + 扌=扌 + k n k € Z), • x =Z )，又 x € [0,2 n )5.若tan x > tan n 且 x 在第三象限，则 x 的取值范围是5 解析：tan x > tan n= tan^,又x 为第三象限角,5 5 ••• k n+ 普＜ x V k n+ € Z).5 2 D .以上均不对4.方程解析：选n, 节故选B.3.函数 y = tan解析：选A 令y = tan ^x —扌=0,则有^x —扌=k n , x = 2k n+严，k €乙再令k = 0 ,n n 即一A n 故 | w|< 1 ,•••一 1 < 3<0.IM答案：[—1,0)7.已知x € — n ，于，，求函数y =―1盯+ 2tan x + 1的最值及相应的 x 的值.」3 4 一 cosx2 . 2卄 1 cosx + sin x解：y = 2 + 2tan x + 1 = 2 + 2tan x + 1 cosx cosx2 2=tan x + 2tan x + 2= (tan x + 1) + 1.T x € — n ，n]= tan x € [—羽,1].当tan x =— 1,即卩x =一 n 时，y 取得最小值1;8.求函数y = tan ?x — 6的定义域、周期及单调区间.解:由 2x —6* n+ k n ，k € Z ,4 n得 x ^-― + 2k n, k € Z ,3 xx M 4n+ 2k n k € ZT = n = 2n ，2由—2 + 也务—n <2 + k n k € Z ,得十 2也<<于+ 2k n ，k € z.所以函数y = tan ；x —n 的单调递增区间为令 2k n 4^"+ 2k n (k € Z).1.求函数y = Atan( 3x+ $)(A , w, $都是常数)的单调区间的方法(1) 若w >0，由于y = tan x 在每一个单调区间上都是增函数，故可用 "整体代换”的思 想，令当tan x = 1,即卩x = ,y 取得最大值5.所以函数y = tan 2x —n 的定义域为所以函数y = tan gx —冒丿的周期为2n.k n- n< wx+ gk n+；,求得X的范围即可.(2) 若w<0，可利用诱导公式先把y= Atan( wx+ $)转化为y= Atan[ —(—w x—$)]=—Atan( —wx—册,即把x的系数化为正值，再利用“整体代换”的思想，求得x的范围即可.2. 运用正切函数单调性比较大小的方法(1) 运用函数的周期性或诱导公式将角化到同一单调区间内.。