数学试题卷参考答案及评分建议

山东省烟台市初三数学第一学期期末考试真题及答案解析（第一部分：基础演练，满分120分）一、 选择题（3′×12=36′）1、 下列智能手机的功能图标中，是中心对称图形但不是轴对称图形的有（ ）A. 1个B. 2个C. 3个D. 4个2、 下列各式从左到右的变形属于因式分解的是（ ）A.（m -2）（m -3）= （2-m ） （3-m ）B. 3a -6b +3=3（a -2b ）C. （x +1）（x -1）=x 2-1D. x 2-7x +12=（x -4）（x -3） 3、下列对代数式12---x x 的变形，不正确的是（ ）A. 1-2--x x B. xx -1-2 C. 12--x x D. xx -12--4、使分式23422++-x x x 的值为零的x 的值是（ ） A ． x =2 B ． x = -2或x =-1 C ． x =±2 D ． x = -2 5、下列命题中，正确的命题是（ ）A. 有一个角是直角的四边形是矩形B. 对角线互相垂直的四边形是菱形C. 对角线互相垂直平分的四边形是正方形D. 对角线互相平分的四边形是平行四边形6、小亮根据演讲比赛中九位评委所给的分数制作了如下表格： 如果要去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（ ）A. 平均数B. 众数C. 方差D. 中位数7、在俄罗斯方块游戏中，所有出现的方格体自由下落，如果一行中九个方格齐全，那么这一行会自动消失．已拼好的图案如图所示，现又出现一小方格体，必须进行以下哪项操作，才能拼成一个完整图案，使其全部自动消失（ ） A ．顺时针旋转90°，向下平移 B ．逆时针旋转90°，向下平移 C ．顺时针旋转90°，向右平移 D ．逆时针旋转90°，向右平移8、如图所示，在平行四边形ABCD 中，对角线AC ，BD 相交于点O ，E ，F 是对角线AC 上的两点，当E ，F 满足下列哪个条件时，四边形DEBF 不一定是平行四边形（ ）A. OE=OFB. ∠ADE=∠CBFC. DE=BFD. ∠ABE=∠CDF 9、如图，在平行四边形ABCD 中，∠A=47°，将平行四边形折叠，使点D ，C 分别落在点F ，E 处（点F ，E 都在AB 所在的直线上），折痕为MN ，则∠AMF 等于（ ） A. 47° B. 86° C. 90° D. 94° 10、如图，在菱形ABCD 中，M ，N 分别在AB ，CD 上，且AM=CN ，MN 与AC 交于点O ，连接BO.若∠DAC=29°，则 ∠OBC 的度数为（ ） A. 29° B. 58° C. 61° D. 71°11、 某次列车平均提速20km/h ，用相同的时间，列车提速前行驶400km ，提速前比提速后多行驶100km ，平均数 中位数 众数 方差 8.5 8.3 8.1 0.15A. 20100400400-+=x xB. 20100400400++=x xC. 20100400400+-=x xD. 20100400400--=x x12、如图，平行四边形ABCD 中，AB=10cm ，AD=15cm ，点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动，点Q 在BC 边上，以每秒3cm 的速度从点C 出发，在CB 间往返运动，两个点同时出发，点P 到达点D 时停止（同时点Q 也停止运动），在运动以后，当以点P 、D 、Q 、B 为顶点组成平行四边形时，运动时间t 为（ ） A. 6秒 B. 6.5秒 C. 7.5秒 D. 15秒 二、填空题（3分×6=18分）13、若关于x 的分式方程33122x m x x +-=--有增根，则m = . 14、用一条宽度相等的足够长的纸条打一个结（如图1所示）然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.图中，∠BAC= .15、如图，四边形ABCD 是菱形，点O 是对角线的交点，三条直线都经过点O ，图中阴影面积为24cm 2，其中一条对角线长为6cm ，则另一条对角线长为 cm.16、如图，将△ABC 沿射线BC 方向移动，使点B 移动到点C ，得到△DCE ，连接AE ，若△ABC 的面积为4，则△ACF 的面积为 .17、如图所示，在△ABC 中，M 是BC 的中点，AN 平分∠BAC ，BN ⊥AN.若AB=14，AC=19，则MN 的长为 . 18、如图，正方形ABCD 的边长为6，E 为BC 上的一点，BE=1，F 为AB 上的一点，AF=3，P 为AC 上一点，则PF+PE 的最小值为 . 三、解答题（66分）19、（12分）先化简，再求值：（1） 2222a b ab b b aab⎛⎫+--÷ ⎪⎝⎭，已知a =b -8.（2）先化简：⎪⎭⎫ ⎝⎛--÷+-+x x x x x x 1121222，再从-2≤x ＜3的范围内选取一个适合的整数代入求值.20、（10分）如图，等边△ABC 的边长是4，D 、E 分别为AB 、AC 的中点，延长BC 至点F ，使CF=21BC ，连接CD 和EF.（1）求证：DE=CF ； （2）求EF 的长．21、（10分）如图，△ABC 三个顶点的坐标分别为A （1，1），B （4，2），C （3，4）． （1）画出△ABC 向下平移5个单位长度后得到的△A 1B 1C 1； （2）画出△ABC 关于原点对称的△A 2B 2C 2； （3）画出△ABC 绕点A 逆时针旋转90°后得到的△AB 3C 3；（3）在x 轴上求作一点P ，使△P AB 的周长最小，画出△P AB ，并直接写出点P 的坐标．22、（12分）某学校在初三级部举行了全员参加的数学运算能力竞赛，试卷题目共10题，每题10分.现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下： 整理数据： 分析数据：根据以上信息回答下列问题：（1）a = ，b = ，c = ，d = ；（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好，请说明理由； （3）已知三班方差为S 32=141，请计算1班方差S 12并判断1班，3班哪个班的成绩比较稳定；（4）为了让学生重视数学运算学习，学校将给竞赛成绩满分的同学颁发奖状，该校初三共1200人，试估计需要准备多少张奖状？23、（10分）先阅读下面的内容，再解决问题. 例题：若m 2+2mn +2n 2-4n +4=0，求m 和n 的值. 解：∵m 2+2mn +2n 2-4n +4=0 ∴m 2+2mn +n 2+n 2-4n +4=0 ∴（m+n ）2+（n -2）2=0 ∴m+n =0，n -2=0 ∴m = -2，n =2.问题解决：（1）若x 2+2y 2-2xy +6y +9=0，求x y 的值；（2）已知a ，b ，c 是△ABC 的三边长，满足a 2+b 2=8a +6b -25，且c 是△ABC 中最长的边，求c 的取值范围． 班 数 人数 分数 60 70 80 90 100 1班 0 1 6 2 1 2班 1 1 3 a 1 3班 1 1 4 2 2 平均数 中位数 众数 1班 83 80 80 2班 83 c d 3班 b 80 8024、（12分）为落实大美福山“七纵十横”的城区路网大框架，区政府计划对城区道路进行了改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的1.5倍，甲队改造360米的道路比乙队改造同样长的道路少用3天．（1）甲、乙两工程队每天能改造道路的长度分别是多少米？（2）若甲队工作一天需付费用7万元，乙队工作一天需付费用5万元，如需改造的道路全长1200米，改造总费用不超过145万元，至少安排甲队工作多少天？（第二部分：能力挑战，满分30分）四、附加题25、（14分）某校八年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC 与AFE按如图1所示位置放置，∠A=90°，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图2，AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．26、（16分）如图1，已知点E，F分别为正方形ABCD的边BC，CD上的点，AF，DE相交于点G，当E，F分别为边BC，CD的中点时，有：①AF=DE；②AF⊥DE成立．试探究下列问题：（1）如图1，若点E不是边BC的中点，F不是边CD的中点，且CE=DF，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）（2）如图2，若点E，F分别在CB的延长线和DC的延长线上，且CE=DF，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；（3）如图3，在（2）的基础上，连接AE和EF，若点M，N，P，Q分别为AE，EF，FD，AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种，并证明你的结论．初三数学试题参考答案及评分建议(如有错误请组长及时更正)一、选择题（每小题3分，满分36分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BDAADDCCBCBC二、填空题（每小题3分，满分18分）13. 3 14．36° 15．16 16．2 17．2.5 18．40(102或) 三、解答题（满分66分）19．（本题共2个小题，满分12分）解：（1）原式222=()22()a b ab ab a a b a b +-⋅-2()2a b a a a b-=⋅-………………2分2a b -=. ………………3分 ∵8a b =-，∴a －b =－8.………………4分∴原式=－4. ……………6分（2）原式=2(1)2(1)(1)(1)x x x x x x x +--÷-- =2(1)(1)(1)1x x x x x x +-⋅-+…………2分 =21x x - ……………3分∵x ≠－1，0，1，∴当x =2时，…………4分 原式=21x x -=2221-=4．…………6分(或当-2x =时，原式=34-……6分） 20. （本题满分10分）解：（1）∵ D ,E 分别是AB ,AC 中点 ∴DE 是△ABC 的中位线…………2分∴DE =21BC ,DE ∥BC ∵ CF =21BC ∴DE =CF ……………………5分 （2）∵ DE =CF DE ∥CF ∴四边形EDCF 是平行四边形 ∴EF =CD …………7分 ∵ D 是AB 的中点，等边△ABC 的边长为4∴CD =32 …………9分∴FE =CD =32 …………10分 21.（本题共10分，每小题画图各2分） （1）△111C B A 如图； ………………2分 （2）△222C B A 如图；………………4分（3）△33C AB 如图，3C 的坐标是（－2,3）；.…………7分 （4）点P 和△P AB 如图，点P 的坐标是（2,0）…………10分22. （本题满分12分）解：（1）设乙工程队每天能改造道路的长度为x 米，则甲工程队每天能改造道路的长度为23x 米，…1分 根据题意得：323360360=-x x ………3分 解得：x =40，…………4分 经检验，x =40是原分式方程的解，且符合题意，…………5分 ∴23x =23×40=60． …………6分 答：乙工程队每天能改造道路的长度为40米，甲工程队每天能改造道路的长度为60米．………7分 （2）设安排甲队工作m 天，则安排乙队工作4060-1200m天，………………8分根据题意得：7m +5×4060-1200m≤145， …………10分解得：m ≥10． …………11分答：至少安排甲队工作10天。

小学期末学业水平检测六年级上册数学试卷评分建议及部分参考答案
卷面整洁、书写端正共2分。

如果卷面有破损、脏乱、用涂改液、书写潦草等，
酌情扣分。

一、填空。

每空1分，共25分。

１．、1 2．96﹪、4﹪3．3、18、20、60 4．b、a 5．6:5、1.2 6．3、 7．、3.14﹪8．60 9．80、160 10．55 11．12.5、
25π 12．18.84、3、28.26二、判断。

每题1分，共5分。

1．√2．×3．×4．√5．×
三、选择。

每题1分，共5分。

1．C 2．B 3．A 4．B 5．C
四、计算。

共26分。

1．直接写出得数。

每道1分，计8分。

（略）2．计算下面各题，能用简便算法的就用简便算法。

每道3分（过程2分，结果1分。

能简算未简算但四则运算过程结果都正确的扣1分）。

（略）3．解方程。

每题3分（过程2分，结果1分）。

（略）
五、算算、画画。

共10分。

1．画圆2分；画对三角形的一个顶点1分。

计5分。

（略）
2．计算圆环面积5分。

（略）
六、解决问题。

共27分。

第1至5题每题4分（列式3分，计算1分）；第6题①每空1分，②列式2分，计算1分，③提出问题1分，解答1分。

（略）。

蓬莱区2024-2025学年第一学期期中学业水平考试初四数学试题一、选择题（本题共10个小题，每小题3分，满分30分）每小题都给出标号为A ，B ，C ，D 四个备选答案，其中有且只有一个是正确的．1．如图，在中，，，，，则下列选项错误的是（）第1题图A ．B ．C ．D ．2．下列关系式中，属于二次函数的是（x 为自变量）（ ）A ．B ．C ．D ．3．在中，∠A 和∠C 都是锐角，且，的形状是（ ）A ．直角三角形 B ．钝角三角形C．等边三角形D ．不能确定4．如果在高为2米，坡度为1:2的楼梯上铺地毯，那么地毯长度至少需要（ ）A ．2米B ．6米C ．米D ．米5．已知反比例函数图像经过点，下列说法中不正确的是（ ）A ．该函数图像在第二、四象限B ．点在该函数图像上C ．当时，D ．y 随x 的增大而增大6．已知二次函数的图像与x 轴有交点，则k 的取值范围是（ ）A ．B ．C ．且D ．且7．如图，在边长相等的小正方形组成的网格中，点A ，B ，C 都在格点上，那么的值（）ABC △90C ∠=︒BC a =AC b =AB c =sin a A c=cos a B c=tan a A b=tan b B c=218y x =y =21y x =22y a x=ABC △sin A =tan C =ABC △2+ky x=-()2,3-()1,6-1x >60y -<<()2321y k x x =-+-2k ≥2k ≤2k ≥3k ≠4k ≥-3k ≠sin ACB ∠第7题图ABCD ．8．如图，在中，O 是角平分线AD ，BE 的交点，若，，则的值是（）第8题图AB ．CD ．9．一次函数和反比例函数在同一平面直角坐标系中的图象如图所示，则二次函数的图象可能是（ ）A ．B ．C ．D ．10．如图①，在中，，，F 是边AB 的中点，P 是边BC 上一动点，设，，图②是y 关于x 的函数图象，图象中的最低点的坐标为，那么的值为（）13ABC △10AB AC ==12BC =tan OBD ∠2312y ax b =+cy x=2y ax bx c =+-ABC △AB AC =120BAC ∠=︒PC x =PA PE y +=(),b a a b +第10题图AB ．C ．D二、填空题（共6个小题，每小题3分，满分18分）11．函数x 的取值范围是______．12．点和点在反比例函数（k 为常数）的图象上，若，则，，0的大小关系为______．（用“<”连接）13．如图，在平面直角坐标系中，点O 是坐标原点，平行四边形ABCD 的顶点A 、B 在x 轴的正半轴上，顶点C 在第一象限内，顶点D 在y 轴的正半轴上，对角线AC 和BD 相交于点E 且，函数的图象经过点E ．若平行四边形ABCD 的面积为8，则k 的值为______．第13题图14．在中，，，则BC 的长为______．15．若抛物线与一次函数的图象都经过同一定点，则代数式的值是______．16．如图，已知开口向下的抛物线对称轴为直线，与x 轴交于点，与一次函数的图象交于，．下列结论正确的有______．（填序号）4+4+y =()11,M x y ()22,N x y 223k k y x-+=120x x <<1y 2y AC AB ⊥()0,0ky k x x=>>ABC △1tan 2B ∠=AB =2AC =()21y x a x a =+--y ax b =+23a ab +-()210y ax bx c a =++≠1x =-()1,0()20y mx n m =+≠()2,A p -()1.5,B q第16题图①；②；③使不等式成立的x 的取值范围是或；④若关于x 的一元二次方程有实数根，则；三、解答题（本大题共9个题．满分72分，解答题要写出必要的计算步骤或文字说明或说理过程）17．（本题满分8分）计算：（1（2）．18．（本题满分6分）如图，AD 是的中线，，，，求：（1）BC 的长；（2）∠ADC 的值．19．（本题满分9分）如图，一次函数与反比例函数的图象相交于，两点，连接AO ，BO ，延长AO 交反比例函数图象于点C ．（1）求一次函数与反比例函数的表达式；（2）当时，自变量x 的取值范围；0abc <20a b +=2ax bx c mx n ++<+2x <- 1.5x >210ax bx cd ++-+=1d a c≥-+6045tan 60︒-︒︒-︒()112cos30tan 602π 3.142-⎛⎫︒+︒-+-+- ⎪⎝⎭ABC △1tan 3B =cos C =AC =1y ax b =+2ky x=()2,8A ()8,B n 1y 2y 12y y <（3）点P 是x 轴上一点，当时，请求出点P 的坐标．20．（本题满分10分）已知二次函数图象的顶点坐标为，且图象经过点，．（1）求二次函数的表达式；（2）将二次函数的图象向右平移个单位，图象经过点，求m 的值；（3）在由（2）平移后的图象上，当时，函数的最小值为－3，求n 的值．21．（本题满分9分）图1，2分别是某吊车在吊一物品时的实物图与示意图，已知吊车底盘CD 的高度为2米，支架BC 的长为4米，BC 的坡度为，吊绳AB 与支架BC 的夹角为80°，吊臂AC 与地面成70°角，求吊车的吊臂顶端A 点距地面的高度是多少米？（精确到0.1米；参考数据：，，，，）22．（本题满分9分）操作与探究：（1）在如图的平面直角坐标系xOy 中画出函数的图象；（2）仔细观察图象，结合所学知识解答下列问题：①当函数值时，自变量x 的取值范围是______；45PAC AOB S S =△△()1,4-()3,0()0,3-()0m m >151,4⎛⎫-⎪⎝⎭21n x n -≤≤+sin10cos800.17︒=︒≈cos10sin 800.98︒=︒≈sin 20cos 700.34︒=︒≈tan 70 2.75︒≈sin 700.94︒≈223y x x =--+0y ≥②当时，y 随x 的增大而增大，则m 的取值范围是______；③当时，函数值，直接写出n 的取值范围______．23．（本题满分9分）中国蓬莱，位于山东半岛东部，以其独特的地理条件和丰富的葡萄种植资源而闻名于世．如今，蓬莱凭借其得天独厚的气候与土壤条件，成功跻身世界七大葡萄海岸之列，吸引着众多葡萄酒爱好者和旅行者前来探索．某店购进一种葡萄酒，每瓶进价为50元，规定销售单价不低于成本．该葡萄酒月销售量y （瓶）与售价x （元/瓶）的变化情况部分数据如下表：售价x （元/瓶）…55606570…销售量y （瓶）…1500140013001200…（1）请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识直接判断y 是关于x 的哪种函数，并求出函数关系式；（2）若该种葡萄酒的每瓶利润不超过进价的30%，设这种葡萄酒每月的总利润为w （元），那么售价定为多少元可获得最大利润？最大利润是多少元？24．（本题满分12分）如图，抛物线与x 轴交于点，，与y轴交于点C ，连接BC ．（1）求抛物线的解析式；（2）点P 在BC 下方的抛物线上，连接BP ，CP ，若，求点P 的坐标；（3）点N 在线段OC 上，若存在最小值n ，求点N 的坐标及n 的值．x m <2x n -≤≤34y ≤≤24y ax bx =+-()1,0A -()4,0B 12BCP BOC S S =△△AN +2024-2025学年度第一学期期中学业水平考试初四数学试题参考答案及评分建议一、选择题（每小题3分，满分30分）题号12345678910答案D A C B D C C D B A 二、填空题（每小题3分，满分18分）11．且12．13．4 14．15．－3 16．③④三、解答题（满分72分）17．（本题满分8分）（1）解：原式（2）原式．18．（本题满分6分）（1）解：过点A作于点E，∵，∴，在中，，∴，在中，，即，∴，∴；（2）解：∵AD是的中线，∴，∴，∵，，∴．19．（本题满分9分）解：（1）将代入得，解得，∴反比例函数的解析式为，1x≥-1x≠12y y<<13352222 ==--=-=22231242=---+=+-=-AE BC⊥cos C=45C∠=︒Rt ACE△cos1CE AC C=⋅=1AE CE==Rt ABE△1tan3B=13AEBE=33BE AE==4BC BE CE=+=ABC△122CD BC==1DE CD CE=-=AE BC⊥DE AE=45ADC∠=︒()2,8A2kyx=82k=16k=216yx=把代入得，，∴，将，代入得，解得，∴一次函数为；（2）由图象可知，当时，自变量x 的取值范围为：或；（3）设一次函数与x 轴的交点为D由题意可知，把∴，代入得，，解得，∴，∴，∵，∴，∴，即，∴，∴或．20．（本题满分10分）解：（1）∵二次函数图象的顶点坐标为，设二次函数解析式为：，∵二次函数图象经过点，，∴，解得：，∴二次函数解析式为；（2）将二次函数的图象向右平移个单位后，二次函数解析式为，∵平移后二次函数图象经过点，∴，()8,B n 1628n ==()8,2B ()2,8A ()8,2B 1y ax b =+2881a b a b +=⎧⎨+=⎩110a b =-⎧⎨=⎩110y x =-+12y y <8x >02x <<1y OA OC =2APC AOP S S =△△0y =110y x =-+10x x =-+10x =()10,0D 111081023022AOB AOD BOD S S S =-=⨯⨯-⨯⨯=△△△44302455PAC AOB S S ==⨯=△△224AOP S =△12242A OP y ⨯⨯=128242OP ⨯⨯=3OP =()3,0P ()3,0P -()1,4-()214y a x =--()3,0()0,3-()23014a -=--1a =()221423y x x x =--=--()0m m >()214y x m =---151,4⎛⎫-⎪⎝⎭()2151144m -=---解得：，（舍去），∴m的值为；（3）由（2）可知：平移后二次函数解析式为，函数图像开口向上，对称轴为，当函数取值为－3时，则有，解得：，，∵当时，函数的最小值为－3，∴x 的取值为或，①当x 的取值为时，则有，解得：，②当x 的取值为时，则有，解得：，∴n 的值为或．21．（本题满分9分）解：如图，由题可知，，，米，米，，，∵BC 的坡度为，∴，∴，∵，∴，∵，∴，∴，过点A 作于M ，∴米，∵在中，米，，∴，∴米，∵在中，米，，112m =212m =-122342y x ⎛⎫=-- ⎪⎝⎭32x =23342x ⎛⎫-=-- ⎪⎝⎭152x =212x =21n x n -≤≤+212x =152x =212x =112n +=12n =-152x =522n -=92n =12-92BH HE ⊥AE HE ⊥2CD =4BC =80ABC ∠=︒70ACE ∠=︒tan BH BCH CH ∠===30BCH ∠=︒180BCH ACB ACE ∠+∠+∠=︒80ACB ∠=︒80ABC ∠=︒ABC ACB ∠=∠AB AC =AM BC ⊥2CM BM ==Rt ACM △2CM =80ACB ∠=︒cos cos800.17CM ACB AC ∠==︒≈22000.170.1717CM AC ===Rt ACE △20017AC =70ACE ∠=︒∴，∴米，∴米，∴点A 到地面的距离为13．1米22．（本题满分9分）（1）列表：x …－3－2－101…y…343…描点，连线，如图，（2）①根据图象可知，当函数值时，自变量x 的取值范围是；②根据图象可知，当时，y 随x 的增大而增大，当时，y 随x 的增大而增大，则m 的取值范围是；③根据图象可知，n 的取值范围是．23．（本题满分9分）解：（1）根据表格信息，设售价x （元/瓶）与销售量y （瓶）的解析式为：，且，，∴，解得，，∴函数解析式为：，当时，；当时，；符合题意，∴y 与x 是一次函数，解析式为：；（2）售价为x （元/瓶），进价为50（元/瓶），∴单件利润为：元/瓶，sin sin 700.94AE ACE AC =∠=︒≈2001880.9411.11717AE =⨯=≈11.1213.1AE CD +=+=0y ≥31x -≤≤1x <-x m <1m ≤-10n -≤≤()0y kx b k =+≠()55,1500()60,1400551500601400k b k b +=⎧⎨+=⎩202600k b =-⎧⎨=⎩202600y x =-+65x =1300y =70x =1200y =202600y x =-+()50x -∴，∴每盒利润不超过进价的30%，∴，解得，，∵，开口向下，且对称轴为，∴当时，w 随x 的增大而增大；当时，w 随x 的增大而减小；∴当时，利润取得最大值，且（元），∴售价为65元时可获得最大利润，最大利润为19500元．24．（本题满分12分）解：（1）将，坐标代入得，，解得，∴抛物线的解析式为：，（2）解：令，得，则；设直线BC 的解析式为，则，解得，∴直线BC 的解析式为，如图，过点P 作轴，交BC 于点D ．设点P 的坐标为，则点D 的坐标为．∴．由，得．解得．∴点P 的坐标为或；（3）解：如图，作，垂足为点E ．()()()25050202600203600130000w x y x x x x =-=--+=-+-505030%x -≤⨯65x ≤200-<()360090220x =-=⨯-90x <90x >65x =2206536006513000019500w =-⨯+⨯-=()1,0A -()4,0B 24y ax bx =+-4016440a b a b --=⎧⎨+-=⎩13a b =⎧⎨=-⎩234y x x =--0x =4y =-()0,4C -y mx n =+404m n n +=⎧⎨=-⎩14m n =⎧⎨=-⎩4y x =-PH x ⊥()2,34m m m --(),4m m -24DP m m =-+12BCP BOC S S =△△()21114444222m m -+⨯=⨯⨯⨯12m =+22m =-()24-()24-NE CB ⊥∵，，∴，∴，∴为等腰直角三角形．∴．∴．当点A ，N ，E 共线时，有最小值．最小值n 为线段AE 的长，∵为等腰直角三角形，∴，∴，∴为等腰直角三角形，∴，∴为等腰直角三角形．∴，即点N 的坐标为．∴．∴n()0,4C -()4,0B 4OB OC ==45OCB ∠=︒NCE △sin 45NE NC =⋅︒=AN AN NE +=+AN NE +NCE △45CNE ∠=︒45ANO CNE ∠=∠=︒AON △45NAO ∠=︒ABE △1ON OA ==()0,1-sin 45AE AB =⋅︒=。

南通市2023届高三第二次调研测试数学参考答案与讲评建议一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若M ，N 是U 的非空子集，M ∩N = M ，则A ．M ⊆NB ．N ⊆MC ．U ðM =ND ．U ðN = M【答案】A2．若i z = (1- 2i )2，则z =A ．4+ 3iB ．4- 3iC ．- 4+ 3iD ．- 4- 3i【答案】C3．已知(x 3+ 22x)n 的展开式中各项系数和为243，则展开式中常数项为A ．60B ．80C ．100D ．120【答案】B4．古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作，也为地图学提供了数学基础．现根据刘徽的《重差》测量一个球体建筑物的高度，已知点A 是球体建筑物与水平地面的接触点（切点），地面上B ，C 两点与点A 在同一条直线上，且在点A 的同侧．若在B ，C 处分别测得球体建筑物的最大仰角为60°和20°，且BC = 100m ，则该球体建筑物的高度约为（cos10°≈0.985）A ．49.25mB ．50.76mC ．56.74mD ．58.60m【答案】B5．在▱ABCD 中，12BE BC = ，13AF AE =．若AB mDF nAE =+ ，则m + n =A ．12B ．34C ．56D ．43【答案】D6．记函数f (x )= sin (ωx + π4)(ω>0)的最小正周期为T ．若ππ2T <<，且f (x )≤|f ( π3)|，则ω=A ．34B ．94C ．154D ．274【答案】C7．已知函数f (x )的定义域为R ，y =f (x )+e x 是偶函数，y =f (x )- 3e x 是奇函数，则f (x )的最小值为A ．eB ．C ．D ．2 e【答案】B8．已知F 1，F 2分别是双曲线C ：22221(00)y x a b a b-=>>，的左、右焦点，点P 在双曲线上，PF 1⊥PF 2，圆O ：22229()4x y a b +=+，直线PF 1与圆O 相交于A ，B 两点，直线PF 2与圆O 相交于M ，N 两点．若四边形AMBN 的面积为9b 2，则C 的离心率为A ．54B ．85C D ．【答案】D二、选择题：本题共4小题，每小题5分，共20分。

二年级数学下册学业水平测试卷（人教版）试卷参考答案和评分标准平罗县城关第四小学安惠霞一、填一填共22分，1小题3分，2、5、8、9小题每空0.5分，其余每小题1分。

参考答案：1. 6×3=18或3×6=18；18 ÷3 = 6或18 ÷3 = 62. ②④③3．2和5或5和2；1和6或6和1，3和8或8和3，4和7或7和44.10，四， 15.126， 580,2374,30036.五千四百六十四7.2008. <， >，=9.千克，克，米10.（1）23,30，38 （2）■◇◆□二、火眼金睛来当老师共8分，每题2分参考答案：1. × 2. × 3．√ 4.√ 5. × 6. √ 7.√ 8. ×三、快乐选择，共5分 ,每题1分参考答案：1. ② 2. ③ 3．③ 4. ③ 5. ① 6. ① 7. ②四、看清题目，精心细算共 39分1.直接写得数共15分，每题1分参考答案： 2 12 4 9 93 8 1 110 90320 1100 1000 900 2002.用竖式计算共8分，每题2分参考答案：520 190 134 12103.用递等式计算共8分，每题2分，按步骤给分参考答案：55 40 4 354.列式计算共8分，每题2分参考答案：① 40÷8=5 ②20÷5=4 ③ 28÷7=4 ④ 25+60=85五、移一移，画一画共3分，答案（略）六、解决问题共22分， 4.5各5分，其余每题3分参考答案：1. 36÷6=6（天） 36÷4=9（页）2.26+30=56（名） 56÷8=7（个）3.116+268=384（元） 500〉384 够或116+268≈400（元） 500〉400 够4. ①打游戏机②看动画片③略④提问和解答各0.5分⑤发现：同学们课余时间喜欢打游戏机和看动画片。

四年级数学试卷参考答案及评分建议一、看清数据，细心计算（8分+14分+9分=31分）1.直接写出得数。

（每题1分，共8分）5 3 7 1600 4 646 92.用竖式计算，带*题要验算。

（前面3题每题3分，验算题5分，每个竖式2分，得数1分。

共14分）7......2 20......25 32......13 67 (40)3.计算下面各题。

（每题3分，共9分）50－15×39÷65 320÷（16＋48）×92 432÷［12×（216÷36）］=50－585÷65 =320÷64×92 =432÷［12×6］……1分=50－9 =5×92 =432÷72 ……1分=41 =460 =6 ……1分二、认真读题，正确填空（每空1分，共22分）1.9000 72.63.4 两 34. 13……200 13……105.546.方块（画图也可以），2 37. 锐角75°直角90°平角180° 8.9.∠2＝140°，∠3＝40°三、反复比较，慎重选择（每题1分，共6分）1．B 2．C 3．C 4．A 5．A 6．C四、明确要求，动手操作（4分+3分+7分+4分=18分）1．量出下面每个角的度数（左右悬殊3°），每小题2分，共4分。

55° 130°2．画出最短路线2分，填空1分，（50）3.（1）图略，每个图2分（2）填空1分，（○3）4.（1）每空1分，共2分△○（2）设计一个按周期排列的图形序列，正确即可。

……2分五、学以致用，解决问题（5分×3+8分=23分）1.600÷20=30（元）……2分30÷2=15（元）……1分600÷15=40（箱）……2分第二个问题也可以用20×20=40(箱)2.（1）（15+18）×20=33×20=660（箱）或15×20+18×20……2分（2）48×18-35×15=864-525=339（元）……3分也可以分步列式，分步赋分3．（1）（23+34+20+28+51+47+21）÷7=32（本）……3分（2）32×32=960（本）……2分4．（1）画出统计图，每个直条1分，如有未填时间-0.5分填空每空1分。

PDEF浙教版八年级第一学期第一次阶段数学试题卷亲爱的同学们：转眼间，你进入八年级的第一个学期已一个多月了，回头看看，你收获到了哪些？通过这份测试卷，检验一下你自己，相信你会给自己、给大家一个惊喜、沉着、冷静，动动脑，开始吧．温馨提示：1.试卷共4页，答题纸4页，满分100分，考试时间90分钟。

2.答案必须写在答题纸相应的位置上，写在试卷、草稿纸上无效。

一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）1．如图，工人师傅砌门时，常用木条EF 固定长方形门框ABCD ，使其不变形，这样做的根据是（）．A ．两点之间的线段最短B ．长方形的四个角都是直角C ．长方形是轴对称图形D ．三角形有稳定性第1题图 第3题图 第4题图 第6题图 2．下面每组数分别是三根小木棒的长度, 它们能摆成三角形的是（ ）. A. 12cm, 3cm, 6cm B. 8cm, 16cm, 8cm C.6cm, 6cm, 13cm D. 2cm, 3cm, 4cm 3．如图，一次数学活动课上，小聪将一副三角板按图中方式叠放，则α∠等于 （ ）． A ．10° B ．15° C ．30° D ．45° 4．如图，已知∠BAC=∠DAC ，那么添加下列一个条件后，仍无法判定△ABC ≌△ADC 的是（ ）. A ．CB=CD B ．AB=AD C ．∠BCA=∠DCA D ．∠B=∠D 5．正n 边形的每个内角都是135°，则n 的值为 （ ）.A ．7B ．8C ．9D ．106．如图，三条直线表示相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) ．A.一处B. 两处C.三处D.四处7．如图，在△ABC 中，∠C=40°，按图中虚线将∠C 剪去后，∠1+∠2等于（ ）. A.140° B.210° C.220° D.320°8．如图，已知∠A=∠B=∠BCD=90°，AB=CD=3，AD=5，BE=10，点C 是BE 的中点，动点P 从点B 出发以每秒1个单位的速度沿BC →CD →DA ，向终点A 运动，设点P 的运动时间为t 秒.当t 为多少秒时，△ABP 与△DCE 全等（）.A ．5B ．3或5C ．3或8D ．5或8CBE F aAxyBCO D C BAE第7题图 第8题图 第9题图 第10题图 9．如图，两组邻边分别相等的四边形我们称它为筝形．如图，在筝形ABCD 中，AB=AD ，BC=DC ，AC 与BD 相交于点O ，则①AC ⊥BD ；②AC 、BD 互相平分；③AC 平分∠BCD ；④∠ABC=∠ADC=90°；⑤筝形ABCD 的面积为BD AC ⋅21.上述判断正确的有（ ）个.A ．2B ．3C ．4D ．510．如图，在六边形ABCDEF 中，∠A+∠F+∠E+∠D =α，∠ABC 的平分线与∠BCD 的平分线交于点P ，则∠P 度数为（ ）. A ．11802α-︒B ．13602α︒-C ．11802α︒-D ． 13602α-︒ 二、填空题（本题有6小题，每小题3分，满分18分）11. 已知：△ABC ≌△A ′B ′C ′，∠A=∠A ′，∠B=∠B ′，∠C=60°，AB=16cm ，则 ∠C ′=_________°，A ′B ′=__________cm.12. 已知一个等腰三角形的两边长为3和6，则它的周长等于_________.13. 如图，在△ABC 中，AD 平分∠CAB ，DE ⊥AB 于点E, DE=2， AC=6,则S △ADC =_________． 14．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=_________°.第13题图 第14题图 第15题图15．如图，在坐标平面内有一等腰直角三角形ABC,直角顶点C （1，0），另一顶点A 的坐标为（－1，4），则点B 的坐标为 _________ ．16. 如图，在第1个△ABA 1，∠B =40°，∠BAA 1=∠BA 1A ；在A 1B 上取一点C ，延长AA 1到A 2，使得在第2个△A 1C A 2中，∠A 1CA 2=∠A 1 A 2C ；在A 2C 取一点D,延长A 1 A 2到A 3，使得在第3个△A 2DA 3中，∠A 2DA 3=∠A 2 A 3D ；…,按此顺序进行下去，第3个三角形中以A 3为顶点的内角的度数为_______°，第n 个三角形中以A n 为顶点的内角的度数为_________°.第16题图AB CDEA nA 4A 3A 2A 1DACBCDCABD21三、解答题（本题有7小题，第17～20题每题6分，第21、22题每题8分，第23题12分，共52分）17.如图，已知△ABC 中，AB=AC ，AD 平分∠BAC ，求证△ABD ≌△ACD第17题图18．如图，在△ABC 中，∠1=∠B ，∠2=∠C ，∠BAC=60°，求∠B 的度数．第18题图19．如图，已知△ABC ≌△A ＇B ＇C ＇，AD 、A ＇D ＇是对应边BC 、B ＇C ＇边上的高． （1）求证AD= A ＇D ＇（2）请用一句话来表述本题的结论．____________________________________________________________________. 第19题图20．如右图，在△ABC 中，∠B=40°，∠C=110°． （1）按要求画图：①作∠A 的角平分线AE （尺规作图）；②作BC 边上的高AD. （2）试求∠DAE 的度数．第20题图21．如图，∠A=∠B ，AE=BE ，点D 在AC 边上，∠1=∠2，AE 和BD 相交于点O ． （1）求证：△AEC ≌△BED ；（2）若AD:CD=3:2，S △EBD =10，求S △BOE -S △AOD第21题图AC22．如图，已知：OP平分∠MON，点A，B 分别在边O M，O N 上，且∠OAP＋∠OBP=180°， PC⊥OM于点C．（1）求证：PA=PB；（2）求证：OA－OB=2AC．第22题图23.（1）观察理解：如图1，在△ABC中，∠ACB=90°，AC=BC，直线l过点C，点A、点B 在直线l同侧，BD⊥l，AE⊥l，垂足分别为D、E，由此可得：∠AEC=∠CDB=90°，所以∠CAE+∠ACE=90°，又因为∠ACB=90°，所以∠BCD+∠ACE=90°，所以∠CAE=∠BCD，又因为AC=BC，所以△AEC≌△CDB（）；（请填写全等判定的方法）（2）理解应用：如图2，AE⊥AB，且AE=AB，BC⊥CD，且BC=CD，利用(1)中的结论，请按照图中所标注的数据计算图中实．线．所围成的图形的面积S= ；（直接写出答案）（3）类比探究：如图3，Rt△ABC中，∠ACB=90°，AC=4，将斜边AB绕点A逆时针旋转90°至AB＇，连结B＇C，求△AB＇C的面积；（4）拓展提升：如图4，等边△EBC中，∠EBC=∠BEC=∠ECB=60°，EC=BC=3cm，点O在BC上，且OC=2cm，动点P从点E沿射线EC以1cm/s速度运动，连结OP，将线段OP绕点O 逆时针旋转120°得到线段OF，当点F恰好落在射线EB上时，请补全图形，并求出点P运动的时间.数学答案参考答案及评分建议一、单选题（共 10 题， 共 30 分）1．D 2．D 3．B 4．A 5．B 6．D 7．C 8．D 9．B 10．A 二、填空题（共 8 题，共 18 分） 11．60，16（对一个得2分） 12．15 13．614．135° 15．（5，2） 16．235（1分），1270-n 或n 2140（2分） 三、解答题（共 8 题 ，共 52 分） 17．（6分）证明略 18．（6分）40°过程略 19．（1）（4分）证明略 （2）（2分） 全等三角形对应边上的高线相等. 20．（1）①（2分） ②（1分）略 （2）35°（3分）略 21．（1）（4分） 略 （2）（4分） 略 22．（8分） （1）（4分）证明略 （2）（4分）证明略 23．（12分） (1)（2分）AAS (2)（2分）50(3)（4分）过 B ′作 B ′E ⊥AC 于 E ，由旋转得：AB=AB ′， ∵∠BAB ′=90°，可证△AEB ′≌△BCA ， ∴AC=B ′E=4， ∴S △ AB ′C= 21AC .B ′E = 21⨯ 4⨯4 = 8(4)（4分）如图，∵∠FOP=120°， ∴∠FOB+∠COP=60°， ∵∠BCE=60°，∴∠COP+∠OPC=60°， ∴∠FOB=∠OPC ，∵OF=OP ，∠OBF=∠OCP=120°， ∴△PCO ≌△OBF ， ∴PC=OB=1=t ﹣3， t=4，即当t=4秒时，点F恰好落在射线EB 上．。

2024学年第一学期七年级期中测试 数学试题卷参考答案及评分建议一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 BDACCBDCBC二、填空题 11. >，< 12. 1 13. 6 14. 1832xx -⋅15. －2024 16. 1 三、解答题17．3112534042-<-<-<<<-，数轴表示略 18．(1)()157366202156912⎛⎫-⨯+-=--+=- ⎪⎝⎭；(2)()32113191099-⨯--=-⨯+=．19．设商品价格为a 元，则甲、乙、丙三个超市的价格分别为a (1－20%)(1－10%)=0.72a ；a (1－15%)2=0.7225a ；a (1－30%)=0.7a ； 所以到丙超市购买最合算 20．a =±5，b =±2，c =－2(1)∵a <b ，∴a =－5 b =±2 ∴a ＋b =－7或－3(2)∵a bc >0，∴ab <0 ∴a =5，b =－2或a =－5，b =2 ∴a －3b －2c ＝15或－7． 21．(1)2132293124--=--=- (2)()222222322233a ab a ab a ab a ab ab ⎛⎫---=--+= ⎪⎝⎭∴当2a =-，b =4时，248ab =-⨯=-．22． (1)115(2)8，3 (3)61，179，(4)设甲诞生的年份为a ，他家的人口数为b （0<b <10），则根据嬉戏规则，结果为()21051050a b a b +⨯+=++，所以当甲告知乙结果时，只要减去50，所得结果的个位数就是甲方家的人口数；结果减去50再除以10，所得的数就是甲方的诞生月份数．23．(1)图1中火柴棒的总数是()31m +根，图2中火柴棒的总数是()52n +根， (2)∵图3中有3 p 个正方形，∴火柴棒的总数是()73p +根，①当p =8时，a =59；∴m =26，575n =不是整数；∴p ≠8 ②由题意得315273a m n p =+=+=+，所以325177m n p --==．因为m ，n ，p 均是正整数，所以当m =17，n =10时，p =7， 此时a 的值最小，3171510277352a =⨯+=⨯+=⨯+==52．。

2024-2025年第一学期高三年级期中试题参考答案及评分建议一．选择题：D B C A B C A B二．选择题：9.BC10.AC 11.BCD 三．填空题:12.14513.)1,21(14.33四．解答题：15.解：（1）由题意得}21|{≤<=x x A ，}0|{>=∴y y B ，]2,1(=∴B A ；………6分（2）由题意得xxax f 22)(+=的定义域为R ，且)(x f 是奇函数，01)0(=+=∴a f ，1-=∴a ，xx x f 212)(-=∴，………9分x x x f 212)(-= 在]2,1(上单调递增，23)1(=f ，415)2(=f ，∴当B A x ∈时，)(x f 的值域为]415,23(.………13分16.解（1）设}{n a 的公比为q ，则⎪⎩⎪⎨⎧===-=-,8,12)1(2132124q a a q q a a a 解得⎩⎨⎧==2,21q a 或⎪⎩⎪⎨⎧-==21,321q a （舍去），)(2*N n a n n ∈=∴；………6分（2）由（1）可得)N (2)4(*∈⨯-=n n b nn ，n n n n n S 2)4(2)5(2)2(2)3(12⨯-+⨯-++⨯-+⨯-=∴- ，①1322)4(2)5(2)2(2)3(2+⨯-+⨯-++⨯-+⨯-=∴n n n n n S ，②①-②，整理得102)5(1+⨯-=+n n n S ，………10分所以对于任意的*N ∈n ，不等式102)4(102)5(1+⨯-≤+⨯-+n n n n λ恒成立，即不等式0)410()2(≥-+-λλn 对于任意的*N ∈n 恒成立，………12分⎩⎨⎧≥-+-≥-∴,04102,02λλλ解得382≤≤λ，∴实数λ的取值范围是]38,2[.………15分17.解：（1）由题意得)62sin(2cos 212sin 23)(π-=-=x x x x f ，………3分1)62sin()(=-=∴πA A f ，20π<<A ，65626πππ<-<-∴A ，=∴A π3，C B sin 3sin 2= ，由正弦定理可得c b 32=，即c b 23=，………5分7=a ，由余弦定理得747cos 22222==-+=c A bc c b a ，2=∴c ，3=b ；………7分（2）由题意得x x x f x g 2cos )22sin()3()(=+=+=ππ，………9分02cos )(==∴B B g ，20π<<B ，π<<∴B 20，4π=∴B ，………10分n m ⋅∴C A C A sin sin cos cos +=)cos(C A -=432cos(π-=A ，………13分24ππ<<A，44324πππ<-<-∴A ，1)432cos(22≤-<∴πA ，n m ⋅∴的取值范围为]1,22(.………15分18.（1）证明：连接OA ，P A AB = ，︒=∠60P AB ，∴△P AB 是正三角形，P A AB PB ==∴，同理可得AB PC =，PC PB =∴，O 是BC 的中点，BC OP ⊥∴，………2分AC AB = ，BC OA ⊥∴，AC AB ⊥ ，BC OB OA 21==∴，BC OP ⊥ ，222OB OP PB +=∴，222222OA OP OB OP PB P A +=+==∴，OA OP ⊥∴，………4分O BC OA = ，⊥∴OP 平面ABC ；………6分（2）由（1）得OA OP ⊥，OB OP ⊥，OB OA ⊥，以O 为原点，OP OB OA ,,所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，设2=AB ，则)0,0,1(A ，)0,1,0(B ，)0,1,0(-C ，)1,0,0(P ，AP BQ = ，)1,1,1(-∴Q ，显然)1,0,0(=OP 是平面ABC 的一个法向量，………8分设),,(z y x m =是平面BCQ 的一个法向量，则⎪⎩⎪⎨⎧⊥⊥,,BQ m BC m ⎩⎨⎧=+-=-∴,0,02z x y 取1=z ，则0,1==y x ，)1,0,1(=∴m ，………10分2221||||,cos ==>=<∴OP m OP m OP m ，∴二面角Q BC A --的大小为︒135；……12分（3）假设存在点M ，设BM =λBQ (0≤λ≤1)，则BM =λBQ =(-λ,0,λ)，QPBCAzOyxM),1,1(λλ--=+=∴BM AB AM ，………13分直线AM 与平面BCQ 所成角的正弦值为77，71|1)1(21||||||||,cos |22=+++-==><∴λλAM m AM m AM m ，………15分21=∴λ或23-=λ（舍去），21=∴BQ BM .………17分19.（1）证明：由题意得曲线)(x f y =在点))(,(n n a f a 处的切线方程为))(()(n n n a x a f a f y -'=-，即)(n a a a x e e y n n -=-，令0=y ，解得1-=n a x ，则11-=+n n a a ，即11-=-+n n a a )(*N n ∈，所以数列}{n a 是以1a 为首项、1-为公差的等差数列；………5分（2）由（1）可得11-=-+n n a a )(*N n ∈，所以ee af a f n n a a n n 1)()(11==-++，所以数列)}({n a f 是以)(1a f 为首项、e1为公比的等比数列，其前4项的和为1)1(431---e e e a )1)(1(231++=-e e e a )1)(1(2++=e e ，所以实数31=a ；………10分（3）原不等式等价于23121xe x x m x-++≥在),0(+∞上恒成立，令23121)(x e x x x h x-++=，0>x ，则322)222)(2()(x e x x x x h x -++-='，令xe x x x t 222)(2-++=，0>x ，则0)1(2)(<-+='xe x x t ，所以)(x t 在),0(+∞上递减，所以0)0()(=<t x t ，令0)(<'x h ，则2>x ；令0)(>'x h ，则20<<x ，所以)(x h 在)2,0(上递增，在),2(+∞上递减，所以47)2()(2e h x h -=≤，所以实数m 的取值范围为),47[2+∞-e .………17分注：以上各题其它解法请酌情赋分.。

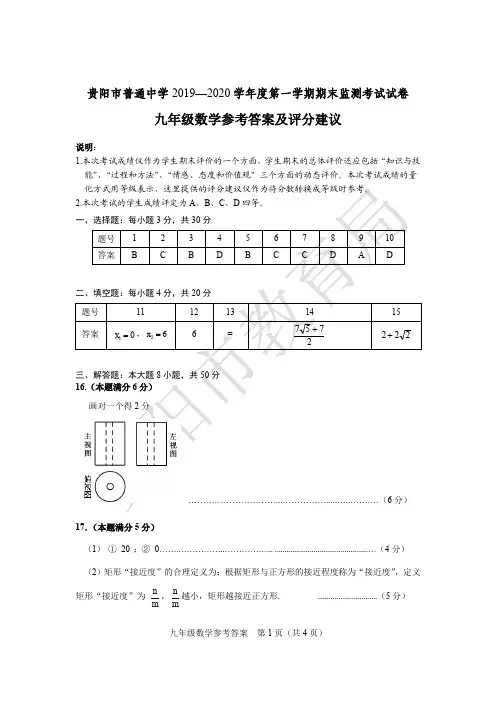
九年级数学参考答案 第1页（共4页）贵阳市普通中学2019—2020学年度第一学期期末监测考试试卷九年级数学参考答案及评分建议说明：1.本次考试成绩仅作为学生期末评价的一个方面，学生期末的总体评价还应包括“知识与技能”、“过程和方法”、“情感、态度和价值观”三个方面的动态评价。

本次考试成绩的量17．（本题满分5分）（1） ① 20 ；② 0…….……………..……………... ................................................…（4分） （2）矩形“接近度”的合理定义为：根据矩形与正方形的接近程度称为“接近度”，定义矩形“接近度”为n n. ...............................（5分）九年级数学参考答案 第2页（共4页）4250)5400)(2540(=+m m －－18．（本题满分5分） 解：（1.…………...........................…..…..……............………（2分） （2） 画树状图如下：19 如图所示，线段FG 即为所求. 20答：八，九这两个月的月平均增长率为25% . ………………………......（4分） （2）设：当农产品每袋降价m 元时，该淘宝网店10月份获利4250元.根据题意可得：解得：m 1=5，m 2=－70（不合题意舍去）．答：当农产品每袋降价5元时，该淘宝网店10月份获利4250元. …. ...（7分）开始第17题图九年级数学参考答案 第3页（共4页）21．（本题满分8分）解：（1） ∵AB ⊥CD ，AC ⊥BC ，∴∠A+∠ACD =90°，∠BCD+∠ACD =90°， ∴∠A =∠BCD ，又∵NM ⊥BM ，AC ⊥BC ，∴∠AMN+∠BMC =90°，∠CBM+∠BMC =90°，22九年级数学参考答案 第4页（共4页）23．（本题满分8分）解：（1） 6－x ； ……………………….............................................................. . ..............（2分） （2）在Rt △ACB 中，由勾股定理有：222AB BC AC =+，且BC=8，AB=10，∴AC=6，又∵A 1是BC 的中点， （3又∵∠A =∠DA 1E ，∠A =∠DA 1E =∠CDA 1 EA 1//AD∴四边形ADA 1E 是平行四边形， ∵DA =DA 1，∴平行四边形ADA 1E 是菱形. .................................................................…….......（8分）（第23题图）（第23题备用图）。

2022-2023学年第一学期高一数学期中质量监测数学参考答案及评分建议一．选择题: 12 3 4 5 6 7 8 D C C B D C B A二．选择题:910 11 12 A CD BCD BC AD三．填空题:13.14 14.(]0，2 15.240 16.1,2 +∞四．解答题： 17.解（1）（2）18.解：(1)因为函数()2x fx a −=的图象经过点11,2， 所以12122a a −==，解得， ...........................................2分 所以()22x f x −=，所以 128t =， 解得3t =−.................................................. 5分011331133293113.223.2− ×−+ =+−=（）（）..........................................2分 (4)分1112212222221225,329,7,25,()5x x x x x x x x x x x x x x −−−−−−−+=++=∴+=∴++=+=∴+−=−=两边平方,得，...............................................5分得.................................6分即，...............................71x x −∴−=分..............................................8分(2).()10102x x x g x x +≤=−> 由（1）可知：,如图：................................... 8分单调增区间为�−1，0)和�0，+∞�. ............................. 10分19.解（1）由33x >，得1x >，所以(1,)A =+∞，则(]R ,1A =−∞ ............... 3分又{}{}2303B x x x x x =−=∣∣0 ， 所以(){}R 3B A x x =≤ . ............................ 5分（2）由B C C = ，得C B ⊆， ........................ 6分 ①当12a a −>，即1a <−时，C =∅，满足题意； ..................... 7分 ②当12a a − ，即1a − 时，C ≠∅，因为C B ⊆，所以10,23,a a − 解得312a . ........................ 9分 综上，实数a 的取值范围是()3,11,2∞ −−∪. ........................ 10分20．（A ）解（1）由题意知，当120x =时，0v =， 代入80150k v x=−−，解得2400k =， ........................ 2分 所以60,030240080,30120150x v x x <≤ = −<≤ −，， 当50x =时，解得56v =，所以车流密度为50辆/千米时，车流速度为56千米/小时. ..................... 5分 （2）由（1）知60,030,240080,30120,150x v x x <≤ = −<≤ −当030x <≤时，6040v =≥，符合题意； ........................ 6分当30120x <≤时，令24008040150x−≥−，解得90x ≤， ..................... 8分 所以3090x <≤. ........................ 9分 所以，若车流速度v 不小于40千米/小时，则车流密度x 的取值范围是(]0,90辆/千米......................... 10分20（B ）解（1）由题意知，当120x =（辆/千米）时，0v =（千米/小时）， 代入80150k v x=−−，解得2400k =， ........................ 2分 所以60,030240080,30120150x v x x <≤ = −<≤ −，， 当50x =时，解得56v =，所以车流密度为50辆/千米时，车流速度为56千米/小时. ................... 5分（2）由题意得60,030,240080,30120,150x x y x x x x <≤ = −<≤ −当030x <≤时，60y x =为增函数，所以1800y ≤，30x =时等号成立；......... 6分当30120x <≤时，240045008080180150150150x y x x x x =−=−−+ −−4800(33667≤≈. 当且仅当4500150150x x−=−，即30(583x =≈时等号成立. ................. 9分 所以，隧道内车流量的最大值约为3667辆/小时，此时车流密度约为83辆/千米........................... 10分21（A ）.解（1）因为91()3x mx f x +=为偶函数， 所以()()f x f x −=，R x ∈， 所以919133x x mx mx −−++=，即239mx x =， ..................... 4分 解得1m =. ..................... 5分（2）由（1）知，91()333x x x x f x −+==+， 由2222()1y y f x −−+≥，得 222332x x y y −+−+≥，因为30x >，30x −>，所以332x x −+≥=，当且仅当33x x −=，即0x =时，33x x −+有最小值2. ..................... 8分 所以22222y y +−≥成立，即 2221y y +−≤恒成立，解得31y −， 所以y 的取值范围是[]31−，. .......................... 10分21.（B ）解（1）因为91()3x mxf x +=为偶函数， 所以()()f x f x −=，R x ∈， 所以919133x x mx mx −−++=，即239mx x =， ..................... 3分 解得1m =. ..................... 4分（2）由（1）知，91()333x x x x f x −+==+， 将222()1y y n f x −−+≥变形为22332x x y y n −+−+≥，因为30x >，30x −>，所以332x x −+≥=，当且仅当33x x −=，即0x =时，33x x −+有最小值2. ..................... 6分 所以R y ∃∈，使得2222y y n +−≥成立，即221y y n +−≤成立，亦即221n y y ≥+−成立， ..................... 8分因为2221(1)22y y y +−=+−≥−，当且仅当1y =−时取等号，所以有2n ≥−， 所以n 的取值范围是[)2,−+∞. ..................... 10分 （注：以上各题，其他正确解法相应付分）。

2020届高三第二次调研测试数学学科参考答案及评分建议一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．．．．．．．．． 1．已知集合{}14A =，，{}57B a =-，．若{}4A B =，则实数a 的值是 ▲ ．【答案】9 2．若复数z 满足2i iz=+，其中i 是虚数单位，则 z 的模是 ▲ ．3． 在一块土地上种植某种农作物，连续5年的产量（单位：吨）分别为9.4，9.7，9.8，10.3，10.8．则该农作物的年平均产量是 ▲ 吨．【答案】104．右图是一个算法流程图，则输出的S 的值是 ▲ ． 【答案】525．“石头、剪子、布”是大家熟悉的二人游戏，其规则是：在石头、剪子和布中，二人各随机选出一种，若相同则平局；若不同，则石头克剪子，剪子克布，布克石头． 甲、乙两人玩一次该游戏，则甲不输的概率是 ▲ ．【答案】236．在△ABC 中，已知B = 2A ，AC，则A 的值是 ▲ ． 【答案】π67．在等差数列{a n } ( n ∈ N *)中，若a 1 = a 2 + a 4，a 8 = -3，则a 20的值是 ▲ ．【答案】-158．如图，在体积为V 的圆柱O 1O 2中，以线段O 1O 2上的点O 为顶点，上下 底面为底面的两个圆锥的体积分别为V 1，V 2，则12V V V+的值是 ▲ ． 【答案】139．在平面直角坐标系xOy 中，双曲线22221(00)y x a b a b-=>>，的左顶点为A ，右焦点为F ，过F作x 轴的垂线交双曲线于点P ，Q ．若△APQ 为直角三角形，则该双曲线的离心率是 ▲ ． 【答案】2（第8题）（第4题）10．在平面直角坐标系xOy 中，点P 在直线2y x =上，过点P 作圆C ：22(4)8x y -+=的一条切线，切点为T ．若PT PO =，则PC 的长是 ▲ ．11．若x > 1，则91211x x x +++-的最小值是 ▲ ．【答案】812．在平面直角坐标系xOy 中，曲线e x y =在点()00e x P x ，处的切线与x 轴相交于点A ，其中e 为自然对数的底数．若点B ( x 0，0 )，△PAB 的面积为3，则0x 的值是 ▲ ．【答案】ln 613．图（1）是第七届国际数学教育大会（ICME -7）的会徽图案，它是由一串直角三角形演化而成的（如图（2）），其中OA 1 = A 1A 2 = A 2A 3 = … = A 7A 8 = 1，则6778A A A A ⋅的值是 ▲ ．14．设函数f ( x )2log 04(8)48x a x f x x ⎧-<⎪=⎨-<<⎪⎩，≤，，． 若存在实数m ，使得关于x 的方程f ( x ) = m 有4个不相等的实根，且这4个根的平方和存在最小值，则实数a 的取值范围是 ▲ ． 【答案】()1-∞，说明：第6题答案写成角度也对；第12题自然对数符合“ln ”书写错误不给分；第14题答案写成“1a <”或者“{}|1a a <”也算正确。

贵阳市2023年普通高中高三年级质量监测试卷数学参考答案与评分建议13. 160 14.12a=−15.6xπ=(或57,66x x ππ=−=等)16.317. 解：（1）∵1,2A B C A B C π+=++=， ∴2,33C A B ππ=+= 由余弦定理得22222cos 3c a b ab π=+−，即222c a b ab =++ ① ∵2a c b +=②，由①②得35,77c c a b ==，由正弦定理得323sin sin sin 737214a A C c π===⨯=. …………………………………………………5分（2）∵ABC ∆的面积为4，∴1sin 24ab C =，即13527724c c ⨯⨯⨯=， ∴7c =，所以AB边上的高5sin 771414h b A ==⨯⨯=. …………………………………………………10分18.解：（1）在长方体1111ABCD A B C D −中，2,1,AB AD E ==是AB 的中点， ∴45AED BEC ∠=∠=︒,∴180180454590DEC AED BEC ∠=︒−∠−∠=︒−︒−︒=︒, 即CE DE ⊥，在长方体1111ABCD A B C D −中，1D D ⊥平面ABCD ，CE ⊂平面ABCD ，∴1CE D D ⊥， 又11,,D DDE D D D DE =⊂平面，∴CE ⊥平面1D DE ，又CE ⊂平面1D EC ，所以平面1D DE ⊥平面1D EC . …………………………………………………6分(2) 建立如图的空间直角坐标系D xyz −,因为在长方体1111ABCD A B C D −中，2,1,AB AD E ==是AB 的中点，(3) 所以1(0,0,1),(1,1,0),(1,2,0),(0,2,0)D E B C ， 因此1(1,1,0),(1,1,1),(0,1,0)CE ED EB =−=−−=，由(1)知平面1D DE 的法向量为(1,1,0)CE =−，设平面1D EB 的法向量为(,,)x y z =n ,则10ED EB ⎧⋅=⎪⎨⋅=⎪⎩n n , 即00x y z y −−+=⎧⎨=⎩,取1,0,1x y z ===，所以(1,0,1)=n ， 因此平面1D DE 与平面1D EB 夹角的余弦为C AC11cos 2CE CE θ⋅===n n. …………………………………………………12分 19. 解:（1）由题意得112n n a a −=⨯，111(12)212n n n a S a a −==⨯−−，所以1111212n n n a a b a λ−+⨯−⨯==， 即1111212nn a a a λ−⨯−+=⨯对于所有*n N ∈恒成立,因此111210a a a λ=⎧⎨−+=⎩，解得11,2a λ==，所以{}n a 的通项公式为11122n n n a −−=⨯=.…………………………………………………6分 （2）由（1）知12log 21n n c n −==−，112n n n c n a −−=，0122101221...22222n n n n n T −−−−=+++++ ① 1231101221 (222222)n n n n n T −−−=+++++ ② ①−②得12111111...22222n n n n T −−=+++−111[1()]1122112212n n n n n −−−+=−=−−所以1122n n n T −+=−.…………………………………………………12分 20.解：(1)设i A = “从第i 个盒子中取到红球”，则1121(),()33P A P A == 21212121121()()()()(|)()(|)P A P A A P A A P A P A A P A P A A =+=+9531313232=⨯+⨯=；…………………………………………………4分（2）∵111111()()()()(|)()(|)n n n n n n n n n n n P A P A A P A A P A P A A P A P A A −−−−−−=+=+1112111()[1()]()3333n n n P A P A P A −−−=⨯+−⨯=+∴1111()[()]232n n P A P A −−=− 所数列1{()}2n P A −是首项为11211()2326P A −=−=，公比为13的等比数列， 因此1111()()263n n P A −−=⨯，∴111()()223n n P A =+⨯；（经验证1n =也成立） …………………………………………………8分 （3）X 的可能值为1,2，111111(1)()1()()223n n n P X P A P A −−−===−=−⨯,11111(2)()()223n n P X P A −−===+⨯, 所以X 的分布列为111111111311()1[()]2[()]()223223223n n n E X −−−=⨯−++=+.由于1113311311()()22223223n −−<++=≤，所以3()22E X <≤.…………………………………………………12分21.解：（1）由题意得(2,0),(2,0)A B −,设(,),(,),(0,2)M m n N m n m m −≠≠±，则224m n +=，直线PA 的方程为(2)2n y x m =++，直线PB 的方程为(2)2ny x m =−−−， 2222222(2)(2)(4)44n n y x x x x m n−−=+−=−=−−−,所以轨迹E 的方程为224(2)x y x −=≠±. …………………………………………………6分（2）当定向直线l 的倾斜角为90︒时，设:,(||2)l x t t =≥，由224x t x y =⎧⎨−=⎩得((,C t D t ，当AC AD ⊥时，0,(2)(2)0AC AD t t ⋅=++−= ∴2t =−，此时:2l x =−经过点A （,,A C D 三点重合），不满足题意.当定向直线l 的倾斜角不为90︒时，假设存在定向直线:l y kx t =+，由224y kx t x y =+⎧⎨−=⎩得222(1)240k x ktx t −−−−=， 当22210,4(44)0k t k −≠∆=−+>时,设1122(,),(,)C x y D x y ，则212122224,11kt t x x x x k k−−+==−− 由AC AD ⊥得,0AC AD ⋅=,即1212(2)(2)()()0x x kx t kx t +++++=， 因此221212(1)(2)()40k x x kt x x t ++++++=，2222242(1)(2)4011t kt k kt t k k−−+++++=−−， 化简得(2)0k t k −=， ∴0k =或2t k =，当0k =时,经验证,满足条件；当2t k =时,():22l y kx k k x =+=+过点A ，不满足条件，综上所述，当0k =即直线l 的一个方向向量为(1,0)时,AC AD ⊥. …………………………………………………12分22.解（1）由1()ax f x xe +=−得1()(1)ax f x e ax +'=−+,(,)x ∈−∞+∞, (i)当0a =时，()0f x e '=−<，函数()f x 在(,)−∞+∞上单调递减，(ⅱ)当0a <时，1,()0x f x a '=−=；1,()0x f x a '<−<；1,()0x f x a '>−>； 函数()f x 在1(,)a −∞−上单调递减,在1(,)a −+∞上单调递增.(ⅲ)当0a >时，1,()0x f x a '=−=; 1,()0x f x a '<−>；1,()0x f x a '>−<；函数()f x 在1(,)a −∞−上单调递增,在1(,)a−+∞上单调递减.…………………………………………………6分（2）当0,0a b >≠时，函数()y f x =的图像与函数y be =−的图像有两个交点1122(,),(,)A x y B x y .(2)①当0,0a b >≠时，函数()y f x =的图像与函数y be =−的图像有两个交点1122(,),(,)A x y B x y ,即方程()f x eb =−有两个不相等的实数根12,x x ，也即曲线1()ax f x xe +=−与直线y eb =−有两个横坐标分别为12,x x 的交点.由（1）知,当0a >时，max ()1)1(f x f a a−==，且当0x <时，()0f x >，(0)0f =，所以10eb a <−<,∴10ab e−<<. ②由①知当10ab e−<<时，12()()f x f x =,即121112ax ax x e x e ++−=−，∴21()12a x x x e x −=， 不妨设120x x <<，∴121x t x =>，∴22()21ln ln ,,11a x tx t t t t e ax ax t t−===−−， 1211()2(ln 2)11t t a x x t t t +−++=−⨯−+， 令221(1)()ln 2,(1),()01(1)t t g t t t g t t t t −−'=−⨯>=>++， 所以函数()g t 在(1,)+∞上单调递增,则()(1)0g t g >=，又1t >，∴101tt+<−， 因此1211()2(ln 2)011t t a x x t t t +−++=−⨯<−+,即12()2a x x +<−. …………………………………………………12分。

2022-2023学年第一学期期末高三数学试题参考答案及评分建议一、选择题：B DC A B CD B 二、选择题:9.A C 10.A B 11.A C D 12.A C D 三、填空题：13.2-14.98-15.2331116.)10,2(四、解答题：17.解：（1）选择条件①212+=a a ，且n n S a a +=12，由题意可得1112+++=n n S a a ，11122+++=-=-∴n n n n n a S S a a ，n n a a 21=∴+，……2分}{n a ∴为公比2=q 的等比数列，212+=a a ，2211+=∴a a ，21=∴a ，)(2*N n a n n ∈=∴；………5分选择条件②}{n a 为等比数列，且满足k S n n +=+12，由题意可得4)4()8(122=+-+=-=k k S S a ，8)8()16(233=+-+=-=k k S S a ，223==∴a a q ，)(2*22N n q a a n n n ∈==∴-；………5分（2）由（1）得)(2*N n a n n ∈=，)32)(12(1log log 1322122++=⋅=∴++n n a a b n n n )321121(21+-+=n n ，………7分n n b b b T +++=∴ 21321121(7151()5131[(21+-+++-+-=n n λ<+-=32131(21n ，λ∴的最小值为61.………10分18.解：（1）由余弦定理得A bc c b a cos 2222-+=,22a bc b =+ ，c A b =+∴)cos 21(，………2分由正弦定理得Cc B b sin sin =,)sin(sin )cos 21(sin B A C A B +==+∴，)sin(sin B A B -=∴，π<<B A ,0 ，π<<<∴A B 0，B A B -=∴，B A 2=∴；………6分（2）由（1）得B A 2=，)cos 21(A b c +=，B b c b cos 26+∴BB cos )1cos 4(262-+=B B cos 4cos 8+=，………8分B A 2= ，30π<<∴B ，1cos 21<<∴B ，………10分12cos 4cos 828<+≤∴B B ，Bb c b cos 26+∴的取值范围为)12,28[.………12分19.解：（1）由题意得033.0200022.0190009.0180002.0170(⨯+⨯+⨯+⨯=x 20010)002.0230008.0220024.0210=⨯⨯+⨯+⨯+，………3分033.0)200200(022.0)200190(009.0)200180(002.0)200170[(22222⨯-+⨯-+⨯-+⨯-=s15010]002.0)200230(008.0)200220(024.0)200210(222=⨯⨯-+⨯-+⨯-+；……6分（2）由题意得200==x μ，15022==s σ，Z ～)150,200(N ，（i）2.12150= ，9544.0)4.2246.175(=<<∴Z P ；………8分（ii）由（i）得从该企业购买了1件这种产品，其质量指标值位于区间)4.224,6.175(的概率为9544.0=p ，X ∴～)9544.0,100(B ，44.959544.0100)(=⨯=∴X E .………12分20.解：（1）O 为BD 的中点，AD AB =，BD AO ⊥∴， 平面⊥ABD 平面BCD ，⊥∴AO 平面BCD ，BC AO ⊥∴；………4分（2）由（1）得⊥AO 平面BCD ，以点O 为原点，OB ，OA 所在的直线分别为x 轴，z 轴，建立如图所示的空间直角坐标系，设a OA =，由题意可得)0,0,0(O ，),0,0(a A ，)0,0,1(B ，)0,23,21(-C ，)32,0,31(a E -，设),,(111z y x m =是平面BCE 的一个法向量，则⎪⎩⎪⎨⎧⊥⊥，BE m BC m ,⎪⎪⎩⎪⎪⎨⎧=+-=+-∴，03234,023231111z a x y x 令31=y ，则⎪⎩⎪⎨⎧==，a z x 2,111，2,3,1(a m =∴，………6分由题意可知)1,0,0(=n 是平面BCD 的一个法向量，||||,cos n m n m n m >=<∴2160cos 112=︒=+=a ，3=∴a ，………10分332,3,1(=∴m ，)3,23,21(--=AC ，||||,cos AC m AC m AC m >=<∴83-=，∴直线AC 与平面BCE 所成角的正弦值为83.………12分21.解：（1） 椭圆C 经过点)2,0(A ，2=∴b ，由题意得直线2AF 的方程为12=+y c x ，即022=-+c cy x ，………2分 直线2AF 与圆222=+y x 相切，2422=+=∴cc d ，2=∴c ，8222=+=∴c b a ，∴椭圆C 的方程为14822=+y x ；………4分（2）设),(11y x P ，),(22y x Q ，点),(00y x N 是PQ 的中点，由⎪⎩⎪⎨⎧=++=148,122y x kx y 得064)21(22=-++kx x k ,221214k k x x +-=+∴，20212k k x +-=∴，………6分PQ MQ PQ MP ⋅+⋅ PQ MQ MP ⋅+=)(02=⋅=PQ MN ，A B C O D E y x zPQ MN ⊥∴，k k MN 1-=∴，………8分∴直线MN 的方程为)(100x x ky y --=-，∴点M 的横坐标为k x k x ky x ++=+=0200)1(221k k +-=k k 211+-=，………10分0>k ，2221≥+∴k k，∴)0,42[-∈x ，∴点M 的横坐标的取值范围为)0,42[-.………12分22.解：（1）由题意得)2)(1()(a e x x f x --='，R x ∈，………1分令0)(='x f ，则1=x 或a x 2ln =，①当12ln <a 时，即20e a <<时，令0)(<'x f ，则12ln <<x a ；令0)(>'x f ，则a x 2ln <，或1>x ，)(x f ∴在)1,2(ln a 上递减，在),1(+∞上递增，)(x f ∴在1=x 处取得极小值，此时不符合题意；………2分②当12ln =a 时，即2e a =时，则0)2)(1()(≥--='a e x x f x ，)(x f ∴在R 上递增，)(x f ∴在1=x 处不取极值，此时不符合题意；………3分③当12ln >a 时，即2e a >时，令0)(<'xf ，则a x 2ln 1<<；令0)(>'x f ，则1<x ，或a x 2ln >，)(x f ∴在)1,(-∞和),2(ln +∞a 上递增，在)2ln ,1(a 上递减，)(x f ∴在1=x 处取得极大值，此时符合题意；综上，)(x f 的单调减区间为)2ln ,1(a ，单调增区间为)1,(-∞和),2(ln +∞a ；………4分（2）由题意得))(2()(ax e x x f x --=，R x ∈，显然2=x 是)(x f 的零点，则方程0=-ax e x，即xe x a =1恰有两个不为2的实数根，………7分令x e x x g =)(，R x ∈，则x e x x g -='1)(，令0)(<'x g ，则1>x ；令0)(>'x g ，则1<x ，)(x g ∴在)1,(-∞上递增，在),1(+∞上递减，当]1,(-∞∈x 时，)(x g 的值域为1,(e -∞；当),1(+∞∈x 时，)(x g 的值域为1,0(e ，……10分e a 110<<∴，且221ea ≠，e a >∴，且22e a ≠，综上，实数a 的取值范围为),2()2,(22+∞e e e .………12分注：以上各题其它解法请酌情赋分.。

数学评分建议一年级二、用竖式计算每题2分，共8分。

竖式正确，但忘记在横式后面写结果，可以用红笔添上，建议不再扣分。

三、填空第1题，4分。

第2题，每小题1分，共2分。

第3题，每个括号1分，共3分。

第4题，3分。

最后一题答案是开放的，能填对一种就可以了。

第5题，2分。

第6题，4分。

第7题，2分。

第8题，每个括号2分，共4分。

五、按要求完成第1题，每行1分，共3分。

第2题，每个图形2分，共4分。

六、解决实际问题第4题6分，其余每题5分，共26分。

二年级一、直接写得数每题1分，合计20分。

二、用竖式计算每题2分，共8分。

竖式正确，但忘记在横式后面写结果，可以用红笔添上，建议不再扣分。

三、填空第1题，每式2分，共4分。

单位名称写错扣1分。

第2题，每空1分，共3分。

第3题，出发时间、结束时间、一共用时各1分，共3分。

第4题，每空1分，共5分。

第5题，每空1分，共4分。

第6题，每空1分，共2分。

第7题，每空1分，共4分。

第8题，每小题2分。

共4分。

五、按要求完成第1题每空1分，共4分。

第2题第（1）题2分，第（2）题4分，共6分。

六、解决实际问题。

第1题6分，其余每题5分，共21分。

第1题，每小题3分。

其中第（2）题，每行站2人、3人、6人、7人、14人、21人，都能正好排成方队。

能写出一种方法就算正确。

第2至4题，都是用两步计算解答的实际问题。

学生分步列式计算，第一步列式、计算都正确，第二步列式正确，但结果算错了；或者第一步列式正确，结果算错了，第二步根据错误的结果列算式，思路正确，建议扣2分。

三年级一、直接写得数每题1分，合计15分。

二、用竖式计算用竖式计算，每题2分；验算每题2分，共8分。

竖式正确，但忘记在横式后面写结果，可以用红笔添上，建议不再扣分。

四、填空第1题，每小题1分，共2分。

其中第（2）有不同的答案，只要填一种就可以。

第2、3、6题，每空1分。

第4、5题，每小题1分。

第7题，每问1分，共3分。