12-晶体学点群

格式：pdf
大小：799.17 KB
文档页数：38

下载文档原格式

固体物理-点群

转角的分反别映为面1，80º和120º，半共角2个为90º和60º
只包含旋转反演轴的点群。其中
共2个
群 —— 立方点群, 含有48个对称操作群 —— 正四面体点群, 含有24个动操作
群 —— 正四面体点群的12个纯转动操作
群
群加上中心反演
晶体的宏观对称只有32个不同类型
用
来描述
—— 绕通过A的转轴的任意对称操作，转过角度 B点转到B′点 —— B′点必有一个格点
A和B两点等价——以通过B点的轴顺时针转过
A点转到A′ 点 —— A′点必有一个格点
且有
— n为整数
—— 任何晶体的宏观对称 1, 2, 3, 4, 6 性只能有以下十种对称素 1, 2, 3, 4, 6
2个二重轴2和2′
绕轴2的转动计为A 绕轴2′的转动计为B
—— 连续进行操作AB 轴上一点N回到原处，轴2转到2″的位置
A和B均为对称操作
—— 是对称操作
—— C的操作则是绕NN′轴转过角度2
300 , 450 , 600 , 900
理论证明由10种对称素只能组成32种不同的点群 —— 晶体的宏观对称只有32个不同类型
十种对称素
—— 长方形、正三角形、正方形和正六方形可以在平面内周期性重复排列 —— 正五边形及其它正n边形则不能作周期性重复排列
点群 —— 以10种对称素为基础组成的对称操作群
—— 由对称素组合成群时，对称轴的数目对称轴之间的夹角将受到严格的限制
两个2重轴之间的夹角只能是
—— 如果存在一个n 重轴和与之垂直的二重轴，就一定存在n 个与之垂直的二重轴
§1.6 点群
—— 晶体中原子的周期性排列形成晶体一定的宏观对称性 —— 不同的形式原子排列形成的宏观对称性，对称操作也

晶体点群

除了Dn群的特征外，还含有n个对称面m。
Sn群
含有一个非真轴Sn(n为偶数)，Sn=Cnh(n为奇数)。
Td与T群
Oh与O群
Ci群
国际符号一般由三个位构成，每个位代表一个窥视方向。每个晶系的晶轴选择都有特别的规定：
注意各晶系点群国际符号中的不同位置所代表的对称性方向！
Raman
0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.1027430 0.1027695 0.1027755 N N N N N N Y Y Y
Point Group=32, Oh
萤石(CaF2) 计算Raman谱
319
分子点群
>32
n
晶体学点群表示
极射赤面投影图
Schonflies符号国际符号
N
O
S
N
S
N P
P’
S
极射赤面投影图
任何分子的全部对称元素交于一点，其全部对称操作必构成点群。点群用熊夫利斯符号表示，如Cn、Dn、Cnh等。
Arthur Schö nflies was a student at the University of Berlin from 1870 to 1875. He obtained a doctorate from Berlin in Arthur Moritz 1877 and the following Schö nflies year he obtained a post as (1853.4.17— a teacher at a school in 1928.5.27) Berlin.

晶体点群、空间群简要归纳

晶体点群、空间群简要归纳本⽂只是很简要的归纳，具体内容还请见李新征⽼师群论书和其在蔻享的群论课。

另外推荐肖瑞春⽼师科学⽹博客的这篇博⽂，介绍了群论及后续的学习：若研究中涉及群论和物理性质相关，其中陈纲的《晶体物理学基础》书特别好，易懂，将主动变换和被动变换等分析得特别清晰，不过此书太厚，注意⽤到什么学什么，⽤minimized的知识来科研，否则被导师批评...1.对称操作、对称元素对称操作：保持系统不变的操作。

对称元素：它是⼀个⼏何实体，对称操作可以依据对称元素施⾏对称操作。

对称元素可以是点、直线、⾯等。

2.点群：1）定义：三维实正交群O(3)群的有限⼦群物理理解：实际上点群是实际的物理系统在三维空间的⼀些对称操作的集合。

这些对称操作会保持⼀个点不动。

2）点群分类第⼀类点群：只包含纯转动元素的点群。

第⼆类点群：点群中，除了纯转动元素，还包含转动反演元素的点群。

因为点群是O(3)群的⼦群，⽽O(3)群中有固有转动和⾮固有转动。

3）点群的性质{()}性质1：点群这个集合可以写成C k(2π/n)、IC k′2π/n′的形式，其中n,→k′,n′取有限个⽅向和值；C k(2π/n)是绕→k轴转2π/n⾓的操作。

性质2：设G是点群，K是G的纯转动部分，由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动⼦群,即K=G∩SO(3)∘.点群G与其有限⼦群K的关系有以下三种可能的情况：1.G=K, 即点群只包含纯转动操作；称为第⼀类点群。

2.若点群G中除了纯转动操作，还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第⼆类点群。

3.若点群G中除了纯转动操作，且G中不包含纯反演操作I时 , 此第⼆类点群G⼀定与⼀个第⼀类G+同构,其中，G+=K∪K+, ⽽K+定义为:K+={Ig∣g∈G,但g∉K}根据这⾥的第3点，可以知道构造这种情况对应的第⼆类点群的⽅法：根据⼀个已知的第⼀类点群K∪K+，即可以构造⼀个第⼆类点群K∪I K+.还可以证明K必须是K∪K+的不变⼦群，其阶数是K∪K+的⼀半。

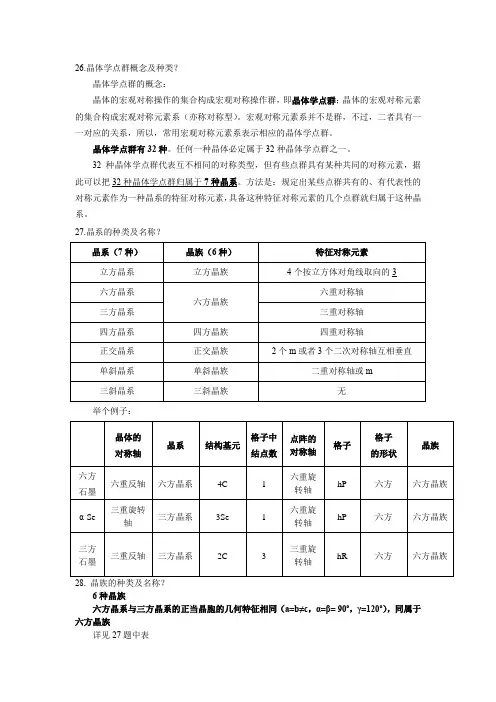
晶体点群分类和晶面指数的计算

26.晶体学点群概念及种类？晶体学点群的概念：晶体的宏观对称操作的集合构成宏观对称操作群，即晶体学点群；晶体的宏观对称元素的集合构成宏观对称元素系（亦称对称型）。

宏观对称元素系并不是群，不过，二者具有一一对应的关系，所以，常用宏观对称元素系表示相应的晶体学点群。

晶体学点群有32种。

任何一种晶体必定属于32种晶体学点群之一。

32种晶体学点群代表互不相同的对称类型，但有些点群具有某种共同的对称元素，据此可以把32种晶体学点群归属于7种晶系。

方法是：规定出某些点群共有的、有代表性的对称元素作为一种晶系的特征对称元素，具备这种特征对称元素的几个点群就归属于这种晶系。

27.晶系的种类及名称？举个例子：28. 晶族的种类及名称？6种晶族六方晶系与三方晶系的正当晶胞的几何特征相同（a=b≠c，α=β= 90º，γ=120º），同属于六方晶族详见27题中表29. Bravais 格子的含义及种类？7种晶系共有14种空间点阵型式，即14种Bravais格子。

平面点阵指标也称为晶面指标或米勒指数，是标志一族平面点阵在晶体中方向的一组3个互质整数(个别晶系有4个整数)，加圆括号记作(h*k*l*)。

晶面指标（h*k*l*）平面点阵指标需要经过三步才能写出：（1）以a、b、c为度量单位，依次写出平面点阵在三条晶轴上的截数r、s、t；（2）求倒易截数1/r、1/s、1/t；（3）求出倒易截数的互质整数比h*：k*：l*，记作（h*k*l*），即为平面点阵指标。

（4）晶面与哪条坐标轴平行，相应的截数就是无穷大。

求倒易截数就是为了消除无穷大。

显然,相互平行的一族平面点阵，其（h*k*l* ）相同。

关于晶体学的一些概念

第21卷　第6期大学化学2006年12月关于晶体学的一些概念周公度(北京大学化学与分子工程学院　北京100871) 大学化学编辑部约我写篇文章,讨论一些晶体学的基本概念和表述方法。

我想藉此机会写一些学习体会,和读者交流,就教于读者。

1　晶体的周期结构和点阵晶体是由原子或分子按照一定的周期性在空间排列形成的固体。

在晶体内部三维空间中,原子的排列按周期规律隔一定距离重复出现,每个重复的单位具有相同的化学组成、相同的化学结构、相同的空间取向和相同的周围环境。

这种重复的基本结构内容叫结构基元。

为了研究晶体中结构基元排列的周期性,将每个结构基元抽象成一个几何上的点表示,而不考虑结构基元的内容和结构,这些点形成点阵。

点阵是在空间任意方向上均为周期排列的无限个全同点的集合。

每个点阵点都有相同的周围环境。

晶体结构可用晶胞表示,将晶胞并置堆积即成晶体。

点阵可用通过点阵点的平行六面体的点阵单位表示。

晶胞和点阵单位是相互对应的。

晶胞参数a,b,c,α,β,γ表达了晶胞的大小和形状,同样它也是表达点阵单位的点阵参数。

将点阵单位用直线划出平行六面体,或将直线通过点阵点外延成格子,称晶格。

点阵和晶格都是从实际晶体结构中抽象出来的,都是表示晶体周期性结构规律的一种抽象的图像。

点阵和晶格在英文中是同一个词(lattice)。

点阵强调的是结构基元在空间的周期排列,它反映的周期排列方式是惟一的;晶格强调的是按点阵单位划出来的格子,由于晶胞和点阵单位的划分有一定的灵活性,所以不是惟一的。

下面通过实例描述晶体周期性结构的重复内容及其点阵。

图1示出α2Se的分子结构、晶体结构和点阵的投影。

α2Se为三重螺旋形的长链分子, Se—Se键长232pm,如图1(a)所示。

在晶体中,这些螺旋长链分子互相平行地堆积在一起,平行螺旋轴的投影结构示于图1(b)。

晶体属D3232点群,实验测得这个三方晶系晶体的晶胞参数a=435.52pm,c=494.95pm,晶胞中包含3个Se原子。

晶体结构空间群点群

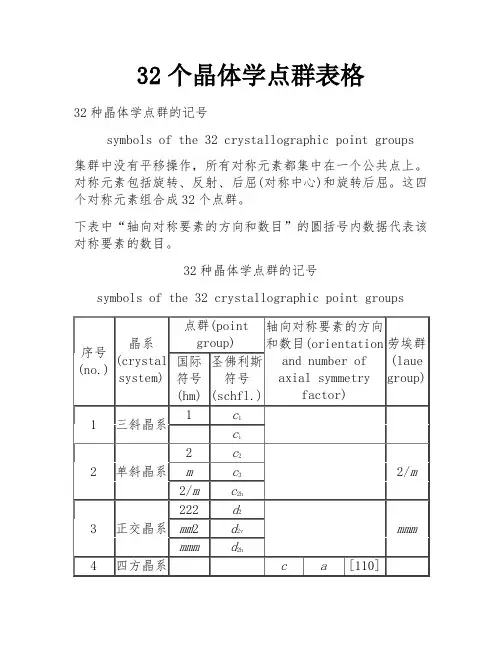
(二)点群、单形及空间群点群：晶体可能存在的对称类型。

通过宏观对称要素在一点上组合运用而得到。

只能有32种对称类型，称32种点群表1- 3 32种点群及所属晶系*2/m表示其对称面与二次轴相垂直，/表示垂直的意思。

其余类推同一晶系晶体可为不同点群的原因：阵点上原子组合情况不同。

如错误!未找到引用源。

，对称性降低，平行于六面体面的对称面不存在，4次对称轴也不存在。

理想晶体的形态―单形和聚形：单形：由对称要素联系起来的一组同形等大晶面的组合。

32种对称型总共可以导出47种单形，如错误!书签自引用无效。

，错误!书签自引用无效。

所示聚形：属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。

大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体，如单形四方柱与平行双面形成了四方柱体的真实晶体形态空间群：描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。

属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群，空间群有230种，见教材中表1- 4国际通用的空间群符号及其所代表的意义为：P：代表原始格子以及六方底心格子（六方底心格子为三方晶系和六方晶系所共有）。

F：代表面心格子。

I：代表体心格子。

C：代表（001）底心格子（即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布）。

A：代表（100）底心格子（即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布）。

R：代表三方原始格子。

其它符号：意义与前述相同表1- 4 晶体的空间群、点群、晶系、晶族一览表续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4点群符号m 43m2晶系等轴晶系晶族高级晶族/k/174/stu/content/1.1.3.2.htm。

32个晶体学点群表格

劳埃群(laue group)
国际符号(hm)
圣佛利斯符号(schfl.)
1三斜晶系1Fra bibliotekc1ci
2
单斜晶系
2
c2
2/m
m
c3
2/m
c2h
3
正交晶系
222
d2
mmm
mm2
d2v
mmm
d2h
4
四方晶系
c
a
[110]
4
c4
4
4/m
s4
4/m
c4h
422
d4
4
2(2)
2(2)
4/mmm
4mm
c4v
4
m(2)
m(2)
32个晶体学点群表格
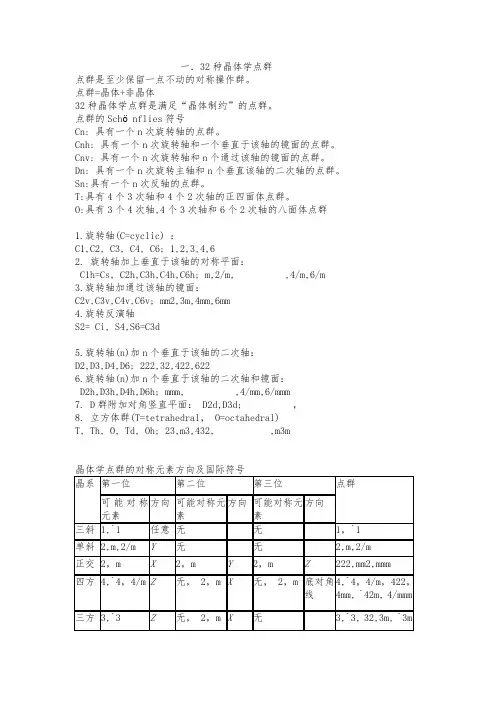
32种晶体学点群的记号
symbols of the 32 crystallographic point groups
集群中没有平移操作，所有对称元素都集中在一个公共点上。对称元素包括旋转、反射、后屈(对称中心)和旋转后屈。这四个对称元素组合成32个点群。
下表中“轴向对称要素的方向和数目”的圆括号内数据代表该对称要素的数目。
[110]
23
t
2(3)
3(4)
m
m
th
(4)
432
o
4(3)
3(4)
2(6)
mm
3m
td
3(3)
3(4)
m(6)
mm
oh
(4)
32种晶体学点群的记号
symbols of the 32 crystallographic point groups
序号(no.)
晶系(crystal system)

12晶体点群与极射赤面投影投影简版解析

2
m
2/m
mm22
222 2 mmm2
3
3
3m 2 32 2 3m 2
4
4
42m
4/m
4mm
422
4/mmm
6
6
62m
6/m
6mm
622 6/mmm
622
23
m3
43m
432
m3m
群的定义，group
元素的集合G={gi}，并且定义了一种乘法: gi gj = gk
1。封闭性：集合中的任意元素和另一元素的乘积仍在这一集合中，gigj =gk G
• 等效点系在空间群表中表示为Wyckoff位置。
Wyckoff位置（1）
在国际表中包含的一个最有用的信息是Wyckoff位置。 Wyckoff位置告诉我们在晶体中何处可以找到原子。
比如：单斜空间群Pm 仅有垂直于b轴的二个镜面。一个在y = 0，另一个在y = ½位置。
通过镜面操作，在x， y， z的原子 --〉在x， - y， z 第二个原子。如果我们安置原子在其中一个镜面(它的Y座标将
❖所有实数，普通加法，单位元素为0； ❖4点群：乘法 -> 旋转,每次旋转90；共
有四个元素：0Biblioteka 90,180,270；单位元素是0； 90和270是互为逆元素，180 的逆元素是其本身；任何两次连续旋转都会是这四个角度之一。
1
1
2
m
2/m
mm22
222 2 mmm2
3
3
3m 2
32 2
3m 2
• 空间群= Pnma 点群= mmm 空间群= I `4c2 点群= `4m2 空间群= P42/n 点群= 4/m

晶体学点群

Sn:具有一个n次反轴的点群。 T:具有4个3次轴和4个2次轴的正四面体点群。 O:具有3个4次轴,4个3次轴和6个2次轴的八面体点群。
32种点群的表示符号及性质
1.旋转轴(C=cyclic) ： C1,C2, C3, C4, C6; 1,2,3,4,6
2. 旋转轴加上垂直于该轴的对称平面：
C1h=Cs, C2h,C3h,C4h,C6h; m,2/m,
外延推演法推导7种晶系32种晶体学点群
国际符号中包含n次旋转轴，所以实际有n个镜面m。
n m表示镜面m垂直于n次旋转轴，nm表示镜面m
熊夫利斯符号Cn表示一个含有Cn， C2 n ，……的点群。Cnh表示这种点群中还含有垂ห้องสมุดไป่ตู้于Cn的镜面，点群Cnh中对称操作数目是Cn群中的两倍。Cnv表示镜面含Cn轴。点群Cnv中对称操作数目也是Cn群的两倍。
2(C2)
m(C1h)
2 (C2 h ) m
外延推演法推导7种晶系32种晶体学点群
3. 正交晶系正交晶系有两个互相垂直的2次轴或两个镜面，因此也必有第三个2次轴。
(1)正交晶系中二次轴必然相互垂直。点群{ 1，2[100] ， 2
[010] ， 2[001] }
2,m,2/m 222,mm2,mmm
四方 4,`4，4/m Z
三方 3,`3 六方 6,`6, 6/m 立方 2,m,4, `4
无， 2，m
X
无， 2，m
底对角线
4,`4，4/m，422， 4mm, `42m, 4/mmm
3,`3, 32,3m, `3m 6,`6, 6/m,622, 6mm, `62m, 6/mmm 23,m3,432, `43m, m`3m
Z Z

点群与晶系分析课件

空间群确定
根据晶体结构分析结果，确定空间群，以便进一步研究晶体结构和性质。
点群与空间群关系
理解点群与空间群之间的关系，有助于理解晶体结构和物理性质。
晶系分析方法
晶系分类
01
根据晶体对称性对晶系进行分类，包括立方、四方、六方等晶
系。
晶格常数
02
测量和计算晶体的晶格常数，有助于确定晶系和进一步研究晶
晶系的特点
每个晶系都有其独特的几何特征和对称元素，这些特征决定了晶体在三维空间中的结构和性质。
晶系的对称性
对称操作
晶体的对称性是指晶体在三维空间中能够通过某些操作保持不变的性质。这些操作包括旋转、平
移和反演等。
对称元素
晶体中存在的对称元素，如对称面、旋转轴和反演中心等，决定了晶体的对称性。通过对称元素可以将晶体分类到不同的晶系。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
点群与晶系的实际应用
材料科学中的点群与晶系应用
晶体结构预测
利用点群和晶系分析，可以预测材料的晶体结构，从而影响其物理和化学性质。
相变研究
通过分析点群和晶系，有助于研究材料在不同温度和压力下的相变行为，为材料制备和应用提供指导。
生物学
在生物学中，点群和晶系分析可用于研究蛋白质的结构和功能，对于药物设计和疾病治疗具有重要意义。
点群与晶系的发展趋势
高压和高温下的点群和晶系研究
随着实验技术的不断发展，人们开始探索高压和高温条件下晶体结构的对称性和稳定性。
点群和晶系的计算模拟
利用计算机模拟技术，可以更准确地预测和理解晶体结构和性质，有助于发现新的材料和化合物。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

晶体转动时极点投影的变化
0º
晶体转动时极点投影的变化
10º
晶体转动时极点投影的变化
20º
晶体转动时极点投影的变化
30º
晶体转动时极点投影的变化
40º
晶体转动时极点投影的变化
50º
晶体转动时极点投影的变化
60º
作业
《结晶学》 p.46: 2，7-9
补充题： 1、试将422,622中的对称操作按共轭类和陪集分类，并说明其中2次轴的关系与32中的三个2次轴有何不同。 2、分析群 n 、 m 群的极性。 n 3、用吴式网将 m 3 m 的所有对称素和一般位置等价点系转动到(111)方向。
第四章：晶体的对称性 § 4.1 对称性的概念 § 4.2 空间变换 § 4.3 对称群的类型和性质 § 4.4 晶体学点群 § 4.5 晶系 § 4.6 空间群和国际表
第四章：晶体的对称性 § 4.4 晶体学点群
对称群的分类 1、按极限群分类——族 7个族，共9个子族 2、按对称变化的类型分类：第一类群：i)，ii），iix）共11个第二类群：iii），iv），v），vi)，vii)，ix）共21个 3、按晶系分类一般位置等价点系构成的凸多面体的外形
⇒ ∞ mm
(1 m = 2 m)
22 → 2
1→2 m
mm → 2
2mm(C2v)，4阶
mm → 2
3 2 m (D3d)，12阶
3→6 m
mm → 2 62 → 2
4 2 m (D4d)，8阶
6 2 m (D6d)，12阶
6=3 m
mm → 2
n m 总：27 （ 7) m (Dnh)，（4n阶） m ⊥ n、 || n ） m 1 3 ⇒ ∞ mmm ( m = mm 2 ) ( m = 6 2 m ) m m 2 4 6 m = mmm m = 4 mmm m = 6 mmm m m m
9) n1 n 2
无极性。
⇒ ∞∞ m
总：32
m 3 (Th)，24阶
4 3 m (Td)，24阶 m 3 m (Oh)，48阶 m 3 (Th)，24阶
4 3 m (Td)，24阶
m 3 m (Oh)，48阶
第四章：晶体的对称性 § 4.4 晶体学点群
不同方向的投影
转动直到两点在一条经线上，读出纬度的差值即为面角
222(D2)，4阶
A ′′′
A ′′
A′
A
32(D4)，6阶
422(D3)，8阶
A ′′′ A ′′ A′
A
622(D6)，12阶
4) n/m (Cnh)，2n阶 m ⊥ n）（
总：17
(1 m = m )
(3 m = 6 ) 2 m 4 m
6 m
⇒ ∞ m
极性&非极性：同3)； 2) 、 4)极限群相同，可看作同一族的两个子族。
第四章：晶体的对称性 § 4.4 晶体学点群
32种晶体学点群 1) 旋转群：n(Cn)，n阶总：5
1
3
⇒ ∞
2
4
6
极性：主轴方向，奇数群中所有方向；非极性：偶数群中垂直于主轴的方向。 2) 反演转动群： (Sn)，（奇：2n阶；偶：n阶）总：10 n
1
2=m
3
4
6=3 m
⇒ ∞ m
极性：偶数群中垂直于主轴的方向； 3 非极性：主轴方向，、1 中垂直于主轴的方向。
2mm(C2v)，4阶
m m
3m(C3v)，6阶
4mm(C4v)，8阶
6mm(C6v)，12阶
(1 m = 2 m) 3 m = 3 2m ( 2 m = 2 mm ) 4 m = 4 2 m
无极性。
总：24 （ 6) n m (Dnd)，（奇：4n阶；偶：2n阶） m || n ）
6 m = 62m
2/m(C2h)，4阶
3/m(C3h)，6阶
4/m(C4h)，8阶
6/m(C6h)，12阶
5) nm (Cnv)，2n阶（ m || n ）
总：21
(1 || m = m ) 3m ⇒ ∞ mm 2 m = 2 mm 4 m = 4 mm 6 m = 6 mm
极性：主轴方向，奇数群中垂直于主轴的方向；非极性：偶数群中垂直于主轴的方向。
无极性。
2 2 2 2 m= ( mmm ) (D2h)，8阶 m m m m
4 m = 4 mmm (D4h)，16阶 m
4 m
m
6 m = 6 mmm (D6h)，24阶 m
8) 转动群 n1 n 2
无极性。
⇒ ∞∞
总：29
23(T)，12阶
432(O)，24阶 23(T)，12阶
432(O)，24阶
3) n2(Dn)，2n阶 2 ⊥ n，否则将产生新的 n ）（
总Байду номын сангаас14
(12 = 2 ) 32 22 = 222 42 = 422 62 = 622
⇒ ∞2
极性：奇数群（32）垂直于主轴的方向；非极性：主轴方向，偶数群2次轴方向。（国际符号要写出所有独立的对称素，故为 222 ，而非22 ）