当前位置：文档之家 › 胶体的运动学性质布朗运动 课件 高中化学课件

胶体的运动学性质布朗运动 课件 高中化学课件

  • 格式：ppt
  • 大小：3.83 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

胶体的性质和应用PPT教学课件

胶体的性质和应用PPT教学课件
D、三氯化铁溶液中滴入氢氧化钠溶 液出现红褐色沉淀
2、下列分散系中能产生丁达
尔现象的是（ C D ）
A、食盐水
B、碘酒
C、淀粉溶液
D、氢氧化铁胶体
3、向含色素的水溶液中加入 活性炭后，一般来说，水溶液 的颜色会变浅，表示这类现象
最适宜的术语是（ C ）
A、盐析 B、乳化
C、吸附 D、凝聚
4、将某溶液滴入Fe(OH)3胶体内， 开始时产生沉淀，继续滴加时沉
昨日的习惯，已经造 就了今日的我们；今日的 习惯，决定明天的我们。 好习惯，益终生！
中学生应该拥有以下几方面的良好 习惯：
保持自己的、 • 有计划消费的习惯
• 勤于劳动的习惯
学习别人的 • 节约时间的习惯
• 卫生习惯
• 锻炼习惯 好习惯
• 学习习惯 • 处事待人习惯
读名言，谈启示。
1、吃不穷，穿不穷，算计不到一 世穷。 2、锄禾日当午，汗滴禾下土。
（3）加入与胶粒带相反电荷的胶 体：胶粒间电性相互中和，相互间 结合成大颗粒而沉降
3、应用：
（1）江河入海口沙州的形成 （2）盐析 （3）AlCl3的净水作用 （4）制豆腐 （5）使用墨水
1.下列事实与胶体性质无关的是( D)
A、在豆浆里加入盐卤做豆腐
B、河流入海处易形成沙州
C、一束平行光线照射蛋白质溶液时， 从侧面可以看到光亮的通路
谁知盘中餐，粒粒皆辛苦。 3、学会理财是每个人都必须具备 的生存技能。
读故事，谈感悟。
洛克非勒是美国著名的石油大亨， 尽管其家族非常富有，但却一直保持着 重视节俭、严格教育子女的家规。在入 学之前，父母从不给孩子零花钱，孩子 上学以后，才给他们少量的零花钱。发 给的零用钱根据年龄而变化，7-8岁时， 每周3角；11-12岁时，每周一元；13岁 以后，每周2元，每周发一次。

胶体及其性质教学PPT课件

胶体及其性质教学PPT课件
作无规则的运动。
普遍存在 的现象
.
7
布朗运动 力学性质
1827年，Brown在用显微镜观察花粉时发现花粉 颗粒不停地做无序运动。
花粉受到不同水分子的无序撞击下产生的运动 颗粒越小，温度越高，布朗运动越剧烈。
布朗运动是使该胶体微粒保持悬浮状态，并不 容易沉淀，这是胶体稳定的原因之一。
布朗运动并不是胶体特有的性质
（溶液）
（胶体）
.
3
浊液分散系 胶体分散系
颗粒直径＞100nm 1nm＜颗粒直径＜100nm
溶液分散系
颗粒直径＜1nm
.
4
原因：胶粒直径大小小于可见光的波长,胶 粒对光有散射作用；而溶液分散质的粒子太 小，不发生散射。
应用：鉴别胶体和溶液。
.
5
.
6
胶体的性质2 布朗运动（动力学性质） 在超显微镜下观察胶体溶液可以看到胶体颗粒不断地
D．全部
.
18
5.将某溶液逐滴加入到Fe(OH)3溶胶内， 开始产生沉淀，继续滴加时沉淀又溶解，该 溶液是( B )
A. 2mol/L NaOH的溶液
B. 2mol/L H2SO4的溶液 C. 2mol/L MgSO4的溶液 D. FeCl3的溶液
.
19
别能中和带有负电荷胶粒的胶体和带有正电荷
胶粒的胶体。
.
12
②加入电性相反的胶粒 破坏胶粒的带电结构
③升温 增加碰撞机会
2、胶体的应用
(1)、工业生产：石油工业中将石油乳状液中
的油水分离，冶金、水泥工业的静电除尘，工
程中泥土和泥炭的脱水，制造有色玻璃、制肥
皂等
.
13
(2)、农业生产：土壤的保肥作用，土壤里的许 多物质如黏土、腐殖质等常以胶体的形式存在

胶体的基本性质PPT课件

胶体的基本性质PPT课件

根据Donnan平衡， 脑脊液中的蛋白质含量较少，故氯化物较高
正常人脑脊液中的氯化物含量比血液高约20%左右， 但脑脊液中的氯化物浓度随血液中氯化物浓度而变；
在正常人血液中，血钠为130～150mmol/L， 血钾为3.5～5.3mmol/L，血钙为..25～2.75mmol/L， 血镁为0.75～1.25mmol/L。氯化钠是其主要成分。 为维持脑脊液与血液之间渗透压的平衡，应当及时适度补盐
↓↓
高分子和胶粒不能通过半透膜， 所以可利用此法测算高分子和稳定胶体的渗透压。
获得高分子的相对分子质量和胶体的胶束聚集数.
.
7
② 渗透的应用－－反渗透（超过滤）
利用超过渗透压的压力， 从相反方向将溶剂自溶液中压出， 称为反渗透。
↓
应用于海水淡化、浓缩溶液 （果汁、放射性污水）。
淡水井
海水在25℃时的渗透压为25 atm， 相当于210m 高水柱，
⑶ 胶体的渗透(osmosis)、渗透压与Donnan平衡
① 渗透压是稀溶液的四个依数性之一， 半透膜：只能透过溶剂、不透过溶质。 对于理想稀溶液、理想半透膜： 渗透压π服从公式： πV＝nRT, π=P2-P1
P1
纯溶剂
P2 T
溶液
.
半透膜 6
实际情况：很难找到不能透过离子的半透膜
因此无法测定盐和小分子引起的渗透压。
.
4
斐克第一定律（Fick’s first law）
设任一截面A上浓度是均匀的，垂直A方向上的浓度梯度为dc/dx 设通过A面的物质质量为m，则扩散速度为dm/dt， 它与浓度梯度和截面积A成正比。
斐克第一定律：
dm = -DA dc
dt
dx

胶体的性质及其应用-PPT课件

胶体的性质及其应用-PPT课件

由于浓差因素，膜内的电解质离子
不断向膜外渗透，经常更换外面的
溶剂，可达到净化溶胶的目的。因
此，利用渗析的方法可以达到净化、
精制胶体的目的。
氢氧化铁胶体渗析
不同直径的微粒比较
由试验可知： 悬浊液和乳浊液
微粒不能透过滤纸， 更不能透过半透膜。
胶粒却可以透过 滤纸但不能透过半膜。
溶液中的离子或 小分子既能透过滤纸， 又能透过半透膜。
二.胶体的重要性质
1.丁达尔现象
原因：胶体粒子较大(1~100nm)，对 光具有散射作 用，光在胶体的通路中出现一条明亮的光带。
记住：这是区别溶液和胶体最简单的方法！
小于1纳米时：
大于1纳米小于 100纳米时：
大于100纳米 时：
用一束强光照射大小不同微粒时的结果比较
丁达尔现象演示
NaCl 溶液
分散质：分散系中分散成微粒的物质。 分散剂：分散系中微粒分散在其中的物质。
例如：氯化钠溶液
分散剂：水 分散质：氯化钠
胶体：分散质微粒直径在1~100nm之间的分 散系（即直径在10-9至10-7米之间）。
胶体的分类： 按照分散剂的状态不同可分为：
液溶胶—— 分散剂为液体 气溶胶—— 分散剂为气体 固溶胶 —— 分散剂为固体
河海的交汇处易形成沙洲(如:长江三角洲),为什么?
课堂练习
1.下列各物质形成分散系,能发生丁达尔现象的是 AB
A. 稀盐酸滴入水玻璃溶液中
B. 牛奶
C. 蔗糖溶解在水中
D. NaCI水溶液
2.有一种橙色胶体溶液，在电泳实验中，其胶粒向阴极移动，
对这种胶粒进行下列处理，不会发生凝聚的是 BD
A. 加Na2SO4溶液 C. 加入硅酸胶体

胶体的性质及其应用ppt_图文

胶体的性质及其应用ppt_图文

胶体与浊液的区别： 将Fe(OH)3胶体和泥水分别进行过滤，可 观察到的实验现象：
过滤后的现象
Fe(OH)3胶体
没得到滤渣，滤液还是红 褐色。
泥水
在滤纸上得到泥沙，滤液 澄清、透明。
自然界的丁达尔现象
早晨的阳光射入森林的美丽景象
(自然界的丁达尔现象)
二、布朗运动
——1827年，布朗把花粉悬浮在水中，用显微镜 观察，发现花粉颗粒作不停的、无秩序的运动。
胶体微粒所带电荷来源于胶体微粒对溶液中存 在的带电微粒的吸附，一般说来具有结构上的“相似 相吸附”。
胶体的应用 ：
1、生产:土壤的保肥作用。土壤里许多物质如粘土, 腐殖质等常以胶体形式存在。 2、卫生:血液透析,血清纸上电泳，利用电泳分离各 种和蛋白质。 3、日常生活:制豆腐原理(胶体的聚沉)和豆浆、粥、 净水。
具体例子：
制豆腐的化学原理
盐卤或石膏为电解质，可使豆浆里的蛋白质胶 粒凝聚并和水等物质一起聚沉而成凝胶（豆腐）
具体例子：江河如海口形成三角洲
具体例子：明矾净水原理
[例题]自来水厂用绿矾和氯水一起净水，试用 离子方程式和简要的文字叙述原理。
分析：净水需要胶体吸附水中悬浮杂质，同时 又要进行消毒杀菌，可从这两个方面思考 解答。
胶体的性质及其应用ppt_图文.ppt
固溶胶
烟水晶
有色玻璃
胶体的性质
丁达尔效应 布朗运动 电泳 聚沉
胶体的制备
分散质粒子在1nm～100nm
之间的分散系，就叫做胶体。
注意事项： A、不能用自来水，自来水 中有电解质会使胶体发生聚 沉，应用蒸馏水。 B、FeCl3也不能过量，过量 的FeCl3也能使胶体发生聚沉 。 C、不能过度加热。 D、书写制备胶体的化学方 程式时，生成的胶体不加沉 淀符号“↓”

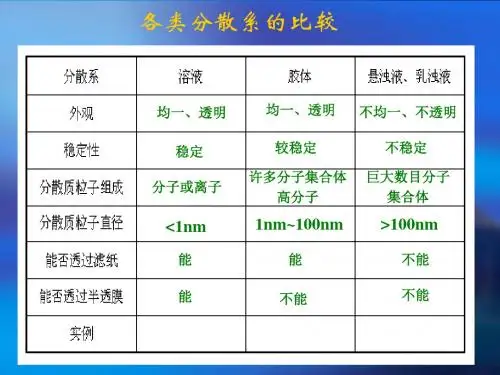
胶体的性质及应用课件

胶体的性质及应用课件

【讨论1】 胶体分散系稳定的原因？
（1）同种胶粒带同种电荷，相互排斥，不易聚沉。
（2）布朗运动克服重力作用，不易聚沉。
【讨论2】 如何破坏胶体的稳定性，使胶体粒子 聚集成大颗粒而沉淀？
5、胶体的聚沉 胶体聚沉后一般情况下都生成沉淀
胶体聚沉的方法
①加少量电解质溶液
②加带有相反电荷胶粒的胶体：互相中和电性，减小 同种电性的相互排斥而使之聚成大颗粒。 ③加热：温度升高，胶粒碰撞速率加快，从而使小颗 粒成为大颗粒而聚沉。
2.胶体粒子直径 较浊液粒子小
能透过滤纸
布朗运动
吸附离子
(带电)
通直流电
中和电荷
比浊液 稳定
电泳
沉聚
常见的胶体
(1)FeCl3溶液，Al2(SO4)3溶液，Fe3+，Al3+水解形成 Fe(OH)3和Al(OH)3胶体
(3)肥皂水，C17H35COO-水解生成硬脂酸胶体 C17H35COO-＋H2O == C17H35COOH(胶体)＋OH-
1、工业除杂、除尘 2、土壤的保肥作用
［例题1］已知土壤胶粒带负电，在土壤里施用含 氮量相等的下列肥料，肥效较差的是
A. （NH4）2SO4 C. NH4NO3
B. NH4HCO3 D. NH4Cl
3、制豆腐的化学原理
盐卤或石膏为电解质，可使豆浆里 的蛋白质胶粒凝聚并和水等物质一起聚 沉而成凝胶（豆腐）
(4)淀粉溶液，蛋白质溶液 (5)江河之水，自然水中除海水，地下水等不是胶体外，
多为胶体。在江河入海口处与海水相遇时胶体凝聚 而形成三角沙洲。 (6)烟、云、雾 (7)血液、墨汁
各类分散系的比较
均一、透明
均一、透明 不均一、不透明

高一化学胶体课件

达到提纯的目的。
胶体制备与提纯的注意事项
注意安全
在制备和提纯过程中，应避免使用有 毒有害的试剂，并确保操作安全。
控制条件
制备和提纯过程中，应控制好温度、 压力、浓度等条件，以保证实验结果 的准确性和可靠性。
实验操作规范
在实验过程中，应遵循实验操作规范 ，避免污染和交叉污染。
实验后处理
实验结束后，应对废液进行妥善处理 ，避免对环境和人体造成危害。
胶体在医学中的应用
胶体在医学中也有着重要的应 用，如医用胶、血液透析等。
医用胶是一种常用的外科手术 材料，具有快速止血、促进伤 口愈合等作用，广泛应用于手 术和创伤治疗中。
血液透析则是利用胶体的渗透 作用，将血液中的毒素和多余 水分滤出，以治疗肾功能衰竭 等疾病。
胶体在其他领域的应用
除了化学工业和医学领域，胶体 在其他领域也有着广泛的应用。
如胶体在环保领域中可以用于污 水处理、土壤修复等；在农业领 域中可以用于农药和肥料的缓释
剂等。
此外，胶体还在化妆品、食品、 墨水等领域中有着广泛的应用， 如隐形眼镜护理液、墨水等产品
中都含有胶体成分。
05
胶体的实验研究
胶体实验的目的与原理
目的
通过实验了解胶体的性质和特点，加深对胶体概念的理解。
原理
胶体是一种分散质粒子直径在1nm-100nm之间的分散系，具有介稳性、丁达 尔效应等特点。实验通过观察胶体的电泳、聚沉等性质，探究胶体的本质。
实验步骤与操作方法
步骤一
制备胶体。将一定量的Fe(OH)3固体溶解在沸水中，得到Fe(OH)3胶体。
步骤二
进行电泳实验。将胶体置于电场中，观察胶体粒子在电场中的移动情况。
氧化铝等。

胶体及其性质ppt课件

2021/4/18
一、胶体的性质
1、丁达尔效应： 光束通过胶体，形成光亮的“通路” 的现象，叫丁达尔效应。
注意：它是胶体特有的性质，可用来鉴别胶体和 其他分散系。
2、布朗运动：胶体分散质粒子作不停的，无秩序的运 动，叫布朗运动。
3、电泳现象：在外加电场作用下，胶体粒子在分散剂 里向电极（阴极或者阳极）作定向移动的现象。
2021/4/18
二、胶 体
1、胶体的外观：类似于溶液，多数均一、透明 2、胶体分散质的构成：
⑴小粒子聚集到在一起形成分散质粒子(Fe(OH)3胶体) ⑵大分子直径达到胶体粒子大小的限度(蛋白质胶体)
3、胶体的分类：（按照分散剂的不同）
胶体
液溶胶 （分散剂是液体如Fe(OH)3胶体） 气溶胶 （分散剂是气体如雾、云、烟）
⑴小粒子聚集到在一起形成分散质粒子(Fe(OH)3胶体) ⑵大分子直径达到胶体粒子大小的限度(蛋白质胶体)
3、胶体的分类：（按照分散剂的不同）
胶体
液溶胶 （分散剂是液体如Fe(OH)3胶体） 气溶胶 （分散剂是气体如雾、云、烟）
固溶胶 （分散剂是固体如烟水晶、有色玻璃）
4、Fe(OH)3胶体的制备：
注意：它是胶体特有的性质，可用来鉴别胶体和 其他分散系。 2、布朗运动：胶体分散质粒子作不停的，无秩序的运
动，叫布朗运动。 3、电泳现象：在外加电场作用下，胶体粒子在分散剂
里向胶体粒子带相同的电荷。一般来 说： 带正电荷：金属氧化物、金属氢氧化物。
胶体（分散质粒子在1nm--100nm之间）
注 ⑴对于溶液溶质是分散质，溶剂是分散剂。溶 意 质、溶剂的概念只适用于溶液，不适用于其他
分散系。
⑵导致三种分散系性质不同的根本原因就是分 散质粒子大小的不同。

胶体的动力学性质.ppt



a X

a M

a X
设浓度很稀： x zm1 x m2 x2
x
m22
zm1 2m2
16
7.5 Donnan (陶南) 平衡
MX膜外 MX膜内
MX MX
m2 -x x
1
zm1 m2
讨论：
① 由于大离子的存在, 平衡时膜内外的MX浓度不等, 将产生
单位体积中的粒子数
高度越高，质量越小的粒子越多 高度越低，质量越小的粒子越少
7.3.2 离心力场中的沉降 (1) 沉降速度
离心力：mx 2
浮力：
阻力： f dx dt
ω - 角速度 11
7.3 沉降
沉降力：
匀速沉降：
V - 粒子偏微比容
m - 粒子质量
kT dx D dt
♦ 定义： 沉降系数
**
比较*和**式得： X 2 2Dt X = 2DT
♦ 扩散和布朗运动的内在联系： 扩散是布朗运动的宏观表现 布朗运动是扩散的微观基础 6
7.2 扩散
7.2.4 Einstein 扩散方程 粒子移动距离： dx
做功： f dx dx dt
反抗阻力： f dx dt
应等于化学势的变化
d= kTd ln c= f dx dt dx = kT d ln c = kT dc *
f : 微观量, 与粒子大小和形状有关.
7.2.5 扩散的应用举例
测定球形质点的半径和粒子量
D KT f
f = 6r
测出 D 而得 r
粒子量： M = 4 r3 NA
3V
V - 粒子的偏微比容
◊ 所测质点的半径为流体力学半径

2021物理化学第九章胶体PPT优秀资料


按胶体溶液的稳定性分类
3）按胶体溶液的稳定性分类
憎液溶胶 半径在1 nm~100 nm之间的难溶物固体粒子 分散在液体介质中，有很大的相界面，易聚沉，是 热力学上的不稳定体系。 一旦将介质蒸发掉，再加入介质就无法再形 成溶胶，是 一个不可逆体系，如氢氧化铁溶胶、 碘化银溶胶等。 这是胶体分散体系中主要研究的内容。
胶粒的结构
胶核吸附离子是有选择性的，首先吸附与胶核中 相同的某种离子，用同离子效应使胶核不易溶解。
若无相同离子，则首先吸附水化能力较弱的负 离子，所以自然界中的胶粒大多带负电，如泥浆水、 豆浆等都是负溶胶。
胶粒的结构
例1：AgNO3 + KI→KNO3 + AgI↓ 胶团的图示式：
过量的 KI 作稳定剂胶团的结构表
当半径大于5 m，Brown运动消失。
Brown运动
Brown运动
Einstein认为，溶胶粒子的Brown运动与分子运动类
似，平均动能为3/2 kT 。并假设粒子是球形的，运用分
子运动论的一些基本概念和公式，得到Brown运动的公式
为：
1
xRLT3tr 2
物理化学第九章胶 体
第九章 胶体化学
9.1分散体系 9.2 溶胶的制备与净化 9.3 溶胶的光学性质 9.4 溶胶的动力学性质 9.5 溶胶的电学性质 9.6 溶胶的流变性质
9.7溶胶稳定性与聚沉
乳状液 大分子概说 大分子的相对摩尔质量 Donnan平衡
一、胶体及其根本特性
1.分散相与分散介质 分散体系分类
（1）当光束通过粗分散体系，由于粒子大于入射 光的波长，主要发生反射，使体系呈现混浊。
（2）当光束通过胶体溶液，由于胶粒直径小于可 见光波长，主要发生散射，可以看见乳白色的光柱。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

作业
1、完成课后习题P29 1、4、5、6 2、家庭小实验：自制豆腐
取适量石膏粉（聚沉剂）用少量生豆浆调拌 均匀，加到煮沸后的豆浆（所用豆浆与石膏 的质量比约为20：1）中，边加边搅拌，豆浆 中的蛋白质会聚沉，与水分离，成豆腐花。 稍冷后，用一湿布包好豆腐花，放入一可漏 水的容器中，稍加压，使水渗出，即成豆腐。
3、“纳米材料”是粒子直径为1~100nm的 材料，纳米碳就是其中一种，若将纳米碳均 匀地分散到蒸馏水中，所形成的物质（ ） C
①是溶液 ②是胶体 ③能产生丁达尔 效应 ④能透过滤纸 ⑤不能透过滤纸 ⑥静置后会析出黑色沉淀
A.①④⑤ D.①③④⑥ B.②③④ C.②③⑤
把混有离子或分子杂质 的胶体装入半透膜袋， 并浸入溶剂中，使离子 4、下列关于胶体的叙述中，不正确的是 或分子从胶体里分离出 （ A ） 去，这样的操作叫做渗 A.向胶体中加入蔗糖溶液，产生聚沉现象 析。通过渗析可以达到 B.一束可见光透过胶体时，产生丁达尔效应 净化、精制胶体的目的
6、Fe(OH)3胶体带正电荷的原因是（ D ） A.在电场作用下， Fe(OH)3胶粒向阴极定向移动 B.Fe3+带正电荷 C.Fe(OH)3带负电荷，吸引阳离子 D.Fe(OH)3胶粒吸附了阳离子 7、在Fe(OH)3胶体中加入Na2SO4饱和溶液，由 SO42- 离子的作用，使胶体形成了沉淀，这 于_______ 凝聚或聚沉 个过程称为_______
2. 胶体的运动学性质——布朗运动
1827年，英国植物学家布 朗把花粉悬浮在水里，用 显微镜观察，发现花粉的 小颗粒在作不停的、无秩 序的运动，这种现象叫做 布朗运动 胶体粒子在分散剂分子的撞击下做无规则运 动，是胶体具有介稳性的次要原因。
注意：凭借肉眼可以看到的微粒的运动不是补朗 运动，如：尘土飞扬、红墨水扩散等。
淀粉溶液、豆浆、蓝黑墨水、 牛奶、血液、黄河水 大气中的飘尘、工厂废气中固体悬物、 纺织厂食品厂弥漫于空气中的有机纤维 或颗粒，矿山开采的粉尘、烟、云、雾 . 有色玻璃 一些纳米材料
2、胶体的应用
（1）石膏或卤水点豆腐、制造果冻 （2）明矾净水原理 （3）江河入海处形成沙洲三角洲 （4）使用蓝色墨水的钢笔抽黑色墨水容易堵塞 （5）喝豆浆放糖不放盐 （6）FeCl3溶液用于伤口止血。 （7）冶金厂大量烟尘用高压电除去。 （8）土壤胶体中离子吸附和交换过程，保肥作 用。 ……
C.用渗析的方法“净化”胶体时，使用的半 透膜只能让分子通过 D.胶体能够吸附阴离子和阳离子，故在电场 的作用下，会产生电泳现象
5、不能用胶体的知识解释的现象是（ C ） A.豆浆中加入石膏做豆腐 B.一支钢笔使用两种不同牌号的墨水，易 出现堵塞 C.向FeCl3溶液中加入NaOH溶液，会出现 红褐色 D.在海水与河水交界处，易形成三角洲
3、胶体的电学性质----电泳现象
在外加电场作用下，胶体粒子在分 ——胶体稳定的主要原因 散剂里向电极（阴极或阳极）做定 胶粒带电，吸附离子； 向移动的现象，叫做电泳。 同种胶粒吸附同种离子，相互排斥。
结论：胶体粒子带电。
规律：金属氧化物、金属氢氧化物的胶体粒 子带正电荷，非金属氧化物、金属硫化物、 土壤、血液、硅酸胶体粒子带负电荷。 带电原因：胶粒具有较大表面积能吸附带电 微粒。（应用：作净水剂）
思考 胶体为什么具有介稳性？
主要原因 胶体粒子可以通过吸附离子
而带有电荷，同种胶粒带同种电荷，而 同种电荷会相互排斥，所以胶体难聚沉。 次要原因 胶体粒子在不停的做布朗运动
五、常见胶体及其应用：
1、常见胶体
烟、云、雾 、有色玻璃、淀粉溶液、豆浆、蓝黑 墨水、牛奶、血液、黄河水、大气中的飘尘、工厂废 气中固体悬物、矿山开采的粉尘、纺织厂或食品厂弥 漫于空气中的有机纤维或颗粒、纳米材料等。 胶 体 的 分 类 液溶胶 气溶胶 固溶胶
小结：
（1）分散系、分散质、分散剂的概念
（2）制备胶体
FeCl3＋3H2O
Fe(OH)3（胶体）＋3HCl
（3）胶体的性质：丁达尔效应、布朗 运动、电泳现象、介稳性和凝聚现象 （4）胶体的应用
练习：
1、胶体和其它分散系的本质区别是（ A ） A.分散质粒子的大小 B.是不是一种稳定的体系 C.会不会产生丁达尔效应 D.粒子有没有带电荷 2、下列分散系中分散质的微粒直径属于纳 米级的是（ C ） A.溶液 D.乳浊液 B.悬浊液 C.胶体
应用：用于高压除尘、疾病检测等。
4、胶体的介稳性和凝聚现象
向胶体中加入少量电解质溶液时，由于加 入的阳离子（或阴离子）中和了胶体粒子 所带的电荷，使胶体粒子聚集成为较大的 颗粒，从而形成沉淀从分散剂里析出，这 个过程叫做聚沉，如：石膏或卤水点豆腐、 FeCl3溶液用于伤口止血等。 胶体凝聚的方法： （1）加热 （2）加电解质溶液（3）加带 相反电荷的胶体（破坏胶粒结构，不可逆）
8、胶体和其他分散系（溶液、浊液）的本质区 别是（ A ） A、分散质粒子的大小 B、是不是一种稳定的体系 C、会不会产生丁达乐效应 D、粒子有没有带电荷 9、以水为分散剂的分散系，按稳定性由弱到强 顺序排列的是( B ) A、溶液、胶体、浊液 B、浊液、胶体、溶液 C、胶体、浊液、溶液 D、浊液、溶液、胶体