第十五章工具变量估计与TSLS-3

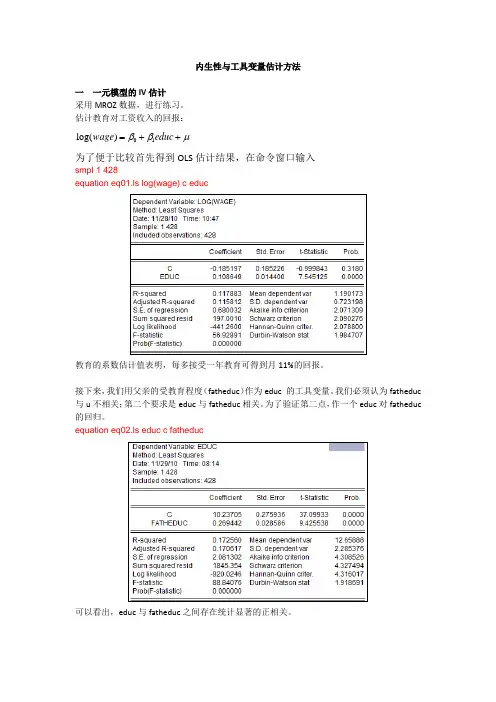
内生性与工具变量估计方法一 一元模型的IV 估计采用MROZ 数据，进行练习。

估计教育对工资收入的回报：01log()wage educ ββμ=++为了便于比较首先得到OLS 估计结果，在命令窗口输入smpl 1 428equation eq01.ls log(wage) c educ教育的系数估计值表明，每多接受一年教育可得到月11%的回报。

接下来，我们用父亲的受教育程度（fatheduc ）作为educ 的工具变量。

我们必须认为fatheduc 与u 不相关；第二个要求是educ 与fatheduc 相关。

为了验证第二点，作一个educ 对fatheduc 的回归。

equation eq02.ls educ c fatheduc可以看出，educ 与fatheduc 之间存在统计显著的正相关。

采用fatheduc 作为educ 的工具变量，进行工具变量回归。

equation eq03.tsls log(wage) c educ @ fatheducIV 估计量的标准误是OLS 标准误的2.5倍，这在我们的意料之中。

二 多元模型的IV 估计 采用card 数据，进行练习。

估计教育对工资收入的回报：012log()var wage educ Control iables βββμ=+++为了便于对照，先做OLS 回归 Smpl 1 3010Equation eq01.ls log(wage) c educ exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669在这个例子中，受教育程度的工具变量是标志着一个人是否在一所四年制大学附近成长的虚拟变量(nearc4)。

为了验证受教育程度与该虚拟变量的偏相关性，先做educ对nearc4以及其他所有外生变量的回归：Equation eq02.ls educ c nearc4 exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669Nearc4的系数估计值意味着，在其他因素固定的情况下，曾住在大学附近的人所受的教育比不在大学附近长大的人平均多出约1/3年。

工具变量法一、工具变量法的主要思想在无限分布滞后模型中，为了估计回归系数，通常的做法是对回归系数作一些限制，从而对受限的无限分布滞后模型进行估计。

在这里，考伊克模型、适应性期望模型与部分调整模型给出了很好的解决此类问题的思路。

经过变换，新的模型中，随机扰动项的表达式为：考伊克模型：1t t t v u u λ-=- （01λ<< ，λ为衰减率） （1.1）； 适应性期望模型：1（1）t t t v u u λ-=--（01λ<< ，λ为期望系数）（1.2）；部分调整模型：（1）t t v u γ=-（01γ≤< ，1γ-为调整系数） （1.3）。

t u 为原无限分布滞后模型中的扰动项，t v 为变换后的扰动项。

在原模型中的随机扰动项满足经典假设的前提下，部分调整模型也满足经典假设，但是考伊克模型与适应性期望模型的随机扰动项由于存在原随机扰动项的滞后项，也就是说考伊克模型与适应性期望模型的解释变量1t Y - 势必与误差项t v 相关，因此，可能会出现上述两个模型的最小二乘估计甚至是有偏的这样严重的问题。

那么，我们是否可以找到一个与1t Y -高度相关但与t v 不相关的变量来替代1t Y -？在这里，一个可行的估计方法就是工具变量法。

在讨论工具变量法之前，我们先来了解一下外生变量和内生变量。

一般来说：一个回归模型中的解释变量有的与随机扰动项无关，我们称这样的解释变量为外生变量；而模型中有的解释变量与随机扰动项相关，我们可称这样的解释变量为内生解释变量。

内生解释变量的典型情况之一就是滞后应变量为解释变量的情形，如上述考伊克模型与适应性期望模型中的1t Y -。

外生解释变量：回归模型中的解释变量与随机扰动项无关； 内生解释变量：回归模型中的解释变量与随机扰动项无关；了解了内生变量和外生变量的概念，我们接着讨论工具变量法的主要思想：工具变量法和普通最小二乘法是模型参数估计的两类重要方法，在多元线性回归模型中，如果出现解释变量与随机误差项相关（即出现内生变量）时，其回归系数的普通最小二乘估计是非一致的，这时就需要引入工具变量。

实证研究中常见的5种工具变量（好用）/ 工具变量（instrumental variable）是社会科学定量分析中解决内生性问题的重要手段,是基于调查数据进行因果推断的前沿方法。

本文在简要介绍工具变量的定义、原理及估算方法的基础上,对实证分析中较为常见的五类工具变量进行回顾梳理,为今后研究寻找工具变量提供了参考。

同时,对工具变量估计量的权重性特征进行了阐述,并结合实例展示了使用工具变量进行因果推断的基本步骤和要点。

最后,就工具变量方法的潜力和局限性进行了剖析。

因果推断的圣杯在反事实因果的框架之下，基于调查数据的社会学定量分析要进行因果推断，难度极大。

其主要原因在于，社会学家一旦要证明某个他们所感兴趣的“因”会带来一定的“果”，就必须面对一个永恒挑战:“内生性”问题( endogeneity) 。

也即: 如果某个潜在的、无法观测的干扰项，既影响“因”，又影响“果”，那么，利用最小二乘法模型( 简称OLS模型) 进行回归分析所得到的估计量就会是有偏误的，而不具有因果推断力。

在实证分析中，无论是经典的教育回报研究( Card，1999)，还是我国学界非常关注的关系网、社会资本研究( Mouw， 2003， 2006; 陈云松、范晓光，2010，2011) ，内生性问题都极为重要且亟待解决。

解决内生性问题的常见方法，主要包括工具变量( instrumental variable，简称IV) 、固定效应模型( fixed effects model，简称FE) 、倾向值匹配( propensity score matching，简称PSM) 、实验以及准实验( experimentsand quasi-experiments) 等等。

近年来，其中不少方法已经逐步在我国社会学界得到评述和应用( 梁玉成， 2010; 陈云松、范晓光， 2010， 2011; 陈云松， 2012; 胡安宁，2012; 魏万青，2012) 。

两阶段最小二乘回归Contents1背景 (3)2理论 (4)3操作 (4)4 SPSSAU输出结果 (5)5文字分析 (6)6剖析 (9)TSLS是用于解决内生性问题的一种方法，除TSLS外还可使用GMM估计。

内生变量是指与误差项相关的解释变量。

对应还有一个术语叫‘外生变量’，其指与误差项不相关的解释变量。

产生内生性的原因通常在三类，分别说明如下：内生性问题的判断上，通常是使用Durbin-Wu-Hausman检验（SPSSAU在两阶段最小二乘回归结果中默认输出），当然很多时候会结合自身理论知识和直观专业性判断是否存在内生性问题。

如果假定存在内生性问题时，直接使用两阶段最小二乘回归或者GMM估计即可。

一般不建议完全依照检验进行判断是否存在内生性，结合检验和专业理论知识综合判断较为可取。

内生性问题的解决上，通常使用工具变量法，其基本思想在于选取这样一类变量（工具变量），它们的特征为：工具变量与内生变量有着相关(如果相关性很低则称为弱工具变量)，但是工具变量与被解释变量基本没有相关关系。

寻找适合的工具变量是一件困难的事情，解决内生性问题时，大量的工作用于寻找适合的工具变量。

关于引入工具变量的个数上，有如下说明：过度识别和恰好识别是可以接受的，但不可识别这种情况无法进行建模，似想用一个工具变量去标识两个内生变量，这是不可以的。

另需要提示，如果是恰好识别状态下是无法进行Durbin-Wu-Hausman检验。

工具变量引入时，有时还需要对工具变量外生性进行检验（过度识别检验），针对工具变量外生性检验上，SPSSAU默认提供Sargan检验和Basmann检验。

特别提示，只有过度识别时才会输出此两个检验指标。

关于两阶段最小二乘法的原理上，其将估计分成两个步骤（阶段）回归。

如下表格说明：第一阶段回归结果为中间过程值，SPSSAU默认没有输出；第二阶段回归结果为最终结果值。

特别提示：●内生性问题涉及以下几点，分别是内生变量判断（Durbin-Wu-Hausman检验和理论判断），内生性问题的解决（两阶段最小二乘回归TSLS或GMM），工具变量引入后过度识别检验（Sargan检验和Basmann检验）等。

工具变量法代码工具变量法（Instrumental Variables，简称IV）是一种常用的估计因果效应的方法。

它主要针对的是存在内生性问题的经济学模型，如回归分析中的自变量与误差项存在相关关系。

下文将介绍工具变量法的基本原理，以及其在实践中的使用方法和代码实现。

一、基本原理工具变量法的基本思想是利用一个或多个与内生性自变量相关但不受误差项影响的外生性变量（即工具变量）来代替内生性自变量，在保证模型符合经济学意义的前提下，得到更精确的因果效应估计。

具体来说，对于回归模型：y = α + βx + u其中，x为内生性自变量，u为误差项，我们考虑引入一个外生变量z作为工具变量，那么可以构建如下两个求解方程：x = δ + ρz + vy = α + β(δ + ρz + v) + u其中，δ和ρ是未知的系数。

第一个方程是用工具变量估计内生性自变量的回归式，第二个方程则是运用估计出的内生性自变量对y进行回归。

对于外生性工具变量z，我们可以假定它只会通过自变量x对y产生影响，而不会通过误差项u对y产生影响，即：Cov(z,u) = 0而通过IV估计，我们可以得到内生性自变量x在z上的部分效应（partial effect），从而得出因果效应的估计。

二、实践应用在实践中，工具变量法常常被用来研究各种经济学问题。

例如，研究教育水平对收入的影响、研究医疗保险对医疗消费的影响等。

下面以一个简单的例子来说明如何使用工具变量法。

假设我们想研究家庭收入对孩子的大学入学率的影响，但是我们发现家庭收入存在内生性问题，因为它与其他一些难以观测的因素（如家庭背景、社会阶层等）存在相关关系。

我们考虑使用父母的教育水平和收入作为工具变量，来估计家庭收入与大学入学率之间的因果关系。

代码实现在工具变量法的实现中，常常需要用到Python中的statsmodels（回归模型和统计测试）和pandas（数据处理）两个库。

我们假设有如下数据集：- family_income：家庭收入（千元） - education：父母教育水平（0-未受过教育，1-小学，2-初中，3-高中，4-大学） - college：是否考入本科（0-否，1-是）- random_var：随机变量，用于混淆我们首先看一下家庭收入与大学入学率是否存在内生性问题，可以通过构建回归模型来检验：import statsmodels.api as sm import pandas as pddf = pd.read_csv('data.csv')x = df[['family_income']] y = df[['college']] x = sm.add_constant(x) results = sm.OLS(y, x).fit() print(results.summary())运行上述代码后，我们可以得到回归模型的结果，其中P值可以判断内生性是否显著。

伍德里奇《计量经济学导论》（第5版）笔记和课后习题详解-第15章工具变量估计与两阶段最小二乘法【圣第15章工具变量估计与两阶段最小二乘法15.1复习笔记一、动机：简单回归模型中的遗漏变量1．面对可能发生的遗漏变量偏误（或无法观测异质性）的四种选择（1）忽略遗漏变量问题，承受有偏而又不一致估计量，若能把估计值与关键参数的偏误方向一同给出，则该方法便令人满意。

（2）试图为无法观测变量寻找并使用一个适宜的代理变量，该方法试图通过用代理变量取代无法观测变量来解决遗漏变量的问题，但并不是总可以找到一个好的代理。

（3）假定遗漏变量不随时间变化，运用固定效应或一阶差分方法。

（4）将无法观测变量留在误差项中，但不是用OLS 估计模型，而是运用一种承认存在遗漏变量的估计方法，工具变量法。

2．工具变量法简单回归模型01y x uββ=++其中x 与u 相关：()Cov 0，x u ≠（1）为了在x 和u 相关时得到0β和1β的一致估计量，需要有一个可观测到的变量z，z 满足两个假定：①z 与u 不相关，即Cov（z，u）＝0；②z 与x 相关，即Cov（z，x）≠0。

满足这两个条件，则z 称为x 的工具变量，简称为x 的工具。

z 满足①式称为工具外生性条件，工具外生性意味着，z 应当对y 无偏效应（一旦x 和u 中的遗漏变量被控制），也不应当与其他影响y 的无法观测因素相关。

z 满足②式意味着z 必然与内生解释变量x 有着或正或负的关系。

这个条件被称为工具相关性。

（2）工具变量的两个要求之间的差别①Cov（z，u）是z 与无法观测误差u 的协方差，通常无法对它进行检验：在绝大多数情形中，必须借助于经济行为或反思来维持这一假定。

②给定一个来自总体的随机样本，z 与x（在总体中）相关的条件则可加以检验。

最容易的方法是估计一个x 与z 之间的简单回归。

在总体中，有01x z vππ=++从而，由于()()1Cov /ar V ，x z z π=所以式Cov（z，x）≠0中的假定当且仅当10π≠时成立。

工具变量法工具变量法具体步骤工具变量法目录概念某一个变量与模型随机解释变量高度相关，但却不与为丛藓科扭口藓项相关，那么就可以用此变量与模型中相应回归系数的一个一致估计量，这个变量就称为方法变量，这种估计方法就叫工具基本原理变量法。

缺点工具变量法的关键是选择一个有效的优先选择工具变量，由于工具自变量变量可以选择中的困难，工具变量法本身存在两方面不足：一是由于工具变量不是惟一的，因而工具变量估计量有一定的任意性；其二由于误差项实际上是不可观测的，因而要寻找严格意义上与误差项无关的与所替代而随机解释变量高度相关的变量总的来说事实上是困难的。

工具变量法与内生解释变量可持续性解释变量会造成解读严重的后果：不一致性inconstent 和有偏biased ，因为频域不满足误差以解释线性为条件的期望值为0。

产生解释变量招盛纯一般有三个原因：一、遗漏变量二、测量误差三、联立性第三种情况是无法逐步解决的，前两种可以采用工具变量（IV ）法。

IV 会带来的唯一坏处是估计方差的增大，也就是说同时采用OLS 和IV 估计，则前者的方差小于后者。

但IV 的应用是有前提条件的：1.IV 与内生解释函数相关，2.IV 与u 不相关。

在小样本情况下，一般用内生解释变量对IV 进行回归，如果R －sq 值很小的话，一般t值也很小，所以对IV 质量的评价没有大的风险问题，但是当采用大样本时，情况则相反，往往是t 值很大，而R －sq 很小，这时如果采用t 值进行关键问题评价则可能出现出现问题。

这时IV 与内生解释变量之间的若干程度不是阐释太大，但是如果与u 之间有轻微的相关机构的话，则：1、导致很小的不一致性；2、有偏性，并且这种有偏性随着R －sq趋于0而趋于OLS 的有偏性。

所以现在在采用IV 时最好采用R －sq 或F －sta 作为评价标准，另外为了观测IV 与u 的关系，可以将IV 作为解释变量放入方程进行回归，如果没有其他的系数没有多的变化，则说明IV 满足第二个条件。

工具变量法 GMM估计1 OverviewModel过程可以分析线性、非线性（对参数或者对变量）的单方程和方程组。

使用的估计方法有：OLS, 2SLS, SUR, ITSUR, 3SLS, IT3SLS,GMM ,FIML。

MODEL过程分析的模型如下：这里，Y是内生变量，X是外生变量，TEHTA是参数。

观测到的变量要么是内生变量，要么是外生变量。

上面的方程组可以简写为：这个形式称为一般形式。

还可以写成标准形式：标准形式把内生变量放在方程的一边。

两种形式的方程（组）都可以使用MODEL过程估计。

经常用当前外生变量、滞后的外生变量、滞后的内生变量来解释当前内生变量。

这就构成了一个动态模型。

滞后变量不论内生还是外生都看作外生变量。

以上并不要求扰动项独立同分布。

自相关、异方差甚至不同的分布都有可能。

对于异方差可以使用加权估计，GARCH模型也可以修正异方差。

如果难以确定异方差的来源和形式，难以确定权重变量的话，可以使用GMM方法得到比OLS方法更加有效的估计。

方程组一个常见的问题就是联立偏倚。

考虑：这个方程组对参数是非线性的，不能使用线性回归估计。

同时这里Y1和Y2是同时决定的，普通非线性最小二乘方法的结果也是有偏和非一致的。

这称为联立性偏倚。

在线性模型中，处理联立性偏倚的可以把出现在方程右边的内生变量换成其预测值。

预测值与扰动项无关从而消除了联立性偏倚。

预测值是通过工具变量法估计得到的，这称为第一步回归。

利用预测值进行第二次回归称为两段最小二乘。

在非线性模型中，使用线性近似，把非线性方程组线性化后使用工具变量法，反复迭代。

在方程组中，方程之间的扰动项可能相关。

对于大样本情况，可以使用系统方法考虑到方程内和方程之间关系得到更有效的估计。

如果不存在联立性问题，即不存在内生变量作为解释变量的话，可以使用SUR估计。

SUR方法需要估计方程之间扰动项的协方差矩阵∑。

估计步骤为先使用OLS估计方程组，从残差得到∧∑，然后使用SUR。

工具变量法（Instrumental Variables Method）是一种用于解决因果关系分析中的内生性问题（Endogeneity Problem）的方法。

在工具变量法中，我们使用一个或多个与内生解释变量相关，但与误差项无关的工具变量来估计因果效应。

关于工具变量法的系数，这里以二阶段最小二乘法（Two-Stage Least Squares）为例进行说明。

在二阶段最小二乘法中，我们首先使用工具变量和内生解释变量来预测内生解释变量的值，然后使用这个预测值和工具变量以及其他外生解释变量来进行回归分析，以估计因果效应。

假设我们的模型是：Y = β0 + β1*X + ε。

其中，X是内生解释变量，Y是因变量，ε是误差项。

我们选择了一个工具变量Z，它与X相关，但与误差项无关。

首先，我们使用Z和其他外生解释变量来预测X的值，得到预测值X_hat。

然后，我们在第二阶段进行回归分析，使用Y对X_hat和其他外生解释变量进行回归。

这个回归的系数就是我们想要估计的因果效应。

需要注意的是，工具变量必须满足与内生解释变量相关，但与误差项无关的条件。

否则，工具变量法将无法准确估计因果效应。

同时，
工具变量的选择也需要有一定的理论依据和实际背景的支持。

经济数据的特点与类型。

1、横截面数据：多个经济个体的变量在同一时间点上的取值，如2012年中国各省的GDP2、时间数列数据：指的是某个经济个体的变量在不同时点上的取值，如1978-2012年山东省每年的GDP3、面板数据：多个经济个体的变量在不同时点上的取值，如1978-2012年中国各省的GDP 小样本OLS（最小二乘法）：单一方程线性回归最常见方法条件：解释变量与扰动项正交、扰动项无自相关、同方差。

拟合优度：衡量线性回归模型对样本数据的拟合程度（R2），越高说明模型拟合程度越好。

单系数T检验：对回归方程扰动项的具体概率进行假设显著性水平进行检验F检验：整个回归方程是否显著STATA操作简介：如果数据中包含1949-10-01或1949/10/01的时间变量，导入stata后可能会被视为字符串，因此对于日度数据，可以使用命令gen newvar=date(varname,YMD),将其转换为整数日期变量，其中YMD说明原始数据的格式为年月日，如果原始数据的格式为月日年则使用MDY；对于月度数据则gen newvar=monthly(varname,YM)。

.describe：数据的概貌.drop keep：删除和保留.su：统计特征Pwcorr：变量之间相关系数Star（.05）：5%显著性水平gen:产生g intc=log（tc）：取自然对数. reg：OLS回归.Vce：协方差矩阵reg。

，noc表示在进行回归时不要常数项大样本OLS：只要求解释变量与同期的扰动项正交即可Robust：稳健标准误，如果存在异方差，则应使用稳健标准误最大似然估计法：如果回归方程存在非线性，则使用最大似然估计法（MLE ）或非线性最小二乘法（NLS ）三类在大样本下渐进等价的统计检验：Wald test LR （似然比检验） LM操作步骤如下：sysuse auto （调用数据集）Hist mpg ，normal （画变量mpg 的直方图，并与正态密度比较）直方图显示，变量mpg 的分布于正态分布有一定差距。