尺寸链计算及例题解释
- 格式:ppt
- 大小:1.92 MB
- 文档页数:10







尺寸链计算(带实例)尺寸链的计算一、尺寸链的基本术语:1.尺寸链——在机器装配或零件加工过程中,由相互连接的尺寸形成封闭的尺寸组,称为尺寸链。
如下图间隙A0与其它五个尺寸连接成的封闭尺寸组,形成尺寸链。
2.环——列入尺寸链中的每一个尺寸称为环。
如上图中的A0、A1、A2、A3、A4、A5都是环。
长度环用大写斜体拉丁字母A,B,C……表示;角度环用小写斜体希腊字母α,β等表示。
3.封闭环——尺寸链中在装配过程或加工过程后自然形成的一环,称为封闭环。
如上图中A0。
封闭环的下角标“0”表示。
4.组成环——尺寸链中对封闭环有影响的全部环,称为组成环。
如上图中A1、A2、A3、A4、A5。
组成环的下角标用阿拉伯数字表示。
5.增环——尺寸链中某一类组成环,由于该类组成环的变动引起封闭环同向变动,该组成环为增环。
如上图中的A3。
6.减环——尺寸链中某一类组成环,由于该类组成环的变动引起封闭环的反向变动,该类组成环为减环。
如上图中的A1、A2、A4、A5。
7.补偿环——尺寸链中预先选定某一组成环,可以通过改变其大小或位置,使封闭环达到规定的要求,该组成环为补偿环。
如下图中的L2。
二、尺寸链的形成为分析与计算尺寸链的方便,通常按尺寸链的几何特征,功能要求,误差性质及环的相互关系与相互位置等不同观点,对尺寸链加以分类,得出尺寸链的不同形式。
1.长度尺寸链与角度尺寸链①长度尺寸链——全部环为长度尺寸的尺寸链,如图1②角度尺寸链——全部环为角度尺寸的尺寸链,如图32.装配尺寸链,零件尺寸链与工艺尺寸链①装配尺寸链——全部组成环为不同零件设计尺寸所形成的尺寸链,如图4②零件尺寸链——全部组成环为同一零件设计尺寸所形成的尺寸链,如图5③工艺尺寸链——全部组成环为同一零件工艺尺寸所形成的尺寸链,如图6。
工艺尺寸指工艺尺寸,定位尺寸与基准尺寸等。
装配尺寸链与零件尺寸链统称为设计尺寸链。
3.基本尺寸链与派生尺寸链①基本尺寸链——全部组成环皆直接影响封闭环的尺寸链,如图7中尺寸链β。

一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中,由相互联系的尺寸,按一定顺序排列成的封闭尺寸组,称为尺寸链。
尺寸链示例2、工艺尺寸链的组成环:工艺尺寸链中的每一个尺寸称为尺寸链的环。
工艺尺寸链由一系列的环组成。
环又分为:(1)封闭环(终结环):在加工过程中间接获得的尺寸,称为封闭环。
在图b所示尺寸链中,A0是间接得到的尺寸,它就是图b所示尺寸链的封闭环。
(2)组成环:在加工过程中直接获得的尺寸,称为组成环。
尺寸链中A1与A2都是通过加工直接得到的尺寸,A1、A2都是尺寸链的组成环。
1)增环:在尺寸链中,自身增大或减小,会使封闭环随之增大或减小的组成环,称为增环。
表示增环字母上面用--> 表示。
2)减环:在尺寸链中,自身增大或减小,会使封闭环反而随之减小或增大的组成环,称为减环。
表示减环字母上面用<-- 表示。
3)怎样确定增减环:用箭头方法确定,即凡是箭头方向与封闭环箭头方向相反的组成环为增环,相同的组成环为减环。
在图b所示尺寸链中,A1是增环,A2是减环。
4)传递系数ξi:表示组成环对封闭环影响大小的系数。
即组成环在封闭环上引起的变动量对组成环本身变动量之比。
对直线尺寸链而言,增环的ξi=1,减环的ξi=-1。
3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。
已知组成环求封闭环的计算方式称作正计算;已知封闭环求各组成环称作反计算;已知封闭环及部分组成环,求其余的一个或几个组成环,称为中间计算。
尺寸链计算有极值法与统计法(或概率法)两种。
用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。
用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。
5.极值法解尺寸链的计算公式(4)封闭环的中间偏差(5)封闭环公差(6)组成环中间偏差Δi=(ES i+EI i)/2(7)封闭环极限尺寸(8)封闭环极限偏差6.竖式计算法口诀:封闭环和增环的基本尺寸和上下偏差照抄;减环基本尺寸变号;减环上下偏差对调且变号。


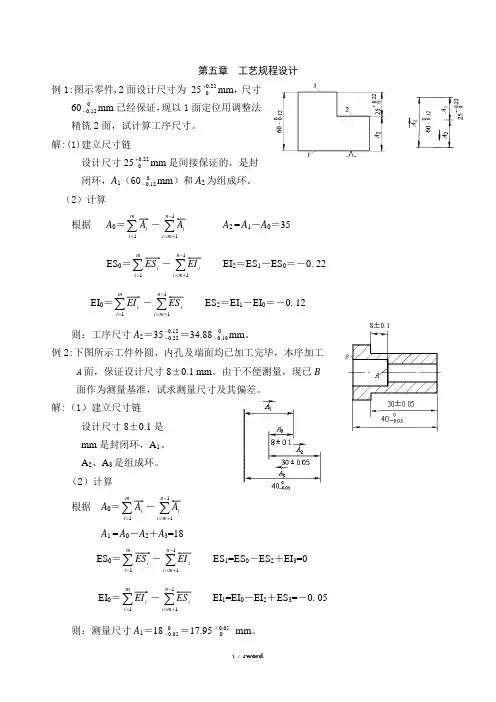
第五章 工艺规程设计例1:图示零件,2面设计尺寸为 2522.00 +mm ,尺寸60012.0-mm 已经保证,现以1面定位用调整法精铣2面,试计算工序尺寸。
解:(1)建立尺寸链设计尺寸2522.00 +mm 是间接保证的,是封闭环,A 1(60012.0-mm )和A 2为组成环。
(2)计算根据 A 0=∑=m i i A 1-∑-+=11n m i i A A 2 = A 1-A 0=35ES 0=∑=mi i ES 1-∑-+=11n m i i EI EI 2=ES 1-ES 0=-0.22 EI 0=∑=mi i EI 1-∑-+=11n m i i ES ES 2=EI 1-EI 0=-0.12则:工序尺寸A 2=3512.022.0--=34.88010.0-mm 。
例2:下图所示工件外圆、内孔及端面均已加工完毕,本序加工A 面,保证设计尺寸8±0.1 mm 。
由于不便测量,现已B面作为测量基准,试求测量尺寸及其偏差。
解:(1)建立尺寸链设计尺寸8±0.1是mm 是封闭环,A 1、A 2、A 3是组成环。
(2)计算根据 A 0=∑=m i i A 1-∑-+=11n m i i AA 1 = A 0-A 2+A 3=18ES 0=∑=m i i ES 1-∑-+=11n m i i EI ES 1=ES 0-ES 2+EI 3=0EI 0=∑=mi i EI 1-∑-+=11n m i i ES EI 1=EI 0-EI 2+ES 3=-0.05 则:测量尺寸A 1=180 05.0-=17.9505.00 + mm 。
例3:一带有键槽的内孔要淬火及磨削,其设计尺寸如图所示。
保证键槽尺寸034 0436..+ mm 的有关工艺过程如下: 1)镗内孔至中01 0396..ϕ+(005 0198.R .+)mm ; 2)插键槽至尺寸A 1;3)淬火(变形忽略不计);4)磨内孔,同时保证内孔直径005 040.ϕ+(0025 020.R +)mm 和键槽深度 034 0436..+mm 两个设计尺寸的要求。
关于尺寸链的简单计算方法之一:坚式法。
1、先确定尺寸链中的组成:增环、减环、封闭环,并画出尺寸链图。
(有一定的难度)
2、根据以下三点把相关的数据填入下表:
a、增环的尺寸及偏差不变,照抄入表格内
b、减环的尺寸及偏差要变号,并上下偏差对调,填入相应表格内。
(此步最重要)
c、封闭环等于增减环尺寸、偏差的代数和。
例如,右图是一个定位套零件,图中已标注了A0及A1的尺寸及偏差,若直接按此图来加工时,A0尺寸不便直接测量,但可通过加工便于测量的尺寸A2来间接保证A0的尺寸。
分析可知A1为增环,A2为减环,A0为封闭环,并画出尺寸链图。
分别
25-X=10,可解得X=15
0-b=0.1,可解得b=-0.1
-0.05-a=-0.1,可解得a=0.05
即尺寸A2=15
此方法可用于计算增环、减环、封闭环的尺寸及其及偏差。
相关概念:
1、封闭环是指尺寸链中在加工或装配过程中最后形成的一环,它的大小是由组成环间接保证的。
如A0。
2、组成环,它包括增环、减环。
a、增环若该环的变动将会引起封闭环的同向变动(同向变动是指该环增大时封闭环也增大,该环减小时封闭环也减小)
b、减环若该环的变动将会引起封闭环的反向变动(反向变动是指该环增大时封闭环减小,该环减小时封闭环增大)
A0
A1
A2
X
a
b
1.零件图
2.尺寸链图
+0.05
-0.1
3.最后可得出便于加工的图PDF created with pdfFactory Pro trial version 。