线性代数B期末试题

线性代数B 期末试题一、判断题(正确填T ，错误填F 。

每小题2分，共10分)1． A 是n 阶方阵，R ∈λ，则有A A λλ=。

（ ）2． A ，B 是同阶方阵，且0≠AB ，则111)(---=A B AB 。

（ ）3．如果A 与B 等价，则A 的行向量组与B 的行向量组等价。

( ) 4．若B A ,均为n 阶方阵，则当B A >时，B A ,一定不相似。

( )5．n 维向量组{}4321,,,αααα线性相关，则{}321,,ααα也线性相关。

（ ）二、单项选择题（每小题3分，共15分）1．下列矩阵中，（ ）不是初等矩阵。

（A ）001010100⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ (B)100000010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ (C) 100020001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(D) 100012001⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦ 2．设向量组123,,ααα线性无关，则下列向量组中线性无关的是（ ）。

（A ）122331,,αααααα--- （B ）1231,,αααα+ （C ）1212,,23αααα- （D ）2323,,2αααα+3．设A 为n 阶方阵，且250A A E +-=。

则1(2)A E -+=（ ） (A) A E - (B) E A + (C) 1()3A E - (D) 1()3A E +4．设A 为n m ⨯矩阵，则有（ ）。

（A ）若n m <，则b Ax =有无穷多解；（B ）若n m <，则0=Ax 有非零解，且基础解系含有m n -个线性无关解向量；（C ）若A 有n 阶子式不为零，则b Ax =有唯一解； （D ）若A 有n 阶子式不为零，则0=Ax 仅有零解。

5．若n 阶矩阵A ，B 有共同的特征值，且各有n 个线性无关的特征向量，则（ ）（A ）A 与B 相似 （B ）A B ≠，但|A-B |=0（C ）A=B （D ）A 与B 不一定相似，但|A|=|B|三、填空题（每小题4分，共20分）1．01210n n -。

同济大学课程考核试卷（B 卷）2009—2010学年第一学期命题教师签名： 审核教师签名：课号：122010 课名：线性代数B 考试考查：考试此卷选为：期中考试( )、期终考试( )、重考( √ )试卷（注意：本试卷共七大题，三大张，满分100分．考试时间为 分钟.要求写出解题过程，否则不予计分） 一、填空题（每空3分，共24分）1．已知4阶方阵为()2131,,,A αααβ=, ()1232,2,,B αααβ=, 且 4A =-，2B =-，则行列式 =+B A 6 。

2. 设行列式1131100021034512D =，j i A 是D 中元素j i a 的代数余子式，则=+2414A A -9 .3. 已知矩阵222222a A a a ⎛⎫⎪= ⎪ ⎪⎝⎭，伴随矩阵0≠*A ，且0=*x A 有非零解，则 C .(A) 2=a ； （B ） 2=a 或4-=a ； (C) 4-=a ； (D) 2≠a 且4-≠a .4. 向量组s ααα，，，21)2(≥s 线性无关，且可由向量组s βββ，，， 21线性表示， 则以下结论中不能成立的是 B(A) 向量组s βββ，，，21线性无关； (B) 对任一个j α(1)j s ≤≤，向量组s j ββα，，，2线性相关； (C) 向量组s ααα，，，21与向量组s βββ，，， 21等价. 5. 已知3阶矩阵A 与B 相似且010100001A -⎛⎫⎪= ⎪⎪-⎝⎭, 则201222B A -=300030001⎛⎫- ⎪ ⎪ ⎪⎝⎭. 6. 设0η是非齐次线性方程组Ax b =的特解，12,,,s ξξξ是齐次方程组0Ax =的基础解系，则以下命题中错误的是 B(A) 001020,,,,s ηηξηξηξ---是Ax b =的一组线性无关解向量；(B) 0122s ηξξξ++++是Ax b =的解；(C) Ax b =的每个解均可表为001020,,,,s ηηξηξηξ+++的线性组合.7. 设4阶矩阵A 有一个特征值为2-且满足5T AA E =，||0A >，则其伴随矩阵*A 的一个特征值为 _________8. 已知实二次型2221,231231323(,)2624f x x x x x x ax x x x =++++正定,则常数a 的取值范围为22a -<<.二、（10分）设矩阵A 的伴随矩阵*110011102A -⎛⎫⎪=- ⎪ ⎪-⎝⎭，且0A >, E BA ABA 311+=--。

共4页第页复旦大学期末考试试卷（B 卷）课程名称线性代数A 考试学期19-20-1得分适用专业非电类专业考试形式闭卷考试时间长度120分钟题号一二三四五六七得分一.（30%）填空题（E 表示单位矩阵）：1.设03a A b ⎛⎫= ⎪⎝⎭，如果10A O =，则参数,a b 满足条件；2.设0k >，向量(,0,)T k k α=，如果矩阵T A E αα=-是1T B E k αα=+的逆矩阵，则参数k =；3.若,A B 都是n 阶可逆矩阵，则分块矩阵O A B E ⎛⎫ ⎪⎝⎭的逆矩阵为；4.若向量组(1,2,3),(1,,3),(1,2,)T T T x y 线性相关，则参数,x y 满足条件；5.3R 的子空间{}(,,)|0T V x y z x y z =--=的维数是；6.假设3阶矩阵A 的秩是2，123,,ηηη是线性方程组Ax b =的解，若12(2,2,4)T ηη+=，13(1,0,1)T ηη-=，则Ax b =的通解是；7.如果2阶矩阵A 的特征值是2和3，则A 的伴随矩阵*A 的特征值是；8.若2是1114335x y -⎛⎫ ⎪= ⎪ ⎪--⎝⎭A 的二重特征值，且A 相似于对角阵，则(,)x y =；9.如果二次型2212124x tx tx x ++是正定的，则参数t 满足条件；10.如果线性方程组31222393x y zx ay z x y bz +-=⎧⎪+-=⎨⎪++=⎩有3个线性无关的解向量，则(,)a b =。

共4页第页二.（14%）设112100010,020002201A B ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，求矩阵方程2()AB B X B +=的解。

三.（10%）已知向量组12110,213αα-⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭与向量组1231110,,120m n βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的秩相同，并且，3β可以由12,αα线性表示。

《线性代数》期末考试试卷B一、(30分)填空题(E 表示相应的单位矩阵).1. 设3阶矩阵A = (α1, α2, α3)的行列式|A | = 3, 矩阵B = (α2, α3, α1), 则矩阵A − B 的行列式|A − B | =______.解: (法一) |A − B | = |α1−α2, α2−α3, α3−α1| = |α1, α2−α3, α3−α1| + |−α2, α2−α3, α3−α1|= |α1, α2−α3, α3| + |−α2, −α3, α3−α1| = |α1, α2, α3| + |−α2, −α3, −α1| = |α1, α2, α3| − |α2, α3, α1| = |α1, α2, α3| − |α1, α2, α3| = 0.(法二) A − B = (α1−α2, α2−α3, α3−α1) = (α1, α2, α3)101110011−⎛⎞⎜⎟−⎜⎟−⎝⎠= AP ,其中P =101110011−⎛⎞⎜⎟−⎜⎟−⎝⎠, |P | =101110011−−−= 0, 故|A − B | = |AP | = |A ||P | = 0.2. 若矩阵A 满足A 2 = O , 则E +A 的逆矩阵(E +A )−1 = _______.解: A 2 = O ⇒ (E +A )(E −A ) = E 2 −A 2 = E ⇒ (E +A )−1 = E −A .3. 若向量组α1 = (1, t , 1), α2 = (1, 1, t ), α3 = (t , 1, 1)的秩为2, 则参数t 满足条件___________.解: 令A = (α1, α2, α3), 则秩(A ) = 秩(α1, α2, α3) = 2 ⇒111111tt t = |A | = 0 ⇒ (t +2)(t −1)2 = 0 ⇒ t = −2或1.当t = −2时, 秩(A ) = 2; 当t = 1时, 秩(A ) = 1. 故t = −2.4. 假设3阶矩阵A 的特征值为1, 2, −1, 矩阵B = E −2A *, 其中A *是A 的伴随矩阵, 则B 的行列式|B |= _______.解: 3阶矩阵A 的特征值为1, 2, −1 ⇒存在P 使得P −1AP =100020001⎛⎞⎜⎟⎜⎟−⎝⎠记为Λ, 而且|A | = 1×2×(−1) = −2.故P −1A −1P = (P −1AP )−1 = Λ−1 =10001/20001⎛⎞⎜⎟⎜⎟−⎝⎠. 由A *A = |A |E 可得A * = |A |A −1 = −2A −1, 于是有|B | = |P |−1⋅|B |⋅|P | = |P −1|⋅|B |⋅|P | = |P −1BP | = |P −1(E −2A *)P | = |P −1EP −2P −1A *P | = |E − 2P −1A *P |= |E + 4P −1A −1P | = |E + 4Λ−1| =500030003−= −45.5. 若矩阵A =10022312x −⎛⎞⎜⎟⎜⎟⎝⎠与矩阵B =03y ⎛⎞⎜⎟⎜⎟⎝⎠相似, 则(x , y ) =________.解: |A | = 2(1−x ), |B | = 0, tr(A ) = 1+x , tr(B ) = 3+y . 因为矩阵A 与B 相似, 所以|A | = |B |, tr(A ) = tr(B ).由此可得x = 1, y = −1. (x , y ) = (1, −1). 6. 设(1, −1, 0)T , (1, 0, −1)T 是3阶实对称矩阵A 的相应于某个非零二重特征值的特征向量. 若A 不可逆,则A 的另一个特征值为______, 相应的一个特征向量为__________.解: 3阶矩阵A 有非零二重特征值而且A 不可逆 ⇒ A 的另一个特征值为0.设ξ为对应于0的特征向量, 则ξ与(1, −1, 0)T , (1, 0, −1)T 正交, 即ξ为12130x x x x −=⎧⎨−=⎩的非零解向量. 由此可得A 的一个对应于0的特征向量为ξ = (1, 1, 1)T .7. 已知3元非齐次线性方程组Ax = b 的系数矩阵的秩为2, 并且α1, α2, α3是Ax = b 的3个解向量, 其中α1 = (1, 1, 1)T , α2 + α3 = (2, 4, 6)T , 则Ax = b 的通解是_______________.解: 3元非齐次线性方程组Ax = b 的系数矩阵的秩为2 ⇒ Ax = 0的基础解系中有且仅有1个解向量.α1, α2, α3是Ax = b 的3个解向量 ⇒ A (α2 + α3 − 2α1) = A α2 + A α3 − 2A α1 = b + b − 2b = 0. α1 = (1, 1, 1)T , α2 + α3 = (2, 4, 6)T ⇒ α2 + α3 − 2α1 = (0, 2, 4)T . 可见ξ = (0, 2, 4)T 是Ax = 0的基础解系,因而Ax = b 的通解是x = k (0, 2, 4)T + (1, 1, 1)T , 其中k 为任意实数. 8. 若4阶方阵A , B 的秩都等于1, 则矩阵A +B 的行列式|A +B | = ________.解: 4阶方阵A , B 的秩都等于1 ⇒ 秩(A +B ) ≤ 秩(A )+秩(B ) = 2 < 4 ⇒ |A +B | = 0. 9. 若矩阵A =211x ⎛⎞⎜⎟⎝⎠与矩阵B =1221⎛⎞⎜⎟−⎝⎠合同, 则参数x 满足条件___________.解: 设λ1, λ2为A 的特征值, µ1, µ2为B 的特征值.µ1µ2 = |B | = −5 < 0 ⇒ µ1, µ2异号 ⇒ B 的秩为2, 正惯性指数为1.A 与B 合同 ⇒ A 的秩为2, 正惯性指数为1 ⇒ λ1, λ2异号 ⇒ 2x − 1 = |A | = λ1λ2 < 0 ⇒ x < 1/2.二、(10分)计算下述行列式的值: D =111+11111+11111111x x x x −−. 解: +1111+111111111111x x x x −−=1111+111111111111x x x −−+1111+11000111111x x x x−−=0000001111x x x−−+ x111+111111x x x −− =000000x x x −−+ x 111+111111x x x −−= x 3 + x 2111+00x x x x x −−= x 3 + x 22111+000x x x x x−= x 3 + (x 4 − x 3) = x 4. 三、(15分)设线性方程组1231231233032314x x x x x x x x x λµ++=⎧⎪++=−⎨⎪−++=⎩. 问: 当参数λ, µ取何值时, 线性方程组有唯一解? 当参数λ, µ取何值时, 线性方程组有无穷多组解? 当线性方程组有无穷多组解时, 求出其通解.解: 该方程组的增广矩阵(A , b ) =1310(3)1323114λµ×−×⎛⎞⎜⎟−⎜⎟−⎝⎠→13100701071λµ⎛⎞⎜⎟−−⎜⎟+⎝⎠→131007010011λµ⎛⎞⎜⎟−−⎜⎟+−⎝⎠. (1) 当λ ≠ −1, µ为任意实数时, 秩(A ) = 秩(A , b ) = 3, 此时线性方程组有唯一解.(2) 当λ = −1, µ = 1时, 秩(A ) = 秩(A , b ) = 2 < 3, 此时线性方程组有无穷多组解,131007010011λµ⎛⎞⎜⎟−−⎜⎟+−⎝⎠=1713100701()0000⎛⎞⎜⎟−−×−⎜⎟⎝⎠→171310010(3)0000⎛⎞⎜⎟×−⎜⎟⎝⎠→37171010100000−⎛⎞⎜⎟⎜⎟⎝⎠由此可得3137127x x x +=−⎧⎨=⎩, 即3137127x x x =−−⎧⎨=⎩. 故通解为x = k (−1, 0, 1)T + (−37,17, 0)T , 其中k 为任意实数.四、(12分)设矩阵A =101012001⎛⎞⎜⎟−⎜⎟⎝⎠, C =103101⎛⎞⎜⎟−⎜⎟⎝⎠, 矩阵X 满足A −1X = A *C + 2X , 其中A *是A 的伴随矩阵,求X .解: |A | = −1, 在A −1X = A *C + 2X 两边同时左乘以A 得X = −C + 2AX . 故(E −2A )X = −C .(E −2A , −C ) =10210(1)0343100101(1)−−−×−⎛⎞⎜⎟−−⎜⎟−−×−⎝⎠→1021003431001014(2)⎛⎞⎜⎟−−⎜⎟××−⎝⎠→13100120303500101−⎛⎞⎜⎟−×⎜⎟⎝⎠→5312100010100101−⎛⎞⎜⎟−⎜⎟⎝⎠. 由此可得X =5312101−⎛⎞⎜⎟−⎜⎟⎝⎠. 五、(10分)已知向量组η1, η2, η3线性无关, 问: 参数a , b , c 满足什么条件时, 向量组a η1+η2, b η2+η3, c η3+η1线性相关?解: (a η1+η2, b η2+η3, c η3+η1) = (η1, η2, η3)011001a b c ⎛⎞⎜⎟⎜⎟⎝⎠. 令P =011001a b c ⎛⎞⎜⎟⎜⎟⎝⎠, 则|P | = abc + 1. 由条件可知:a η1+η2,b η2+η3,c η3+η1线性相关 ⇔ 秩(a η1+η2, b η2+η3, c η3+η1) < 3 ⇔ 秩(P ) < 3 ⇔ |P | = 0 ⇔ abc = −1. 六、(15分)已知二次型f (x 1, x 2, x 3) = x 12 + 2x 22 + x 32 − 2x 1x 3.1. 写出二次型f 的矩阵;2. 求一正交变换x = Qy , 将f 变成其标准形(并写出f 的相应的标准形)；3. 求当x T x = 1时f (x 1, x 2, x 3)的最大值.解: 1. 二次型f 的矩阵A =101020101−⎛⎞⎜⎟⎜⎟−⎝⎠.2. |λE −A | =101020101λλλ−−−= (λ−2)2λ, 可见A 的特征值为λ1 = λ2 = 2, λ3 = 0.解(2E −A )x = 0得对应于λ1 = λ2 = 2的两个正交的特征向量ξ1 = (1, 0, −1)T , ξ2 = (0, 1, 0)T ,解(0E −A )x = 0得对应于λ3 = 0的一个特征向量ξ3 = (1, 0, 1)T .令Q = (11||||ξξ,22||||ξξ,33||||ξξ) =1/00101/0⎛⎜⎜⎜−⎝, 则正交变换x = Qy 将f 变成标准形2y 12 + 2y 22.3. x T x = 1 ⇔ (Qy )T (Qy ) = 1 ⇔ y T Q T Qy = 1 ⇔ y T y = 1 ⇔ y 12 + y 22 + y 32 = 1, 此时y 12 + y 22 ≤ 1. 故当x T x = 1时f (x 1, x 2, x 3) = 2y 12 + 2y 22的最大值为2.七、(8分)证明题.1. 设向量组α1, α2, α3, α4中, α1, α2, α3线性相关, α2, α3, α4线性无关, 证明: α1能由α2, α3, α4线性表示. 证明: 因为α1, α2, α3线性相关, 所以α1, α2, α3, α4线性相关.又因为α2, α3, α4线性无关, 所以α1能由α2, α3, α4线性表示.2. 设A 是n 阶正定矩阵, 证明: 矩阵A +A −1−E 也是正定矩阵.证明: 设λ1, …, λn 为A 的特征值, Λ =1n λλ⎛⎞⎜⎟⎜⎟⎝⎠O . A 是n 阶正定矩阵 ⇒ 存在可逆矩阵P 使得P −1AP = Λ, 其中λ1, …, λn > 0⇒ P −1(A +A −1−E )P = P −1AP + P −1A −1P − P −1EP = Λ + Λ−1 − E =111111n n λλλλ+−⎛⎞⎜⎟⎜⎟⎜⎟+−⎝⎠O, 其中 λ1+11λ−1, …, λn +1n λ−1> 0 ⇒ A +A −1−E 也是正定矩阵.。

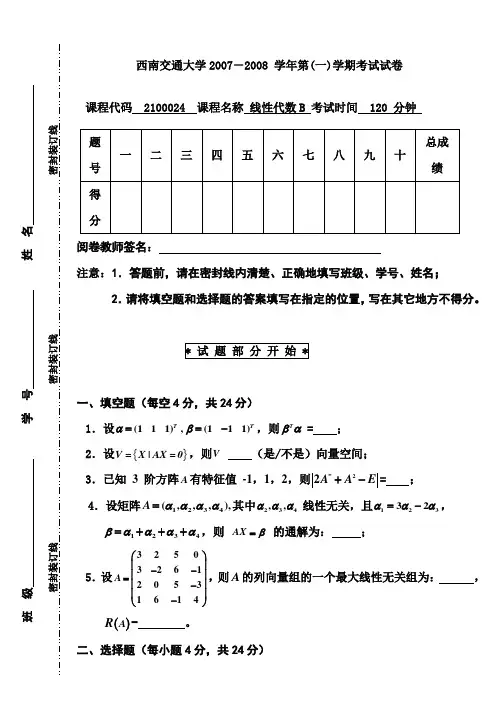
西南交通大学2007－2008 学年第(一)学期考试试卷课程代码 2100024 课程名称 线性代数B 考试时间 120 分钟阅卷教师签名：注意：1．答题前，请在密封线内清楚、正确地填写班级、学号、姓名；2．请将填空题和选择题的答案填写在指定的位置，写在其它地方不得分。

一、填空题（每空4分，共24分）1．设(111),(111)T T αβ==-，则T βα= ； 2．设{}V =X |AX =0，则V （是/不是）向量空间； 3．已知 3 阶方阵A 有特征值 -1，1，2，则2*2A A E +-= ； 4．设矩阵1234(,,,),A =αααα其中234,,ααα线性无关，且12332ααα=-，1234=+++βαααα，则 AX β= 的通解为： ；5．设3250326120531614A ⎛⎫⎪-- ⎪= ⎪- ⎪-⎝⎭，则A 的列向量组的一个最大线性无关组为： ， ()A R = 。

二、选择题（每小题4分，共24分）班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6．行列式 001100010020100003A ⎛⎫⎛⎫⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭求1A -=（ ）（A ） 100010121⎛⎫ ⎪ ⎪ ⎪⎝⎭ （B ）1001002103⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ （C ） 001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭ （D ） 00110021003⎛⎫ ⎪ ⎪⎪⎪ ⎪⎝⎭7．设 21201123()132013x x x f x x x x--=，则()f x 中3x 的系数为( )。

(A) -1 ； (B) 1 ； (C) -17 ； (D) 17 。

8．设 A B 、 均为 n 阶可逆方阵，下列各式正确的是( )。

(A) ||||A A λλ=； (B) 111()AB B A ---=； (C) ()T T T AB A B =； (D)||||||A B A B +=+。

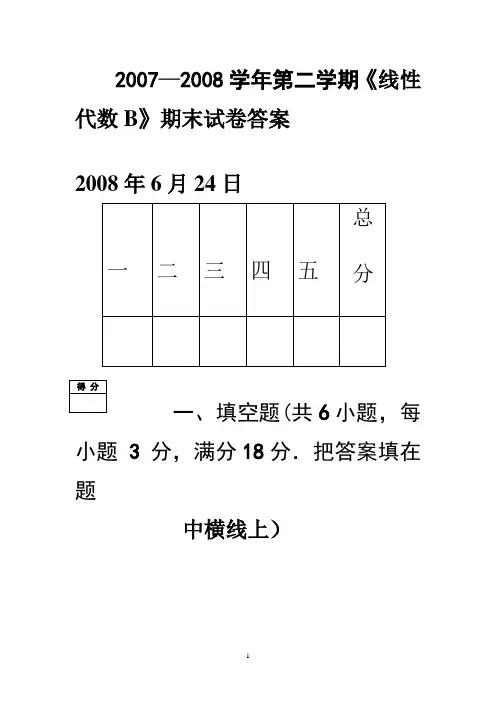
2007—2008学年第二学期《线性代数B》期末试卷答案2008年6月24日一、填空题(共6小题，每小题 3 分，满分18分．把答案填在题中横线上）1．设12-103524-1A 轾犏犏=犏犏臌，*A 是A 的伴随矩阵，则*A = 9 ．2．设3维向量组α1＝(1,2,3)，α2＝(2,5,6)，α3＝(3,6,k )线性相关，则k ＝ 9 ．3．已知3阶矩阵A 满足A 2-E =O ，则秩R(A )= 3 ．4．设实二次型22212312123(,,)3322f x x x =x x tx x x+++正定，则t 的取值范围是 |t |<3 ．5．已知矩阵⎥⎦⎤⎢⎣⎡=513a A 只有一个线性无关的特征向量，则=a-1 ．6．设⎥⎦⎤⎢⎣⎡=000111E ，⎥⎦⎤⎢⎣⎡=001012E ，⎥⎦⎤⎢⎣⎡=010021E ，⎥⎦⎤⎢⎣⎡=100022E 为数域F 上的线性空间22⨯F 的一组基，向量⎥⎦⎤⎢⎣⎡-=3102α在这组基下的坐标为 (2,0,-1,3)T ．二、选择题（共6小题，每小题3分，满分18分．在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后的括号内）2．与矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=900042021A 等价的矩阵是[ B ]．(A)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000001；(B) 100010000轾犏犏犏犏臌； (C) 100010001轾犏犏犏犏臌；(D) 000000000轾犏犏犏犏臌． 1．设A 是4×3矩阵，列向量组线性无关，B 为3阶可逆矩阵，则秩R(AB ) 为[ C ]．(A) 1 ； (B) 2；(C) 3； (D) 4．3．线性方程组b Ax =的系数矩阵A 是4×5矩阵，且A 的行向量组线性无关，则错误的命题是[ D ]．(A) 齐次线性方程组0=x A T只有零解；(B) 齐次线性方程组A T Ax =0必有非零解；(C) 对任意向量b ，非齐次线性方程组Ax =b 必有无穷多解；(D) 对任意向量b ，非齐次线性方程组b x A =T必有无穷多解．4．设A 是n 阶实对称矩阵，P 是n 阶可逆矩阵，已知n 维列向量α是A 的属于特征值λ的特征向量，则矩阵P -1AP 属于特征值λ的特征向量是[ A ]．(A) P -1α； (B) P T α；(C) P α； (D) α．5．下列矩阵中，正定矩阵是[ D ]．(A) 120250003轾犏犏犏犏-臌；(B) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡624293431；(C)123257370轾-犏犏犏犏臌；(D)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----2115222．6．设3阶矩阵A的特征值为-1，-2，3，则A的迹为[ A ]．(A)0；(B) 1；(C) 2；(D) 3．三、解答题（共５小题，每小题9分，满分45分）1．求向量组α1＝(1,2,-1,1)T,α2＝(0,-4,5,-2)T ，α3＝(2,0,4,0)T ，α4＝(3,-2,8,-1)T的秩和一个极大无关组．解 令A =(α1, α2，α3，α4)，则102310231024020448011~~1548056110011120103470000⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-----⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦A ．………（5分）所以R(A )=3，且α1, α2，α3是α1, α2，α3，α4的一个极大无关组． ………（9分）2．已知α＝(2,1,4)，β＝(1,2,－3)，令A ＝αT β，求A n ．解 由于A ＝αT β=22461(1,2,3)123.44812-⎡⎤⎡⎤⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦ ………（4分）所以A n =αT β αT β αT β… αT β=(-8) n -1A =1246(8)1234812n --⎡⎤⎢⎥--⎢⎥⎢⎥-⎣⎦． ……（9分）3．设矩阵A 的伴随矩阵A *=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-420010001，且0>A ，E BA ABA 3-1-1+=，其中E 为3阶单位矩阵，求矩阵B ． 解 在ABA -1=BA -1+3E 等号的两边左乘矩阵A *，右乘矩阵A ，且|A |=2，得2B =A *B +6E，………（3分）即2B -A *B =6E ，亦即(2E -A *)B =6E ，故B =6(2E -A *)-1， ………（6分）即 11006006010060022063-⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦B ． ………（9分）4．验证1231231,1,1032ααα轾轾轾犏犏犏犏犏犏=-==犏犏犏犏犏犏臌臌臌为R 3的基，并将507β轾犏犏=犏犏臌用这个基线性表示．解 设A =（α1，α2，α3），要证α1，α2，α3是R 3的一个基，只须证A E 即可．由于123512351235(,)~1110~0345~0345032703270022120812081002 ~0309~0103~0103001100110011⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦A β（5分）显然，A E ，所以α1，α2，α3是R 3的一个基．且 ……………（7分）β=2α1+3α2-α3． ……………（9分）5．求一组3维列向量α1，α2，使之与α3＝(1,1,1)T正交，并把α1，α2，α3化成两两正交的单位向量． 解 设所求的向量为x ，依题意得(x , α3)=0，即x 1+x 2+x 3=0，解之得 1232233,,.x x x x x x x =--⎧⎪=⎨⎪=⎩ 即121231110,01x x k k x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦k 1,k 2为任意常数．取12111,001--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦αα，则α1，α2与α3正交． ………（５分）对α1，α2施行施密特标准正交化，令b 1=α1，单位化得11110-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦e . b 2=α2－2111(,)( ,) αe e e e 1=11122-⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦.单位化得21112-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦e . 将α3单位化，得31111⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦e . 则e 1,e 2,e 3即为所求的两两正交的单位向量． ………（９分）四、（满分11分）已知非齐次线性方程组1234123412341,32420,31x x x x x x x x ax x x bx +++=-⎧⎪++-=⎨⎪+++=⎩ 有3个线性无关的解。

,考试作弊将带来严重后果！期末考试《 线性代数》试卷A1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)； ．考试形式：开（闭）卷；单项选择题（每小题2分，共30分）。

．设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=6 35 24 1C ,6 5 43 2 1B ,4 32 1A ，则下列矩阵运算无意义的是【 】A . BAC B. ABC C . BCA D. CAB设n 阶方阵A 满足A 2–E =0，其中E 是n 阶单位矩阵，则必有 【 】A. A=A -1B. A=-EC. A=ED. det(A)=1设A 为3阶方阵，且行列式det(A)=12-,则*A = 【 】 A. 14-B. 14C. 1-D. 1 设A 为n 阶方阵，且行列式det(A)=0，则在A 的行向量组中 【 】A.必存在一个行向量为零向量B.必存在两个行向量，其对应分量成比例C. 存在一个行向量，它是其它n-1个行向量的线性组合D. 任意一个行向量都是其它n-1个行向量的线性组合．设向量组321,,a a a 线性无关，则下列向量组中线性无关的是 【 】A ．133221,,a a a a a a --- B. 212132,,a a a a - C. 32322,2,a a a a + D. 3121,,a a a a +6.向量组(I): )3(,,1≥m a a m 线性无关的充分必要条件是 【 】A.(I)中任意一个向量都不能由其余m-1个向量线性表出B.(I)中存在一个向量,它不能由其余m-1个向量线性表出C.(I)中任意两个向量线性无关D.存在不全为零的常数0,,,111≠++m m m a k a k k k 使7．设a 为n m ⨯矩阵，则n 元齐次线性方程组0=Ax 存在非零解的充分必要条件是【 】A ．A 的行向量组线性相关B . A 的列向量组线性相关 C. A 的行向量组线性无关 D. A 的列向量组线性无关 8.设i a 、i b 均为非零常数（i =1，2，3），且齐次线性方程组⎩⎨⎧=++=++00332211332211x b x b x b x a x a x a的基础解系含2个解向量，则必有 【 】 A.03221= b b a a B.02121≠ b b a a C.332211b a b a b a == D. 02131= b b a a 9.方程组⎪⎩⎪⎨⎧=++=++=++ax x x x x x x x x 32132132123 3 12 12 有解的充分必要的条件是【 】A. a=-3B. a=-2C. a=3D. a=210. 设η1，η2，η3是齐次线性方程组Ax = 0的一个基础解系，则下列向量组中也为该方程组的一个基础解系的是 【 】A. 可由η1，η2，η3线性表示的向量组B. 与η1，η2，η3等秩的向量组C.η1－η2，η2－η3，η3－η1D. η1，η1+η3，η1+η2+η3 11. 已知非齐次线性方程组的系数行列式为0，则【 】A. 方程组有无穷多解B. 方程组可能无解，也可能有无穷多解C. 方程组有唯一解或无穷多解D. 方程组无解12. n 阶方阵A 相似于对角矩阵的充分必要条件是A 有n 个 【 】A.互不相同的特征值B.互不相同的特征向量C.线性无关的特征向量D.两两正交的特征向量13. 下列子集能作成向量空间R n 的子空间的是 【 】A. }0|),,,{(2121=a a a a a nB. }0|),,,{(121∑==ni in aa a aC. 121{(,,,)|1}n a a a a = D. }1|),,,{(21∑=n inaa a a14. 下列矩阵中为正交矩阵的是 【 】A. ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1- 1 01 1 00 0 1 B. ⎥⎦⎤⎢⎣⎡1- 22 151C. 1 -10 -1⎡⎤⎢⎥⎣⎦ D. 1 00 -1⎡⎤⎢⎥⎣⎦15.若矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=8020001 a a A 正定,则实数a 的取值范围是 【 】 A ．a < 8 B. a ＞4 C ．a ＜-4 D ．-4 ＜a ＜4二、填空题（每小题2分，共20分）。

2008 -2009学年第二学期《线性代数 B 》试卷量组1，2， ，m ， 的秩为5. 设A 为实对称阵，且AI M 0,则二次型f =x T A x 化为f =y T A -1 y 的线性变换是x= __________ .T6. 设 R 3 的两组基为 a 11,1,1 ，a 2 1,0, 1 ，a 3 1,0,1 ；2,3,4 , 3 3,4,3 ，则由基 a !,a 2,a 3到基 1, 2, 3的过渡矩阵为、单项选择题（共6小题，每小题3分，满分18 分）一一一-二二 -三四五六总分(共 0 0 12. A 为n 阶方阵,AA T = E 且A 0,则A E |.3•设方阵A1 2 24 t 3 , B 为三阶非零矩阵，且AB=O,则t 3114.设向量组m线性无关，向量 不能由它们线性表示，贝U 向1(1,2,1,)T ，22009年6月22日6小题，每小题3分，满分18分）、填空题 1 0 0 10 01.设D n 为n 阶行列式，则D n = 0的必要条件是[]. (A) D n 中有两行元素对应成比例； (B) D n 中各行元素之和为零； (C) D n 中有一行元素全为零；(D)以D n 为系数行列式的齐次线性方程组有非零解.2.若向量组 ，，线性无关，，， 线性相关，则[](A)必可由，， 线性表示； (B)必可由，， 线性表示； (C)必可由，， 线性表示； (D)必可由，，线性表示.3.设3阶方阵A 有特征值0,— 1,1，其对应的特征向量为P i , P 2,P 3, 令1 亠( P 1, P 2, P 3)，则 P —1AP =[ ].1 0 00 0 0(A) 01 0 ；(B) 01 0 ；0 0 0 0 0 10 01 0(C) 0 10 ；(D) 0 00 .0 0 —10 0—14. 设 a 1, a, a 线性无关，则下列向量组线性相关的是[](A) a, a, a - a ；(B) a 1,a + a, a 1+ a ；(C) a +( 也， a + a, a + a ； (D) a 1- a, a - a, a - a .5. 若矩阵A a x 4有一个3阶子式不为0,则A 的秩R ( A )=[]. (A) 1； (B) 2; (C) 3；(D) 4.6. 实二次型f 二X T A X 为正定的充分必要条件是[].(A) A 的特征值全大于零； (B) A 的负惯性指数为零；(C)AI > 0 ；(D) R(A) = n .、解答题(共5小题，每道题8分，满分40分)。

线性代数B期末试卷及答案2008 – 2009学年第⼆学期《线性代数B 》试卷⼀⼆三四五六总分⼀、填空题(共6⼩题，每⼩题 3 分，满分18分）1。

设??-=*8030010000100001A ,则A ＝。

2。

A 为n 阶⽅阵，T AA =E 且=+3．设⽅阵12243,311t -??=-A B 为三阶⾮零矩阵，且AB=O ，则=t . 4。

设向量组m ααα,,,21 线性⽆关，向量不能由它们线性表⽰，则向量组,,,,21m ααα的秩为。

5．设A 为实对称阵，且｜A |≠0,则⼆次型f =x T A x 化为f =y T A —1 y 的线性变换是x = ．６．设3R 的两组基为()T11,1,1a =，()21,0,1a T=-，()31,0,1a T=；),1,2,1(1=βT ，()()232,3,4,3,4,3ββ==T T，则由基123,,a a a 到基123,,βββ的过渡矩阵为 .得分6⼩题，每⼩题3分，满分18分）1.设D n为n阶⾏列式，则D n＝0的必要条件是[ ].（A）D n中有两⾏元素对应成⽐例；(B) D n中各⾏元素之和为零;(C） D n中有⼀⾏元素全为零；（D）以D n为系数⾏列式的齐次线性⽅程组有⾮零解．2．若向量组，，线性⽆关，，，线性相关，则[ ].(A)必可由，,线性表⽰；（B) 必可由，,线性表⽰;(C）必可由,,线性表⽰；(D）必可由，，线性表⽰.３．设3阶⽅阵A有特征值0，－1，1,其对应的特征向量为P1，P2，P3,令P＝（P1，P2，P3），则P－1AP＝[ ]。

（A)100010000-；（B)000010001-；（C)000010001－； (D）100000001－．４．设α1，α2，α3线性⽆关，则下列向量组线性相关的是[ ］.（A）α1，α2，α3 - α1；（B)α1，α1+α2，α1+α3；(C)α1+α2，α2+α3，α3+α1； (D)α1-α2，α2—α3，α3—α1.５．若矩阵A3×4有⼀个3阶⼦式不为0，则A的秩Ｒ（A） =[ ].（A) 1； (B）2；（C）3； (D）4．６．实⼆次型f＝x T Ax为正定的充分必要条件是［］.（A) A的特征值全⼤于零；（B） A的负惯性指数为零；（C）｜A| > 0 ; （D) R(A) = n .得分三、解答题（共5⼩题，每道题8分，满分40分）1。

一、填空题(共 6 题，每题 3 分，共 18分)1. n 阶行列式122222222222322222122222n n−的值为______.2. 设矩阵001110123010,010,023*********A C D −⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，且3阶方阵B 满足ABC D =，则1B −=______. 3. 已知2R 中两组基为ααββ===−=1212(1,1),(0,1);(1,1),(1,2),T TTT则从基αα12,到基ββ12,的过渡矩阵是 ， 已知α在基αα12,下的坐标为(3,0)T ，则α在基ββ12,下的坐标为 .4.设111101,1101a A b α−−⎛⎫⎛⎫ ⎪ ⎪=−=− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭为A 的属于特征值2−的特征向量，则a =______，b =______.5.设3阶实对称矩阵A 的秩()2r A =且A 满足22A A O −=(O 表示零矩阵)，则4I A −=______.6. 已知实二次型22212312313(,,)2f x x x x ax x x x =+++经正交变换x Py =可化为标准型221223f y y =+，则a =______.二、选择题(共 8题，每题 3分，共 24分) 1. 下列(2)n n ≥阶行列式的值必为0的是（ ）.(A) 行列式主对角线上的元素均为0 (B) 行列式零元素的个数多于n 个 (C) 行列式零元素的个数多于2n n −个 (D) 行列式非零元素的个数比+1n 少2. 将2阶方阵A 的第二列加到第一列得方阵B ，再交换B 的第一行与第二行得单位矩阵， 则A =（ ）.（A ）0111⎛⎫ ⎪⎝⎭ （B ）0111⎛⎫ ⎪−⎝⎭ （C ）1110⎛⎫ ⎪⎝⎭ （D ）1110−⎛⎫ ⎪⎝⎭3．设A 是n 阶矩阵，O A =3，则 =−−1)(A I （ ）.（A ）2A A I +− （B ）2A A I ++ （C ）2A A I −+ （D ）2A A I −−4. 齐次线性方程组2123123123000x x x x x x x x x λλλλ⎧++=⎪++=⎨⎪++=⎩的系数矩阵记为A ，若存在3阶非零矩阵B 使得AB O =，则（ ）.中国海洋大学《线性代数》2017-2018学年第一学期期末试卷B卷（A ）2λ=−且0B = （B ）2λ=−且0B ≠ （C ）1λ=且0B = （D ）1λ=且0B ≠ 5. 已知12,ββ是方程组Ax b =的两个不同解，12,αα是对应齐次方程组0Ax =的基础解系， 则Ax b =的一般解是（ ）.（A ）1211212()2k k ββααα−+++ （B ）1211221()2k k ββααα++−+（C ）1211212()2k k ββαββ−+++ （D ）1211212()2k k ββαββ++−+6.下列矩阵中不能对角化的是（ ）.（A ）1101⎛⎫ ⎪⎝⎭ (B) 1102⎛⎫ ⎪⎝⎭ (C) 1112⎛⎫ ⎪⎝⎭ （D ）1212⎛⎫ ⎪⎝⎭注：以下两道为多选题 7. 对向量组12,,,m ααα，其中,1,2,,n i R i m α∈=，下列说法正确的是（ ）.(A)设A 为n 阶方阵，若12,,,m ααα线性相关，则12,,,m A A A ααα也线性相关 (B) 设A 为n 阶方阵，若12,,,m ααα线性无关，则12,,,m A A A ααα也线性无关(C) 12,,,m ααα线性相关的充要条件是其中至少有一个向量可由其余向量线性表出 (D) 若12,,,m ααα中有一个是零向量，则此向量组线性相关(E)零向量可由12,,,m ααα线性表出8. 下列说法正确的是（ ）.(A)对矩阵A 不管施行初等行变换还是初等列变换都不会改变矩阵的秩的值 (B)若A 、B 均可逆，则()()r ACB r C =(C)若n 阶方阵A 的秩()1r A n =−，则*()0r A =，其中*A 为A 的伴随矩阵 (D)若1212=(,,,),=(,,,),m n a a a b b b αβ，其中,i j a b (1,2,,;1,2,,i m j n ==)均非零，则()1T r αβ=三、计算题 (共 3题，共24分)1．（8分）已知4阶行列式42134102315211152D =−,ij A 表示第i 行第j 列元素ij a 的代数余子式，求1323432A A A ++的值。

河海大学2019–2020学年第二学期期末考试《线性代数》试题（B）卷考核方式：闭卷课程性质：必修课适用对象：2018级、2019级相关专业题号一二三四总分复核人满分102016得分一、填空题（将正确答案填在题中横线上。

每小题2分，共10分）1、设1D =3512，2D =345510200，则D =12D D O O=_____________。

2、四阶方阵A B 、，已知A =116，且=B ()1-12A 2A --，则B =_____________。

3、三阶方阵A 的特征值为1，-1，2，且32B=A -5A ，则B 的特征值为_____________。

4、若n 阶方阵A 满足关系式2A -3A-2E O =，若其中E 是单位阵，那么1A -=_____________。

5、设()11,1,1α=，()21,2,3α=，()31,3,t α=线性相关，则t=_____________。

二、单项选择题（每小题2分，共20分）1、若方程13213602214x x xx -+-=---成立，则x 是（）（A ）-2或3；（B ）-3或2；（C ）-2或-3；（D ）3或2；2、设A 、B 均为n 阶方阵，则下列正确的公式为（）（A ）()332233A B+3AB +B A B A +=+；（B ）()()22A B A+B =A B --；（C ）()()2A E=A E A+E --；（D ）()222AB =A B3、设A 为可逆n 阶方阵，则()**A=（）54100（A ）A E ；（B ）A ；（C ）nA A ；（D ）2n A A -；4、下列矩阵中哪一个是初等矩阵（）（A ）100002⎛⎫ ⎪⎝⎭；（B ）100010011⎛⎫⎪ ⎪ ⎪⎝⎭；（C ）011101001-⎛⎫ ⎪- ⎪ ⎪⎝⎭；（D ）010002100⎛⎫ ⎪- ⎪ ⎪⎝⎭；5、下列命题正确的是（）（A ）如果有全为零的数1,k 2k 3,,,m k k 使1122m m k k k αααθ+++= ，则1,α2α，，mα线性无关；（B ）向量组1,α2α， ，mα若其中有一个向量可由向量组线性表示，则1,α2α， ，m α线性相关；（C ）向量组1,α2α， ，m α的一个部分组线性相关，则原向量组本身线性相关；（D ）向量组1,α2α， ，m α线性相关，则每一个向量都可由其余向量线性表示。

上海海洋大学试卷诚信考试承诺书本人郑重承诺：我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”，承诺在考试中自觉遵守，如有违反，按有关条款接受处理。

承诺人签名： 日 期：考生姓名： 学号： 专业班名：一、选择题（每题4分，共20分）1．矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1001110001100011的元素12a 的代数余子式值为（ ）.A. 1B. 1-C. 2D. 2-2．已知3阶矩阵A 的行列式为1，则A 2的行列式为（ ）.A. 2B. 3C. 4D. 8 3．设n 阶方阵A 不可逆，则必有（ ）.A. A 的秩小于nB. A 的秩等于1n -C. 0A =D. 线性方程组0=Ax 只有零解4．已知34⨯阶矩阵A 的列向量组线性无关，则T A 的秩为（ ）.A. 1B. 2C. 3D. 45. 设Ax=b 是一非齐次线性方程组，12,ηη是其任意2个解，则下列结论错误的是（ ） A. 12ηη-是Ax=0的一个解 B.121122ηη+是Ax=b 的一个解 C. 12ηη+是Ax=0的一个解D. 122ηη-是Ax=b 的一个解二、填空题（每题4分，共20分）1．设矩阵⎥⎦⎤⎢⎣⎡--=3211A ，⎥⎦⎤⎢⎣⎡--=1111B ，则AB = . 2．已知向量组)3,1,2(1-=α，)6,,4(2-=k α线性相关，则=k .3．设3阶矩阵A 的秩为2，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101020001P ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001010100Q ，则PAQ 的秩为 . 4．设3151A ⎛⎫= ⎪-⎝⎭，则A 的特征值为 .5．设3阶可逆方阵A 与它的伴随矩阵*A 相等，则=A . 三、计算题（共54分）1. （8分）计算行列式1234112331101205---，并求1121314122A A A A +-+。

2．（8分）已知⎥⎦⎤⎢⎣⎡=1101A ，求n A .3．（8分）已知100025013A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，求1-A .4．（10分）设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101020101A ，且X A AX +=，求X .5．（10分）求矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡422222323101的秩及其列向量组的一个极大无关组，并将不属于这个极大无关组的列向量用极大无关组线性表示.6．（10分）求线性方程组12341234123423222547x x x x x x x x x x x x +++=⎧⎪++-=⎨⎪+++=⎩的通解.四、证明题（6分）证明：若方阵A 的行列式0 A ，则A 可逆.课程考试标准答案和评分标准一、选择题（每题4分，共20分） 1. B 2. D 3. A 4. C 5. C 二、填空题（每题4分，共20分）1． 2255-⎡⎤⎢⎥-⎣⎦. 2． 2- .3． 2 . 4． 122,4λλ=-= . 5． 1 三、计算题（共54分）1. （8分）计算行列式1234112331101205---，并求1121314122A A A A +-+。

线性代数b期末考试题一、单项选择题（每题3分，共30分）1. 以下哪个矩阵是可逆的？A. \(\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}\)B. \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)C. \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\)D. \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\)2. 若矩阵A的行列式为0，则矩阵A是：A. 可逆的B. 不可逆的C. 正定的D. 负定的3. 向量\(\alpha = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\)和\(\beta = \begin{bmatrix} 2 \\ 4 \end{bmatrix}\)是否线性相关？A. 是B. 否4. 线性方程组\(Ax = b\)有解的条件是：A. \(A\)是可逆的B. \(b\)在\(A\)的列空间中C. \(A\)是对称的D. \(A\)是正交的5. 矩阵\(A\)的特征值是指：A. 矩阵\(A\)的对角线元素之和B. 矩阵\(A\)的对角线元素之积C. 满足\(\det(A - \lambda I) = 0\)的\(\lambda\)D. 矩阵\(A\)的迹6. 若\(A\)和\(B\)是同阶方阵，则\(AB\)和\(BA\)的行列式关系是：A. \(\det(AB) = \det(A)\)B. \(\det(AB) = \det(A) \cdot \det(B)\)C. \(\det(AB) = \det(BA)\)D. \(\det(AB) = \det(A) + \det(B)\)7. 向量\(\alpha\)和\(\beta\)的内积定义为：A. \(\alpha \cdot \beta = \sum_{i=1}^{n} \alpha_i \beta_i\)B. \(\alpha \cdot \beta = \sum_{i=1}^{n} \alpha_i / \beta_i\)C. \(\alpha \cdot \beta = \sum_{i=1}^{n} \alpha_i - \beta_i\)D. \(\alpha \cdot \beta = \sum_{i=1}^{n} \alpha_i \times\beta_i\)8. 矩阵\(A\)的秩是指：A. \(A\)中非零行的数量B. \(A\)中非零列的数量C. \(A\)的行空间的维数D. \(A\)的列空间的维数9. 若\(A\)是\(n \times n\)矩阵，\(\lambda\)是\(A\)的一个特征值，则\(\lambda^n\)是：A. \(A^n\)的一个特征值B. \(A^T\)的一个特征值C. \(A^{-1}\)的一个特征值D. \(A^*\)的一个特征值10. 线性变换\(T: \mathbb{R}^n \rightarrow \mathbb{R}^m\)的矩阵表示依赖于：A. 定义域\(\mathbb{R}^n\)的选择基B. 值域\(\mathbb{R}^m\)的选择基C. 定义域\(\mathbb{R}^n\)和值域\(\mathbb{R}^m\)的选择基D. 线性变换\(T\)的定义二、填空题（每题4分，共20分）1. 若矩阵\(A\)和\(B\)相似，则\(\det(A) = \det(B)\)。

西南交通大学2012－2013学年第(1)学期考试试卷课程代码 6010500 课程名称 线性代数B 考试时间 120 分钟阅卷教师签字：一、 选择题（共4小题，每题4分，总计16分）1. 设A 为n 阶矩阵，且2=A ，令T B A A =，则B =（ ）． （A ）n2 （B ）12-n （C ）12+n （D ）42. 设向量组1α，2α，3α，4α线性无关，则向量组12αα+，23αα+，34αα+，41αα+ （ ）． （A ）线性相关 （B ）线性无关（C ）既可能线性相关也可能线性无关 （D ）是否线性相关与向量的维数有关 3. 设A 是n m ⨯矩阵，b 为n 维非零列向量，则下列结论正确的是（ ）． （A ）若0=Ax 仅有零解，则b Ax =必有唯一解 （B ）若0=Ax 有非零解，则b Ax =必有无穷多个解 （C ）若b Ax =有无穷多个解，则0=Ax 仅有零解 （D ）若b Ax =有无穷多个解，则0=Ax 必有非零解4. 若n 阶矩阵B A ,有共同的特征值，且各有n 个线性无关的特征向量，则（ ）． （A ）A 与B 相似 （B ）B A ≠，但0=-B A （C ）B A = （D ）A 与B 不相似,但B A =二、填空题（4小题，每题4分，共16分）5. 设矩阵123456111A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，1224510110B ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，初等矩阵P 满足AP B =，则P = ．6. 设A 为三阶可逆阵，1100220321A -⎛⎫⎪= ⎪ ⎪⎝⎭，则*A = ．7. 设A 为86⨯的矩阵，已知它的秩为4，则0=Ax 的解空间维数为 ．8. 若31212322212232x x x tx x x x f -+++=为正定二次型，则t 的取值范围是 ．班 级 学 号 姓 名密封装订线 密封装订线 密封装订线三、解答下列各题（共3小题，每题8分，总计24分）9. 计算n 阶行列式011111011111011111011111D =．10. 设n 阶方阵A 满足0422=--E A A ．证明3A E -可逆，并求1(3)A E --．11. 齐次线性方程组12341234123423503240230x x x x x x x x x x x x ⎧⎪⎨⎪⎩-++=-++-=--++=的一个基础解系及其通解．四、解答题（共3小题，每题8分，总计24分）12. 求向量组11211α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦--，22521α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦-，33574α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦--，416179α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦-的秩及一个极大线性无关组，并将其余向量通过该极大线性无关组表示出来．13. 设矩阵),,,(4321a a a a A =，其中432,,a a a 线性无关，3212a a a -=，1234b a a a a =+++，求方程组b Ax =的通解．14. 设三阶矩阵A 的特征值为1,1,2-． 求矩阵E A A B -+=2*的行列式B ．五、解答下列各题（共3小题，总计20分）15. （12分）用正交变换x Py =化二次型323121232221321844552),,(x x x x x x x x x x x x f --+++=为标准形，并求出正交变换矩阵P ．这里，T T x x x x ),,(321=，T T y y y y ),,(321=．16. （4分）用特征值定义证明：n 阶实对称的正交矩阵A 的特征值只能是1±．17. （4分）已知3阶矩阵A 与3维列向量α，若2,,A A ααα线性无关，且3232A A A ααα=-。

8.设A 为三阶方阵, 且3=A , 则 12-=A .一、填空题（每小题2分，共20分）1.行列式=-203297302233241.2.设014111112--=D ，则=++333231A A A .3.设 , 231102 ⎪⎪⎭⎫ ⎝⎛-=A , 102324171⎪⎪⎪⎭⎫ ⎝⎛-=B 则= )( TAB . 4.设052=-+I A A ，则=+-1)2(I A .5.已知矩阵⎪⎪⎪⎭⎫⎝⎛-=100120121A ，*A 是A 的伴随矩阵，则=-1*)(A .6.A 、A 分别为线性方程组b AX =的系数矩阵与增广矩阵，则线性方程组b AX =有解的充分必要条件是 .7.设⎪⎪⎪⎭⎫ ⎝⎛-=30511132a A ，且秩(A )=2，则=a .9.向量组1(1,2,1,1),T α=-,)0,3,0,2(2T=αT )1,4,2,1(3--=α的秩等于 . 10.设21,αα是)3(≥n n 元齐次线性方程组OAX =的基础解系，则=)(A r .二、选择题（每小题2分，共20分）1.已知101yxy x aA =，则A 中元素a 的代数余子式11A 等于（ ）.A.1- B .1 C .a - D .a2.已知4阶矩阵A 的第三列的元素依次为2,2,3,1-，它们的余子式的值分别为1,1,2,3-，则=A （ ）.A .3B .3-C .5D .5-3.B A ,均为n 阶矩阵，且2222)(BAB AB A ++=+，则必有（ ）.A.B A = B .I A = C .I B = D .BA AB =4.设A 、B 均为n 阶矩阵，满足O AB =，则必有（ ）.A.0=+B A B .））B r A r ((= C .O A =或O B = D .0=A 或0=B5.设33⨯阶矩阵),,(1γβα=A ，),,(2γβα=B ，其中γβαα,,,21均为3维列向量，若2=A ，1-=B ，则=+B A （ ）.A.4 B .4- C .2 D .16.设B AX =为n 个未知数m 个方程的线性方程组，,)(r A r =下列命题中正确的是（ ）.A .当n m =时，B AX =有唯一解 B .当n r =时，B AX =有唯一解C .当m r =时，B AX =有解D .当n r <时，B AX =有无穷多解7.若齐次线性方程组⎪⎩⎪⎨⎧=λ++=+λ+=++λ000321321321x x x x x x x x x 有非零解,则=λ（ ）.A .1或2B .1或－2C .－1或2D .－1或－28.n 阶矩阵A 的秩r n =的充分必要条件是A 中（ ）.A.所有的r 阶子式都不等于零 B .所有的1r +阶子式都不等于零 C.有一个r 阶子式不等于零 D .有一个r 阶子式不等于零, 且所有1r +阶子式都等于零9.设向量组,),,1(21T a a =α,),,1(22T b b =αT c c ),,1(23=α，则321,,ααα线性无关的充分必要条件是 （ ）.A.c b a ,,全不为0 B .c b a ,,不全为0 C .c b a ,,互不相等 D .c b a ,,不全相等10.已知21,ββ为b AX =的两个不同的解，21,αα为其齐次方程组0A X =基础解系，21,k k 为任意常数，则方程组b AX =的通解可表成（ ）.A.2)(2121211ββααα-+++k kB .2)(2121211ββααα++-+k k线性代数期末试题答案一、填空题（每小题2分，共20分）1.52.03. ⎪⎪⎪⎭⎫⎝⎛-1031314170 4. )(31I A - 5.1/211/2011/2001/2-⎛⎫⎪⎪ ⎪⎝⎭6.)()(A r A r =7.6=a8. 38 9.2 10.2-n二、选择题（每小题2分，共20分）1.B2.C3.D4.D5.A6.C7.B8.D9.C 10.B 三、（8分)解：3211324-824823592373(1)373125212412411131D -===-----18361836(1)1313241=-=-=-四、（10分）解：（1）⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=14191269629303212114321011324TAA （2）⎪⎪⎪⎭⎫⎝⎛-----=--461351341)2(1E A (3) 由XA AX2+=，得A XE A =-)2(A E A X 1)2(--=⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫⎝⎛-----=9122692683321011324461351341五、（12分）解：将方程组的增广矩阵A 用初等行变换化为阶梯矩阵：22112411411242110228018211240134(1)(4)00(4)2k k k k k k k k k k k ⎡⎤⎢⎥----⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥=-→-→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎣⎦⎣⎦+-⎢⎥-⎣⎦A所以，⑴ 当1k≠-且4k ≠时，()()3r r ==A A ，此时线性方程组有唯一解．⑵ 当1k =-时，()2=A r ，()3=A r ，此时线性方程组无解．⑶ 当4k=时，()()2==A A r r ，此时线性方程组有无穷多组解．此时，原线性方程组化为132334x x x x =-⎧⎨=-⎩ 因此，原线性方程组的通解为13233334x x x x x x=-⎧⎪=-⎨⎪=⎩或者写为123034101x x C x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x (C R)∈六、（10分）解：记向量组4321,,,αααα对应矩阵为A 并化为行阶梯形矩阵为12341223122324130212(,,,)12030013062300002634000A αααα--⎛⎫⎛⎫⎪ ⎪-----⎪ ⎪ ⎪ ⎪==→- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭所以向量组4321,,,αααα的秩为3且它的一个最大无关组为：123,,ααα或124,,ααα1004101020013000000A -⎛⎫⎪ ⎪- ⎪→⎪ ⎪ ⎪ ⎪⎝⎭41231432αααα=--+ 七、（12分）解：（1）.⎪⎪⎪⎪⎪⎭⎫⎝⎛--------→⎪⎪⎪⎪⎪⎭⎫⎝⎛--------=61826239131039131024511810957245113322311312A⎪⎪⎪⎪⎪⎭⎫⎝⎛----→0000000039131015801为自由未知量。

一、选择题（每小题3分，共18分）1．设行列式 111222333a b c a b c d a b c =，则111111222222333333223223223c b c a b c c b c a b c c b c a b c ++++++=+++（ ）。

A ．2d -； B ．d -； C ．d ； D ．2d 。

2．已知A 为n 阶非零方阵，E 为n 阶单位矩阵，若3A O =，则（ ）。

A ．A E +不可逆，E A -不可逆；B ．A E -不可逆，A E +可逆；C ．A E +可逆，E A -可逆；D ．AE +不可逆，E A -可逆。

3．向量1α，2α，3α线性无关，则下列向量组线性相关的是（ ）。

A ．12αα+，23αα+，31αα+； B ．1α，12αα+，123ααα++； C ．12αα-，23αα-，31αα-； D ．12αα+，232αα+，313αα+。

4．若3阶方阵2E A -及E A +，3A E -都不可逆，则A 的特征多项式中常数项为（ ）。

A ．23； B ．2 ； C ．23-； D ．43。

5．下列命题错误的是（ ）。

A ．相似矩阵有相同的特征多项式； B ．1n +个n 维向量必线性相关；C ．矩阵Q 是n 阶正交矩阵的充分必要条件是1T QQ -=；D ．若矩阵A 的秩是r ，并且存在1r -阶子式，则其所有的1r -阶子式全为0。

6．下列命题正确的是（ ）。

A ．若A ，B 为同阶方阵，且TA A =，则TB AB 也是对称阵；厦门大学《线性代数》课程试卷学院＿＿＿年级＿＿姓名＿＿＿＿学号＿＿＿＿主考教师： 试卷类型：（B 卷） 2017.06.28B ．若AX AY =，且A O ≠，其中O 为零矩阵，则X Y =；C ．齐次线性方程组AX O =（A 是m n ⨯矩阵）有唯一解的充分必要条件是()r A m =；D ．设非齐次线性方程组AX b =有无穷多解，则相应的齐次线性方程组AX O =有唯一解。