下载文档原格式
第十章：多元线性回归与曲线拟合――Regression菜单详解〔上〕回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
在医学领域中，此类问题很普遍，如人头发中某种金属元素的含量与血液中该元素的含量有关系，人的体外表积与身高、体重有关系；等等。
回归分析就是用于说明这种依存变化的数学关系。
§10.1Linear过程调用此过程可完成二元或多元的线性回归分析。
在多元线性回归分析中，用户还可根据需要，选用不同筛选自变量的方法〔如：逐步法、向前法、向后法，等〕。
例10.1：请分析在数据集Fat surfactant.sav中变量fat对变量spovl的大小有无影响？显然，在这里spovl是连续性变量，而fat是分类变量，我们可用用单因素方差分析来解决这个问题。
但此处我们要采用和方差分析等价的分析方法--回归分析来解决它。
回归分析和方差分析都可以被归入广义线性模型中，因此他们在模型的定义、计算方法等许多方面都非常近似，下面大家很快就会看到。
这里spovl是模型中的因变量，根据回归模型的要求，它必须是正态分布的变量才可以，我们可以用直方图来大致看一下，可以看到根本服从正态，因此不再检验其正态性，继续往下做。
在菜单中选择Regression==>liner，系统弹出线性回归对话框如下：除了大家熟悉的容以外，里面还出现了一些特色菜，让我们来一一品尝。
【Dependent框】用于选入回归分析的应变量。
【Block按钮组】由Previous和Next两个按钮组成，用于将下面Independent框中选入的自变量分组。
由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法，如果对不同的自变量选入的方法不同，那么用该按钮组将自变量分组选入即可。
下面的例子会讲解其用法。
【Independent框】用于选入回归分析的自变量。
【Method下拉列表】用于选择对自变量的选入方法，有Enter〔强行进入法〕、Stepwise〔逐步法〕、Remove〔强制剔除法〕、Backward〔向后法〕、Forward〔向前法〕五种。
SPSS多元线性回归分析实例操作步骤多元线性回归是一种常用的统计分析方法，用于探究多个自变量对因变量的影响程度。
SPSS（Statistical Package for the Social Sciences）是一款常用的统计软件，可以进行多元线性回归分析，并提供了简便易用的操作界面。
本文将介绍SPSS中进行多元线性回归分析的实例操作步骤，帮助您快速掌握该分析方法的使用。
步骤一：准备数据在进行多元线性回归分析之前，首先需要准备好相关的数据。
数据应包含一个或多个自变量和一个因变量，以便进行回归分析。
数据可以来自实验、调查或其他来源，但应确保数据的质量和可靠性。
步骤二：导入数据在SPSS软件中，打开或创建一个新的数据集，然后将准备好的数据导入到数据集中。
可以通过导入Excel、CSV等格式的文件或手动输入数据的方式进行数据导入。
确保数据被正确地导入到SPSS中，并正确地显示在数据集的各个变量列中。
步骤三：进行多元线性回归分析在SPSS软件中，通过依次点击"分析"-"回归"-"线性"，打开线性回归分析对话框。
在对话框中，将因变量和自变量移入相应的输入框中。
可以使用鼠标拖拽或双击变量名称来快速进行变量的移动。
步骤四：设置分析选项在线性回归分析对话框中，可以设置一些分析选项，以满足具体的分析需求。
例如，可以选择是否计算标准化回归权重、残差和预测值，并选择是否进行方差分析和共线性统计检验等。
根据需要，适当调整这些选项。
步骤五：获取多元线性回归分析结果点击对话框中的"确定"按钮后，SPSS将自动进行多元线性回归分析，并生成相应的分析结果。
结果包括回归系数、显著性检验、残差统计和模型拟合度等信息，这些信息可以帮助我们理解自变量对因变量的贡献情况和模型的拟合程度。
步骤六：解读多元线性回归分析结果在获取多元线性回归分析结果之后，需要对结果进行解读，以得出准确的结论。
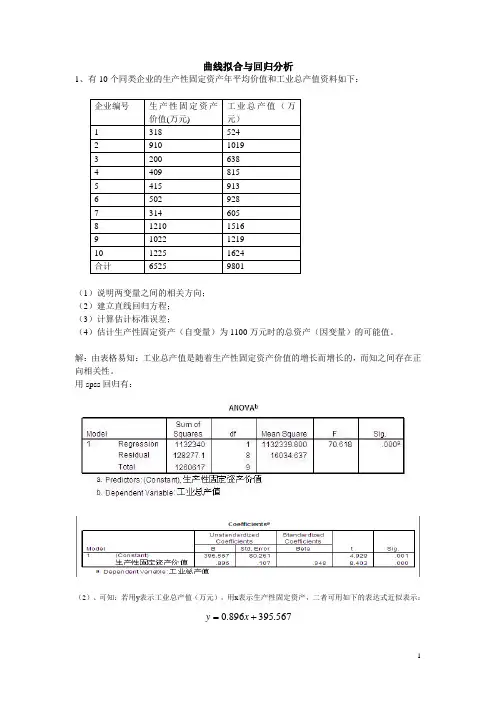
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下：（1）说明两变量之间的相关方向；（2）建立直线回归方程；（3）计算估计标准误差；（4）估计生产性固定资产（自变量）为1100万元时的总资产（因变量）的可能值。
解：由表格易知：工业总产值是随着生产性固定资产价值的增长而增长的，而知之间存在正向相关性。
用spss回归有：（2）、可知：若用y表示工业总产值（万元），用x表示生产性固定资产，二者可用如下的表达式近似表示：=x.0+y.567395896（3）、用spss回归知标准误差为80.216（万元）。
（4）、当固定资产为1100时，总产值可能是（0.896*1100+395.567-80.216~0.896*1100+395.567+80.216）即（1301.0~146.4）这个范围内的某个值。
另外，用MATLAP也可以得到相同的结果：程序如下所示：function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示：b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值（万元）工业总价值（万元）2、设某公司下属10个门市部有关资料如下：（1）、确定适宜的 回归模型； （2）、计算有关指标，判断这三种经济现象之间的紧密程度。
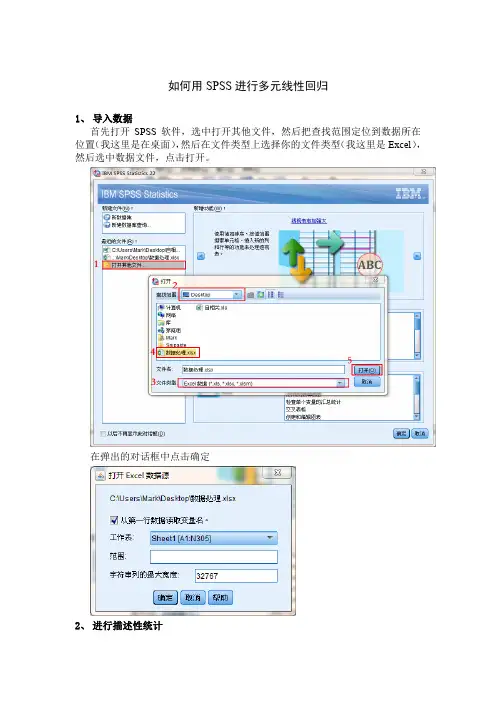
如何用SPSS进行多元线性回归1、导入数据首先打开SPSS软件，选中打开其他文件，然后把查找范围定位到数据所在位置（我这里是在桌面），然后在文件类型上选择你的文件类型（我这里是Excel），然后选中数据文件，点击打开。
在弹出的对话框中点击确定2、进行描述性统计首先点击菜单栏中的分析-描述统计-描述出现如下页面，选中想要进行描述性统计的变量到右边变量框中。
如图所示，点击选项，选择需要SPSS汇报的描述性统计：结果如图，这里只选择平均值、标准偏差、最小值和最大值：得出描述性统计如图：注意：结果是可以复制粘贴到Excel里面的。
3、相关性分析首先点击菜单栏中的分析-相关-双变量同样按照描述性统计的操作，把想要进行分析的变量选中，选择Pearson相关系数，并进行双尾检验（一般性操作），点击确定即可。
得出如下结果：一般来讲，相关系数大于0.6就说明可能会存在多重共线性问题，而且相关系数比较显著（右上角有两个星号，说明结果在0.01的水平上显著），结论：GYZCZ和SCALE可能存在多重共线性。
4、回归以及回归诊断首先点击分析-回归-线性因变量和自变量选择好，如图所示：点击右上角的Statistics，出现如下菜单，选择共线性诊断和Durbin-Watson检验（检验序列相关性），然后点击继续。
点击右上角的绘图，出现如下界面，按照图示进行选择，这一步是为了进行异方差的初步验证，然后点击继续。
以上全部设定好了之后，点击确定即可。
主要结果分析：可决系数R方值为0.432，调整后的R方是0.414，说明模型拟合程度还不错（一般大于0.3都还能接受）。
D.W.值为0.828，说明存在正的序列相关性（如果是横截面数据，则不需要考虑，如果是时间序列数据就需要考虑用差分法、广义最小二乘、可行的广义最小二乘等方法）F值通过检验（显著性为0.000），说明模型的整体线性性满足。
共线性诊断：看方差膨胀因子（VIF），GYZCZ与SCALE的VIF值大于10，说明存在多重共线性，需要剔除这两个变量。
SPSS如何进行线性回归分析操作本节内容主要介绍如何确定并建立线性回归方程。
包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。
为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。
也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。
另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。
一、一元线性回归分析用SPSS进行回归分析，实例操作如下：1.单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。
从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。
在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。
所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。
具体如下图所示：2.请单击Statistics…按钮，可以选择需要输出的一些统计量。
如RegressionCoefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。
Model fit 项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。
上述两项为默认选项，请注意保持选中。
设置如图7-10所示。
设置完成后点击Continue返回主对话框。
回归方程建立后，除了需要对方程的显著性进行检验外，还需要检验所建立的方程是否违反回归分析的假定，为此需进行多项残差分析。
由于此部分内容较复杂而且理论性较强，所以不在此详细介绍，读者如有兴趣，可参阅有关资料。
3.用户在进行回归分析时，还可以选择是否输出方程常数。
SPSS如何进行线性回归分析操作本节内容主要介绍如何确定并建立线性回归方程。
包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。
为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。
也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。
另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。
一、一元线性回归分析用SPSS进行回归分析，实例操作如下：1.单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。
从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。
在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。
所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。
具体如下图所示：2.请单击Statistics…按钮，可以选择需要输出的一些统计量。
如RegressionCoefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。
Model fit 项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。
上述两项为默认选项，请注意保持选中。
设置如图7-10所示。
设置完成后点击Continue返回主对话框。
回归方程建立后，除了需要对方程的显著性进行检验外，还需要检验所建立的方程是否违反回归分析的假定，为此需进行多项残差分析。
由于此部分内容较复杂而且理论性较强，所以不在此详细介绍，读者如有兴趣，可参阅有关资料。
3.用户在进行回归分析时，还可以选择是否输出方程常数。
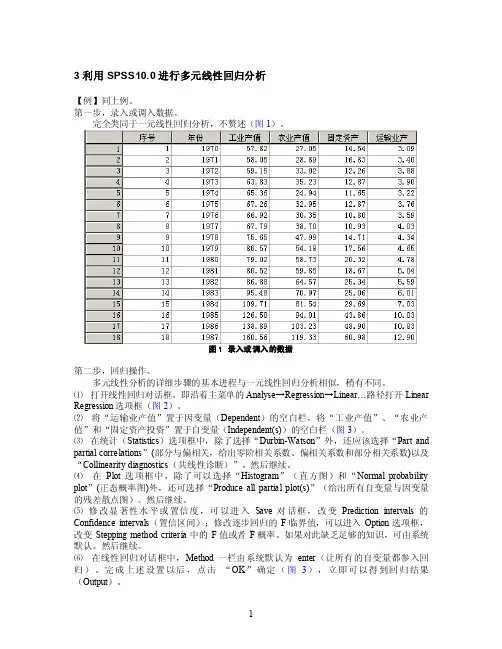
3 利用SPSS10.0进行多元线性回归分析【例】同上例。
第一步，录入或调入数据。
完全类同于一元线性回归分析，不赘述（图1）。
图1 录入或调入的数据第二步，回归操作。
多元线性分析的详细步骤的基本进程与一元线性回归分析相似，稍有不同。
⑴打开线性回归对话框。
即沿着主菜单的Analyse→Regression→Linear…路径打开Linear Regression选项框（图2）。
⑵将“运输业产值”置于因变量（Dependent）的空白栏，将“工业产值”、“农业产值”和“固定资产投资”置于自变量（Independent(s)）的空白栏（图3）。
⑶在统计（Statistics）选项框中，除了选择“Durbin-Watson”外，还应该选择“Part and partial correlations”(部分与偏相关，给出零阶相关系数、偏相关系数和部分相关系数)以及“Collinearity diagnostics（共线性诊断）”。
然后继续。
⑷在Plot选项框中，除了可以选择“Histogram”（直方图）和“Normal probability plot”(正态概率图)外，还可选择“Produce all partial plot(s)”（给出所有自变量与因变量的残差散点图）。
然后继续。
⑸修改显著性水平或置信度，可以进入Save对话框，改变Prediction intervals的Confidence intervals（置信区间）；修改逐步回归的F临界值，可以进入Option选项框，改变Stepping method criteria中的F值或者F概率。
如果对此缺乏足够的知识，可由系统默认。
然后继续。
⑹在线性回归对话框中，Method一栏由系统默认为enter（让所有的自变量都参入回归）。
完成上述设置以后，点击“OK”确定（图3），立即可以得到回归结果（Output）。
图2 线性回归对话框图3 设置变量图4 统计选项框的设置图5 图形对话框的设置在Variables Entered/Removed （变量取舍即变量的输入或剔除）表中，给出的采用的变量、剔除的变量和回归方法（enter ）,此表中没有剔除变量。
SPSS如何进行线性回归分析操作本节内容主要介绍如何确定并建立线性回归方程。
包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。
为了确保所建立的回归方程符合线性标准，在进行回归分析之前，我们往往需要对因变量与自变量进行线性检验。
也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验，这里不再重复。
另外，通过散点图还可以发现数据中的奇异值，对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。
一、一元线性回归分析用SPSS进行回归分析，实例操作如下：1.单击主菜单Analyze / Regression / Linear…，进入设置对话框如图7-9所示。
从左边变量表列中把因变量y选入到因变量（Dependent）框中，把自变量x选入到自变量（Independent）框中。
在方法即Method一项上请注意保持系统默认的选项Enter，选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。
所以该方法可命名为强制进入法（在多元回归分析中再具体介绍这一选项的应用）。
具体如下图所示：2.请单击Statistics…按钮，可以选择需要输出的一些统计量。
如RegressionCoefficients(回归系数)中的Estimates，可以输出回归系数及相关统计量，包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。
Model fit 项可输出相关系数R，测定系数R2，调整系数、估计标准误及方差分析表。
上述两项为默认选项，请注意保持选中。
设置如图7-10所示。
设置完成后点击Continue返回主对话框。
回归方程建立后，除了需要对方程的显著性进行检验外，还需要检验所建立的方程是否违反回归分析的假定，为此需进行多项残差分析。
由于此部分内容较复杂而且理论性较强，所以不在此详细介绍，读者如有兴趣，可参阅有关资料。
3.用户在进行回归分析时，还可以选择是否输出方程常数。
SPSS多元线性回归分析教程.doc
1. 软件安装和数据导入
安装完SPSS软件，打开软件，在主界面中选择“Open an existing data source”选项，找到导入的数据文件，点击“Open”按钮将数据导入SPSS。
2. 变量检查和描述性统计分析
在“Variable View”选项卡中，查看每个变量的数据类型和属性是否正确。
在“Data View”选项卡中，选中变量列表，点击“Analyze”菜单中的“Descriptive Statistics”选项，进行数据描述性统计分析。
3. 模型构建和回归分析
在“Regression”菜单中，选择“Linear”选项，进入线性回归分析设置页面。
将自
变量和因变量移动到变量框中，点击“OK”按钮进行回归分析。
在分析结果界面中，查看
回归分析的显著性和方程式，判断回归模型的拟合程度和自变量对因变量的解释度。
4. 结果解释和模型优化
根据分析结果，解释各个变量对因变量的影响程度和统计显著性。
如果存在模型缺陷，可以考虑添加、删除或转换自变量，优化回归模型并重新进行分析。
同时，需要注意验证
模型的可靠性和稳定性，避免过度拟合或欠拟合的情况。
5. 结果呈现和报告撰写
将回归分析结果进行图表制作和文字描述，清晰、简洁地呈现分析结果。
在报告撰写
过程中，需要注意逻辑性和一致性，避免遗漏关键内容和出现明显错误。
总之，SPSS多元线性回归分析需要掌握数据导入、变量检查、描述性统计分析、模型构建、回归分析、结果解释、模型优化、结果呈现和报告撰写等技能，才能有效地进行数
据分析研究。
SPSS 10.0高级教程十二：多元线性回归与曲线拟合回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
在医学领域中，此类问题很普遍，如人头发中某种金属元素的含量与血液中该元素的含量有关系，人的体表面积与身高、体重有关系；等等。
回归分析就是用于说明这种依存变化的数学关系。
§10.1Linear过程10.1.1 简单操作入门调用此过程可完成二元或多元的线性回归分析。
在多元线性回归分析中，用户还可根据需要，选用不同筛选自变量的方法（如：逐步法、向前法、向后法，等）。
例10.1：请分析在数据集Fat surfactant.sav中变量fat对变量spovl的大小有无影响？显然，在这里spovl是连续性变量，而fat是分类变量，我们可用用单因素方差分析来解决这个问题。
但此处我们要采用和方差分析等价的分析方法--回归分析来解决它。
回归分析和方差分析都可以被归入广义线性模型中，因此他们在模型的定义、计算方法等许多方面都非常近似，下面大家很快就会看到。
这里spovl是模型中的因变量，根据回归模型的要求，它必须是正态分布的变量才可以，我们可以用直方图来大致看一下，可以看到基本服从正态，因此不再检验其正态性，继续往下做。
10.1.1.1 界面详解在菜单中选择Regression==>liner，系统弹出线性回归对话框如下：除了大家熟悉的内容以外，里面还出现了一些特色菜，让我们来一一品尝。
【Dependent框】用于选入回归分析的应变量。
【Block按钮组】由Previous和Next两个按钮组成，用于将下面Independent框中选入的自变量分组。
由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法，如果对不同的自变量选入的方法不同，则用该按钮组将自变量分组选入即可。
下面的例子会讲解其用法。
【Independent框】用于选入回归分析的自变量。
【Method下拉列表】用于选择对自变量的选入方法，有Enter（强行进入法）、Stepwise（逐步法）、Remove（强制剔除法）、Backward（向后法）、Forward（向前法）五种。
该选项对当前Independent框中的所有变量均有效。
【Selection Variable框】选入一个筛选变量，并利用右侧的Rules钮建立一个选择条件，这样，只有满足该条件的记录才会进入回归分析。
【Case Labels框】选择一个变量，他的取值将作为每条记录的标签。
最典型的情况是使用记录ID 号的变量。
【WLS>>钮】可利用该按钮进行权重最小二乘法的回归分析。
单击该按钮会扩展当前对话框，出现WLS Weight框，在该框内选入权重变量即可。
【Statistics钮】弹出Statistics对话框，用于选择所需要的描述统计量。
有如下选项：o Regression Coefficients复选框组：定义回归系数的输出情况，选中Estimates可输出回归系数B及其标准误，t值和p值，还有标准化的回归系数beta；选中Confidence inter vals则输出每个回归系数的95%可信区间；选中covariance matrix则会输出各个自变量的相关矩阵和方差、协方差矩阵。
以上选项默认只选中Estimates。
o Residuals复选框组：用于选择输出残差诊断的信息，可选的有Durbin-Watson残差序列相关性检验、超出规定的n倍标准误的残差列表。
o Model fit复选框：模型拟合过程中进入、退出的变量的列表，以及一些有关拟合优度的检验：，R，R2和调整的R2, 标准误及方差分析表。
o R squared change复选框：显示模型拟合过程中R2、F值和p值的改变情况。
o Descriptives复选框：提供一些变量描述，如有效例数、均数、标准差等，同时还给出一个自变量间的相关矩阵。
o Part and partial correlations复选框：显示自变量间的相关、部分相关和偏相关系数。
o Collinearity diagnostics复选框：给出一些用于共线性诊断的统计量，如特征根（Ei genvalues）、方差膨胀因子(VIF)等。
以上各项在默认情况下只有Estimates和Model fit复选框被选中。
【Plot钮】弹出Plot对话框，用于选择需要绘制的回归分析诊断或预测图。
可绘制的有标准化残差的直方图和正态分布图，应变量、预测值和各自变量残差间两两的散点图等。
【Save钮】许多时候我们需要将回归分析的结果存储起来，然后用得到的残差、预测值等做进一步的分析，Save钮就是用来存储中间结果的。
可以存储的有：预测值系列、残差系列、距离（Dis tances）系列、预测值可信区间系列、波动统计量系列。
下方的按钮可以让我们选择将这些新变量存储到一个新的SPSS数据文件或XML中。
【Options钮】设置回归分析的一些选项，有：o Stepping Method Criteria单选钮组：设置纳入和排除标准，可按P值或F值来设置。
o Include constant in equation复选框：用于决定是否在模型中包括常数项，默认选中。
o Missing Values单选钮组：用于选择对缺失值的处理方式，可以是不分析任一选入的变量有缺失值的记录（Exclude cases listwise）而无论该缺失变量最终是否进入模型；不分析具体进入某变量时有缺失值的记录（Exclude cases pairwise）；将缺失值用该变量的均数代替（Replace with mean）。
10.1.1.2 输出结果解释根据题目的要求，我们只需要在Dependent框中选入spovl，Independent框中选入f at即可，其他的选项一律不管。
单击OK后，系统很快给出如下结果：Regression这里的表格是拟合过程中变量进入/退出模型的情况记录，由于我们只引入了一个自变量，所以只出现了一个模型1（在多元回归中就会依次出现多个回归模型），该模型中fat为进入的变量，没有移出的变量，具体的进入/退出方法为enter。
上表为所拟合模型的情况简报，显示在模型1中相关系数R为0.578，而决定系数R2为0.3 34，校正的决定系数为0.307。
这是所用模型的检验结果，可以看到这就是一个标准的方差分析表！有兴趣的读者可以自己用方差分析模型做一下，就会发现出了最左侧的一列名字不太一样外，其他的各个参数值都是相同的。
从上表可见所用的回归模型F值为12.059，P值为0.002，因此我们用的这个回归模型是有统计学意义的，可以继续看下面系数分别检验的结果。
由于这里我们所用的回归模型只有一个自变量，因此模型的检验就等价与系数的检验，在多元回归中这两者是不同的。
上表给出了包括常数项在内的所有系数的检验结果，用的是t检验，同时还会给出标化/未标化系数。
可见常数项和fat都是有统计学意义的，上表的内容如果翻译成中文则如下所示：10.1.2.1 分析实例例10.2：请分析在数据集plastic.sav中变量extrusn、additive、gloss和opacity对变量tear_r es的大小有无影响？已知extrusn对tear_res的大小有影响。
显然，这里是一个多元回归，由于除了extrusn确有影响以外，我们不知道另三个变量有无影响，因此这里我们将extrusn放在第一个block，进入方法为enter（我们有把握extrusn一定有统计学意义）；另三个变量放在第二个block，进入方法为stepwise（让软件自动选择判断），操作如下：1.Analyze==>Regression==>Liner2.Dependent框：选入tear_res3.Independent框：选入extrusn；单击next钮4.Independent框：选入additive、gloss和opacity；Method列表框：选择stepwise5.单击OK钮10.1.2.2 结果解释最终的结果如下：Regression上面的表格依次列出了模型的筛选过程，模型1用进入法引入了extrusn，然后模型2用ste pwise法引入了additive，另两个变量因没有达到进入标准，最终没有进入。
上面的表格翻译出来如下：上表是两个模型变异系数的改变情况，从调整的R2可见，从上到下随着新变量的引入，模型可解释的变异占总变异的比例越来越大。
上表是所用两个模型的检验结果，用的方法是方差分析，可见二个模型都有统计学意义。
上表仍然为三个模型中各个系数的检验结果，用的是t检验，可见在模型2中所有的系数都有统计学意义，上表的内容翻译如下：这是新出现的一个表格，反映的是没有进入模型的各个变量的检验结果，可见在模型1中，未引入模型的候选变量additive还有统计学意义，可能需要引入，而模型2中没有引入的两个变量其P值均大于0.05，无需再进行分析了。
10.2 Curve Estimation过程Curve Estimation过程可以用与拟合各种各样的曲线，原则上只要两个变量间存在某种可以被它所描述的数量关系，就可以用该过程来分析。
但这里我们要指出，由于曲线拟合非常的复杂，而该模块的功能十分有限，因此最好采用将曲线相关关系通过变量变换的方式转化为直线回归的形式来分析，或者采用其他专用的模块分析。
10.2.1 界面详解Curve Estimation过程中有特色的对话框界面内容如下：下面我们分别解释一下它们的具体功能。
【Dependent框】用于选入曲线拟和中的应变量，可选入多个，如果这样，则对各个应变量分别拟合模型。
【Independent单选框组】用于选入曲线拟和中的自变量，有两种选择，可以选入普通的自变量，也可以选择时间作为自变量，如果这样做，则所用的数据应为时间序列数据格式。
【Models复选框组】是该对话框的重点，用于选择所用的曲线模型，可用的有：∙Linear：拟合直线方程，实际上与Linear过程的二元直线回归相同；∙Quadratic：拟合二次方程Y = b0+b1X+b2X2；∙Compound：拟合复合曲线模型Y = b0×b1X；∙Growth：拟合等比级数曲线模型Y = e(b0+b1X)；∙Logarithmic：拟合对数方程Y = b0+b1lnX；∙Cubic：拟合三次方程Y = b0+b1X+b2X2+b3X3；∙S：拟合S形曲线Y = e(b0+b1/X)；∙Exponential：拟合指数方程Y = b0 eb1X；∙Inverse：数据按Y = b0+b1/X进行变换；∙Power：拟合乘幂曲线模型Y = b0X b1；∙Logistic：拟合Logistic曲线模型Y = 1/（1/u + b0×b1X），如选择该线型则要求输入上界。
