当前位置：文档之家 › 第四章_快速傅里叶变换(FFT)

第四章_快速傅里叶变换(FFT)

  • 格式：pdf
  • 大小：1.41 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

快速傅里叶变换FFT

快速傅里叶变换FFT
第4章 迅速傅里叶变换(FFT)
本章主要内容
▪ 引言 ▪ 基2FFT算法 ▪ 进一步降低运算量旳措施
4.1 引言
▪ DFT是信号分析与处理中旳一种主要变换。但直接计算DFT旳 计算量与变换区间长度N旳平方成正比，当N较大时，计算量 太大，直接用DFT算法进行谱分析和信号旳实时处理是不切 实际旳。
▪ 1965年发觉了DFT旳一种迅速算法，使DFT旳运算效率提升1－2 个数量级，为数字信号处理技术应用于多种信号旳实时处理 发明了条件，推动了数字处理技术旳发展。
r 0
x2 ( r )WN2 kr
X (k) x(n)WNkn x(n)WNkn
n
n
X(k) x(n)WNkn x(n)WNkn
n
n
X (k )
x(n)WNkn
x(n)WNkn
N / 21
N / 21
N / 21
N / 21
n
n
x(2r)WN2kr
x(2r 1)WNk(2r1) x(2r)WN2kr x(2r1)WNk(2r1)
4.2 基2FFT算法
2.旋转因子旳变化规律
N点DIT―FFT运算流图中，每个蝶形都要乘以旋转因子WpN，p 称为旋转因子旳指数。N＝8 ＝23 时各级旳旋转因子
第一级：L=1， 有1个旋转因子：WNp =WN/4J =W2LJ J=0 第二级：L=2，有2个旋转因子：WNp =WN/2J =W2LJ J=0,1 第三级：L=3，有4个旋转因子：WNp =WNJ =W2LJ J=0,1,2,3 对于N＝2M 旳一般情况，第L级共有2L-1个不同旳旋转因子：
▪ 1984年，提出了分裂基迅速算法，使运算效率进一步提升；
4.2 基2FFT算法

数字信号处理课件第4章快速傅里叶变换FF

数字信号处理课件第4章快速傅里叶变换FF
雷达信号压缩
通过FFT对雷达信号进行频谱分析，实现雷 达数据的压缩，减小存储空间和传输带宽。
谢谢聆听
05 FFT的局限性与挑战
浮点运算的开销问题
浮点运算开销
快速傅里叶变换（FFT）算法在实 现过程中需要进行大量的浮点运 算，这可能导致计算成本较高， 尤其是在处理大规模数据时。
硬件资源需求
由于FFT的浮点运算密集特性，对 计算设备的硬件资源（如CPU、 GPU等）要求较高，需要具备高 性能的计算能力。
FFT的软件实现
C/C实现
01
使用C或C等通用编程语言实现FFT算法，具有较好的通用性和
可移植性。
优化编译器
02
利用现代编译器的优化功能，如向量化、内联等，可以提高软
件实现的计算速度。
并行计算框架
03
利用OpenMP、CUDA等并行计算框架，可以实现多核或多
GPU上的并行计算。
FFT的优化方法
算法改进
FFT的历史与发展
历史
FFT的诞生可以追溯到1960年代，其发展经历了多个阶段，包括库利-图基算法、威尔金森算法、桑德斯算法等 。
发展
随着计算机技术的不断进步，FFT算法在实现方式、精度、并行化等方面不断得到优化和改进，以满足不同应用 场景的需求。
02 FFT的基本算法
递归算法
递归算法是一种基于数学归纳法的算法，通过将问题分解为更小的子问题来解决 问题。在FFT中，递归算法将一个长度为N的DFT问题分解为两个长度为N/2的 DFT问题，直到最后分解为基本的DFT问题。
特别是在信号处理领域，FFT的应用非常广泛。
FFT与Z变换的关系
定义
Z变换是离散时间信号 到复平面上的扩展，而 FFT是频域的一种快速 计算方法。

数字信号处理 第4章 快速傅里叶变换(FFT)-资料

数字信号处理 第4章 快速傅里叶变换(FFT)-资料

x[0]
x[2]
W20
x[1]
x[3] W20
X1[0]
2点DFT X1[1] 1 X2[0]
2点DFT X2[1] 1
W40
1
W41
1
X [0] X [1] X [2] X [3]
4点基2时间抽取FFT算法流图
x[0]
x[2]
W40
x[1]
x[3]
W40
X1[0]
X1[1] 1
X2[0]
W40 1
W80 W80
2点DFT XX111[11[]1]
1 X4X1点21[20[]D0W] FW80T40
2点DFT XX121[21[]1W] W82411
1
1
xx[[11]]
XX212[10[]0]
xx[[35]] xx[[53]] xx[[77]]
W80 W80
2点DFT XX212[11[]1]
X2[1]
W41
1
1
X[0] X[1] X[2] X[3]
X[8mX点[m4基]]2X时X11[[间mm]]抽WW取88mmFXXF22[[Tmm算]],, 法mm流 00图,,11,,22,,33
x[0]
X1[0]
X [0]
x[2]
X1[1]
X [1]
x[4]
4点DFT
X1[2]
X [2]
x[6]
N=2
x[k]={x[0], x[1]}
X[0] x[0] W20 x[1] X [1] x[0] W21x[1] x[0] W20 x[1]
x[0]
X [0]
x[1] W20
-1
X [1]

《快速傅里叶变换(FFT) 第四章》

《快速傅里叶变换(FFT) 第四章》

方法： 分解N为较小值：把序列分解为几个较短的 序列，分别计算其DFT值； 利用旋转因子WNk的周期性、对称性、可 约性进行合并、归类处理，以减少DFT的运 算次数。 k ( kn WN m WNN m WN ( nlN ) WNk lN ) n WN 周期性： N m m N m N m m m m 对称性：Wm WNm [W WN N WNN [WNNN m ]] WN WN 2 WN WN 可约性：W mN N W knmW kn / m W kn m kmn ,m 2 2
x ( r ) W x ( r )W x ( r ) W x ( r )W e (r W x r) xxr) W( r ) W (WW (r )W W e W (2 ) x x x(2 r 1)
W e
2 j 2 kr 2 kr N N /2
N 2
2 这样将N点DFT分解为两个N/2点的DFT
N X (k ) X 1 (k ) W X 2k(k ) k 0,1, 1 N X (k ) X 1 (k ) WN X 2 (k ) k 0,1, N 1 2 k X (kN X 1 (k ) WN X 2 (k ) k 0,1, 2 1 ) N2 k X (k N X 1 (k ) WN X 2 (k ) k 0,1, 1 N ) k X (k 2 N X 1 (k ) WN X 2 (k ) k 0,1, N 1 ) 2 k 2 X (k ) X (k ) W X (k ) k 0,1, 2 1
4.1 离散傅里叶变换的高效计算思路 DFT是信号分析与处理中的一种重要变换。但直接 计算DFT的计算量与变换区间长度N的平方成正比， 当N较大时，计算量太大，直接用DFT算法进行谱分 析和信号的实时处理是不切实际的。

详解FFT(快速傅里叶变换FFT

详解FFT(快速傅里叶变换FFT

knN W N N第四章 快速傅里叶变换有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长 序列.但其计算量太大,很难实时地处理问题,因此引出了快速傅里叶变换 (FFT). 1965 年，Cooley 和 Tukey 提出了计算离散傅里叶变换（DFT ）的快 速算法，将 DFT 的运算量减少了几个数量级。

从此，对快速傅里叶变换（FFT ） 算法的研究便不断深入，数字信号处理这门新兴学科也随 FFT 的出现和发 展而迅速发展。

根据对序列分解与选取方法的不同而产生了 FFT 的多种算 法，基本算法是基２DIT 和基２DIF 。

FFT 在离散傅里叶反变换、线性卷积 和线性相关等方面也有重要应用。

快速傅里叶变换（FFT ）是计算离散傅里叶变换（DFT ）的快速算法。

DFT 的定义式为N −1X (k ) = ∑ x (n )W NR N (k )n =0在所有复指数值 W kn 的值全部已算好的情况下，要计算一个 X (k ) 需要 N 次复数乘法和 N －1 次复数加法。

算出全部 N 点 X (k ) 共需 N 2次复数乘法和 N ( N − 1) 次复数加法。

即计算量是与 N 2成正比的。

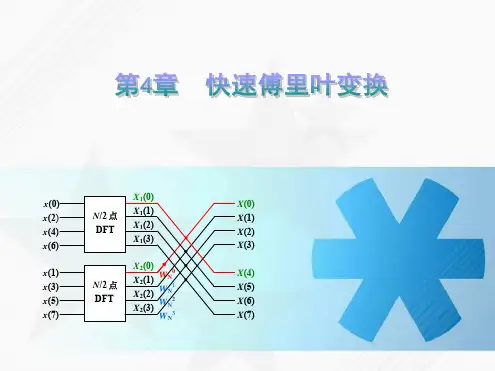
FFT 的基本思想：将大点数的 DFT 分解为若干个小点数 DFT 的组合， 从而减少运算量。

W N 因子具有以下两个特性，可使 DFT 运算量尽量分解为小点数的 DFT运算：（1） 周期性：( k + N ) nN= W kn= W ( n + N ) k（2） 对称性：W( k + N / 2 )= −W kNN利用这两个性质，可以使 DFT 运算中有些项合并，以减少乘法次数。

例子：求当N＝4 时，X(2)的值4 NNN3∑44444X (2) = n =0x (n )W 2 n = x (0)W 0 + x (1)W 2 + x (2)W 4 + x (3)W 6= [ x (0) + x (2)]W 0 + [ x (1) + x (3)]W 2(周期性)4＝[ x (0) + x (2)]－[ x (1) + x (3)]W 04(对称性)通过合并，使乘法次数由 4 次减少到 1 次，运算量减少。

数字信号处理第四章 fft

数字信号处理第四章 fft

第四章 快速傅立叶变换（FFT)
基2FFT算法
FFT的基本思想 长为N的序列x(n)的) N
N 1

x ( n )W N
nk
0 k N 1
nk
n0 N 1

X ( k )W N
0 n N 1
x ( n )
n0
N 2
x(
N 2
rn


N 2
1
x1 ( n )W N
2
rn
n0
基2频域抽取FFT(Sande-Tukey算法 ，DIF-FFT)
X ( 2 r 1)
x ( n ) x ( N 2
n0 1
N 2
N 2
1
n ) W N
( 2 r 1) n

nk
将k分成偶和奇数，即将X(k)分解成奇偶两组，在偶数组中k=2r, e 则 ； jk 1 在奇数组中k=2r+1,则 e 1；有：
jk
X (2r )
x ( n )
n0 1
N 2
1
x ( N n ) W N 2 n) N W
2
2 rn

实序列的FFT算法
Z(k)与H(k)、G(k)的关系 一般而言，H(k)，G(k)均是复函数，因此，关键是怎样从Z(k)中分 离出H(k)和G(k)。Z(k)可写作：
WN W
N 2
N 2
k N
e
j
2 N N 2
W N W N
k
k
) X 1 (k
) WN
k
(k
N 2
)
X 2 (k

数字信号处理_程佩青_PPT第四章

数字信号处理_程佩青_PPT第四章
第四章 快速傅里叶变换 （FFT）
主要内容
DIT-FFT算法 DIF-FFT算法 IFFT算法 Chirp-z算法 线性卷积的FFT算法
§4.0 引言
FFT: Fast Fourier Transform
1965年，Cooley&Turky 发表文章《机器计算傅 里叶级数的一种算法》，提出FFT算法，解决 DFT运算量太大，在实际使用中受限制的问题。 FFT的应用。频谱分析、滤波器实现、实时信 号处理等。 DSP芯片实现。TI公司的TMS 320c30，10MHz 时钟，基2-FFT1024点FFT时间15ms。
又WN
k
N 2
W
N /2 N
W W
k N
k N
k X (k ) X1 (k ) WN X 2 (k )，k 0,1,2,...N / 2 1 (2) X ( N k ) X ( N k ) W ( N / 2 k ) X ( N k ) 1 N 2 2 2 2 k X1 (k ) WN X 2 (k )，k 0,1,2,...N / 2 1


n为偶
n为奇
N / 2 1

rk k rk x ( r ) W W x ( r ) W 1 N /2 N 2 N /2 r 0 r 0 X1 ( k )
N / 2 1
2 rk rk （这一步利用： WN WN /2
） r , k 0,1,...N / 2 1
N为2的整数幂的FFT算法称基-2FFT算法。
将序列x(n)按n的奇偶分成两组：
x1 (r ) x(2r ) ，r 0， 1， 2， ...N/ 2 1 x2 (r ) x(2r 1)

数字信号处理课件第4章

数字信号处理课件第4章
N 2
N −1
2 ( = ∑ x(2r )WN rk + ∑ x(2r + 1)WN2 r +1) k r =0
N 2
−1
N 2
−1
r =0
2 k 2 = ∑ x1 (r )(WN ) rk + WN ∑ x2 (r )(WN ) rk r =0 r =0
−1
N 2
−1
根据可约性，W = e
2 N
N 2
X1(k + N ) = X3 (k) −WNk X4 (k), k = 0,1,L, N −1 4 4
2
(二) N/4点DFT
同样对n为奇数时 ， 点分为两个N/4点的 同样对 为奇数时， N/2点分为两个 为奇数时 点分为两个 点的 序列: 序列 x5 (l) = x2 (2l), l = 0,1,L, N −1 4
3
k 则有：X ( k ) = X 1 (k ) + WN X 2 (k ) k X (k + 4) = X 1 (k ) − WN X 2 (k ), k = 0,1,2,3
(一) N/2点DFT 一 点
整个过程如下图所示: 整个过程如下图所示
x1(0)=x(0) )= ( x1(1)= (2) )=x( x1(2)= (4) )=x( x1(3)= (6) )=x( x2(0)= (1) )=x( x2(1)= (3) )=x( x2(2)= (5) )=x( x2(3)= (7) )=x( X1(0) N/2点 N/2点 X1(1) X1(2) DFT X1(3) X2(0) X2(1) X2(2) X2(3)
2
N 2 N2 ( ) = 2 4 N N ( − 1) 2 2

DSP--FFT-深入浅出-详细讲解快速傅里叶变换

DSP--FFT-深入浅出-详细讲解快速傅里叶变换
第四章 迅速付里叶变换 (FFT) Fast Fourier Transforming
第一节 引言
一、迅速付里叶变换FFT
• 有限长序列经过离散傅里叶变换 (DFT)将其频 域离散化成有限长序列.但其计算量太大(与N 旳平方成正比）, 极难 实时地处理问题 , 因 此 引 出 了 快 速 傅 里 叶 变 换(FFT) .
• 一种复数乘法涉及4个实数乘法和2个实数相 法。
(a+jb)(c+jd)=(ac-bd)+j(bc+ad)
2次实数加法
4次实数乘法
4.计算DFT需要旳实数运算量
N 1
X (k) {(Re[x(n)]Re[WNkn ] Im[x(n)]Im[WNkn ]) n0
j(Re[x(n) Im[WNkn ] Im[x(n)]Re[WNkn ])}
4
4
X (k) N X (k) N
(
N
)
4 2
4
+
(
N 4
4
)2
=
N 4
2
这么一直分下去，剩余两点旳变换。
2、将长序列DFT利用对称性和 周期性分解为短序列DFT--结论
• 迅速付里时变换(FFT)就是在此特征基础上 发展起来旳，并产生了多种FFT算法，其基 本上可提成两大类：
• 按抽取措施分： 时间抽取法(DIT);频率抽取法(DIF)
r 0
r 0
W 2
j 2 2
e N
j 2
e N/2
W
3.求出子序列旳DFT
上式得：
N / 21
N / 21
X（k)
x1(r)WNrk/ 2
x2 (r)WNrk/ 2WNk

第4章快速傅里叶变换

第4章快速傅里叶变换

例如： x(n)：
N=1024，N2=1048576
4
x(n)为N长，DFT变换对：
N 1
X (k ) x(n)WNkn n0
k 0,1, N 1
x(n)
1 N
N 1
X (k )WNnk
k 0
n 0,1, N 1
x(n)：时域信号，X(k)：频域频谱
物理意义不同，
但它们都是N长的序列，如果作为程序入口，没有什么
x1(r)= x(2r)
x2(r)= x(2r+1) r =0,1…N/2-1（长度为N/2）
N 1
则 X (k)
x(
n)W
nk N
x(n)WNnk
x(n)WNnk
n0
n为 偶 数
n为 奇 数
N / 21
N / 21
x(
2r
)W
2 rk N
x(2r 1)WN(2r1)k
r0
r0
N / 21
N2次
经过一次分解，运算量减少将近一半！
经过一次分解后，N→N/2； N/2仍为偶数，仍可进一步分解：
N/2 →N/4
l 0,1,
,
N 4
1
x(n)
x1(r) x(2r)
r 0,1,
,
N 2
1
x2(r) x(2r 1)
x3(l) x1(2l) (偶中偶) x4(l) x1(2l 1) (偶中奇)
问题是如何分最有效？
其中：基-2 FFT 是最基本的 FFT 算法，它要求 FFT 的 点数 N=2L（L为正整数）；
如果序列长度不满足这一条件，需要用后补零值点的 方法来补齐。
4.3 按时间抽取（DIT）的基-2FFT算法

第4章 快速傅里叶变换(FFT)

第4章 快速傅里叶变换(FFT)
第4章 快速傅里叶 变换(FFT)
本章主要内容
直接计算DFT的问题及改进的途径 按时间抽取的基2-FFT算法 按频率抽取的基2-FFT算法 快速傅里叶逆变换(IFFT)算法
2
4.1 引言
DFT在实际应用中很重要: 可以计算信号 的频谱、功率谱和线性卷积等。
直接按DFT变换进行计算，当序列长度N很
5.4 512 262 144 2 304 113.8
8.0 1024 1 048 576 5 120 204.8
12.8 2048 4 194 304 11 264 372.4
64 4049 192
21.4
24
4.2.5 按频率抽取的基2-FFT算法
算法原理
先把输入按n的顺序分成前后两半
再把输出X(k)按k的奇偶分组
所以 整个N点DFT运算共需要： 实数乘法次数： 4 N2
实数加法次数： N×2(2N-1)= 2N(2N-1)
6
DFT运算量的结论
N点DFT的复数乘法次数举例
N
N2
N
N2
2
4
64
4049
4
16
128
16384
8
64
256
65 536
16
256
512
262 144
32
1028
1024
1 048 576
N / 21
x(n)WNnk
n0

N / 21
x(n
n0

N 2
(n N )k
)WN 2

N / 21 x(n)
n0

x(n

N 2

快速傅立叶变换(fft)

快速傅立叶变换(fft)

快速傅立叶变换(fft)快速傅里叶变换(FFT)是一种广泛应用于信号处理、图像处理、音频处理、科学数据处理等领域的数学算法。

它可以将时域信号（即时序信号）转换成频域信号，便于对信号进行分析和处理，以便更好地理解和应用信号的特征。

FFT算法的提出的历史非常悠久。

早在1809年，法国数学家Poisson和Laplace就提出了一些有关傅里叶级数的理论。

1965年，J.W. Cooley和J.W. Tukey等人发布了经典的Cooley-Tukey FFT算法，从而大幅提升了FFT的效率，使其利于实际应用。

FFT的原理是将一个离散的、周期性的时域信号，通过离散傅里叶变换（DFT，或称为“离散频谱分析”）、快速卷积公式等方法，转换成一个频域的信息序列，包含了原信号在复平面上的所有幅度、相位信息。

通过FFT转换后的频域信息，可以较容易地对信号进行频谱分析、滤波、变换和还原等处理过程。

FFT算法具有众多的优势。

首先，FFT算法可以将时间复杂度从O(N*N)大幅降低为O(N log N)，大大提高了数据处理的速度。

其次，FFT算法在数字信号处理领域中拥有广泛的应用，如用于信号重构、信号滤波、降噪、音频处理等等。

此外，由于FFT所得到的频域信号表达了各个频率波形的信息，因此可以在多个领域中运用，例如图像的快速变换、高质量视频文件传输等等。

不过，FFT算法也存在不少的局限性，其中最常见的就是其对时间步骤的依赖，并且对于非周期信号的处理效果可能不够理想。

此外，FFT算法对于像素点的数量是有要求的，不能过少或过多，过少的话会导致数据量太少，过多的话会导致计算机内存爆炸，计算时间也会变得非常长。

综上所述，虽然FFT算法存在着一定的局限性，但是其作为一种广泛应用于信号处理、图像处理、音频处理、科学数据处理等领域的数学算法，其高速、准确、可靠等优点，还是使其得到了广泛的应用。

如果在使用FFT算法时能充分了解其原理和应用场景，遵循其设计规范，就可以更好地发挥出其优势，提高数据处理的效率，为人们生产生活带来更多便利。

4-快速傅里叶变换解析

4-快速傅里叶变换解析

k 0,1,, N 1 2
X

k

N 2


X1 (k )
WNk
X 2 (k)
k 0,1,
, N 1 2
x1(0 )＝x(0 ) x1(1 )＝x(2 )
X1(0 )
X1(1 ) N点
X(0 ) X(1 )

x(2r x(2r
) x1(r) 1) x2
从上面的统计可以看到，直接计算DFT，乘法次数和加法 次数都是和N2成正比的，当N很大时，运算量是很可观的，有 时是无法忍受的。
6
第4章 快速傅里叶变换(FFT)
例3-1 根据式（3-1），对一幅N×N点的二维图像进行DFT 变换，如用每秒可做10万次复数乘法的计算机，当N=1024时， 问需要多少时间（不考虑加法运算时间）？
X1(k) WNk X 2 (k) ,
k 0,1,, N 1 2
13
第4章 快速傅里叶变换(FFT)
X (k) X1(k) WNk X 2 (k) , k 0,1,
, N 1 2
（4-11）
X

k

N 2


X1

k

N 2

W
k

N 2
22
(2)两个N/2点的DFT运算量:复乘次数: N 2
2
复加次数: N ( N 1)
2
(3)N/2个蝶形运算的运算量:复乘次数: N
复加次数:
2 2
N
N
2
总共运算量:
复乘: 复加:
N2 N

N ( N 1)/ 2 N 2

第4章 快速傅里叶变换(FFT)

第4章 快速傅里叶变换(FFT)
DIF-FFT）。
第4章 快速傅里叶变换(FFT)
4.2.2 时域抽取法基2FFT基本原理
先设序列点数为N=2M，M为整数。如果不满足这个条 件，可以人为地加上若干零值点，使之达到这一要求。 这种N为2的整数幂的FFT称基-2 FFT。
(一)N/2点DFT
按n的奇偶把x(n)分解为两个N/2点的子序列
第4章 快速傅里叶变换(FFT)
(3)对X1(k)和X 2 (k)进行蝶形运算,前半部为
X(0)~X(3),后半部分为 X(4) ~ X(7) 整个过程如图4.2.2 所示:
x(0 )
X1(0 )
X(0 )
x(2 )
N/2点 X1(1 )
X(1 )
x(4 )
X1(2 )
X(2 )
DFT
x(6 )
X1(3 )
WNk
X2(k)
X(N 2

k)

X1(k) WNk
X 2 (k )
(后一半)
计算X(k)包含N/2个蝶形运算和两个N/2点DFT运算
计算工作量分析
第4章 快速傅里叶变换(FFT)
(1)1个N/2点的DFT运算量:
复乘次数: ( N )2 N 2 复加次数: N ( N 1)
24
22
(2)两个N/2点的DFT运算量:
例如,N=8时的DFT可分解为四个N/4的DFT, 具体步骤如下:
(1) 将原序列x(n)的“偶中偶”部分:
x3(l) x1(r) x(n) x3(0) x1(0) x(0) x3(1) x1(2) x(4)
第4章 快速傅里叶变换(FFT)
第4章 快速傅里叶变换(FFT)
4.1 引言 4.2 基2FFT算法 4.3 进一步减少运算量的措施

第4章 快速傅里叶变换(FFT)

第4章 快速傅里叶变换(FFT)

A(2) A(3) A(4) A(5) A(6)
WN
0
W
2 N
A(4) A(5)
WN
0
X(4) X(5) X(6) A(7) X(7)
W
0 N
WN
1
A(6)
0 WN
WN
WN
3
2
A(7)
W
2 N
A(7)
图4.2.4 N点DIT―FFT运算流图(N=8)
第4章 快速傅里叶变换(FFT)
4.2.3 DIT―FFT算法与直接计算DFT运算量的比较
N=23=8时的各级旋转因子表示如下：
L=1时，WpN=WJ N/4=WJ2L， J=0 L=2时， WpN =WJ N/2=WJ2L， J=0，1 L=3时， WpN =WJN=WJ2L， J=0，1，2，3 对N=2M的一般情况，第L级的旋转因子为
WNp W2J L, J 0,1, 2, , 2 L1 1 2 L 2 M 2 L M N 2 L M W W
第4章 快速傅里叶变换(FFT)
第4章 快速傅里叶变换(FFT)
4.1 引言
4.2 基2FFT算法
4.3 进一步减少运算量的措施
4.4 分裂基FFT算法
4.5 离散哈特莱变换(DHT)
第4章 快速傅里叶变换(FFT)
4.1 引言
DFT是信号分析与处理中的一种重要变换。因直 接计算DFT的计算量与变换区间长度N的平方成正比， 当N较大时，计算量太大，所以在快速傅里叶变换(简 称FFT)出现以前，直接用DFT算法进行谱分析和信号 的实时处理是不切实际的。直到1965年发现了DFT的 一种快速算法以后，情况才发生了根本的变化。
P N J N 2 L M

第四章快速傅理叶变换FFT

第四章快速傅理叶变换FFT

= 372.4 log 2 N
显然,FFT要比直接DFT运算快得多。
（2）原位运算结构（同址运算） 原位运算结构（ ）
FFT运算结构很有规律，它具有强烈的对称性， 它的所有运算都可以由左下图所示的基本运算构成。 由于运算结构规律，所以硬件实现起来简单，软件 编程方便。 FFT的蝶形运算结构很经济，它可以采用原位运 算。原位运算—— 指当数据输入到存储器中以后， 每一级运算的结果仍然储存在同 一组存储器中，直到最后输出， 中间无需其它任何存储器，称为 原位运算。
n w Nk 的周期性和对称性，求出X(k)的后N/2点的DFT。
(2)求：X ( k + N )＝？
2
k ＝0，1,...,
rk
N
N
−1
2
X 1 (k ) =
N / 2 −1 r =0
∑ x1 (r ) W
令 k= k +
N 2
2
X 1 (k +
N 2
)=
N / 2 −1
∑
r =0
x1 (r ) w
∑
nk x(n )w N +
奇数 n = 1
∑
N −1 nk x(n )w N
∑
r =0
2 x ( 2 r ) w Nrk +
2π 2 rk − j N
N / 2 −1
∑
r =0
( x ( 2 r + 1) w N2 r + 1 ) k
2 Q w N rk = e
=e
− j
2π
N
rk
2
rk = wN
结论：
nk 1) 利用系数 w N 的周期性 对称性 周期性和对称性 周期性 对称性可以提高DFT的
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

X(
N k +k = X 2 (k ) ) X 1 (k ) − WN 2
按时间抽取的 8 点 FFT 算法
x ( 0) x1 (0) = x(0) x3 (0) = x1 (0) = x(0) x(1) x (1) = x(2) x3 (l ) x3 (1) = x1 (2) = x(4) 1 x1 (r ) x ( 2) x1 (2) = x(4) x4 (0) = x1 (1) = x(2) x4 (l ) x4 (1) = x1 (3) = x(6) x1 (3) = x(6) x(3) x (n) ⇒ ⇒ x5 (0) = x2 (0) = x(1) x2 (0) = x(1) x ( 4) x5 (l ) x(5) x5 (1) = x2 (2) = x(5) x2 (1) = x(3) x2 ( r ) x x x = = ( 0 ) ( 1 ) ( 3 ) x x ( 2 ) ( 5 ) = x ( 6 ) 6 2 2 x6 (l ) x (7 ) x x x = = ( 1 ) ( 3 ) ( 7 ) x x ( 3 ) ( 7 ) = 6 2 2

(2)
显然： X (2r ), X (2r + 1)对应两个N / 2点的DFT。
令：
N x ( n ) x ( n ) x ( n = + + 1 2) n N x2 (n) = [ x(n) − x(n + 2 )] WN
用蝶型结构图表示为：
x ( n) x(n + )
N 2
x ( n) + x ( n + N 2)
x ( 2)
W
0 N
2 WN
X ( 2)
X (3)
0 WN
x ( 6)
x(1)
W
0 N
W
1 N
X ( 4)
x(5)
0 WN
X (5)
2 WN
3 WN
x(3)W0 NFra bibliotek2 WN
X ( 6)
X (7 )
x (7 )
第一级
m=0
.... ...... .......... .. .......... ..........
第四章 快速傅里叶变换 （FFT）
主要内容
DIT-FFT算法 DIF-FFT算法 重叠相加法 重叠保留法
学习目标
理解按时间抽选的基-2FFT算法的算法原理、 运算流图、所需计算量和算法特点 理解按频率抽选的基-2FFT算法的算法原理、 运算流图、所需计算量和算法特点 理解IFFT算法 了解混合基算法 理解线性卷积的FFT算法及分段卷积方法
§4.2 直接计算DFT的问题及改进途径
1、 DFT与IDFT
N 点有限长序列x(n)
X (k ) = ∑ x(n)W
n =0 N −1 kn N
1 x ( n) = N
复数加法 N–1 N (N – 1)
∑ X (k )W
k =0
N −1
− kn N
一个X(k) N个X(k) (N点DFT)
复数乘法 N N2
W
2 2 W N N
x2(2)
3 3 W NN W x2(3)
x1(0)
x3(0) N/4点 DFT
X3(0)=X1(0)=X(0)
x1(1)
x3(1)
X3(1)=X1(2)=X(4)
x1(2)
-1
0 0 W WN / 2N x4(0)
k WN
k X 1 ( k ) + WN X 2 (k )
-1
k X 1 ( k ) − WN X 2 (k )
注：a. 上支路为加法，下支路为减法； b. 乘法运算的支路标箭头和系数。
N =8=2 用“蝶形结”表示上面运算的分解：
3
X = (k ) X 1 (k ) + WNk X 2 (k )
mF ( DFT ) N2 2N = = mF ( FFT ) N log N log 2 N 2 2
§4.4 按频率抽取（DIF）的FFT算法
（Decimation In Frequency) 一、算法原理
与DIT-FFT算法类似分解，但是抽取的是X(k)。 即分解X(k)成奇数与偶数序号的两个序列。 设： N = 2L，L 为整数。将X(k)按k的奇偶分 组前，先将输入x(n)按n的顺序分成前后两半：
[
]
n为偶
n为奇
=
rk k rk x r W + W x r W ( ) ( ) ∑ N /2 1 N ∑ 2 N /2 r =0 r =0 X1 ( k ) X 2 (k )
N / 2 −1
N / 2 −1
2 rk rk = r , k 0,1,... N / 2 − 1 （这一步利用： WN ） = WN /2
−j 2π mnk mN
− nk N
( N −n ) k N
n ( N −k ) N
周期性 = W W = W
可约性
↓
−j 2π N ⋅ N 2
e = e = −1 e ↑ 0 ( k + N / 2) k 特殊点： WN = 1 WNN / 2 = −1 WN = −WN
− jπ
FFT 算法的基本思想： 利用DFT 系数的特性，合并DFT 运算中的某些项， 把长序列DFT → 短序列DFT，从而减少其运算量。
X (2 = r + 1) =
N / 2 −1
k = 2 r , 2 r + 1 的 X ( k )：
2 rn N ( ) ( ) x n x n W + + N 2 nr N ( ) ( ) x n x n W + + 2 N /2 x1 ( n )
x ( n + ) WN
k
]
nk
Nk / 2 N
= (−1)
=
N / 2 −1
∑
n =0
N nk k x ( n ) + ( −1) x n + 2 WN
= k 0,1,..., N − 1
按k的奇偶将X(k)分成两部分：
下面讨论
X (2 r) = =
1． N=2L时，共有L级运算；每一级有N/2个蝶形结, 每个蝶形有1次复数乘法2次复数加法。 2．每一级有N个中间数据，且每级只用到本级的转 入中间数据，适合于迭代运算。 3．计算量： N N mF = L log 2 N 复数乘法： = 2 2 复数加法： a = NL = N log 2 N F 比较DFT
X = (k ) X 1 (k ) + W X 2 (k )
k N
再利用周期性求X(k)的后半部分
W
r ( N / 2+ k ) N /2
=W
rk N /2
N / 2 −1 N / 2 −1 N / 2+ k ) rk ( ) X 1 + k = ∑ x1 (r )WNr (/ N x r W = ∑ 2 N / 2 = X 1 (k ) 1 r =0 2 r =0 N + k N k k X 2 + k = X 2 (k ) 又WN 2 = WNN / 2WN = −WN 2
第二级
m =1
第三级
m=2
(2) W 因子的分布
k N
X 1 (k )
X 2 (k )
WNk
X 1 (k ) + WNk X 2 (k )
X 1 (k ) − WNk X 2 (k )
由上可知： m = 0级，W m = 1级，W
k 2 0 2 k 4 k 8 0 4
-1
k = 0 W =W
0 8 1 4 0 8 2 8 3 8
k X k X k W ( ) ( ) = + N X 2 ( k )，k = 0,1,2,...N / 2 − 1 1 (2) X ( N + k ) = X ( N + k ) + W ( N / 2+ k ) X ( N + k ) N 1 2 2 2 2 N k X( +k = k 0,1, 2,... N / 2 − 1 ) X 1 (k ) − WN X 2 (k )，= 2
3、降低DFT运算量的考虑
W 的特性 WNnk = e
对称性
nk * N
nk N
−j
2π nk N
= W = W (W= ) W ↓ ↓ − nk nN − nk ⋅ WN WN WNNk ⋅ WN
nk N ( N +n ) k N n ( N +k ) N
nk mnk nk nk / m WN = WmN WN = WN /m
FFT算法分类:
时间抽选法 DIT: Decimation-In-Time 频率抽选法 DIF: Decimation-In-Frequency
§4.3 按时间抽取（DIT）的FFT算法
（Decimation In Time）
1、算法原理
设序列点数 N = 2L，L 为整数。 若不满足，则补零
∑
n =0
N / 2 −1
∑
n =0
n =0

(1)
N / 2 −1
∑
(2 r +1) n N x ( n ) − x ( n + ) W N 2
N / 2 −1
∑
n =0
n nr N x ( n ) − x ( n + ) W W N N /2 2 x2 ( n )