XXGX第4章 部分相干理论

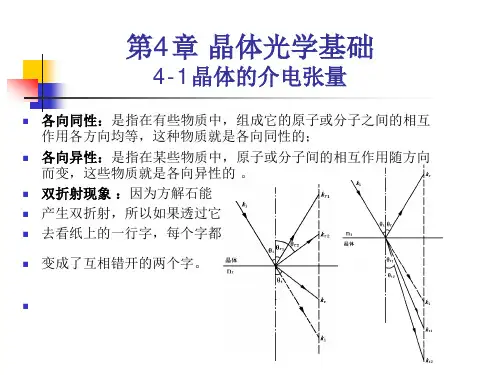
相干现象的基本原理相干现象是光学中一种重要而复杂的现象，其基本原理是光波的叠加和干涉。

在光的传播过程中，当两束或多束光波相遇时，它们会发生干涉现象，这种干涉现象就被称为相干现象。

相干现象广泛应用于光学、物理等领域，如干涉仪、光栅、光波导等。

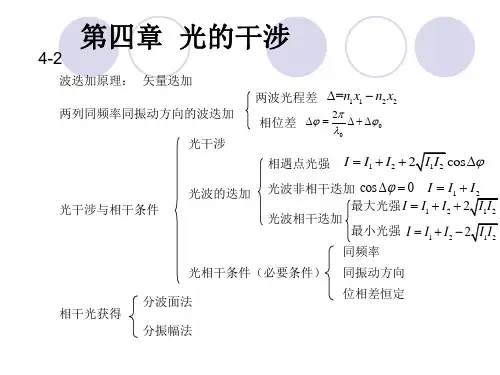
一、光波的叠加光波的叠加是相干现象的基础。

当两束或多束光波在空间中相遇时，它们会叠加在一起，形成新的光波。

光波的叠加是指两个或多个光波的振幅相加，其中正相加会使振幅增大，负相加会使振幅减小。

二、相干性相干性是指两束或多束光波在空间和时间上的关系。

在干涉现象中，如果两束或多束光波的频率、相位、波长等都相等或相差一个整数倍时，它们就具有相干性。

相干性是决定相干现象产生的关键因素。

三、干涉现象当两束或多束相干光波相遇时，它们会发生干涉现象。

干涉可以分为波前干涉和波动干涉。

波前干涉是指不同光源发出的光波经过空间中的不同路径传播后，在某一点上相遇，产生干涉现象。

波动干涉是指单一光源发出的光波经过不同路径传播后，在某一点上相遇，产生干涉现象。

四、干涉的类型干涉现象可分为两种类型：构成干涉和破坏干涉。

构成干涉是指两束或多束光波在相遇处会相互加强或相互减弱，产生明暗交替的条纹或干涉图样。

破坏干涉是指两束或多束光波相互叠加后会彼此消除或部分消除，不会产生干涉图样。

五、应用领域相干现象的应用非常广泛。

在光学领域，相干现象是干涉仪的基础理论，干涉仪可以用于测量非常小的长度、角度和折射率等物理量。

光栅也是相干现象的重要应用之一，利用光波的干涉现象可以实现光栅的制作和应用。

另外，相干现象还广泛应用于光学成像、光学信息处理、光学通信等领域，对于提高光学器件的性能和实现高精度测量具有重要作用。

总结：相干现象是光学中重要的现象之一，它是光波叠加和干涉的结果。

相干性是决定相干现象产生的关键因素，而干涉现象可分为波前干涉和波动干涉。

在应用上，相干现象广泛应用于光学、物理等领域，并在干涉仪、光栅等设备中发挥着重要的作用。

信息光学习题答案信息光学习题答案第一章线性系统分析简要说明以下系统是否有线性和平移不变性. g?x??df?x?;g?x???f?x?dx; dx?g?x??f?x?;g?x??????f????h?x????d?;2???f???exp??j2????d? 解：线性、平移不变；线性、平移不变；非线性、平移不变；线性、平移不变；线性、非平移不变。

证明comb(x)exp(j?x)?comb(x) ???comb????x? ?x??1?证明：左边＝comb???????n?????(x?2n)??2??(x?2n) ?2?n????2?n????2?n??????x??2?右边?comb(x)?comb(x)exp(j?x)?? ?n?????(x?n)??exp(j?x)?(x?n)n?????n???? ??(x?n)??exp(jn?)?(x?n)n???? n?????(x?n)??(?1)n???n?(x?n)?当n为奇数时，右边＝0，当n为偶数时，右边＝2所以当n为偶数时，左右两边相等。

n?????(x?2n) (x) 证明??(sin?x)?comb证明：根据复合函数形式的δ函数公式?[h(x)]??i?1n?(x?xi)h?(xi ),h?(xi)?0 式中xi是h(x)=0的根，h?(xi)表示h(x)在x?xi处的导数。

于是??(sin?x)??n?????(x?n)???co mb(x) 1 计算图题所示的两函数的一维卷积。

解：设卷积为g(x)。

当-1≤x≤0时，如图题(a)所示，g(x)??1?x0(1??)(1?x??)d??111?x?x3 326 图题当0 2??2?2??2?2?2?x?2设卷积为g(x)，当x≤0时，如图题(a)所示，g(x)??0d??x?2 当0 2 图题g(x)??d??2?x x2?x?1?2,x?0 g(x)?2?x?1?,x?0?2即g(x)?2??? ?x??2?(x)?rect(x)?1已知exp(??x2)的傅立叶变换为exp(???2)，试求?exp?x2???exp?x2/2?2解：设y??????????? ?x,z??? 即??exp(??y2)??exp(???2) 1????F?,? 得ab?ab?2坐标缩放性质??f(ax,by)???exp?x2???????exp(?y2/??? exp(??z2)??exp(??2?2)2??exp?x/2???2?????exp??y?/2??2 ? ??2??exp(?2??2z2)?2??exp(?2??2?2)计算积分.????sinc?x?dx?? 4??2?x?cos?xdx?? sinc?解：应用广义巴塞伐定理可得? sinc(x)sinc(x)dx?????2222 ?(?)?(?)d??(1?? )d??(1??)d??????103??021???1?1?1?????s inc(x)cos?xdx????(?)?????d????(?)?????d ??2???2?2????????2?1??1??1??1 ??????????? 2??2??2?? 应用卷积定理求f?x??sinc?x?sinc?2x?的傅里叶变换. 3解：??sinc(x)sinc(2x)????sinc(x)????sinc( 2x)??1???rect(?)?rect?? 2?2?当?31????时，如图题(a)所示，2211??3 G(?)??2du??? 2?12当?11???时，如图题(b)所示，2211??2 G(?)??1du?1 2??2当13???时，如图题(c)所示，22113 G(?)??1du??? 2??222G(ξ)的图形如图题(d)所示，图可知G(?)?3???1?????????? 4?3/2?4?1/2? 图题 4 设f?x??exp??x，??0，求??f?x????解：?exp(??x)???????f?x?dx?? ?0?? ?0??exp(?x)exp(?j2??x)dx??exp(??x)exp(? j2??x)dx ?2??2??(2??)2??? exp(??x)dx?2??2?(2??)2???02? 设线性平移不变系统的原点响应为h?x??exp??x?step?x?，试计算系统对阶跃函数step?x?的响应. 解：阶跃函数定义step(x)??线性平移不变系统的原点响应为h?x??exp??x?step?x??exp??x?,所以系统对解阶跃函数step?x?的响应为g(x)?step(x)?h(x)??1,?0,x?0得x?0x?0 ??0exp[?(x??)]d??1?exp(?x), x?0 有两个线性平移不变系统，它们的原点脉冲响应分别为h1?x??sinc?x?和h2?x??sinc?3x?.试计算各自对输入函数f?x??cos2?x的响应g1?x?和g2?x?. 解：已知一平面波的复振幅表达式为U(x,y,z)?Aexp[j(2x?3y?4z)] 试计算其波长λ以及沿x,y,z方向的空间频率。

量子相干论-概述说明以及解释1.引言1.1 概述量子相干是量子力学中一项重要的概念，它描述了量子系统中的一种非常特殊的状态。

相干性是指量子态中的物理量之间存在特定的相互关系，这种相互关系可以用波函数的幅度和相位来描述。

在量子相干中，不同物理量之间的相位关系非常重要，任何对相位的微小改变都可能导致量子系统的状态发生巨大变化。

量子相干的产生可以通过一系列的操作和控制来实现，例如激光的干涉、原子的束缚和耦合等。

相较于经典的相干，量子相干具有一些独特的性质。

首先，量子相干是一种量子态，其存在于一个复杂的希尔伯特空间中，这种空间与经典物理领域中的相位空间具有本质的区别。

其次，量子相干不仅仅包含了经典相干的波动特性，还涵盖了量子性的波粒二象性。

这使得量子相干成为实现量子信息与量子计算的重要基础。

量子相干的性质非常丰富多样。

首先，量子相干的幅度和相位之间存在非常特殊的关系，可以根据不同的相位关系对量子相干进行分类。

例如，存在着相位完全相同或相反的相干态，以及相位在某种方式下均匀分布的相干态。

其次，量子相干的性质还包括时间演化、热力学行为和量子态的纠缠等方面。

这些性质使得量子相干成为研究和应用的热点领域。

量子相干在众多领域中有着广泛的应用。

在量子信息科学中，量子相干是实现量子比特之间相互操作和传输的基础。

在量子计算领域，量子相干是存储和操作量子信息的重要手段。

此外，量子相干还在量子通信、量子测量和量子传感等领域中发挥着关键作用。

随着量子技术的快速发展，量子相干将继续成为研究和应用的热点领域，并为人类社会带来深远的影响。

综上所述，量子相干作为量子力学中的一个重要概念，具有丰富多样的性质和广泛的应用。

对于深入理解量子系统的性质以及实现量子信息和计算的目标，探究和研究量子相干是非常必要和有价值的。

在未来的发展中，我们可以进一步挖掘量子相干的特性，拓展其应用领域，并致力于实现量子技术的革命性突破。

1.2文章结构1.2 文章结构本文将按照以下结构进行展开：1. 引言：介绍量子相干的重要性和相关背景知识。