2017年春季学期新版北师大版九年级数学下册1.1锐角三角函数同步练习5

北师大九年级数学下册 1.1 锐角三角函数同步训练学校：__________ 班级：__________ 姓名：__________ 考号：__________一、选择题（本题共计 8 小题，每题 3 分，共计24分，）1. 如图，的三个顶点都在方格纸的格点上，则A. B. C. D.2. 若为锐角，且，则A.小于B.大于C.大于且小于D.大于3. 若，则下列说法不正确的是（）A.随的增大而增大B.随的增大而减小C.随的增大而增大D.、、的值都随的增大而增大4. 如果在中，，，，那么下列各式正确的是（）A. B.C. D.5. 若把一个直角三角形的两条直角边都扩大倍，（是大于的自然数），则两个锐角的三角函数值（）A.都变大为原来的倍B.都缩小为原来的C.不变化D.各个函数值变化不一致6. 比较，，的大小关系是（）A. B.C. D.7. 如图，在中，，，的平分线与的外角平分线交于，连接，则的值是（）A. B. C. D.8. 如图，在中，点在上，，垂足为，若，，则等于（）A. B. C. D.二、填空题（本题共计 8 小题，每题 3 分，共计24分，）9. ________ （填大小关系）10. 在中，，如果，，那么________．11. 在中，，当已知和时，求，则、、关系式是________．12. 已知在中，为直角，，，________．13. 已知为锐角，且，那么的范围是________．14. 在中，，、、分别是、、的对边，下列式子：① ，② ，③ ，④，必定成立的是________．15. 如图，是的边上一点，且点坐标为，则________________．16. 如图，直角三角形纸片的两直角边长分别为，，现将如图那样折叠，使点与点重合，折痕为，则的值是________．三、解答题（本题共计 8 小题，每题 9 分，共计72分，）17. 在中，，若，写出的四个三角函数的值．18. 分别求出图中、的正弦值、余弦值和正切值．19. 在中，，、、分别是、、的对边．请利用三角函数的定义探讨能否用边的式子表示？请写出你必要的理由．20. 如图，点在第一象限，与轴所夹的锐角为，，求的值．21. 在中，，，，求的值．22. 如图，在中，，是直角边上一点，于点，，，求的值．23. 如图，在中，，，．求的长；利用此图形求的值（精确到，参考数据：，，）24. 如图，在四边形中，平分，，，求的值．答案1. D2. D3. D4. A5. C6. D7. D8. D9.10.11.12.13.②15.16.17. 解：，，由勾股定理，得，，，．18. 解：如图，，，，，，，．如图，，，，，，，．如图 ， ，，，，，，． 19. 解：∵，， ∴，即 ．20. 解：过 作 轴于 ．∴， ∵ ， ∴， ∵ ，∴ ，∴ ，∴．21. 解：在中，，，，∵，∴，则．22. 解：∵ ，，∴ ，又∵ ，∴ ，∴，设，，由勾股定理得：，在中，．23. 解：过作，交的延长线于点，如图所示：在中，，∵ ，∴ ，∴，，在中，，∴ ，∴；在边上取一点，使得，连接，如图所示：∵ ，∴ ，．24. 解：∵ 平分，∴ ．又∵ ，∴ ．∴，在中，∵，∴．。

北师大版数学九年级下册1.1锐角三角函数课时练习一、单选题（共15题）1．在Rt △ABC 中，∠C =90°，若斜边AB 是直角边BC 的3倍，则tanB 的值是（ ）A ．13B ．3C ．4D ．答案：D解析：解答：设BC =x ，则AB =3x ，由勾股定理得，，tanB=AC BC ==故选：D ． 分析: 设BC =x ，则AB=3x ，由勾股定理求出AC ，根据三角函数的概念求出tanB 。

2. 如图，在△ABC 中，∠C =90°，AB =5，BC =3，则cosA 的值是（ ）∴AC=4，∴cosA=45AC AB =故选D ． 分析: 根据锐角的余弦等于邻边比斜边求解即可3. 如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是（ ）A ．2BCD ．12 答案：D解析：解答:如图，由勾股定理，得tan∠B=12 ACAB=故选：D．分析: 根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案。

4. 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是（）A．BDBCB．BCABC．ADACD．CDAC答案：C解析：解答: ∵AC⊥BC，CD⊥AB，∴∠α+∠BCD=∠ACD+∠BCD，∴∠α=∠ACD，∴cosα=cos∠ACD=BD BC DC BC AB AC==，只有选项C错误，符合题意．分析: 利用垂直的定义以及互余的定义得出∠α=∠ACD，进而利用锐角三角函数关系得出答案．5. 已知sin6°=a，sin36°=b，则sin26°=（）A．a2 B．2a C．b2 D．b答案：A解析：解答: ∵sin6°=a，∴sin26°=a2．故选：A．分析: 根据一个数的平方的含义和求法，由sin6°=a，可得sin26°=a2，据此解答即可．6. 在Rt△ABC中，各边的长度都扩大两倍，那么锐角A的各三角函数值（）A．都扩大两倍B．都缩小两倍C．不变D．都扩大四倍答案：C解析：解答: ∵各边的长度都扩大两倍，∴扩大后的三角形与Rt△ABC相似，∴锐角A的各三角函数值都不变．故选C．分析: 根据三边对应成比例，两三角形相似，可知扩大后的三角形与原三角形相似，再根据相似三角形对应角相等解答．7. △ABC中，a、b、c分别是∠A、∠B、∠C的对边，如果a2+b2=c2，那么下列结论正确的是（）A．b cosB=c B．c sinA=a C．a tanA=b D．tanB＝b c答案：B解析：解答：∵a2+b2=c2，∴△ABC是直角三角形，且∠C=90°，∴sinA=ac即csinA=a，∴B选项正确．故选B．分析: 由于a2+b2=c2，根据勾股定理的逆定理得到△ABC是直角三角形，且∠C=90°，再根据锐角三角函数的定义即可得到正确选项．8. 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（）A．b=a tanB B．a=c cosB C．c＝asinAD．a=b cosA答案：D解析：解答: ∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，∴A.tanB=ba，则b=a tanB，故本选项正确，B.cosB=ac，故本选项正确，C.sinA=ac，故本选项正确，D.cosA=bc，故本选项错误，故选D ．分析: 根据三角函数的定义就可以解决.9. 在Rt △ABC 中，∠C=90°，AB=13，AC=12，则cosA=（ ）A ．513B ．512C ．1213D ．125答案：C解析：解答: ∵Rt △ABC 中，∠C=90°，AB=13，AC=12，∴cosA=1213AC AB 故选C ．分析: 直接根据余弦的定义即可得到答案．10. 如果∠A 为锐角，且sinA=0.6，那么（ ）A ．0°＜A≤30°B ．30°＜A ＜45°C ．45°＜A ＜60°D ．60°＜A≤90°答案：B解析：解答: ∵sin30°=12 =0.5，sin45°=2≈0.707，sinA=0.6，且sin α随α的增大而增大，∴30°＜A ＜45°．故选B ．分析:此题考查了正弦函数的增减性与特殊角的三角函数值．此题难度不大，注意掌握sin α随α的增大而增大.11. 在Rt △ABC 中，如果各边长度都扩大为原来的2倍，那么锐角A 的正弦值（ ）A.扩大2倍 B ．缩小2倍 C ．扩大4倍 D ．没有变化答案：D解析：解答: 根据锐角三角函数的概念，知若各边长都扩大2倍，则sinA 的值不变． 故选D ．分析: 理解锐角三角函数的概念：锐角A 的各个三角函数值等于直角三角形的边的比值．12. 如图，梯子跟地面的夹角为∠A ，关于∠A 的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）A ．sinA 的值越小，梯子越陡B ．cosA 的值越小，梯子越陡C．tanA的值越小，梯子越陡D．陡缓程度与上A的函数值无关答案：B解析：解答: sinA的值越小，∠A越小，梯子越平缓；cosA的值越小，∠A就越大，梯子越陡；tanA的值越小，∠A越小，梯子越平缓，所以B正确．故选B．分析: 根据锐角三角函数的增减性即可得到答案13. sin70°，cos70°，tan70°的大小关系是（）A．tan70°＜cos70°＜sin70° B．cos70°＜tan70°＜sin70°C．sin70°＜cos70°＜tan70° D．cos70°＜sin70°＜tan70°答案：D解析：解答：根据锐角三角函数的概念，知sin70°＜1，cos70°＜1，tan70°＞1．又cos70°=sin20°，正弦值随着角的增大而增大，∴sin70°＞cos70°=sin20°．故选D．分析: 首先根据锐角三角函数的概念，知：sin70°和cos70°都小于1，tan70°大于1，故tan70°最大；只需比较sin70°和cos70°，又cos70°=sin20°，再根据正弦值随着角的增大而增大，进行比较14. 随着锐角α的增大，cosα的值（）A．增大B．减小C．不变D．增大还是减小不确定答案：B解析：解答：随着锐角α的增大，cosα的值减小．故选B．分析: 当角度在0°～90°间变化时，余弦值随着角度的增大而减小，依此求解即可．15. 当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是（）A．正弦和余弦B．正弦和正切C．余弦和正切D．正弦、余弦和正切答案：B解析：解答：当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是正弦和正切．故选B．分析: 当角度在0°到90°之间变化时，正弦和正切函数值随着角度的增大而增大．二、填空题（共5题）1. 如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB=____________答案：7 13解析：解答: ∵在Rt△ABC中，∠C=90°，AB=13，AC=7，∴sinB=ACAB=713故答案是：7 13分析:根据锐角三角函数定义直接进行解答。

第一章 直角三角形的边角关系1.1 锐角三角函数 第1课时 正切基础题 知识点1 正切(tanA ＝∠A的对边∠A的邻边)1.如图，已知在Rt△ABC 中，∠C＝90°，BC ＝1，AC ＝2，则tanA 的值为(B) A .2 B.12C.55 D.2552.在△ABC 中，若BC∶CA∶AB＝3∶4∶5，则tan B ＝(C) A.45 B.35 C.43 D.343.如图，点A(t ，3)在第一象限，OA 与x 轴所夹的锐角为α，tan α＝32，则t 的值是(C)A .1B .1.5C .2D .34.(教材P4习题T2变式)(2019·广州)如图，Rt△ABC 中，∠C＝90°，BC ＝15，tanA ＝158，则AB＝17.5.如图，在Rt△ABC 中，∠C＝90°，BC ＝12 cm ，AB ＝20 cm ，求tanA 和tanB 的值. 解：∵∠C＝90°，BC ＝12 cm ， AB ＝20 cm ，∴AC＝AB 2－CB 2＝16 cm. ∴tanA＝BC AC ＝1216＝34，tanB ＝AC BC ＝1612＝43.知识点2 坡度(坡度i ＝铅直高度h水平长度l)6.为测量如图所示的上山坡道的倾斜度，小明测得图中所示的数据(单位：米)，则该坡道的坡度是(A)A.14B .4C.117D.4177.都匀市某新修“商业大厦”的一处自动扶梯如图，已知扶梯的长l 为10米，该自动扶梯到达的高度h 为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于34.8.如图，斜坡AB 的坡度是1∶4，如果从点B 测得离地面的铅垂线高度BC 是6米，那么斜坡AB 的长度是617米.易错点 对正切的概念理解不清9.在Rt△ABC 中，∠C＝90°，若三角形各边同时扩大三倍，则tanA 的值(B) A .扩大为原来的三倍 B .不变 C .缩小为原来的13 D .不确定中档题10.如图，在Rt△ABC 中，CD 是斜边AB 上的中线，已知CD ＝5，AC ＝6，则tan∠DBC 的值是(D) A.45 B.35 C.43 D.3411.如图，一座公路桥离地面高度AC 为6米，引桥AB 的水平宽度BC 为24米，为降低坡度，现决定将引桥坡面改为AD ，使其坡度为1∶6，则BD 的长是(C)A .36米B .24米C .12米D .6米12.在Rt△ABC 中，∠C＝90°，a ，b ，c 分别是∠A，∠B，∠C 的对边.若c ＝4a ，则tanA ＝1515. 13.(教材P4练习T1变式)如图，等腰△ABC 的腰AB ，AC 的长为5，底边长为6，则tanC ＝43.14.已知∠B 是Rt△ABC 的一个锐角，且AB ＝5，AC ＝3，则tanB 的值为34或35.15.(教材P3例1变式)如图所示，方方和圆圆分别将两根木棒AB ，CD 斜立在墙AE 上，其中AB ＝10 cm ，CD ＝6 cm ，BE ＝6 cm ，DE ＝2 cm ，你能判断谁的木棒更陡吗？请说明理由. 解：∵AB＝10 cm ，BE ＝6 cm ， ∴AE＝AB 2－BE 2＝8 cm. ∴斜坡AB 的坡度为AE BE ＝43.∵CD＝6 cm ，DE ＝2 cm ， ∴CE＝CD 2－DE 2＝4 2 cm.∴斜坡CD 的坡度为CE DE ＝422＝2 2.∵43＜22， ∴圆圆的木棒CD 更陡.16.直角三角形纸片的两直角边长分别为6，8，现将△ABC 如图那样折叠，使点A 与点B 重合，折痕为DE ，求tan∠CBE 的值. 解：由折叠性质，得BE ＝AE. 设CE ＝x ，则BE ＝AE ＝8－x. 在Rt△BCE 中，根据勾股定理，得BE 2＝BC 2＋CE 2，即(8－x)2＝62＋x 2，解得x ＝74.∴tan∠CBE＝CE CB ＝724.综合题17.如图，在Rt△BAD 中，延长斜边BD 到点C ，使DC ＝12BD ，连接AC.若tanB ＝53，则tan∠CAD 的值为(D) A.33 B.35C.13D.15第2课时 锐角三角函数基础题 知识点1 正弦和余弦(sinA ＝∠A的对边斜边，cosA ＝∠A的邻边斜边)1.(2019·孝感)如图，在Rt△ABC 中，∠C＝90°，AB ＝10，AC ＝8，则sinA 等于(A)A.35B.45C.34 D.432.(2019·哈尔滨)在Rt△A BC 中，∠C＝90°，AB ＝4，AC ＝1，则cosB 的值为(A) A.154 B.14 C.1515 D.417173.在Rt△ABC 中，∠C＝90°，sinA ＝35，BC ＝6，则AB ＝(D)A .4B .6C .8D .104.(2019·怀化)如图，在平面直角坐标系中，点A 的坐标为(3，4)，那么sin α的值是(C) A.35 B.34 C.45 D.435.(教材P6练习T1变式)已知，如图，在△ABC 中，AB ＝AC ＝6，BC ＝8，AD⊥BC 于点D. (1)求AD 的值； (2)求sinB ，cosC 的值. 解：(1)∵AB＝AC ，AD⊥BC， ∴BD＝CD ＝12BC ＝12×8＝4.∴AD＝AB 2－BD 2＝62－42＝2 5. (2)sinB ＝AD AB ＝256＝53，cosC ＝CD AC ＝46＝23.知识点2 锐角三角函数6.在Rt△ABC 中，∠C＝90°，∠A＝α，AC ＝3，则AB 的长可以表示为(A) A.3cos α B.3sin αC .3sin αD .3cos α 7.(2019·滨州)在△ABC 中，∠C ＝90°.若tanA ＝12，则sinB ＝255.知识点3 互余两角之间正、余弦，正切之间的关系8.(教材P7习题T3变式)如图，在Rt△ABC 中，∠C＝90°，a ，b ，c 分别表示Rt△ABC 中∠A，∠B，∠C 的对边. (1)求sinA ，cosB ； (2)求tanA ，tanB ；(3)观察(1)(2)中的计算结果，你能发现sinA 与cosB ，tanA 与tanB 之间有什么关系吗？ (4)应用：①在Rt△ABC 中，∠C＝90°，若sinA ＝23，则cosB 的值为23；②在Rt△ABC 中，∠C＝90°，若tanA ＝2，则tanB ＝12.解：(1)在Rt△ABC 中，∠C＝90°， ∴sinA＝BC AB ＝ac ，cosB ＝BC AB ＝a c.(2)在Rt△ABC 中，∠C＝90°， ∴tanA＝BC AC ＝ab ，tanB ＝AC BC ＝b a.(3)由(1)知sinA ＝cosB ， 由(2)知tanA·tanB＝1. 易错点 点的位置不确定9.已知，正方形ABCD 的边长为2，点P 是直线CD 上一点.若DP ＝1，则sin∠BPC 的值是255或21313.中档题10.如图，点A 为∠α边上任意一点，作AC⊥BC 于点C ，CD⊥AB 于点D ，下列用线段比表示cos α的值，错误的是(C)A.BD BCB.BCAB C.AD AC D.CD AC11.如图，在菱形ABCD 中，AE⊥BC 于点E ，EC ＝4，sinB ＝45，则菱形ABCD 的周长是(C)A .10B .20C .40D .28 12.在Rt△ABC 中，∠C＝90°，AB ＝2BC ，现给出下列结论：①sinA＝32；②cosB＝12；③tanA＝33；④tanB＝3，其中正确的结论是②③④(只需填上正确结论的序号).13.如图，在△ABC 中，CD⊥AB，垂足为D.若AB ＝12，CD ＝6，tanA ＝32，求sinA ＋cosB 的值.解：在Rt△ACD 中，CD ＝6，tanA ＝CD AD ＝32，∴AD＝4. ∴BD＝AB －AD ＝8.在Rt△BCD 中，BC ＝82＋62＝10.∴cosB＝BD BC ＝45.在Rt△ADC 中，AC ＝42＋62＝213. ∴sinA＝DC AC ＝6213＝31313.∴sinA＋cosB ＝31313＋45. 14.如图，在△ABC 中，AD 是边BC 上的高，E 为AC 的中点，BC ＝14，AD ＝12，sinB ＝45.求：(1)线段CD 的长； (2)tan∠EDC 的值.解：(1)∵AD 是边BC 上的高， ∴△ADB 为直角三角形. ∵AD＝12，sinB ＝45，∴AB＝AD sinB ＝1245＝15.∴BD＝AB 2－AD 2＝152－122＝9. ∴CD＝BC －BD ＝14－9＝5.(2)∵E 是Rt△ADC 斜边AC 的中点， ∴DE＝EC. ∴∠EDC＝∠C.∴tan∠EDC＝tanC ＝AD DC ＝125.综合题15.如图，已知△ABC 的三个顶点均在格点上，则cosA 的值为(D) A.33 B.55 C.233 D.255。

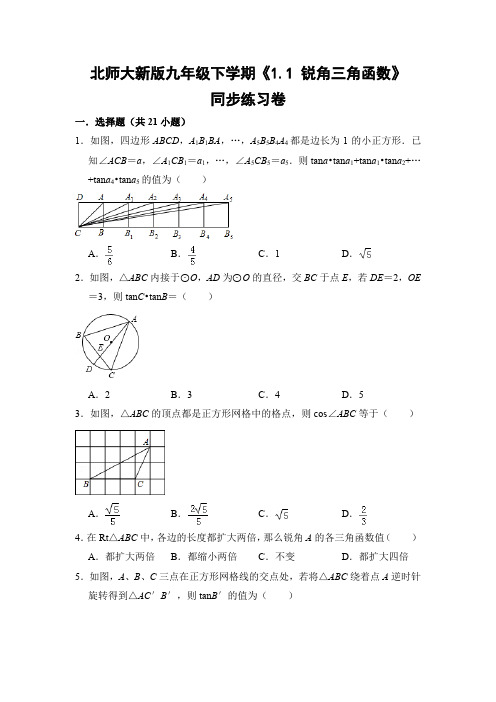
北师大新版九年级下学期《1.1 锐角三角函数》同步练习卷一．选择题（共21小题）1．如图，四边形ABCD，A1B1BA，…，A5B5B4A4都是边长为1的小正方形．已知∠ACB＝a，∠A1CB1＝a1，…，∠A5CB5＝a5．则tan a•tan a1+tan a1•tan a2+…+tan a4•tan a5的值为（）A．B．C．1D．2．如图，△ABC内接于⊙O，AD为⊙O的直径，交BC于点E，若DE＝2，OE ＝3，则tan C•tan B＝（）A．2B．3C．4D．53．如图，△ABC的顶点都是正方形网格中的格点，则cos∠ABC等于（）A．B．C．D．4．在Rt△ABC中，各边的长度都扩大两倍，那么锐角A的各三角函数值（）A．都扩大两倍B．都缩小两倍C．不变D．都扩大四倍5．如图，A、B、C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC′B′，则tan B′的值为（）A．B．C．D．6．如图，∠A的正弦与余弦值分别为（）A．，B．，C．，D．，7．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的中线，若BC＝6，AC＝8，则tan∠ACD的值为（）A．B．C．D．8．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝，AB的垂直平分线ED交BC的延长线于D点，垂足为E，则sin∠CAD＝（）A．B．C．D．9．在正方形网格中，△ABC的位置如图所示，则tan∠A的值为（）A．B．C．D．10．在Rt△ABC中，∠C＝90°，AC＝，BC＝，则cos B的值是（）A．B．C．D．11．在Rt△ABC中，∠C＝90°，AB＝4，BC＝3，则cos B等于（）A．B．C．D．12．Rt△ABC中，∠C＝90°，∠A、∠C所对的边分别为a、c，下列式子中，正确的是（）A．a＝c•cot A B．a＝c•tan A C．a＝c•cos A D．a＝c•sin A 13．在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则∠A的正弦值等于（）A．B．C．D．14．在Rt△ABC中，∠C＝90°，a＝5，b＝12，则tan B的值为（）A．B．C．D．15．如图，在Rt△ACB中，∠C＝90°，∠A＝37°，AC＝4，则BC的长约为（）（sin37°≈0.80，cos37°≈0.60，tan37°≈0.75）A．2.4B．3.0C．3.2D．5.016．在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C对边，如果3a ＝4b，则cos B的值是（）A．B．C．D．17．若锐角三角函数tan55°＝a，则a的范围是（）A．0＜a＜1B．1＜a＜2C．2＜a＜3D．3＜a＜4 18．对于任意锐角α，下列结论正确的是（）A．sinα＜tanαB．sinα≤tanαC．sinα＞tanαD．sinα≥tanα19．已知0＜α＜45°，关于角α的三角函数的命题有：①0＜sinα＜，②cosα＜sinα，③sin2α＝2sinα，④0＜tanα＜1，其中是真命题的个数是（）A．1个B．2个C．3个D．4个20．已知∠A为锐角，且tan A＝，则∠A的取值范围是（）A．0°＜∠A＜30°B．30°＜∠A＜45°C．45°＜∠A ＜60°D．60°＜∠A＜90°21．在Rt△ABC中，∠C＝90°，当∠A的度数不断增大时，cos A的值的变化情况是（）A．不断变大B．不断减小C．不变D．不能确定二．填空题（共14小题）22．在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cos A＝．23．已知△ABC中，AB＝AC，CH是AB边上的高，且CH＝AB，则tan B＝．24．水管的外部需要包扎，包扎时用带子缠绕在管道外部．若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为1，水管直径为4，则α的余弦值为．25．如图，在平面直角坐标系中，已知点A（3，0），点B（0，﹣4），则cos∠OAB等于．26．如果方程x2﹣4x+3＝0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，那么tan A的值为．27．如图，∠1的正切值等于．28．在△ABC中，∠C＝90°，如果AC＝4，sin B＝，那么BC＝．29．在Rt△ABC中，∠C＝90°，AC＝4，AB＝5，则cos A的值是．30．已知△ABC中，∠ACB＝90°，BC＝12，AB＝15，则cos B的值为．31．比较sin53°tan37°的大小．32．比较大小：sin40°cos50°（填“＞”、“＜”或“＝”）33．如图所示的网格是正方形网格，∠BAC∠DAE．（填“＞”，“＝”或“＜”）34．用不等号“＞”或“＜”连接：sin50°cos50°．35．在△ABC中，∠C＝90°，如果sin A＞cos A，那么∠A的度数范围是．三．解答题（共6小题）36．如图，将含30°角的直角三角板ABC（∠A＝30°）绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得到Rt△A′B′C，A′C与AB交于点D，过点D作DE∥A′B′交CB′于点E，连接BE．易知，在旋转过程中，△BDE为直角三角形．设BC＝1，AD＝x，△BDE的面积为S．（1）当α＝30°时，求x的值．（2）求S与x的函数关系式，并写出x的取值范围；（3）以点E为圆心，BE为半径作⊙E，当S＝时，判断⊙E与A′C的位置关系，并求相应的tanα值．37．如图，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作c tanα，即c tanα＝＝，根据上述角的余切定义，解下列问题：（1）c tan30°＝；（2）如图，已知tan A＝，其中∠A为锐角，试求c tan A的值．38．如图所示，在平面直角坐标系xoy中，四边形OABC是正方形，点A的坐标为（m，0）．将正方形OABC绕点O逆时针旋转α角，得到正方形ODEF，DE与边BC交于点M，且点M与B、C不重合．（1）请判断线段CD与OM的位置关系，其位置关系是；（2）试用含m和α的代数式表示线段CM的长：；α的取值范围是．39．如图，AB为⊙O的直径，且弦CD⊥AB于E，过点B的切线与AD的延长线交于点F．（1）若M是AD的中点，连接ME并延长ME交BC于N．求证：MN⊥BC．（2）若cos∠C＝，DF＝3，求⊙O的半径．40．如图，△ABC是等腰三角形，AB＝AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F．（1）求证：DE是⊙O的切线；（2）若⊙O的半径为2，BE＝1，求cos A的值．41．如图，已知：AC是⊙O的直径，P A⊥AC，连接OP，弦CB∥OP，直线PB 交直线AC于D，BD＝2P A．（1）证明：直线PB是⊙O的切线；（2）探究线段PO与线段BC之间的数量关系，并加以证明；（3）求sin∠OP A的值．北师大新版九年级下学期《1.1 锐角三角函数》同步练习卷参考答案与试题解析一．选择题（共21小题）1．如图，四边形ABCD，A1B1BA，…，A5B5B4A4都是边长为1的小正方形．已知∠ACB＝a，∠A1CB1＝a1，…，∠A5CB5＝a5．则tan a•tan a1+tan a1•tan a2+…+tan a4•tan a5的值为（）A．B．C．1D．【分析】根据锐角三角函数的定义，分别在Rt△ACB，Rt△A1CB1，…，Rt△A5CB5中求tan a，tan a1，tan a2，…，tan a5的值，代值计算．【解答】解：根据锐角三角函数的定义，得tan a＝＝1，tan a1＝＝，tan a2＝＝…，tan a5＝＝，则tan a•tan a1+tan a1•tan a2+…+tan a4•tan a5＝1×+×+×+×+×＝1﹣+﹣+﹣+﹣+﹣＝1﹣＝．故选：A．【点评】本题考查了锐角三角函数的定义．关键是找出每个锐角相应直角三角形，根据正切的定义求值．2．如图，△ABC内接于⊙O，AD为⊙O的直径，交BC于点E，若DE＝2，OE ＝3，则tan C•tan B＝（）A．2B．3C．4D．5【分析】由DE＝2，OE＝3可知AO＝OD＝OE+ED＝5，可得AE＝8，连接BD、CD，可证∠B＝∠ADC，∠C＝∠ADB，∠DBA＝∠DCA＝90°，将tan C，tan B 在直角三角形中用线段的比表示，再利用相似转化为已知线段的比．【解答】解：连接BD、CD，由圆周角定理可知∠B＝∠ADC，∠C＝∠ADB，∴△ABE∽△CDE，△ACE∽△BDE，∴＝，＝，由AD为直径可知∠DBA＝∠DCA＝90°，∵DE＝2，OE＝3，∴AO＝OD＝OE+ED＝5，AE＝8，tan C•tan B＝tan∠ADB•tan∠ADC＝＝＝＝＝＝4．故选：C．【点评】求锐角的三角函数值的方法：利用锐角三角函数的定义，或者利用同角（或余角）的三角函数关系式求三角函数值．3．如图，△ABC的顶点都是正方形网格中的格点，则cos∠ABC等于（）A．B．C．D．【分析】找到∠ABC所在的直角三角形，利用勾股定理求得斜边长，进而求得∠ABC的邻边与斜边之比即可．【解答】解：由格点可得∠ABC所在的直角三角形的两条直角边为2，4，∴斜边为＝2．∴cos∠ABC＝＝．故选：B．【点评】难点是构造相应的直角三角形利用勾股定理求得∠ABC所在的直角三角形的斜边长，关键是理解余弦等于邻边比斜边．4．在Rt△ABC中，各边的长度都扩大两倍，那么锐角A的各三角函数值（）A．都扩大两倍B．都缩小两倍C．不变D．都扩大四倍【分析】根据三边对应成比例，两三角形相似，可知扩大后的三角形与原三角形相似，再根据相似三角形对应角相等解答．【解答】解：∵各边的长度都扩大两倍，∴扩大后的三角形与Rt△ABC相似，∴锐角A的各三角函数值都不变．故选：C．【点评】本题考查了锐角三角形函数的定义，理清锐角的三角函数值与角度有关，与三角形中所对应的边的长度无关是解题的关键．5．如图，A、B、C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC′B′，则tan B′的值为（）A．B．C．D．【分析】过C点作CD⊥AB，垂足为D，根据旋转性质可知，∠B′＝∠B，把求tan B′的问题，转化为在Rt△BCD中求tan B．【解答】解：过C点作CD⊥AB，垂足为D．根据旋转性质可知，∠B′＝∠B．在Rt△BCD中，tan B＝＝，∴tan B′＝tan B＝．故选：B．【点评】本题考查了旋转的性质，旋转后对应角相等；三角函数的定义及三角函数值的求法．6．如图，∠A的正弦与余弦值分别为（）A．，B．，C．，D．，【分析】先根据勾股定理求出AC的长，再利用正弦与余弦的定义分别求出∠A 的正弦与余弦．【解答】解：∵AC＝＝4；∴sin A＝＝，cos A＝＝．故选：A．【点评】本题考查了锐角三角函数的定义和勾股定理，找到三角函数的对边、邻边和斜边是解题的关键．7．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的中线，若BC＝6，AC＝8，则tan∠ACD的值为（）A．B．C．D．【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD＝AD，再根据等边对等角的性质可得∠A＝∠ACD，然后根据正切函数的定义列式求出∠A的正切值，即为tan∠ACD的值．【解答】解：∵CD是AB边上的中线，∴CD＝AD，∴∠A＝∠ACD，∵∠ACB＝90°，BC＝6，AC＝8，∴tan∠A＝＝＝，∴tan∠ACD的值．故选：D．【点评】本题考查了锐角三角函数的定义，直角三角形斜边上的中线等于斜边的一半的性质，等边对等角的性质，求出∠A＝∠ACD是解本题的关键．8．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝，AB的垂直平分线ED交BC的延长线于D点，垂足为E，则sin∠CAD＝（）A．B．C．D．【分析】设AD＝x，则CD＝x﹣3，在直角△ACD中，运用勾股定理可求出AD、CD的值，即可解答出；【解答】解：设AD＝x，则CD＝x﹣3，在直角△ACD中，（x﹣3）2+＝x2，解得，x＝4，∴CD＝4﹣3＝1，∴sin∠CAD＝＝；故选：A．【点评】本题考查了线段垂直平分线的性质定理及勾股定理的运用，求一个角的正弦值，可将其转化到直角三角形中解答．9．在正方形网格中，△ABC的位置如图所示，则tan∠A的值为（）A．B．C．D．【分析】连接CD，即可证明△ACD是直角三角形，利用正切函数的定义即可求解．【解答】解：连接CD，则CD2＝2，AC2＝4+16＝20，AD2＝9+9＝18∴AC2＝CD2+AD2，AD＝＝3，CD＝∴∠ADC＝90°∴tan∠A＝＝＝．故选：C．【点评】本题主要考查了正切函数的定义，正确证明△ACD是直角三角形是解决本题的关键．10．在Rt△ABC中，∠C＝90°，AC＝，BC＝，则cos B的值是（）A．B．C．D．【分析】首先利用勾股定理计算出AB的长，再根据余弦的定义可得答案．【解答】解：∵∠C＝90°，AC＝，BC＝，∴AB＝＝，∴cos B＝＝＝，故选：D．【点评】此题主要考查了三角函数，关键是掌握余弦：锐角A的邻边b与斜边c 的比叫做∠A的余弦，记作cos A．11．在Rt△ABC中，∠C＝90°，AB＝4，BC＝3，则cos B等于（）A．B．C．D．【分析】根据锐角三角函数的定义求出即可．【解答】解：∵在Rt△ABC中，∠C＝90°，AB＝4，BC＝3，∴cos B＝＝．故选：D．【点评】本题考查了锐角三角函数的定义的应用，能熟记锐角三角函数的定义是解此题的关键，难度不是很大．12．Rt△ABC中，∠C＝90°，∠A、∠C所对的边分别为a、c，下列式子中，正确的是（）A．a＝c•cot A B．a＝c•tan A C．a＝c•cos A D．a＝c•sin A 【分析】根据三角函数的定义分别分析得出答案．【解答】解：∵∠C＝90°，∠A、∠B、∠C所对的边分别为a、b、c，∴A、cot A＝，则a＝，故本选项错误，B、tan A＝，则a＝b•tan A，故本选项错误，C、cos A＝，则b＝c•cos A，故本选项错误，D、sin A＝，则a＝c•sin A，故本选项正确，故选：D．【点评】此题考查了直角三角形中两锐角的三角函数之间的关系，正确把握边角关系是解题关键．13．在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则∠A的正弦值等于（）A．B．C．D．【分析】直接利用勾股定理得出BC的长，再利用锐角三角函数关系得出答案．【解答】解：如图所示：∵∠C＝90°，AB＝10，AC＝8，∴BC＝＝6，∴∠A的正弦值等于：＝＝．故选：A．【点评】此题主要考查了锐角三角函数关系，正确得出BC的长是解题关键．14．在Rt△ABC中，∠C＝90°，a＝5，b＝12，则tan B的值为（）A．B．C．D．【分析】根据锐角三角函数的定义得出tan B＝，代入求出即可．【解答】解：∵在Rt△ABC中，∠C＝90°，a＝5，b＝12，∴tan B＝＝，故选：D．【点评】本题考查了锐角三角函数的定义，能熟记锐角三角函数的定义的内容是解此题的关键．15．如图，在Rt△ACB中，∠C＝90°，∠A＝37°，AC＝4，则BC的长约为（）（sin37°≈0.80，cos37°≈0.60，tan37°≈0.75）A．2.4B．3.0C．3.2D．5.0【分析】根据正切的定义列式计算即可．【解答】解：在Rt△ACB中，tan A＝，则BC＝AC•tan A≈4×0.75＝3，故选：B．【点评】本题考查的是正切的定义，掌握锐角A的对边a与邻边b的比叫做∠A 的正切是解题的关键．16．在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C对边，如果3a ＝4b，则cos B的值是（）A．B．C．D．【分析】根据锐角三角函数的定义可得cos B＝，然后根据题目所给3a＝4b可求解．【解答】解：因为在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C 对边，如果3a＝4b，令b＝3x，则a＝4x，所以c＝5x，所以cos B＝故选：D．【点评】本题考查了锐角三角函数的定义，解答本题的关键是掌握cos B＝，17．若锐角三角函数tan55°＝a，则a的范围是（）A．0＜a＜1B．1＜a＜2C．2＜a＜3D．3＜a＜4【分析】由tan45°＝1，tan60°＝且锐角范围内tanα随∠α的增大而增大，知tan45°＜tan55°＜tan60°，即1＜a＜，从而得出答案．【解答】解：∵tan45°＝1，tan60°＝，且锐角范围内tanα随∠α的增大而增大，∴tan45°＜tan55°＜tan60°，即1＜a＜，则1＜a＜2，故选：B．【点评】本题主要考查锐角三角函数的增减性，解题的关键是掌握特殊锐角的三角函数值及tanα随∠α的增大而增大．18．对于任意锐角α，下列结论正确的是（）A．sinα＜tanαB．sinα≤tanαC．sinα＞tanαD．sinα≥tanα【分析】直接利用锐角三角函数关系分析得出答案．【解答】解：∵sinα＝，tanα＝，且斜边＞α的邻边，∴sinα＜tanα．故选：A．【点评】此题主要考查了锐角三角函数关系，正确把握定义是解题关键．19．已知0＜α＜45°，关于角α的三角函数的命题有：①0＜sinα＜，②cosα＜sinα，③sin2α＝2sinα，④0＜tanα＜1，其中是真命题的个数是（）A．1个B．2个C．3个D．4个【分析】根据锐角函数的正弦是增函数，余弦是减函数，正切是增函数，可得答案．【解答】解：由0＜α＜45°，得0＜sinα＜，故①正确；cosα＞sinα，故②错误；sin2α＝2sinαcosα＜2sinα，故③错误；0＜tanα＜1，故④正确；故选：B．【点评】本题考查了锐角函数的增减性，熟记锐角函数的正弦是增函数，余弦是减函数，正切是增函数是解题关键．20．已知∠A为锐角，且tan A＝，则∠A的取值范围是（）A．0°＜∠A＜30°B．30°＜∠A＜45°C．45°＜∠A ＜60°D．60°＜∠A＜90°【分析】首先明确tan45°＝1，tan60°＝，再根据正切值随角增大而增大，进行分析．【解答】解：∵tan45°＝1，tan60°＝，正切值随角增大而增大，又1＜＜，∴45°＜∠A＜60°．故选：C．【点评】熟记特殊角的三角函数值，了解锐角三角函数的增减性是解题的关键．21．在Rt△ABC中，∠C＝90°，当∠A的度数不断增大时，cos A的值的变化情况是（）A．不断变大B．不断减小C．不变D．不能确定【分析】当角度在0°～90°间变化时，余弦值随着角度的增大（或减小）而减小（或增大）；依此即可求解．【解答】解：在Rt△ABC中，∠C＝90°，当∠A的度数不断增大时，cos A的值的变化情况是不断减小．故选：B．【点评】此题考查了锐角三角函数的增减性，当角度在0°～90°间变化时，①正弦值随着角度的增大（或减小）而增大（或减小）；②余弦值随着角度的增大（或减小）而减小（或增大）；③正切值随着角度的增大（或减小）而增大（或减小）．二．填空题（共14小题）22．在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cos A＝．【分析】作出图形，根据锐角的余弦等于邻边比斜边，列式计算即可得解．【解答】解：如图，∵∠C＝90°，AB＝10，AC＝8，∴cos A＝＝＝．故答案为：．【点评】本题考查了锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．23．已知△ABC中，AB＝AC，CH是AB边上的高，且CH＝AB，则tan B＝或3．【分析】作高AD，根据等腰三角形的性质得到BC＝2BD，设AB＝5x，则CH ＝AB＝3x，根据三角形面积公式有AD•BC＝CH•AB，即2BD•AD＝15x2，根据勾股定理得到BD2+AD2＝AB2＝25x2，然后进行等式变形有（BD+AD）2﹣2BD•AD＝25x2，即（BD+AD）2﹣15x2＝25x2，（BD﹣AD）2+2BD•AD＝25x2，即（BD﹣AD）2+15x2＝25x2，易得BD+AD＝2x，BD﹣AD＝x或AD ﹣BD＝x，可求出BD＝x，AD＝x或AD＝x，BD＝x，然后在Rt△ABD中根据正切的定义得到tan B＝，再把DB与AD的值代入计算即可．【解答】解：如图，作高AD，∵AB＝AC，∴BC＝2BD，设AB＝5x，则CH＝AB＝3x，∵AD•BC＝CH•AB，∴2BD•AD＝15x2，∵BD2+AD2＝AB2＝25x2，∴（BD+AD）2﹣2BD•AD＝25x2，即（BD+AD）2﹣15x2＝25x2，∴BD+AD＝2x，∴（BD﹣AD）2+2BD•AD＝25x2，即（BD﹣AD）2+15x2＝25x2，∴BD﹣AD＝x或AD﹣BD＝x，∴BD＝x，AD＝x或AD＝x，BD＝x，在Rt△ABD中，tan B＝，∴tan B＝＝或tan B＝＝3．故答案为：或3．【点评】本题考查了正切的定义：在直角三角形中，一锐角的正切等于这个角的对边与邻边的比值．也考查了等腰三角形的性质、勾股定理以及代数式的变形能力．24．水管的外部需要包扎，包扎时用带子缠绕在管道外部．若要使带子全部包住管道且不重叠（不考虑管道两端的情况），需计算带子的缠绕角度α（α指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC，其中AB为管道侧面母线的一部分）．若带子宽度为1，水管直径为4，则α的余弦值为．【分析】本题使带子全部包住管道且不重叠（不考虑管道两端的情况），即斜边长为水管的周长为4π．根据锐角三角函数的定义即可求得α的余弦值．【解答】解：∵水管直径为4，∴水管的周长为4π，∴cos∠α＝．故答案为：．【点评】本题考查锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．25．如图，在平面直角坐标系中，已知点A（3，0），点B（0，﹣4），则cos∠OAB等于．【分析】由题意可得，OA＝3，OB＝4．根据勾股定理得AB＝5．运用三角函数的定义求解．【解答】解：∵在平面直角坐标系中，点A的坐标为（3，0），点B的坐标为（0，﹣4），∴OA＝3，OB＝4．根据勾股定理得AB＝5．∴cos∠OAB＝．【点评】本题考查锐角三角函数的概念：在直角三角形中，余弦等于邻边比斜边．26．如果方程x2﹣4x+3＝0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，那么tan A的值为或．【分析】先求出方程的两个根是1和3，再根据边长3是直角边和斜边两种情况讨论．【解答】解：解方程x2﹣4x+3＝0得，x1＝1，x2＝3，①当3是直角边时，∵△ABC最小的角为A，∴tan A＝；②当3是斜边时，根据勾股定理，∠A的邻边＝＝2，∴tan A＝＝；所以tan A的值为或．【点评】本题注意因为较长边是直角边还是斜边不明确，所以要分情况讨论．27．如图，∠1的正切值等于．【分析】根据同弧所对的圆周角相等，可以把求三角函数的问题，转化为直角三角形的边的比的问题．【解答】解：根据圆周角的性质可得：∠1＝∠2．∵tan∠2＝，∴∠1的正切值等于．故答案为：．【点评】本题考查圆周角的性质及锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．28．在△ABC中，∠C＝90°，如果AC＝4，sin B＝，那么BC＝2．【分析】先根据正弦函数的定义求出AB，再利用勾股定理求出BC即可．【解答】解：∵在△ABC中，∠C＝90°，AC＝4，sin B＝，∴sin B＝＝＝，∴AB＝6，∴BC＝＝＝2．故答案是2．【点评】本题考查了正弦函数的定义：在Rt△ABC中，∠C＝90°，我们把锐角A的对边a与斜边c的比叫做∠A的正弦，记作sin A．即sin A＝∠A的对边除以斜边＝．也考查了勾股定理．29．在Rt△ABC中，∠C＝90°，AC＝4，AB＝5，则cos A的值是．【分析】根据余弦的定义计算即可．【解答】解：如图，在Rt△ABC中，cos A＝＝，故答案为：．【点评】本题考查的是锐角三角函数的定义，掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键．30．已知△ABC中，∠ACB＝90°，BC＝12，AB＝15，则cos B的值为．【分析】根据锐角三角函数的定义即可得到结论．【解答】解：cos B＝＝＝，故答案为：．【点评】本题考查了锐角三角函数的定义，熟练掌握锐角三角函数是解题的关键．31．比较sin53°＞tan37°的大小．【分析】本题比较特殊，勾三股四弦五的直角三角形中的勾三对的角刚好是37°，【解答】解：如图，Rt△ABC中，∠C＝90°，∠A＝53°，∠B＝37°．则AC ＝3，BC＝4，AB＝5，∵sin53°＝＝＝0.8，tan37°＝＝＝0.75，∴sin53°＞tan37°．故答案为＞【点评】本题考查锐角三角函数，解题的关键是记住：勾三股四弦五的直角三角形中的勾三对的角刚好是37°．32．比较大小：sin40°＝cos50°（填“＞”、“＜”或“＝”）【分析】直接利用锐角三角函数关系得出答案．【解答】解：∵cos50°＝sin（90°﹣50°）＝sin40°，∴sin40°＝cos50°．故答案为：＝．【点评】此题主要考查了锐角三角函数关系，正确转换正余弦关系是解题关键．33．如图所示的网格是正方形网格，∠BAC＞∠DAE．（填“＞”，“＝”或“＜”）【分析】作辅助线，构建三角形及高线NP，先利用面积法求高线PN＝，再分别求∠BAC、∠DAE的正弦，根据正弦值随着角度的增大而增大，作判断．【解答】解：连接NH，BC，过N作NP⊥AD于P，S△ANH＝2×2﹣﹣×1×1＝AH•NP，＝PN，PN＝，Rt△ANP中，sin∠NAP＝＝＝＝0.6，Rt△ABC中，sin∠BAC＝＝＝＞0.6，∵正弦值随着角度的增大而增大，∴∠BAC＞∠DAE，故答案为：＞．【点评】本题考查了锐角三角函数的增减性，构建直角三角形求角的三角函数值进行判断，熟练掌握锐角三角函数的增减性是关键．34．用不等号“＞”或“＜”连接：sin50°＞cos50°．【分析】先由互余两角的三角函数的关系得出cos50°＝sin40°，再根据当角度在0°～90°间变化时，正弦值随着角度的增大而增大得出sin50°＞sin40°，从而得出结果．【解答】解：∵cos50°＝sin40°，sin50°＞sin40°，∴sin50°＞cos50°．故答案为＞．【点评】本题考查了锐角三角函数的增减性：当角度在0°～90°间变化时，①正弦值随着角度的增大（或减小）而增大（或减小）；②余弦值随着角度的增大（或减小）而减小（或增大）；③正切值随着角度的增大（或减小）而增大（或减小）．也考查了互余两角的三角函数的关系．35．在△ABC中，∠C＝90°，如果sin A＞cos A，那么∠A的度数范围是45°＜∠A＜90°．【分析】根据锐角三角函数的增减性即可求解．【解答】解：在△ABC中，∠C＝90°，∵sin A＞cos A，∴∠A的度数范围是45°＜∠A＜90°．故答案为：45°＜∠A＜90°．【点评】考查了锐角三角函数的增减性，当角度在0°～90°间变化时，①正弦值随着角度的增大（或减小）而增大（或减小）；②余弦值随着角度的增大（或减小）而减小（或增大）．三．解答题（共6小题）36．如图，将含30°角的直角三角板ABC（∠A＝30°）绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得到Rt△A′B′C，A′C与AB交于点D，过点D作DE∥A′B′交CB′于点E，连接BE．易知，在旋转过程中，△BDE为直角三角形．设BC＝1，AD＝x，△BDE的面积为S．（1）当α＝30°时，求x的值．（2）求S与x的函数关系式，并写出x的取值范围；（3）以点E为圆心，BE为半径作⊙E，当S＝时，判断⊙E与A′C的位置关系，并求相应的tanα值．【分析】（1）根据等腰三角形的判定，∠A＝∠α＝30°，得出x＝1；（2）由直角三角形的性质，AB＝2，AC＝，由旋转性质求得△ADC∽△BCE，根据比例关系式，求出S与x的函数关系式；（3）当S＝时，求得x的值，判断⊙E和DE的长度大小，确定⊙E与A′C的位置关系，再求tanα值．【解答】解：（1）∵∠A＝a＝30°，又∵∠ACB＝90°，∴∠ABC＝∠BCD＝60°．∴AD＝BD＝BC＝1．∴x＝1；（2）∵∠DBE＝90°，∠ABC＝60°，∴∠A＝∠CBE＝30°．∴AC＝BC＝，AB＝2BC＝2．由旋转性质可知：AC＝A′C，BC＝B′C，∠ACD＝∠BCE，∴△ADC∽△BEC，∴＝，∴BE＝x．∵BD＝2﹣x，∴s＝×x（2﹣x）＝﹣x2+x．（0＜x＜2）（3）∵s＝s△ABC∴﹣+＝，∴4x2﹣8x+3＝0，∴，．①当x＝时，BD＝2﹣＝，BE＝×＝．∴DE＝＝．∵DE∥A′B′，∴∠EDC＝∠A′＝∠A＝30°．∴EC＝DE＝＞BE，∴此时⊙E与A′C相离．过D作DF⊥AC于F，则，．∴．∴．（12分）②当时，，．∴，∴，∴此时⊙E与A'C相交．同理可求出．【点评】本题考查的知识点：等腰三角形的判定，直角三角形的性质，相似三角形的判定以及直线与圆的位置关系的确定，是一道综合性较强的题目，难度大．37．如图，定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作c tanα，即c tanα＝＝，根据上述角的余切定义，解下列问题：（1）c tan30°＝；（2）如图，已知tan A＝，其中∠A为锐角，试求c tan A的值．【分析】（1）根据直角三角形的性质用AC表示出AB及AC的值，再根据锐角三角函数的定义进行解答即可；（2）由于tan A＝，所以可设BC＝3x，AC＝4x，则AB＝5x，再根据锐角三角函数的定义进行解答即可．【解答】解：（1）∵Rt△ABC中，α＝30°，∴BC＝AB，∴AC＝＝＝AB，∴c tan30°＝＝．故答案为：；（2）∵tan A＝，∴设BC＝3x，AC＝4x，∴c tan A＝＝＝．【点评】本题考查的是锐角三角函数的定义及直角三角形的性质，熟知锐角三角函数的定义是解答此题的关键．38．如图所示，在平面直角坐标系xoy中，四边形OABC是正方形，点A的坐标为（m，0）．将正方形OABC绕点O逆时针旋转α角，得到正方形ODEF，DE与边BC交于点M，且点M与B、C不重合．（1）请判断线段CD与OM的位置关系，其位置关系是垂直；（2）试用含m和α的代数式表示线段CM的长：CM＝m•tan；α的取值范围是0°＜α＜90°．【分析】（1）连接CD，OM．根据旋转的性质得出MC＝MD，OC＝OD，再证明△COM≌△DOM，得出∠COM＝∠DOM，然后根据等腰三角形三线合一的性质得出CD⊥OM；（2）首先用含α的代数式表示∠COM，然后在Rt△COM中，根据正切函数的定义即可得出CM的长度；由OD与OM不能重合，且只能在OC右边，得出α的取值范围．【解答】解：（1）连接CD，OM．根据旋转的性质可得，MC＝MD，OC＝OD，又OM是公共边，∴△COM≌△DOM，∴∠COM＝∠DOM，又∵OC＝OD，∴CD⊥OM；（2）由（1）知∠COM＝∠DOM，∴∠COM＝，在Rt△COM中，CM＝OC•tan∠COM＝m•tan；因为OD与OM不能重合，且只能在OC右边，故可得α的取值范围是0°＜α＜90°．【点评】解答本题要充分利用正方形的特殊性质，注意在正方形中的特殊三角形的应用，搞清楚矩形、菱形、正方形中的三角形的三边关系，有助于提高解题速度和准确率．39．如图，AB为⊙O的直径，且弦CD⊥AB于E，过点B的切线与AD的延长线交于点F．（1）若M是AD的中点，连接ME并延长ME交BC于N．求证：MN⊥BC．（2）若cos∠C＝，DF＝3，求⊙O的半径．【分析】（1）连接AC．欲求MN⊥BC，只需证MN∥AC即可．由于直径AB⊥CD，由垂径定理知E是CD中点，而M是AD的中点，故EM是△ACD的中位线，可得ME（即MN）∥AC，由此得证．（2）由于∠A、∠C所对的弧相同，因此cos A＝cos C，由此可得BF、AF、AB 的比例关系，用未知数表示出它们的长．连接BD，证△BDF∽△ABF，根据所得比例线段即可求得未知数的值（也可利用切割线定理求解），从而得到直径AB的长，也就能求出⊙O的半径．【解答】（1）证明：（方法一）连接AC．∵AB是⊙O的直径，且AB⊥CD于E，由垂径定理得，点E是CD的中点；又∵M是AD的中点，∴ME是△DAC的中位线，∴MN∥AC．∵AB是⊙O的直径，∴∠ACB＝90°．∴∠MNB＝90°，即MN⊥BC；（方法二）∵AB⊥CD，∴∠AED＝∠BEC＝90°．M是AD的中点，∴ME＝AM，即有∠MEA＝∠A．∵∠MEA＝∠BEN，∠C＝∠A，∴∠C＝∠BEN．又∵∠C+∠CBE＝90°，∴∠CBE+∠BEN＝90°，∴∠BNE＝90°，即MN⊥BC；（方法三）∵AB⊥CD，∴∠AED＝90°．由于M是AD的中点，∴ME＝MD，即有∠MED＝∠EDM．又∵∠CBE与∠EDA同对，∴∠CBE＝∠EDA．∵∠MED＝∠NEC，∴∠NEC＝∠CBE．∵∠C+∠CBE＝90°，∴∠NEC+∠C＝90°，即有∠CNE＝90°，即MN⊥BC．（2）解：连接BD．∵∠BCD与∠BAF同对，∴∠C＝∠A，∴cos A＝cos C＝．∵BF是⊙O的切线，∴∠ABF＝90°．在Rt△ABF中，cos A＝＝，设AB＝4x，则AF＝5x，由勾股定理得：BF＝3x．∵AB是⊙O的直径，∴BD⊥AD，∴△ABF∽△BDF，∴，即，x＝．∴直径AB＝4x＝4×，则⊙O的半径为．【点评】此题主要考查了垂径定理、圆周角定理、三角形中位线定理以及相似三角形的判定和性质等知识，难度适中．40．如图，△ABC是等腰三角形，AB＝AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F．（1）求证：DE是⊙O的切线；（2）若⊙O的半径为2，BE＝1，求cos A的值．【分析】（1）连接AD、OD，根据AC是圆的直径，即可得到AD⊥BC，再根据三角形中位线定理即可得到OD∥AB，这得到OD⊥DE，从而求证，DE是圆的切线．（2）根据平行线分线段成比例定理，即可求得FC的长，即可求得AF，根据余弦的定义即可求解．【解答】（1）证明：连接AD、OD∵AC是直径∴AD⊥BC∵AB＝AC∴D是BC的中点又∵O是AC的中点∴OD∥AB∵DE⊥AB∴OD⊥DE∴DE是⊙O的切线（2）解：由（1）知OD∥AE，∴∠FOD＝∠F AE，∠FDO＝∠FEA，∴△FOD∽△F AE，∴∴∴解得FC＝2∴AF＝6∴Rt△AEF中，cos∠F AE＝＝＝＝．【点评】本题考查了切线的判定，垂径定理等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．并且本题还考查了三角函数的定义．41．如图，已知：AC是⊙O的直径，P A⊥AC，连接OP，弦CB∥OP，直线PB 交直线AC于D，BD＝2P A．（1）证明：直线PB是⊙O的切线；（2）探究线段PO与线段BC之间的数量关系，并加以证明；（3）求sin∠OP A的值．【分析】（1）连接OB．证OB⊥PB即可．通过证明△POB≌△POA得证．（2）根据切线长定理P A＝PB．BD＝2P A，则BD＝2PB，即BD：PD＝2：3．根据BC∥OP可得△DBC∽△DPO，从而得出线段PO与线段BC之间的数量关系．（3）根据三角函数的定义即求半径与OP的比值．设OA＝x，P A＝y．则OD＝3x，OB＝x，BD＝2y．在△BOD中可求y与x的关系，进而在△POB中求OP与x的关系，从而求比值得解．【解答】（1）证明：连接OB．∵BC∥OP，∴∠BCO＝∠POA，∠CBO＝∠POB，∴∠POA＝∠POB，又∵PO＝PO，OB＝OA，∴△POB≌△POA．∴∠PBO＝∠P AO＝90°．∴PB是⊙O的切线．（2）解：2PO＝3BC．（写PO＝BC亦可）证明：∵△POB≌△POA，∴PB＝P A．∵BD＝2P A，∴BD＝2PB．∵BC∥PO，∴△DBC∽△DPO．∴，∴2PO＝3BC．（3）解：∵CB∥OP，∴△DBC∽△DPO，∴，即DC＝OD．∴OC＝OD，∴DC＝2OC．设OA＝x，P A＝y．则OD＝3x，OB＝x，BD＝2y．在Rt△OBD中，由勾股定理得（3x）2＝x2+（2y）2，即2x2＝y2．∵x＞0，y＞0，∴y＝x，OP＝＝x．∴sin∠OP A＝＝＝＝．【点评】此题考查了切线的判定、切线长定理、相似三角形的判定和性质、勾股定理、三角函数等知识点，综合性强，难度大．。

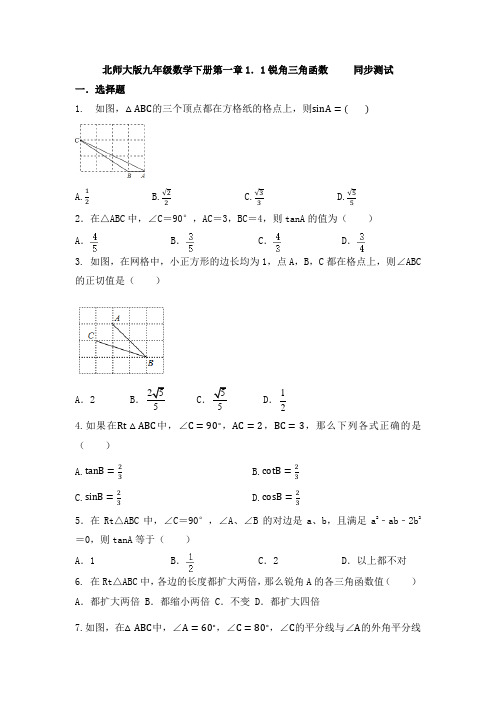
北师大版九年级数学下册第一章1．1锐角三角函数 同步测试 一．选择题1. 如图，△ABC 的三个顶点都在方格纸的格点上，则sinA =( )A.12B.√22C.√33D.√552．在△ABC 中，∠C ＝90°，AC ＝3，BC ＝4，则tanA 的值为（ ） A ．B ．C ．D ．3. 如图，在网格中，小正方形的边长均为1，点A ，B ，C 都在格点上，则∠ABC 的正切值是（ ）A ．2B ．5 C ．5 D ．124.如果在Rt △ABC 中，∠C =90∘，AC =2，BC =3，那么下列各式正确的是（ ） A.tanB =23 B.cotB =23 C.sinB =23D.cosB =235．在Rt △ABC 中，∠C ＝90°，∠A 、∠B 的对边是a 、b ，且满足a 2﹣ab ﹣2b 2＝0，则tanA 等于（ ） A ．1B ．C ．2D ．以上都不对6. 在Rt △ABC 中，各边的长度都扩大两倍，那么锐角A 的各三角函数值（ ） A ．都扩大两倍 B ．都缩小两倍 C ．不变 D ．都扩大四倍7.如图，在△ABC 中，∠A =60∘，∠C =80∘，∠C 的平分线与∠A 的外角平分线交于D，连接BD，则tan∠BDC的值是（）A.1B.12C.√3 D.√338．如图，在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，则sinA的值为（）A．B．C．D．9. 在Rt△ABC中，∠C=90°，AB=13，AC=12，则cosA=（）A．513B．512C．1213D．12510．在Rt△ABC中，各边都扩大5倍，则∠A的三角函数值（）A．不变B．扩大5倍C．缩小5倍D．不能确定11. 如图，梯子跟地面的夹角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（）A．sinA的值越小，梯子越陡 B．cosA的值越小，梯子越陡C．tanA的值越小，梯子越陡 D．陡缓程度与上A的函数值无关12．sin58°、cos58°、cos28°的大小关系是（）A．cos28°＜cos58°＜sin58°B．sin58°＜cos28°＜cos58°C．cos58°＜sin58°＜cos28°D．sin58°＜cos58°＜cos28°二．填空题13. 如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB=____________14．在Rt△ABC中，∠C＝90°，如果cosB＝，BC＝4，那么AB的长为 6 ．15. 比较下列三角函数值的大小：sin40°___________sin50°16.在Rt△ABC中，∠C=90∘，如果AC=5，AB=13，那么sinA=________．17．比较大小：sin40°＝cos50°（填“＞”、“＜”或“＝”）18．如图，在Rt△ABC中，∠C＝90°，BC＝2，且tanA＝，则AC＝．19．比较大小：（1）cos35°cos45°，tan50°tan60°；（2）若sinα＝0.3276，sinβ＝0.3274，则αβ．20.如图，直角三角形纸片的两直角边长分别为4，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是________．三.解答题21. 如图，在Rt△ABC中，∠C=90°，AB=2BC，求sinB的值22. 在Rt△ABC中，∠C=90∘，若tanA=20，写出∠B的四个三角函数的值．23. 在Rt△ABC中，∠C=90°，如果AC：BC=3：4，求cosA的值24.．如图，在Rt△ABC中，∠C＝90°，tanA＝，BC＝2，求AB的长．25. 在Rt△ABC中，∠C=90∘，a、b、c分别是∠A、∠B、∠C的对边．请利用三角函数的定义探讨能否用边c的式子表示bcosA+acosB？请写出你必要的理由．26．在Rt△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c．若a＝2，sin，求b和c．27.如图，在Rt△ABC中，∠C=90∘，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cosB的值．28．（1）如图，锐角的正弦和余弦都随着锐角的确定而确定，也随着其变化而变化，试探索随着锐角度数的增大，它的正弦值和余弦值的变化规律；（2）根据你探索到的规律，试比较18°，34°，52°，65°，88°，这些角的正弦值的大小和余弦值的大小；（3）比较大小：（在空格处填写“＜”或“＞”或“＝”）若∠α＝45°，则sinαcosα；若∠α＜45°，则sinαcosα；若∠α＞45°，则sinαcosα；（4）利用互余的两个角的正弦和余弦的关系，比较下列正弦值和余弦值的大小：sin10°，cos30°，sin50°，cos70°．答案提示1. D.2.C．3.D．4. A.5.C．6.C．7. D.8.A．9.C．10.A．11.B．12.C．13.713. 14.6． 15.＜． 16. 1213. 17.＝． 18.6． 19.（1）＞，＜；（2）＞． 20. 34 21. 解: ∵AB=2BC ，∴=∴sinB=AC AB ==故答案为222. 解：tanA =BCAC =20，BC =20AC ， 由勾股定理，得AB =√BC 2+AC 2=√401AC ， sinA =BCAB =√401AC =20√401401， cosA =AC AB =√401AC=√401401， cotA =AC CB =AC20AC =120．24.解：∵在Rt △ABC 中，∠C ＝90°， ∴tanA ＝＝．∵BC ＝2， ∴＝，AC ＝6．∵AB 2＝AC 2+BC 2＝40， ∴AB ＝．25. 解：∵cosA =ACAB =bc ，cosB =BCAB =ac ，∴bcosA+acosB=b⋅bc +a⋅ac=b2c+a2c=a2+b2c=c2c=c，即bcosA+acosB=c．26.解：如图，∵a＝2，sin，∴c＝＝＝6，则b＝＝＝4．27. 解：∵∠C=90∘，MN⊥AB，∴∠C=∠ANM=90∘，又∵∠A=∠A，∴△AMN∽△ABC，∴ACAB =ANAM=34，设AC=3x，AB=4x，由勾股定理得：BC=√AB2−AC2=√7x，在Rt△ABC中，cosB=BCAB =√7x4x=√74．28.解：（1）在图（1）中，令AB1＝AB2＝AB3，B1C1⊥AC于点C1，B2C2⊥AC于点C 2，B3C3⊥AC于点C3，显然有：B1C1＞B2C2＞B3C3，∠B1AC＞∠B2AC＞∠B3AC．∵sin∠B1AC＝，sin∠B2AC＝，sin∠B3AC＝，而＞＞．∴sin∠B1AC＞sin∠B2AC＞sin∠B3AC．在图（2）中，Rt△ACB3中，∠C＝90°，cos∠B1AC＝，cos∠B2AC＝，cos∠B3AC＝，∵AB3＜AB2＜AB1，∴＞＞．即cos∠B3AC＞cos∠B2AC＞cos∠B1AC．（2）sin88°＞sin65°＞sin52°＞sin34°＞sin18°；cos88°＜cos65°＜cos52°＜cos34°＜cos18°．（3）若∠α＝45°，则sinα＝cosα；若∠α＜45°，则sinα＜cosα；若∠α＞45°，则sinα＞cosα．（4）cos30°＞sin50°＞cos70°＞sin10°．。

第2课时 正弦和余弦..知识点 1 正弦..1．2017·安顺模拟在Rt △ABC 中，∠C ＝90°，则下列等式成立的是( ) A ．sin A ＝AC AB B ．sin A ＝BC ABC ．sin A ＝AC BCD ．sin A ＝BCAC.图1－1－132．如图1－1－13，在Rt △ABC 中，∠C ＝90°，AB ＝5，BC ＝3，则sin A 的值是..( ) A .34 B .43 C .35 D .453．[2017·日照] 在Rt △ABC 中，∠C ＝90°，AB ＝13，AC ＝5，则sin A 的值为( ) A .513B .1213C .512D .1254．在△ABC 中，∠C ＝90°，AC ＝8，sin B ＝45，则BC ＝________．知识点 2 余弦图1－1－145．[2017·湖州] 如图1－1－14，已知在Rt △ABC 中，∠C ＝90°，AB ＝5，BC ＝3，则cos B 的值是( )A .35B .45C .34D .436．在Rt △ABC 中，∠B ＝90°，BC ＝2AB ，则cos A ＝( ) A .52B .12C .2 55D .557．在等腰三角形ABC 中，若AB ＝AC ＝4，BC ＝6，则cos B 的值是________． 8．如图1－1－15，一架梯子斜靠在墙上，若梯子底端到墙的距离AC ＝3 m ，cos ∠BAC ＝34，则梯子长AB ＝________m .图1－1－15 1－1－169．如图1－1－16，∠AOB 放置在正方形网格中，则cos ∠AOB 的值为________． 知识点 3 锐角三角函数10．在△ABC 中，∠C ＝90°，若BC ＝3，AB ＝4，则下列说法正确的是( ) A ．sin B ＝35B ．cos B ＝34C ．tan B ＝34D ．tan B ＝4311．在Rt △ABC 中，∠C ＝90°.若sin A ＝513，则cos A 的值是( )A .512B .813C .23D .121312．已知∠α是锐角，且cos α的值为45，则tan α＝________．13．2017·贵阳模拟在Rt △ABC 中，∠C ＝90°，AC ＝2，下列结论中，正确的是( ) A ．AB ＝2sin A B ．AB ＝2cos AC ．BC ＝2tan AD ．BC ＝2cot A14．在Rt △ABC 中，∠ACB ＝90°，CD 是斜边AB 上的中线，CD ＝4，AC ＝6，则sin B 的值是________．15．如图1－1－17所示，△ABC 的顶点是正方形网格的格点，则sin A 的值为________．1－1－17 1－1－1816．如图1－1－18，在Rt △ABC 中，∠C ＝90°，D 是AB 的中点，过点D 作AB 的垂线交AC 于点E.若BC ＝6，sin A ＝35，则DE ＝________．17．如图1－1－19，四边形ABCD 的对角线AC ，BD 相交于点O ，且BD 平分AC.若BD ＝8，AC ＝6，sin ∠AOB ＝32，则四边形ABCD 的面积为________．(结果保留根号)图1－1－1918．在Rt △ABC 中，∠C ＝90°，BC ＝6，且sin B ＝35，试分别求出AC ，AB 的长．19．已知：如图1－1－20，在△ABC 中，AD 是边BC 上的高，E 为边AC 的中点，BC＝14，AD ＝12，sin B ＝45.(1)求线段DC 的长； (2)求tan ∠EDC 的值．图1－1－2020．如图1－1－21，矩形ABCD 的周长为30 cm ，两条邻边AB 与BC 的长度之比为2∶3. 求：(1)AC 的长；(2)∠α的正弦、余弦和正切．图1－1－2121．如图1－1－22，在Rt△ABC中，∠C＝90°，AC＝12，BC＝5.(1)求sin2A＋cos2A的值；(2)比较sin A和cos B的大小；(3)想一想，对于任意直角三角形中的锐角，是否都有与上述两问题相似的结果？若有，请说明理由．图1－1－221．B [解析] 如图所示，sin A ＝BCAB.故选B.2．C 3.B 4.6 5.A 6.D7.34[解析] 如图，作AD ⊥BC 于点D ，∵AB ＝AC ＝4，BC ＝6， ∴BD ＝12BC ＝3.在Rt △ABD 中，cos B ＝BD AB ＝34.故答案为34.8．4 9.55[解析] 将∠AOB 放在一直角三角形中，相邻的直角边为1，对边为2，由勾股定理得斜边为5，则cos ∠AOB ＝15＝55. 10．B 11.D 12.3413．C [解析] 如图，∵∠C ＝90°，AC ＝2，∴cos A ＝AC AB ＝2AB ，故AB ＝2cos A，故选项A ，B 错误；tan A ＝BC AC ＝BC2，则BC ＝2tan A ，故选项C 正确，选项D 错误．故选C.14．3415．55 [解析] 设每个小正方形的边长为1，过点C 作CD ⊥AB 于点D ，则CD ＝2，AC ＝10.在Rt △ACD 中，sin A ＝CD AC ＝210＝55.16．15417．12 3[解析] 如图，过点A 作AE ⊥BD ，垂足为E ，∵sin ∠AOB ＝32，OA ＝3， ∴AE ＝3×sin ∠AOB ＝3 32，∴S △ABD ＝12BD ·AE ＝12×8×3 32＝6 3，同理S △BCD ＝6 3.∴四边形ABCD 的面积为12 3. 18．解：∵在Rt △ABC 中，∠C ＝90°， ∴sin B ＝AC AB ＝35.设AC ＝3x ，则AB ＝5x .又由AB 2＝AC 2＋BC 2，知 (5x )2＝(3x )2＋62＝9x 2＋36， 解得x ＝32(负值已舍去)．∴AC ＝3x ＝92，AB ＝5x ＝152.19．解：(1)在Rt △ABD 中，∵AD ＝12，sin B ＝45，即AD AB ＝45，∴AB ＝5AD4＝15.由勾股定理，得BD ＝AB 2－AD 2＝152－122＝9， ∴DC ＝BC －BD ＝14－9＝5.(2)在Rt △ACD 中， ∵DE 是斜边AC 上的中线， ∴DE ＝12AC ＝EC ，∴∠EDC ＝∠C ，∴tan ∠EDC ＝tan C ＝AD DC ＝125.20．解：(1)∵AB ＋BC ＝15 cm ，AB ∶BC ＝2∶3， ∴AB ＝6 cm ，BC ＝9 cm ， ∴AC ＝AB 2＋BC 2＝313cm. (2)在Rt △ABC 中， sin α＝AB AC ＝21313，cos α＝BC AC ＝31313，tan α＝AB BC ＝23. 21．[全品导学号：77264016]解：∵∠C ＝90°，AC ＝12，BC ＝5， ∴AB ＝AC 2＋BC 2＝122＋52＝13.∴sin A ＝BC AB ＝513，cos A ＝AC AB ＝1213，cos B ＝BC AB ＝513.(1)∵sin 2A ＝(513)2＝25169，cos 2A ＝(1213)2＝144169，∴sin 2A ＋cos 2A ＝25169＋144169＝1.(2)sin A ＝cos B .(3)由这个特例的解答过程可猜想，对于任意直角三角形中的锐角，都有与上述两问题相似的结果，即对任意直角三角形中的锐角A ，有sin 2A ＋cos 2A ＝1；在Rt △ABC 中，若∠C 为直角，则sin A ＝cos B .理由如下：设在任意Rt △ABC 中，∠C ＝90°，sin 2A ＝⎝⎛⎭⎫BC AB 2，cos 2A ＝⎝⎛⎭⎫AC AB 2， ∴sin 2A ＋cos 2A ＝⎝⎛⎭⎫BC AB 2＋⎝⎛⎭⎫AC AB 2＝BC 2＋AC 2AB 2＝AB2AB 2＝1.∵sin A ＝BC AB ，cos B ＝BCAB ，∴sin A ＝cos B .。

北师大版初中数学九年级下册全册同步练习1.1锐角三角函数一、选择题1．在△ABC中，∠C＝90°，BC＝2，AB=3，则下列结论正确的是( )A． sin A=53B．cos A=23C．sin A=23D．tan A=522．如图l－2l所示的是一水库大坝横截面的一部分，坝高h＝6 m，迎水坡AB＝10 m，斜坡的坡角为a，则tan a的值为 ( )A．35B．45C．43D．343．如图1－22所示，在矩形ABCD中，DE⊥AC于E，设∠ADE＝a，且cos a＝35，AB＝4，则AD的长为 ( )A．3 B．16 3C. 203D．165二、填空题4．如图1－23所示，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，cos∠BAC＝34，则梯子AB的长度为米．5．若a是锐角，且sin2 a+cos2 48°＝1，则a= .6．如图l－24所示，在Rt△ACB中，∠C＝90°，AB＝3，BC＝1，求∠A的三角函数值．三、计算与解答题7．如图1－25所示，在Rt△ACB中，∠ACB=90°，CD为AB边上的高，BD＝3，AD =163，求sin A，cos A，tan A的值．8．如图1－26所示，在平面直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO=5，sin∠BOA＝35．(1)求点B的坐标；(2)求cos∠BAO的值．9．请你画出一个以BC为底边的等腰三角形ABC，使底边上的高AD＝BC(1)求tan∠ABC和sin∠ABC的值；(2)在你所画的等腰三角形ABC中，假设底边BC＝5米，求腰上的高BE．参考答案 1．C[提示：sinA=BCAB．] 2．D[提示：过A 点作垂线交底部于C 点，则△ACB 为直角三角形，∴BC ＝2222106AB AC -=-＝8(m)，∴tan a ＝68＝34．故选D ．]3．B[提示：∠ADE 和∠EDC 互余，∴cos a ＝sin ∠EDC ＝35，sin ∠EDC ＝3,45EC EC DC ==∴EC =125.由勾股定理，得DE ＝165．在Rt △AED 中，cos a ＝16355DE AD AD ==,∴AD＝163．故选B ．] 4．4[提示：在Rt △BCA 中，AC ＝3米，cos ∠BAC ＝34AC AB =，所以AB ＝4米，即梯子的长度为4米．]5．48°[提示：∵sin 2a ＋cos 2a ＝l ，∴a ＝48°．] 6．提示：sin A ＝13，cos A ＝223，tan A =24.7．解：∵∠ACB ＝90°，CD ⊥AB ，∴△ACD ∽△CBD ，∴CD 2＝AD ·DB ＝16，∴CD =4，∴AC =22203AD CD +=．∴sin A ==35CD AC =，cos A ＝45AD AC =，tan A =34CD AD =. 8．解：(1)如图l －27所示，作BH ⊥OA ， 垂足为H ．在Rt △OHB 中，∵BO ＝5，sin ∠BOA ＝35，∴BH =3，∴OH ＝4，∴点B 的坐标为(4，3)． (2)∵OA ＝10，OH ＝4，∴AH ＝6．在Rt △AHB 中，∵BH =3，∴AB ＝22223635BH AH +=+=，∴cos ∠BAO=635AH AB == 255． 9．解：(1)根据题意画出图形，如图1－28所示，∵AB ＝AC ，AD ⊥BC ，AD ＝BC ，∴BD ＝12B C = 12AD ，即AD ＝2BD ，∴AB ＝225BD AD +=BD ，∴tan ∠ABC=ADBD=2,sin ∠ABC=AD AB =255 (2)作BE ⊥AC 于E ，在Rt △BEC 中，sinC=sin ∠ABC=255.又∵sin C=,BEBC.5BE故BE=.1.2 30°，45°，60°角的三角函数值一．选择题：1.在△ABC 中，∠A ，∠B 都是锐角，且 sin A ＝21，cos B ＝22，则△ABC 三个角的大小关系是（ ）A ．∠C ＞∠A ＞∠B B ．∠B ＞∠C ＞∠A C ．∠A ＞∠B ＞∠CD ．∠C ＞∠B ＞∠A2.若0°＜＜90°，且|sin －41|＋223cos ⎪⎪⎭⎫ ⎝⎛-θ，则tan 的值等于（ ）A ．3B ．33 C ．21 D ．233．如图1—37所示，在△ABC 中，∠A =30°，tan B ＝32，AC ＝23，则AB 的长是 ( ) A ．3＋3 B ．2＋23 C. 5 D ．924．等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a ，则其底边上的高是( ) A ．32a B ．a C.12a D ．12a 或32a 二、选择题5．在Rt △ACB 中，∠C ＝90°，AC ＝3，AB ＝2，则tan2B= ． 6．若a 为锐角，且sin a =22,则cos a = ． 7．在Rt △ACB 中，若∠C ＝90°，sin A ＝32,b ＋c ＝6，则b = ． 8．(1)在△ABC 中，∠C ＝90°，sin A ＝21，则 cos B ＝________； (2)已知为锐角，且cos(90°－)＝21，则 ＝________；(3)若1)10(tan 3=︒+α，则锐角 ＝________．三、计算与解答9．计算（1）sin 60°·cos 30°－12.(2) 2 cos 230°－2 sin 60°·cos 45°；(3) 2 sin30°－3 tan 45°＋4 cos 60°；10．如图1—38所示，在Rt △ACB 中，∠BCA ＝90°，CD 是斜边上的高，∠ACD ＝30°，AD ＝1，求AC ，CD ，BC ，BD ，AB 的长．11．如图1—39所示，在相距100米的A ，B 两处观测工厂C ，测得∠BAC ＝60°，∠ABC ＝45°，则A ，B 两处到工厂C 的距离分别是多少?12．在△ABC中，a，b，c分别是∠A，∠B，∠C的对边，且c＝53,若关于x的方程(53＋b)x2＋2ax＋(53－b)=0有两个相等的实数根，方程2x2－(10sin A)x＋5sin A＝0的两个实数根的平方和为6，求△ABC的面积．参考答案 1． D ； 2 。

1.1锐角三角函数一、选择题1．在△ABC中，∠C＝90°， BC＝2，AB=3，则下列结论正确的是( )A． sin A．cos AC．sin A．tan A2．如图l－2l所示的是一水库大坝横截面的一部分，坝高h＝6 m，迎水坡AB＝10 m，斜坡的坡角为a，则tan a的值为 ( )A3．如图1－22所示，在矩形ABCD中，DE⊥AC于E，设∠ADE＝a，( )5A．3 B二、填空题4．如图1－23所示，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，cos∠BAC AB 的长度为米．5．若a是锐角，且sin2 a+cos2 48°＝1，则a= .6．如图l－24所示，在Rt△ACB中，∠C＝90°，AB＝3，BC＝1，求∠A的三角函数值．三、计算与解答题7．如图1－25所示，在Rt△ACB中，∠ACB=90°，CD为AB边上的高，BD＝3，AD sin A，cos A，tan A的值．8．如图1－26所示，在平面直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO=5，sin∠BOA(1)求点B的坐标；(2)求cos∠BAO的值．9．请你画出一个以BC为底边的等腰三角形ABC，使底边上的高AD＝BC(1)求tan∠ABC和sin∠ABC的值；(2)在你所画的等腰三角形ABC中，假设底边BC＝5米，求腰上的高BE．参考答案1．C[提示：] 2．D[提示：过A 点作垂线交底部于C 点，则△ACB 为直角三角形，∴BC＝8(m)，∴tan aD ．] 3．B[提示：∠ADE 和∠EDC 互余，∴cos a ＝sin ∠EDCsin ∠EDC＝EC由勾股定理，得DE在Rt △AED 中，cos a∴AD故选B ．]4．4[提示：在Rt △BCA 中，AC ＝3米，cos ∠BACAB ＝4米，即梯子的长度为4米．] 5．48°[提示：∵sin 2 a ＋cos 2 a ＝l ，∴a ＝48°．]6．提示：sin Acos Atan A7．解：∵∠ACB ＝90°，CD ⊥AB ，∴△ACD ∽△CBD ，∴CD 2＝AD ·DB ＝16，∴CD =4，∴AC∴sin Acos Atan A8．解：(1)如图l －27所示，作BH ⊥OA ， 垂足为H ．在Rt △OHB 中，∵BO ＝5，sin ∠BOABH =3，∴OH ＝4，∴点B 的坐标为(4，3)． (2)∵OA ＝10，OH ＝4，∴AH ＝6．在Rt △AHB 中，∵BH =3，∴AB＝cos ∠9．解：(1)根据题意画出图形，如图1－28所示，∵AB ＝AC ，AD ⊥BC ， AD ＝BC ，∴BD，即AD ＝2BD ，∴AB，∴tan ∠∠作BE ⊥AC 于E ，在Rt △BEC 中，sinC=sin ∠又∵.。

第一章直角三角形边角关系1.1.1 锐角三角函数（一）1、如图，△ABC是等腰直角三角形，你能根据图中所给数据求出tanC吗?2、如图，某人从山脚下的点A走了200m后到达山顶的点B，已知点B到山脚的垂直距离为55m，求山的坡度.(结果精确到0.001)3、若某人沿坡度i＝3：4的斜坡前进10米，则他所在的位置比原来的位置升高________米.4、菱形的两条对角线分别是16和12.较长的一条对角线与菱形的一边的夹角为θ，则tan θ＝______.5、如图，Rt△ABC是一防洪堤背水坡的横截面图，斜坡AB的长为12 m，它的坡角为45°，为了提高该堤的防洪能力，现将背水坡改造成坡比为1：1.5的斜坡AD，求DB的长.(结果保留根号)6、填空：⑴、在Rt△ABC中,∠C=90°,AB=3,BC=1,则tanA= _______.⑵、在△ABC中,AB=10,AC=8,BC=6,则tanA=_______.⑶、在△ABC中,AB=AC=3,BC=4,则tanC=______.7、在Rt△ABC中,∠C是直角,∠A、∠B、∠C的对边分别是a、b、c,且a=24,c= 25,求tanA、tanB的值.8、若三角形三边的比是25:24:7,求最小角的正切值.9、如图,在菱形ABCD中,AE⊥BC于E,EC=1,tanB=, 求菱形的边长和四边形AECD的周长.10、已知:如图,斜坡AB的倾斜角a,且tanα=,现有一小E DB A C球从坡底A处以20cm/s 的速度向坡顶B处移动,则小球以多大的速度向上升高?11、探究:⑴、a克糖水中有b克糖(a>b>0),则糖的质量与糖水质量的比为_______; 若再添加c克糖(c>0),则糖的质量与糖水的质量的比为________.生活常识告诉我们: 添加的糖完全溶解后,糖水会更甜,请根据所列式子及这个生活常识提炼出一个不等式: ____________.⑵、我们知道山坡的坡角越大,则坡越陡,联想到课本中的结论:tanA的值越大, 则坡越陡,我们会得到一个锐角逐渐变大时,它的正切值随着这个角的变化而变化的规律,请你写出这个规律:_____________.⑶、如图,在Rt△A BC中,∠B=90°,AB=a,BC=b(a>b),延长BA、BC,使AE=CD=c, 直线CA、DE交于点F,请运用(2) 中得到的规律并根据以上提供的几何模型证明你提炼出的不等式.。