感知器的学习算法

多层感知器算法原理多层感知器（Multilayer Perceptron，MLP）是一种前馈结构的人工神经网络，可以对一组输入向量进行非线性映射，从而实现分类或回归等任务。

MLP由多个节点层组成，每一层都与上一层和下一层相连，每个节点都是一个带有非线性激活函数的神经元。

MLP 的学习过程主要依赖于反向传播算法，即通过计算输出误差对网络权重进行反向调整，从而达到最优化的目的。

网络结构MLP的网络结构一般包括三层或以上，分别是输入层、隐藏层和输出层。

输入层接收外部输入的数据，输出层产生网络的预测结果，隐藏层位于输入层和输出层之间，可以有多个，用于提取输入数据的特征。

每一层中的节点都与相邻层中的所有节点相连，每条连接都有一个权重，表示该连接的强度。

每个节点除了接收来自上一层的加权输入外，还有一个偏置项，表示该节点的阈值。

每个节点的输出由其输入和激活函数共同决定，激活函数的作用是引入非线性，增强网络的表达能力。

常用的激活函数有Sigmoid函数、双曲正切函数、ReLU函数等。

学习过程MLP的学习过程主要分为两个阶段，即前向传播和反向传播。

前向传播是指从输入层到输出层逐层计算节点的输出，反向传播是指从输出层到输入层逐层计算节点的误差，并根据误差对权重进行更新。

具体步骤如下：前向传播从输入层开始，将输入数据乘以相应的权重，加上偏置项，得到每个节点的输入。

对每个节点的输入应用激活函数，得到每个节点的输出。

将每个节点的输出作为下一层的输入，重复上述过程，直到达到输出层。

在输出层，根据预测结果和真实标签，计算损失函数，评估网络的性能。

反向传播从输出层开始，根据损失函数对每个节点的输出求导，得到每个节点的误差。

对每个节点的误差乘以激活函数的导数，得到每个节点的梯度。

将每个节点的梯度作为上一层的误差，重复上述过程，直到达到输入层。

在每一层，根据节点的梯度和输入，计算权重的梯度，并根据学习率对权重进行更新。

MLP的学习过程可以采用批量梯度下降、随机梯度下降或小批量梯度下降等优化方法，也可以使用动量、自适应学习率或正则化等技术来提高收敛速度和泛化能力。

delta规则Delta规则，也称为delta学习规则或感知器算法，是一个经典的人工神经网络学习算法。

这个算法主要用于训练一个由具有权重的神经元构成的网络，使得网络能够正确地预测给定的输入和输出。

当神经元收到一个输入时，它会计算输入与其权重的加权和作为神经元的激活函数输入。

激活函数通常采用一些非线性的函数，例如sigmoid函数，以产生更高的复杂性。

Delta规则的核心思想是基于误差的学习，即对于给定的输入，通过比较神经元的实际输出和期望输出之间的差异来调整权重。

这个差异被称为误差项，也可以被看作是网络预测与实际结果之间的差异。

具体来说，Delta规则可以被描述为下面的步骤：1.随机初始化权重。

2.使用网络进行预测。

3.计算误差项。

4.根据误差项调整权重。

5.重复以上步骤，直到误差收敛或达到预定的迭代次数。

在第一步中，权重的初始值通常被设置为随机值，以便训练开始时网络能够探索许多可能的解决方案。

在第二步中，网络接收输入并根据初始的权重计算输出。

这个输出通常与期望输出不同，因此满足误差项的条件。

在第三步中，误差项被计算为期望输出与实际输出之间的差异。

这个差异可以使用一个成本函数来度量。

在第四步中，权重被通过误差项的反向传播来调整，即越大的误差项产生更多的权重调整。

在第五步中，程序使用新的权重再次执行第二至第四步，以获得更准确的输出结果。

这个过程持续进行直到误差足够小，或达到规定的迭代次数。

需要注意的是，Delta规则的效率和准确度很大程度上取决于两个因素：学习速率和激活函数。

学习速率决定了神经元根据误差项调整权重的幅度，如果学习速率太大，网络可能会无法收敛；如果太小，网络的训练过程可能会变得过于缓慢。

激活函数对网络所能解决的问题的复杂度具有重要的影响。

如果激活函数是线性的，那么神经网络只能处理线性可分问题，并且不能处理高度非线性的问题。

总之，Delta规则是一种简单而有效的网络训练算法，它在许多机器学习应用中被广泛使用。

感知器算法的基本原理与应用感知器算法是一种简单而有效的机器学习算法，于1957年被Frank Rosenblatt所提出。

在过去几十年里，感知器算法一直被广泛应用在识别模式，分类数据和垃圾邮件过滤等领域。

本文将会介绍感知器算法的基本原理，如何使用感知器完成模式分类，以及如何优化感知器算法。

感知器算法的基本原理感知器算法基于神经元（Perceptron）模型构建，神经元模型的基本原理是对输入信号进行加权，然后通过激活函数的计算输出结果。

通常情况下，神经元被认为是一个输入层节点，一个或多个输入是接收的，以及一个输出层。

感知器算法的核心思想是，给定一组输入和对应的输出（通常成为标签），通过多个迭代来调整模型中的权重，以最大限度地减少模型的误差，并尽可能准确地预测未知输入的输出。

感知器算法的主要流程如下：1. 初始化感知器参数，包括权重（最初为随机值）和偏置（通常为零）。

2. 对于每个输入，计算预测输出，并将预测输出与实际标签进行比较。

3. 如果预测输出与实际标签不同，则更新权重和偏置。

更新规则为$\omega_{j} \leftarrow \omega_{j} + \alpha(y-\hat{y})x_{j}$，其中$x_{j}$是输入的第$j$个特征，$\alpha$是学习率（控制权重和偏置的更新量），$y$是实际标签，而$\hat{y}$是预测输出。

4. 重复步骤2和步骤3，直到满足停止条件（例如，经过N次重复迭代后误差不再显著降低）。

如何使用感知器完成分类让我们考虑一个简单的情况：我们要学习使用感知器进行两类别（正面和负面）的文本情感分类。

我们可以将文本转换为一组数字特征，例如文本中出现特定单词的频率或数量，并将每个文本的情感作为输入，正面或负面情感被记为1或0。

我们可以将感知器视为一个二元分类器，用它来预测每个输入文本的情感值。

对于每个输入，我们计算出感知器的输出，并将其与实际情感进行比较。

如果它们没有匹配，那么我们将使用上面提到的更新规则调整每个特征的权重，重复该过程，直到达到收敛为止。

i
y = f (∑ wi xi − θ )
i =1
d
而且f为一阶跃函数， 而且 为一阶跃函数，即： 为一阶跃函数
d 1, ∑ wi xi − θ ≥ 0 i =1 y = f ( x) = = sgn( w0T x − θ ) d −1, w x − θ < 0 ∑ i i i =1
四、感知器训练算法在多类问题中的应用 就第二章中的第三种情况为例说明） （就第二章中的第三种情况为例说明） 判决规则：对于c种类型 存在k个判决函 种类型， 判决规则：对于 种类型，存在 个判决函 数 d j ( x)( j = 1, 2,⋯, k ) ，若 di ( x) > d j ( x)( j = 1, 2,⋯ , k , j ≠ i) ， x ∈ ωi 则判： 则判： 假设k=c, 多类问题的感知器算法的步骤如下： 多类问题的感知器算法的步骤如下： 假设 (1) 赋给初值： 赋给初值： 赋初值，选择正常数c, 给 Wi 赋初值，选择正常数 把训练样本 变成增广型， 变成增广型，k=0; x (2) 输入训练样本 xk，k ∈{x1 , x2 ,⋯, xn }，假定 x ∈ ωi ；
训练样本
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101
W(K)Tx
+ + + 0 0 + 0 + + + -
(3) 计算 个判决函数值： 计算c个判决函数值 个判决函数值：
di ( xk ) = [Wi (k )]T xk , i = 1, 2,⋯ , c

多层感知器学习算法研究中文摘要多层感知器学习算法研究中文摘要多层感知器是一种单向传播的多层前馈网络模型，由于具有高度的非线性映射能力，是目前神经网络研究与应用中最基本的网络模型之一，广泛应用于模式识别、图像处理、函数逼近、优化计算、最优预测和自适应控制等领域。

而多层感知器采用的是BP算法。

BP算法的收敛速度慢是个固有的缺点，因为它是建立在基于只具有局部搜索能力的梯度法之上的，是只具有局部搜索能力的方法，若用于多个极小点的目标函数时，是无法避免陷入局部极小和速度慢的缺点的。

因此，对BP算法的研究一直以来都是非常重要的课题。

毕业设计课题旨在对多层感知器的学习算法进行研究，并提出一种新的学习算法。

由于BPWE (权值外推BP)算法和TBP (三项BP)算法都是基于权值调整的改进算法，而考虑将TBP算法中的均衡因子融入到BPWE算法中，从而使后者对权值的调整由原来的两项增加为三项，从而提出一种新的学习算法---TWEBP算法。

为了验证本算法的优点，采用了三个例子，分别对异或问题、三分类问题和函数逼近问题进行了实验，发现其收敛速度和逃离局部极小点的能力都优于传统算法。

关键词：多层感知器学习算法趋势外推均衡因子TWEBP作者：王之仓指导教师：邓伟Research on Multilayer Perceptron Learning AlgorithmABSTRACTMultilayer Perceptron is a sort of multilayer feed-forward single direct propagation network model. Because of its good nonlinear mapping ability, it is one of the basic models in the research and application of neural network at present, which has been widely applied to pattern recognition, image processing, function approximation, optimization computation, optional prediction, adaptation control and so on. Multilayer Perception trained with BP algorithm often has a low convergence speed as a natural drawback，because it is based on gradient descent method which is only local searching. When applied to an object function with many local minimums, it is not possible for BP algorithm toAbstract Research on Multilayer Perceptron Learning Algorithm avoid being trapped in local minimum and to have a low converges speed. In a word, the research on BP algorithm has become very important for a long time.The purpose of this design task is to study the algorithms of Multilayer Perceptron, and a new BP algorithm is presented. Both BPWE algorithm (back-propagation by weight extrapolation) and TBP algorithm (a three-term back propagation algorithm) are based on weight value adjusted. Considered to add the proportional factor of the TBP algorithm into BPWE algorithm, it made the latter can adjust weight value by three terms too. A new BP algorithm，named TWEBP (the three-term weight extrapolation back propagation algorithm), is presented based on the two algorithm proposed just now. This new TWEBP algorithm is tested on three examples and the convergence behavior of the TWEBP and BP algorithm are compared. The results show that the proposed algorithm generally out-perfoims the conventional algorithm in terms of convergence speed and the ability to escape from local minima. Keywords：Multilayer Perceptron, learning algorithm, extrapolation, proportional factor, TWEBP目录攸顺 ......................................... ............. .. (I)ABSTRACT .................... (II)第一章绪论 (1)1.1基本概念 (1)1.2神经网络的发展过程 (2)1.2.1产生背景 (2)1.2.2发展历史 (2)1.2.3现状 (4)1.3多层感知器 (5)1.3.1基本概念 (5)1.3.2多层感知器学习算法存在的问题 (6)1.3.3多层感知器学习算法的研究成果 (7)1.4毕业设计工作及论文结构 (8)1.4.1毕业设计工作 (8)1.4.2论文结构 .......................................................... . (8)第二章反向传播算法 (9)2.1反向传播算法 (9)2.1.1学习规则 (9)2.1.2学习过程 (9)2.1.3反向传播算法的步骤 (11)2.2反向传播算法的贡献和局限性 (12)2.2.1反向传播算法的贡献 (12)2.2.2反向传播算法的局限性 (12)2.3对反向传播算法的进一步讨论 (13)2.3.1激活函数 (13).2.3.2 ............................... ...................................................................................... ；162.3.3云力量项 (16)2.3.4学习速率 (17)2.3.5误差函数.................. . (19)2.4小结 (20)第三章性能优化 (21)3.1性能优化的理论基础 (21)3.2最速下降法 (23)3.3牛顿法 (24)3.4共轭梯度法 (25)3.5小结 (27)第四章TWEBP算法 (29)4.1趋势外推思想 (29)4.1.1趋势外推 (29)4.1,2 BPWE 算法 (30)4.2TBP 算法 (32)4.3TWEBP 算法 (32)4.4计算机仿真 (33)4.4.1 XOR 问题 (33)4.4.2三分类问题 (37)4.4.3函数逼近问题 (42)4.5 4^ (46)第五章总结与展望 (47)#%娜.......... .. (48)攻读学位期间公幵发表的论文 (50)® (51)第一章绪论一个神经元有两种状态，即兴奋和抑制，平时处于抑制状态的神经元，其树突和胞体接收其他神经元经由突触传来的兴奋电位，多个输入在神经元中以代数和的方式叠加；如果输多层感知器学习算法研究第一韋绪论入兴奋总量超过某个阈值，神经元就会被激发进入兴奋状态，发出输出脉冲，并由轴突的突触传递给其他神经元。

感知器的训练算法
已知两个训练模式集分别属于ω1类和ω2类，权向量的初始值为w(1)，可任意取值。

若0x )k (w ,x k T 1k >∈ω，若0x )k (w ,x k T 2k ≤∈ω，则在用全部训练模式集进行迭代训练时，第k 次的训练步骤为：
- 若1k x ω∈且0x )k (w k T ≤，则分类器对第k 个模式x k 做了错误分类，此时应校正权向量，使得w(k+1) = w(k) + Cx k ，其中C 为一个校正增量。

- 若2k x ω∈且0x )k (w k T >，同样分类器分类错误，则权向量应校正如下：w(k+1) = w(k) - Cx k
- 若以上情况不符合，则表明该模式样本在第k 次中分类正确，因此权向量不变，即：w(k+1) = w(k)
若对2x ω∈的模式样本乘以(-1)，则有：
0x )k (w k T ≤时，w(k+1) = w(k) + Cx k
此时，感知器算法可统一写成：
⎩⎨⎧≤+>=+0
x )k (w if Cx )k (w 0x )k (w if )k (w )1k (w k T k k T。

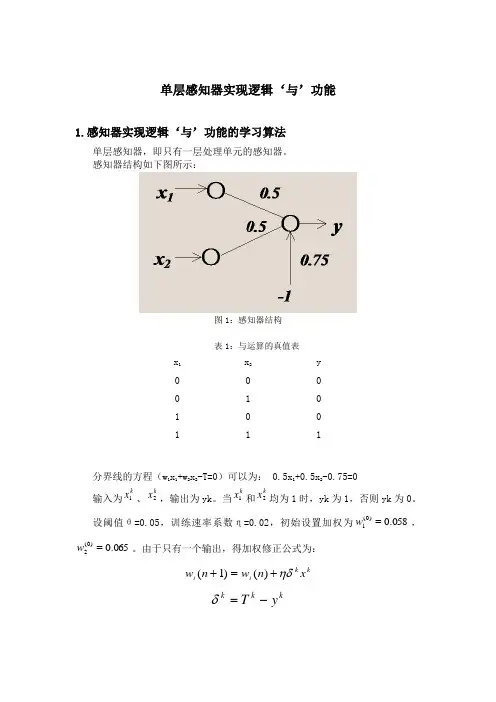
单层感知器实现逻辑‘与’功能1.感知器实现逻辑‘与’功能的学习算法单层感知器，即只有一层处理单元的感知器。

感知器结构如下图所示：图1：感知器结构表1：与运算的真值表x 1 x 2 y 0 0 0 0 1 0 1 0 0 111分界线的方程（w 1x 1+w 2x 2-T=0）可以为： 0.5x 1+0.5x 2-0.75=0输入为k x 1、k x 2，输出为yk 。

当k x 1和k x 2均为1时，yk 为1，否则yk 为0。

设阈值θ=0.05，训练速率系数η=0.02，初始设置加权为058.0)0(1=w ，065.0)0(2=w 。

由于只有一个输出，得加权修正公式为：k k i i x n w n w ηδ+=+)()1(k k k y T -=δ第一步：w(0)=(0.058, 0.065)，加入x1=(0, 0)，05.01221111-=-+=θxwxws，则y1=0。

由于T1=0，δ1= T1- y1=0，故w(1)=(0.058, 0.065)第二步：加入x2=(0, 1)，015.02222112=-+=θxwxws，则y2=1。

由于T 2=0，则δ2= T2- y2=-1，故w(2)=w(1)+0.02(-1)x2=(0.058, 0.045)第三步：加入x3=(1, 0)，008.03223113=-+=θxwxws，则y3=1。

由于T 3=0，则δ3= T3- y3=-1，故w(3)=w(2)+0.02(-1)x3=(0.038, 0.045)第四步：加入x4=(1, 1)，033.04224114=-+=θxwxws，则y4=1。

由于T 4=1，则δ4= T4- y4=0，故w(4)=w(3)=(0.038, 0.045)第五步：加入x1=(0, 0)，S1=-0.05，则y1=0。

由于T1=0，δ1=0，故w(5)=(0.038,0.045)第六步：加入x2=(0, 1)，S2=-0.005，则y2=0。

感知器模型及其学习算法1感知器模型感知器模型是美国学者罗森勃拉特（rosenblatt）为研究大脑的存储、学习和认知过程而提出的一类具有自学习能力的神经网络模型，它把神经网络的研究从纯理论探讨引向了从工程上的实现。

rosenblatt明确提出的感知器模型就是一个只有单层排序单元的前向神经网络，称作单层感知器。

2单层感知器模型的自学算法算法思想：首先把连接权和阈值初始化为较小的非零随机数，然后把有n个连接权值的输入送入网络，经加权运算处理，得到的输出如果与所期望的输出有较大的差别，就对连接权值参数按照某种算法进行自动调整，经过多次反复，直到所得到的输出与所期望的输出间的差别满足要求为止。

?为简单起见，仅考虑只有一个输出的简单情况。

设xi(t)是时刻t感知器的输入（i=1,2,......,n），ωi(t)是相应的连接权值，y(t)是实际的输出，d(t)是所期望的输出，且感知器的输出或者为1，或者为0。

3线性不可分问题单层感知器无法抒发的问题被称作线性不容分后问题。

1969年，明斯基证明了“异或”问题就是线性不容分后问题：“异或”（xor）运算的定义如下：由于单层感知器的输出为y(x1,x2)=f(ω1×x1+ω2×x2-θ)所以，用感知器实现简单逻辑运算的情况如下：（1）“与”运算（x1∧x2）令ω1=ω2=1，θ=2，则y=f(1×x1+1×x2-2)显然，当x1和x2均为1时，y的值1；而当x1和x2有一个为0时，y的值就为0。

（2）“或”运算（x1∨x2）令ω1=ω2=1,θ=0.5y=f(1×x1+1×x2-0.5)显然，只要x1和x2中有一个为1，则y的值就为1；只有当x1和x2都为0时，y的值才为0。

（3）“非”运算（～x1）令ω1=-1，ω2=o，θ=-0.5，则y=f((-1)×x1+1×x2+0.5))显然，无论x2为何值，x1为1时，y的值都为0；x1为o时，y的值为1。

• τij—— 输入输出间的突触时延； 输入输出间的突触时延； • Tj —— 神经元 的阈值； 神经元j的阈值 的阈值； • wij—— 神经元 到 j 的突触连接系数或称 神经元i到 权重值； 权重值； • f ( ) —神经元转移函数。 神经元转移函数。 神经元转移函数
o j (t + 1) = f {[
满足y=x1.x2逻辑与关系。 。
逻辑或： 二个兴奋性输入） 令T=1，I=0，E=x1+x2（二个兴奋性输入） ， ， 当x1=1, x2=1, E=1+1=2, 当x1=1, x2=0, E=1+0=1, 当x1=0, x2=1, E=0+1=1, 当x1=0, x2=0, E=0+0=0, 满足y=x1+x2逻辑或关系 触发 y=1 触发 y=1 触发 y=1 不触发 y=0
x1 0 0 1 1
x2 0 1 0 1
y 0 0 0 1
感知器结构
x1 x2
○ ○
0.5 0.5
○
0.75 -1
y
wix1+w2x2 -T=0 0.5x1+0.5x2-0.75=0
感知器的学习算法
感知器学习规则的训练步骤：
(1) 对各权值w0j(0),w1j(0),┄,wnj(0)，j=1, 2,┄,m （m为计算层的节点数）赋予较小的非零随机数； (2) 输入样本对{Xp,dp}，其中Xp=(-1,x1p,x2p,┄,xnp)， dp为期望的输出向量（教师信号），上标p代表 样本对的模式序号，设样本集中的样本总数为P， 则p=1,2,┄,P；
(4)概率型转移函数 概率型转移函数
P(1) =
1 1+e
− x/T

基于模式识别的判别函数分类器的设计与实现摘要：本文主要介绍了模式识别中判别函数的相关概念和感知器算法的原理及特点，并例举实例介绍感知器算法求解权向量和判别函数的具体方法，最后按照线性函数判决函数的感知算法思想结合数字识别，来进行设计，通过训练数字样本（每个数字样本都大于120），结合个人写字习惯，记录测试结果，最后通过matlab 编码来实现感知器的数字识别。

关键字：模式识别 判别函数 感知器 matlab1 引言模式识别就是通过计算机用数学技术方法来研究模式的自动处理和识别。

对于人类的识别能力我们是非常熟悉的。

因为我们在早些年就已经会开发识别声音、脸、动物、水果或简单不动的东西的技术了。

在开发出说话技术之前，一个象球的东西，甚至看上去只是象个球，就已经可以被识别出来了。

所以除了记忆，抽象和推广能力是推进模式识别技术的关键技术。

最近几年我们已可以处理更复杂的模式，这种模式可能不是直接基于通过感知器观察出来的随着计算机技术的发展，人类对模式识别技术提出了更高的要求。

本文第二节介绍判别函数分类器，具体介绍了判别函数的概念、特点以及如何确定判别函数的正负；第三节介绍了感知器的概念、特点并用感知器算法求出将模式分为两类的权向量解和判别函数，最后用matlab 实现感知判别器的设计。

2 判别函数分类器2.1 判别函数概念直接用来对模式进行分类的准则函数。

若分属于ω1，ω2的两类模式可用一方程d (X ) =0来划分，那么称d (X ) 为判别函数，或称判决函数、决策函数。

如，一个二维的两类判别问题，模式分布如图示，这些分属于ω1，ω2两类的模式可用一直线方程 d (X )=0来划分。

其中0)(32211=++=w x w x w d X 式中： 21,x x 为坐标变量。

图2-1 两类二维模式的分布将某一未知模式 X 代入：若0)(>X d ，则1ω∈X类； 若0)(<X d ，则2ω∈X 类；若0)(=X d ，则21ωω∈∈X X 或或拒绝维数=3时：判别边界为一平面。

lpips函数LPIPS（Learned Perceptual Image Patch Similarity）是一种基于深度学习的图像质量度量方法，旨在模拟人类视觉感知的方式，通过对图像中各个区域的相似度进行计算，从而得出一个数值化的图像质量评估结果。

LPIPS算法的核心思想是基于感知学习，即通过训练一个深度神经网络，使其能够对人类视觉感知的特征进行模拟和学习，并基于这些特征来评估图像质量。

这个神经网络被称为感知器，它接收两个输入图像，并输出它们之间的差异度量值。

在训练感知器时，需要为其提供一个大量的图像对，每对图像都包含一个原始图像和一个被处理过的图像，这个处理过的图像可能是被压缩、缩放、裁剪或者加噪处理过的，通过这些处理，可以模拟出现实生活场景中的各种图片处理情况。

感知器将原图像和处理后的图像作为输入，输出它们之间的差异度量值，这个差异度量值可以用来评估图像质量的差异程度。

感知器的训练是一个基于监督学习的过程，需要将其与大量人工标注的图像质量评估数据进行训练。

这些数据可以来自于各种真实生活场景中的图像，例如自然风光、人像、文档等，这些图像经过人工标注后，给出了它们的图像质量评估值。

依据这些标注数据，感知器可以通过反向传播算法对自己进行参数训练，从而不断提高自己对图像质量的估计准确性。

感知器的输出结果是两个图像之间的差异度量值，通常是一个实数，取值范围为0-1。

当输入的两个图像完全相输出为0；而当它们差异最大时，输出为1。

通过这个度量值，可以对图像质量进行定量评估，以为图像处理及修复等应用提供数据和指导。

LPIPS算法已经在许多应用场景中得到了验证和应用，例如图像无损和有损压缩、图像超分辨率、图像放大等。

在图像压缩领域，LPIPS算法可以用来评估各种不同压缩率下图像质量的差异，以便找到最优的压缩率；在图像超分辨率领域，LPIPS算法可以用来评估不同超分辨率算法对图像质量的影响，以便找到最佳的超分辨率算法等。

机器学习算法--Perceptron（感知器）算法概括Perceptron(感知器)是⼀个⼆分类线性模型，其输⼊的是特征向量，输出的是类别。

Perceptron的作⽤即将数据分成正负两类的超平⾯。

可以说是机器学习中最基本的分类器。

模型Perceptron ⼀样属于线性分类器。

对于向量X=x1,x2,...x n，对于权重向量（w）相乘，加上偏移（b），于是有：f(x)=N∑i=1w i x i+b设置阈值threshold之后，可以的到如果f(x)>threshold,则y(标签)设为1如果f(x)<threshold,则y(标签)设为0即，可以把其表⽰为：y=sign(w T x+b)参数学习我们已经知道模型是什么样，也知道Preceptron有两个参数，那么如何更新这两个参数呢？⾸先，我们先Preceptron的更新策略：1. 初始化参数2. 对所有数据进⾏判断，超平⾯是否可以把正实例点和负实例点完成正确分开。

3. 如果不⾏，更新w，b。

4. 重复执⾏2，3步，直到数据被分开，或者迭代次数到达上限。

那么如何更新w，b呢？我们知道在任何时候，学习是朝着损失最⼩的地⽅，也就是说，我的下⼀步更新的策略是使当前点到超平⾯的损失函数极⼩化。

在超平⾯中，我们定义⼀个点到超平⾯的距离为：(具体如何得出，可以⾃⾏百度~~~ )，此外其中1|w|是L2范数。

意思可表⽰全部w向量的平⽅和的开⽅。

1‖w‖w T x+b 这⾥假设有M个点是误差点，那么损失函数可以是：L(w,b)=−1‖w‖∑x i∈M yi(w T x+b)当然，为了简便计算，这⾥忽略1|w|。

1|w|不影响-y(w,x+b)正负的判断，即不影响学习算法的中间过程。

因为感知机学习算法最终的终⽌条件是所有的输⼊都被正确分类，即不存在误分类的点。

则此时损失函数为0，则可以看出1|w|对最终结果也⽆影响。

既然没有影响，为了简便计算，直接忽略1|w|。

1、用感知器算法求解向量,训练样本为:(1) ω1}(1,1,0),(1,0,1),(1,0,0),{(0,0,0):TT T T (2) ω2:}(1,1,1),(0,1,0),(0,1,1),{(0,0,1)T T T T（1）训练样本分量增广化及符号规范化。

)10,0,0(1'=，x )10,0,1(2'=，x )11,0,1(3'=，x )10,1,1(4'=，x )1-1-,0,0(5'=，x )1-1-,1-,0(6'=，x )1-0,1-,0(7'=，x )1-1-,1-,1-(8'=，x （2）运用感知器训练算法，任意给增广权矢量赋初值：)111,1()1(w '=， 取增量1=ρ则： )10,0,0(1'=，x )10,0,1(2'=，x )11,0,1(3'=，x )10,1,1(4'=，x )1-1-,0,0(5'=，x)1-1-,1-,0(6'=，x)1-0,1-,0(7'=，x)1-1-,1-,1-(8'=，x)111,1()1(w '=，)1()2(,01)()(,,11w w x k w x d x x k k k k=>='=== )2()3(,02)()(,,22w w x k w x d x x k k k k=>='=== )3()4(,03)()(,,33w w x k w x d x x k k k k=>='=== )4()5(,03)()(,,44w w x k w x d x x k k k k=>='===)00,1,1()5()6(,02)()(,,555'=+=<-='===，x w w x k w x d x x k k k k)1-1-,0,1()6()7(,01)()(,,666'=+=<-='===，x w w x k w x d x x k k k k)7()8(,01)()(,,77w w x k w x d x x k k k k=>='=== )8()9(,01)()(,,88w w x k w x d x x k k k k=>='===)01-,0,1()9()10(,01)()(,,911'=+=<-='===，x w w x k w x d x x k k k k)10()11(,01)()(,,102w w x k w x d x x k k k k=>='===)0,1,0,2()11()12(,0)()(,,1133'=+=='===，x w w x k w x d x x k k k k)12()13(,03)()(,,124w w x k w x d x x k k k k=>='===)01-,0,2()13()14(,01)()(,,1355'=+=<-='===，x w w x k w x d x x k k k k)14()15(,01)()(,,146w w x k w x d x x k k k k=>='===)1-1-,1,2()15()16(,0)()(,,1577'-=+=='===，x w w x k w x d x x k k k k)16()17(,01)()(,,168w w x k w x d x x k k k k=>='===)0,1,1,2()17()18(,01)()(,,1711'--=+=<-='===x w w x k w x d x x k k k k)18()19(,02)()(,,182w w x k w x d x x k k k k=>='=== )19()20(,01)()(,,193w w x k w x d x x k k k k=>='=== )20()21(,01)()(,,204w w x k w x d x x k k k k=>='=== )21()22(,01)()(,,215w w x k w x d x x k k k k=>='=== )22()23(,02)()(,,226w w x k w x d x x k k k k=>='=== )23()24(,01)()(,,237w w x k w x d x x k k k k=>='===)1,2,2,1()24()25(,0)()(,,2488'---=+=='===x w w x k w x d x x k k k k)02-,2,1()25()26(,01)()(,,2511'-=+=<-='===，x w w x k w x d x x k k k k)26()27(,01)()(,,262w w x k w x d x x k k k k=>='===)1,1,2,2()27()28(,01)()(,,2733'--=+=<-='===x w w x k w x d x x k k k k)28()29(,01)()(,,284w w x k w x d x x k k k k=>='===)0,2,2,2()29()30(,0)()(,,2955'--=+=='===x w w x k w x d x x k k k k)30()31(,04)()(,,306w w x k w x d x x k k k k=>='=== )31()32(,02)()(,,317w w x k w x d x x k k k k=>='=== )32()33(,02)()(,,328w w x k w x d x x k k k k=>='===)1,2,2,2()33()34(,0)()(,,3311'--=+=='===x w w x k w x d x x k k k k)34()35(,03)()(,,342w w x k w x d x x k k k k=>='===)35()36(,01)()(,,353w w x k w x d x x k k k k=>='===)36()37(,01)()(,,364w w x k w x d x x k k k k=>='=== )37()38(,01)()(,,375w w x k w x d x x k k k k=>='=== )38()39(,03)()(,,386w w x k w x d x x k k k k=>='=== )39()40(,01)()(,,397w w x k w x d x x k k k k=>='=== )40()41(,01)()(,,408w w x k w x d x x k k k k=>='=== )41()42(,01)()(,,411w w x k w x d x x k k k k=>='===由上边结果可以看出，经过，，，，，，，，87654321x x x x x x x x一轮迭代后表明使用)34(w异能对所有样本正确分类，增广权矢量的值不再变化，所以算法收敛于)34(w ，)34(w 就是所求的解向量，即)1,2,2,2()34(*'--=w。

3.5 感知器算法对于线性判别函数，当模式的维数已知时判别函数的形式实际上就已经定了下来，如二维 121122T()x x d w x w x w ==++（,），X X三维123112233T,()+x x x d w x w x w x w==++（,），X X剩下的问题也就是确定权向量W ，只要求出权向量，分类器的设计即告完成。

非线性判别函数也有类似的问题。

本章的后续部分将主要讨论一些基本的训练权向量的算法，或者说学习权向量的算法，它们都是都是用于设计确定性分类器的迭代算法。

1. 概念理解在学习感知器算法之前，首先要明确几个概念。

1）训练与学习训练是指利用已知类别的模式样本指导机器对分类规则进行反复修改，最终使分类结果与已知类别信息完全相同的过程。

从分类器的角度来说，就是学习的过程。

学习分为监督学习和非监督学习两大类。

非监督学习主要用于学习聚类规则，没有先验知识或仅有极少的先验知识可供利用，通过多次学习和反复评价，结果合理即可。

监督学习主要用于学习判别函数，判别函数的形式已知时，学习判别函数的有关参数；判别函数的形式未知时，则直接学习判别函数。

训练与监督学习方法相对应，需要掌握足够的与模式类别有关的先验信息，这些先验信息主要通过一定数量的已知类别的模式样本提供，这些样本常称作训练样本集。

用训练样本集对分类器训练成功后，得到了合适的判别函数，才能用于分类。

前面在介绍线性判别函数的同时，已经讨论了如何利用判别函数的性质进行分类，当然，前提是假定判别函数已知。

2）这种分类器只能处理确定可分的情况，包括线性可分和非线性可分。

只要找到一个用于分离的判别函数就可以进行分类。

由于模式在空间位置上的分布是可分离的，可以通过几何方法把特征空间分解为对应不同类别的子空间，故又称为几何分类器。

当不同类别的样本聚集的空间发生重叠现象时，这种分类器寻找分离函数的迭代过程将加长，甚至振荡，也就是说不收敛，这时需要用第4章将要介绍的以概率分类法为基础的概率分类器进行分类。

感知器算法原理感知器算法是一种二分类的分类算法，基于线性模型的思想。

其原理是通过输入的特征向量和权重向量的线性组合，经过阈值函数进行判别，实现对样本的分类。

具体来说，感知器算法的输入为一个包含n个特征的特征向量x=(x₁, x₂, ..., xn)，以及对应的权重向量w=(w₁, w₂, ..., wn)，其中wi表示特征xi对应的权重。

感知器算法的目标是找到一个超平面，将正负样本正确地分离开来。

如果超平面上方的点被判为正样本，超平面下方的点被判为负样本，则称超平面为正类超平面；反之，则称超平面为负类超平面。

感知器算法的具体步骤如下：1. 初始化权重向量w和阈值b。

2. 对于每个样本(xᵢ, yᵢ)，其中xᵢ为特征向量，yᵢ为样本的真实标签。

3. 计算样本的预测输出值y_pred=sign(w·x + b)，其中·表示向量内积操作，sign为符号函数，将预测值转化为+1或-1。

4. 如果预测输出值与真实标签不一致（y_pred ≠ yᵢ），则更新权重向量w和阈值b：- w:=w + η(yᵢ - y_pred)xᵢ- b:=b + η(yᵢ - y_pred)，其中η为学习率，用于控制权重的更新速度。

5. 重复步骤3和4，直到所有样本都被正确分类，或达到预定的迭代次数。

感知器算法的核心思想是不断地通过训练样本来优化权重向量和阈值，使得模型能够将正负样本准确地分开。

然而，感知器算法只对线性可分的问题有效，即存在一个超平面能够完全分开正负样本。

对于线性不可分问题，感知器算法无法收敛。

因此，通常需要通过特征工程或使用其他复杂的分类算法来解决线性不可分的情况。

感知器算法的基本步骤嘿，咱今儿个就来聊聊感知器算法的那些事儿哈！你知道不，这感知器算法就像是一个神奇的魔法盒子，里面装着好多奇妙的步骤呢！首先啊，得有一堆数据，就好像是一堆五颜六色的糖果，每颗糖果都有它独特的味道和特征。

然后呢，就要开始给这些数据分分类啦！这就好比把不同口味的糖果放进不同的小盒子里。

怎么分呢？这就得靠感知器算法的魔力啦！它会先观察这些数据，就像我们仔细观察糖果的颜色、形状一样。

接着，它会试着找到一些规律，一些能把这些数据区分开来的关键之处。

这可不是一件容易的事儿啊，就好像在一堆乱糟糟的东西里找线索一样。

找到规律后，它就开始行动啦！它会根据这些规律来判断新的数据该归到哪一类。

这就好像来了一颗新糖果，它能马上判断出这颗糖果该放进哪个小盒子里。

你说神奇不神奇？而且哦，这个过程就像是一场有趣的游戏，不断地尝试、调整，直到找到最合适的分类方法。

想象一下，如果没有这个神奇的感知器算法，那我们面对那么多复杂的数据该咋办呀？不就像无头苍蝇一样乱撞啦！它的基本步骤虽然听起来简单，可实际操作起来可不容易呢！得小心翼翼地处理每一个数据，就像对待珍贵的宝贝一样。

在这个过程中，可能会遇到各种问题呢。

有时候会发现分错类啦，那就得赶紧调整策略，重新再来。

有时候数据太多太复杂啦，就好像走进了一个巨大的迷宫，得慢慢摸索着找到出口。

但正是因为有了这些挑战，才让感知器算法变得更加有趣和有意义呀！它就像是一个勇敢的探险家，在数据的海洋里不断探索、前行。

总之呢，感知器算法的基本步骤就像是搭积木一样，一块一块地堆积起来，最后建成一座坚固的城堡。

虽然过程中会有困难，但只要我们用心去理解、去实践，就一定能掌握这个神奇的算法，让它为我们服务呀！所以，还等什么呢，赶紧去探索感知器算法的奥秘吧！。

训练样本
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101
wkTx
+ + + 0 0 + 0 + + + -
12
k 8 , xk x4 , d ( xk ) w(k )xk 1 0 , k 9 , xk x1 , d ( xk ) w(k )xk 0 , k 10 , xk x2 , d ( xk ) w(k )xk 2 0 , k 11 , xk x3 , d ( xk ) w(k )xk 1 0 , k 12 , xk x4 , d ( xk ) w(k )xk 0 , k 13 , xk x1 , d ( xk ) w(k )xk 0 , k 14 , xk x2 , d ( xk ) w(k )xk 1 0 , k 15 , xk x3 , d ( xk ) w(k )xk 2 0 , k 16 , xk x4 , d ( xk ) w(k )xk 2 0 , k 17 , xk x1 , d ( xk ) w(k )xk 1 0 ,
13
14
解：此为线性不可分问题，利用感知器法求权向量 权向量产生循环(-1, 2, 0), (0, 2, 2), (-1, 1, 1), (-1, 1, 1) (-1, 1, 1), (0, 0, 0), (-1, 2, 0) 因此算法不收敛，我们可以取循环中任一权值，例如取 W=(0,2,2)T 则判别函数为： g(x)= 2x1+2x2 判别面方程为： g(x)= 2x1+2x2＝0 所以x1+x2＝0 由图看出判别面H把二类分开，但其中x2错分到ω1类， 而x1错分到ω2类，但大部分分类还是正确的。